“教是为了不教”教育思想的实践探索

摘 要：“教是为了不教”中的“教”与“不教”是辩证统一关系. 以“教”即教给学生未来能自己学习的本领为基础，让学生“学会”对后续学习有支撑意义的核心知识与一般观念；以“不教”即以培养学生自学能力为目的，让学生自己去发现问题、解决问题，实现“会学”的素养目标. 从“学会”到“会学”的结构化学习，正是“学·用”结构教学策略的核心要义，也是从“教”到“不教”的实践方略.

关键词：教与不教；“学·用”结构；自主学习；实践探索

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）09-0020-05

引用格式：朱先东.“教是为了不教”教育思想的实践探索：“学·用”结构教学策略［J］. 中国数学教育（初中版），2024（9）：20-24.

“教是为了不教”是我国现代著名教育家叶圣陶先生创立的具有中国特色的教育思想. 这一教育思想与新课程理念所倡导的学生观、教学观非常一致. 当前课程改革背景下重提“教是为了不教”就显得更有现实意义.

一、“教是为了不教”教育思想的核心理念

“教是为了不教”教育思想辩证而缜密地指出了“教”与“不教”的关系，它们相互依存、相互作用. 其中，“教”是立足点、是途径，“不教”是目标与价值，即“使学生养成自主全面发展，能够离开教者、超越教者，终身自学、创新实践的现代中国人为目的和价值，构成了‘教是为了不教’的本质内涵和核心理念”.

从“教”到“不教”是一个发展的逻辑，体现了人的成长与教育内在本质的发展过程，如同导儿学步，其目的在于“独行”. 教师首先要“教”，而且要运用科学的方法、有效的策略，将学生教好、教到位，最终达到终身自学之“不教”的目标，而“教好”恰恰是“不教”的前提和保障.

二、实现“教是为了不教”教育思想的教学策略——“学·用”结构教学策略

陶行知先生曾言：“好的先生不是教书，不是教学生，乃是教学生学.”这一精辟的见解深刻地揭示了教师的责任不仅在于使学生“学会”，更重要的是让学生“会学”. 经过近10年的实践探索，笔者总结出了“学·用”结构教学策略，使“教是为了不教”教育思想的落实有了具体的实践方略.

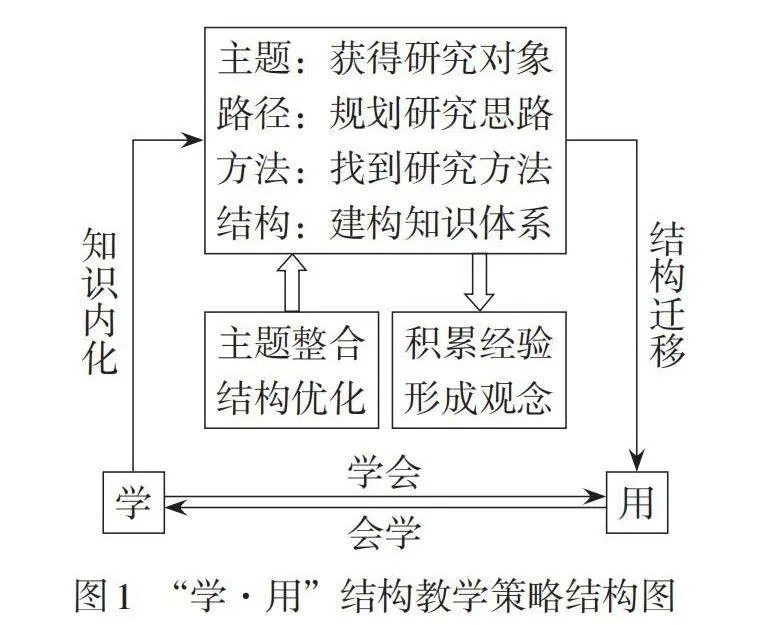
“学·用”结构教学策略是以学生的“学”为中心，以“用”知识和方法学习新知、解决问题为目标，把具有相同或类似结构的一类课进行关联思考和整体设计，即通过对主题内容整合与结构优化，将同一个结构单元或者不同单元但结构类似的内容的教学过程分为“学结构”和“用结构”两个阶段（如图1）.

在“学结构”阶段，要发挥教师的引导作用. 首先，要结合具体情境，引导学生通过直观想象、数学抽象认识事物的本质、关系及其规律，获得数学的研究对象，这是开展整体性学习的基础；其次，需要根据研究对象的特点确定合适的类比对象并构建研究路径，通过类比、联想、特殊化、一般化等推理活动发现和提出数学问题，形成研究思路，找到研究方法，这既是感悟数学思想、积累数学活动经验的关键，也是实现数学学习以简驭繁的关键；最后，在整体思路和方法指引下，组织学生进行自主探究，建构知识体系，完善认知结构，这是教学设计的核心. 在“用结构”阶段，重在发挥学生的主体作用，运用先行组织者策略，将获得的学习结构（框架结构、过程结构和方法结构的总称）和学习经验主动迁移到新的情境中，研究新知识，解决新问题，发展结构化思维，这是实现“会学”的保证.

三、“学·用”结构教学策略的实践

以“函数”主题的学习为例，初中阶段的“函数”主题包含“一次函数”“反比例函数”“二次函数”三个单元，其中“一次函数”是“函数”主题的起始单元，对“函数”主题的其他单元教学有先行组织、结构统领并孕伏一种生长力量的作用. 因此，一次函数的研究是“学结构”阶段，反比例函数和二次函数的研究是“用结构”阶段.

1. 学会一次函数研究的一般观念

教师可以采用启发式、探究式等教学方式“教”学生研究一次函数，积累具体函数研究的原初经验，形成一次函数研究的一般观念，即构建三大学习结构，积累四条具体经验.

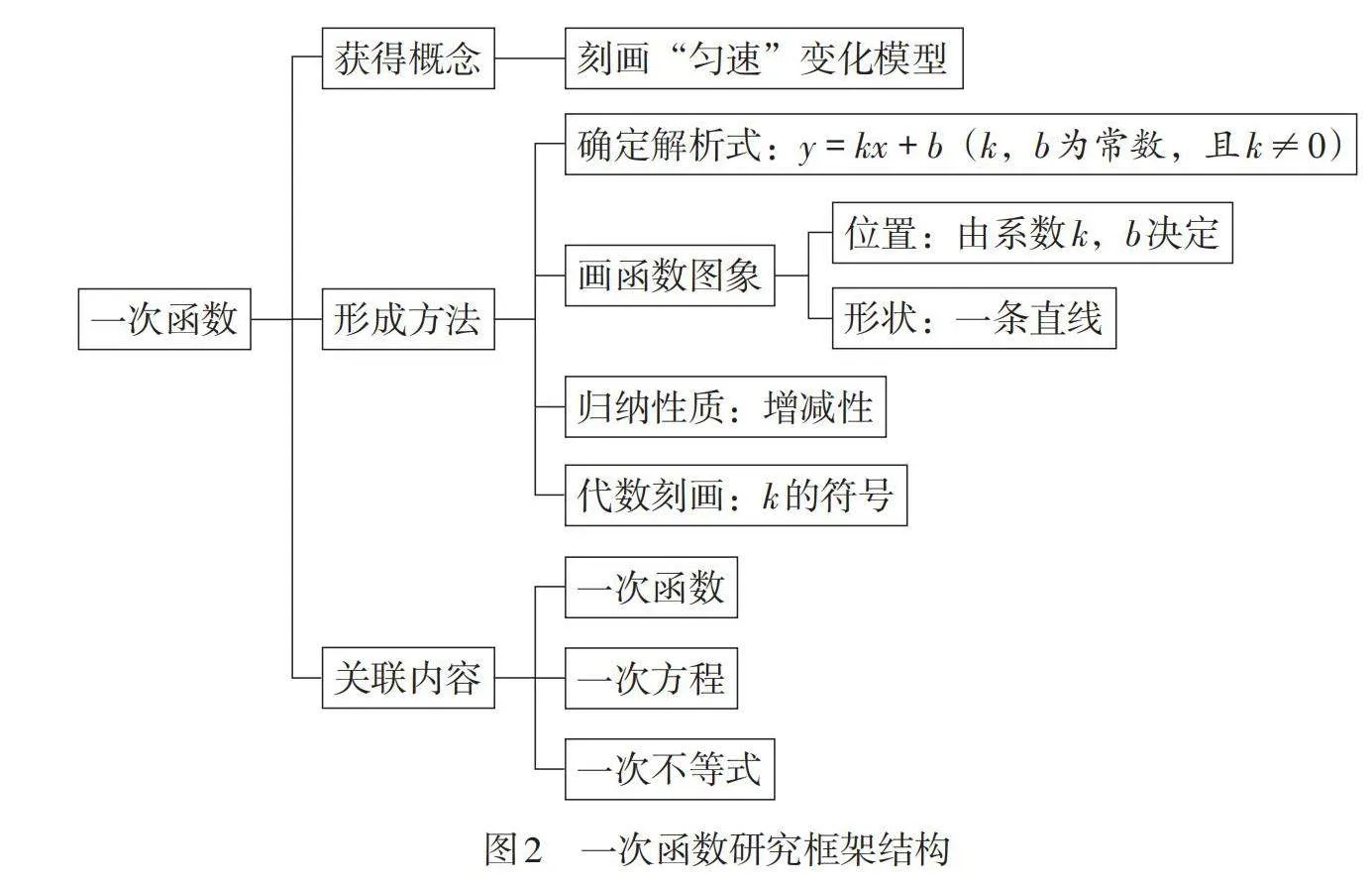
一次函数研究的框架结构如图2所示.

一次函数研究的过程结构：抽象模型—给出定义—画出图象—研究性质—应用性质.

一次函数研究的方法结构：抽象、归纳、模型、分类、数形结合、对应、转化.

数学抽象的活动经验：函数学习要经历两次抽象过程，一是将实际问题通过数学化抽象得到函数概念模型，二是将函数概念模型归纳形成抽象的函数概念.

函数图象画法经验：列表，描点，连线.

函数性质研究经验：考查函数解析式中参数变化对图象位置特点和几何特征的影响，对函数自变量和函数值之间关系的影响. 而利用图象的特征确定函数特性是研究函数性质的基本方法.

问题解决的活动经验：建立函数模型，解决实际问题.

上述一次函数的研究为学生主动研究其他函数知识提供了“脚手架”，为“不教”提供了学力保障. 教师后续的“少教”甚至“不教”的程度，取决于学生对已有知识经验、过程经验和方法经验的理解与掌握、检索与提取、应用与迁移的能力.

2. 运用一次函数研究的一般观念，类比研究新函数

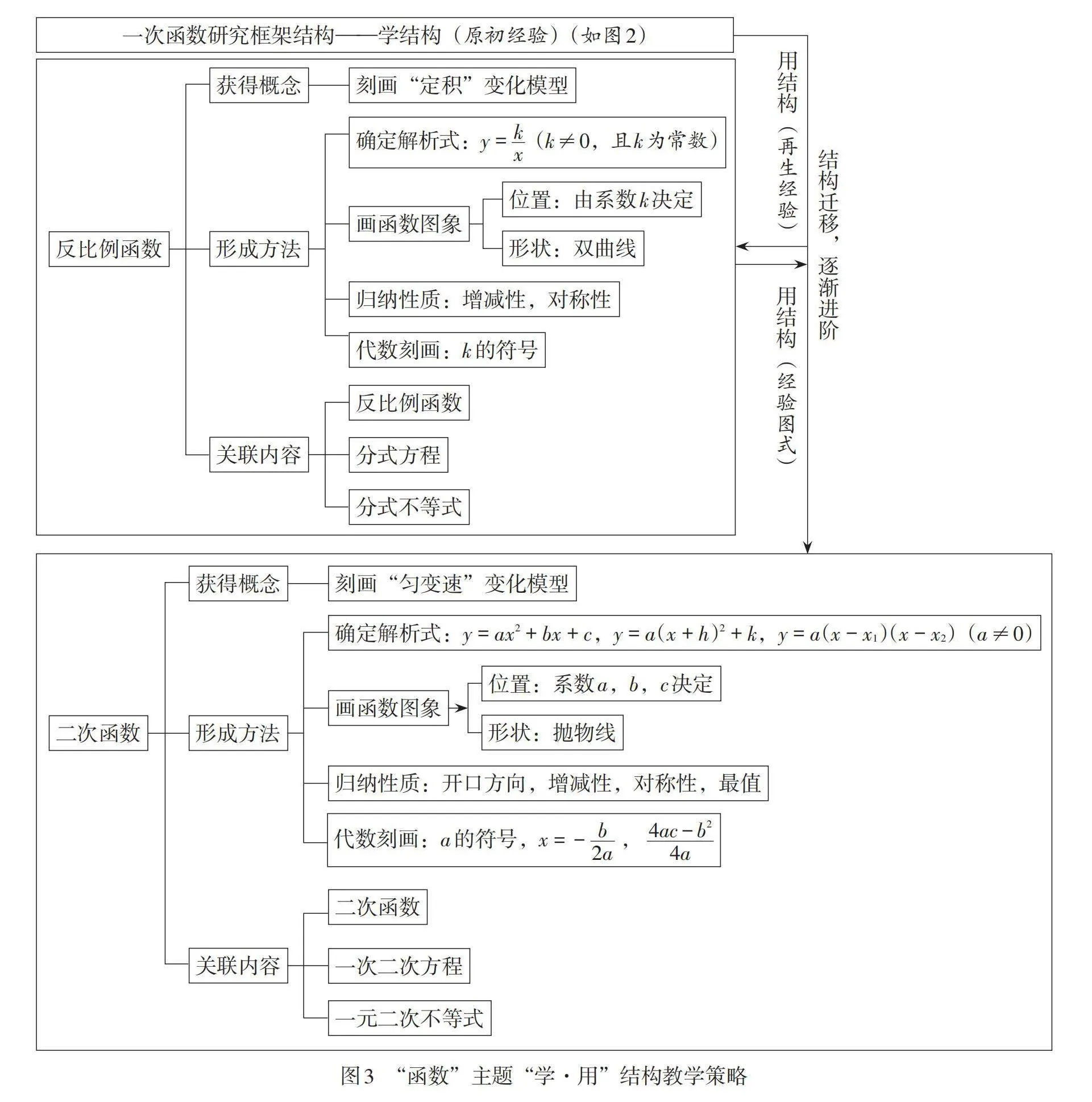
反比例函数和二次函数与一次函数在结构上是并列关系，它们具有类似的结构，是“用结构”学习阶段. 对于这两类函数，主要让学生运用在“学结构”阶段所形成的知识、过程、方法等进行类比学习和主动学习，甚至可以放手让学生自主学习，即类比一次函数自主研究反比例函数和二次函数，其框架结构如图3所示.

这样的教学策略既充分体现了数学学科知识的整体性、逻辑的连贯性、方法的普适性、思维的系统性和思想的一致性，也体现了内容和方法的进阶性，着力培养学生的学习力和迁移力，实现从“学会”到“会学”的育人目标.

3. 从“学会”到“会学”教之策略

从“教”到“不教”，从“学会”到“会学”，要处理好“教什么”和“怎么教”的问题，关键是“怎么教”的问题. 从学科内容来看，课程标准对“教什么”都做了具体规定，提出了明确的要求；从学的需求来看，知识体系中的重要节点、关键环节，即对学生来说经过努力仍然存在困难的内容，就在教师“教”的范围之内，不但要教，而且要教好.

对于“怎么教”的问题，按照《义务教育数学课程标准（2022年版）》（以下简称《标准》）的建议，改变单一讲授式教学方式，注重启发式、探究式、参与式、互动式等，探索大单元教学，积极开展跨学科的主题式学习和项目化学习等综合性教学活动.

（1）认准目标，致力于导.

教之道在于“导”. 教师之为教，不在全盘授予，而在相机诱导. 为了让学生实现“会学”之目标，教师更要想方设法让学生先学先思，自奋其力，自求得之.

例如，对于一次函数图象的研究，学生在列表时往往存在两个问题：一是所取的数都是正整数，缺少代表性；二是列表时缺少省略号. 这时教师不仅要“教”，而且要从定义出发启发学生思考：一次函数自变量的取值范围是什么？如何取数？数取不尽怎么办？让学生理解列表、取数的基本要求，实现“领悟之源广开，纯熟之功弥深”.

教师的“导”固然重要，但学习的主体是学生. 教学本质上是以学生自主学习成长为中心的师生学习共同体. 叶圣陶先生曾指出：“达到不需要教，就是要教给学生自己学习的本领，让他们自己学习一辈子.”因此，教师要为“不需要教”打基础，一定要锚定让学生“会学”的目标. 教师的教学要结合具体的学情和内容，指导学生掌握科学有效的学习方法，逐渐实现从“扶”到“放”，并且能放手时坚决放手，让学生学会自己学习. 例如，在研究二次函数时，教师要引导学生类比正比例函数[y=kx]的研究经验自主研究二次函数[y=ax2]. 尽管两者内容不同，但研究方法相同，体现了思想方法的一致性. 进而放手让学生自主研究[y=ax2+c → y=ax+m2 → y=ax+m2+ℎ → y=ax2+][bx+c]，由特殊到一般，逐级递进，培养学生自学的主体精神和能力. 这也是学生应具备的最基本、最核心的素养.

（2）整体思考，结构教学.

教学是一个系统工程，需要根据学生的认知规律、数学的学科逻辑，以及教学的各个要素之间的关系进行整体性策划和结构化教学.

结构化教学是指基于学科知识结构和学生的认知能力，运用核心概念和一般观念，统摄学习目标与内容、学习过程与方法，使学生形成较完善的认知结构和思维结构的教学. 主要体现在以下三个方面.

① 教学目标结构化. 即追求主题、单元、课时及教学要素目标的一致性，形成完整的目标结构.《标准》指出：“教学目标的设定要体现整体性和阶段性. 要依据核心素养的内涵和不同学段的主要表现，结合具体的教学内容，全面分析主题、单元和课时的特征，基于主题、单元整体设计教学目标，围绕单元目标细化具体课时的教学目标.”

例如，在“一次函数”单元教学设计中，首先，要结合学生的认知规律，全面分析“函数”主题、“一次函数”单元和各课时的内容与特征，基于“函数”主题确定“一次函数”单元的教学目标；其次，在“一次函数”单元目标的统领下，借助美国威金斯提出的“以终为始”设计理念设计“一次函数”单元的评价任务、分课时教学目标，以及单元目标引领下的课时作业设计与检测；最后，经过归纳与整理、反思与提炼，形成一次函数研究的一般观念，建立单元目标下的学习结构（如图4）.

② 教学内容结构化. 即匹配教学目标，通过结构化再组织、再加工，把相互之间具有关联的内容进行有机整合，形成完整的知识结构. 通过核心概念建立关联，使学生更好地理解和掌握数学概念和原理，实现知识和方法的迁移.《标准》指出：“在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系.”

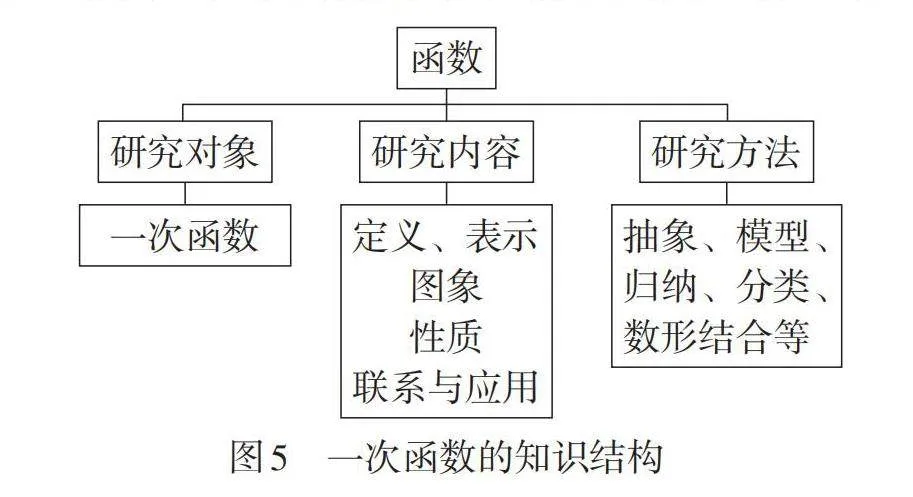
例如，在研究一次函数内容后，教师要引导学生自主整理知识与方法，绘制个性化思维导图，然后让学生交流分享，完善知识结构（如图5），积累函数研究的基本活动经验. 随着“函数”主题内容学习的推进，通过类比、分析、比较、综合，在新、旧知识之间建立联系，使所学知识构成清晰、稳定、整合的知识体系.

③ 教学任务结构化. 即匹配教学目标与内容，以大问题、大任务驱动学生思维主动介入，自主检索与关联，形成问题研究的过程结构和方法结构. 在“用结构”阶段，要运用好先行组织者教学策略，为学生学习新知识提供类比或分辨的参照，提供学习线索，帮助学生获得研究内容、形成研究思路、找到研究方法. 下面以“反比例函数”单元的研究为例.

问题1：你能总结一下“一次函数”单元研究的问题、过程与方法吗？

【设计意图】先让学生明确一个类比对象，使他们逐步养成用函数研究的一般观念思考问题的习惯.

问题2：类比一次函数的研究，你能勾画出反比例函数研究的问题、过程和方法吗？

【设计意图】引导学生类比一次函数，建构研究反比例函数的大框架，把握反比例函数研究的大方向，让学生“先见森林，再见树木”，激发学生的学习兴趣.

经过学生的类比、归纳，猜想得到研究反比例函数的整体研究框架结构如图6所示.

四、结束语

“学·用”结构教学策略不仅重视教师的“教”，倡导教师成为“善教者”，而且注重培育学生主动类比发现结构、形成结构并加以拓展的学习心态和学习方法，以及培育学生自觉将已有经验迁移到新的问题情境，解决挑战性问题的能力. 这正是“教是为了不教”最深层、最根本的精神内涵和价值追求.

参考文献：

［1］任苏民. 论“教是为了不教”的科学内涵和理论体系［J］. 课程·教材·教法，2018，38（2）：69-77.

［2］陈波. 陶行知教育文选［M］. 杭州：浙江大学出版社，2014.

［3］朱先东. 数学整体性教学设计［M］. 北京：中国农业大学出版社，2022.

［4］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.