温故建构新知 论证生成巧思

摘 要：平行四边形的对角线互相平分是三角形中位线定理的最近知识生长点，由此引出三角形中位线定理的概念并建构模型探讨不同视角下的论证方法，最后通过古题新做打破学生固有思维，完成对新知的吸收和内化，使学生的探究水平和知识的迁移能力得到稳步提升.

关键词：中位线定理；定理证明；类比探究

中图分类号：G633.6 文献标识码：A 文章编号：1673-8284（2024）09-0033-04

引用格式：王玉娇，郑林. 温故建构新知 论证生成巧思：三角形中位线定理的探究［J］. 中国数学教育（初中版），2024（9）：33-36.

数学是研究数量关系和空间形式的科学. 三角形的中位线定理既体现了线段之间的数量关系，又体现了线段之间的位置关系，是衔接三角形和平行四边形知识的桥梁. 本文主要从三角形中位线定理的生成、论证和知识的巩固三个部分出发进行探究. 在人教版《义务教育教科书·数学》（以下统称“人教版教材”）中，三角形的中位线定理被安排在八年级下册第十八章“平行四边形”中，体现了需要利用平行四边形的知识来探究三角形中位线定理的设计意图. 但是大部分教师在设计引入三角形中位线定理或概念的生成时均是与平行四边形分开的，内容衔接上不够自然，且缺少探索发现该定理的过程. 事实上，三角形和平行四边形内容是相互关联的. 这样直接切入教学显得生硬，容易出现知识的断层. 笔者以平行四边形的一道习题变式作为引入，利用平行四边形的性质顺势发现、提出和论证三角形的中位线定理，前后衔接过渡自然. 现将教学过程呈现如下.

一、类比联想获新知：概念的生成过程

在三角形中位线定理的教学中，由平行四边形的性质关联到三角形中位线定理的发现过程，以此激发学生的学习潜能和学习数学的兴趣. 若能从学生熟悉的原教材、旧例题中挖掘出具有启发性的知识，则更能激发学生的求知欲. 在概念的生成过程环节立足于学生已有的认知，从学生思维的最近发展区出发探究新知，这样的教学设计有助于激发学生独自钻研的主动性和发现数学知识之间的环环相扣之美.

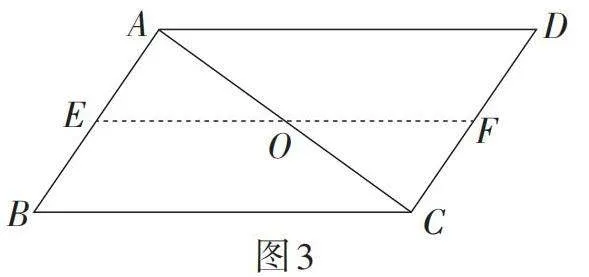
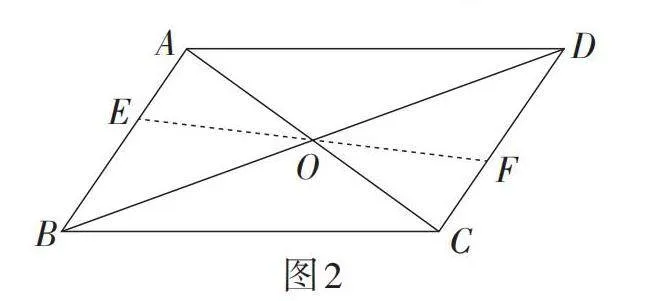
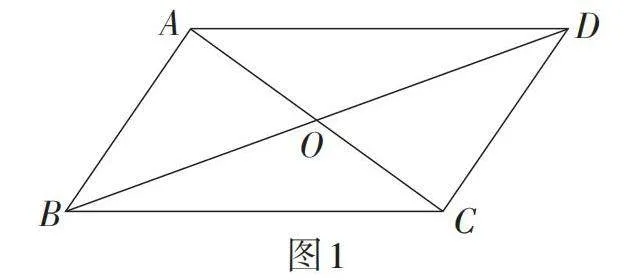
例 如图1，▱ABCD的对角线AC，BD相交于点O.

（1）点O平分了哪些线段？

（2）如图2，将线段BD所在的直线绕点O旋转，分别交线段AB，CD于点E，F，则点O平分线段EF吗？

（3）如图3，在旋转的过程中，当点E为线段AB的中点时，我们可以得到哪些特殊的结论？

由第（3）小题，可以得到结论：F为线段CD的中点，EF∥BC，且[EO=12BC].

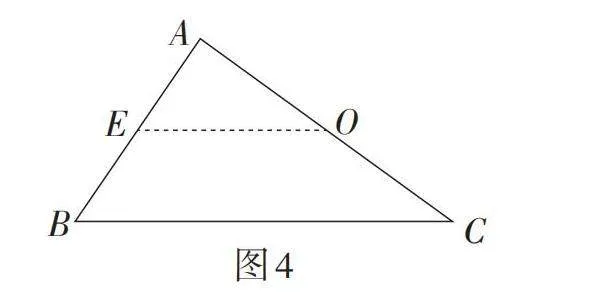
将图3中▱ABCD的对角线AC的右侧部分去掉，得到如图4所示的三角形，则EO是连接△ABC的边AB，AC的中点的线段. 像EO这样，连接三角形两边中点的线段叫作三角形的中位线.

探究：三角形的中位线有什么性质？

由第（3）小题的结论，得到三角形的中位线定理：三角形的中位线平行于三角形的第三边，并且等于第三边的一半.

【教学说明】该例题是学习平行四边形的性质时的经典拓展题. 之前学生通过平行四边形的性质易证无论EF所在直线绕点O如何旋转，总有△AOE ≌ △COF. 本节课继续探究当EF所在直线旋转到平行四边形一边中点的特殊位置时，可以自然得出三角形的中位线定理. 该例题不但实现了知识点之间的衔接，而且实现了平行四边形和三角形之间的相互转化，为后面三角形的中位线定理的论证提供了添加辅助线的思路. 同时，让学生明白对已有知识与已学例题进行深入挖掘往往会有意想不到的收获.

二、探索碰撞生巧思：定理的论证过程

如何让知识在思维里生长？学生只有在自我探索、实践中不断建构、优化、类比，才能深刻体会三角形与平行四边形之间的相互转化关系. 我们借助三角形中位线定理的论证过程来继续深化学生的认知. 本环节可以遵循“分析思路—添加辅助线—进行论证”三步原则进行. 借助对上述例题的分析，从不同视角得出不同的论证方法.

1. 建构平行四边形

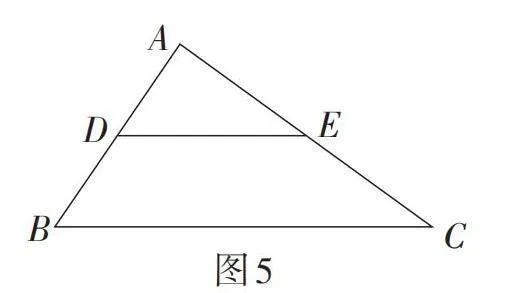
如图5，在△ABC中，D，E分别是边AB，AC的中点，连接DE. 求证：DE∥BC，且[DE=12BC].

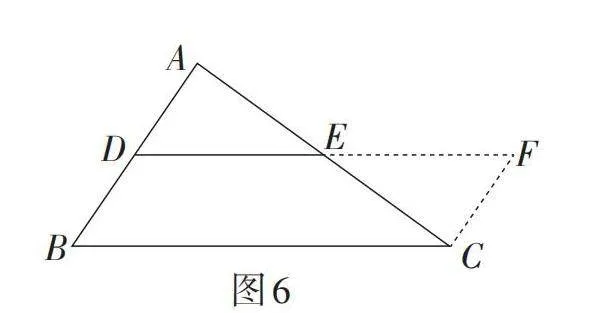
思路1（倍长中线模型1）：如图6，延长DE至点F，使EF = DE，连接CF. 易证得△ADE ≌ △CFE. 从而证得四边形DBCF是平行四边形，即可得到DE∥BC，且DE =[12BC].

思路2（构造平行模型1）：如图6，过点C作AB的平行线，交DE的延长线于点F. 以下同理思路1，即可证得DE∥BC，且[DE=12BC].

【教学说明】思路1和思路2是学生比较容易想到的. 虽然添加辅助线后的图形一样，但是有不一样的辅助线作法. 通过倍长线段或作平行线将线段倍分关系转化为线段相等关系，其本质是一样的，都是最终转化为平行四边形来解决问题，为学生今后证明线段平行积累了经验，即要证明线段平行，不仅可以依据角之间的数量关系，还可以依据平行四边形的性质.

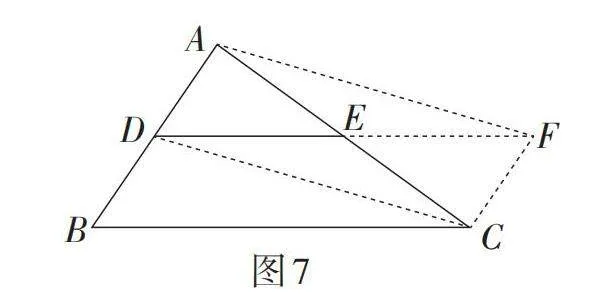
思路3（倍长中线模型2）：如图7，延长DE至点F，使EF = DE，连接DC，AF，CF，则四边形ADCF为平行四边形，进而得四边形DBCF为平行四边形. 以下同理思路1，即可证得DE∥BC，且[DE=12BC].

【教学说明】思路1至思路3都是将三角形问题转化为平行四边形来解决. 之前研究平行四边形时是用三角形的知识来解决的，此时我们又利用平行四边形的知识解决了三角形的问题，让学生体会到了相互转化的数学思想方法.

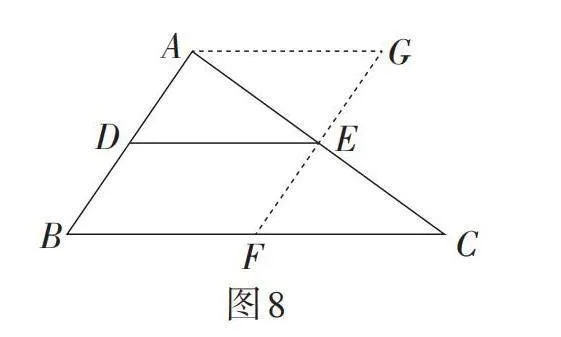
思路4（构造平行模型2）：如图8，过点A作AG∥BC，过点E作EF∥AB，直线EF交BC于点F，交AG于点G，则四边形ABFG是平行四边形. 易证△AEG ≌ △CEF，则四边形ADEG和四边形DBFE分别为平行四边形，从而可证得DE∥BC，且[DE=12BC].

【教学说明】通过呈现四种论证思路，引导学生对四种论证思路进行比较，从作辅助线、思考问题的方式、证明方法的不同视角出发，旨在让学生体会每种证明方法的本质都是将三角形问题转化为平行四边形问题来解决.

2. 汲取古书的精华，体会古人的智慧

在数学教学过程中，我们可以适当培养学生追本溯源的优良数学品质，而考查问题的本源和发展历史是最行之有效的方法.《九章算术注》和《几何原本》是古代中外数学史上的两部重要著作，接下来看看这两部著作对三角形的中位线定理的论证.

古希腊数学家欧几里得在其著作《几何原本》中证明三角形中位线定理的方法是：先将线段之间的关系转化为三角形面积之间的关系，再将三角形面积之间的关系转化为直线的位置关系. 具体思路如下.

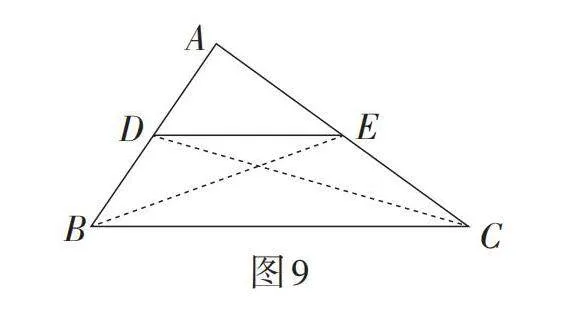
思路5：如图9，在△ABC中，点D，E分别是边AB，AC的中点，连接BE和DC. 因为AD = BD，AE = CE，所以[S△EAD=S△EDB，S△EAD=S△CED.] 所以[S△EDB=][S△CED.] 所以△EDB和△CED的高相等，则DE∥BC. 因为[S△BCE=S△ABE=2S△BDE]，且△BCE和△BDE的高相等，所以[DE=12BC].

我国魏晋时期的数学家刘徽在《九章算术注》中通过“割补法”来推导三角形的中位线定理，其思路如下.

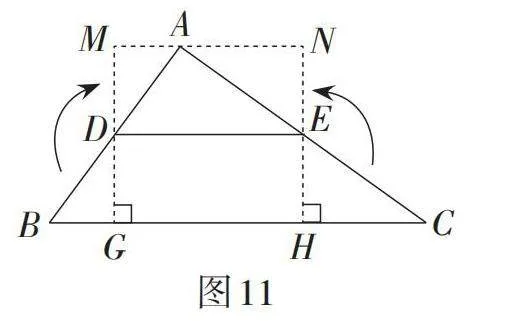
思路6：如图10，连接△ABC两边的中点，即得到中位线DE. 过点A作中位线DE的垂线AH，垂足为点H. 将中位线DE上方的△ADE分割成Rt△AHD和Rt△AHE，分别将它们补到相应的位置，得到矩形BCNM，则矩形BCNM的长为△ABC的底BC，则DE∥BC，且[DE=12BC].

问题1：观察图10，你还有其他类似的方法吗？

生1：如图11，利用“割补法”构造矩形MGHN.

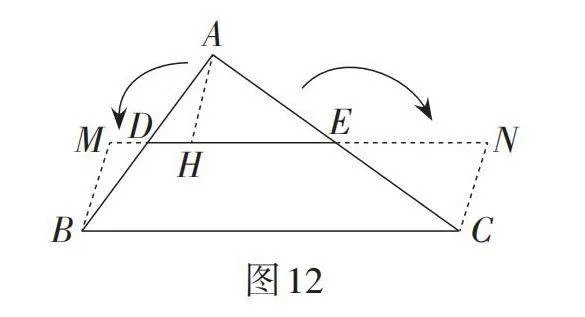
问题2：如果不作中位线DE的高线，而是在DE上任取点H，连接AH，你能借用刘徽的“割补法”来证明三角形中位线定理吗？

生2：如图12，利用“割补法”构造▱BCNM.

【教学说明】在教学中融入历史上证明三角形中位线定理的方法，使学生在追寻历史足迹的过程中感受数学学科深厚的文化底蕴，感受中外数学家为数学学科发展做出的卓越贡献. 近代教材中还出现了“同一法”“反证法”等，受篇幅限制在此不作拓展. 用多种方法来论证三角形的中位线定理，不仅能让学生巩固所学知识，而且能通过一题多解让学生分析、比较并观察方法之间的差异性，培养学生的创造性思维. 一题多解的精华不在于“多”而在于归纳. 在发散思维之后，观察到题目的解法可以分为“同质异形”和“异质同形”两类. 例如，在论证中发现不同的构造方法实质都是将三角形问题转化为平行四边形的问题，这就是“同质异形”；同样的构造方法不同的思维角度，这就是“异质同形”. 教师要引导学生对上述证法进行对比、归纳，让学生透彻理解不同的证明方法，从而学会举一反三.

3. 旧题新做固认知：知识的巩固过程

三角形的中位线定理可用于解决土地分割问题. 例如，某农场有四位兄弟幸福和睦地生活着，而父亲去世打破了四兄弟平静的生活，他们为分割父亲留下的一块土地而争论不休，谁都不肯吃亏. 已知土地的形状为三角形，利用你所学的数学知识设计土地分割方案，并给出方案的理论依据，以此说服四兄弟接受方案. 通过构造三角形的中线和中位线可以得到六种不同的分割方案，分别如图13 ～ 图18所示.

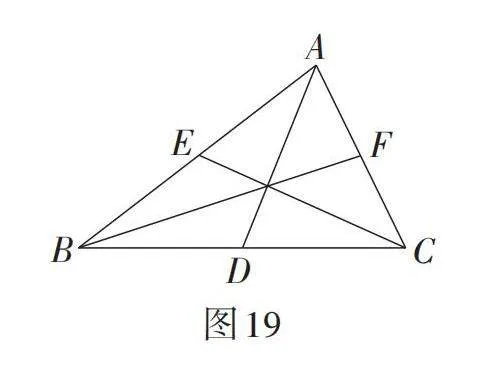
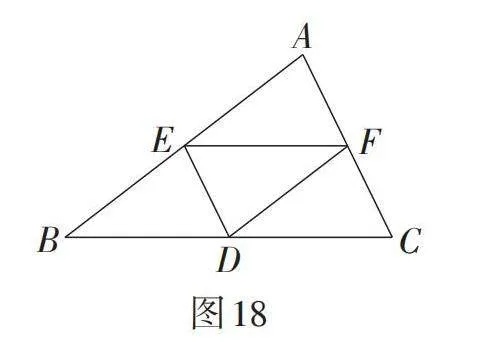
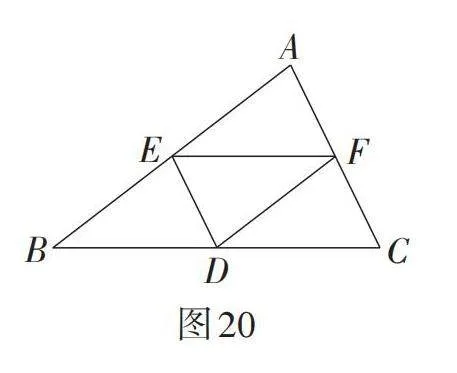
【教学说明】在构造的过程中，可以让学生辨析三角形的中线与中位线的概念，引导学生从数量、位置、性质和构造图形的角度分别阐述三角形的中线与中位线的不同之处. 如图19，任何三角形都有三条中线，它们在三角形的内部且交于一点，且中线平分三角形的面积. 如图20，任何三角形都有三条中位线，中位线EF，DE和DF把原三角形分成四个全等的三角形，即△AEF ≌ △EBD ≌ △DFE ≌ △FDC；三条中位线与原三角形可以构成▱AEDF，▱EBDF，▱EDCF. 上述“土地分割”问题除了用三角形的中线知识解决，也可以利用三角形的中位线定理解决. 此问题引导学生从多角度思考. 同时，从理论到实际，锻炼了学生的应用意识和能力，体现了“数学既来源于生活，又服务于生活”的宗旨.

三、意犹未尽话教学：探究后的几点思考

1. 思之美——在于精益求精

在证明三角形中位线定理的过程中，通过构造平行线和倍长中线的方法把三角形转化成平行四边形来研究，培养了学生的几何直观素养，渗透了类比、转化等数学思想. 学生之后在解决相关问题时能通过分析问题联想到有关的知识，从而解决问题，这样有利于提升学生思维的灵活性.

2. 师之慧——在于俯瞰全局

我们为什么要学习三角形中位线定理？为什么要将三角形中位线定理安排在平行四边形的性质之后学习？这都是教师应该思考的问题. 一切数学的探索均源自需求. 分土地问题需要用到三角形的中位线定理来解决，且需要利用平行四边形的性质来论证三角形的中位线定理，所以将三角形的中位线定理安排在本章. 教师应该站在一定的知识高度上俯瞰整个教学体系，寻找新知教学的出发点和落脚点，架构贯穿其中的最佳路径. 基于“四个理解”来设计教学方案，打破学生的思维定式，在三角形中位线定理的证明中引入多种方法，可以拓展学生的思维，发展学生的数学核心素养.

3. 史之趣——在于文化传承

本节课抓住“概念生成—论证探究—古题新做”的教学主线，并且将古今中外对三角形中位线定理的探究渗透其中. 不论是欧几里得的“面积法”还是刘徽的“割补法”，都向我们展示了图形之美、建构之妙. 在这样的教学过程中，师生共同感受到了数学的博大精深和历史悠久. 这么优秀和多元化的知识需要我们薪火相传并且发扬光大.

参考文献：

［1］吴增生. 三角形中位线定理教材设计之我见［J］. 中国数学教育（初中版），2018（12）：3-5，10.

［2］欧几里得. 几何原本［M］. 燕晓东，译. 南京：江苏人民出版社，2011.