基于混合策略的DBO算法对TSP的研究

摘要：旅行商问题（Traveling Salesman Problem， TSP）是一个经典的 NP（Non-deterministic Polynomial）问题，具有重要的实际应用价值。蜣螂算法（Dung Beetle Optimizer， DBO）是一种新兴的启发式算法，兼顾了全局搜索和局部开发，具有收敛速度快和求解精度高的特点。为了进一步提升 DBO 算法的性能并探究其在 TSP 问题上的表现，对蜣螂算法进行了改进，提出了混合策略引导的改进蜣螂算法（Levy-Improved Sine Algorithm Dung Beetle Optimizer， L-MSADBO）。该算法在原始蜣螂算法的基础上，增加了混沌映射策略用于初始化种群，采用正弦算法引导滚球蜣螂的位置更新，并使用 Levy 飞行策略引导偷窃蜣螂的位置更新。此后，对更新完成的最优个体进行高斯-柯西变异扰动，并采用贪婪原则对扰动前后的值进行择优选择。使用改进的 DBO 算法解决 TSP 问题，并将其与原始 DBO 及其他广泛研究的智能算法，如 MSADBO（Improved Sine Dung Beetle Optimizer）、GWO（Grey Wolf Optimizer）、PSO（Particle Swarm Optimization）和 Tabu（Tabu Search），进行对比，发现改进的 DBO 在 TSP 问题的求解效果上优于其他算法。

关键词：旅行商问题；混沌映射；Levy飞行策略

中图分类号：TP399 文献标识码：A

文章编号：1009-3044（2024）24-0019-06

开放科学（资源服务）标识码（OSID）

0 引言

TSP 问题（旅行商问题）是一种具有广泛应用背景和重要理论意义的组合优化问题[1]。传统的算法在解决 TSP 问题时通常通过直接处理问题约束条件或使用暴力枚举的方法。虽然这种传统方式能够获得 TSP 相关问题的精确解，但随着问题规模的增大（组合爆炸），计算量也显著增加，导致这些方法失效。智能算法虽然不能提供精确解，但能够将误差控制在很小范围内，并且快速给出求解结果。因此，大量智能算法被应用于解决 TSP 问题。

高珊等[2]提出了一种贪婪随机自适应灰狼优化算法，该算法利用贪婪随机自适应算法生成初始解，并在局部搜索阶段使用灰狼算法优化结果。与其他算法相比，该算法在求解 TSP 问题时表现出较高的效率和稳定性。申晓宁等[3]在粒子群算法中引入了启发信息，并将其应用于低碳 TSP 模型，与 Tabu 算法等代表性算法相比，其所提出的算法具有更高的求解精度。除此之外，一些新提出的算法也用于解决 TSP 问题。孟范立等[4]提出了增加消除机制的乌鸦优化算法，并在 TSPLIB 数据集上进行了实验，结果显示该方法相比其他算法具有更好的优化精度和稳定性。王芬等[5]将猎人猎物优化算法应用于 TSP 问题，结果表明该算法具有收敛速度快、寻优能力强的特点，在解决旅行商问题时能够得到较好的优化结果。

考虑到目前尚未有关于蜣螂及其改进算法在 TSP 问题上的研究，本文提出了用于解决 TSP 问题的混合策略引导的改进蜣螂算法，并将其求解的最短距离与 DBO、MSADBO、GWO、PSO 及 Tabu 算法进行对比，以研究其在 TSP 问题上的表现。

1 TSP 问题概述

旅行商问题可以描述为：一位商人需要从若干个城市集合中的某一个城市出发，经过所有城市且每个城市只能经过一次，最后返回到出发城市。目标是制定一条最优路线使总路程最短。其数学模型如下：

[mininjndijxij] （1）

[j=1nxij=1 i=1，⋅⋅⋅，n，] （2）

[i=1nxij=1 j=1，⋅⋅⋅，n，] （3）

[i，j∈Sxij≤S-1] （4）

[xij∈0，1 i，j=1，⋅⋅⋅，n.] （5）

其中：式（1）为目标函数，[dij]表示城市[i]，[j]之间的距离；式（2）和式（3）表示旅行商经过每个城市有且只有一次；式（4）即旅行商不能重复经过任何一个城市；式（5）为决策变量约束，表示已经过的城市，0表示未经过的城市。

2 蜣螂算法

蜣螂算法是 Xue 等人[6]在 2022 年提出的一种新兴算法，其灵感来源于蜣螂的滚球、跳舞、觅食、繁殖和偷窃行为。与其他算法不同的是，蜣螂算法会根据蜣螂的种类进行生存。在蜣螂优化算法中，每个蜣螂种群由4个不同的代表组成，即滚球蜣螂个体、孵卵蜣螂个体、小蜣螂个体和小偷蜣螂个体。

2.1 滚球蜣螂

滚球蜣螂需要在整个搜索空间中通过获取自然界的信息（主要受光照强度影响）并沿着给定的方向移动。在滚动过程中，滚球蜣螂的位置迭代公式可以用 （6）、（7） 表示：

[xit+1=xit+α×k×xit-1+b×]

[Δx，k∈0，0.2，b∈（0，1）] （6）

[Δx=xit-XW] （7）

式中：[t]为当前迭代次数；[xit]为第[i]只蜣螂在第[t]次迭代时的位置信息；[α]为一个取值为1或-1的变量，[Δx]用于模拟光强的变化；[XW]为全局最差位置。遇到障碍物时，蜣螂会爬到球的上方进行“跳舞”，以获取信息并找到新的移动方向。蜣螂的跳舞行为可以通过公式（8）表示：

[xit+1=xit+tanθ][xit-xit-1，θ∈0，π] （8）

式中：[θ]是一个介于0到[π]的值，一旦蜣螂成功确定了一个新的方向，它将继续向后滚动。值得注意的是，当[θ]等于0、[π2]或[π]时，蜣螂的位置将不会更新。

2.2 繁殖蜣螂

在自然界中，蜣螂会将球滚到安全的区域进行隐藏，以为后代提供安全的环境。因此，选择合适的产卵地点对蜣螂而言至关重要。受此启发，使用边界策略来模拟产卵区域，边界的定义由公式 （9）、（10） 来表示：

[Lb∗=maxX∗×1-R，Lb] （9）

[Ub∗=minX∗×1+R，Ub] （10）

式中：[X*]表示当前局部最优位置；[Lb*]和[Ub*]分别表示产卵区域的下界和上界；[Lb]和[Ub]分别表示优化问题的下界和上界；[R=1-t/Tmax]，[Tmax]为最大迭代次数。产卵区的边界范围随着[R]的变化而变化，因此孵化球的位置在迭代过程中也是动态变化的，由公式（11）定义：

[Bit+1=X∗+b1×Bit-Lb∗+][b2×Bit-Ub∗] （11）

式中：[Bit]为第[i]个育雏球在第[n]次迭代时的位置；[b1]和[b2]表示大小为[1×D]的两个独立随机向量，[D]表示优化问题的维数。

2.3幼小蜣螂

一些已经出生的蜣螂会从地下钻出寻找食物，成为觅食蜣螂。为了模拟这一行为，我们需要建立觅食区域，觅食区域的定义由公式（12）、（13）表示：

[Lbb=maxXb×1-R，Lb] （12）

[Ubb=minXb×1+R，Ub] （13）

式中：[Xb]为全局最佳位置，[Lbb]和[Ubb]分别是觅食区域的下界和上界。因此，幼小蜣螂在觅食过程中的位置更新公式如（14）所示：

[xit+1=xit+C1×xit-Lbb+C2×xit-Ubb] （14）

式中：[C1]表示服从正态分布的随机数；[C2]表示取值在 0到1的随机向量。

2.4偷窃蜣螂

在众多蜣螂中，有些蜣螂会偷走其他蜣螂的球，这在自然界中是一种常见现象。由公式 （12）、（13） 可知，[Xb]为最优食物源，因此我们可以假设其周围的[Xb]表示争夺食物的最佳地点。在迭代过程中，小偷蜣螂的位置更新可描述为 （15）：

[xit+1=Xb+S1×g×xit-X∗+xit-Xb] （15）

式中：[g]为一个大小为[1×D]的随机向量，并服从正态分布，[S1]表示一个常数。

3 改进蜣螂算法求解 TSP 问题

3.1 Bernoulli 混沌映射策略

原蜣螂算法通过随机生成位置的方式来初始化种群的位置。这种方式可能导致初始种群的多样性相对较低，不能充分遍历所有可能位置。为了增强种群的多样性，本文采用 Bernoulli 映射来初始化种群。Bernoulli 映射在 0 到1的分布更加均匀，同时其周期性也更加稳定[7]。Bernoulli 映射如公式 （16） 所示：

[Zk+1=Zk1-λ， 0≤Zk≤1-λZk-1-λλ， 1-λ≤Zk≤1 ] （16）

式中：[z=（x1，x2，x3…，xd）]表示生成的混沌序列，[d]表示维度。

3.2 改进正弦算法引导和Levy飞行策略

改进正弦算法（Improved Sine Algorithm， MSA）[8] 策略受到与正余弦算法（Sine Cosine Algorithm， SCA）相关的多种算法[9-11] 的启发。该算法利用数学中的正弦函数进行迭代优化，具有较强的全局探索能力。在本文中，引入改进正弦算法的同时，在位置更新过程中加入自适应的可变惯性权重系数，使算法能够对局部区域进行充分搜索。这不仅弥补了原始 DBO 算法全局搜索能力较弱的缺点，还解决了全局与局部搜索不平衡的问题。改进正余弦算法的位置更新公式如下所示：

[xit+1=ωtxit+r1×sinr2×r3pit-xit]（17）

式中：[t]为当前迭代次数；[ωt]为惯性权重参数，其定义如公式（18）所示；[pit]为第[t]次迭代中最佳个体位置变量的第[i]个分量，[r1]为一个非线性递减函数，其定义如公式（19）所示，[r2]是区间[0，2π]上的随机数，[r3]是区间[-2，2]上的随机数。

[ωt=ωmax-ωmax-ωmin×tTmax] （18）

其中，[ωmax]和[ωmin]分别表示[ωt]的最大值和最小值；[t]表示当前迭代次数；[Tmax]表示最大迭代次数。

[r1=ωmax-ωmin2cosπtTmax+ωmax+ωmin2] （19）

更新后的滚球蜣螂公式如下：

[xit+1=xit+α×k×xit-1+b×Δx， δ<STωtxit+r1×sinr2×r3pit-xit， δ≥ST ] （20）

式中：[δ=rand（1）]，表示0到1的随机数，[ST∈0.5，1]。当[δ<ST]时，表示蜣螂进行有目标的滚动；[δ≥ST]时，通过正弦函数进行引导。这种机制不仅改善了DBO算法在位置更新策略上过于随机的缺陷，还通过[pit]的存在增加了种群之间的信息交流，弥补了原算法中个体之间缺乏交流的短板。由[r1]的公式可以看出，它控制了蜣螂方向和移动距离。由公式（19）可以看出，随着迭代次数的增加，惯性权值在不断减小，这使得算法在前期具备较强的全局搜索能力，而在后期提高局部开发能力。

Levy 飞行是一种交替进行高频短距离探索和低频长距离探索的策略，它在大范围内寻找最优解的同时，可以避免陷入局部最优解[12-13]。本文在偷窃蜣螂的位置更新公式中引入了 Levy 飞行策略，以使这部分个体探索更广阔的搜索空间。Levy 是一种特殊的随机游走策略，其步长分布服从重尾特征[14]概率分布。Levy 飞行策略主要由公式 （21）、（22）、（23） 构成：

[Levyβ=μv-β] （21）

其中，[Levyβ]是服从参数为[β]的Levy分布的随机变量，[0<β<2]；[μ]服从标准正态分布[N（0，σ2）]；[ν]服从标准正态分布[N0，1]，[σ]可以由公式（22）计算得到：

[σ=Γ1+βsinπβ2βΓ1+β22β-12] （22）

式中，[Γ]表示Gamma分布函数。

原偷窃蜣螂的位置更新在迭代初期逼近全局最优解时，可能导致搜索范围不足，从而陷入局部最优。为了克服这一弊端，在改进后的更新公式中加入了动态权重系数[w]，其公式如 （23） 所示。由 Levy 飞行策略引导的偷窃蜣螂位置更新公式如 （24） 所示：

[w=exp2×1-tTmax-exp-2×1-tTmaxexp2×1-tTmax+exp-2×1-tTmax] （23）

[xit+1=Levy×Xb+S1×g×xit-X∗+xit-w×Xb] （24）

式中，在迭代初期，具有较大值，有助于全局搜索；而在迭代后期，它逐渐变小，以促进局部搜索并加快收敛速度。

3.3 自适应高斯-柯西混合变异扰动与贪婪原则

在蜣螂算法的迭代后期，由于蜣螂个体的快速同化，种群会迅速聚集到当前的最优位置。然而，当前位置并非真正的最优位置时，种群容易集中在当前最优位置附近进行搜索，导致无法找到真正最优位置的问题。为了解决这种情况，使用自适应的高斯-柯西变异扰动对最优的蜣螂进行扰动，以提高蜣螂种群的多样性，帮助其跳出局部最优。

由于柯西变异的搜索范围比高斯变异更大，但更容易跳过最优值[15]，而高斯变异在较小的搜索范围内表现出良好的搜索能力[16]，因此定义高斯-柯西混合扰动后的位置如下：

[Hbt=Xbt1+μ1×Gaussσ+μ2×cauchyσ] （25）

其中，[Xbt]为个体[X]在第[t]次迭代的最优位置，[Hbt]为高斯-柯西混合扰动后的位置， [Gaussσ]为高斯变异算子，[cauchyσ]为柯西变异算子，[μ1=t/Tmax]，[μ2=1-t/Tmax]，变异算子的权重系数[μ1]，[μ2]以一种一维线性的方式逐步变化。

从公式 （25） 可以看出，算法在迭代初期，主要通过柯西分布函数对个体进行较大幅度的变异扰动，使算法能够进行全局探索并快速收敛；随着算法迭代的进行，大多数蜣螂个体的位置变化不大，此时算法主要通过高斯分布函数对种群进行扰动，以帮助算法跳出局部最优解。

由于无法确定变异扰动之后得到的新位置的适应度值一定优于原位置，因此加入了贪婪原则。通过比较扰动前后两个位置的适应度值，决定是否进行位置更新。贪婪原则公式如式 （26） 所示。

[Xb=Hbt，fHbt<fXbtXbt，fHbt≥fXbt] （26）

其中，[fx]表示[x]位置的适应度值。若[fHbt<fXbt]，则选取[Hbt]；反之，则保留之前的位置信息[Xbt]。

3.4 L-MSADBO算法

本文对蜣螂算法进行了改进，提出了混合策略引导的改进蜣螂算法L-MSADBO。在原始蜣螂算法的基础上，该算法在种群初始化时增加了混沌映射的策略，采用正弦算法引导滚球蜣螂的位置更新公式，以及Levy飞行策略引导偷窃蜣螂的位置更新公式。对更新完后的最优个体进行高斯-柯西变异扰动，并采用贪婪原则来择优选取扰动前后的值。其主要步骤如下：

a）输入相关参数，根据公式（16）对蜣螂种群进行初始化。

b）根据公式（1）计算各个蜣螂的适应度值。

c）判断[δ]和[ST]，若[δ<ST]，则按照公式（6）更新滚球蜣螂；反之，则按公式（17）进行更新。

d）根据公式（11）和（14）更新繁殖蜣螂和幼小蜣螂的位置，偷窃蜣螂则依据公式（24）进行更新。

e）对各个蜣螂进行边界判定，并根据公式（1）计算其适应度值。

f）使用公式（25）对当前最优解进行高斯-柯西变异扰动，并依据公式（1）计算扰动后的适应度值。

g）通过公式（26）的贪婪原则选取最优解。

h）判断迭代次数[t]，或[t<Tmax]，则[t=t+1]，并返回步骤c）继续更新；否则，输出最优蜣螂的适应度值。

L-MSADBO算法的流程图如图1所示：

图1 L-MSADBO算法流程图

4 L-MSADBO求解TSP问题仿真分析

为了探究 L-MSADBO 的有效性及其在 TSP 问题中的应用效果，以 Oliver30 数据集为例。我们分别使用 MSADBO、DBO、PSO、GWO 和 Tabu 方法对该 TSP 问题进行了求解，并将所得结果与 L-MSADBO 进行了对比分析。其中，30 个位置的坐标数据如表 1 所示：

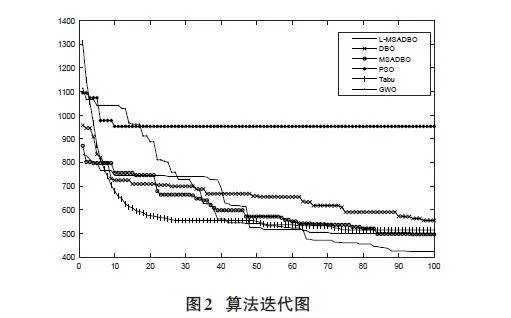
各个算法的迭代对比图如图 3 所示。图 4 到图 10 分别为各个算法的最优路线图。表 2 和表 3 分别为各个算法的最优结果对比表和最优路线表。

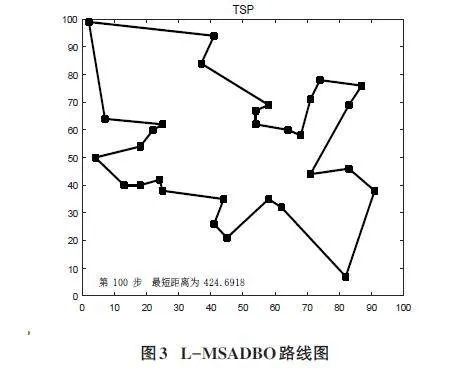
由图 3 可以看出，在迭代初期，L-MSADBO 对于 TSP 问题的解已经优于其他算法。经过 60 次迭代后，L-MSADBO 的解开始趋于稳定，并在 80 多次迭代后完成收敛，得到的最优值为 424.9618，优于其他算法，且与 Oliver 数据集的最优值 423.7 最为接近。不难看出，通过对 DBO 算法的改进，混沌映射使得原本过于随机的 DBO 初始种群多样性得以提高，从而使在迭代初期 L-MSADBO 的解优于原始 DBO 算法。通过正弦算法和 Levy 飞行策略对种群更新进行优化，增强了算法的搜索能力和平衡性，使得可以找到优于 MSADBO 的解。最后，通过高斯-柯西变异以及贪婪原则对迭代后期的最优解进行优化，进一步提升了该算法求得最优解的能力。

5 结束语

本研究提出了一种混合策略引导的改进蜣螂算法，并将其应用于 TSP 问题，对 Oliver 数据集进行求解，并与 MSADBO、DBO、GWO、PSO、Tabu 的求解效果进行了对比。实验表明，L-MSADBO 算法在解决 TSP 问题时获得的路线距离最短，并且趋近于最优值。后续的工作将致力于将 L-MSADBO 算法应用在更多的 TSP 数据集和其他问题上，以更深入和广泛地探究其解决问题的效果。

参考文献：

[1] CAMPBELL P J. The traveling salesman problem： A computational study[J]. Mathematics Magazine， 2007， 80（3）： 238-364.

[2] 高珊，孟亮.贪婪随机自适应灰狼优化算法求解TSP问题[J].现代电子技术，2019，42（14）：46-50，54.

[3] 申晓宁，潘红丽，陈庆洲，等.引入启发信息的粒子群算法在低碳TSP中的应用[J].计算机工程与科学，2022，44（6）：1114-1125.

[4] 孟范立.基于改进的乌鸦搜索算法求解旅行商问题[J].电脑知识与技术，2023，19（12）：22-25.

[5] 王芬，杨媛.基于猎人猎物优化算法求解TSP问题[J].宁夏师范学院学报，2022，43（7）：59-63，71.

[6] XUE J K，SHEN B.Dung beetle optimizer：a new meta-heuristic algorithm for global optimization[J].The Journal of Supercomputing，2023，79（7）：7305-7336.

[7] 陈建东，聂斌，雷银香，等.多策略增强型麻雀搜索算法[J].现代信息科技，2023，7（13）：39-45，52.

[8] LUO Y B，DAI W M，TI Y W.Improved sine algorithm for global optimization[J].Expert Systems with Applications，2023，213：118831.

[9] 曲良东，何登旭.一个简化的正弦余弦算法：正弦算法[J].计算机应用研究，2018，35（12）：3694-3696，3728.

[10] 刘勇，马良.转换参数非线性递减的正弦余弦算法[J].计算机工程与应用，2017，53（2）：1-5，46.

[11] 徐松金，龙文.求解高维优化问题的改进正弦余弦算法[J].计算机应用研究，2018，35（9）：2574-2577.

[12] 谢金宵，高岳林，于宏利.基于高斯变异与Levy飞行策略的混合粒子群优化算法[J].宝鸡文理学院学报（自然科学版），2021，41（1）：5-10.

[13] 张玉，卢子广，卢泉，等.基于Levy飞行改进鸟群算法的光伏直流微电网优化配置研究[J].太阳能学报，2021，42（5）：214-220.

[14] 王贺贺.基于重尾分布布谷鸟算法的非线性系统辨识研究[D].北京：北京化工大学，2018.

[15] 贾鹤鸣，林建凯，吴迪，等.融合学习行为策略的改进黑猩猩优化算法[J].计算机工程与应用，2023，59（16）：82-92.

[16] 毛清华，张强.融合柯西变异和反向学习的改进麻雀算法[J].计算机科学与探索，2021，15（6）：1155-1164.

【通联编辑：唐一东】