金融科技对商业银行全要素生产率的技术溢出效应研究

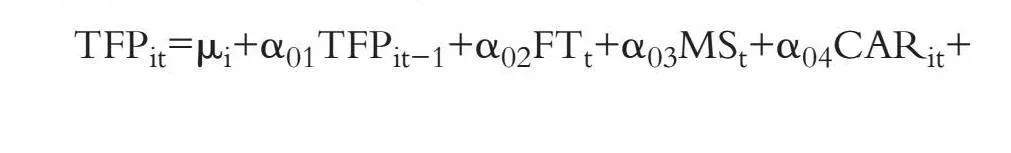
【摘要】本文基于技术溢出理论， 研究金融科技对商业银行全要素生产率的非线性影响。首先通过DEA—Malmquist模型测算出商业银行全要素生产率， 然后使用文本挖掘法筛选出高相关性的关键词构建金融科技发展指数， 最后分别以金融科技发展指数、 金融科技企业融资总额、 金融科技机构新增数量作为转换变量， 建立面板平滑转换回归（PSTR）模型，检验金融科技的非线性影响。实证结果表明： 金融科技对商业银行全要素生产率呈现出先抑制后促进的非线性影响， 随着金融科技的不断发展， 技术溢出效应逐渐增强。

【关键词】金融科技；全要素生产率；技术溢出；PSTR模型；门槛效应

【中图分类号】 F832.33 【文献标识码】A 【文章编号】1004-0994（2024）17-0121-8

一、 引言

伴随着金融科技（Fintech）的蓬勃发展， 大数据、 区块链、 云计算、 人工智能等新兴技术给传统金融行业带来了机遇与挑战。从被称为中国金融科技元年的2016年起， 科技对于金融的促进作用就不仅仅局限于渠道等浅层次上， 而是真正开启了的“金融+科技”的深度融合。金融科技利用信息技术向传统金融领域渗透： 一方面可以通过技术创新发展出高壁垒的新产品和新服务， 通过与商业银行的合作， 促进商业银行盈利模式的改进， 提高银行的运行效率； 另一方面， 金融科技的风险通过不同业务渠道传染到商业银行， 加重了商业银行的风险承担， 冲击着传统金融的稳定性。金融科技与传统商业银行之间的关系已经转变成更高层次的“竞合”。因此， 金融科技发展带来的数字技术创新逐渐成为金融行业以及相关学者关注的热点问题。

已有文献对金融科技给商业银行带来的影响进行了相关研究， 但是在定量分析两者的关系时， 学者们主要集中在两者的线性关系上， 从挤出效应或者技术溢出效应单方面进行阐述， 而未关注两种效应共同作用的结果， 且对于门槛效应的研究不足。实际上， 在转换变量发展的不同时期， 挤出效应和技术溢出效应可能分别占据主导地位， 产生非线性影响。金融科技对传统商业银行全要素生产率到底是具有促进作用还是抑制作用？金融科技是否会对商业银行产生技术溢出或挤出效应？假设存在正向的技术溢出效应， 其溢出程度是否会由于某些因素的影响而发生变化， 技术溢出是否存在门槛效应？回答以上问题不仅对金融科技的健康发展和政策制定具有重要意义， 而且可以促使商业银行和金融科技相辅相成， 更蓬勃健康地发展。

鉴于此， 本文利用面板平滑转换回归（PSTR）模型探究金融科技对商业银行全要素生产率的非线性影响。本文的贡献主要体现在两个方面：一是， 利用PSTR模型研究发现金融科技和商业银行全要素生产率之间具有非线性关系， 丰富了两者之间的非线性关系研究。现有文献主要集中于通过平方项研究U型或者倒U型关系以及使用Hansen的门槛效应模型， PSTR模型考虑了平滑的门槛转换问题， 更符合现实经济意义。二是， 基于技术溢出理论， 分析金融科技发展对商业银行的技术溢出效应和挤出效应， 并总结相关研究的技术溢出传导路径， 拓展了金融科技的非线性影响。

二、 文献综述

（一） 金融科技对商业银行的影响

随着金融科技的不断深化， 现有文献主要从银行的风险承担水平、 全要素生产率和经营效率角度研究金融科技对商业银行的影响， 但是并没有取得一致性结论， 主要表现为正向技术溢出效应和负向挤出效应。

一方面， 金融科技和传统商业银行在融合过程中相互促进， 对商业银行产生正向的技术溢出效应。金融科技通过技术溢出效应， 为商业银行带来技术和产品的创新， 形成新型业务模式， 并优化渠道管理， 推动商业银行自身效率的提升。Philippon（2016）认为， 正是金融科技产生的技术进步对传统金融机构的商业模式创新带来了启发， 其通过更广泛的客户数据使商业银行效率得到提升。沈悦和郭品（2015）、 林彧等（2020）均发现， 金融科技通过技术溢出效应提高了商业银行的全要素生产率， 由于吸收能力的差异， 其对不同类型商业银行的影响程度明显不同。

另一方面， 金融科技也会给商业银行带来一定程度的冲击， 形成负向的挤出效应。金融科技主要从信贷、 负债和风险等方面对商业银行业务形成冲击， 分流银行的存款、 挤占银行中间业务和资产业务， 威胁银行的盈利。邱晗等（2018）、 沈悦和郭品（2019）发现， 金融科技通过作用于利率市场化， 使银行的负债端结构发生改变， 资产端承受的风险随之上升， 从而对传统商业银行造成一定冲击， 冲击程度随商业银行规模的增大而降低。刘孟飞和蒋维（2020）研究了金融科技对我国商业银行效率的影响， 发现金融科技对不同商业银行利润和成本的影响不同， 其对商业银行盈利具有正向促进作用， 降低了商业银行的成本效率。

上述结论的不一致也反映出金融科技对商业银行影响的复杂性， 意味着二者之间并非简单的线性关联， 可能存在非线性关系。

（二） 技术溢出的门槛效应

技术溢出效应的相关研究认为， 技术具有较强的外部性， 技术领先企业的技术扩散会对其他企业产生积极作用， 促进其他企业的技术创新和业务发展。大量文献对外商直接投资（FDI）的技术溢出效应进行了研究， 如钟娟和张庆亮（2010）、 王华等（2012）、 吴书胜和李斌（2015）、 金春雨和王伟强（2016）等分别使用技术差距、 人力资本、 对外开放程度、 外资规模等作为转换变量， 发现FDI的技术溢出存在门槛效应。这种技术溢出的门槛效应同样适用于金融科技与商业银行之间， 因此有必要深入研究金融科技对商业银行效率的非线性影响。

近几年， 关于金融科技非线性影响的研究主要通过二次项衡量U型或者倒U型关系， 以及通过面板门槛回归（PTR）模型研究突变的门槛效应。汪可等（2017）、 刘孟飞等（2021）、 岳华等（2022）的研究均发现， 金融科技对商业银行的绩效和风险承担产生先升后降的倒U型影响。田新民和张志强（2020）研究发现， 不同金融科技水平下， 金融科技和金融资源配置效率对经济增长的影响表现为门槛效应。熊健等（2021）使用分段回归研究金融科技和银行绩效的关系， 发现随着金融科技发展水平的不断提高， 挤出效应逐渐减弱， 由鲶鱼效应和关联效应产生的技术溢出效应不断增强， 金融科技对商业银行经营绩效产生先抑制后促进的非线性影响。孟娜娜和粟勤（2020）使用金融科技与银行业竞争的交互项衡量技术溢出效应， 认为金融科技通过产业竞争机制对普惠金融产生挤出效应， 通过技术溢出机制产生鲶鱼效应， 但是随着竞争加剧， 鲶鱼效应逐步减弱。基于以上文献回顾发现， 上述文献并未使用PSTR模型， 而是仅考虑了突变的门槛效应， 但是金融科技对商业银行全要素生产率的影响会产生平滑的变化， 因此采用PSTR模型更加合理。

三、 研究假设

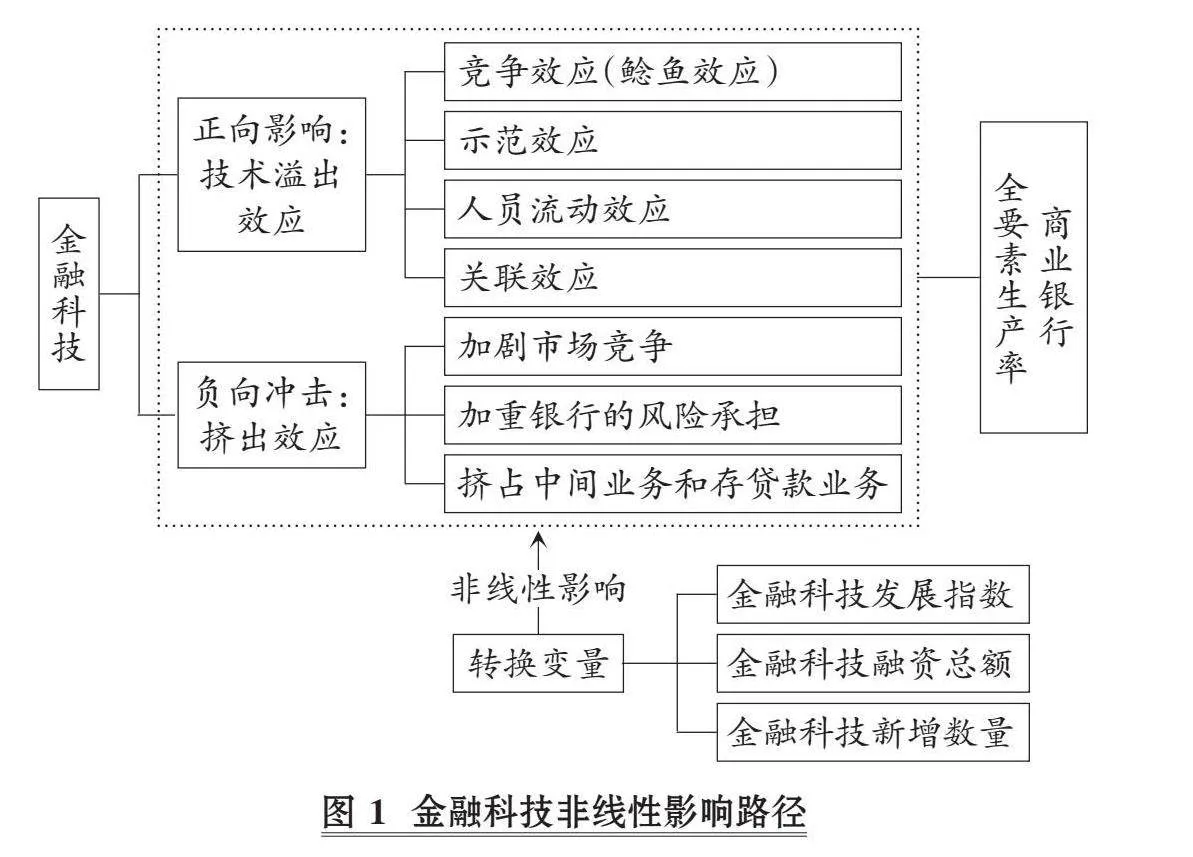
沈悦和郭品（2015）、 孙洁（2017）、 杨傲和王力（2019）、 卜亚和张倩（2021）、 刘孟飞等（2021）、 王秀意（2022）等借鉴FDI的技术溢出理论， 研究发现金融科技可以通过竞争效应、 示范效应、 人员流动效应以及关联效应影响商业银行全要素生产率。基于以上研究， 本文总结了金融科技对商业银行全要素生产率的技术溢出影响路径， 如图1所示。

金融科技对商业银行全要素生产率的技术溢出效应分析如下：

一是竞争效应（鲶鱼效应）。金融科技的发展通过加剧市场竞争挤压商业银行的业务， 动摇传统商业银行的垄断地位， 改变商业银行的投入与产出要素， 倒逼商业银行改革经营模式、 创新业务和产品， 进而提升经营效率。例如：随着数字银行的兴起， 其在点对点、 个性化服务中取得进展， 从而冲击了传统商业银行的零售业务； 第三方支付工具和区块链技术下电子记账本等的兴起， 对信用卡和借记卡等传统支付结算带来了负面影响； 智能投顾所展现的机器人可以代替人脑进行分析， 配置最优资产组合， 对传统资产管理业务造成了冲击。

二是示范效应。金融科技所带来的丰富的技术应用和完备的数据分析系统给传统商业银行创造了新的发展契机。随着多年的发展， 传统商业银行在各方面已经形成了一套完备的体系和服务方式， 其技术水平相对落后、 风险管控比较保守， 无法在保持高安全性的同时保持低成本。而金融科技所展现的创新理念、 便利又低成本的服务、 包容的风险管控， 均能给传统商业银行注入新活力。

三是人员流动效应。不同主体之间的劳动力流动可以带来技术溢出。具体来看， 其包括两个方面：一方面， 金融科技领域优质技术人才的流入， 对商业银行构建网上银行、 提供数字化财富管理等产生正向作用； 另一方面， 传统商业银行的优秀工作者投身金融科技产业， 使传统商业银行的经营管理能力受到冲击。

四是关联效应。掌握新兴金融科技技术能够对传统商业银行的数据分析和科学决策能力产生积极作用， 且有助于缓解信息不对称问题。商业银行与金融科技公司合作， 吸收金融科技公司先进的技术与经验； 与此同时， 传统商业银行拥有的完备管理体系、 丰富客户群以及多样化金融业务也能给金融科技产业带来新的思考。两者之间相互推动、 相互促进， 迎来整个金融业可持续发展的新时代。

金融科技对商业银行全要素生产率的非线性影响研究主要认为：金融科技企业和传统金融企业之间的技术差距越大， 金融科技企业产生的鲶鱼效应、 示范效应和关联效应越明显， 商业银行的模仿空间越广阔。随着传统金融企业的技术水平逐渐接近金融科技企业， 传统金融企业可模仿的空间缩小， 吸收和模仿的成本增加， 从而降低了进一步技术溢出的可能。金融科技作为新技术， 在应用初期的接受程度相对较低（发展程度低、 融资总额低、 机构新增数量低）， 呈现的技术溢出效应较弱， 此时挤出效应成为主导， 金融科技与商业银行形成竞争关系。但是当具有一定认同基础之后， 技术溢出效应明显加强， 技术溢出效应占据主导地位， 商业银行会做出加快金融科技平台建设、 与金融科技公司联盟等行为。随着金融科技发展的不断深入， 技术差距逐渐缩小， 技术溢出效应可能会再次降低。目前相关研究缺乏关于金融科技技术溢出对商业银行效率非线性影响的深入分析， 本文认为， 金融科技对商业银行全要素生产率的技术溢出效应会随着金融科技发展程度的不同而呈现平滑的非线性变化。

基于以上分析， 本文提出如下假设：

假设1： 将金融科技发展指数、 金融科技企业融资总额、 金融科技机构新增数量作为转换变量， 随着转换变量数值的不断提高， 金融科技的挤出效应逐渐减弱、 技术溢出效应逐渐增强， 金融科技对商业银行全要素生产率产生平滑转换的非线性影响。

四、 研究设计

（一） 样本选择

本文主要选取26家上市商业银行作为研究样本， 具体包括5家国有商业银行、 8家股份制商业银行以及13家城市商业银行①。时间窗口设置为2011 ～ 2020年， 相关数据来源于Wind数据库与各大商业银行年报。

（二） 变量选取

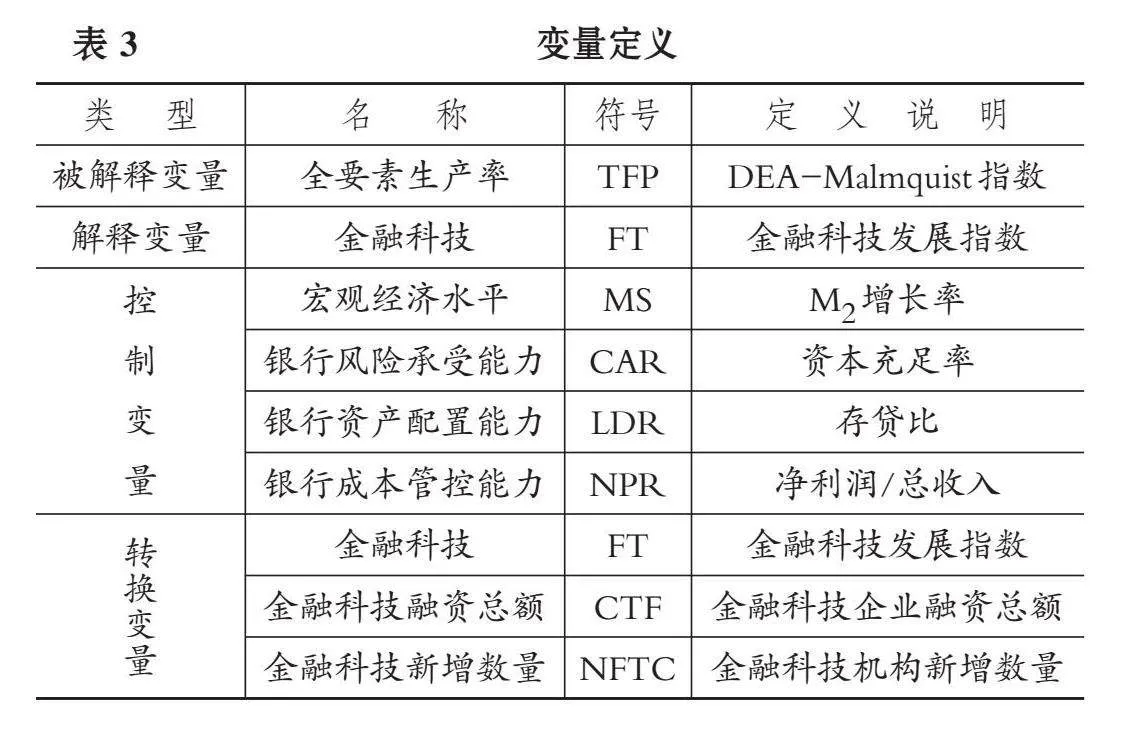
1. 被解释变量：商业银行全要素生产率（TFP）。测算商业银行全要素生产率的方法主要有两类， 即参数法和非参数法。其中， 非参数法能够更准确、 客观地测量商业银行的全要素生产率， 原因在于其所需要的样本量较小， 不必构造生产函数， 能减少计算中的误差。数据包络分析（DEA）作为非参数效率分析方法的典型代表， 能得到更准确的结果。在商业银行系统中， 存款不断派生， 存款既可以看作商业银行的投入指标， 又可以看作商业银行的产出指标。故为避免误差， 将存款作为中间指标使用， 建立无导向DEA模型。为了更好地度量生产率的跨期变化， Färe等（1994）建立了基于DEA的Malmquist生产率指数。该指数可以很好地衡量决策单元生产率的变化， 故本文用其测量商业银行全要素生产率（TFP）。Malmquist指数可以表示为：

（1）

其中， Dt+1（·）和Dt（·）分别表示第t+1期和第t期观测点到前沿面的距离函数， 、 、 和 、

、 分别表示第t+1期和第t期商业银行q的投入、 产出、 中间指标。

在指标选取方面： 将资产总额（X1）和营业费用（X2）作为投入变量， 其反映了银行的资金投入和管理经营投入； 税前利润（Y1）和贷款总额（Y2）是银行存贷款业务以及中间业务以后的产出， 记为产出变量； 存款总额（Z）作为银行的派生变量， 记为中间变量。

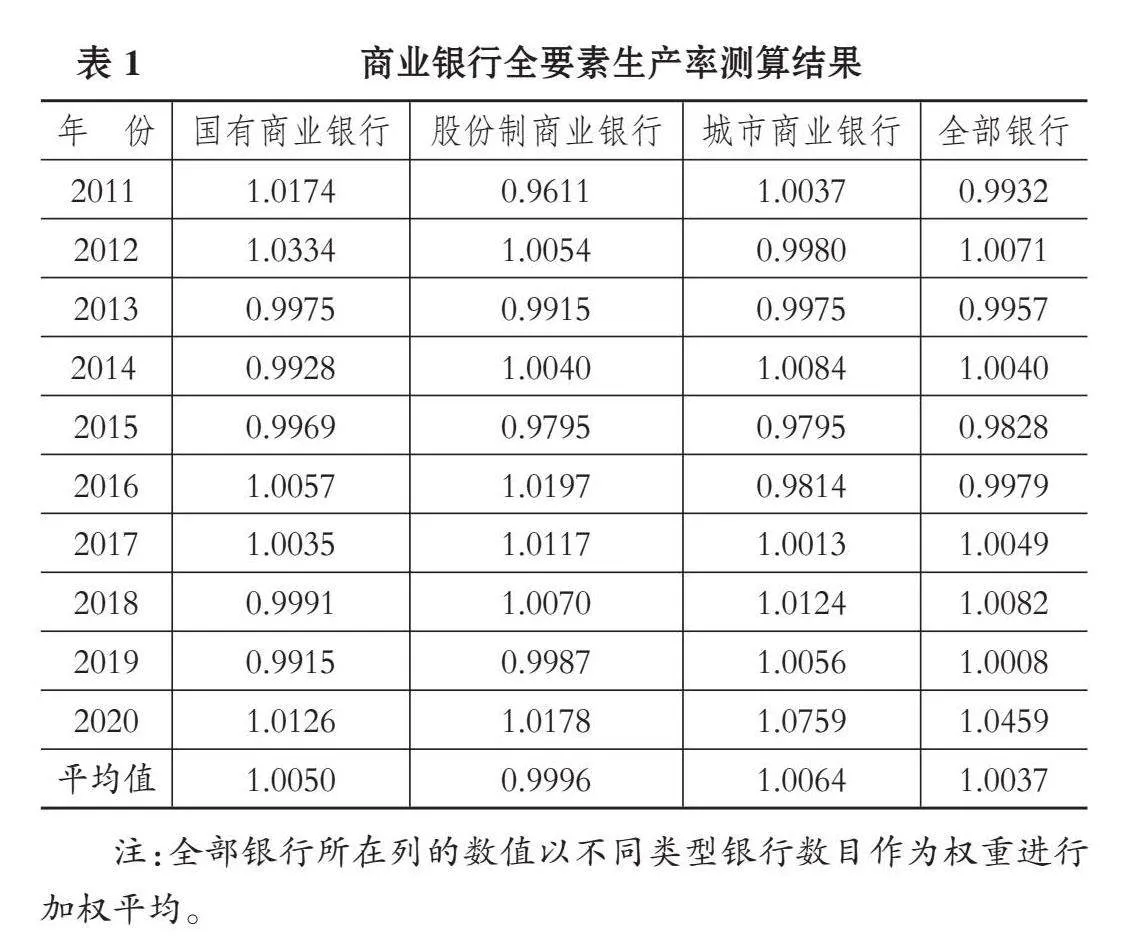
根据模型（1）和测算的相关投入、 产出、 中间指标， 运用Matlab 9.0测算得到各商业银行的全要素生产率， 分类汇总后的结果如表1所示。由表1可知， 2011～2020年间， 我国商业银行全要素生产率的整体平均数值为1.0037， 表明整体效率有所提升。但由于商业银行体系较为陈旧， 改革力度较小， 以及受到金融科技的冲击， 并没有表现出强势的持续增长态势， 而是呈平缓波动性调整。

从不同类型商业银行全要素生产率的测算结果来看， 大型国有商业银行在金融科技发展初期表现良好， 整体效率增长情况超过股份制商业银行和城市商业银行， 这与其良好的改革政策、 示范带头效应和技术层面的引进有关； 但是其后期的效率增长不明显， 主要是因为其存在资产规模庞大、 创新激励机制不健全、 管理决策延迟等问题， 造成银行自主进行技术创新的动力不足、 人员流失严重、 技术溢出的吸收能力不足。股份制商业银行不断进行业务创新和多元化发展， 通过人员流动和示范效应， 使得其技术溢出吸收能力在近几年略高于国有商业银行。城市商业银行全要素生产率相对较高， 近几年也在不断发展， 其与金融科技企业服务对象相似， 更容易吸收优质示范效应。城市商业银行由于经营规模较小、 体制灵活， 抵制技术创新冲击的能力较弱， 迫切需要进行数字化转型改革， 因此其全要素生产率的提升效果更加明显。

2. 核心解释变量：金融科技（FT）。由于金融科技近年来才发展为金融领域的热点， 其测算没有统一标准。相关文献使用的金融科技指数衡量方法大致分为三类：文本挖掘法、 北京大学数字普惠金融指数、 以第三方支付和线上支付交易量等作为替代指标。本文借鉴沈悦和郭品（2015）、 汪可等（2017）、 李春涛等（2020）、 王小华等（2022）的做法， 采用文本挖掘法， 通过爬虫技术构建金融科技发展指数（FT）。该方法的优势在于， 能够全面地覆盖金融科技的各个维度， 保证各维度数据性质的统一与稳定。具体做法如下：

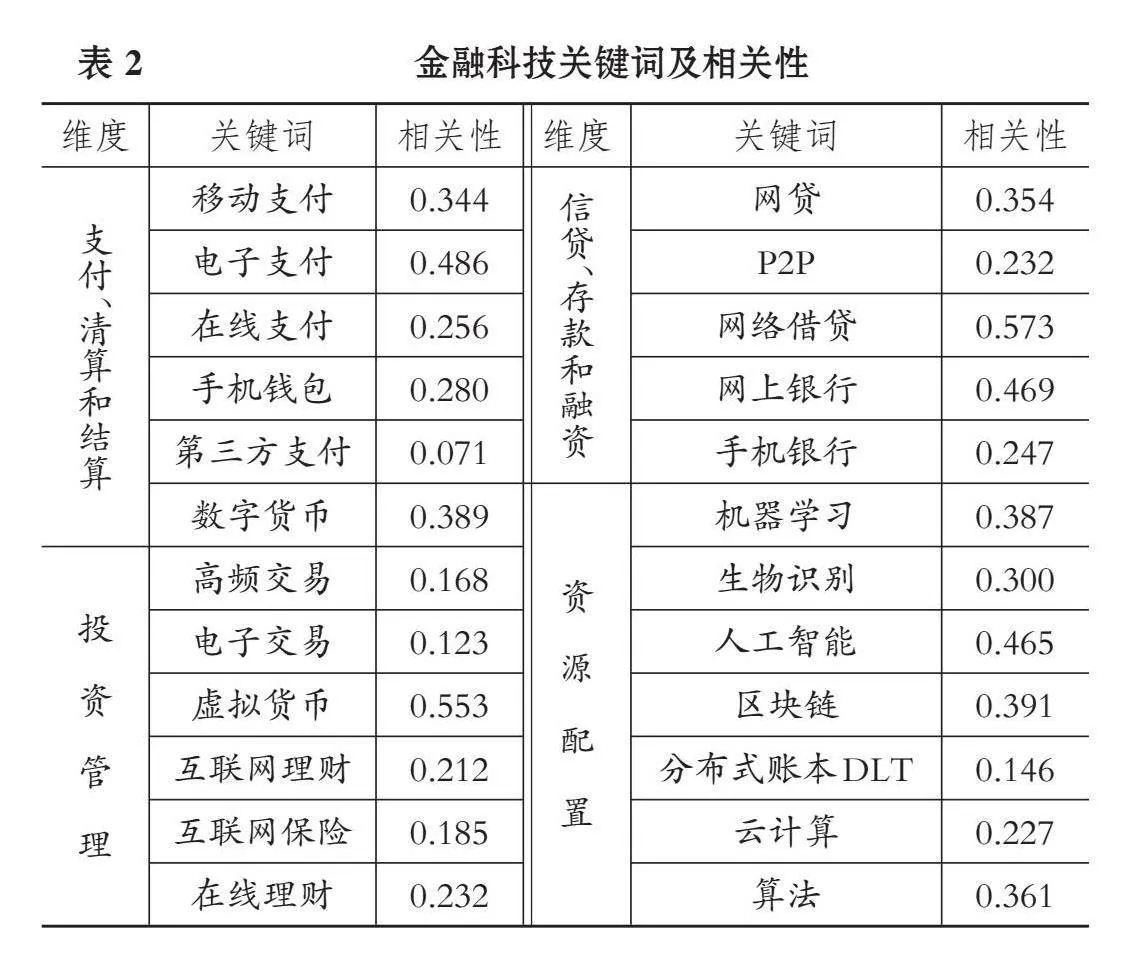
首先， 由于金融科技的金融属性， 其在支付清算结算、 信贷融资、 投资管理、 资源配置等方面很大程度地影响了传统金融业。据此， 基于支付、 清算和结算， 信贷、 存款和融资， 投资管理， 资源配置四个维度构建关键词词库， 并选出其中具有代表性的关键词。与以往学者基于金融IT阶段、 互联网金融阶段构建的关键词词库相比， 本文选取的人工智能等关键词囊括了金融科技3.0阶段的最新特性， 最终得到如表2所示的金融科技关键词词库。

其次， 利用爬虫技术， 得到年度词频。本文爬取的数据分析平台为百度指数， 这是由于百度搜索是目前我国应用最广泛的搜索引擎， 在一定程度上反映了人们对金融科技的关注。通过每个指标的日搜索词频， 可以得到年度词频。

最后， 利用主成分分析法得到金融科技发展指数。通过计算商业银行全要素生产率和各个关键词词频的相关系数（如表2所示）， 选取相关性大于0.3的关键词进行主成分分析， 按照方差贡献率合成各维度指数和金融科技发展指数， 指数变化趋势如图2所示。综合来看， 各维度指数均基本保持上升的趋势， 其中支付、 清算和结算维度指数的变化幅度较大， 而金融科技发展指数由于受到各维度的影响， 趋势较为平稳。从2018年以后， 我国金融科技发展速度明显放缓， 主要受到市场空间收窄、 监管政策趋严等因素的影响。金融监管体系的完善有利于减轻金融科技发展过程中存在的非法集资和庞氏骗局等野蛮生长问题， 从而缓解金融科技对商业银行效率的冲击， 弱化挤出效应， 可能带来技术溢出效应的不断增强。

3. 控制变量。商业银行的效率还会受到宏观因素和微观因素的影响。宏观层面因素主要为宏观经济水平， 以货币供应量（M2）的增长率（MS）衡量。微观层面因素包括商业银行的风险承受能力、 资产配置能力和成本管控能力， 其中银行风险承受能力用资本充足率（CAR）衡量， 银行资产配置能力用存贷比（LDR）衡量， 银行成本管控能力用非利息收入占比（NPR）， 即净利润/总收入衡量。

4. 转换变量。本文选择衡量金融科技发展水平的变量作为转换变量， 具体包括金融科技发展指数（FT）、 金融科技企业融资总额（FCT）和金融科技机构新增数量（NFTC）。从金融科技关注度的角度分析， 随着金融科技发展指数的不断增大， 当其超过一定阈值时， 由于商业银行的吸收和学习能力不断增强， 可能会对商业银行全要素生产率产生先抑制后促进的影响。相关非线性模型研究一般使用解释变量作为转换变量。选择金融科技企业融资总额作为转换变量， 是从金融科技投融资方角度进行的考虑， 在金融科技发展初期， 由于行业监管宽松， 金融科技领域的融资总额快速增加， 有利于提高金融科技企业跨界业务整合能力及科技创新能力， 提高市场竞争力， 其对商业银行全要素生产率可能存在先抑制后促进的影响； 随着监管趋严以及市场环境的变化， 金融科技行业边际投资收益递减， 金融科技融资总额不断降低， 可能会再次出现抑制商业银行全要素生产率的情况。从金融科技企业发展的角度来看， 选择金融科技机构新增数量作为转换函数， 在金融科技发展初期， 金融科技机构新增数量不断增加， 与传统商业银行形成业务上的竞争， 随后又通过技术溢出促进商业银行全要素生产率的提升。

具体变量的定义说明如表3所示。

（三） 模型设定

1. 面板平滑转换模型。为探究金融科技与商业银行全要素生产率的非线性关系， 可采用Hansen（1999）提出的PTR模型进行估计和检验。但该模型规定发生的突变是离散和间断的， 存在门槛值前后的跳跃性转换， 具有一定的局限性。因此， 本文采用González等（2005）提出的PSTR模型， 加入连续的转换函数， 捕捉连续平滑的非线性关系， 这更符合经济变量之间的因果连续渐进关系， 同时还可以捕捉面板数据的截面异质性， 作为外生回归的固定效应模型。PSTR模型如下：

TFPit=μi+α01TFPit-1+α02FTt+α03MSt+α04CARit+

α05LDRit+α06NPRit+（α11TFPit-1+α12FTt+α13MSt+

α14CARit+α15LDRit+α16NPRit）×h（qit；γ，c）+εit （2）

在模型（2）中：被解释变量TFPit为第[i]家银行[t]时刻的全要素生产率； 核心解释变量为金融科技发展指数FTt； qit为转换变量， 分别选取金融科技发展指数（FT）、 金融科技企业融资总额（FCT）、 金融科技机构新增数量（NFTC）作为转换变量； γ为转换函数的斜率， 即平滑参数， 可以通过其大小反映一种机制到另一种机制的转换速率； c为位置参数， 即从一种机制转到另一种机制的临界值； h（qit；γ，c）为转换函数。该模型允许模型参数随转换变量做缓慢平滑的非线性转换。

2. 转换函数说明。根据相关研究， 转换函数一般采用Logistic形式：

h（qit；γ，c）={1+exp［-γ （qit-cj）］}-1，γ>0，c1≤…≤cm （3）

在模型（3）中， m为位置参数的个数， 一般取m=1或m=2。h（qit；γ，c）在0到1之间变化， 当h（qit；γ，c）=0时， 模型处于低机制， 此时变成线性模型； 当h（qit；γ，c）=1时， 模型处于高机制。转换函数在0 ～ 1之间平滑转换， 模型则在两种机制之间平滑转换。

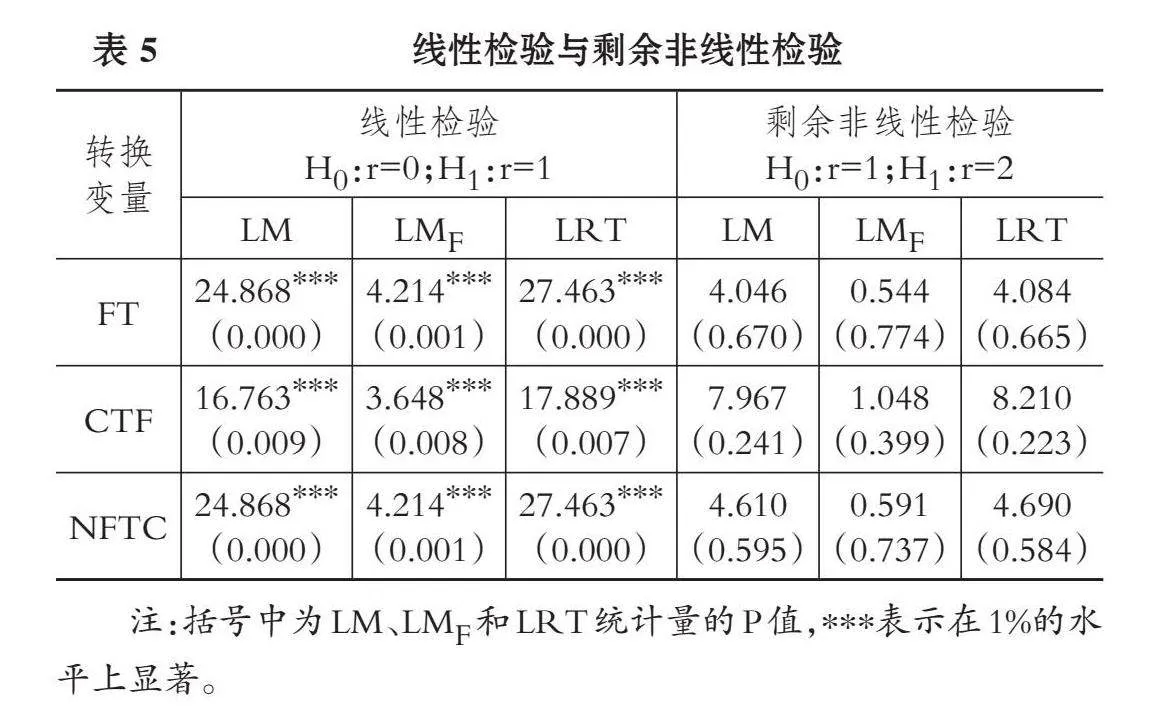
3. 线性检验与剩余非线性检验。为判断商业银行全要素生产率与金融科技发展指数之间是否存在非线性效应， 需要先进行线性检验“H0：r=0；H1：r=1”。由于在转换函数h（qit；γ，c）中存在未识别干扰参数γ和c， 本文借鉴Luukkonen等（1988）的做法， 将h（qit；γ，c）在r=0处构造一阶泰勒展开式， 以检验“H0：r=0；H1：r=1”。据此分别得到H0和H1假设下的残差平方和SSR0和SSR1， 采用Colletaz和Hurlin（2006）构造的三个检验统计量（LM、 LMF和LRT）进行检验， 其中LM和LRT检验统计量服从χ2（mk）分布， LMF检验统计量近似服从F（mk，TN-N-mk）分布。三个检验统计量的具体公式如下：

（4）

（5）

（6）

其中， N代表商业银行个数， T为年份， k为外生变量个数。若结果拒绝线性检验的原假设， 则通过非线性检验， 为确定转换函数的个数， 还需进行剩余非线性检验， 提出假设“H0：r=1；H1：r=2”。继续构造泰勒展开式并进行上述三个检验， 若结果拒绝原假设， 说明转换函数的个数至少为2个， 然后继续提出假设“H0：r=2；H1：r=3”。以此类推， 直到不再拒绝原假设， 最终确定PSTR模型最优的转换函数个数。

五、 实证结果分析

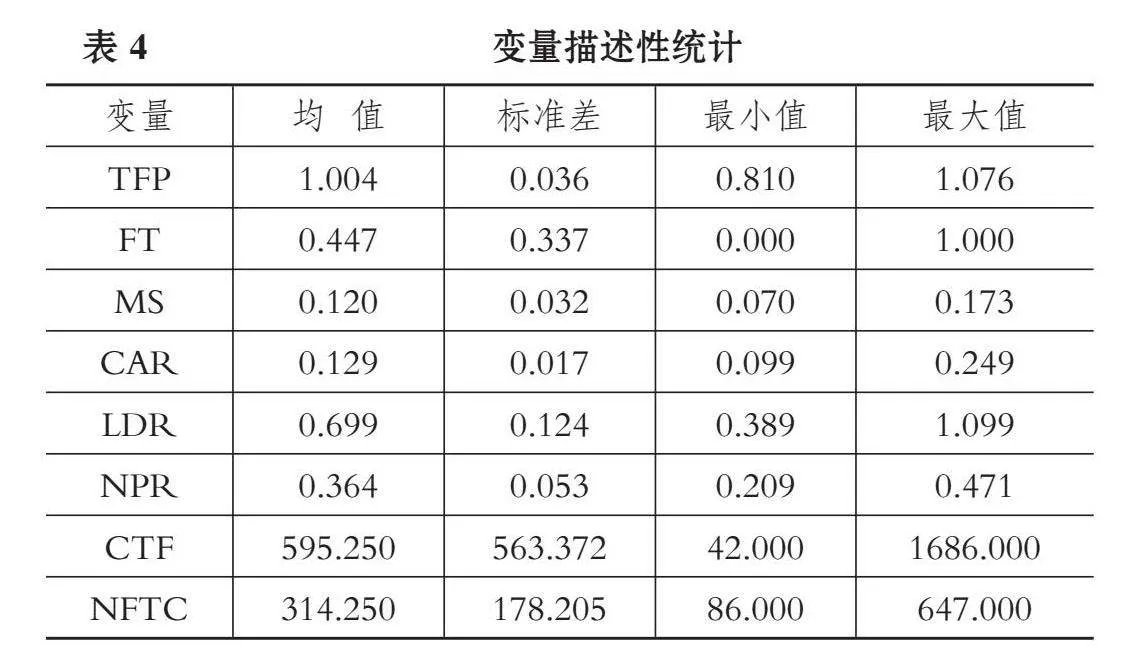
（一） 描述性统计

本文主要变量的描述性统计结果如表4所示。

（二） 线性检验与剩余非线性检验

基于上文构建的PSTR模型②， 按照其检验步骤首先进行线性检验（H0：r=0）， 如果拒绝原假设， 则认为具有非线性关系， 需要继续进行剩余非线性检验（H0：r=1）， 直到无法拒绝原假设， 最终确定转换函数的个数。表5中的线性检验结果显示， 在1%的置信水平下， 三个检验均显著拒绝原假设， 说明随着金融科技发展指数、 金融科技企业融资总额、 金融科技机构新增数量的变化， 商业银行全要素生产率与金融科技之间呈现非线性关系。在剩余非线性检验中， 三个检验均无法拒绝原假设（H0：r=1）， 说明在三个不同转换变量模型中， 均只存在1个最优转换函数。

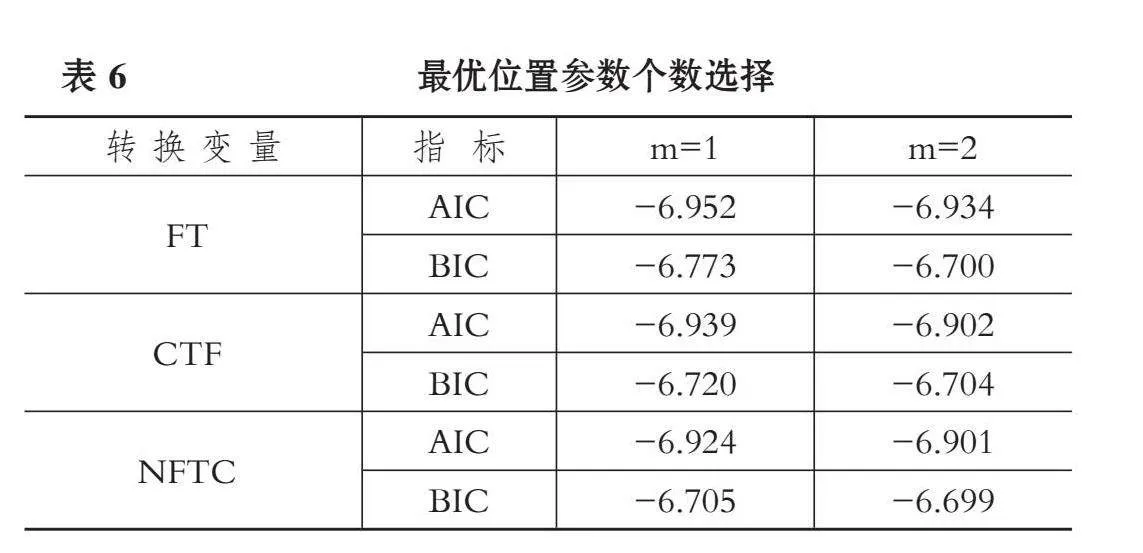
（三） 确定最优位置参数个数的检验

为确定最优位置参数的个数， 计算m=1和m=2时对应的AIC值和BIC值， 根据AIC和BIC准则， 选择数值较小的模型， 得到表6所示的结果。根据结果对比可知， m=1时三个转换变量模型的AIC值和BIC值均小于m=2时的数值， 因此只存在一个最优位置参数。这个结论与Colletaz和Hurlin（2006）、 王欣和姚洪兴（2017）提出的较少的机制个数足以反映PSTR模型截面以及时间的一致性结论保持一致。

（四） PSTR模型估计结果分析

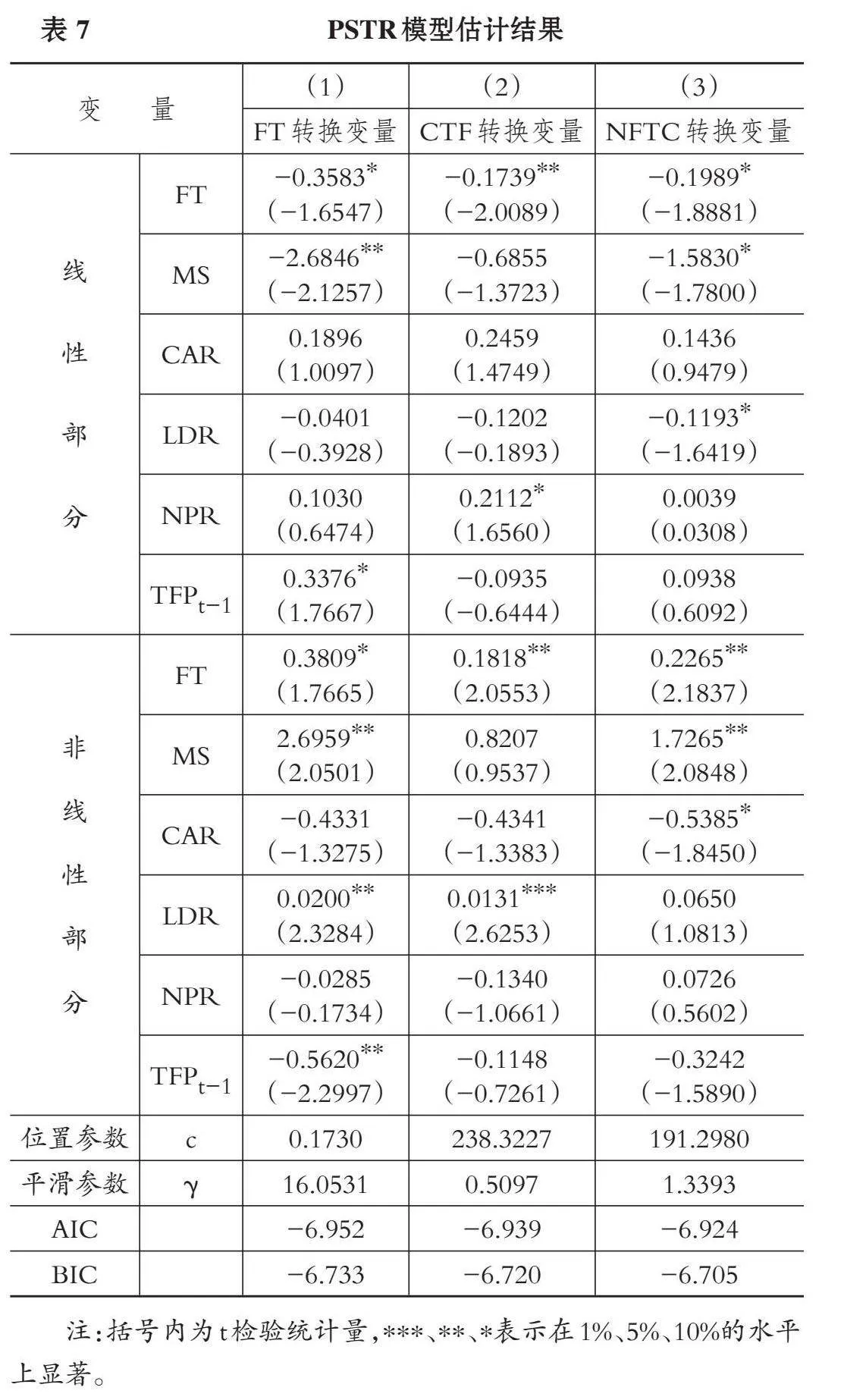
借鉴Colletaz和Hurlin（2006）的研究， 对模型（2）进行估计， 结果如表7所示。根据表7中的结果， 下文分别讨论金融科技发展指数、 金融科技企业融资总额、 金融科技机构新增数量和相关控制变量对商业银行全要素生产率的影响。

表7第（1）列以金融科技发展指数作为转换变量， 首先α02+α12>0（线性部分FT的系数-0.3583与非线性部分FT的系数0.3809之和大于0）， 并且显著， 说明金融科技对商业银行全要素生产率呈现出促进作用。当h=0时， 金融科技发展指数处于低机制状态（FT≤0.1730）， 金融科技对商业银行全要素生产率的线性影响系数为-0.3583， 呈现出抑制作用； 当h=1时， 金融科技发展指数处于高机制状态（FT>0.1730）， 金融科技对商业银行全要素生产率的抑制作用被有效减弱并转变为促进作用。其次， 转换函数的平滑参数为16.0531， 说明转换函数随金融科技发展水平的提高从低机制到高机制的变化相对适中③。这一结论与我国近几年的情况相符。金融科技发展早期， 自身尚存在发展阻碍， 其对商业银行的技术溢出效应主要体现在竞争效应上； 随着金融科技发展水平的提高， 其对商业银行的示范效应逐步增强， 商业银行更加注重二者的耦合作用， 从而促进全要素生产率的提升。最后， 就样本区间来看， 2013年以后金融科技发展指数均跨越了门槛值， 即近年来商业银行正在逐步吸收金融科技所带来的技术溢出， 其自身研发能力和创造能力不断增强， 从而使全要素生产率不断提高。

表7第（2）列以金融科技企业融资总额作为转换变量， α02+α12>0（线性部分FT的系数-0.1739与非线性部分FT的系数0.1818之和大于0）， 并且显著， 说明金融科技对传统商业银行全要素生产率总体上呈现出促进作用。该转换函数的平滑参数为0.5097， 可见转换函数随金融科技企业融资总额的变化同样发生缓慢变化。与金融科技发展指数作为转换变量情况下的变化趋势略有不同， 此时金融科技对商业银行全要素生产率的影响呈现出“抑制—促进—抑制”的变化趋势。这也与实际情况相符， 金融科技企业融资总额在一定程度上反映了金融科技发展水平， 其值越大， 金融科技发展水平越高。在本文所选时间窗口上： 2015年以后金融科技企业融资总额超过了238.3227亿元， 表明2015年以后金融科技企业融资总额对商业银行全要素生产率的正向技术溢出效应显著； 2018年金融科技企业融资规模达到顶点， 2019年出现断崖式下降， 降到门槛值238.3227亿元以下， 2020年受到疫情以及行业监管政策的影响， 金融科技企业融资总额达到最低值， 2021年后才出现反弹。

表7第（3）列以金融科技机构新增数量作为转换变量， 当金融科技机构新增数量跨过门槛值时， 金融科技的影响逐渐从低机制状态向高机制状态转换， 金融科技对商业银行全要素生产率呈现出先抑制后促进的作用， 最终表现为促进作用的趋势， 与预期相符。除此之外， 从2013年开始金融科技机构新增数量均超过了位置参数191.2980， 表现出正向促进作用。

表7第（1）列、 第（2）列和第（3）列中控制变量表现出的变化趋势基本一致。M2增长率（MS）对商业银行全要素生产率的影响系数由负变正， 且α03+α13>0， 说明总体来看宏观经济水平的提升有利于商业银行全要素生产率的提高。这也与商业银行的顺周期性相吻合。当经济处于繁荣时期时， 投资增加， 货币需求增加， 银行利息收入增加， 同时不良贷款率下降， 企业偿付能力提升， 使得整个银行业的全要素生产率提高， 反之则降低。

资本充足率（CAR）对商业银行全要素生产率的影响系数由正变负， 且α04+α14＜0。当金融科技发展程度较低时， 资本充足率对商业银行全要素生产率有正向促进作用； 随着金融科技的不断发展， 商业银行全要素生产率的提升更加依赖于对技术的需求， 而不是对资本的需求。

存贷比（LDR）对商业银行全要素生产率的影响系数总体为负， α05+α15＜0， 可以看出， 商业银行资产配置能力越强， 其全要素生产率越高。当模型处于低机制， 即金融科技发展水平较低时， 商业银行资产配置能力对全要素生产率的影响较大； 而金融科技发展到高机制水平后， 其对商业银行全要素生产率的技术溢出效应在不断增加， 商业银行自身资源配置能力的影响程度降低。

非利息收入占比（NPR）对商业银行全要素生产率的影响系数总体为正， α06+α16>0。金融科技对传统商业银行的示范效应超过竞争效应， 商业银行的创新能力也在不断发展以提高其全要素生产率。

（五） 稳健性检验

为确保上述结果具有可靠性， 本文进行了如下稳健性检验：

首先， 依次采用支付清算结算指数、 信贷融资指数、 投资管理指数、 资源配置指数作为金融科技发展指数的替代变量， 发现检验结果趋于稳定（限于篇幅， 具体结果已省略）。如以FT为转换变量的情况下， 替换变量后得到的对应门槛值分别为0.1432、 0.1651、 0.1721、 0.2338， 各变量的变化趋势与表7基本一致。

其次， 改变样本容量， 采用2011 ～ 2017年的数据进行实证研究， 以FT、 CTF、 NFTC为转换变量的情况下， 得到的门槛值分别为0.1321、 243.4381、 189.5327。由此可以看出， 金融科技和商业银行全要素生产率之间的非线性关系具有稳定性。

六、 结论与建议

（一） 结论

本文基于技术溢出理论， 首先运用无导向DEA—Malmquist指数模型对具有代表性的26家商业银行全要素生产率进行测度， 然后通过网络爬虫技术和主成分分析法构建金融科技发展指数， 最后采用PSTR模型对金融科技发展指数和商业银行全要素生产率之间的非线性关系进行探究。结论如下：第一， 金融科技对商业银行全要素生产率具有非线性影响。随着金融科技的发展， 其对商业银行全要素生产率的抑制作用逐渐减弱， 最终转换为促进作用， 有利于商业银行逐步实现技术进步。第二， 从时间范围来看， 自2015年开始金融科技发展指数均跨越门槛值且逐年上升， 反映出近年来金融科技所表现出的技术溢出不断被商业银行吸收， 使商业银行逐步调整为自身最优状态。第三， 随着金融科技的不断发展， 传统商业银行的资本等对其全要素生产率的影响有所减弱， 转为更加依赖技术进步所带来的溢出效应。

（二） 建议

基于以上实证研究结果， 本文提出以下三点建议：

1. 商业银行提升技术水平和技术应用能力， 充分发挥金融科技技术溢出效应， 推动银行数字化转型。一方面， 商业银行可以通过设立金融科技子公司等方式， 加大核心技术自主研发力度， 缩小技术差距， 提高金融科技利用率， 增强获客和展业能力； 另一方面， 商业银行需加强与金融科技公司的多渠道深入合作， 形成金融科技生态系统。商业银行本身掌握着较为全面的客户信息数据， 若其能更好地掌握金融科技公司所拥有的完备数据分析能力， 更有效率地提取相应信息并进行分析， 则其成本将会大大降低， 从而更有利于全要素生产率的提升。对于以上两种技术创新模式的选择， 可以根据不同类型商业银行的自身条件、 人才队伍建设、 创新成本等方面进行综合衡量。

2. 金融科技企业坚持优势， 加强前沿技术的研发， 控制好自身风险。金融科技企业最大的优势就是利用技术的不断创新来形成数据生态系统， 以便进行科学决策， 实现技术升级。与此同时， 技术带来的潜在风险日趋复杂， 因此金融科技企业更应该提高自身风险应对能力， 警惕技术风险的交叉传染导致商业银行过度的风险承担， 协助商业银行优化信用风险控制模型， 完善征信体系建设， 提升风险识别和预警能力， 更好地推进金融科技服务发展。

3. 政府充分认识金融科技公司和商业银行的耦合作用， 调整监管力度和范围。一方面， 政府应促进二者在保持竞争的同时更加注重合作， 促使整个金融业健康发展； 另一方面， 由于技术创新， 传统商业银行的生存压力增大， 政府需规范金融科技服务中新技术的应用， 进行谨慎监管来降低风险。政府应该加快完善监管体制改革， 优化监管工具， 提升监管的数字化水平， 平衡创新和审慎监管， 为金融科技和商业银行的竞合发展提供良性的制度环境。

【 注 释 】

① 5家国有商业银行为中国银行、中国农业银行、中国工商银行、中国建设银行、中国交通银行，8家股份制商业银行为中信银行、招商银行、浦发银行、兴业银行、光大银行、平安银行、华夏银行、民生银行，13家城市商业银行为北京银行、常熟银行、成都银行、杭州银行、江苏银行、江阴银行、南京银行、宁波银行、上海银行、无锡银行、长沙银行、郑州银行、贵阳银行。

② 为避免伪回归问题，在进行线性检验之前，对面板数据进行了平稳性检验，各个变量的一阶差分序列均平稳，不存在单位根。由于篇幅限制，相关结果已省略，如有需要请联系作者。

③ 由于篇幅限制，对于转换函数与转换变量的图形，如需要相关结果请联系作者。

【 主 要 参 考 文 献 】

卜亚，张倩．金融科技对商业银行效率的影响研究——基于技术溢出视角的分析［ J］．经济论坛，2021（5）：37 ～ 49．

金春雨，王伟强．FDI对我国高技术产业技术溢出的非线性效应——基于13个细分行业内资企业和外资企业面板数据的实证检验［ J］．产经评论，2016（5）：41 ～ 50．

林彧，钟俊滨，李镇南．大数据时代下金融科技对商业银行效率的影响——基于文本挖掘与DEA-Malmquist指数的分析［ J］．科技创新发展战略研究，2020（4）：1 ～ 9．

刘孟飞，蒋维，王琦．金融科技、技术进步与银行业全要素生产率增长［ J］．华南理工大学学报（社会科学版），2021（3）：32 ～ 44．

刘孟飞，蒋维．金融科技促进还是阻碍了商业银行效率？——基于中国银行业的实证研究［ J］．当代经济科学2020（3）：56 ～ 68．

孟娜娜，粟勤．挤出效应还是鲶鱼效应：金融科技对传统普惠金融影响研究［ J］．现代财经（天津财经大学学报），2020（1）：56 ～ 70．

邱晗，黄益平，纪洋．金融科技对传统银行行为的影响——基于互联网理财的视角［ J］．金融研究，2018（11）：17 ～ 29．

沈悦，郭品．互联网金融、技术溢出与商业银行全要素生产率［ J］．金融研究，2015（3）：160 ～ 175．

孙洁．谈互联网金融、技术溢出与商业银行全要素生产率［ J］．商场现代化，2017（19）：113 ～ 114．

田新民，张志强．金融科技、资源配置效率与经济增长——基于中国金融科技门槛作用的分析［ J］．统计与信息论坛，2020（7）：25 ～ 34．

汪可，吴青，李计．金融科技与商业银行风险承担——基于中国银行业的实证分析［ J］．管理现代化，2017（6）：100 ～ 104．

王华，祝树金，赖明勇．技术差距的门槛与FDI技术溢出的非线性——理论模型及中国企业的实证研究［ J］．数量经济技术经济研究，2012（4）：3 ～ 18．

王小华，邓晓雯，周海洋．金融科技对商业银行经营绩效的影响：促进还是抑制？［ J］．改革，2022（8）：141 ～ 155．

王秀意．金融科技与上市商业银行全要素生产率的研究——基于三阶段SBM-DEA模型［ J］．技术经济，2022（8）：34 ～ 46．

吴书胜，李斌．中国对外直接投资逆向技术溢出非线性效应研究——基于面板平滑转换模型的实证分析［ J］．世界经济研究，2015（9）：74 ～ 85+128．

熊健，张晔，董晓林．金融科技对商业银行经营绩效的影响：挤出效应还是技术溢出效应？［ J］．经济评论，2021（3）：89 ～ 104．

杨傲，王力．互联网金融技术溢出对商业银行效率提升的影响研究［ J］．北京化工大学学报（社会科学版），2019（1）：23 ～ 29+47．

岳华，王海燕，陈欣媛．金融科技与商业银行盈利能力：冲击抑或助推？——基于银行财报文本挖掘的实证检验［ J］．东南大学学报（哲学社会科学版），2022（4）：70 ～ 81+147．

钟娟，张庆亮．金融市场发展对中国FDI技术溢出效应的影响及其门槛效应检验［ J］．财贸研究，2010（5）：98 ～ 104．

Colletaz G.， Hurlin I.. Threshold Effects of the Public Capital Productivity： An International Panel Smooth Transition Approach［R］． Document de Recherche du Laboratoire d'Économie d'Orléans，2006．

Färe R.， Grosskopf S.， Norris M.， Zhang Z.. Productivity Growth， Technical Progress， and Efficiency Change in Industrialized Countries［ J］． American Economic Review， 1994（1）：66 ～ 83．

González A.， Teräsvirta T.， Dijk D.V.. Panel Smooth Transition Regression Models［R］． SSE/EFI Working Paper Series in Economics and Finance，2005．

Hansen B. E.. Threshold Effects in Non-dynamic Panels： Estimation， Tes-ting and Inference［ J］． Journal of Econometrics，1999（2）：345 ～ 368．

Luukkonen R.， Saikkonen P.， Teräsvirta T.. Testing Linearity Against Smooth Transition Autoregression［ J］． Biometrika，1988（3）：491 ～ 499．

Philippon T.. The Fintech Opportunity［R］． National Bureau of Economic Research Working Paper，2016．