杠杆的动态变化分析题型归类

类型题一：杠杆静止型动态变化类

【解题策略】首先明确杠杆处于静止状态时，阻力、阻力臂和动力臂三个量中哪些量不变；然后分析直接变量如何变化；最后根据杠杆平衡条件[F1l1=F2l2]判断动力的变化。注意：①此类题通常还有两种细分类型，即阻力和阻力臂不变型、阻力移动型，对于阻力移动型，阻力和动力臂不变，变化的是阻力臂；②力的作用点与支点的连线为最大力臂。

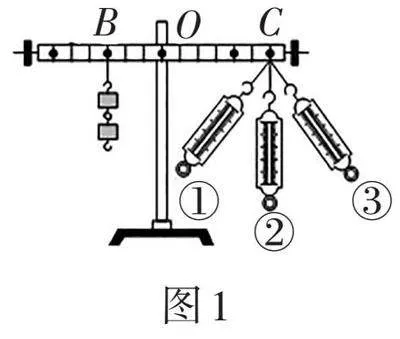
例1 如图1是小明探究“杠杆平衡条件”的实验装置，实验中杠杆始终处于水平平衡状态。若在C处逐渐改变弹簧测力计拉力的方向，依次为①→②→③，则拉力的变化情况是（ ）。

A. 先变小后变大" B. 先变大后变小

C. 逐渐变大" " " D. 保持不变

答案：A

类型题二：杠杆匀速转动常规型动态变化类

【解题策略】首先明确杠杆处于匀速转动时，阻力、阻力臂和动力臂三个量中哪些量不变；然后化动为静，分别作出初、末两状态时的力臂，并比较二者大小变化情况；最后根据杠杆平衡条件[F1l1=F2l2]判断动力的变化。注意：①杠杆转动到竖直位置时，阻力臂为零，杠杆转动到水平位置时，阻力臂最大；②若动力方向时刻与杠杆垂直，则动力臂不变；③若杠杆没有悬挂物体，则杠杆自重提供阻力。

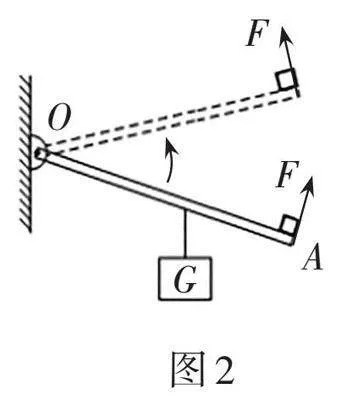
例2 如图2所示，轻质杠杆OA某处悬挂一重G = 60 N的物体，在A端施加一个始终与轻质杠杆垂直的拉力F，当杠杆由图中实线位置匀速转动到虚线位置时，则拉力F（ ）。

A. 一直增大" " " " " B. 一直减小

C. 先增大后减小 " " D. 先减小后增大

答案：C

类型题三：杠杆匀速转动特殊型——动力臂和阻力臂的比值不变

【解题策略】此类题的显著特点是：在杠杆匀速转动的过程中，动力作用线与阻力作用线时刻保持平行，且二者大小变化趋势是一致的，即同时增大或同时减小。解法如下：首先明确阻力是不变量；然后化静为动，分别作出初、末两状态的动力臂和阻力臂，通过相似三角形找寻力臂之比的变化规律；最后根据杠杆的平衡条件[F1l1=F2l2]分析动力F的变化规律。注意：杠杆在匀速转动时，若动力臂和阻力臂之比保持不变，则动力与阻力之比也不变。

例3 如图3所示，用方向不变的力F，将杠杆从A位置匀速提升到B位置的过程中，F的大小变化情况有（ ）。

A. 逐渐变大 B. 逐渐变小

C. 保持不变 D. 无法判定

解析：如图4所示，将杠杆从A位置匀速提升到B位置的过程中，阻力不变，动力臂和阻力臂均减小。杠杆在A位置时动力臂为OA，阻力臂为OC。因为杠杆平衡，所以可列等式F × OA = G × OC，即[F=G × OCOA]；杠杆在B位置时，OA'为动力臂，OC'为阻力臂，因为杠杆平衡，可列等式F × OA′ = G × OC′，即[F=G × OC'OA']。又因为" △OC′D ∽ △OA′B，推出[OC'OA'=ODOB=OCOA]。因此将杠杆从A位置匀速提到B位置的过程中，力F的大小不变。答案：C。

类型题四：生活中的杠杆模型类动态变化类

【解题策略】首先构建杠杆模型，明确动力和阻力；然后分析力臂变化情况；最后根据杠杆平衡条件[F1l1=F2l2]判断动力的变化。注意：若是分析生活中的杠杆静止型动态变化类，则化静为动，先找杠杆的支点，然后再根据以上步骤分析解答。

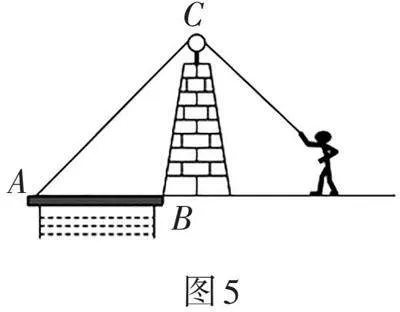
例4 在我国古代，简单机械就有了许多巧妙的应用，护城河上安装的吊桥装置就是一个例子，如图5所示。在拉起吊桥的过程中，吊桥可看作杠杆，其支点为 " " （选填“A”“B”或“C”）点；从图示位置开始缓慢拉起吊桥的过程中，在刚开始的一小段时间内绳子的拉力 （选填“变大”“变小”或“不变”）。

解析：在拉起吊桥的过程中，吊桥可看作杠杆，绕着B点转动，因而其支点为B点，绳子在A点的拉力为动力，阻力为吊桥受到的重力。从图示位置开始缓慢拉起吊桥的过程中，吊桥的重心在中点，重力的方向是竖直向下的，在拉起吊桥的过程中，从支点O到重力的作用线的距离变小，即阻力臂变小。根据杠杆平衡条件，阻力不变，阻力臂变小而动力臂变大，则动力变小，即在刚开始的一小段时间内绳子的拉力变小。答案：B；变小。

（作者单位：山东省枣庄市薛城区教学研究中心）