基于渗流场-应力场耦合作用的基坑土体变形特性研究

摘 要：对渗流场-应力场耦合理论及耦合作用下土体固结特性进行分析，建立耦合作用下有限元方程及有限元模型。从理论联系实际的角度出发，利用岩土有限元分析软件PLAXIS对某采用复合土钉支护方案的基坑工程进行有限元模拟分析，分别建立不考虑渗流场影响及考虑渗流场-应力场耦合作用的2种计算模型，模拟分步开挖时复合土钉支护结构下基坑土体变形特性，并对2种模型计算结果进行对比分析，通过模拟结果与现场实测数据的对比，结果表明耦合作用下的基坑土体变形计算值与现场实测值较为一致。说明考虑渗流场-应力场耦合作用下的有限元数值模拟方法是可行的，计算结果是合理的，对类似工程具有一定的指导意义。

关键词：渗流场；应力场；耦合；有限元；复合土钉

中图分类号：TU753 文献标志码：A 文章编号：2095-2945（2024）24-0058-05

Abstract： The coupling theory of seepage field and stress field and the consolidation characteristics of soil under coupling are analyzed， and the finite element equation and finite element model under coupling are established. From the point of view of combining theory with practice， the finite element simulation analysis of a foundation pit with composite soil nailing is carried out by using geotechnical finite element analysis software PLAXIS. Two calculation models without considering the influence of seepage field and considering the coupling effect of seepage field and stress field are established respectively， and the soil deformation characteristics of foundation pit under composite soil nailing structure during step-by-step excavation are simulated. The calculation results of the two models are compared and vqMW7+o/vhLmRw02y6Pv+Y4YdehuWePq4RH+jslRc80=analyzed. The simulation results are compared with the field measured data. The results show that the calculated value of foundation pit soil deformation under the coupling action is consistent with the field measured value. It is shown that the finite element numerical simulation method considering the coupling of seepage field and stress field is feasible， the calculation results are reasonable， and has a certain guiding significance for similar projects.

Keywords： seepage field; stress field; coupling; finite element method; composite soil nail

工程建设领域内基坑工程越来越多，但是，从研究现状看，对于基坑工程的研究大多停留在对应力与土体变形的分析上。由于渗流场的复杂性，目前进行基坑支护方案设计时普遍忽略渗流场的影响，或者只进行水土分算处理，并未考虑渗流场与应力场的耦合作用。因此，研究渗流场-应力场耦合作用的基坑土体变形特性研究，具有一定的理论和实践意义。

1 渗流场-应力场耦合理论研究现状

岩土工程是多种作用（如渗流场、应力场等）交织的领域，耦合作用即这种多种作用联合在一起的现象[1]。Tsang C. F.对这些耦合作用进行了归纳与分类，总结出了4种典型的耦合作用：水力学和力学（HM）；水力学、力学和化学（HMC）；热学、水力学和力学（THM）；热学、力学、水力学和化学（TMHC）。在岩土工程当中对工程质量影响最大的是渗流场与应力场的耦合作用，即Tsang C F四大耦合分类当中的水力学和力学的耦合作用[2]。渗流场与应力场耦合又可以根据岩土体介质的特性分为2类：①等效连续介质；②裂隙孔隙介质。

渗流场与应力场耦合作用下的土体变形又可称为土体固结。1925年美籍奥地利土力学家泰尔扎吉（Terzaghi）提出了有效应力理论，由此奠定了现代土力学的基础，并在有效应力理论的基础上提出了土体固结理论。Terzaghi固结理论又被称为一维固结理论，这是因为在这一理论当中，Terzaghi假定渗流只在竖直方向运动且土体变形只在竖直方向发生。然而，经过后续科学家的研究发现，土体固结是一个复杂的空间三维问题，一维固结理论具有很大的局限性，理论推导与实际情况存在较大差异。1936年Rendulic在Terzaghi理论的基础上，考虑到渗流的空间三维特性，提出了Terzaghi-Rendulic理论，即目前耦合分析研究中比较常用的准三维固结理论。1941年Biot在考虑孔隙水压力损失函数时，改善了Terzaghi-Rendulic理论，得到了Biot固结理论即真三维固结理论。

李培超等[3-4]在渗流力学的基础上提出了适用于多孔介质的有效应力原理，弥补了Terzaghi有效应力原理的不足。王媛[5]在Biot理论的基础上提出了以结点位移和孔隙水压力为未知量的渗流场与应力场耦合的计算方法。

2 渗流场-应力场耦合理论

渗流场-应力场耦合问题可以按照围岩材料确定性本构模型的力学特征，可将其分类为：弹性耦合理论、黏弹性耦合理论、弹塑性耦合理论和弹黏塑性耦合理论[3]。

1）弹性耦合理论。弹性耦合理论假设微分控制方程是关于孔隙比及有效应力的函数，其中土骨架被设定为连续弹性介质，符合胡克定律。

2）黏弹性耦合理论。黏弹性耦合理论假设含水层底部总应力保持不变，并且只有在土壤骨架的垂直方向上产生弹性变形，固结速率与残余次固结量存在一定的函数关系。

3）弹塑性耦合理论：在弹性耦合理论的基础上，假设满足介质塑性屈服准则。

4）弹黏塑性耦合理论：在弹塑性耦合分析的基础上，加入时间因素。

3 工程案例分析

3.1 工程概况

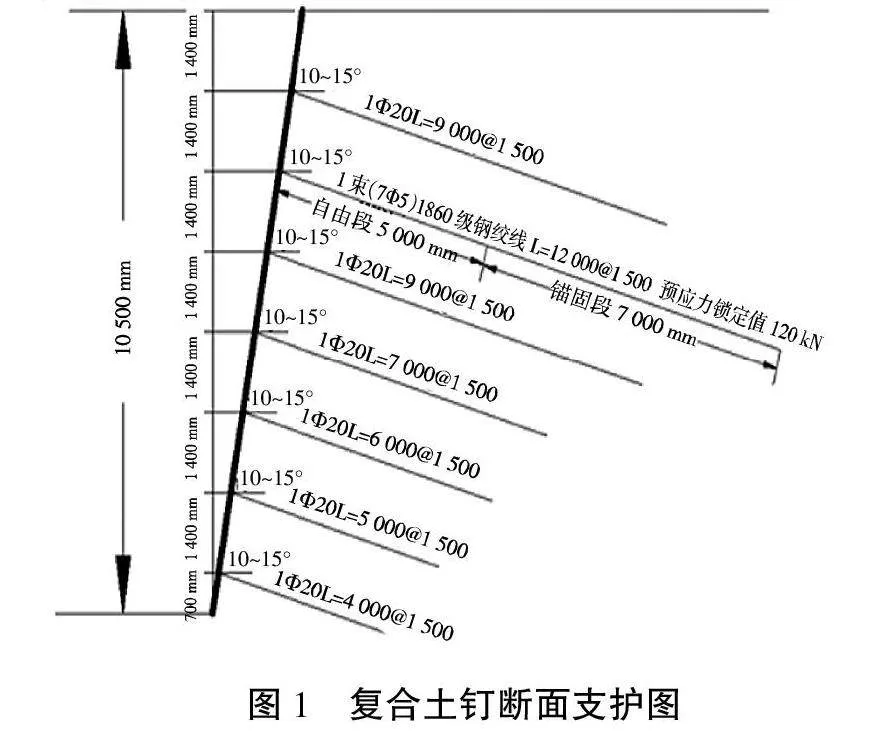
某基坑工程由主楼与地下车库连成一体。建筑基坑面积约6 400 m2，基坑开挖深度10.5 m，基坑平面尺寸约80 m×80 m，基坑周长约320 m。拟建场地周边建筑物距离建筑物基础外皮均在20 m以外。该剖面位于工程南部，设计采用复合土钉支护方案。复合土钉支护深度10.5 m；放坡系数1∶0.2；土钉孔直径100 mm，横向间距1.5 m，锚杆孔直径150 mm，垂直间距1.40 m，土钉采用注浆式土钉。具体复合土钉布置如图1所示。

3.2 计算模型建立

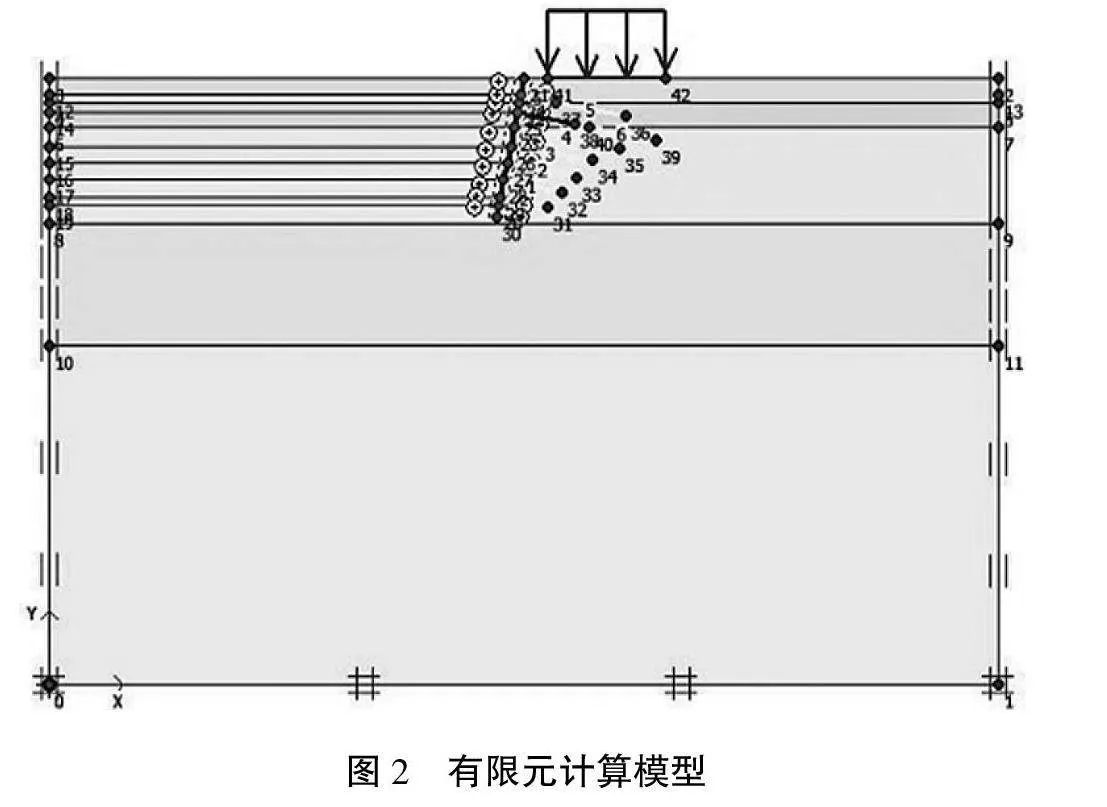
基坑开挖深度10.5 m，分7次开挖；每步开挖深度分别为1.4、1.4、1.4、1.4、1.4、1.5、3.0 m。基坑PLAXIS计算模型尺寸为80 m×50 m，建立模型如图2所示。计算模型中地层共分为5层：填土层、粉质黏土层、圆砾层、卵石层及强风化砾岩层，层厚分别为1.8、1.0、9.2、10、28 m。

本文进行有限元数值模拟之前，对计算模型作如下假定：①降水阶段土体的应力-应变关系符合弹性应力-应变关系，且土骨架不可压缩；②土体各向同性；③地下水渗流运动规律符合达西定律；④按平面应变问题考虑。

3.3 有限元模型建立

根据勘察报告，基坑剖面所在地层共分为5层：填土层、粉质黏土层、圆砾层、卵石层及强风化砾岩层，层厚分别为1.8、1.0、9.2、10、28 m。运用PLAXIS建立模型如图2所示。

3.4 参数选取

3.4.1 土体参数选取

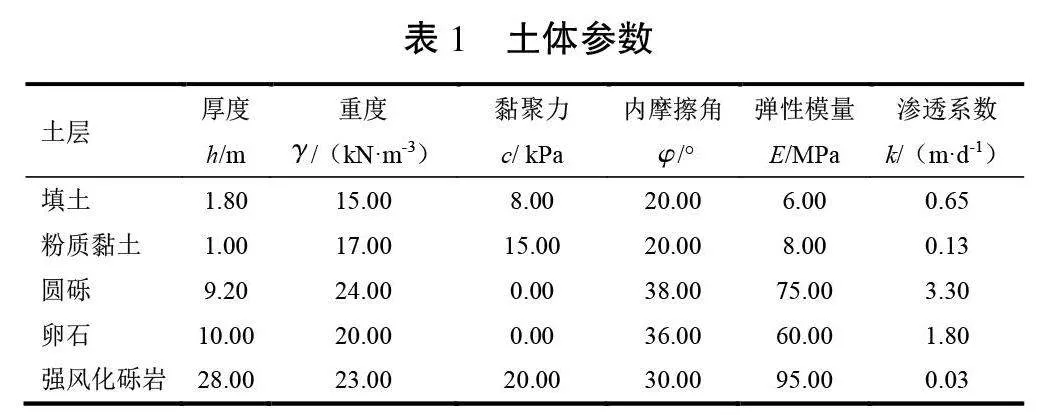
土体参数见表1。

3.4.2 材料参数

1）土钉参数：弹性模量EA=9.8×104 kN/m，钻孔直径120 mm，钢筋直径20 mm，土钉为弹性材料且仅承受拉力。

2）锚杆参数：轴向刚度EA=1.23×105 kN/m，钻孔直径150 mm，预应力120 kN。

3）面板参数：法向刚度EA=3×107 kN/m，抗弯刚度EA=2.5×103 kN·m2/m，密度＝2.5×103 kN/m3，泊松比＝0.2，厚度h=0.1 m。

3.5 数值模拟计算结果与分析

3.5.1 基坑土体位移分析

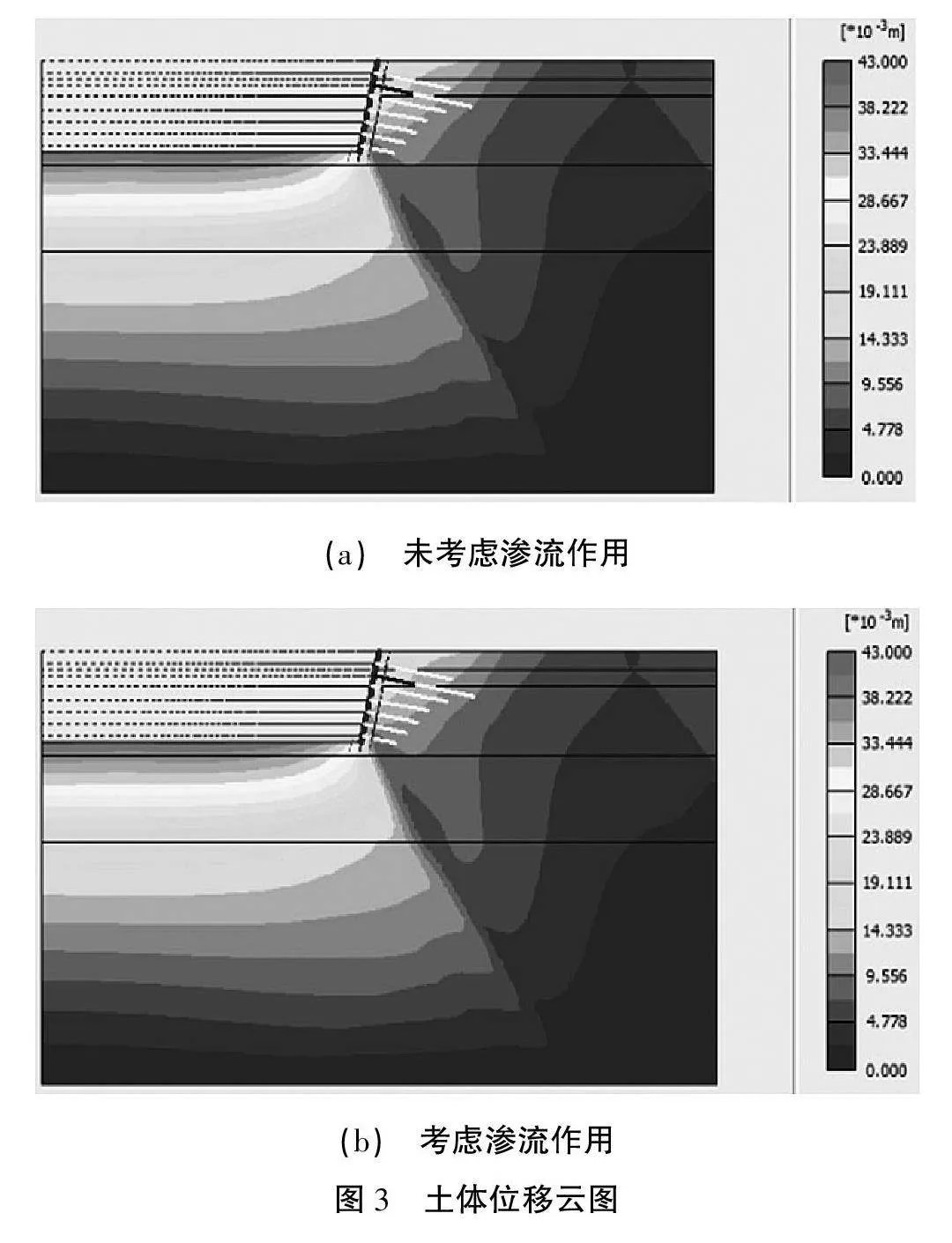
基坑分步开挖结完obUqFh1McSkd7FStbwewaQ==成后，土体位移云图如图3所示。

基坑分步开挖完成后，土体位移矢量图如图4所示。

对比渗流场、应力场耦合作用土体位移云图及位移矢量图进行分析，可以得出以下规律。

1）随着基坑逐步开挖，基坑整体位移场的影响范围也逐步加大，且位移量也随之不断增大，这与前面模型中土体位移规律是一致的。

2）坑后土体位移总体趋势向下，坑底土体位移总体趋势向上，渗流场耦合前后这一土体位移规律并未出现变化。

3）渗流场、应力场耦合作用下，基坑坑后土体的位移量较耦合之前出现明显的增大，而坑底隆起量明显减小，这是由于基坑在降水过程中产生的土体固结作用引起的。

4）渗流场、应力场耦合前后土体最大位移分别为43、30 mm，土体均未产生很大变形，说明复合土钉支护结构对基坑坑壁周围土体的变形起到了比较理想的约束作用。

5）基坑底部土体位移量在坑壁周围要明显小于坑底其他部位，但坑底以下土体随着深度的加深，支护结构对土体变形的影响逐渐减弱，土体变形差异逐渐增大。

3.5.2 水平位移分析

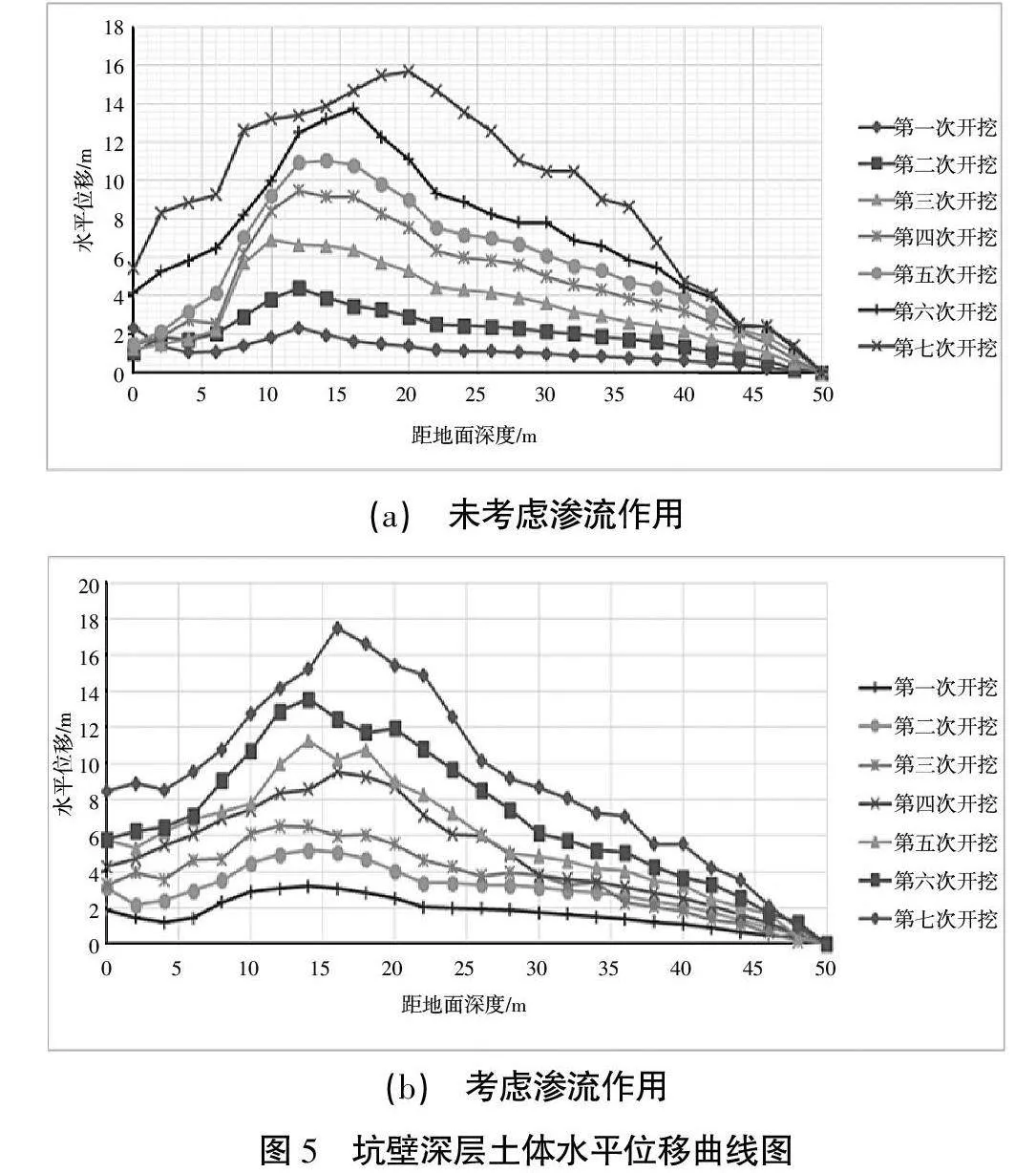
基坑开挖坑壁深层土体水平位移的曲线图如图5所示。

水平位移是最能反映基坑坑壁安全状态的指标，对比渗流场、应力场耦合前后的坑壁深层土体水平位移的曲线图，可得出如下结论。

1）耦合前后基坑坑壁的变形特征是相同的，基本呈现出向基坑开挖一侧的“鼓出”现象。

2）基坑坑壁同一位置土体的水平位移，随着基坑开挖深度的增加而不断增大。

3）基坑坑壁水平位移整体较小，但在进行渗流场-应力场耦合分析之后较耦合之前略有增加。开挖结束时坑壁最大水平位移出现在基坑坡脚，最大水平位移为15 mm。复合土钉支护结构对上层土体即基坑坑壁的水平变形起到了很好的约束作用。

4）基坑开挖各步坑壁轴线土体最大水平位移值随着基坑开挖的进行不断增大，且土体最大水平位移出现位置不断加深。坑壁轴线土体最大水平位移位置均位于开挖底面以下4～8 m处，远离了坑壁及坡脚，基坑整体稳定性得到了很大提高。

3.5.3 竖直位移分析

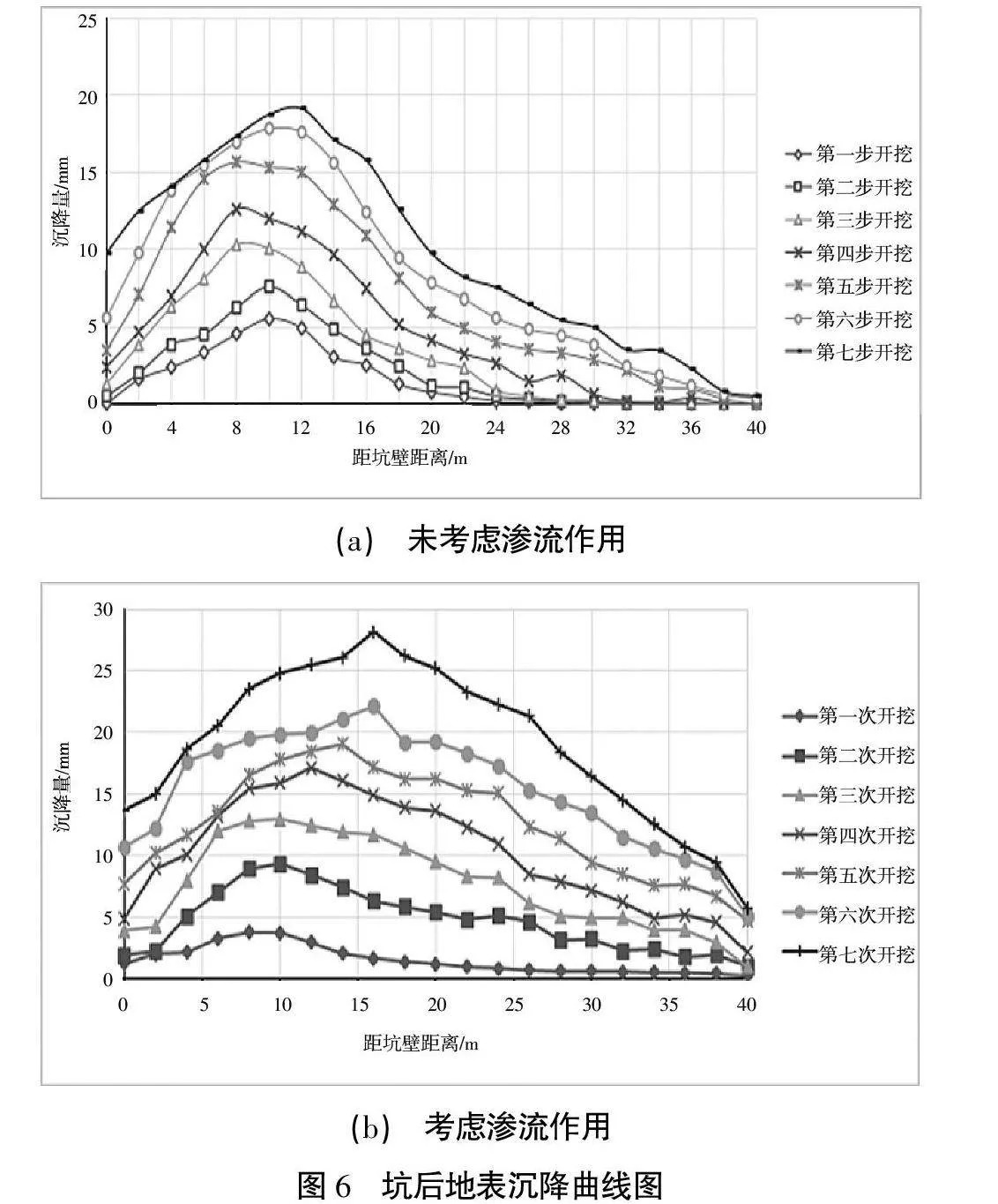
根据数值模拟结果分析，坑后地表沉降及坑底土体隆起曲线图如图6所示。

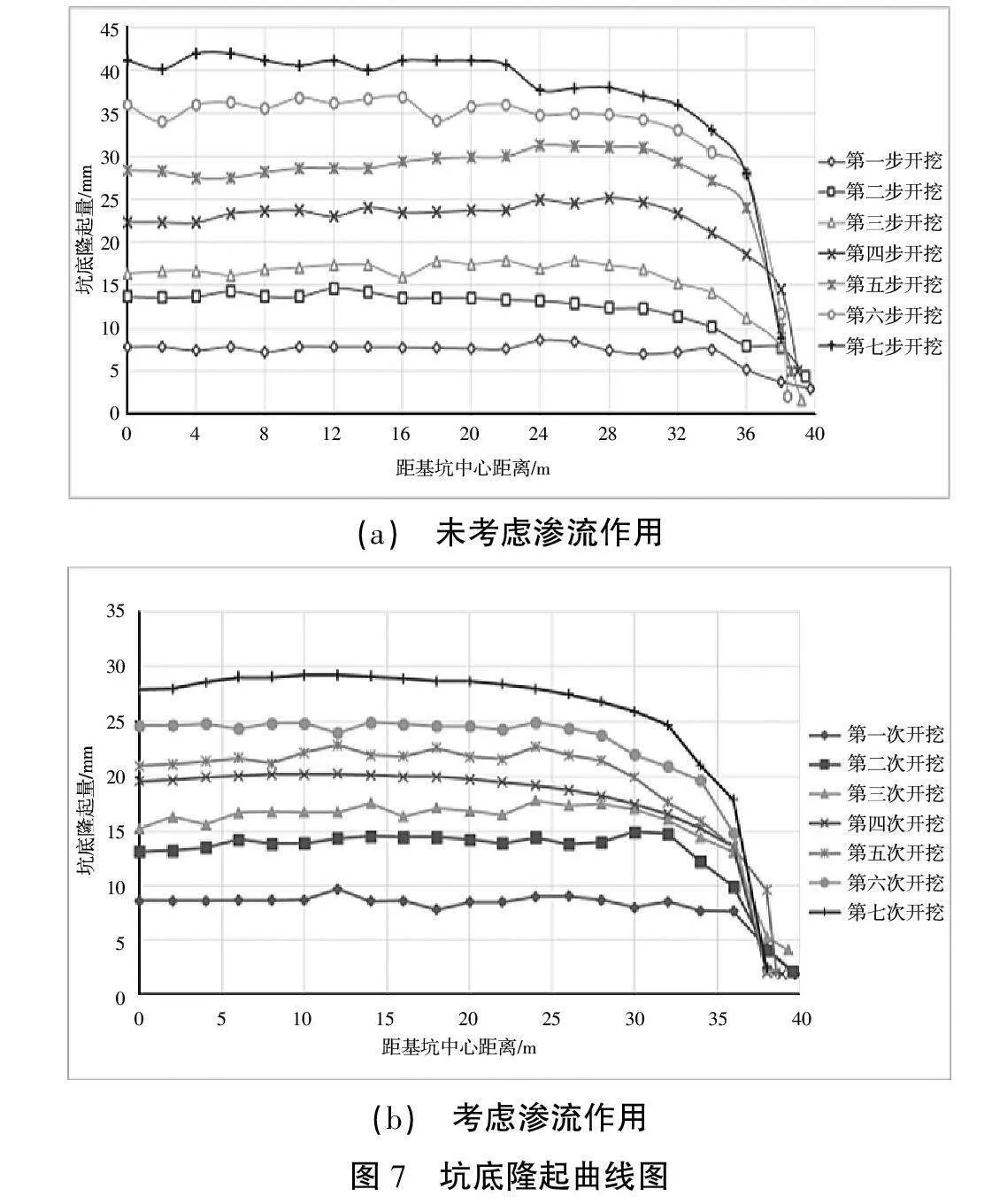
坑底土体隆起曲线图，如图7所示。

对渗流场、应力场耦合作用前后下基坑开挖各步坑后地表沉降及坑底隆起曲线进行对比分析，可得出如下结论。

1）耦合前后，坑底土体的隆起以及坑后地表的沉降量随着开挖的进行逐渐增大的变化规律是一致的。

2）距基坑坑壁5 m之外的区域坑底土体隆起位移较大，基坑坡脚处位移量较小，坑后5～10 m的范围内土体的沉降变形较大，基坑边缘土体变形量较小，可见在耦合前后复合土钉支护结构均很好地控制了坑壁周围土体的变形。

3）基坑开挖和工程施工，大幅降低基坑及周边地下水位，土体产生固结沉降，地表土体沉降量较耦合之前有较明显的增大，而土体固结压密作用使得坑底土体变形量一定程度减小。

4）由于基坑采用坑外管井降水，地下水位呈漏斗状，降水对地表沉降产生的影响也总体体现为沿远离坑壁的方向变化幅度逐渐减小。但由于支护结构的作用，土体最大位移发生的位置均离坑壁较远。

3.6 数值模拟与实测值的对比分析

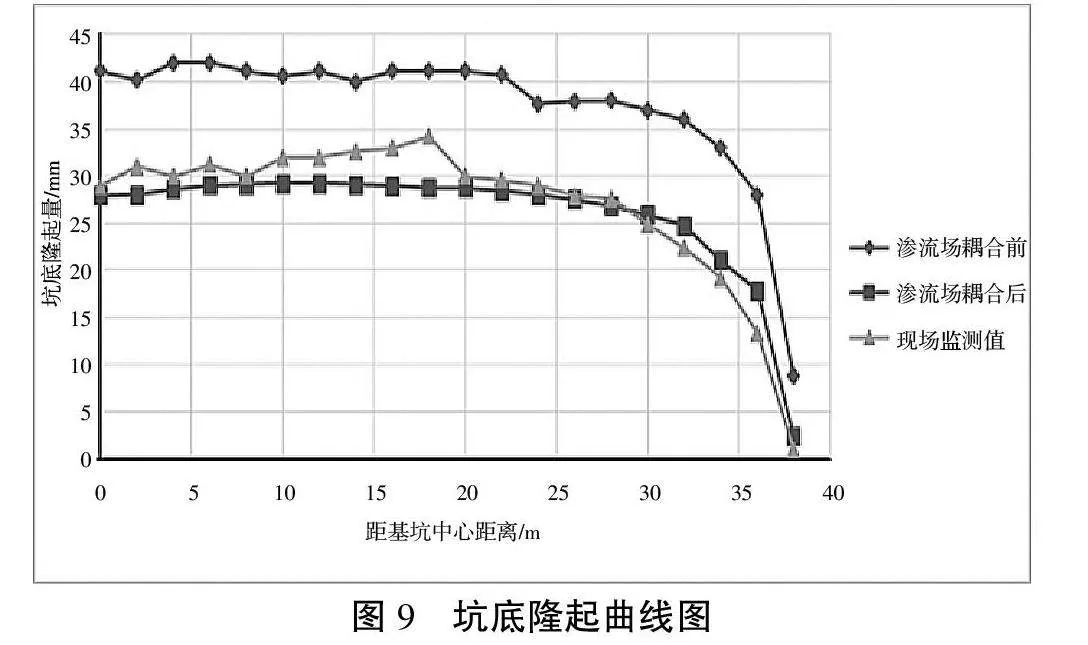
基坑开挖完成时有限元数值模拟结果与现场监测数据对比结果如图8、图9所示。

分析图8、图9可发现渗流场耦合前后基坑土体变化趋势与现场监测结果是一致的，说明有限元数值模拟可以有效地指导基坑工程设计工作。耦合之前数值模拟结果显示地表最大沉降位置发生在距坑壁10～12 m的区域，耦合之后最大沉降位置位于14～16 m的范围内，而现场监测显示最大位移发生在12～15 m的区域，耦合前后结果与现场结果对比均存在一定的误差，但耦合之后误差远小于耦合之前。分析图8与图9可以发现，渗流场耦合之后模拟结果曲线与现场监测数据所得曲线极为接近，而耦合之前的结果与现场实测数据具有比较大的出入，说明渗流场-应力场耦合作用下的数值模拟结果更符合实际工程。

4 结论

本文运用岩土软件PLAXIS对某基坑工程进行了有限元数值模拟计算，分别建立了不考虑渗流场影响及考虑渗流场-应力场耦合作用的2种有限元模型，对比2种模型数值模拟结果，可得到以下结论。

1）随着基坑分步开挖的进行，土体变形影响范围逐步加大，且土体变形量也随开挖的进行不断增大。

2）基坑坑壁变形趋势以水平为主，基本呈现出向基坑开挖一侧“鼓出”的趋势。

3）基坑开挖过程中，坑后土体位移总体趋势向下，宏观表现为地表沉降；坑底土体位移整体趋势向上，表现为坑底隆起。

4）考虑渗流场-应力场耦合作用下的数值模拟计算结果与现场实测值较为接近，说明本文所采用的计算方法是可行的，模拟结果是可靠的。

参考文献：

[1] 曹书文，杨璐，孔涛涛，等.基坑降水对支护结构和地面沉降影响的有限元分析[J].建筑科学，2011，27（9）：37-40.

[2] LUBINSKI.Theory of elastieity for porous bodies dislaying a strong pore strueture[J].Proe.U.S.Natinnal Congress of Applied Meehanies，1954.

[3] 李培超，孔祥言，卢德唐.饱和多孔介质流固耦合渗流的数学模型[J].水动力学研究与进展（A辑），2003（4）：419-426.

[4] 李培超，孔祥言，李传亮，等.地下各种压力之间关系式的修正[J].岩石力学与工程学报，2002（10）：1551-1553.

[5] 王媛.多孔介质渗流与应力的耦合计算方法[J].工程勘察，1995（2）：33-37.