NURBS体参数化模型的无支撑打印算法

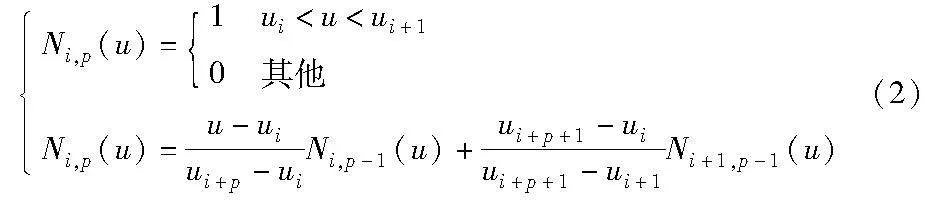
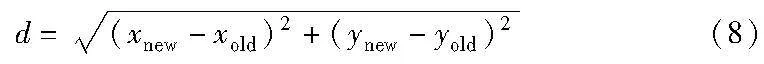
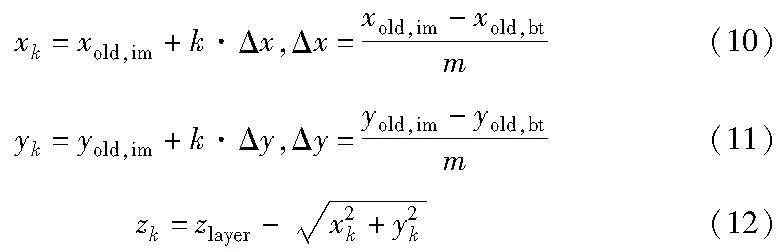
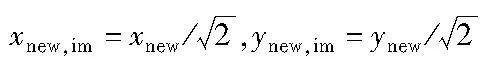
摘 要：处理大角度悬垂结构的打印问题是无支撑打印的主要挑战。针对NURBS（non-uniform rational B-spline）体参数化模型的多自由度无支撑三维打印技术，提出一种锥形切片算法。通过对模型的三维文件进行几何映射，利用水平切片算法对其进行切片，得到模型变形后的连续打印路径G-code；然后对得到的G-code进行逆映射，生成适用于六轴机械臂的多自由度连续打印路径。利用锥形切片算法规划打印路径，可以在无须支撑的情况下，依靠自支撑结构实现对悬空结构部分的打印。最后，通过仿真实验和对比实验，验证了锥形切片算法的准确性、可行性和有效性。锥形切片算法的引入为NURBS体参数化模型的无支撑三维打印提供了一种更加高效、经济和环保的解决方案。

关键词：NURBS体参数化； 无支撑打印； 锥形切片； 几何映射； 六轴机械臂

中图分类号：TP391.9 文献标志码：A 文章编号：1001-3695（2024）07-030-2141-06

doi：10.19734/j.issn.1001-3695.2023.10.0535

Unsupported printing algorithm of NURBS volume parametric mode

Abstract：Achieving unsupported 3D printing still faces challenges in handling large-angle overhangs and improving printing precision. This paper presented a cone slicing algorithm for multi-freedom unsupported 3D printing of NURBS volume parametric models. Though the geometric mapping of the 3D model file of the model， it applied a horizontal slicing algorithm to this mapped model， resulting in a continuous print path G-code of the deformed model. This G-code was then subjected to inverse mapping， generating multi-degree-of-freedom continuous printing paths suitable for six-axis robotic arms. Utilizing the conical slicing algorithm to plan printing paths enabled printing of overhanging structures without the need for support. It validates the accuracy， feasibility， and effectiveness of the conical slicing algorithm through simulation experiments and comparative trials. The introduction of the conical slicing algorithm offers a more efficient， economical， and green solution for unsupported 3D printing of NURBS-based parametric models.

Key words：NURBS volume parameterization; unsupported printing; conical slicing; geometric transformation; six-axis robotic ARM

0 引言

非均匀有理B样条（NURBS）是计算机辅助设计（CAD）中表示对象的事实标准［1］。增材制造（AM）的输入数据为CAD模型，而CAD模型主要采用NURBS曲面作为边界表示。NURBS以数据交换格式（如初始图形交换规范IGES、STEP）为基础，允许在计算机辅助设计（CAD）与计算机辅助制造（CAM）系统或几何库之间进行精确的数据传输。此外，基于权值和控制点的NURBS不仅可以准确地表达几何形状，还能够表达解析形式［2］。通过在CAD系统中生成准确的NURBS模型，并将其多边形近似值引入到适用于多轴机械臂的多自由度打印工艺中，极大地增强了增材制造路径规范的灵活性［3］。

增材制造技术是一种基于现代CAD/CAM技术、激光技术、计算机数控技术、精密伺服驱动技术以及新材料技术的先进制造方法［4］。该技术已在生物技术、航空航天、电子、建筑、医药等多个领域广泛应用［5，6］。增材制造技术可以直接从CAD数据模型生成三维产品模型，通常采用分层制造逐层叠加的方法进行材料堆积制造［7，8］。当前，已有多项相关研究将NURBS体参数化模型成功应用于增材制造领域，其中包括切片算法、支撑点的求解 ［9］以及生成非均匀NURBS体参数化模型的三维打印通用AMF（additive manufacturing file format）文件［10］等研究。

具有悬垂结构的模型的无支撑打印是增材制造3D打印中的难点。传统的熔融沉积成型（fused deposition modeling，FDM）三轴3D打印工艺通常需要使用支撑结构来实现成型［11，12］，同时也带来了一系列的问题，例如制造成本的增加、后期人工处理的烦琐以及材料浪费。在无支撑的情况下，悬空部分的稳定性是一个关键问题。这些部分容易变形、下垂或坍塌，因此，如何确保打印头能够准确地定位并在不添加支撑的情况下完成打印是一个挑战［13］。在这一背景下，对无支撑打印技术的深入研究是一个亟待解决的问题。通过研究无支撑打印技术，可以更好地满足不同行业对于精细、复杂结构的需求，促进3D打印技术朝着更加智能化的方向发展［14，15］。由于机械臂具备高自由度和灵活的运动轨迹，能够构建空间中的任意无干涉曲线。所以将机械臂技术与3D打印工艺相融合，可以突破传统3D打印工艺在成型复杂度方面的限制，实现对多方向复杂曲面的无支撑一体化成型［16，17］。

FDM是一种层层堆叠的制造过程。在面对存在悬垂结构的模型时，因其水平切片算法和Z轴垂直堆叠的特性，所以在无支撑情况下打印具有悬垂结构的模型时会出现坍塌的情况。因此，需要设计一种高效的切片算法来规划打印路径，以实现无支撑打印。近年来，为了突破传统的“2.5D 打印”限制［18］，国内外学者纷纷进行了机械臂3D打印及无支撑曲面打印切片算法的研究。例如：Wüthrich等人［19］提出一种非平面切片算法，可以通过改变喷头打印方向来实现一定悬垂角度的无支撑打印，但是该算法无法解决大悬垂模型的无支撑打印问题；Allen等人［20］提出了一种具有Z值可逆性的打印方法，通过在三轴打印机上动态调整Z值，实现曲面路径的生成，但该方法仅适用于三自由度打印机，并且模型的悬垂部分仍需要支撑；Chen等人［21］提出了一种适用于薄壳结构的弯曲层路径规划方法，该方法要求事先打印与薄壳形状相匹配的模具作为支撑，然后在模具表面进行路径规划，然而，该方法的适用场景具有诸多限制，仅适用于薄壳零件的打印，没有真正解决无支撑打印问题。为此，本文提出了一种锥形切片算法。该算法通过倾斜每个打印层，使其呈现一种圆锥形状，而非传统的平行于打印平面；同时，通过调整打印喷嘴在Z轴上的旋转角度，使当前打印层附着在上一层已完成打印的部分上，形成自支撑结构。该算法在无须额外支撑的情况下可以实现大悬垂结构的无支撑打印。

综上所述，为了解决具有悬垂特征模型的无支撑打印问题，本文提出了一种基于NURBS体参数化模型的锥形切片算法。基于NURBS体参数化模型的基础理论，对模型进行等参线网格单元划分和三角网格划分；然后，对模型进行几何映射，并使用锥形切片技术生成映射后模型的连续打印路径G-code；最后，对生成的G-code进行逆映射，以获得原始模型的多轴机械臂多自由度无支撑连续打印路径。

1 NURBS体参数化模型定义和网格划分

1.1 NURBS体参数化模型定义

三维几何空间中NURBS体参数化模型的参数方程具体表达式为

其中：Pi，j，k为控制点；ωi，j，k为权因子；Ni，p（u）、Nj，q（v）、Nk，r（w）是分别定义在节点矢量空间U、V、W上的NURBS基函数，其阶数分别为p、q、r。U、V、W的节点矢量空间为

NURBS在U方向上的基函数表达式为

NURBS在V、W方向上的基函数定义与U方向上的类似。

1.2 等参线网格单元划分

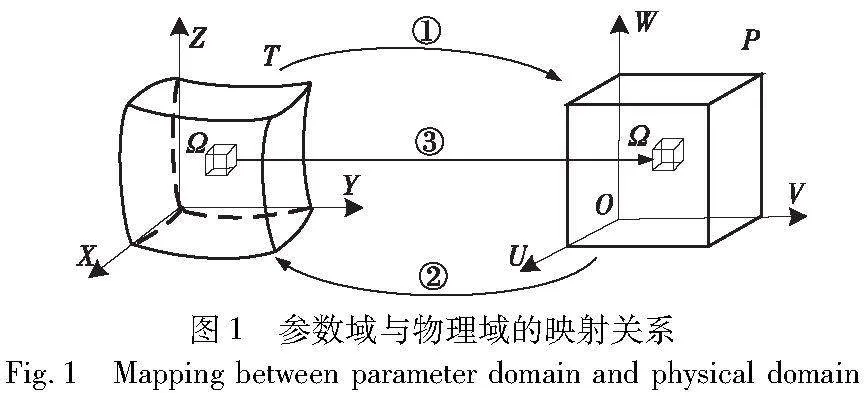
NURBS体参数化模型通过三变量张量体参数化模型T与规则的立方体P建立一一映射关系［10］。如图1所示，T是指在（X，Y，Z）三维坐标中具有物理域边界的三维模型，P是指在正交参数域坐标（U，V，W）中构建的立方体。其中：①②为物理域与参数域之间的映射关系，③为物理域在参数域相对应的单元。

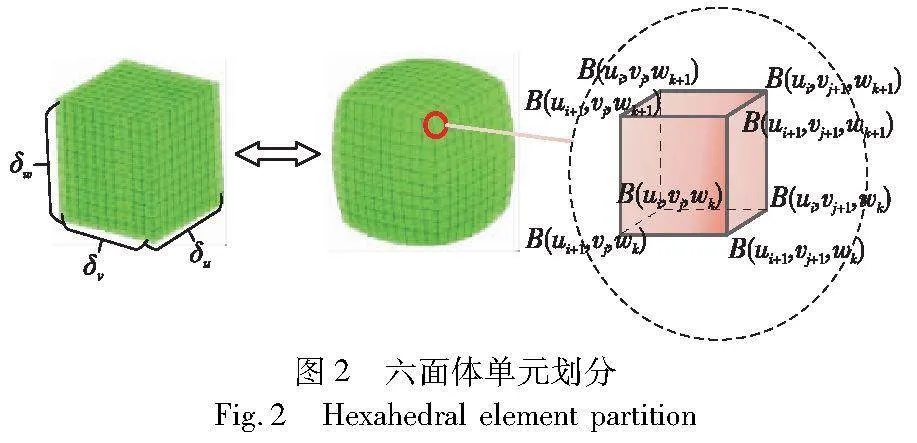
在参数域u、v、w三个参数方向上，将节点矢量空间U、V、W分别细分为 δu、δv、δw等份，得到等参数线网格单元。相应地，在物理域中，通过在三变量张量方向上进行细分，可以获得六面体单元，如图2所示。

当δu、δv、δw的细分次数足够大时，等参线网格单元可被视为规则的六面体结构，其在物理域中的八个顶点分别为B（ui，vj，wk）、B（ui+1，vj，wk）、B（ui，vj+1，wk）、B（ui，vj，wk+1）、B（ui+1，vj+1，wk）、B（ui，vj+1，wk+1）、B（ui+1，vj，wk+1）、B（ui+1，vj+1，wk+1）。等参线网格单元的数量K的计算方法如式（3）所示，其中K（u）、K（v）、K（w）分别为u、v、w三个参数方向的细分次数。

K=K（u）·K（v）·K（w）（3）

1.3 三角形网格划分

标准三角语言（standard triangle language，STL）是三维模型用于增材制造的主要文件格式，其主要通过三角形网格来拟合三维实体的外表面。因此在对模型进行等参线网格单元划分后，还需要进行三角形网格划分。

根据等参线网格单元的六面体单元结构，其每个表面皆可划分出两个三角形。通过连接参数域的正方形对角线划分出两个直角三角形，对应的物理域就可获得两个NURBS曲面三角形。图3为NURBS曲面的三角形网格划分，左侧为物理域划分，右侧为对应的参数域划分。

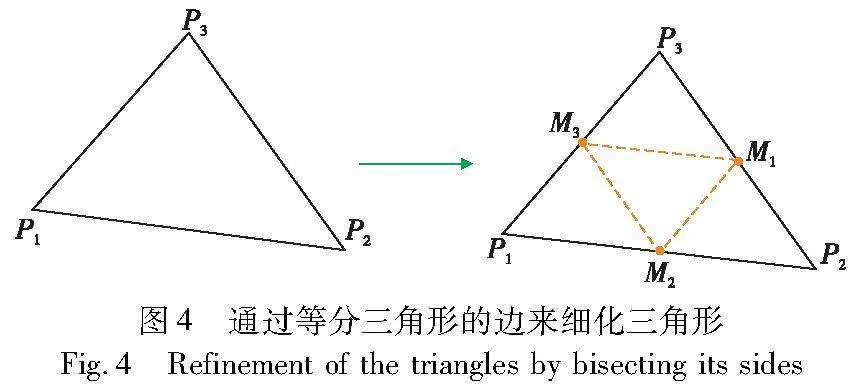
当u、v、w三个参数方向的细分次数足够多时，划分的三角形网格可视为直线三角形。随着细分次数的增多，划分的三角形网格也会增多。目前有很多不同的方法来细化三角形，其中最便捷的是将每个三角形的边进行等分，然后把3个新生成的中点连接起来，这样1个三角形可以产生4个更小的三角形，如图4所示。同时，1个六面体单元可以划分为5个相同大小的四面体。

模型划分的三角形网格数量和细分次数之间的关系如式（4）（5）所示。

n=K（u）+K（v）+K（w）（4）

Q=4n·N（5）

其中：Q为划分的三角形网格总数；n为在参数域u、v、w三个参数方向上细分次数总和;N为三角形网格基数。

2 锥形切片算法

2.1 锥形切片算法原理

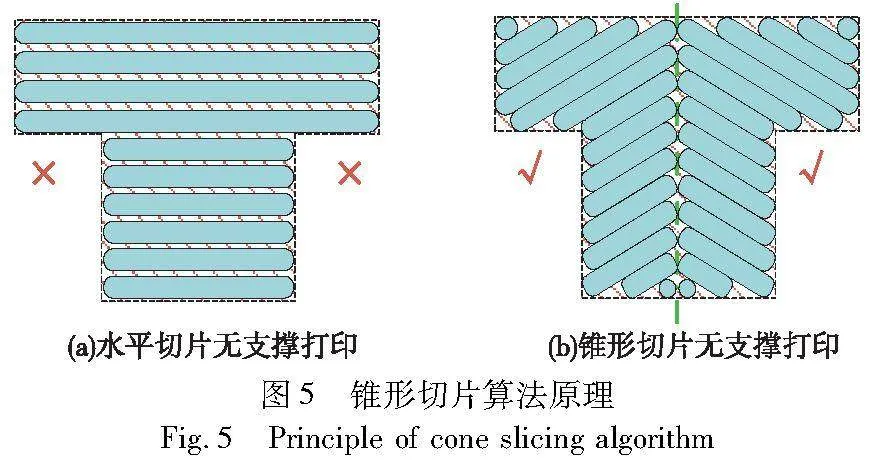
常见的FDM 3D打印机通常能够打印具有适度倾斜角度的模型，但在处理大角度倾斜或悬空部位时，必须添加支撑结构。而锥形切片算法的原理在于使每个打印层倾斜，形成一种圆锥形状，如图5所示。这种方法确保即使在打印水平悬空部位时，只有最外层的部分会悬空打印，而当前打印层的绝大部分仍然附着在周围的层上，充当支撑。通过这种方式，可以实现对悬空的复杂几何形状进行打印，而无须添加额外的支撑结构。

传统的切片软件以固定的Z值将模型水平划分为层，而锥形切片算法是利用锥形层对模型进行划分。锥形层由同心圆组成，每个圆具有不同的Z值和半径。锥形层的生成主要是通过如式（6）所示的几何映射S来完成。

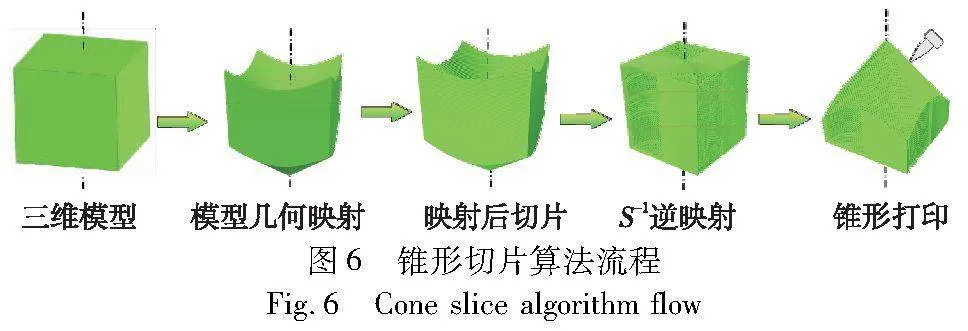
图6展示了所提出的锥形切片算法的工作流程。首先，对三维模型的三角形网格文件进行几何映射；然后，对映射后的文件进行切片；最后，使用S-1对G-code进行几何逆映射，得到多自由度连续打印路径。

2.2 模型几何映射

三维模型由三角形网格进行拟合，通过对三角形网格的所有顶点执行如式（6）所示的几何映射，完成对所有三角形网格的变换，实现模型的几何映射。图7展示了原始三维模型及其转换的示例。

三角形网格文件通过单位法线和三角形的顶点在三维笛卡尔坐标系中描述三角曲面。其通用表示定义为

在计算机图形学和计算机辅助设计领域，通常会选择边长适中的三角形网格，以在模型准确性和计算效率之间取得平衡。当三角形网格的边长小于1 mm时，几何模型的精度高，有助于提高仿真的准确性，但同时会增加顶点和面片数量，导致数据储存和计算复杂度的上升；而当边长大于2 mm时，计算量减小，但切片时可能产生伪影，严重降低打印模型的表面质量。因此，将三角形网格的边长控制在1～2 mm，能够在保证精度的前提下，提高计算效率。

将三角形网格文件存储为mesh（网格）对象。利用该对象的points、normals和vector等属性，对对象所有的点、面的法向量和三角形数组进行描述，以完成三角形网格的几何映射。具体过程如下：

a）读取三角形网格文件并将其存储为mesh对象。

b）使用vector属性提取描述对象的三角形数组。

c）通过给定次数的细化步骤来细化三角形划分。如果有N个三角形，细化步骤执行m次，则输出为4m×N。

d）对划分后的三角形网格进行几何映射。

e）将转换后的三角网格数据存储为mesh对象，并将其保存在一个新的三角网格文件中。

2.3 G-code逆映射

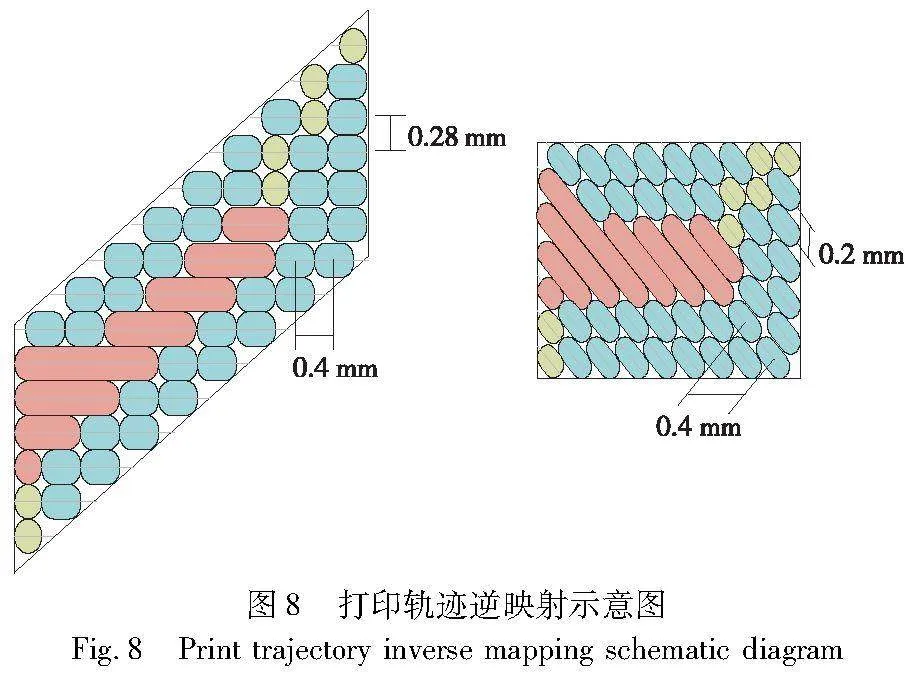
将模型进行几何映射后，对其进行水平切片，然后将生成的打印轨迹G-code进行逆映射，得到最终的锥形打印轨迹。图8为逆映射前后打印轨迹及填充的示意图，其中蓝色截面表示层打印边界周长，绿色表示可调整宽度的边界周长，红色表示打印填充（参见电子版）。

在传统的打印机设置中，新打印的层总是有很好的支撑，并且它在挤出过程中会被压平和加宽。锥形切片旨在实现无支撑打印，因此打印层不会加宽，挤出宽度也不会超过喷嘴的直径，以确保现挤出线层与已打印的部分有良好的连接。例如，将切层高度为0.28 mm的G-code进行逆映射，由于逆映射的特点，切层高度减小为0.2 mm的锥形层矩形距离，挤压宽度保持0.4 mm不变，这导致挤压宽度和层高度之间的比例为2∶1。两个不同层的单线之间有50%的良好重叠，这也是保证实现无支撑打印的主要原因。

G-code是打印头的一组移动指令，其中每条移动命令定义了打印头移动到的端点。因此，打印头在指令执行前的位置被定义为“旧”点，而打印头在执行后的位置被定义为“新”点。每走一步，“新”点就会变成新的“旧”点。经过逆映射后坐标值定义如下，其中经过逆映射后的值用“im”标记。

假设当前层的z坐标为zlayer，旧点坐标为xold，yold，新点坐标为xnew，ynew。

逆映射后旧点的坐标可以表示为

逆映射后新点的坐标可以表示为

逆映射的“新旧”两点之间的距离不应过大，否则会导致逆映射后打印失真。如图9（a）所示，当打印轨迹为较长线段时，喷嘴将在位置P1（“旧”点），移动到线的端点P2（“新”点）。当这条由起点和终点组成的轨迹用S-1进行逆映射后，喷头将沿着直线再次从P1到P2。然而，对于逆映射后的锥形打印轨迹，喷嘴必须在一个圆锥截面上移动，图9中用蓝色双曲线表示（参见电子版）。因此，长线条轨迹必须被分割成长度相等的小段，以达到适当的精度，如图9（b）所示。

根据式（8）计算两点之间轨迹长度：

当轨迹长度最大为lmax时，由式（9）得出分割后轨迹的数量m为

在对每一点的轨迹进行逆映射后，得到分割后打印喷嘴位置，即运动轨迹点的坐标（xk，yk，zk），如式（10）～（12）所示，其中k=0，1，…，m。

多自由度增材制造方式需要知道机械臂末端每个点的位姿信息，除了上述的x、y、z位置坐标外，还需要求得每个点的姿态信息。通过打印路径的方向计算出机械臂末端喷头的角度，使其可以垂直于打印路径。

欧拉角是一种将位姿分解为绕坐标轴的旋转角度的常见表示方式。通常，欧拉角包括绕X、Y和Z轴的旋转角度，分别称为滚转角（roll）、俯仰角（pitch）和偏航角（yaw）。已知一段打印路径中相邻的两点pi、pi+1的坐标，如图10所示，连接这两点形成段lpipi+1，这个线段视为两点之间的打印轨迹。其次过线段lpipi+1创建平面Su，使平面Su垂直于打印平台，令平面Su作为约束平面。同时定义向量Ni为喷嘴在线段lpipi+1内的欧拉角，即喷嘴打印方向，Ni在平面Su内，即与平面Su平行。然后向量Ni需要垂直于线段lpipi+1，并指向Z轴负方向，也就是与Z轴的夹角大于90°。通过使用反三角函数，可以分别计算出滚转角、俯仰角和偏航角，此时可求得向量Ni的唯一值。最后使用NURBS样条曲线对打印轨迹中每个路径点的位姿进行插值平滑计算，以消除噪声和错误路径点的影响，从而提高打印路径的鲁棒性。

3 仿真实例

本文在Anaconda Python（Python3）编程环境下开发了一套用于NURBS体参数化模型的锥形切片程序，并在RobotStudio仿真软件中验证了该切片算法在机械臂多自由度无支撑打印应用场景中的可行性。此外，为了验证锥形切片算法无支撑打印的有效性，针对具有悬垂结构的模型，设计了锥形切片算法和水平切片算法的对比实验。

3.1 仿真实验

本文采用了两个具有悬空部分的NURBS体参数化模型，这种类型的模型通常需要在传统的3D打印方式下添加支撑结构才能实现成型，如图11所示。

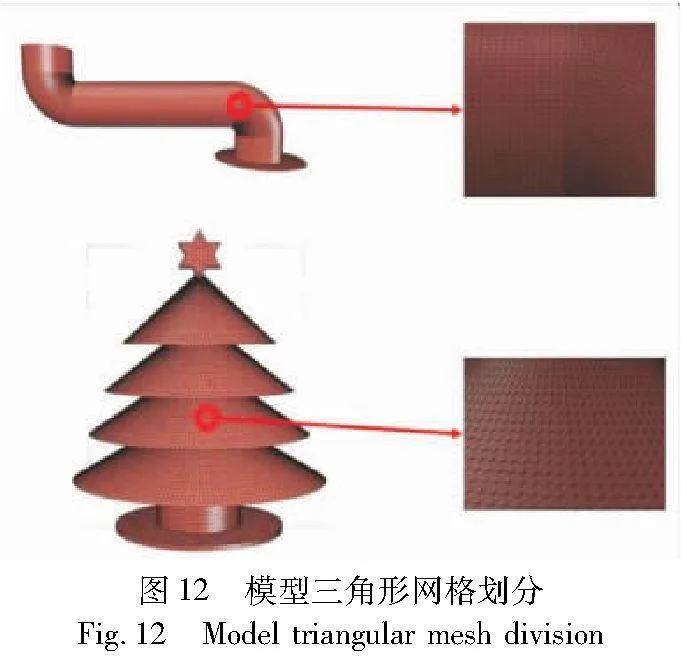
针对实验模型，采用本文提出的锥形切片算法对模型进行切片，以生成多轴机械臂的多自由度打印轨迹，在无支撑的情况下实现对具有悬空结构模型的三维打印。为了提高模型的精度和几何映射的准确性，必须对模型的三角网格进行精细的划分。然而，如果三角形网格被过度细分，将会导致模型数据的增加。将三角形网格的边长控制在1～2 mm，如图12所示。这既可以确保模型文件的数据量不会过大，又能够保证打印件具有良好的表面质量。

对模型进行三角形网格划分后，对模型进行几何映射，图13为两个模型进行映射后的可视化模型。经过映射后的模型，在xy方向倍数扩大，在z方向上平移相关位移，模型整体向下呈锥形。

将模型进行几何映射后，通过水平切片算法对其进行水平切片，然后将生成的打印轨迹G-code进行逆映射，得到连续的锥形无支撑打印轨迹，如图14所示。

在传统的打印条件下，实验模型无论如何摆放都需要添加支撑结构。然而，支撑结构会增加额外的材料消耗，导致材料的浪费，并延长打印时间。此外，支撑结构难以清除，可能会导致打印物体表面不够光滑，进而需要进行额外的表面处理和修复。

锥形切片算法生成的多自由度打印轨迹不仅包括路径点的位置信息，还包含姿态信息。通过RobotStudio仿真软件，采用规格型号为IRB1410的六轴机械臂，建立ABB机械臂多自由度打印工作站，读取位姿轨迹信息，可以控制六轴机械臂对两个实验模型进行多自由无支撑打印仿真。IRB1410六轴机械臂打印仿真平台如图15所示，管道模型和圣诞树模型的六轴机械臂多自由无支撑打印仿真分别如图16、17所示。

通过仿真实验，验证了锥形切片算法对具有悬垂结构的模型的无支撑打印的可行性。利用机械臂六自由度优势，打印喷嘴可以实时垂直于当前打印路径切线，保证当前层能够始终依托上一层有足够的支撑，从而使得悬空结构可以以自支撑方式实现无支撑打印。

3.2 对比实验

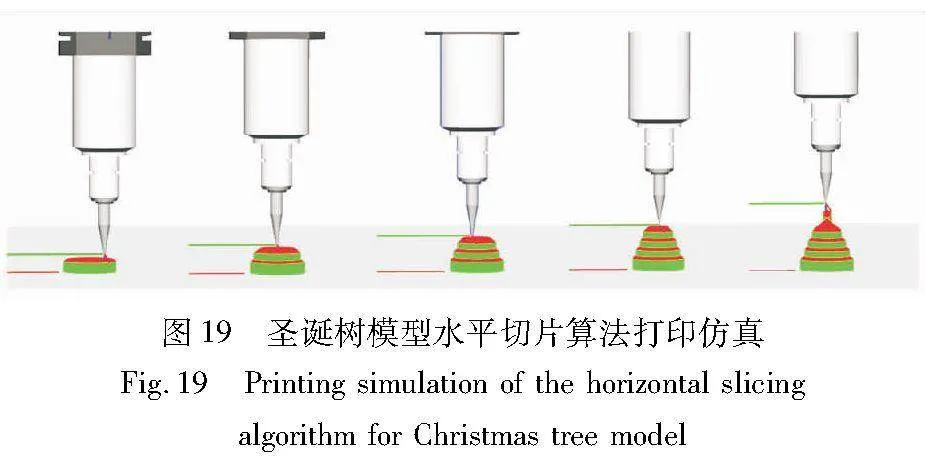
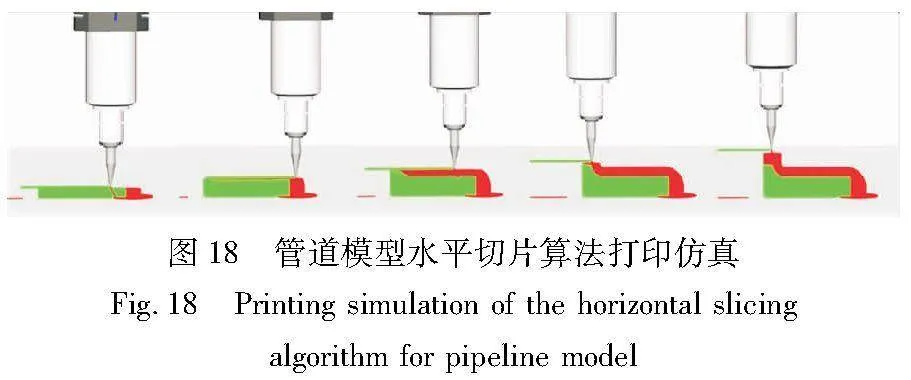
为了验证锥形切片算法的有效性，针对具有悬垂结构的模型，将其与水平切片算法的打印效果进行对比。图18和19分别展示了水平切片算法对管道模型和圣诞树模型的打印过程。对比图16和17中锥形切片算法对管道模型和圣诞树模型的打印过程可以看出，水平切片算法在打印悬垂结构时需要先打印出支撑结构，然后在支撑结构上完成对悬垂结构的打印。由于水平切片算法相对于锥形切片算法需要额外打印支撑结构，所以会增加打印时间和成本。

表1展示了锥形切片算法和水平切片算法的打印时间，锥形切片算法的无支撑打印方式比水平切片算法带支撑结构的打印方式分别节约了18.15%和20.19%的时间。通过对比实验，可以看到对于具有悬垂结构的模型，锥形切片算法的无支撑打印方式可以有效节约打印时间和成本，减少材料浪费，是一种更加高效、经济和环保的打印方式。

4 结束语

本文在NURBS体参数化模型的基础上，针对带有悬空结构模型的无支撑打印问题，首次提出了一种NURBS体参数化模型锥形切片算法。该算法首先对模型进行等参数网格单元划分和三角形网格细分；然后利用几何映射、水平切片和轨迹逆映射实现对模型的锥形切片，并生成适用于多轴机械臂的多自由度打印的路径轨迹；最后控制多轴机械臂完成对带有悬空结构的模型进行多自由度无支撑打印。通过在机械臂仿真软件中实施的无支撑打印仿真实验，验证了该算法能够准确生成多轴机械臂多自由度无支撑打印的路径轨迹。该方法旨在提高打印效率，减少材料浪费，为制造领域中无支撑打印提供了一种创新的解决方案。本文所提出的锥形切片算法生成的多自由度打印轨迹适用于六轴机械臂。而非六轴以下机械臂因自由度的限制，缺少机械臂末端打印角度的灵活性，需要更多地去考虑打印喷嘴与已完成打印部分的碰撞问题。未来将进一步探讨如何实现其他自由度机械臂的无支撑打印，以及结合曲面切片算法和锥形切片算法对带有非对称悬空结构模型进行无支撑打印。

参考文献：

［1］Chacón J M， Sánchez-Reyes J， Vallejo J， et al. G-code generation in a NURBS workflow for precise additive manufacturing ［J］. Rapid Prototyping Journal， 2022，28（11）： 65-76.

［2］Wang Lin， Guo Kaijin， He Kunjin， et al. Bone morphological feature extraction for customized bone plate design［J］. Scientific Reports， 2021，11（1）： 15617.

［3］Ezair B， Fuhrmann S， Elber G. Volumetric covering print-paths for additive manufacturing of 3D models［J］. Computer-Aided Design， 2018，100： 1-13.

［4］Yao Yuan， Zhang Yichi， Aburaia M， et al. 3D printing of objects with continuous spatial paths by a multi-axis robotic FFF platform［J］. Applied Sciences， 2021， 11（11）： 4825.

［5］吴陈铭， 戴澄恺， 王昌凌，等. 多自由度3D打印技术研究进展综述［J］. 计算机学报， 2019， 42（9）： 1918-1938. （Wu Chenming， Dai Chengkai， Wang Changling， et al. Recent progress on multi-DOF 3D printing： a survey［J］. Chinese Journal of Computers， 2019，42（9）： 1918-1938.）

［6］Salet T A M， Ahmed Z Y， Bos F P， et al. Design of a 3D printed concrete bridge by testing［J］. Virtual and Physical Prototyping， 2018，13（3）： 222-236.

［7］Lensgraf S， Mettu R R. An improved toolpath generation algorithm for fused filament fabrication［C］//Proc of IEEE International Conference on Robotics and Automation. Piscataway， NJ： IEEE Press， 2017： 1181-1187.

［8］石立伟， 陈兴， 王军伟，等. 基于自适应分层的3D打印成型方向优化［J］. 计算机应用研究， 2021，38（4）： 1139-1144. （Shi Liwei， Chen Xing， Wang Junwei， et al. Optimization of build orientation in 3D printing based on adaptive layering［J］. Application Research of Computers， 2021，38（4）： 1139-1144.）

［9］陈龙， 韩文瑜， 何文彬，等. 复杂非均质体参数化模型的切片及支撑点求解［J］. 机械工程学报， 2019， 55（15）： 99-108. （Chen Long， Han Wenyu， He Wenbin， et al. The algorithm of slicing and obtaining support points for complex heterogeneous volume paramete-rization model［J］. Journal of Mechanical Engineering， 2019， 55（15）： 99-108.）

［10］陈龙， 韩文瑜， 徐岗. 非均质NURBS体参数化模型的AMF通用文件生成方法［J］. 系统仿真学报， 2019， 31（10）： 2010-2018. （Chen Long， Han Wenyu， Xu Gang. A generation method of AMF general files for heterogeneous NURBS volume parametric model［J］. Journal of System Simulation， 2019，31（10）： 2010-2018.）

［11］Dai Chengkai， Wang C C L， Wu Chenming， et al. Support-free vo-lume printing by multi-axis motion［J］. ACM Trans on Graphics， 2018， 37（4）： 1-14.

［12］Zhao Donghua， Guo Donghua. Shape and performance controlled advanced design for additive manufacturing： a review of slicing and path planning［J］. Journal of Manufacturing Science and Enginee-ring， 2020，142（1）： 1-87.

［13］Fang Guoxin， Zhang Tianyu， Zhong Sikai， et al. Reinforced FDM： multi-axis filament alignment with controlled anisotropic strength［J］. ACM Trans on Graphics， 2020，39（6）： 1-15.

［14］Zhang Tianyu， Fang Guoxin， Huang Yuming， et al. S3-slicer： a general slicing framework for multi-axis 3D printing［J］. ACM Trans on Graphics， 2022，41（6）： 1-15.

［15］Shan Yujie， Shui Yiyang， Hua Junyu， et al. Additive manufacturing of non-planar layers using isothermal surface slicing［J］. Journal of Manufacturing Processes， 2023， 86： 326-335.

［16］张帆， 魏培祥， 赵圆圆，等. 基于体素的机械臂连续碳纤维3D打印路径规划［J］. 计算机集成制造系统， 2023，29（5）： 1517-1527. （Zhang Fan， Wei Peixiang， Zhao Yuanyuan， et al. Voxel-based path planning method for continuous carbon fiber 3D printing with robot arm［J］. Computer Integrated Manufacturing System， 2023， 29（5）： 1517-1527.）

［17］Fortunato G M， Nicoletta M， Batoni E， et al. A fully automatic non-planar slicing algorithm for the additive manufacturing of complex geometries［J］. Additive Manufacturing， 2023， 69： 103541.

［18］Lau T Y， Chen Li ， He Dong， et al. Partition-based print sequence planning and adaptive slicing for scalar field-based multi-axis additive manufacturing［J］. Computer-Aided Design， 2023，163： 103576.

［19］Wüthrich M， Gubser M， Elspass W J， et al. A novel slicing strategy to print overhangs without support material［J］. Applied Sciences， 2021， 11（18）： 8760.

［20］Allen R J， Trask R S. An experimental demonstration of effective curved layer fused filament fabrication utilising a parallel deposition robot［J］. Additive Manufacturing， 2015，8： 78-87.

［21］Chen Lufeng， Chung M F， Tian Yaobin， et al. Variable-depth curved layer fused deposition modeling of thin-shells［J］. Robotics and Computer-Integrated Manufacturing， 2019， 57： 422-434.