跨脉冲传播的深度脉冲神经网络训练方法

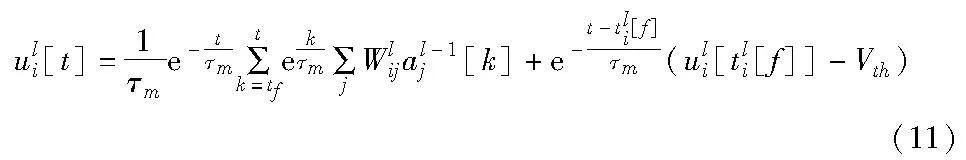
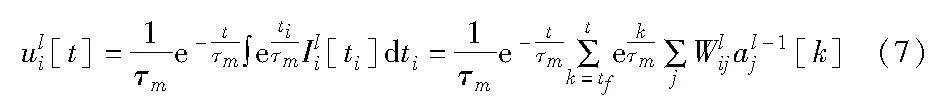
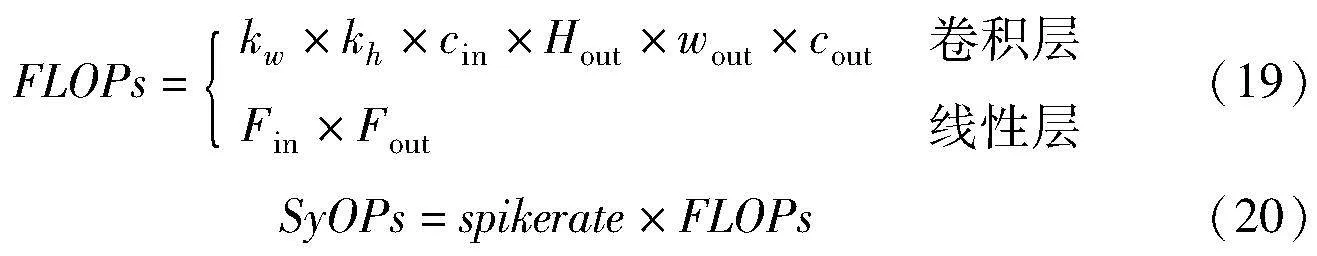
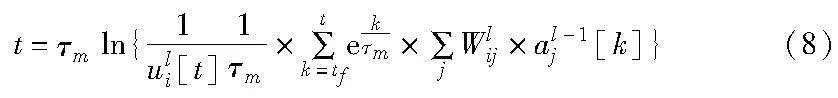
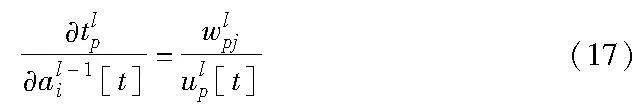
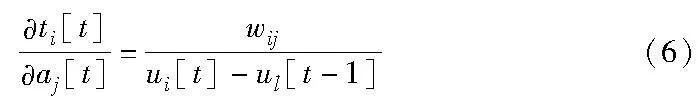
摘 要：基于反向传播的脉冲神经网络（SNNs）的训练方法仍面临着诸多问题与挑战，包括脉冲发放过程不可微分、脉冲神经元具有复杂的时空动力过程等。此外，SNNs反向传播训练方法往往没有考虑误差信号在相邻脉冲间的关系，大大降低了网络模型的准确性。为此，提出一种跨脉冲误差传播的深度脉冲神经网络训练方法（cross-spike error backpropagation，CSBP），将神经元的误差反向传播分成脉冲发放时间随突触后膜电位变化关系和相邻脉冲发放时刻点间的依赖关系两种依赖关系。其中，通过前者解决了脉冲不可微分的问题，通过后者明确了脉冲间的依赖关系，使得误差信号能跨脉冲传播，提升了生物合理性。此外，并对早期脉冲残差网络架构存在的模型表示能力不足问题进行研究，通过修改脉冲残余块的结构顺序，进一步提高了网络性能。实验结果表明，所提方法比基于脉冲时间的最优训练算法有着明显的提升，相同架构下，在CIFAR10数据集上提升2.98%，在DVS-CIFAR10数据集上提升2.26%。

关键词：脉冲神经网络； 脉冲时间依赖； 误差反向传播； 脉冲神经网络训练算法

中图分类号：TP183 文献标志码：A 文章编号：1001-3695（2024）07-029-2134-07

doi：10.19734/j.issn.1001-3695.2023.11.0562

Deep spiking neural network training method across spiking propagation

Abstract：Backpropagation-based training methods for SNNs still face many problems and challenges， including that the spike firing process is non-differentiable and spike neurons have complex spatiotemporal dynamics processes. In addition， SNNs backpropagation training methods often do not consider the relationship of the error signal between adjacent spikes， greatly reducing the accuracy of the model. To this end， this paper proposed a cross-spike error backpropagation training method for deep spiking neural networks（CSBP）， which divided the error backpropagation of neurons into two dependencies： the dependency of spike firing time with the postsynaptic membrane potential（DSFT） and the dependency between spike firing time（DBSFT）. Among them， DSFT solved the problem of spike non-differentiability and DBSFT clarified the dependence between spikes， allowing error signals to propagate across spikes， improving biological rationality. In addition， this paper solved the problem of insufficient expressive ability in early spiking ResNet network architecture by modifying the structural order of the spike residual block. Experimental results show that the proposed method is significantly improved compared to the SOTA（state-of-the-art） training algorithms based on spike time. Under the same architecture， the improvement is 2.98% on the CIFAR10 dataset， and 2.26% on the DVS-CIFAR10 dataset.

Key words：spiking neural networks（SNNs）; spike time dependency; error backpropagation; spiking neural network training algorithm

0 引言

近年来，脉冲神经网络（SNNs）因其比传统神经网络（artificial neural networks，ANNs）具有更高的生物真实性而备受关注。独特的信息编码方式使其能高效地利用时间信息，并且能在神经形态硬件上实现显著的低功耗的性能。由于SNNs所具有的复杂的神经元动力学模型和脉冲发放过程不可微分的特性，其训练仍然是一个具有挑战性的问题。

近几年，研究人员提出了许多方法来训练SNNs，主流方法包括ANN-to-SNN的转换方法［1～4］和SNNs误差反向传播（BP）方法［5～11］。其中，基于转换的方法通常需要较大的时间步才能获得与深度ANNs相当的精度，这增大了模型的推理时间成本。相反，SNNs BP方法能高效地利用脉冲时间信息，在极少的时间步下，就能训练具备高精度性能的SNNs。但是，由于脉冲神经网络的脉冲发放过程具有不可微分的特性，传统的误差反向传播算法无法直接应用于SNNs的训练。为了解决脉冲不可微分问题，使得传统的BP算法能适用于SNNs的训练，研究人员提出了代理梯度［5～7］和基于脉冲时间［8～10］的SNNs BP训练方法。

代理梯度［5～7］方法是指在误差反向传播过程中采用平滑函数来代替不可微的脉冲激活函数。其中，Shrestha等人［5］提出用概率密度函数来代替脉冲激活函数，并在时间维度上分配误差信用。文献［6，7］提出了在时间和空间两个维度进行误差反向传播（backpropagation through time，BPTT），并引入了几个连续的替代函数来解决脉冲不可微的问题。虽然采用代理梯度的方法使SNNs能够进行直接训练，但代理梯度是对真实梯度的一种近似，其值一般都很小，在BPTT框架下，网络模型的梯度消失问题会变得更加显著，使得其无法直接应用到深层网络上。并且由于该类方法采用的是频率编码，其所需的时间步为几十到几百个［6，7］，这进一步导致了模型的训练及推理时长高。

基于脉冲时间编码的训练方法［8～10］能够充分利用脉冲的时间信息，极大程度地减少网络所需的时间步。其中，大多数基于脉冲时间的方法［8，9］只允许每个神经元最多触发一个脉冲，因而有着不错的时延性能，但这也导致了网络中脉冲数不足、精度低的问题。Zhang等人［10］将该类方法应用于LIF（leaky integrate-and-fire）神经元模型上，允许每个神经元发放多个脉冲，从而在较低的时延下也能获取优越的精度性能。然而，该方法通过脉冲时间与膜电位间的线性假设计算脉冲时间与膜电位的梯度，在膜电位变化平缓时，存在梯度爆炸问题，导致无法应用于深层的网络架构，减低了实际的应用价值。此外，现有的SNNs反向传播训练算法往往对膜电位进行归零重置，使得在反向传播期间相邻脉冲间的误差信号被截断，导致误差信号无法跨脉冲传播，大大降低了误差信号的准确性。

为了解决上述问题，本文首先依据膜电位与脉冲发放时间的动力学模型，推导脉冲发放时间随突触后电位变化的依赖关系，以此解决了脉冲发放过程中不可微分的问题。如2.2.2节所分析，通过该依赖关系能进一步地避免现有基于线性假设的方法［10］存在的梯度爆炸问题，使得该训练算法能进一步应用到深层网络架构下，提高其实际应用价值。其次，本文采用减法复位对膜电位进行重置，通过残余膜电位项构建相邻脉冲发放时刻点间的依赖关系，使得误差信号能够跨脉冲传播，从而提升误差信号的准确性。最终，本文提出一种跨脉冲误差传播的深度脉冲神经网络训练算法，将神经元的误差反向传播分成脉冲发放时间随突触后膜电位变化关系和相邻脉冲发放时刻点间的依赖关系两种依赖关系。前者通过脉冲发放时间与突触后电位的依赖性明确了误差信号在空间维度上的分配，解决了脉冲不可微分问题；后者则明确了脉冲间的依赖关系，使得误差信号能够跨脉冲传播。此外，针对Fang等人［11］提出的残差网络模型中表达能力不足的问题，本文还改进了残差网络模型中的残差单元块，进一步提升网络的性能。

本文的主要贡献可以归纳为以下几点：

a）依据膜电位与脉冲发放时间的动力学模型，推导脉冲发放时间随突触后膜电位变化的关系，明确了误差信号在空间维度上的分配，解决了脉冲不可微分问题，突破了线性假设情况下梯度爆炸的问题。

b）采用减法复位对膜电位进行重置，并基于残余膜电位项推导相邻脉冲发放时刻点间的依赖关系，使得误差信号能够跨脉冲传播，从而提升误差信号的准确性。

c）本文分析了残差网络模型［11］表达能力不足的问题，对该模型的残差单元进行调整，提出了改进后的残差网络模型。

d）本文在静态数据集MNIST、Fashion-MNIST、CIFAR10和神经形态数据集N-MNIST和DVS-CIFAR10上进行了实验。实验结果表明，本文相对于现有基于脉冲时间的深度脉冲神经网络训练算法，取得了SOTA（state-of-the-art）精度。与其他同类方法比较，本文方法在时延和精度上也有着较大优势。

1 LIF神经元模型

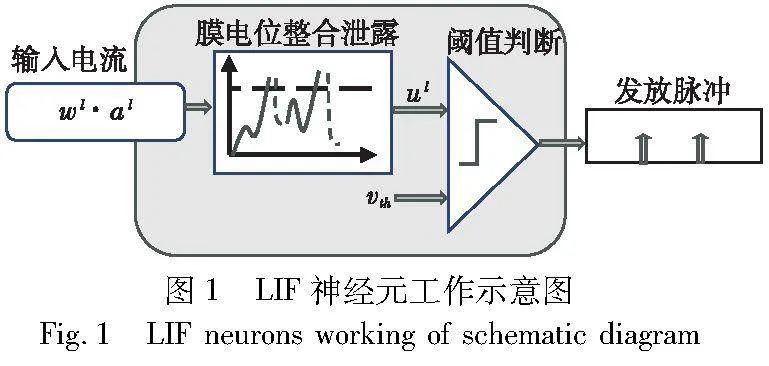
本文采用LIF神经元模型（图1）和指数衰减突触模型作为脉冲神经元模型［10］。将脉冲的发放时间作为神经元的输出，神经元输出的脉冲序列Γ可表示为

Γ={tj［1］，tj［2］，…，tj［n］}（1）

其中：Γ表示神经元j的输出脉冲序列;n表示脉冲个数;tj表示神经元的输出脉冲。脉冲序列Γ是按时间排序的，如tj［1］<tj［2］<…<tj［n］。输入脉冲通过突触模型转换为神经元的突触后电位（postsynaptic potentials，PSP）a［t］，然后，LIF神经元将其接收到的PSP整合为膜电位u，其动力学可以被描述为

其中：uli［t］表示第l层中i神经元的膜电位；τm是膜电位的时间常数；R是有效的泄露电阻；Ili［t］表示输入电流；Wlij表示第l层中突触前神经元j到突触后神经元i的突触权重；al-1j［t］表示由突触前神经元j脉冲产生的突触后电位。LIF的前馈工作过程如图1所示，输入电流经过膜电位的整合、泄露后，其膜电位uli［t］会跟预设的阈值Vth进行比较，一旦膜电位超过设定的阈值，神经元将会发射一个脉冲并重置膜电位。在实际的前馈计算应用中，一般会把LIF神经元的微分模型离散化为如下公式：

其中：R被整合到了突触权重中。本文使用指数衰减形式的突触模型作为脉冲响应核函数，转换脉冲为（PSP）a［t］。

其中：τs表示突触时间常数；tli［f］是i神经元的输出脉冲；tli［f］∈Γlij，H（·）是阶跃函数，当t<tli［f］时，H（t-tli［f］）=0。

2 跨脉冲误差传播的深度脉冲神经网络训练算法

2.1 跨脉冲误差反向传播的依赖关系推导

2.1.1 脉冲发放时间随突触后膜电位变化的关系（DSFT）

基于线性假设［10］来处理脉冲不可微的问题，其梯度中的不可导项的计算如式（6）所示。

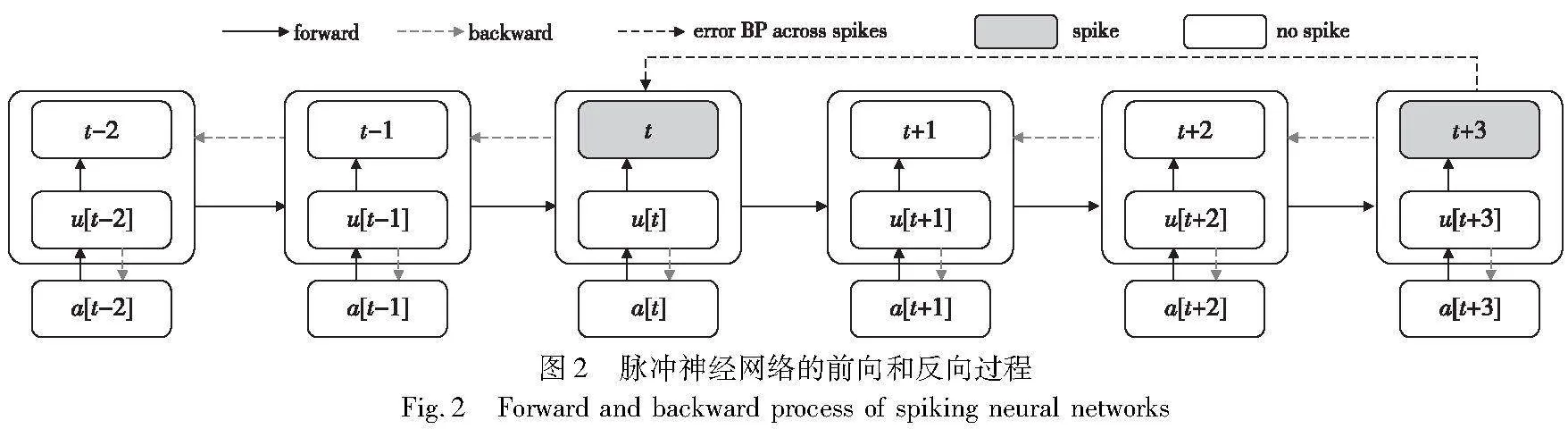
从式（6）可知，在膜电位变化平缓时，ui［t］-u［t-1］的值趋于0，这容易造成梯度爆炸问题，尤其在深度网络架构下，这使得其无法直接应用于超过10层的网络架构。为此，本文依据膜电位与脉冲发放时间的动力学模型（式（2）），推导出膜电位在单个脉冲周期内的模型公式（式（7）），如图2所示，脉冲周期是指首个输入脉冲到发放脉冲的整个时间周期。

其中：tf表示脉冲周期内的首个输入脉冲时间。

为了进一步推导脉冲发放时间随突触后膜电位变化的关系，本文将式（7）中参数t看成脉冲的发放时间，从而得出脉冲发放时间随突触后电位变化的关系，如式（8）所示。在后续2.2.2节，本文讨论了与基于线性假设的方法的区别，解决了其存在的梯度爆炸问题。

2.1.2 相邻脉冲发放时刻点间的依赖关系（DBSFT）

为了计算简便，现有的脉冲网络误差反向训练算法中往往对膜电位进行归零重置操作，使得误差信号只能在单个脉冲周期内传播，并不能跨脉冲进行反向传播，导致误差信号被截断，降低了误差信号的准确性。实际上，残余膜电位对于后续脉冲发放有着重要的影响［12］，在输入电流恒定的情况下，脉冲发放时刻的残余膜电位越大，后续脉冲越早发放。因此，本文保留神经元的残余膜电位信息作为脉冲周期的初始膜电位，以此来构建脉冲发放时刻点间的依赖关系，提升误差信号的准确性，如图2深黑色虚线所示，本文增加了发放脉冲间的误差信号传递路径。本文采用的减法复位的重置机制如式（9）所示。

uli［t］=uli［t］-Vth if uli［t］≥Vth（9）

其中：tli［f］是神经元i在该脉冲周期前最近的一个脉冲发放时间。由此，增加了残余膜电位项的膜电位的动力学方程，如式（11）所示。

2.2 误差的反向传播

2.2.1 反向传播

本文采用Van Rossum distance ［13］测量实际输出突触后电位和渴望输出突触后电位。如式（12）所示，损失函数L被定义为

a）输出层。如果l层是输出层，使用式（12）可以得到损失函数关于ali［t］的偏导数：

其中：T表示仿真时长；n表示神经元i的脉冲序列Γ={tli［1］，tli［2］，…，tli［n］}的脉冲个数；tli［g］是在发射脉冲tli［f］后的下一个脉冲，即f<g<n。如果神经元i没有生成脉冲时，则令δli=0；对于ali［t］/tli［f］由式（5）可得。

其中：Nl表示l层的神经元个数；tlp是受al-1i［t］影响的脉冲周期的发射脉冲，详见算法1。最终，可以得到损失L对每一层突触权重W（l）ij的梯度，如式（16）所示。

2.2.2 不可微分问题

式（15）中，tlp/al-1i［t］就是脉冲神经网络训练算法中的不可求导项，本文指出基于线性假设的方法中该梯度的计算存在梯度爆炸问题，为此，本文通过DSFT来解决该问题。根据式（8）计算得

从式（17）可看出，本文方法即使在膜电位变化较为平缓时，也不会出现分母为零的情况，从而避免了梯度爆炸的问题。实验结果显示，本文方法能更好地应用到深层网络中。

2.2.3 跨脉冲误差传播

从上述公式可以看出，相邻输出脉冲tli［g］与tli［f］之间的误差梯度不仅与膜电位相关，还与其脉冲时间相关。

2.3 脉冲残余块（spiking residual blocks）

在残差网络中，脉冲残余块是实现恒等映射的重要网络结构。图3展示了不同的脉冲残余块，其中conv表示卷积层，BN表示块标准化，SN表示脉冲神经元模型（在本文中SN表示LIF神经元）。早期SNNs训练方法［14～16］使用的脉冲残余块如图3（a）所示，层与层之间的信息是经过一层SN传递的。由于SN是一种非线性模型，这使得早期的脉冲残余块无法实现恒等映射，即Ol+1i=SN（Oli）≠Oli。为了实现恒等映射，Fang等人［11］提出了如图3（b）所示的脉冲残余块，其中g表示数据的处理函数，本文实验仅使用ADD函数。Fang等人［11］通过将层间的SN层移到加法运算之前，使得脉冲信息能直接传递整个网络，实现了恒等映射。但是，从图3（b）中可以观察到将SN移到加法运算前将会导致两条路径传递的都是非负的脉冲序列。以频率编码方式为例，随着使用的脉冲残余块的层数越多，输出脉冲序列的频率就越大，越无法表示低频的信息，这极大地制约了模型的表达能力。同理地，用脉冲时间编码信息也会存在同样的问题。为此，本文把文献［11］提出的脉冲残余块调整成如图3（c）所示结构，将BN以及SN放到残余路径的顶部，使得在脉冲残余块之间通过加权后的突触后膜电位Ili传递信息，其值有正有负，从而避免了上述问题。对下采样块（downsample blocks）进行同样操作。

3 实验

本文在几个常用数据集上测试了所提方法的准确性，包括静态数据集MNIST、Fashion-MNIST、CIFAR10和神经形态数据集N-MNIST、DVS-CIFAR10。实验中的相关超参数设置：神经元的膜电位阈值Vth、膜电位时间常数τm和突触时间常数τs被设置为1，仿真时间T设置为5。为了更好地评估本文方法，与现有基于脉冲时间信息脉冲神经网络误差反向传播训练算法及其他同类训练算法均做了对比。此外，本文还进行了跨脉冲传播的消融性实验以及功耗分析等以证明本文方法和网络模型的有效性。实验结果均经过三次实验取平均获得。硬件平台为GPU：NVIDIA GeForce RTX 3060。

3.1 实验结果

3.1.1 与当前先进的基于脉冲时间信息的训练算法比较

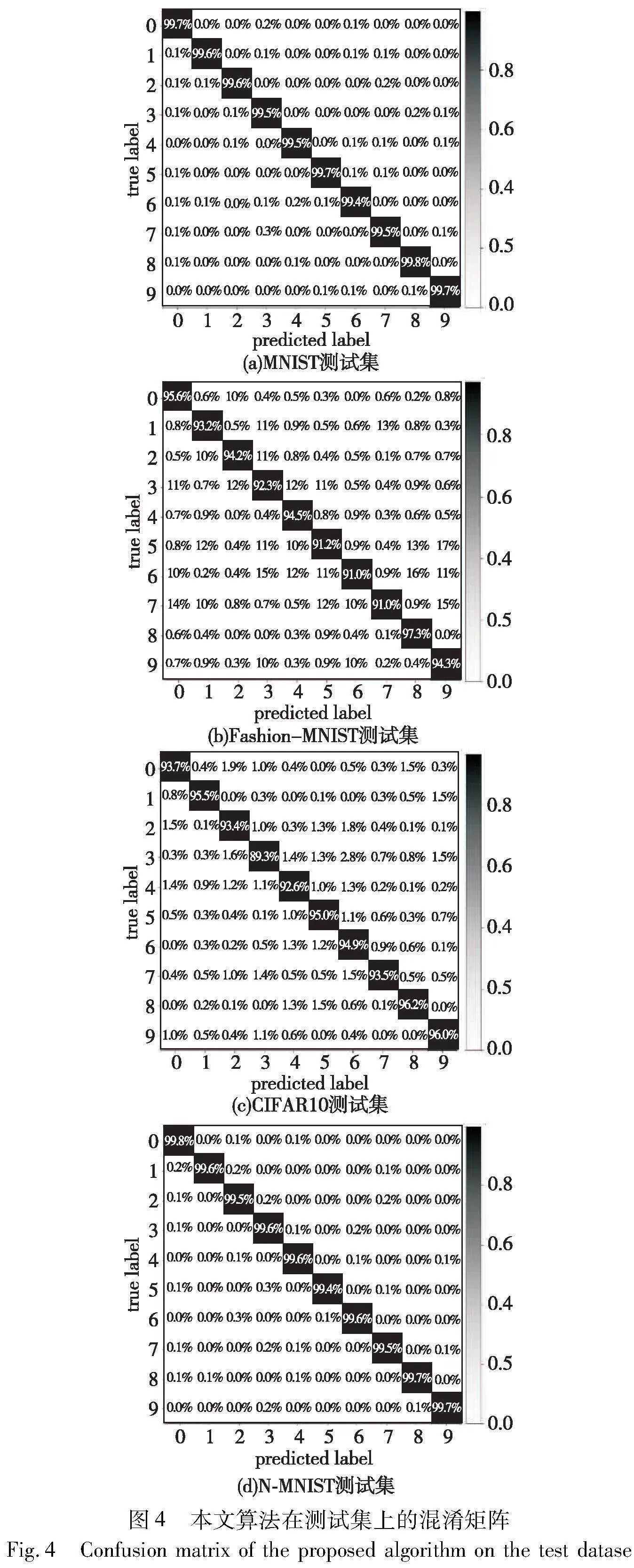
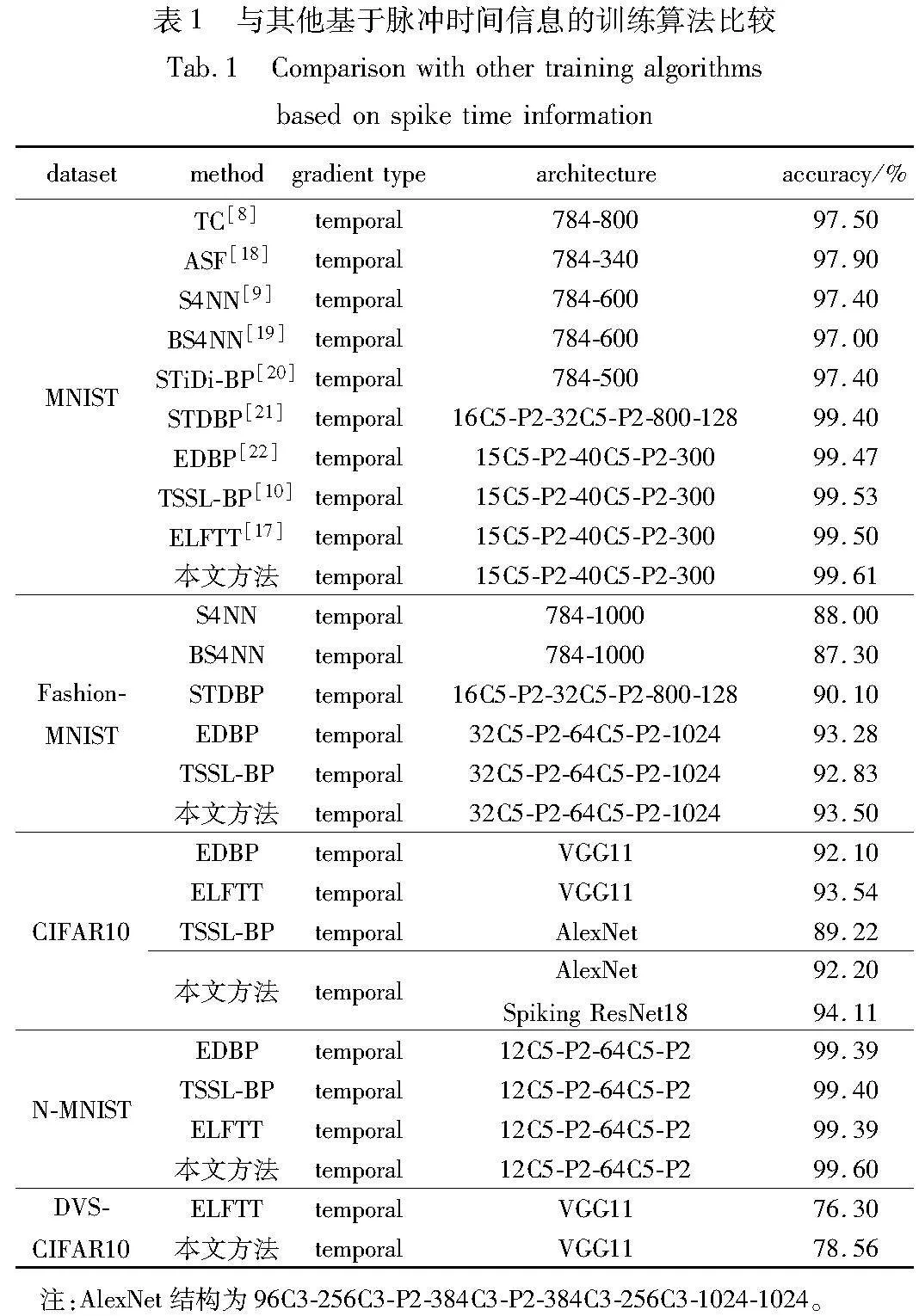
首先将本文方法与当前先进的基于脉冲时间的SNNs训练方法进行比较。如表1所示，本文给出了MNIST、Fashion-MNIST、CIFAR10、N-MNIST及DVS-CIFAR10数据集的实验结果及其测试集下的混淆矩阵（图4）。在MNIST、Fashion-MNIST以及N-MNIST简单数据集上，本文方法的测试精度分别为99.61%、93.50%以及99.60%。而在其他较复杂的数据集上，本文训练算法明显优于其他基于脉冲时间的SNNs训练方法。在CIFAR10数据集中，本文方法在使用AlexNet网络架构时取得了92.20%的测试精度。在相同架构下，较之前基于脉冲时间的训练方法的SOTA SNNs的准确率提高了2.98%以上。在DVS-CIFAR10数据集上，本文使用了VGG11的网络架构。本文方法取得了78.56%的测试精度。与使用同样网络架构的基于时间的SOTA算法［17］相比，精度提高约2.26%。

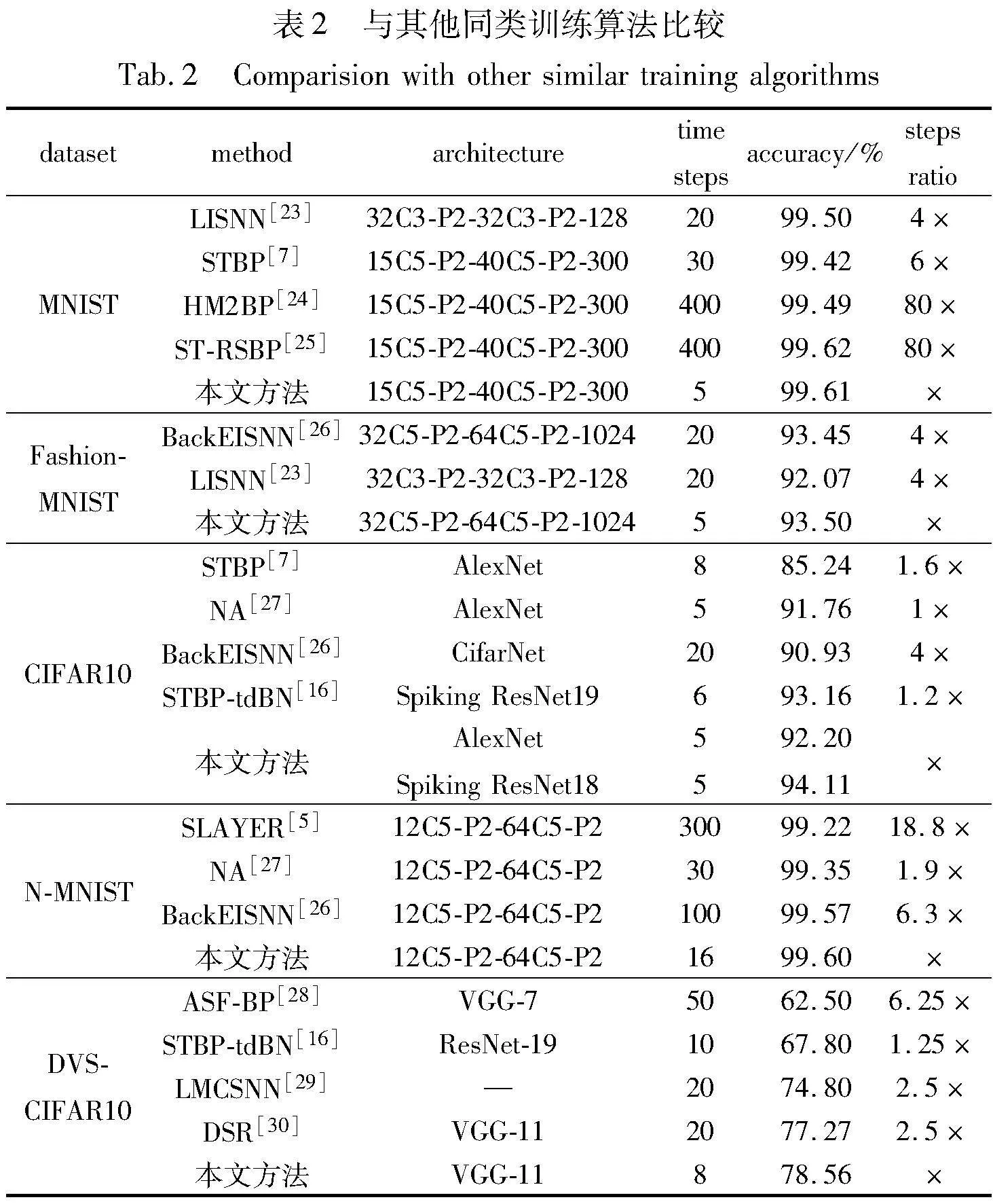
3.1.2 与其他同类训练算法比较

此外，本文还与其他同类训练算法（非脉冲时间）进行了比较，实验结果如表2所示。从表2可以看出，与这部分算法相比，本文方法在精度上虽然提升不是很高，但在时间步上却有着较为明显的提升，这对于减少脉冲神经网络的训练及推理时延有着极大的影响。从表2可以清晰地看出，本文方法在时间步上最大能减少80倍。

3.2 消融性实验

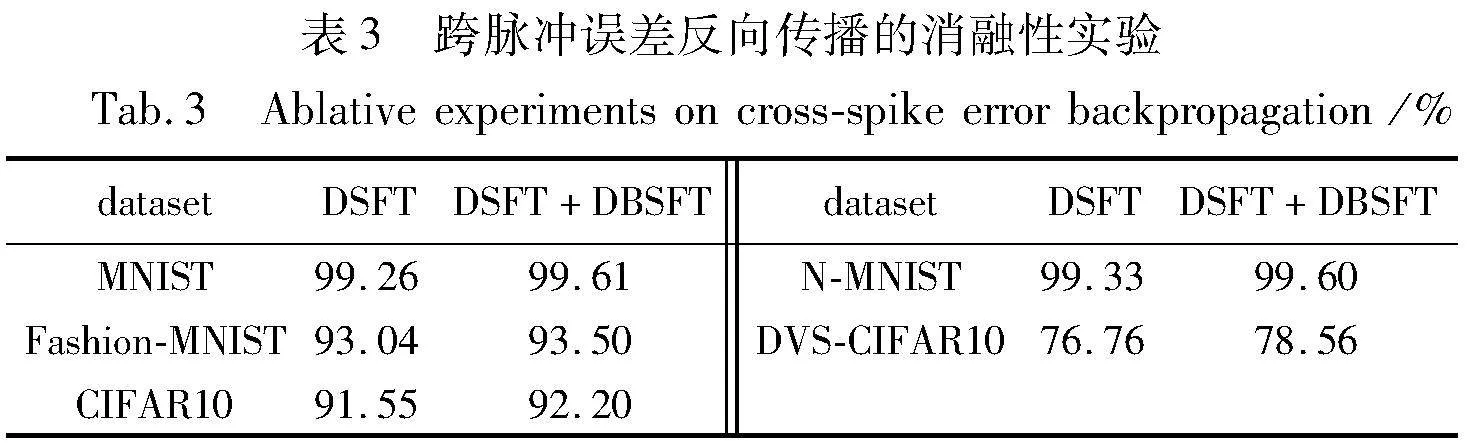
在本节中，对所提出的DSFT和DBSFT在不同数据集上进行消融实验。实验中除了跨脉冲误差梯度项，其余超参数设置均相同（如第3章实验所介绍参数）。实验结果如表3 所示。从表3中可以看出，加入跨脉冲误差传播（DBSFT）可以有效提高SNNs模型的准确性。特别是在DVS-CIFAR10上，测试精度提高了1.8%。实验结果表明，DBSFT可以有效提升误差信号的准确性。

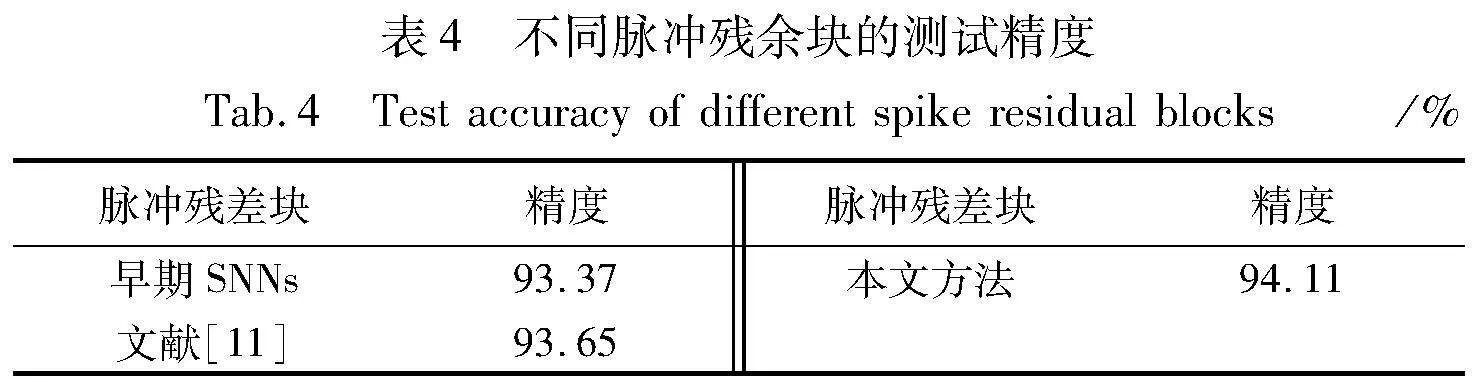
此外，为了测试本文所改进的脉冲残余块结构的测试精度。本文给出了CIFAR10数据集在不同脉冲残余块的测试精度曲线。针对如图3所示的不同脉冲残余块，其测试集精度如表4所示，在其他实验条件均相同的情况下，本文所提改进脉冲残余块相比于其余两种脉冲残余块在CIFAR10数据集上的测试精度分别提升了0.74%及0.5%左右PSpUcrJG7N0pX+f4DvnB8A==。

3.3 复杂度分析

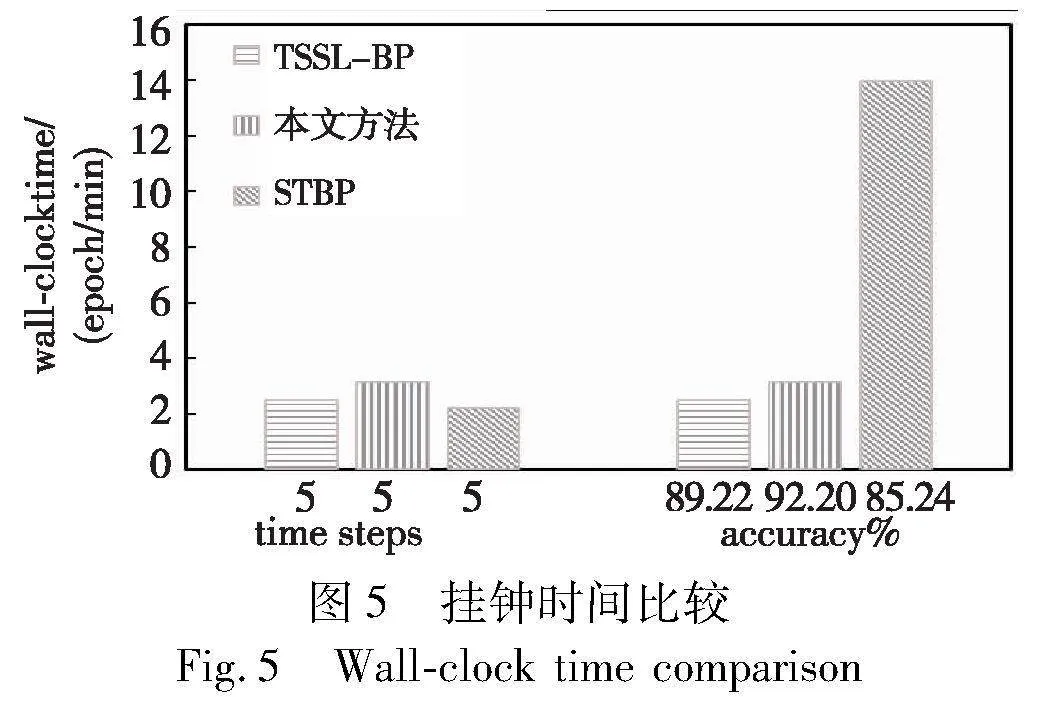
本文方法的时间复杂度为O（N×T），其中N为隐藏层神经元个数，T为时间步。为了更加直观地展示本文方法与其他经典算法在时间上的差异，将两个经典的脉冲神经网络训练算法STBP［7］、TSSL-BP［10］与本文方法在CIFAR10数据集下（NVIDIA GeForce RTX 3060，块大小为64）的每一次迭代所消耗的时间（wall-clock time）进行对比，如图5所示。其中，STBP是基于代理梯度的经典训练算法，而TSSL-BP是基于脉冲时间的经典算法。从图5可以看出，在相同的时间步下，本文方法所消耗的时间会略多于TSSL-BP和STBP算法，这主要是由于本文方法需要依据DNSFT关系，额外地计算误差信号跨脉冲传播的梯度项。但是在精度性能相近时，本文方法消耗的时间仅为STBP算法的22.64%。

3.4 脉冲发放稀疏性及功耗分析

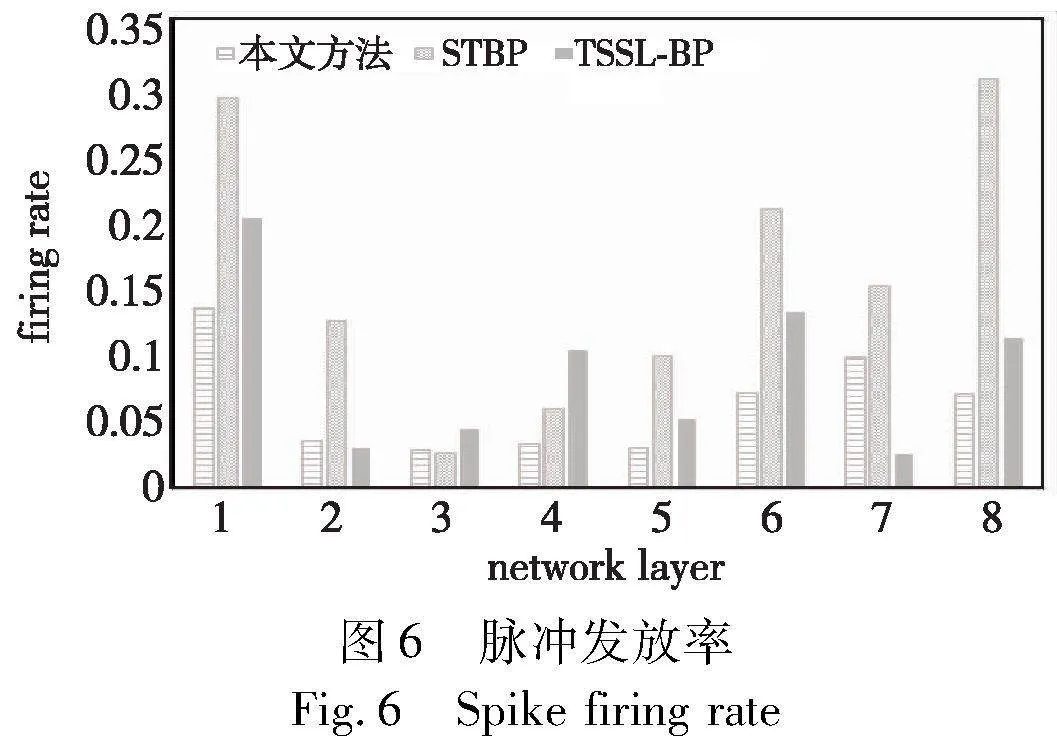
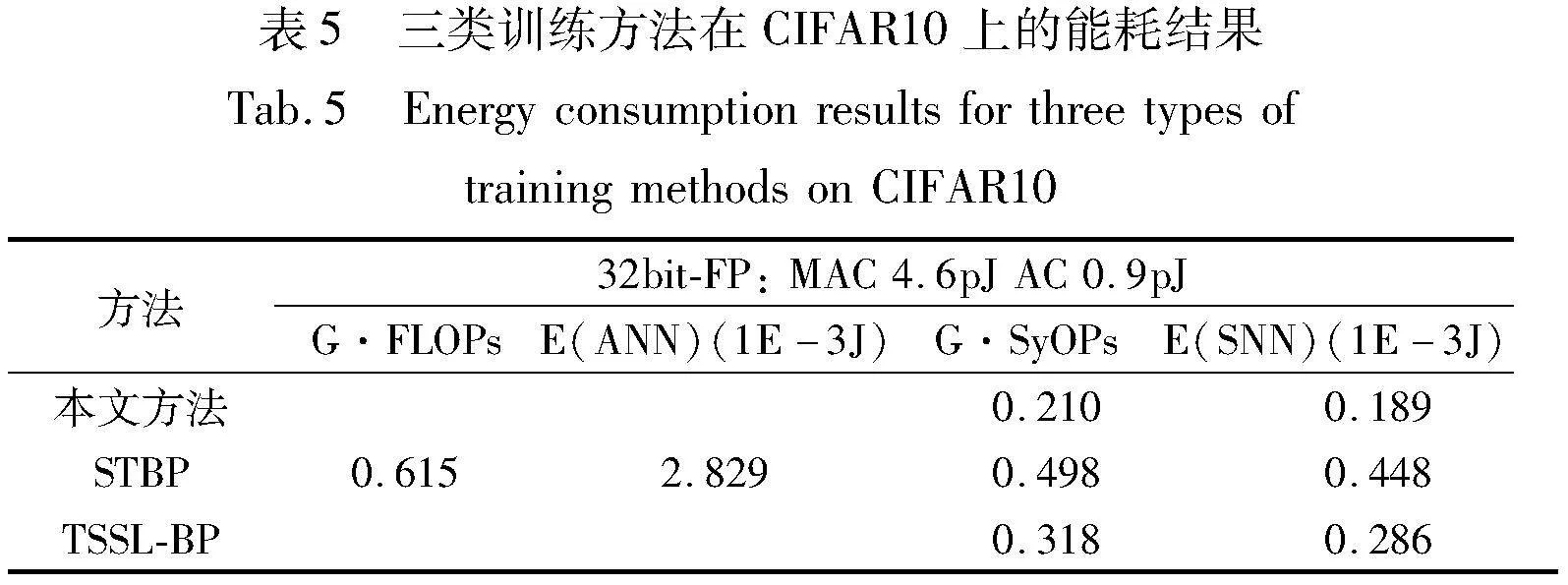
为了更好地比较各SNNs方法的综合性能，本文进行了各方法的能耗分析。在ANNs中，每个浮点运算（floating-point operations，FLOPs）都包括一个浮点（floating-point，FP）乘法和一个浮点加法运算（multiplication and addition computation，MAC）。由于脉冲的二进制化，SNNs每个浮点运算操作仅只有一个浮点加法（addition computation，AC），称之为突触运算（synaptic operations，SyOPs）。本文根据文献［31］通过运算操作次数和每种运算操作在45 nm技术下的能耗数据［32］的方法来评估各训练方法的能耗性能，即

其中：kw（kh）是卷积核的宽度（高度）；cin（cout）是指输入（输出）的通道数；Hout（wout）是指输出特征图的高度（宽度）；Fin（Fout）表示输入（输出）特征的数量；spikerate是指SNNs每层的发放率，其计算公式为

其中：T表示训练、推理中总的时间步；Stotal是指该网络层在T时间内总的脉冲数量;Ntotal表示该层神经元数量。由上述公式可以知道，越低的脉冲发放率其能耗越低。实验数据集使用CIFAR10，网络模型架构采用AlexNet： 96C3-256C3-P2-384C3-P2-384C3-256C3-1024-1024。其中，STBP的时间步为8，另外两种均为5。如图6所示，本文给出了不同方法每层脉冲发放率的柱状图，其中，相比于其他两类训练方法，本文方法的脉冲发放率相对较低，这有效地使得网络模型保持稀疏性。

由此，根据式（19）（20）进一步分析各SNNs BP训练方法的能耗性能。如表5所示，本文方法在能耗估计中仅为0.189，低于其他两类训练方法，为ANNs的6.7%，STBP方法的42.2%和TSSL-BP的66.1%。

3.5 在实际交通数据的应用

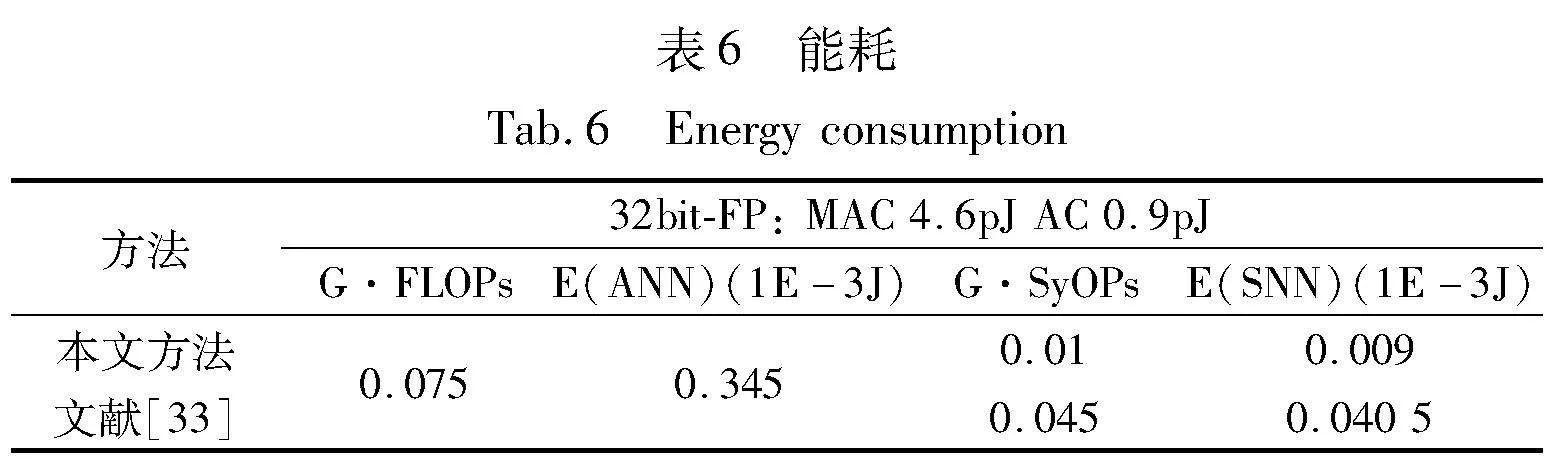
相比于传统的ANNs，SNNs由于独特的脉冲处理方式，其具有显著的低功耗性能，这使得其在边缘设备、机器人及无人机等终端设备有着很好的应用场景。本文对比了联邦学习中的SNNs训练算法文献［33］在实际交通数据（https：//www. kaggle.com/vishnu0399/emergency-vehicle-siren-sounds，https：// www.kaggle.com/hj23hw/pedestrian-augmented-traffic-light-dataset）的单机识别精度和功耗性能。该数据集一共872张图片，包括160张自行车、205张汽车以及507张交通灯，其中本文使用80%的数据作为训练集。实验所用网络架构均为1728-2500-3的三层简单网络架构。在单机设备上，本文方法精度为90.6%，而文献［33］精度仅为87.4%。本文考虑到在边缘设备联邦学习中，能耗是相对重要的一个评价指标，为此，本文进一步测试了两种方法的能耗指标，如表6所示，本文方法仅为文献［33］的22.2%，表明算法在能耗上有着更好的表现。这主要由于本文方法高效地利用了脉冲时间编码信息，能有效地降低网络的时间步。本文后续工作就是将所提方法应用于多边缘智能终端的联邦学习中，探索在联邦学习上的性能优势。

4 结束语

本文首先依据膜电位与脉冲发放时间的动力学模型，推导脉冲发放时间随突触后电位变化的关系，避免线性假设条件下梯度过大的问题。其次采用减法复位对膜电位进行重置，并基于残余膜电位项构建相邻脉冲发放时刻点间的依赖关系，使得误差信号能够跨脉冲传播，从而提升误差信号的准确性。此外，针对脉冲残余块间信息值不断累加增长的问题，本文修改了原有的脉冲残余块，进一步提高了网络模型的性能。实验表明，本文方法相对于现有基于脉冲时间的深度脉冲神经网络训练算法，取得了SOTA精度。与其他同类方法比较，本文方法在时延和精度上也有着较大优势。

参考文献：

［1］张驰， 唐凤珍. 基于自适应编码的脉冲神经网络［J］. 计算机应用研究， 2022，39（2）： 593-597. （Zhang Chi， Tang Fengzhen. Self-adaptive coding for spiking neural network［J］. Application Research of Computers， 2022， 39（2）： 593-597.）

［2］王浩杰， 刘闯. 用于双阈值脉冲神经网络的改进自适应阈值算法［J］. 计算机应用研究， 2024，41（1）： 177-182，187. （Wang Haojie， Liu Chuang. Improved adaptive threshold algorithm for double threshold spiking neural network［J］. Application Research of Computers， 2024，41（1）： 177-182，187.）

［3］Chen Yunhua， Mai Yingchao， Feng Ren， et al. An adaptive thre-shold mechanism for accurate and efficient deep spiking convolutional neural networks［J］. Neurocomputing， 2022， 469： 189-197.

［4］冯忍， 陈云华， 熊志民， 等. 自校准首脉冲时间编码神经元模型［J］. 计算机科学， 2024， 51（3）： 244-250. （Feng Ren， Chen Yunhua， Xiong Zhimin， et al. Self-calibrating first spike temporal encoding neuron model［J］. Computer Science， 2024， 51（3）： 244-250.）

［5］Shrestha S B， Orchard G. SLAYER： spike layer error reassignment in time［C］//Proc of the 32nd International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2018： 1419-1428.

［6］Wu Yujie， Deng Lei， Li Guoqi， et al. Spatio-temporal backpropagation for training high-performance spiking neural networks［J］. Frontiers in Neuroscience， 2018， 12： article No.331.

［7］Wu Yujie， Deng Lei， Li Guoqi， et al. Direct training for spiking neural networks： faster， larger， better［C］//Proc of the 33rd AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2019： 1311-1318.

［8］Mostafa H. Supervised learning based on temporal coding in spiking neural networks［J］. IEEE Trans on Neural Networks and Lear-ning Systems， 2017，29（7）： 3227-3235.

［9］Kheradpisheh S R， Masquelier T. Temporal backpropagation for spiking neural networks with one spike per neuron［J］. International Journal of Neural Systems， 2020，30（6）： 2050027.

［10］Zhang Wenrui， Li Peng. Temporal spike sequence learning via backpropagation for deep spiking neural networks［C］//Proc of the 34th International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2020： 12022-12033.

［11］Fang Wei， Yu Zhaofei， Chen Yanqi， et al. Deep residual learning in spiking neural networks［C］//Proc of the 35th Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2021： 21056-21069.

［12］Han Bing， Srinivasan G， Roy K. RMP-SNN： residual membrane potential neuron for enabling deeper high-accuracy and low-latency spiking neural network［C］//Proc of IEEE/CVF Conference on Compu-ter Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2020： 13555-13564.

［13］Van Rossum M C W. A novel spike distance［J］. Neural Computation， 2001，13（4）： 751-763.

［14］Hu Yangfan， Tang Huajin， Pan Gang. Spiking deep residual networks［J］. IEEE Trans on Neural Networks and Learning Systems， 2023，34（8）： 5200-5205.

［15］Lee C， Sarwar S S， Panda P， et al. Enabling spike-based backpropagation for training deep neural network architectures［J/OL］. Frontiers in Neuroscience，2020，14. （2020-02-28）. https：//doi.org/10.3389/fnins.2020.00119.

［16］Zheng Hanle， Wu Yujie， Deng Lei， et al. Going deeper with directly trained larger spiking neural networks［C］//Proc of the 35th AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2021： 11062-11070.

［17］Zhu Yaoyu， Fang Wei， Xie Xiaodong， et al. Exploring loss functions for time-based training strategy in spiking neural networks［C］//Proc of the 37th Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2023： 65366-65379.

［18］Com瘙塂a I M， Potempa K， Versari L， et al. Temporal coding in spiking neural networks with alpha synaptic function： learning with backpro-pagation［J］. IEEE Trans on Neural Networks and Learning Systems， 2021， 33（10）： 5939-5952.

［19］Kheradpisheh S R， Mirsadeghi M， Masquelier T. BS4NN： binarized spiking neural networks with temporal coding and learning［J］. Neural Processing Letters， 2022，54（2）： 1255-1273.

［20］Mirsadeghi M， Shalchian M， Kheradpisheh S R， et al. STiDi-BP： spike time displacement based error backpropagation in multilayer spiking neural networks［J］. Neurocomputing， 2021， 427： 131-140.

［21］Zhang Malu， Wang Jiadong， Wu Jibin， et al. Rectified linear postsy-naptic potential function for backpropagation in deep spiking neural networks［J］. IEEE Trans on neural networks and learning systems， 2021， 33（5）： 1947-1958.

［22］Zhu Yaoyu， Yu Zhaofei， Fang Wei， et al. Training spiking neural networks with event-driven backpropagation［C］//Proc of the 36th International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2022： 30528-30541.

［23］Cheng Xiang， Hao Yunzhe， Xu Jiaming， et al. LISNN： improving spiking neural networks with lateral interactions for robust object recognition［C］//Proc of the 29th International Joint Conference on Artificial Intelligence. 2020： 1519-1525.

［24］Jin Yingyezhe， Zhang Wenrui， Li Peng. Hybrid macro/micro level backpropagation for training deep spiking neural networks［C］//Proc of the 32nd International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2018： 7005-7015.

［25］Zhang Wenrui， Li Peng. Spike-train level backpropagation for trai-ning deep recurrent spiking neural networks［C］//Proc of the 33rd International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2019： article No. 701.

［26］Zhao Dongcheng， Zeng Yi， Li Yang. BackEISNN： a deep spiking neural network with adaptive self-feedback and balanced excitatory-inhibitory neurons［J］. Neural Networks， 2022， 154： 68-77.

［27］Yang Yukun， Zhang Wenrui， Li Peng. Backpropagated neighborhood aggregation for accurate training of spiking neural networks［C］//Proc of the 38th International Conference on Machine Learning.［S.l.］： PMLR， 2021： 11852-11862.

［28］Wu Hao， Zhang Yueyi， Weng Wenming， et al. Training spiking neural networks with accumulated spiking flow［C］//Proc of the 35th AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2021： 10320-10328.

［29］Fang Wei， Yu Zhaofei， Chen Yanqi， et al. Incorporating learnable membrane time constant to enhance learning of spiking neural networks［C］//Proc of IEEE/CVF International Conference on Computer Vision. Piscataway， NJ： IEEE Press， 2021： 2641-2651.

［30］Meng Qingyan， Xiao Mingqing， Yan Shen， et al. Training high-performance low-latency spiking neural networks by differentiation on spike representation［C］//Proc of IEEE/CVF Conference on Compu-ter Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2022： 12434-12443.

［31］Rathi N， Roy K. DIET-SNN： a low-latency spiking neural network with direct input encoding and leakage and threshold optimization［J］. IEEE Trans on Neural Networks and Learning Systems， 2023， 34（6）： 3174-3182.

［32］Horowitz M. 1.1 computing’s energy problem （and what we can do about it）［C］//Proc of IEEE International Solid-State Circuits Conference Digest of Technical Papers. Piscataway， NJ： IEEE Press， 2014： 10-14.

［33］Yang Helin， Lam K Y， Xiao Liang， et al. Lead federated neuromorphic learning for wireless edge artificial intelligence［J］. Nature Communications， 2022， 13（1）： article No. 4269.

［34］Gerstner W， Kistler W M. Spiking neuron models： single neurons， populations， plasticity［M］. Cambridge： Cambridge University Press， 2002.