时变路网下考虑碳排放的需求响应型公交调度优化模型

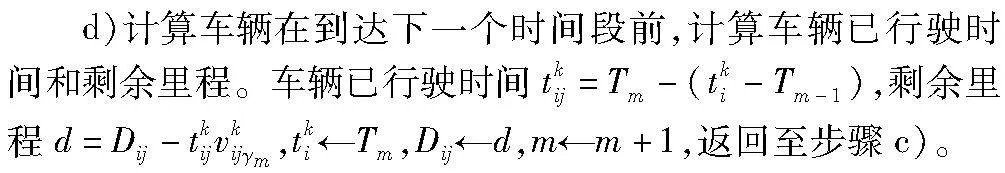
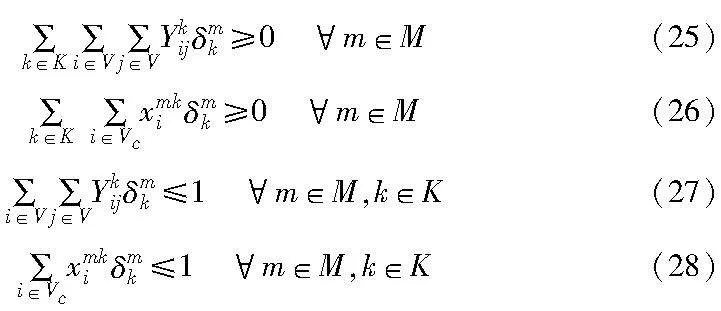
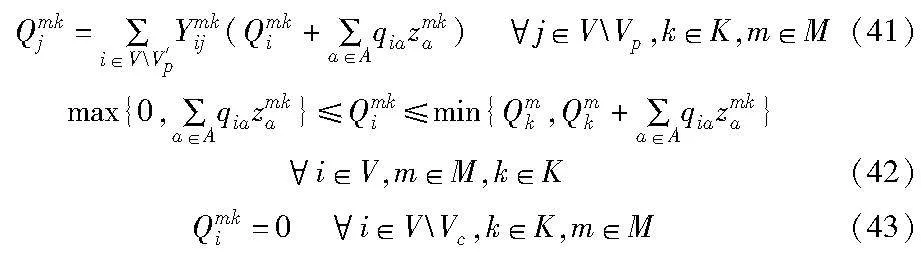
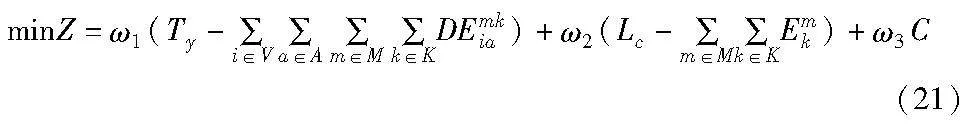
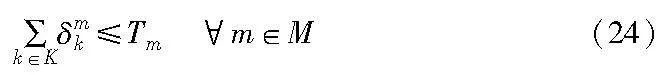
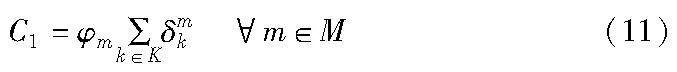
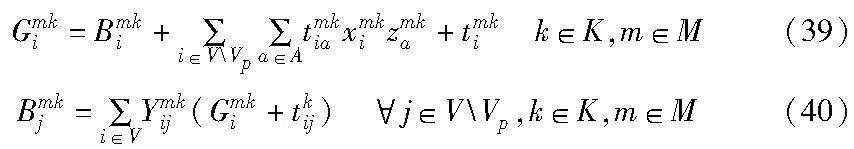
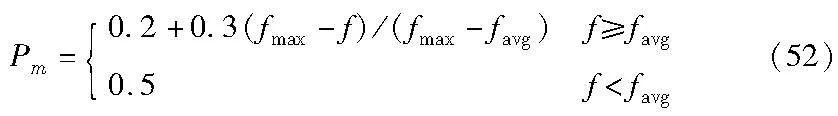
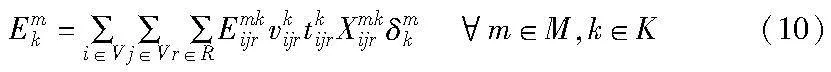
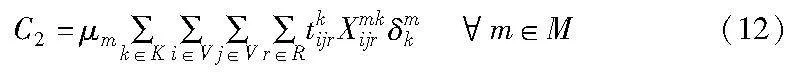
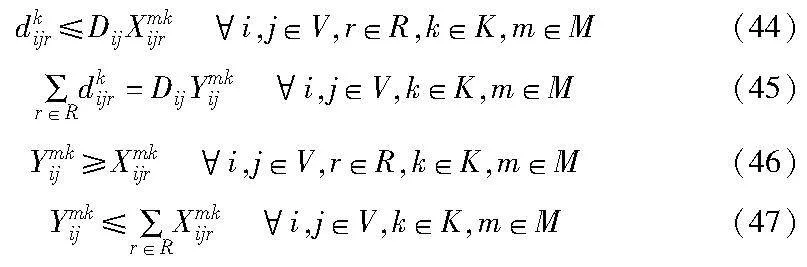
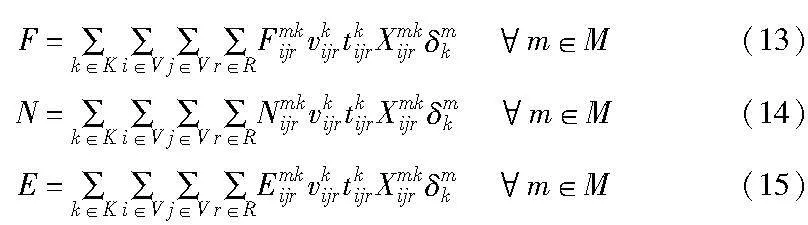
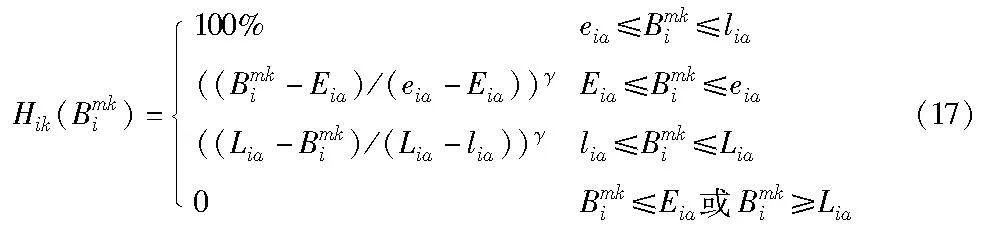
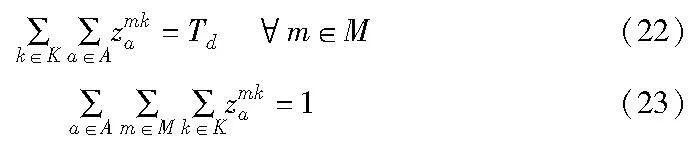
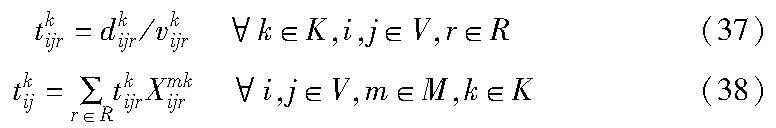
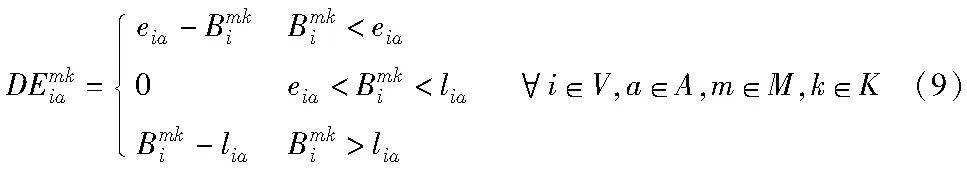
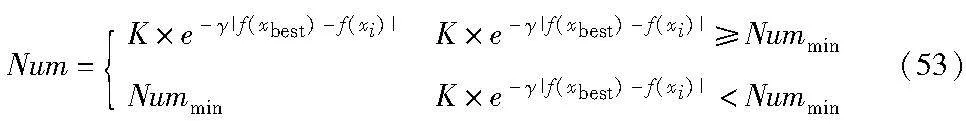
摘 要：以往对需求响应型公交的研究中，鲜有考虑到时变路网、碳排放等因素对车辆调度的影响，需要对现有研究的局限性进行改进。针对当前“双碳”背景下存在传统燃油公交与电动公交混合运行的现状，结合两者特性分别给出约束条件、成本和碳排放测算方法，建立包含延误时间、碳排放和运营成本作为优化目标的调度优化模型，并提出了自适应遗传-萤火虫算法用以求解该模型。实验结果表明：a）所提算法改善了传统遗传算法中易陷入局部最优的问题，在基于仿真路网的实验中能使目标函数减少9.1%，平均车辆使用数、平均途经节点数和平均行驶里程数分别减少了0.3辆、4.9个和104.57 km，提高了求解精度；b）模型考虑碳排放影响最高能减少9%的碳排放量，运营成本降低2.9%；c）动态阻抗下的车辆调度方案既贴近实际情况，又能同时降低7.5%的碳排放以及节约5%的运营成本；d）电动公交的引入能得到显著的碳减排效果，但由此带来的成本上升也是不容忽视的。

关键词：时变路网； 碳排放； 需求响应型公交； 自适应遗传-萤火虫算法

中图分类号：U491.2 文献标志码：A 文章编号：1001-3695（2024）07-025-2098-12

doi：10.19734/j.issn.1001-3695.2023.10.0506

Demand-responsive bus scheduling optimisation model considering

carbon emissions under time-varying road network

Abstract：Previous studies on demand-responsive buses rarely considered the impact of time-varying road networks and carbon emissions on vehicle scheduling， indicating the need for improvement in the limitations of existing studies. In response to the current scenario of mixed operation involving traditional fuel buses and electric buses under the backdrop of “dual-carbon”， this study outlined constraints， costs， and methods for measuring carbon emissions based on the characteristics of these two types of buses. It established a scheduling optimization model that incorporates delay time， carbon emissions， and operational costs as optimization objectives， it proposed the use of an adaptive genetic-firefly algorithm. The experimental results show that： a）The proposed algorithm addresses the issue of local optimality common in traditional genetic algorithms. In experiments based on a simulated road network， it achieves a 9.1% reduction in the objective function， along with decreases of 0.3 vehicles， 4.9 nodes， and 104.57 km in average vehicle usage， average route nodes， and average travel distance respectively， enhancing the precision of the solution. b）Considering the impact of carbon emissions， the model can achieve a maximum reduction of 9% in carbon emissions and a 2.9% reduction in operating costs. c）The vehicle scheduling scheme under dynamic impedance is both realistic and achieves simultaneous reductions of 7.5% in carbon emissions and 5% in operating costs. d）The introduction of electric buses yields a significant reduction in carbon emissions， but the associated cost increase is noteworthy.

Key words：time-varying road network; carbon emission; demand-responsive public transport; adaptive genetic-firefly algorithm

0 引言

如今大多城市基建的发展水平逐渐跟不上汽车保有量的快速增长，导致城市供需矛盾日益凸显，由此带来的环境污染问题也愈发突出。传统公交运营模式固化，服务覆盖范围有限，不可能完全实现“门对门”服务，若是转而选择网约车或私家车出行会进一步加剧城市交通拥堵。在此背景下，国家开始大力支持多元化的出行方式来替代以往私家车出行模式，由此需求响应型公交（demand-responsive bus，DRB）得到发展和应用。DRB具有无须换乘、乘坐体验好、准点率高的特点，可以为具有相似需求（例如出行时间和出行地点）的乘客提供便捷出行服务［1］。DRB的运营规划主要包含车辆调度、站点规划、路线规划以及时刻表编制等等，运营企业根据用户需求提前设计路线，并将这些信息提供给乘客，以实现高效率的运营模式。

除了研究DRB的调度优化外，车辆碳排放与成本控制也是本文关心的问题之一。“双碳”目标的提出使得新能源汽车在公交领域得到了广泛应用，许多燃油公交将会被电动公交所取代，但目前并未被全部替代，两种类型公交混合运行的现状仍然存在，因此本文研究的是一个多车型VRP。电动公交尽管采用清洁能源作为燃料，但并不代表其不产生碳排放，只是将碳排放的产生从下游转移到了上游，并且其运行里程受到电池容量限制，无法完成长距离行驶需求，这就需要配置更多车辆完成任务，因此电动公交的使用成本也会更高。如何在混合车型车队的运营模式下，通过合理配置不同类型的车辆使用比例来达到平衡车辆碳排放和运营成本就成为公交企业需要解决的问题。

1 相关研究

当前学者对于DRB调度优化模型的研究集中在模型及算法设计这两个方面。孙倩等人［2］考虑到车辆到站时间的不确定性对车辆调度的影响，以运营商成本和乘车时间成本等组成的系统总成本最小为优化目标；胡迪等人［3］设计了D-K-means聚类算法来确定固定站点和备选站点，并以企业运营成本最小、拒绝预约需求数最小为优化目标；管德永等人［4］通过分析历史乘车请求信息确定需求响应型公交的停靠节点；贺韵竹等人［5］则是根据预约乘客的在站等待时间对票价进行差异化定价，根据客流量变化更新公交发车时刻；Huang等人［6］将实时乘客需求纳入线路优化中，并证明了该方案的可行性；孙会君等人［7］提出了折返站与换乘站协同承担客流疏散任务的应急公交接驳方案，以乘客等待时间最小、公交满载率最大为优化目标；Shen等人［8］将公交线路设计模型分为求解VRPTW和乘客-车辆匹配问题这两个问题进行求解；Chen等人［9］考虑了车辆容量约束、时间约束等条件，以额外旅行时间最小和运营成本最小构建模型；王正武等人［10］研究了同时接送模式下响应型接驳公交运行路径与车辆调度的协调优化问题，以系统运营利润最大为目标构建模型，该模型属于VRPSPD问题；王志建等人［11］引入信任度和用户偏好来衡量每位乘客的信任水平，以行驶距离最短和总信任度最高为目标构建模型；杜太升等人［12］为乘客设置了柔性时间窗惩罚函数，以包括车辆固定成本和延误惩罚成本在内的总成本最小为优化目标构建模型。靳文舟等人［13］将多车型多车场等要素加入到DRB模型中，以车辆固定成本、运输成本和时间窗惩罚函数之和最小为优化目标。

DRB调度优化问题本质还是车辆路径问题，求解算法的精度和速率会直接影响到求解结果的质量。目前，学者们主要采用精确算法和启发式算法作为求解方法。文献［3，14］采用精确算法求解DRB调度优化问题，尽管精确算法能够保证最终的求解结果为最优解，但受限于算例规模限制，若算例规模过大，便无法在可接受时间内找到NP难题的最优解，因此启发式算法的应用更为广泛。孙倩等人［2］设计了遗传-邻域搜索算法用于求解模型，通过与lingo求解器的对比实验证明该算法在求解复杂模型时更有优势；管德永等人［4］采用基于LNS策略的遗传算法求解静态DRB调度问题，算法中注重对初始种群的设计，最后证明该算法具有较好的求解稳定性；Huang等人［6］设计了动态遗传算法来生成静态的初始行车路径，并不断更新动态行车路径以满足实时需求；王正武等人［10，15］首先采用传统遗传算法求解同时接送模式下的公交调度问题，并采用双链编码方式求解，之后对传统遗传算法进行改进，设计了遗传模拟退火算法求解高自由度DRB调度优化问题；Shu等人［16］通过改进后的蚁群优化算法求解模型，采用K-means聚类算法得到车辆停靠节点；靳文舟等人［13，17］首先采用基于精英选择策略的遗传算法求解DRB调度问题，后续的研究对算法进行了提升，提出了混合遗传-蚁群算法对多车型多车场DRB模型进行求解。两种算法都表现出了优质且稳定的求解结果，前者通过在选择操作中以精英选择策略代替传统的轮盘赌选择操作，而后者通过设计初始种群、改进变异操作以及两种算法的有机结合。文献［18，19］都设计了变邻域搜索算法求解DRB调度模型；任婧璇等人［20］在模拟退火算法的基础上引入了自适应邻域机制，以解决带有全服务时间窗约束、容量约束，车队规模确定的DRB调度问题。

当今在以绿色发展为主基调下研究DRB调度问题时，其优化目标中不应只关注用户出行体验以及经济成本，还需要兼顾环境目标，达到节能减排的目的。为此，Erdogan等人［21］提出了绿色VRP（green VRP，GVRP），以油耗最小化作为优化目标建立VRP模型。但车辆在行驶过程中的碳排放会受到实时路况的影响，城市路段在早晚高峰时期可能会形成交通拥堵，考虑以恒速行驶的路径规划方案不符合实际情况，因此在GVRP的基础上，Kuo等人［22］提出了时间依赖型GVRP（time-dependent green VRP，TDGVRP），以油耗最小化作为优化目标构建模型，并采用模拟退火算法求解；Franceschetti等人［23］根据道路拥堵或通畅两种路况设置旅行时间分段函数，并以油耗最小化作为目标函数；Heidari 等人［24］以总成本和碳排放量最小为目标构建模型；珠兰等人［25］以包括油耗成本在内的总成本最小为目标函数构建绿色车辆路径模型，模型中允许车辆选择合适的时间出发以规避拥堵；周鲜成等人［26］基于路段划分策略计算车辆行驶时间，以包括油耗成本、碳排放成本及车辆固定成本等在内的总成本之和作为目标函数构建模型，仿真结果表明该模型能有效降低配送总成本并减少碳排放。

结合以上对DRB模型及算法设计的研究，本文进行了一系列改进。首先，出于实际情境考虑，模型研究场景拓展至同时接送模式下的多车型多车场。其次，为反映城市路网的时变特性，采用了基于时间段划分的车辆行驶时间计算方法。在算法构建方面，现有学者主要在传统启发式算法基础上进行改进，通过调整搜索方式或是将两种算法有机结合以弥补不足，这对于设计新型高效算法来说是不错的思路。

然而，当前DRB调度模型研究多集中于带容量和时间窗约束的VRP，通过对单链染色体中的编码进行变换操作以实现路径的优化，但这一操作在VRPSPD模型中会产生非可行解。文献［10］的编码方式为本文提供了借鉴，采用双层编码系统优化车辆调度和行驶路径，解决了单链染色体编码方式可能产生非可行解的问题。在初始种群设计方面，本文强调了初始种群质量对算法收敛速率的重要性。另外，对于遗传算法的选择、交叉和变异策略，现有方法较为死板，缺乏灵活性，概率的选取较为主观，对于迭代中出现的重复染色体的情况也并未进行处理。鉴于这些不足，设计了自适应遗传-萤火虫算法进行改进。

最后，不同于常见的目标函数构建思路，是以最小化总成本为目标，将乘客延误以及碳排放等转换为惩罚成本，然后与其他运营成本进行加权组合。尽管达到了简化模型的目的，但可能导致为了降低总运营成本而牺牲了乘客乘坐体验和碳排放等因素。与之相反的是本文模型着重关注乘客体验，控制碳排放量，最后才是优化运营成本。为此分别为这三个目标设置了权重并且仅在满足特定条件下才优化运营成本。这一建模思路旨在实现对服务质量、碳排放和运营成本的综合兼顾。文章设置了可允许延误时间和可允许碳排放量，并根据各决策目标的重要程度设置权重系数，构建带容量和时间窗约束的DRB模型，该模型属于TDMDGVRPSPD问题，并设计了新型混合启发式算法对其进行求解。最后通过实际路网案例表明构建的模型及算法能科学规划车辆出发时间及车辆停靠点，相较于改进前的求解算法，所设计算法得到了更好的收敛效果和收敛速度。通过几组仿真实验讨论了碳排放、时间窗、路网阻抗变化以及车型选择对仿真结果的影响，期望本文对于当前“双碳”背景下DRB的大规模应用提供理论参考。

2 模型构建

2.1 问题描述与模型假设

本文主要关注时变路网下需求响应型公交车队的调度优化问题，关键问题包括调度车辆、规划车辆路径、确定出发时间、平衡优化目标等。此外，还需考虑碳排放、乘客体验和路网实时变化等因素，尽管增加了问题的复杂性，但解决这些问题有助于提高运营效益、降低成本，并适应实时变化的交通环境。

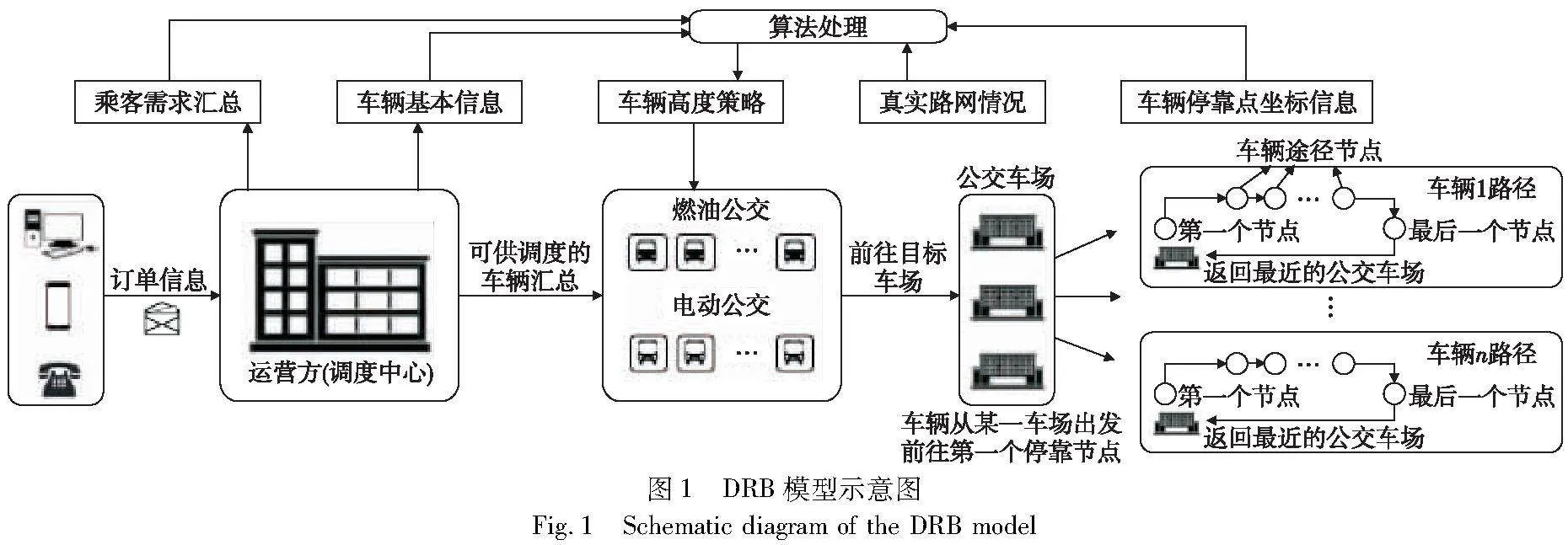
文章构建的具体场景为：在一服务区域内某运营企业拥有多个公交场站以及多辆可供使用的公交车辆，这些车辆可分为燃油和电动两种车型且每种车型的车辆数存在上限。运营方同时开设了若干个车辆停靠点，车辆只会停靠运营方设定的节点，不会随意停靠。乘客中可以任意选择某两个节点作为上下点，并且上下车时间窗、乘客数量都是明确的。运营方会在公交发车前收集信息并通过算法处理完成车辆调度和路径规划工作，平台将优化后的车辆-乘客匹配及路径优化结果等发布给每辆车后，车辆会提前到达某一车场并在规定时间发车。公交从车场开出后行驶至各停靠点接送乘客，并在完成所有乘客的接送任务返回最近的公交场站，其DRB模型示意图如图1所示。

对于前文所研究问题的描述，因其复杂度较高，所以需要对部分条件给出相应假设来降低模型的构建及求解难度。需求响应型公交调度模型在车辆指派过程中应遵循以下基本假设：a）车辆初始状态为空载并且按照调度信息准时从某车场出发；b）默认乘客会在时间窗开始时刻准时等候在预定的上车点，不存在迟到现象；若车辆提前到达，则必须等待目标乘客全部到达并且上车完毕后，才会前往下一地点；c）路网中所有节点都是可连通的，任意两两节点之间距离已知，并且车辆在行驶过程中不考虑红绿灯或者突发事件，也不考虑道路坡度和车辆加速度对碳排放的影响；d）车辆型号以及自重等信息已知，车辆载重等于乘客自重乘以乘客数量，为方便计算，每位乘客自重设定为一固定值，不考虑乘客行李等额外载重。

2.2 时变路网下的车辆行驶时间计算

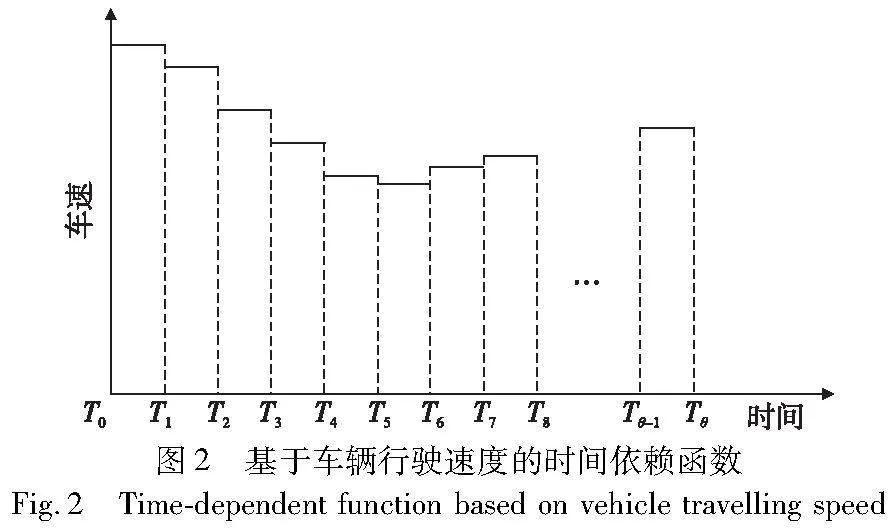
实际道路中路段阻抗具有时变性，车速随着时间的变化而不断变化，使得在时变路网下计算某一路段的行驶时间变得较为困难。本文参考Ichoua等人［27］关于时变路网下车辆行驶时间的计算方法，采用基于行驶车速的时间依赖函数来表现路段的时变性。

如图2所示，将全天中某一段时间T细分为θ个时间段，每一个时间段用γm（m=1，2，…，θ）表示，其中γm=［Tm-1，Tm］，Tm表示第m个时间段的结束时刻。假设车辆k在时间段γm内行驶在路段（i，j）上的行驶速度为vkijγm保持不变，Dij为路段（i，j）的长度，那么车辆k在路段（i，j）上行驶时间的计算步骤如下：

a）令m=1、tkij=0，其中m表示时间段序数，tkij表示已行驶时间。

b）判断车辆出发时间tki的时间段序号。若车辆出发时间tki早于Tm，则直接进入步骤c），否则m←m+1，若车辆出发时间tki仍大于第m+1个时间段的结束时刻Tm+1，则继续累加，直到确认出发时间的时间段序号m，进入步骤c）。

2.3 不同动力能源公交的碳排放测算

本文对于模型中不同能源公交碳排放的测算，主要采用基于距离理论的碳排放测算方法。

2.3.1 燃油公交碳排放计算

燃油公交运行时产生的碳排放量由行驶距离乘以CO2排放因子得到，计算公式如下：

Mc=∑i∑j∑kDijk×Eijk（1）

Eijk=∑i∑j∑kCijk×ρi×qi×ei（2）

式（1）中：i为燃料类型；j为车辆类型；k为行驶条件；Mc为燃油公交的碳排放总量（kg）；Dijk为车辆行驶距离（km）；Eijk为车辆每公里的CO2排放因子（kg/km）。式（2）中：Cijk为车辆每公里油耗（L/km）；ρi为燃料密度（kg/L）；qi为燃料热值（TJ/kg）；ei为所消耗燃料的CO2排放系数（kg/TJ）。

2.3.2 电动公交碳排放计算

电动公交运行时产生的碳排放量估算也是类似思路，但不同之处在于CO2排放因子由当地电力排放因子决定，计算公式如下：

Me=∑i∑j∑kDik×Eijk（3）

Eijk=∑i∑j∑kSECijk×EFij/（Mi×（1-TDLj））（4）

SEC=Cij×ρi×Qi×ηi/3600（5）

式（3）中：i为车辆类型；j为年份；k为行驶条件；Me为车辆出行CO2排放量（kg）；Dik为车辆行驶距离（km）；Eijk为车辆每公里的CO2排放因子（kg/km）。式（4）中：SECijk为车辆每公里耗电率（kW·h/km）；EFij为当地的电力排放因子（kg/kW·h）；Mi为电动公交的充电效率（%）；TDLj为电力传输与分配的平均损耗（%）。式（5）参考国标GB/T 19754—2021，将传统能源公交的油耗量转换为电动公交的耗电量，其中ρi为燃料密度 （g/cm3）； Qi为燃料的低热值（kJ/kg）；ηi为燃料发动机的平均工作效率（%）；Cij为燃油公交在同样行驶条件下的油耗量（L/km）。

2.3.3 车辆油耗计算

由于2.3.1节和2.3.2节中两种能源公交的碳排放测算都会涉及到对车辆油耗的计算，所以这一部分主要通过Barth等人［28］提出的综合排放模型（CMEM）计算得到，本文进行了一定简化，并同时计算了车辆行驶和怠速时的油耗使用量：

式（6）中：Ptract为车辆牵引功率；Cd为空气阻力系数；A为前表面面积（m2）；ρ为空气密度（kg/m3）；v为车辆速度（m/s）；G为车辆净重（kg）；μ为载重量（kg）；g为重力加速度（m/s2）；Cr为滚动阻力系数。式（7）中：P为发动机输出功率（kw）；ε为车辆传动效率；Pacc为车辆附件消耗功率。式（8）中：FR为燃油消耗率（g/s）；为当量燃空比；N为发动机转速（r/s）；Nidle为发动机的怠速转速（r/s）；V为发动机排量（L）；η为发动机的指示热效率；K为发动机摩擦因子，Kidle为怠速时的发动机摩擦因子。

2.4 符号说明

模型中参数、变量及决策变量释义如表1所示。

2.5 数学模型

1）决策目标

用户出行体验是公交调度优化过程中所需考虑的第一要务，因此将其列为重要目标进行优化。出行体验的一个重要衡量标准即乘车延误时间，在车辆调度中应尽可能保证车辆到达目的地的时间位于时间窗范围内。车辆延误时间的计算公式如式（9）所示。

模型中需要保证乘客总延误时间不高于允许延误时间Ty，当Ty=0时，表明模型要求每一位乘客都能准时上下车。当总延误时间超出允许延误时间Ty时，会严重影响解的优越性。当车型为m时，车辆k的碳排放量计算公式如式（10）所示。

模型的第二要务为限制碳排放量，若是简单以碳排放量最小化作为目标函数，那么可能会忽略运营成本对车辆调度的影响。因此，只需要保证所有车辆的碳排放不高于允许排放量Lc即可，同样地，当碳排放量超出允许排放量Lc时，也会影响解的优越性。

为了确保企业能够持续性的运营，在保证乘客出行体验并且较好地控制碳排放量后，应以尽可能低的运营成本来完成所有乘客的出行需求。运营成本主要由车辆固定使用成本、车辆使用时间成本、车辆油耗成本（车辆充电成本）、碳排放成本以及车辆延误时间成本组成。

车辆固定使用成本C1主要包含司机、设备使用等一系列费用，与车辆行驶里程、车辆损耗等无关，只与车辆使用数有关，可由式（11）表示为

车辆使用时间成本C2一般与各车型车辆的时间使用长度有关，可由式（12）表示为

路网中所有车辆的燃油消耗量F（耗电量N）和碳排放量E可表示为

那么车辆油耗及充电成本C3、车辆碳排放成本C4可以表示为

C3=αf×F+αe×N，C4=αc×E（16）

车辆延误时间成本只与车辆延误时间有关，当车辆在乘客期望时间窗之内到达预定节点时，便不会产生延误费用，反之，通过车辆到达各节点的延误时间DEmkia乘以单位延误时间的惩罚费用αh得到，延误时间的计算如式（9）所示。

车辆单位延误时间的惩罚费用αh由乘客满意度惩罚成本乘以满意度函数得到。引入最大可容忍的早到时间及晚到时间t1、t2，则Eia=eia-t1、Lia=lia+t2。当车辆在乘客期望时间窗之内到达时，乘客满意度为100%；当车辆在乘客期望时间窗［eia，lia］之外但在最大可容忍时间窗［Eia，Lia］之内到达时，乘客满意度便会随着到达时间与期望时间窗差值的增大而减小，呈现非线性的变化趋势；当车辆在时间窗［Eia，Lia］之外到达，乘客满意度为0，即车辆到达乘客节点时间的满意度函数Hik（Bmki）如式（17）所示，其中γ表示满意度敏感系数，本文设定γ≠1，即乘客满意度与距期望时间窗的差值呈非线性关系：

引入满意度惩罚成本Cr，则车辆单位延误时间的惩罚费用αh以及车辆延误时间成本C5可由式（18）（19）得到：

由此，企业运营成本C如式（20）所示。

C=C1+C2+C3+C4+C5（20）

综上所述，采用线性加权法对各个决策目标赋予相应的权重系数后进行加权求和得到最终的目标函数。权重系数的设定应当反映出各决策目标的关键程度。鉴于本文将乘客延误时间列为首要优化目标，其次是碳排放，最后是运营成本，假设乘客延误时间、碳排放以及运营成本对应的权重系数分别为ω1、ω2、ω3，则权重系数的设置应保证ω1>>ω2>>ω3。由此，可以将运营商的目标函数写为如下形式：

2）相关约束条件

对于乘客所提交的所有订单，运营方都必须提供服务，并且任意一订单有且只有一辆车为其进行服务：

运营方对于m车型车辆的总使用数不能超过该车型的最大可使用车辆数：

本文考虑的是在车辆停靠节点固定的情况下对乘客的配送问题，某一节点可能会作为多位乘客的下车点或者是上车点，也会被车辆多次访问，因此，某一节点也可能会存在车辆停靠多次的情况，也可能只停靠一次或不停靠；同样地，某一路段可能存在多辆车都需经过的情况，但也可能存在车辆只经过一次或不经过的情况。但同一辆车在同一节点上最多停靠1次，在同一路段上也最多经过1次，不允许折返：

车辆实际使用数量不超过最大可使用车辆数，并且每辆车最多只能使用1次，所有车辆从某一公交车场出发，完成乘客配送任务后必须返回公交车场进行燃油（电量）补充和人员休息：

车辆在到达与离开的停靠节点必须是同一个节点，节点处的车流量必须保持守恒：

车辆单程行驶距离不能超过最大单程行驶距离限制：

式（37）（38）表示车辆在路段（i，j）上全程行驶时间的计算方法：

车辆离开某节点的时间等于其到达该节点时间加上车辆服务时间和车辆等待时间；且车辆到达某节点的时间等于其离开前面停靠节点时刻加上两节点之间的行程时间：

式（41）表示车辆到达某一节点的载客量等于车辆到达前一个节点时的载客量加上该节点的上车人数；式（42）确保每条车辆路径中，车辆载客量不超过车辆最大载客量；式（43）确保车辆从公交车场出发以及结束配送任务后返回车场时，车辆载客量为0：

式（44）（45）显示了变量dkijr与Dij之间的限制关系；式（46）（47）显示变量Xmkijr与Ymkij之间的限制关系：

其他变量约束为

3 算法设计

本文考虑同时接送模式、多中心多车型配送、时变路网等因素对配送方案制定的影响，属于NP-hard问题，求解过程复杂，因此采用启发式算法进行求解。遗传算法（genetic algorithm，GA）引入自然界中的进化思想，具有较优的全局搜索能力，但搜索具有盲目性，对初始种群有一定依赖性。萤火虫算法（firefly algorithm，FA）是一种模拟萤火虫交配行为的启发式算法，寻优能力强并且能保证更好的收敛速度，将两种算法进行结合，从而提高算法的整体求解能力。本文根据模型特点，设计自适应遗传-萤火虫算法（adaptive genetic and discrete firefly algorithm，AGDFA）进行求解。

3.1 算法流程设计

针对本文构建的DRB模型，设计了相应的AGDFA进行求解，如图3所示。大致流程如下：

a）通过订单上车点的时间窗下限对所有订单进行分组后生成初始种群，对种群中各染色体进行编解码，得到目标函数值和适应度值，将在3.3节中详细阐述；

b）判断算法迭代次数是否达到算法终止条件，若是，则直接输出最优解，否则继续进行迭代操作；

c）通过自适应遗传算法对染色体分别进行选择、交叉和变异操作，将在3.5节中详细阐述；

d）删除种群中重复染色体，之后随机产生的染色体补齐种群规模；

e）通过离散萤火虫算法再对染色体进行进化操作后，更新车辆出发及返回地点和时间，将在3.6节中详细阐述；

f）更新种群中染色体后，对种群中各染色体进行解码，得到目标函数值和适应度值，返回至流程b）。

3.2 初始种群生成

初始解的质量很大程度上影响算法的求解质量和求解效率，若是随机生成初始种群，在产生大量不可行解的同时，还会增加迭代次数。为保证生成的初始种群中各染色体的有效性，设计“先订单后节点”的两阶段方法生成可行解。首先对订单进行分组并确定归属，之后确定车辆到达各节点顺序，最后确定发车时间、车辆在配送任务完成后返回的车场编号以及车辆到达各节点的具体时间。此方式不仅保证初始种群中全体染色体均为可行解，并且具有一定随机性，增加了初始种群的多样性。

具体步骤如下：

假定运营方准备为n个乘客订单提供服务，最大可使用车辆数为k。

阶段1：订单分组并确定归属。

a）随机派遣一辆车（车型不限），再随机生成正整数num（n/k≤num≤2n/k），根据订单中上车点期望时间窗的下限从早到晚对所有未服务订单进行排序，从前面若干个未服务的订单中随机选取一个作为新派车辆的第一个服务对象，距离第一服务对象最近的公交车场会作为该车辆的出发点。

b）对于前一个订单上车点的时间窗下限eia，从剩余未服务订单中找出所有上车点晚于eia的订单，并从前几个订单中随机抽取一个订单作为后续服务对象；若不存在上车点晚于eia的订单，那么从未服务订单中找出上车时间窗下限离eia最近的订单作为后续服务对象。

c）如果当前车辆的服务订单数未达到num，则返回步骤b）；否则当前车辆的订单分配完成并重新派遣一辆车。若剩余未服务订单数少于num，则新派车辆会接收所有的未服务订单，进入下一步，否则返回步骤a）。

d）检查是否有某些冲突订单分配在同一车辆的情况（某订单的上车点为另一订单的下车点，其上车点又是前一订单的下车点，车辆需往返服务，不符合约束），若是，返回步骤a）重新分配订单，否则在所有乘客的配送任务和车辆调配都安排完毕后，调度层编码完毕。

阶段2：确定车辆具体行驶路径以及车辆出发时刻。

e）根据车辆调配和订单分配信息提取车辆出发点和需服务订单的上下车点，首先将每辆车的出发点以及需服务订单的上车节点进行组合，根据乘客上下车顺序插入各订单的下车节点后组成车辆行驶路径。

f）检查车辆行驶路径是否能够精简，是否存在某节点多次停靠的情况，如果是，按照乘客上下站点约束对车辆重复经过的节点进行合并，否则进入下一步。

g）判断车辆在行驶过程中是否存在不满足容量约束的情况，如果是，那么对车辆行驶路径进行调整，使其满足容量约束，否则车辆行驶路径生成完毕。

h）距离车辆行驶路径首个途径节点最近的车场会作为车辆出发点，距离最后一个途径节点最近的车场会作为车辆最终目的地。以各车辆服务的首个订单的时间窗下限作为车辆到达该订单上车点的时刻，由此计算车辆从公交车场出发的时刻。若计算得到车辆出发时刻早于可允许的最早出发时刻，那么以最早出发时刻作为车辆出发时刻。

3.3 染色体编解码方式

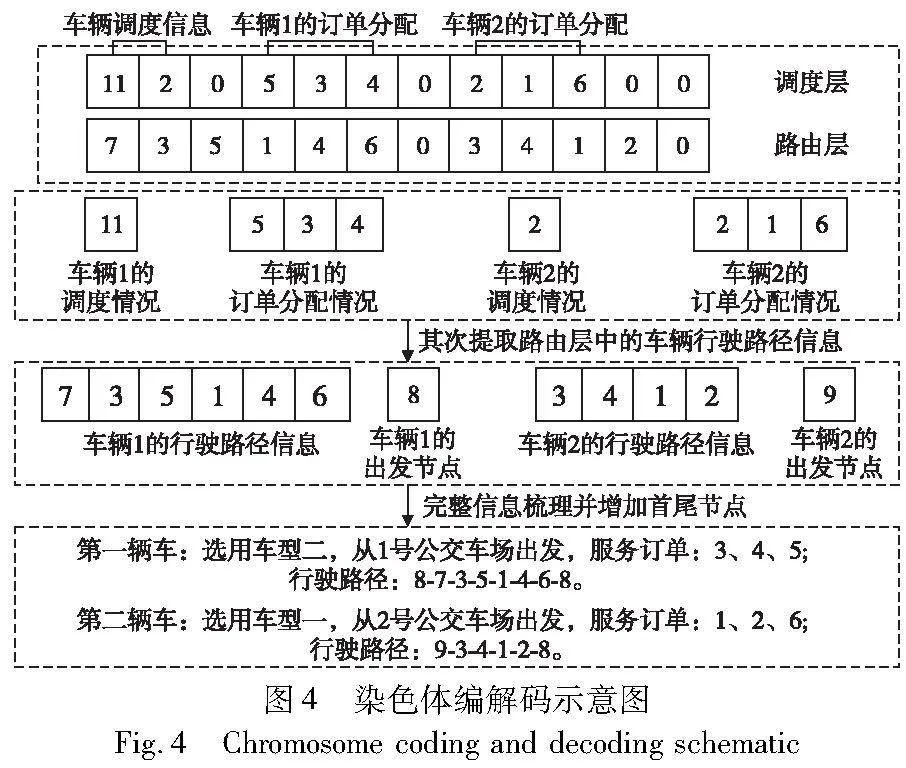
为了解决TDMDGVRPSPD中关于车辆行驶路径和订单分配的双重决策问题，设计了一个双层整数编码系统，它包含调度层和路由层，其中调度层主要包含车型选择、出发点以及订单分配信息，而路由层包含车辆途径节点的全部信息。这两层编码是以调度层为先、路由层在后的顺序构造染色体。

图4为染色体编解码方式示意图，以6个订单、7个途径节点（编号1～7）和2个公交车场（编号8、9，假设1号车场编号为8，二号车场编号为9）为例。每辆公交的调度信息采用10（k-1）+n的表达方式，即第k种车型的公交从n号公交车场中出发，车辆调度信息末端加入0后作为调度层最前端存在；而后将每辆公交的需服务订单号加入0后依次添加到调度层中，因此在调度层中，第i辆车需服务的订单编号为第i个0到第i+1个0之间的所有编号，这些订单不存在先后服务顺序，而是订单分配结果。调度层生成完毕后开始对路由层进行编码。提取每辆车的调度信息和订单分配情况，依据每个需服务订单的具体上下节点编号，生成车辆依次途径的节点顺序，不同车辆间途径的节点用自然数0隔开，在路由层末端加入0以表示编码结束。如图4所示车辆1需服务订单3、4、5号，调度信息11，由此可知车辆1为1号车型，从1号车场（节点编号8）出发，再根据服务订单的上下节点随机生成车辆1需依次途径的节点顺序，图4中的示例为7、3、5、1、4、6，再通过计算得到车辆目的地后得到最终的车辆1行驶路径，出发时刻计算见3.2节步骤h），车辆2的具体行驶信息生成也是同理。

3.4 染色体适应度值计算

由于本文目标函数为最小化问题，所以染色体的适应度值可设置为目标函数值的倒数乘以某一定值，适应度值越大，表明该染色体越优秀，传承到下一代的几率也就越大。

3.5 AGA进化操作

AGA进化操作是指采用遗传算法思想将染色体从较劣解转变为较优解的操作，主要包括选择操作、交叉操作以及变异操作，通过不停地迭代达到优化车辆调度、车辆行驶路径和车辆使用数的目的。

3.5.1 选择操作

选择操作主要采用精英选择策略和随机遍历选择策略相结合的方式。首先采用精英选择策略按一定比例从种群中筛选出较优个体直接进入下一代，对于剩余个体则采用随机遍历选择策略挑选出合适个体填充子代种群。随机遍历选择策略可以看做改进版的轮盘赌法，采用单次多个体选取方式替代轮盘赌中单次单个体选取方式，使得表现不佳的个体也有较大的机会被选择，保证了种群多样性。

3.5.2 交叉操作

为提升算法收敛性能，本文设置了自适应交叉概率，根据新生成个体的适应度调整交叉概率，在迭代前期以较大的概率进行交叉操作，增加解的多样性，在迭代后期以较小的概率进行交叉操作，避免破坏较优解。自适应交叉概率计算方法如式（51）所示。

其中：fbest是交叉操作中父代最优个体的适应度值；favg是所有个体的平均适应度值；fmax为所有个体适应度的最大值。

交叉操作包含订单信息交换和节点信息交换。订单信息交换是将两条父代染色体中分别随机选取一辆车的订单信息进行交换，之后再对交换后的染色体进行修复；节点信息交换是将某一车辆路径内的随机两个节点位置进行互换。

3.5.3 变异操作

变异操作的目的在于增加种群的多样性，加强算法的搜索能力，结合目前各种变异方式和本文所研究问题，采用两种不同变异操作达到减少车辆使用数量和改善车辆行驶路径的目的。对于变异概率的选取，这与交叉概率的选取理念一致，设置自适应变异概率，根据新个体适应度调整变异概率。自适应变异概率的计算方法如式（52）所示。

其中：fmax为所有个体适应度的最大值；f为个体适应度值；favg为所有个体的平均适应度值。

变异操作包含车型使用变异和订单分配变异。车型使用变异是指在不影响原有车辆行驶路径且不违反约束的基础上，改变某一车辆的使用车型；订单分配变异的目的是尽可能减少染色体中所使用的车辆数，具体操作是在父代染色体中随机挑选出订单数最少的车辆，删除该车辆需服务订单以及订单对应的行驶路径，然后将删除后的订单重新插入到其他车辆中去，在满足所有约束的前提下依据订单分配情况重新生成行驶路径。

3.6 DFA进化操作

首先模拟萤火虫自然行为按适应度值将染色体分为最优染色体（第一类染色体）、除最优外的较优染色体（第二类染色体）以及除去前面两类后的剩余染色体（第三类染色体）三类。其次人为假设染色体活动顺序，第一类染色体有且仅有一个，并且是不活动的，目的是为了保存当前最优解，但是在迭代过程中，最优染色体的角色是动态变化的。第二类染色体最先开始位置更新，它们不会受到最优染色体的影响，而是搜索空间中四处搜寻，扩大搜索范围，继续寻找最优解。若在搜索过程中发现比当前最优解更好的解，则替换掉当前最优染色体。而后则是第三类染色体按随机顺序开始更新位置，在收到最优染色体的吸引后，向其方向移动。若在移动过程中发现比当前最优解更好的解，则立刻替换掉当前最优解，尚未移动的染色体也会向新的最优染色体移动。

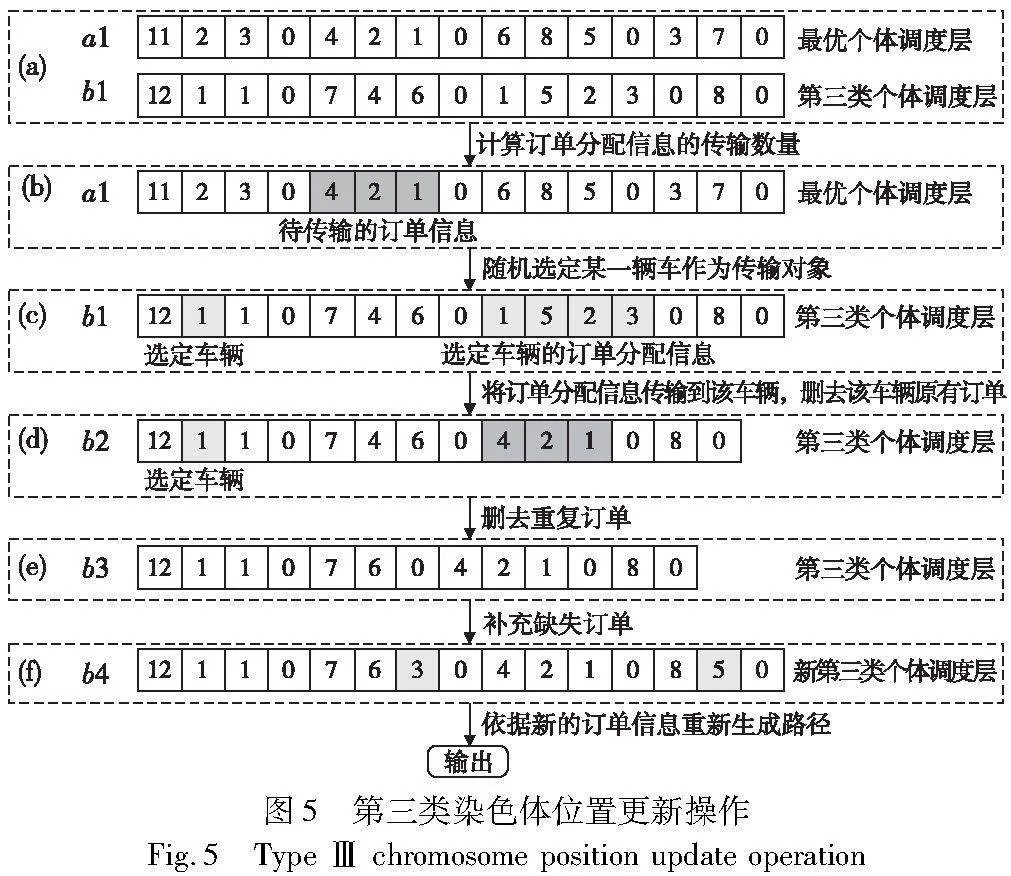
由于在离散优化问题中对个体移动方向、移动步长的确定较为困难，所以针对本文编码方式设计了一种有效的解决方法。第二类染色体在位置更新的过程中不会受到最优染色体的影响，因此更新过程模仿3.5.3节中的变异操作。第三类个体受到最优个体的影响，会逐渐向最优个体移动，通过将最优个体中某一车辆的（全部或部分）订单分配信息传输到第三类个体中，从而达到逐渐向最优个体靠拢的目的。订单分配信息的传输数量根据个体与最优个体两者间适应度差值的大小而决定，并随着适应值差的增大而逐渐减小，计算公式如下：

其中：Num代表订单分配信息的传输数量；Nummin表示最少传输数量；K代表最大可传输信息数，以最优个体中单辆车的最大分配订单数为准；γ表示光吸收系数；f（xbest）表示最优个体的适应度；f（xi）表示个体i的适应度。

为了进一步理解本文第三类个体的位置更新操作过程，采用共计8个订单、3辆车和3个车场为例对第三类个体的位置更新操作进行说明。图5（a）分别模拟了最优个体调度层和第三类个体调度层的情况，假设在经过计算后Num数值为3，并且最优个体中第一辆车和第二辆车中订单信息数量均可满足传输条件，图5（b）中选择将第一辆车的调度信息传输给第三类个体。

在第三类个体随机选择一辆车作为传输对象，将订单分配信息传输到该车辆后，删去该车辆原有订单后再将重复订单删去，假如某一车辆的所有订单都被删去，那么该车辆对应车型、行驶路径也会一并删去，总使用车辆数-1。将缺失订单补充到除选定车辆之外的其他车辆上，最后依据新的车辆调度信息重新生成符合约束的路径，由此，新的第三类个体构建完毕。以图5（c）～（f）为例，选定第二辆车作为传输对象，在将订单4、2、1传输到该车辆后，再将该车辆的原有订单全部删除。将缺失订单3、5分配到除第二辆车之外的其他车辆上，根据新的订单信息生成路径后输出。

3.7 其他处理操作

为了进一步增加种群中染色体的多样性，提高收敛效率，在染色体每次经过GA进化操作（选择、交叉、变异）和DFA进化操作后，还需要进行以下处理操作。

a）更新车辆出发和返回信息。在所有进化操作完成后，根据车辆首个途径节点所在的位置，选择距离最近的公交车场作为该车辆的出发点，距离车辆最后一个途径节点最近的车场会作为车辆的最终目的地。首个订单的时间窗下限作为车辆到达该订单上车点的时刻，由此计算车辆从公交车场出发的时刻。若计算得到的车辆出发时刻早于可允许的最早出发时刻，那么以最早出发时刻作为车辆出发时刻。倘若更新后的染色体适应度并不优于更新前的染色体适应度，那就不更新车辆出发和返回信息。

b）重复染色体删除操作。算法中自适应交叉概率值和自适应变异概率值均小于1，因此会有一定概率出现重复染色体。当概率较小时，染色体种群中出现重复染色体的几率就越大，重复的染色体过多会影响算法的求解性能，因此将重复的染色体进行删除是有必要的，能够在一定程度上加快算法收敛速度。对于重复染色体也不是全部删除，而是根据删除概率ε进行随机删除，ε的取值分为两种情况：

对于ε1和ε2的取值，应保证0<ε1<ε2≤1，原因在于与最优解相同的染色体不应被过多删去。保证算法进一步收敛，与最优解不同的染色体可以少量保留或者不保留，保证种群多样性。

在删除重复染色体后，为了增加种群多样性，将会随机生成新染色体来补齐种群规模，这能够进一步提升算法的收敛能力，避免算法陷入局部最优。

4 实际路网仿真实验与分析

首先通过MATLAB R2017a对多个标准算例进行编程求解，验证模型和算法的有效性和可靠性。此外，为模拟真实情况，构建基于实际路网的仿真实验，以检验在不同情况下的仿真结果。

4.1 仿真环境简介及相关参数取值

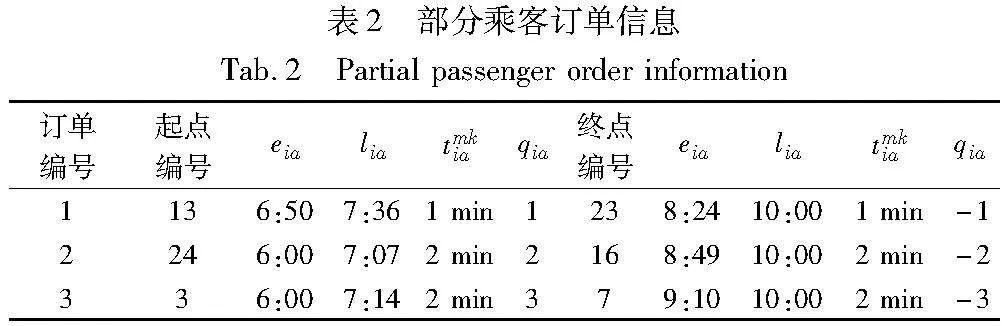
为了准确验证DRB模型以及求解算法的有效性与可靠性，需要结合实际路网进行仿真与分析。仿真对象包括25辆车和53个乘客订单，仿真区域包括上海市闵行区、松江区和徐汇区，在仿真区域内随机选取了25个地点作为车辆停靠点（编号1～25），并额外选取了3个地点作为公交车场（编号26～28），各节点间距离以车辆导航时显示的最短行驶距离为准，如图6所示，表2给出了部分乘客订单信息。

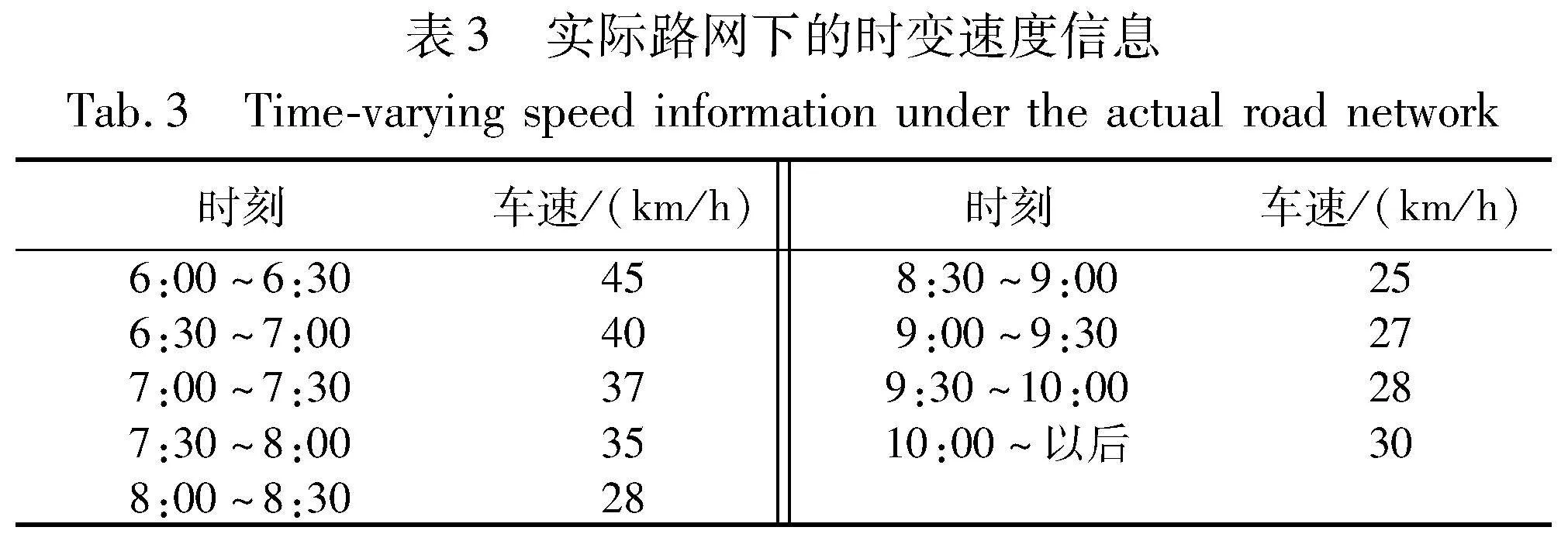
假设车辆最早出发时刻为6：00，允许总延误时间Ty=1 500 min，碳排放标准Lc=1 t CO2，传统能源公交的最大可使用车辆数T1=15，纯电动公交的最大可使用车辆数T2=10，两种车型的最大载客量均为20，两种车型车辆的最大单程行驶距离限制d1max=500、d2max=200，满意度惩罚费用Cr=10，最大可容忍的早到时间t1及晚到时间t2分别为40 min和20 min，满意度敏感系数γ=0.4，燃油公交的固定使用费用φ1=50，使用时间成本μ1=10，单位油耗成本αf=7.31；电动公交的固定使用费用φ2=100，使用时间成本μ2=20，单位油耗成本αe=0.6，车辆碳排放成本αc=0.07，种群规模为30，最大迭代次数为500次，道路时变速度信息如表3所示，单位：km/h。

4.2 模型及算法有效性与可靠性验证

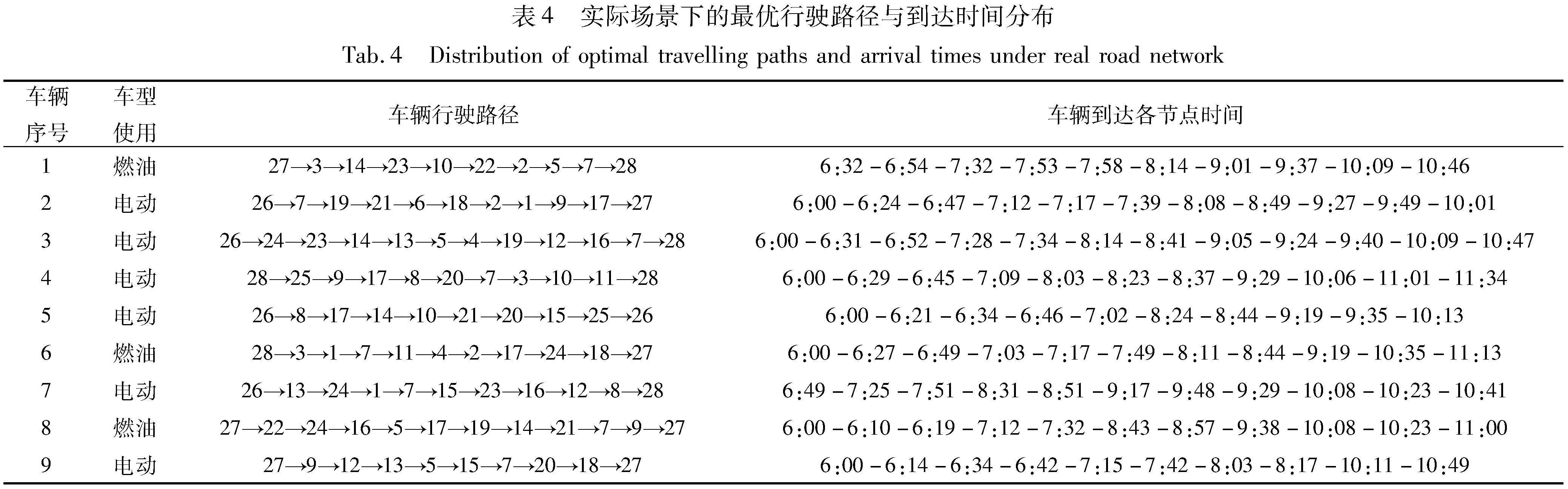
首先采用AGDFA对上文中基于实际路网状况下的仿真实验进行求解，程序共运行10次，得到的最优车辆路径及配送时间分布如表4所示。

表4中“车辆行驶路径”一栏中，第一个数字表示车辆出发车场编号，最后一个数字表示车辆完成任务后返回的车场编号，其余数字代表车辆途径节点。在“车辆到达各节点时间”一栏中，第一个数字表示车辆从某公交车场出发的具体时间，最后一个数字代表车辆完成配送任务后回到公交车场的时间，其余数字代表到达各节点时间。

由表4可知：a）经过AGDFA的500次迭代后，能够生成符合模型约束的可行解，不同类型车辆的使用限制、乘客上下节点约束等均能得到满足。b）各车辆的途径节点数差异不大，大约都在10个节点左右，并且大部分车辆出发能够在最早出发时刻出发，只有1号和7号在完成配送任务返回车场时，仍有部分车辆尚未出发。之所以出现这样的差别，其原因在于每一个订单上下点的时间窗都有较大差异，并且目标函数值的计算很大程度上与延误时间相关。c）电动公交的使用数量远多于燃油公交使用数，其原因在于前者行驶过程中的单位碳排放量较少，且在决策目标中，碳排放优化的优先级高于运营成本。

4.3 自适应遗传-萤火虫算法与其他同类算法的对比

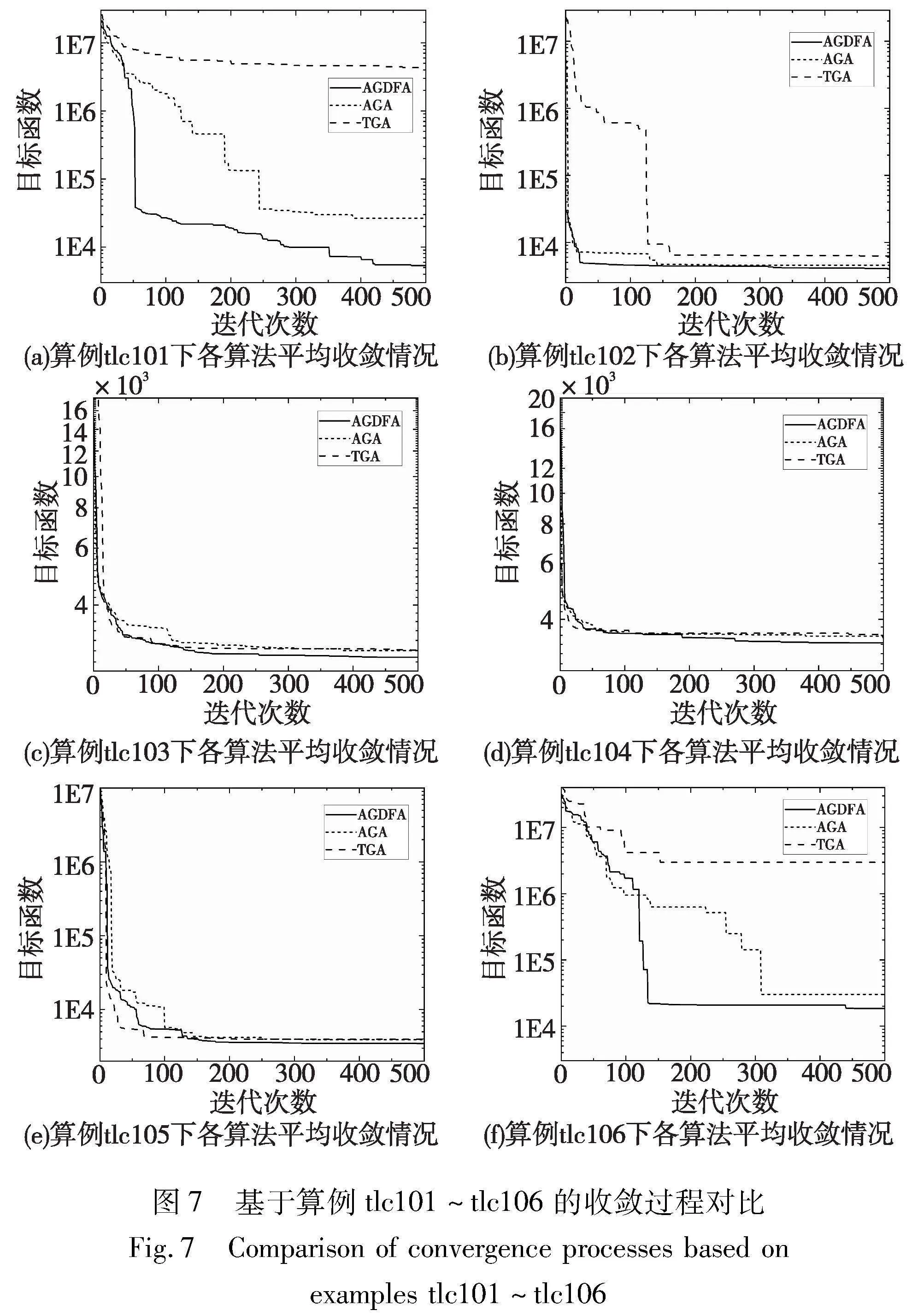
为了对比本文所设计的自适应遗传-萤火虫算法与同类求解算法的收敛性能和求解结果差异，本文分别采用传统遗传算法（TGA）、自适应遗传算法（AGA）和自适应遗传-萤火虫算法（AGDFA）三种算法，采用Li and Lim标准算例来进行测试。由于Li and Lim算例是针对VRPPD相关模型开发的算例，所以为了使算例适用于本文提出的模型，对原算例进行了一定修改后生成新算例tlc101～tlc106。

算例较先前实验有略微不同，因此部分参数有一定改变。分别对算例tlc101～tlc106进行逐一求解，经过10次迭代后的算法平均收敛过程如图7所示。

由图7所示，与传统遗传算法相比（TGA），本文设计的自适应遗传算法（AGA）和自适应遗传-萤火虫算法（AGDFA）在求解DRB调度模型时得到了较优的收敛性能。由于算例tlc101和tlc106中各订单的时间窗长度较短，所以不太容易得到乘客总延误时间低于允许延误时间的解。从收敛曲线可以看出，TGA对于这类问题的求解能力一般，并且容易在收敛早期就陷入局部最优中，在此基础上得到进一步改进的AGA显示了较好的求解能力，能够分别在较短的迭代次数内接近问题的最优解，AGDFA在AGA的基础上引入萤火虫算法思想，进一步加强了算法的全局搜索能力。

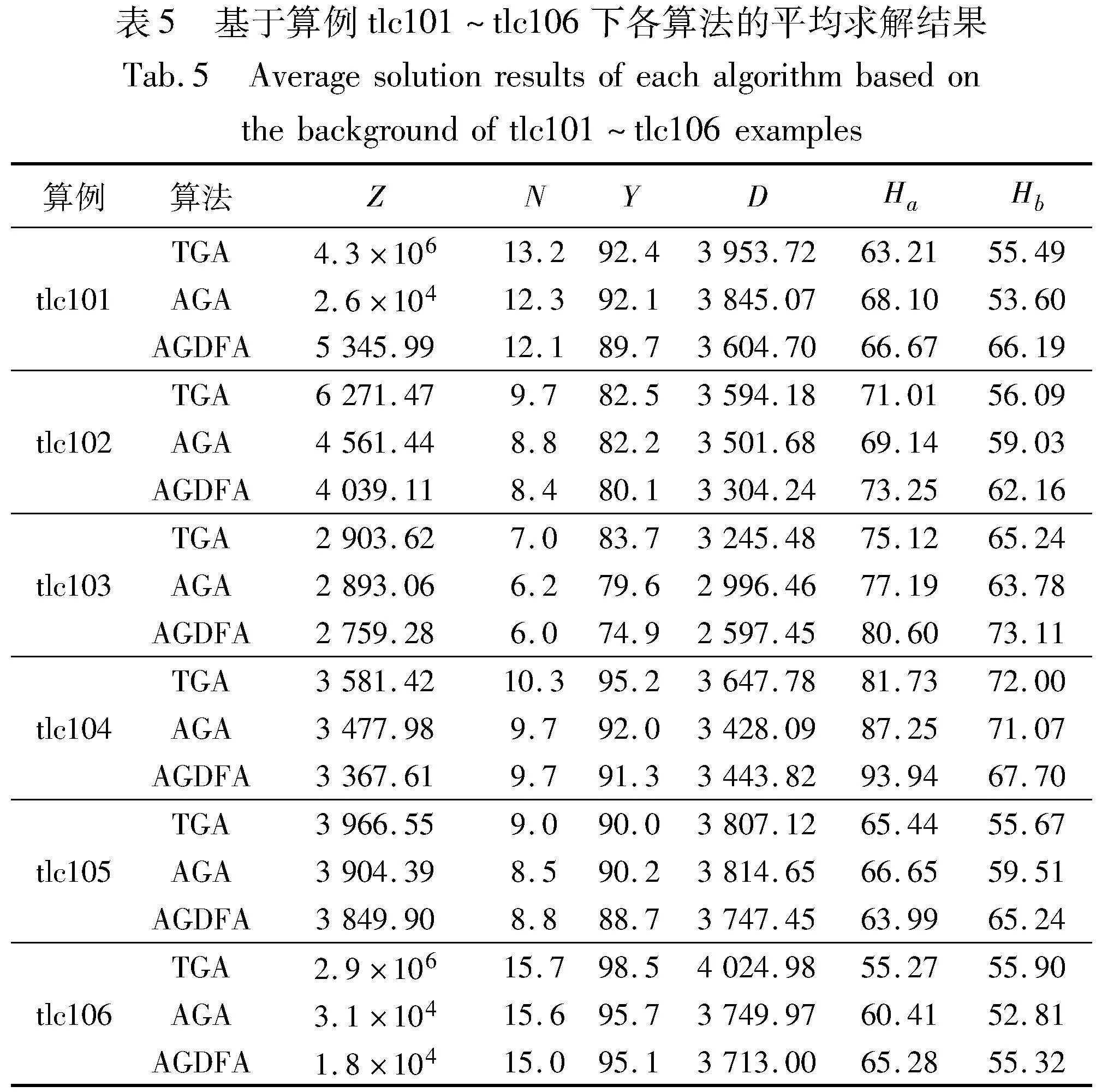
此外，基于算例tlc101～tlc106和一个基于仿真路网的算例下各算法运行10次的平均求解结果如表5所示。其中：Z代表目标函数；N代表车辆使用数；Y代表车辆总途径节点数；D代表车辆总行驶里程；Ha代表乘客上车时的满意度（%）；Hb代表乘客下车时的满意度（%）。

由表5可知，与自适应遗传-萤火虫算法的优点主要有以下两点：

a）在求解质量上，相比较于TGA、AGA与AGDFA在求解质量上有显著的提升， 6个算例上的表现都有一定优势，尤其是算例tlc101和tlc106中存在整体时间窗约束较紧的情况下，AGDFA仍能够获得较好解。AGA求解下的车辆使用数平均减少了0.65辆，车辆总途径节点数平均减少了1.75个，车辆总行驶里程减少了156.3；AGDFA求解下的车辆使用数减少了0.81辆，车辆总途径节点数平均减少了3.75个，车辆总行驶里程减少了310.4。

b）在乘客满意度方面，由于乘客的最大可容忍早到时间及晚到时间并不相同，所以本文分别统计了乘客上下车时的满意度。经过计算，AGA求得的结果中平均上车满意度增加了4.1%，平均下车满意度增加了0.1%；AGDFA求得的结果中平均上车满意度增加了7.3%，平均下车满意度增加了8.1%。

通过在算例tlc101～tlc106下应用不同算法求解，结果显示出本文设计的自适应遗传-萤火虫算法在需求响应型公交调度模型的求解中表现更为优越，能够获得更高质量的解决方案。

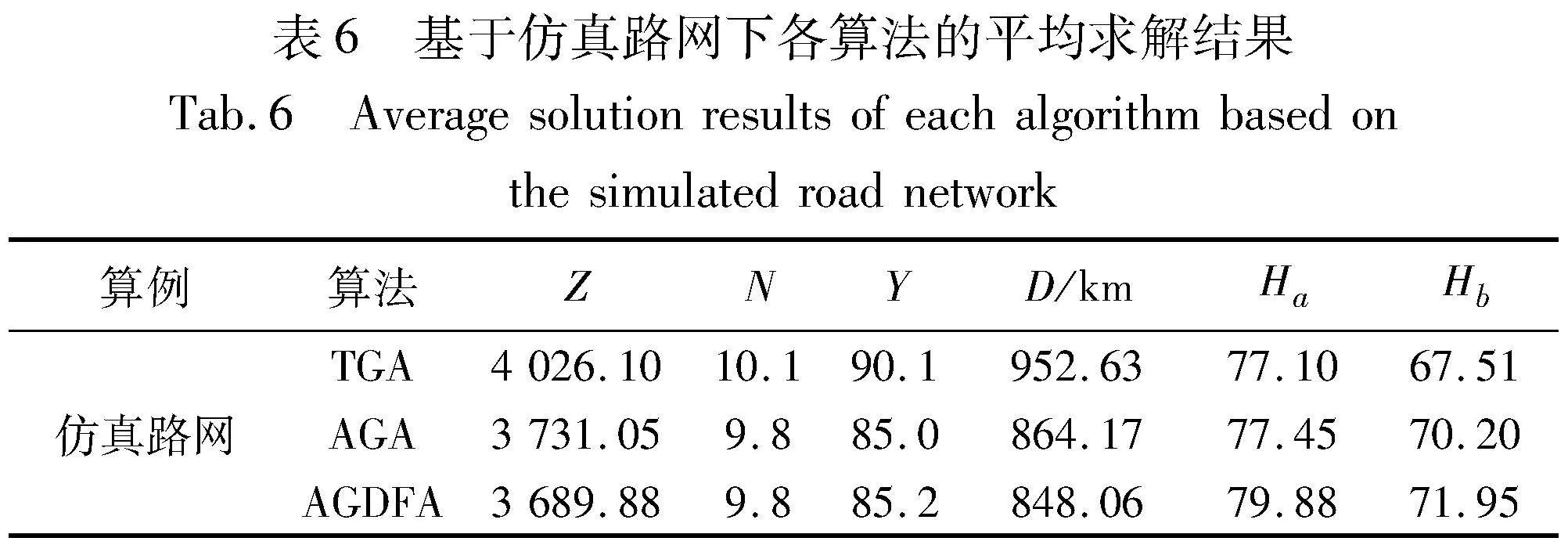
之后又通过一个基于仿真路网的算例进行测试，实验10次后的平均测试结果如表6所示，结果显示在自适应-萤火虫算法的优化下，目标函数减少了9.1%，车辆使用数、途径节点数和行驶里程数分别减少了0.3辆、4.9个和104.57 km。与此同时，乘客上下车时的满意度也显著提升，分别增加了2.78%和4.44%。这些结果都表明自适应遗传-萤火虫算法在解决该问题时的有效性和性能优越性。

4.4 路网仿真实验及分析

4.4.1 碳排放标准对仿真结果的影响分析

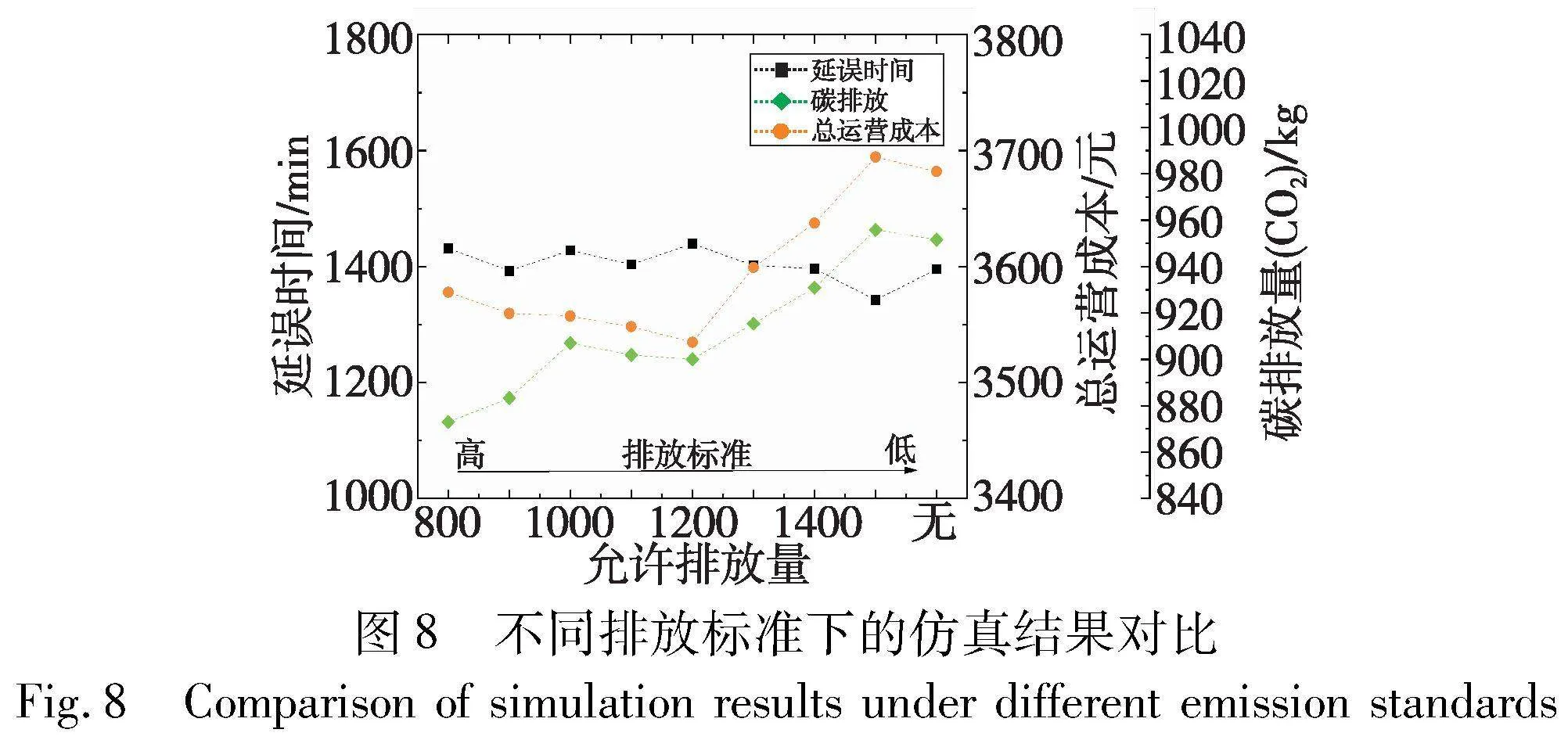
为验证碳排放因素对模型仿真效果的影响，在其他参数不变的情况下，对模型中允许对排放量的取值进行一定改变。将排放标准Lc的取值在某一范围内从小到大依次进行实验，并进行了不考虑碳排放下的模型仿真效果实验，对应了排放标准从严到宽的变化趋势。通过实际路网状况进行仿真实验，每种取值情况分别计算10次后取平均值，计算结果如图8所示。

由图8可知：随着排放标准的逐渐宽松，路网总碳排放量呈现逐渐增高的趋势，运营成本则是呈现先平稳下降而后急剧上升的变化过程。相比于不考虑碳排放影响的情况，当模型考虑碳排放且排放标准Lc=800 kg CO2的情况时，碳排放量下降了9%，成本下降了2.9%，表明合理制定排放标准能够在一定程度上控制碳排放量并降低成本，若排放标准过于宽松，对于企业和环境方面都是不利的。

4.4.2 乘客时间窗与允许延误时间对仿真结果的影响分析

在算法程序其他条件不变的情况下，对乘客时间窗与允许延误时间进行修改，以验证这两者对仿真结果的影响。引入时间窗修正系数ε，修正后时间窗宽度等于原有时间窗宽度乘以ε，ε数值越小，表明乘客对时间窗要求越严格。将不同Ty取值和时间窗要求下的情况分别计算10次后取平均值，图9显示了实验结果。

由图9可知：当乘客时间窗要求越高，对于乘客、企业以及环境方面的收益就越不利。当时间窗宽度缩小到原来的50%时，延误时间、碳排放量和成本分别增加了25%、35%和40%。当允许延误时间的取值逐渐收紧后，能为乘客提供更佳的服务体验，但同时也会增加碳排放和运营成本，因此，为了使模型在这两个方面达到平衡，Ty数值的合理选取是相当重要的。

4.4.3 路网阻抗的动态性对仿真结果的影响

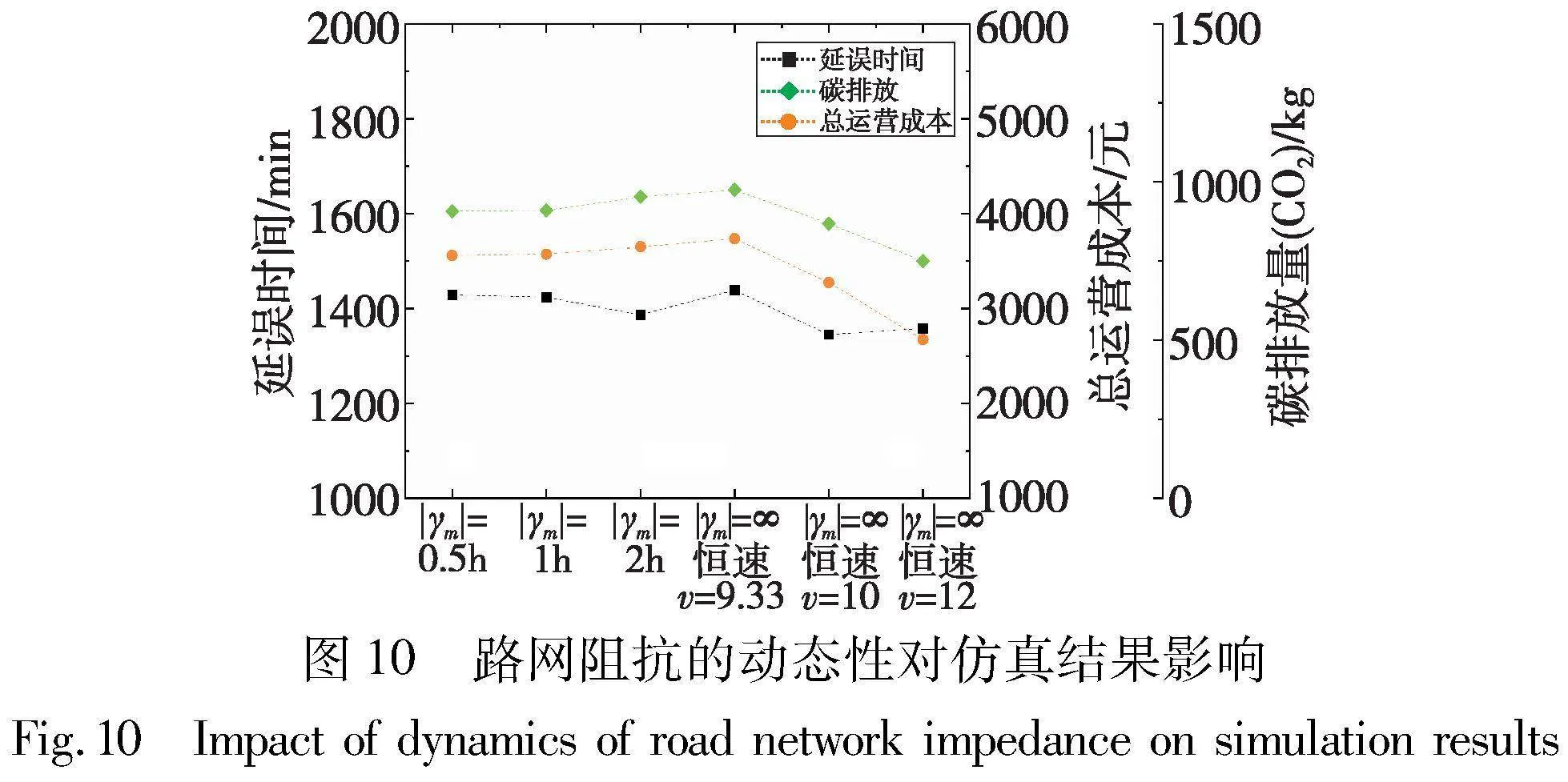
由于不同路段之间的行驶速度变化会对车辆的准点率，整个系统的碳排放量和运营成本等产生影响，所以，路网内时间阻抗的变化情况对于需求响应型公交的调度优化至关重要。本文针对每一时间段γm为各个路段都单独设置行驶速度，以模拟时变路网。然而，关于γm长度的设置存在主观因素，需要了解到路网阻抗变化的时间间隔是否对仿真结果的优劣有一定的变化规律。为验证这一猜想，在其他参数不变的情况下，对时间段的长度进行调整。调整后各时间段内的行驶速度取其包含的所有原本时间段内行驶速度的均值。本文分别设置了若干种实验场景，针对每种场景分别将各算例运算10次后取均值作为运算结果，如图10所示。

图10可知，在考虑动态阻抗的情况下，随着时间段γm长度由0.5 h不断增加至无限大，车辆碳排放和运营成本都逐渐增加，仿真结果呈现出不断劣化的趋势，表明路网阻抗变化对仿真结果优劣确实存在变化规律，路网中考虑静态阻抗时得到的仿真结果不如动态阻抗下的结果。根据不同车辆行驶速度的分析表明，车速对仿真结果有较大影响，随着恒定车速逐渐增加，碳排放与成本都有一定程度下降。

4.4.4 车型比例对仿真结果的影响

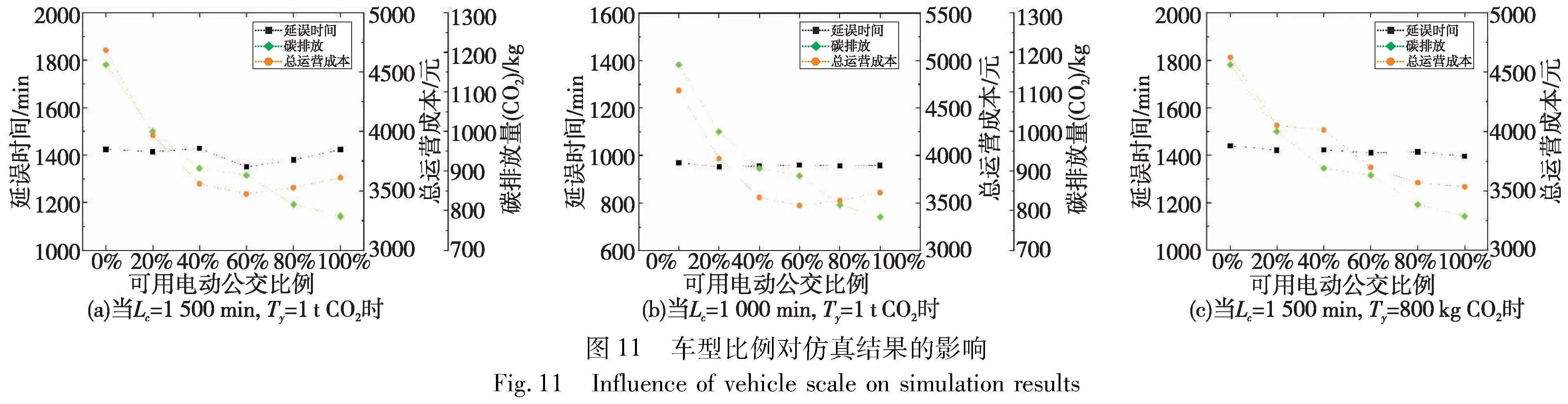
前文提到盲目增加电动公交使用数量极有可能导致运营成本增加，因此对可用车辆中电动公交的比例进行修改以验证这一想法。本文分别实验在正常标准、高时间窗标准、高排放标准三种情况下各个车型比例对仿真结果的影响，每种情况分别对应不同Lc和Ty的取值。实验10次后取均值作为运算结果，如图11所示。

由图11可知，随着电动公交车型比例的增加，三种情况下车辆碳排放量都在不断降低，这是由于电动公交的单位碳排放较低导致的。在正常标准和高时间窗标准下，运营成本呈现先急剧下降而后缓慢上升的趋势，当电动公交与燃油公交比例达到6∶4时，运营成本达到最佳，基本证实了前文提到的猜想。但在高排放标准的情况下，碳排放和成本的变化呈现单边下降趋势，表明在该情况下，尽可能多地起用电动公交是完全可取的。

5 结束语

本文主要考虑的是时变路网背景下的DRB调度优化，针对当下公交运营中存在油、电两种不同类型公交共同服务的现状，分别给出了碳排放估算方法。之后结合多车场、多车型、同时接送模式等要素建立模型，该模型属于TDMDGVRPSPD问题，根据延误时间、碳排放及运营成本的重要程度分别设置权重系数后加权进行优化，并设计自适应遗传-萤火虫算法进行求解，最后通过实验验证了算法和模型的有效性，获得主要结论如下：

a）本文所采用的自适应遗传-萤火虫算法有效改善了传统遗传算法中易陷入局部最优的问题，提高了算法的求解精度。

b）模型在考虑碳排放影响后能够减少9%的碳排放并省下2.9%的费用支出。

c）乘客时间窗的宽松程度与仿真结果的优劣相关，乘客时间窗要求越高，对于乘客、企业以及环境方面的收益就越不利。

d）相比于静态路网，考虑动态路网阻抗背景下的车辆调度即符合实际情况，也能够获得更优解，根据不同车辆行驶速度的分析表明，车速对仿真结果有较大影响，因此在制定方案时车速设置应尽可能贴近现实。

e）电动公交的加入能够大幅度降低碳排放和运营成本，但对于目前新能源技术尚未完全成熟的时期，企业仍需根据自身以及外部情况合理调度车辆，实现减排效益与成本控制两者间的平衡。

尽管本文对于DRB的调度优化研究已经有了一定成果，但对于此类问题还有很多值得深入研究的地方，未来对于DRB调度优化问题的研究仍可以从以下三个方面考虑：

a）在研究需求响应型公交调度优化模型时，并未运用现实生活中的实际案例进行分析，而是采用算例结合模拟仿真的方法进行研究。由于这种研究方式可能导致得出的结论与实际情况存在一定偏差，为提高研究的实证性和可信度，未来的研究可采用实际路网中的案例，以获取更真实、更具说服力的数据。

b）本文只考虑了乘客静态的出行需求，即车辆发车前，乘客提前预约的需求。但并未考虑到车辆在运行过程中收到的实时动态需求，在后续的研究中，可以引入动态规划的方法，对乘客的动态需求进行处理，使得DRB实现实时响应的功能。

c）尽管本研究提出的算法在求解当前DRB调度问题时取得较好的成果，但仍需承认的是，这一算法仍存在一些局限性和不足，未来的研究可集中于改进算法的鲁棒性、扩展性以及提高应对更复杂情景的适应能力，以更好地应对未来需求的挑战。

参考文献：

［1］Sun Qian， Chien S， Hu Dawei，et al. Optimizing multi-terminal customized bus service with mixed fleet［J］. IEEE Access， 2020， 8： 156456-156469.

［2］孙倩， 胡大伟， 钱一之， 等. 考虑车辆随机到站时间的动态需求响应型接驳公交线路优化［J］. 交通运输系统工程与信息， 2022， 22（5）： 196-204，292. （Sun Qian， Hu Dawei， Qian Yizhi，et al. Dynamic bus routing optimization for demand-responsive feeder transit considering stochastic bus arrival time［J］. Journal of Transportation Systems Engineering and Information Technology， 2022， 22（5）： 196-204，292.）

［3］胡迪， 靳文舟. 基于站点优化的需求响应公交调度研究［J］. 深圳大学学报： 理工版， 2022， 39（2）： 209-215. （Hu Di， Jin Wenzhou. Flex-route demand response transit scheduling based on station optimization［J］. Journal of Shenzhen University Science and Engineering， 2022，39（2）： 209-215.）

［4］管德永， 吴晓芳， 赵杰， 等. 需求响应型公交车辆调度及路径优化［J］. 公路交通科技， 2022，39（5）： 140-148. （Guan Deyong， Wu Xiaofang， Zhao Jie，et al. Dispatch and route optimization of demand-responsive bus［J］. Journal of Highway and Transportation Research and Development， 2022，39（5）： 140-148.）

［5］贺韵竹， 贾鹏， 李海江， 等. 新型需求响应公交发车时刻和票价优化［J］. 系统工程理论与实践， 2022， 42（4）： 1060-1071. （He Yunzhu， Jia Peng， Li Haijiang， et al. Optimization of the departure time and fare of new demand responsive transit systems［J］. Systems Engineering-Theory & Practice， 2022，42（4）： 1060-1071.）

［6］Huang Ailing， Dou Ziqi， Qi Liuzi， et al. Flexible route optimization for demand-responsive public transit service［J］. Journal of Transportation Engineering Part A：Systems， 2020，146（12）： 15.

［7］孙会君， 冯宗旭， 郑汉坤. 考虑地铁运营中断下多站协同的接驳公交优化研究［J］. 交通运输系统工程与信息， 2023， 23（2）： 111-120，175. （Sun Huijun， Feng Zongxu， Zheng Hankun， et al. Optimization of bus bridging considering multi-station coordination under me-tro disruption［J］. Journal of Transportation Systems Engineering and Information Technology， 2023， 23（2）： 111-120，175.）

［8］Shen Chan， Sun Yao， Bai Zijian， et al. Real-time customized bus routes design with optimal passenger and vehicle matching based on column generation algorithm［J］. Physica A-Statistical Mechanics and Its Applications， 2021， 571： 125836.

［9］Chen Xi， Wang Yinhai， Wang Yong， et al. Customized bus route design with pickup and delivery and time windows： model， case study and comparative analysis［J］. Expert Systems with Applications， 2021， 168： 114242.

［10］王正武， 陈涛， 宋名群. 同时接送模式下响应型接驳公交运行路径与调度的协调优化［J］. 交通运输工程学报， 2019， 19（5）： 139-149. （Wang Zhengwu， Chen Tao， Song Mingqun. Coordinated optimization of operation routes and schedules for responsive feeder transit under simultaneous pick-up and delivery mode［J］. Journal of Traffic and Transportation Engineering， 2019，19（5）： 139-149.）

［11］王志建， 郭健， 张强. 考虑乘客信任程度的营运车辆合乘线路规划［J］. 计算机应用研究， 2023，40（4）： 996-999. （Wang Zhijian， Guo Jian， Zhang Qiang. Planning of ride-sharing routes for operating vehicles considering degree of passenger trust［J］. Application Research of Computers， 2023，40（4）： 996-999.）

［12］杜太升， 陈明明. 考虑时间窗的通勤定制公交线路优化［J］. 交通运输工程与信息学报， 2023， 21（1）： 152-163. （Du Taisheng， Chen Mingming. Optimization of customized bus routes for commuting considering time windows［J］. Journal of Transportation Enginee-ring and Information， 2023， 21（1）： 152-163.）

［13］靳文舟， 胡为洋， 邓嘉怡， 等. 基于混合算法的需求响应公交灵活调度模型［J］. 华南理工大学学报：自然科学版， 2021，49（1）： 123-133. （Jin Wenzhou， Hu Weiyang， Dengjiayi， et al. Flexible scheduling model of demand response transit based on hybrid algorithm［J］. Journal of South China University of Technology：Natural Science Edition， 2021，49（1）： 123-133.）

［14］郑汉， 张星臣， 王志美. 混合车型需求响应公交服务定制问题研究［J］. 交通运输系统工程与信息， 2018，18（2）： 157-163. （Zheng Han， Zhang Xingchen， Wang Zhimei. Design of demand-responsive service by mixed-type vehicles［J］. Journal of Transportation Systems Engineering and Information Technology， 2018，18（2）： 157-163.）

［15］王正武， 袁媛， 高志波. 高自由度响应公交分区路径与调度的协调优化［J］. 长沙理工大学学报： 自然科学版， 2018，15（1）： 41-48. （Wang Zhengwu， Yuan Yuan， Gao Zhibo. Coordination optimization for partition path and scheduling with high degree of freedom demand response transit［J］. Journal of Changsha University of Science and Technology： Natural Science， 2018，15（1）： 41-48.）

［16］Shu Wanneng， Li Yan. A novel demand-responsive customized bus based on improved ant colony optimization and clustering algorithms［J］. IEEE Trans on Intelligent Transportation Systems， 2023， 24（8）： 8492-8506.

［17］靳文舟， 郭献超， 龚隽. 基于精英选择遗传算法的需求响应公交规划［J］. 公路工程， 2020，45（2）： 44-49. （Jin Wenzhou， Guo Xianchao， Gong Jun. Based on elitist selection genetic algorithm for demand responsive transit planning［J］. Highway Engineering， 2020， 45（2）： 44-49.）

［18］Aktas D， Sorensen K， Vansteenwegen P. A variable neighborhood search algorithm for a public bus line with a demand-responsive operation during peak hours［J］. Transportation Planning and Techno-logy， 2023，46（5）： 615-652.

［19］李欣， 林小敬， 许航， 等. 需求响应公交网络化运营优化模型［J］. 计算机应用， 2023， 43（S1）： 288-292. （Li Xin， Lin Xiaojing， Xu Hang， et al. Optimization model of networked operation for demand-responsive transit［J］. Journal of Computer Applications， 2023， 43（S1）： 288-292.）

［20］任婧璇， 常孝亭， 巫威眺， 等. 考虑候选站点和全服务过程的需求响应接驳公交调度［J］. 交通运输系统工程与信息， 2023，23（5）： 202-214. （Ren Jingxuan， Chang Xiaoting， Wu Weitiao， et al. Demand responsive feeder transit scheduling considering candidate stops and full-service process［J］. Journal of Transportation Systems Engineering and Information Technology， 2023， 23（5）： 202-214.）

［21］Erdogan S， Miller-Hooks E. A green vehicle routing problem［J］. Transportation Research Part E-Logistics and Transportation Review， 2012，48（1）： 100-114.

［22］Kuo Yiyo. Using simulated annealing to minimize fuel consumption for the time-dependent vehicle routing problem［J］. Computers & Industrial Engineering， 2010，59（1）： 157-165.

［23］Franceschetti A， Honhon D， Van Woensel T， et al. The time-dependent pollution-routing problem［J］. Transportation Research Part B-Methodological， 2013，56： 265-293.

［24］Heidari A， Imani D M， Khalilzadeh M， et al. Green two-echelon closed and open location-routing problem： application of NSGA-Ⅱ and MOGWO metaheuristic approaches［J］. Environment Development and Sustainability， 2023， 25（9）： 9163-9199.

［25］珠兰， 马潇， 刘卓凡. 时间依赖型绿色车辆路径问题研究［J］. 交通运输系统工程与信息， 2021， 21（6）： 187-194. （Zhu Lan， Ma Xiao， Liu Zhuofan. Time-dependent green vehicle routing problem［J］. Journal of Transportation Systems Engineering and Information Technology， 2021，21（6）： 187-194.）

［26］周鲜成， 刘长石， 周开军， 等. 时间依赖型绿色车辆路径模型及改进蚁群算法［J］. 管理科学学报， 2019， 22（5）： 57-68. （Zhou Xiancheng， Liu Changshi， Zhou Kaijun， et al. Improved ant colony algorithm and modelling of time-dependent green vehicle routing problem［J］. Journal of Management Science in China， 2019， 22（5）： 57-68.）

［27］Ichoua S， Gendreau M， Potvin J Y. Vehicle dispatching with time-dependent travel times［J］. European Journal of Operational Research， 2003，144（2）： 379-396.

［28］Barth M， Boriboonsomsin K. Energy and emissions impacts of a freeway-based dynamic eco-driving system［J］. Transportation Research Part D-Transport and Environment， 2009，14（6）： 400-410.