车路协同下的无信号交叉口车辆通行调度策略

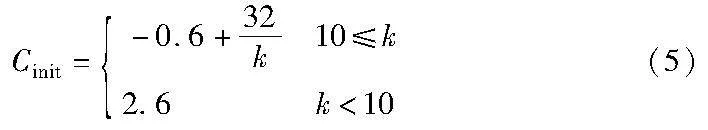
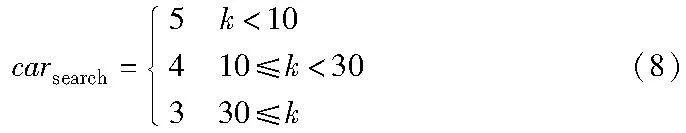
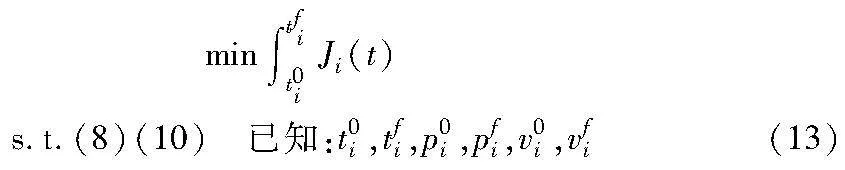
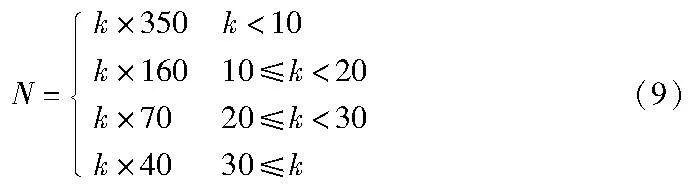
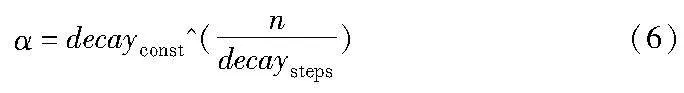
摘 要：无信号交叉口车辆通行调度问题是智能交通领域的研究重点，由于车辆通行顺序决策问题的解空间随着车辆数增加而指数级增长，在保证实时性的同时找到较优通行顺序成为无信号交叉口通行调度的一大问题。针对该问题提出一种基于自适应蒙特卡罗树搜索算法的无信号交叉口车辆通行调度方法，采用分层式框架，上层集中式顺序决策，下层分布式轨迹规划。首先，建立基于冲突点的交叉口模型，将网联车加入到待搜索队列中，根据交叉口中的车辆通行特点设计通行顺序的蒙特卡罗树搜索流程，以总通行时间为指标建立评价函数，然后针对不同交通情景设计自适应探索系数及其他超参数，使算法在求解不同车辆数时以及搜索的不同时期保持最佳状态。轨迹规划环节以加速度二范数为目标函数，以速度、加速度以及始终点位置等为约束，建立最优控制命题求解车辆轨迹。最后，进行实验，结果表明该算法相较于其他算法在数值仿真和微缩平台实验中最大优化幅度分别达到33.42%和38.04%，为无信号交叉口车辆通行调度提供了一个有效解决方案。

关键词：智能交通； 无信号交叉口车辆通行调度； 蒙特卡罗树搜索； 智能网联车； 微缩平台

中图分类号：U495 文献标志码：A 文章编号：1001-3695（2024）07-023-2087-06

doi：10.19734/j.issn.1001-3695.2023.11.0544

Vehicle traffic scheduling strategy at unsignalized intersectionsunder vehicle road coordination

Abstract：The vehicle traffic scheduling problem at unsignalized intersections is the research focus in the field of intelligent transportation. Because the solution space of vehicle traffic order decision problem increases exponentially with the increase of the number of vehicles， finding the optimal traffic sequence while ensuring the real-time performance has become a major problem for traffic scheduling at unsignalized intersections. To solve this problem， this paper proposed a vehicle traffic scheduling method at unsignalized intersections based on adaptive Monte Carlo tree search algorithm， which used a hierarchical framework， upper level centralized sequential decision-making， and lower level distributed trajectory planning. Firstly， the intersection model based on the conflict point was established， the connected vehicles were added to the queue to be searched， the Monte Carlo tree search process of the traffic sequence was designed according to the vehicle traffic characteristics in the intersection， the evaluation function was established with the total traffic time as the index， and then the adaptive exploration coefficient and other super parameters were designed for different traffic situations， so that the algorithm could maintain the best state in solving different vehicle numbers and different search periods. In the trajectory planning process， the acceleration two norm was taken as the objective function， and the speed， acceleration and the position of the starting point were taken as constraints to establish the optimal control proposition to solve the vehicle trajectory. Finally， experiments were carried out， and the results show that compared with other algorithms， the maximum optimization amplitude of this algorithm in numerical simulation and micro platform experiment is 33.42% and 38.04% respectively， which provides an effective solution for vehicle traffic scheduling at unsignalized intersections.

Key words：intelligent transportation; unsignalized intersection vehicle traffic scheduling; Monte Carlo tree search（MCTS）; connected automatic vehicle（CAV）; miniature platform

0 引言

近年来，新能源汽车迅速发展，汽车电动化技术逐渐成熟，汽车智能化拉开序幕［1］。早在2011年，国家科技部已设立“智能车路协同关键技术研究”主题项目，到2022年清华大学智能研究院牵头发表《面向自动驾驶的车路协同关键技术与展望》2.0版本，“车路协同”概念在被逐步完善与实践。在所有交通场景中，约50%的城市交通事故发生在交叉口［2］，是造成城市交通拥堵的主要原因。因此无信号交叉口是车路协同技术的重点应用场景，被认为是缓解交通拥堵和提高安全性的最有潜力的方法之一［1，3］。智能网联车（CAV）的V2X（vehicle to everything）技术使得CAV可以与相邻车辆共享其驾驶状态和意图［4］，实现车路协同控制，更好地协调其运动，缓解交通拥堵。

在无信号交叉口对CAV进行协同控制的关键问题是确定CAV通过交叉口的最优顺序［5，6］。国内外学者对交叉口通行顺序决策问题进行了相关研究［7～9］。文献［10］首先提出了基于预留的算法来控制不同车道上两车经过同一路口时避免发生碰撞，该算法的核心思路是先到先服务（first come first service，FCFS）。也有学者在FCFS的基础上对路口多车协同的求解方法和优化目标作出进一步改进［11，12］。Carlino等人［13］在FCFS基础上提出了基于拍卖的路口场景协同决策方法，其性能优于先进先出策略，但中高车流场景下的通行效果仍不理想。基于预留的方法核心在于获得无冲突通行顺序，并未考虑到通行顺序的最优性。为提高通行效率，基于优化的顺序决策方法被提出。Müller等人［14］将车辆通过冲突区的顺序转换为一个混合整数规划问题，在确定好车辆通行顺序之后，再据此规划车辆的时空轨迹。Ahn等人［15］在优化模型中进一步考虑了安全因素。然而优化方法的解空间随着车辆数的增多呈指数增长，使其难以满足实时性要求。为提高求解速度，已有研究对交叉口模型做了较多简化，比如将整个交叉口视为冲突点，这也使得算法求解出的通行顺序与真实交叉口车辆通行情况有一定差距。Chen等人［16］建立了基于冲突点的交叉口模型，采用图搜索的方法进行求解，但其重点在于获得无冲突车辆通行顺序，并未对结果的最优性进行论证。Li等人［6］将车辆通行顺序规划问题的解空间描述成一个树型结构，采用蒙特卡罗树搜索方法求解车辆通行顺序。Xu等人［17］沿用文献［6］提出的树型解空间表示法，并结合启发式规则以提高搜索效率，但两者在交叉口的建模上均采用了将交叉口冲突区分解为小块冲突区的方式，并未考虑交叉口内同时通行多辆车的情况。Pei等人［18］定义了车辆通行状态，构建小尺度的状态空间，并通过动态规划搜索出通行顺序，尽管获取到了小尺度状态空间中的最优解，但存在压缩状态空间过程中丢失最优解的问题。李磊等人［19］通过选取局部最优组合的方式，快速获取到了安全可行的通行解，但对全局最优性欠缺考虑。

如前所述，现有工作大多侧重于通过特定的方法获得通行顺序，侧重于无冲突解决方案的可行性，忽视了交通效率。有些研究为了弱化最优性和计算复杂度的矛盾，对交叉口冲突模型进行简化，使得其搜索空间已失去全局最优性。因此，考虑最优通行顺序的无信号交叉口调度问题尚未得到较好解决。本文提出了一种无信号交叉口通行调度方法，将问题解耦为上层集中式顺序决策和下层分布式控制两部分。上层顺序决策环节中建立基于冲突点的无信号交叉口模型，并改进蒙特卡罗树搜索流程，对算法的超参数进行优化，平衡搜索结果的最优性与搜索的实时性。下层轨迹规划根据给出的车辆到达时间建立最优控制命题求解最优轨迹。最后进行仿真和实验，证明该方法的有效性和优越性。

1 无信号交叉口车辆协同调度框架

1.1 无信号交叉口模型

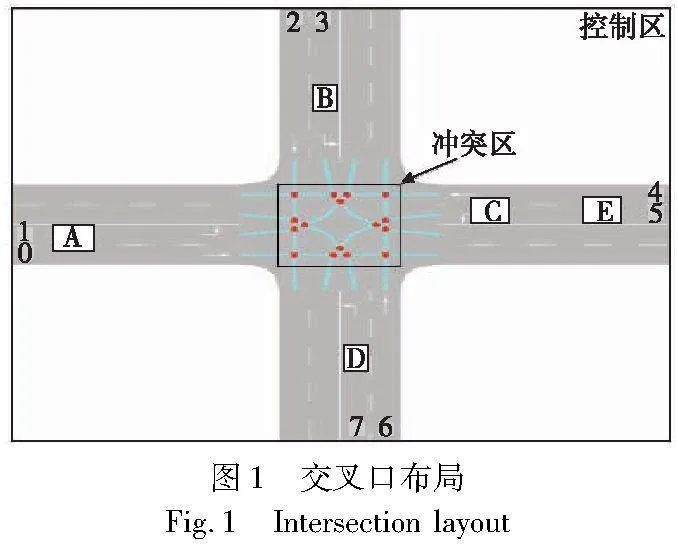
由于交叉口存在多重形态，本文选择典型双向四车道交叉口进行研究，后续可拓展至更为复杂的交叉口。如图1所示，由于右拐车道的路径未与其他车道相冲突，所以并未包含右拐车道。入口车道编号为0～7，每条道路包含左转和直行车道。整个交叉口区域分为冲突区和控制区。其中，控制区内冲突区外的车道长度为L ，单个车道宽度为W，冲突区域边长为LS。

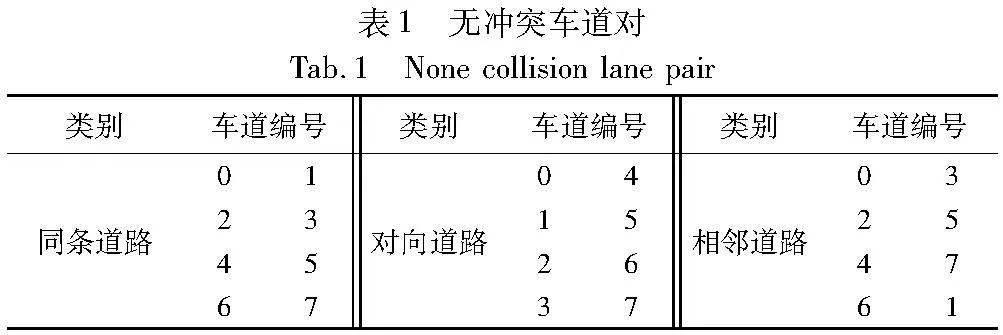
交叉口的车辆冲突主要发生在冲突区内，将各车道在冲突区内通行路径的交点定义为冲突点，图1冲突区内一共包含16个冲突点。根据车辆所在的车道信息可确定其通过交叉口的路径，当两车在冲突区内的路径存在交点且交点处两车的通行时间窗存在重叠，则两车有碰撞关系，如图1中车辆所示，A车和C车、E车属于无碰撞关系，A车和B车、D车属于有碰撞关系。不存在碰撞关系的车道在表1中列出。

每辆进入控制区的CAV都将被分配一个唯一的标识Vi，车辆间是否存在冲突关系可以通过车道编号在表1中进行查询。针对无信号交叉口车辆通行顺序决策问题，提出如下假设：a） 交叉口内所有车辆均为CAV；b） CAV在进入控制区前已换道至目标车道；c） 不考虑CAV与其他设备通信过程中丢包的情况；d） 车辆在冲突区内的行驶速度恒定。

1.2 车辆协同调度框架

本文针对集中式调度复杂度高的问题，采用双层控制框架，上层为交叉口管理层，下层为车辆控制层，将通行顺序决策和车辆轨迹规划控制进行解耦，降低问题复杂度，如图2所示。交叉口管理层采用集中式架构，交叉口中央服务器获取交叉口内的车辆信息，完成车辆通行顺序决策。车辆控制层采用分布式架构，各CAV独自完成轨迹规划和控制的工作。为避免全连接通信带来的巨大通信负担，采用车辆分组通信机制。交叉口管理层只与车辆通行组中的组长进行通信，通行组组长与同组的车辆进行通信。通行组组长定义为同组中最接近冲突区的车辆。

交叉口管理层需要具有高动态响应能力，以应对动态变化的交通情况。因此设计了一种以固定时间周期更新的顺序决策策略，服务器以固定时间间隔检测交叉口内的车辆情况，若交叉口内存在新增车辆，则调用顺序决策算法，否则保持上次的决策结果。

2 顺序决策方法

在车辆数目较多时，树搜索方法通常无法在有限的计算资源和时间内探索完所有的节点。本文使用MCTS与剪枝规则来提高搜索效率，并使搜索结果尽可能接近最优解。

2.1 基于蒙特卡罗树搜索的通行顺序决策算法

蒙特卡罗树搜索包含选择、拓展、模拟和反向传播四个主要步骤。搜索结束的条件为达到设定迭代次数或计算时间，或搜索结果超过一定回合数不发生变化。

搜索中各步骤的功能为：a）选择。选择UCB值最大的节点。b）拓展。在未完全拓展的节点下添加一个新子节点。c）模拟。对新创建的子节点使用随机策略进行探索，直到叶节点（最底层节点），对结果进行评价。d）反向传播。将模拟的结果沿新节点向上反馈至根节点，更新所有父节点的信息。

其中，使用置信上界（upper confidence bound，UCB）对节点价值进行评估，不仅考虑该节点的当前价值，也将节点的被选择次数纳入考量，其计算公式为

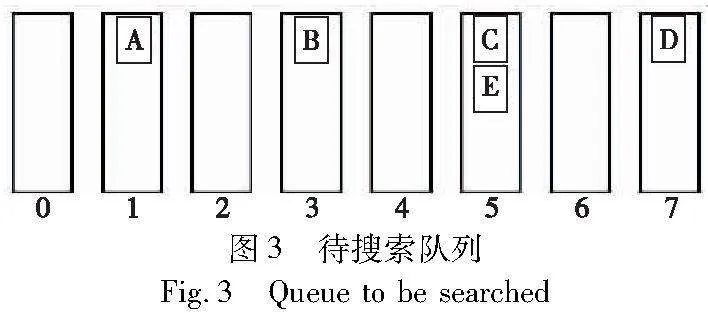
首先对车辆信息进行预处理，由于控制区内不允许换道，车辆具有先进先出的特征，所以采用队列的数据结构保存交叉口各车道的车辆。以图1中的车辆为例，生成的待搜索队列如图3所示。车辆通行顺序决策问题可转换为由所有可能的通行顺序组成的解空间中的树搜索问题，每个叶节点包含车辆通行顺序信息和待搜索队列信息。其中，ROOT节点的通行顺序为空且待搜索队列中包含所有的车辆。

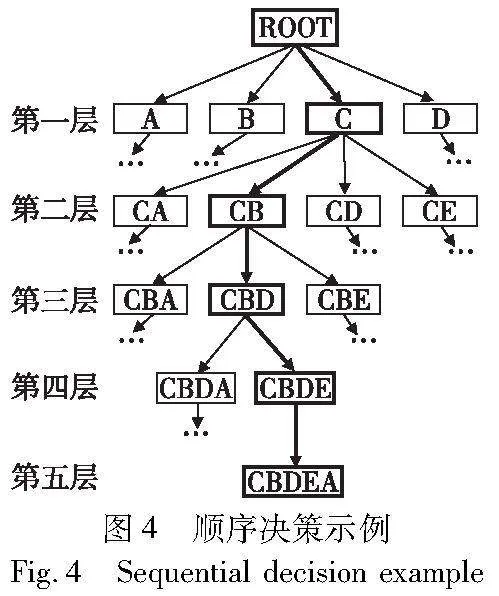
以图3所示的待搜索队列为例，介绍如何运用树搜索方法进行通行顺序决策。首先创建根节点ROOT，根节点中的通行顺序置为空，初始化根节点的待搜索队列。在搜索的第一层，ROOT节点从待搜索队列的头部选择拓展车辆，可选的车辆包括A、B、C、D，以选择C车为例，生成子节点C，其待搜索队列继承自ROOT节点并删除其中的车辆C。子节点重复以上拓展流程，直到待搜索队列中的车辆为空。搜索过程如图4所示，其中红色加粗节点的待搜索队列信息如图5所示。

2.2 车辆通行组

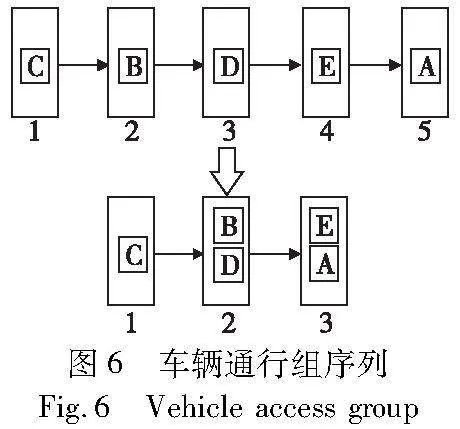
通过上述树搜索获得的通行顺序如图4所示为CBDEA，仅包含车辆通过交叉口时的先后顺序信息，因而将其称为车辆通行序列（order of car，OC），其无法体现同一时刻交叉口内通过多辆CAV。为提高车辆通行效率，尽可能让无碰撞关系的车辆同时通过交叉口冲突区。在此将可同时通过交叉口的无碰撞车辆组合称为车辆通行组。车辆通行组可有效减少冲突区中无车辆通行的空窗期，提高交叉口冲突区的利用率。需要注意的是，若上一通行组中包含多台车辆，则下一通行组中的车辆需要全面考虑与上一通行组中不同车辆的碰撞关系，进而设置无碰撞的最快到达时间。将车辆通行序列转换为车辆通行组序列（order of group，OG）的方法如算法1所示。

算法1 成组通行算法

其中：tg为成组阈值，若两车的到达时间相差超过tg，则两车将单独成组，其取值为车辆在交叉口冲突区中的平均通行时间。

通过算法1将搜索出的通行序列转换为车辆通行组序列，结果如图6所示，通行组由5组缩减少到了3组，有效提高了交叉口冲突区的利用率。

2.3 通行组序列价值评估

对车辆通行组序列进行价值评估是搜索过程中的重要环节，其评价的准确性直接影响到算法求解出的通行顺序的优劣。首先计算第i辆车最快到达交叉口的时间，假设Vi前方不存在其他车辆且不存在冲突车辆，Vi以自由流速度从其当前所在位置行驶到冲突区所需要的时间为最小到达时间，如式（2）所示。

其中：disi为第i辆车距离冲突区的距离；vf为自由流速度。

由于通行组中可能存在多辆车，所以估算通行组的到达时间时需要考虑到前一通行组中的所有车辆，存在冲突的车辆先后经过同一冲突点时需要保持安全跟车距离dsafe，采用恒定车头时距（constant time headway，CTH）进行计算。

dsafe=th×v+dminsafe（3）

其中：th为固定车头时距；dminsafe为最小安全距离。

本文目标在于提高交叉口整体的通行效率，因而对通行组序列的评价指标与其总通行时间相关，关于车辆通行组序列总通行时间test的计算如算法2所示。

算法2 通行顺序评估算法

算法2中，tassign，OG［i］［j］为OG中第i组中的第j辆车的安排到达时间；tmin，OG［i］［j］为第i组中的第j辆车的最快到达时间。

评价通行组序列优劣的原则为总通行时间短的叶节点评分高，反之评分低，通行时间与评价分数呈负相关。因此采用恒大于通行时间的值减去通行时间作为该通行顺序的评分，评价公式如下：

goal=（tmin+tsafe×k）-test（4）

其中：goal为当前通行顺序的得分；tmin为通行组中最快到达冲突区的车辆的到达时间；tsafe为不同车辆通过同一冲突点的安全间隔时间;k为通行组序列中包含的车辆数。其中，tmin+tsafe×k是按照逐车通行的方式估算出的最长通行时间，其恒大于等于估算出的通行时间。

2.4 自适应参数

MCTS的搜索性能受到多个参数的影响，其中探索系数直接影响到搜索的速度和搜索结果的质量。当探索系数越大时，算法越倾向于探索新的节点，使得搜索结果质量更高，但也增加了搜索时间。而探索系数减小时，算法倾向于选择已知的利益最大的节点，减少对新节点的探索，提高了搜索速度，但求得的通行顺序可能与最优解差距较大。过去一般将探索系数设置为一定值，由于参与顺序决策的车辆数在不断变化，若以恒定的探索系数，在车辆数较少时将出现过早结束搜索的情况，导致结果不够理想，而车辆数较多时可能导致求解失败。为了在搜索速度和结果质量间取得较好的平衡，应根据参与顺序决策的车辆数目来初始化探索系数。车辆数增多时，探索系数应适当减小以提高搜索速度，反之探索系数可适当增大以提高求解质量。不同车辆数时的初始探索系数如式（5）所示。

其中：Cinit为初始探索系数。当车辆数小于10时，探索系数增大到2.6后继续增加并未提高通行效率，而搜索时间却随之增大。当车辆数大于10辆后，采用线性递减的方法计算探索系数，车辆数达到50时，探索系数为0.04。

树搜索前期时，由于探索的车辆较少，由此节点模拟出来的通行顺序存在较大随机性，不能真实地反映出当前节点的价值，所以要保持一定的探索能力，加强对较优解的发掘。随着搜索的进行，探索到的车辆数增多，节点模拟出的通行顺序已能大致反映当前节点的价值，因此可以减小探索系数以提高搜索速度。参考机器学习中的学习率衰减方法定义了衰减系数，用于实现算法的探索能力随探索深入而下降，如式（6）所示。

其中：α为衰减系数；decayconst为衰减常数；decaysteps为衰减步长；n为当前迭代次数。衰减后的探索系数为Cdecay=α×Cinit（7）

其中：Cdecay为随迭代次数衰减的探索系数。

剪枝规则同样是影响搜索速度的一重要因素，增大剪枝力度可以有效减小解空间。当参与顺序决策的车辆较多时，优先探索较快到达的车辆，有利于提高搜索速度，对于距离较远的车辆进行剪枝，剪枝参数如式（8）所示。

其中：可探索节点按车辆的到达时间进行排序；carsearch为需要探索的子节点数，此范围外的车辆即被剔除。

另一影响搜索的参数是总迭代次数，迭代次数过少可能导致探索不完全甚至无法获得完整通行顺序。迭代次数过多则可能导致算法计算时间过长，对已知最优的通行顺序进行重复探索。对不同车辆数进行测试，标定结果为

其中：N为总迭代次数，当车辆数达到50辆时，搜索时间为0.8 s。结合上述定义，最终的交叉口车辆通行顺序决策如算法3所示。

算法3 基于自适应蒙特卡罗树搜索的通行顺序决策算法

3 车辆轨迹规划

交叉口管理层求解最优通行顺序后可由算法2求得每辆CAV的分配到达时间。各CAV在获取到分配的到达时间后，结合自车所在位置以及当前行驶状态信息进行轨迹规划。由于控制区内车辆不需要进行换道，只需进行车辆纵向运动控制，在此采用二阶运动学模型：

其中：pi（t）为车辆i在t时刻的位置；vi（t）为车辆i在t时刻的速度；ui（t）为车辆i在t时刻的加速度。已知当前状态和末端状态的情况下，可以使用优化方法获得车辆的轨迹，为使车辆能耗尽可能降低，目标函数设置为加速度的二范数，如式（11）所示。

为确保车辆的控制输入和速度能在允许的范围内，优化过程中对其进行了如下限制：

其中：umin为最小加速度；umax为最大加速度；vmin为最小速度；vmax为最大速度。

车辆的始末状态可直接获得，初始时间为t0i，末端时间为tfi=t0i+tassigni，tassigni为车辆i的安排行驶时间，初始位置为p0i，末端位置为pfi，初始速度为v0i，末端速度定义为冲突区的车辆行驶速度vfi。最终建立轨迹规划最优控制命题如下：

采用商用求解器Cplex求解式（13），获得车辆的加速度控制量。

4 仿真与实验

为了验证算法的有效性，选择经典的先到先得算法（文献［10］）、基于图优化的决策算法（文献［16］）、基于MCTS的树搜索算法（文献［17］）进行对比，对比的指标为交叉口车辆通行时间，验证方法包含数值仿真和微缩平台实验。

4.1 数值仿真

在不同车流量情况下每个决策时刻参与决策的车辆数将有所不同，选择10、20、30、40、50辆五种不同车辆数的场景对算法的计算效率和车辆通行时间进行数值仿真，每种车辆数进行五组仿真取平均通行时间作为结果。更高车流量的情况可通过滚动时域法对交叉口内的车辆进行滚动求解通行顺序。仿真所使用电脑的CPU为i5-12400，内存为16 GB，操作系统为Windows 10，编程语言为Python。

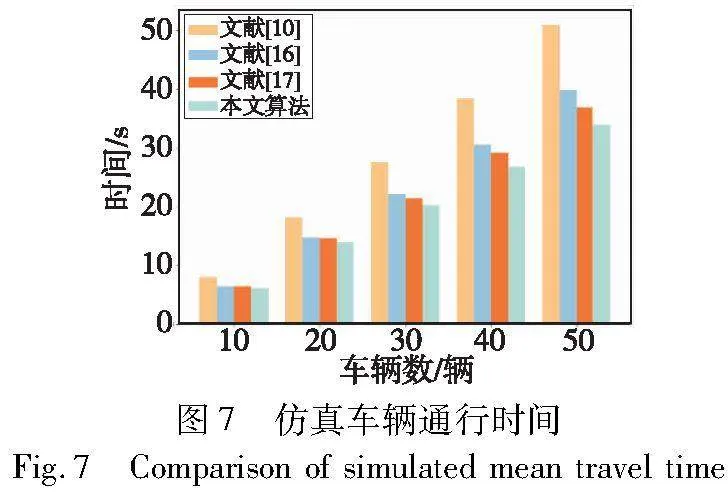
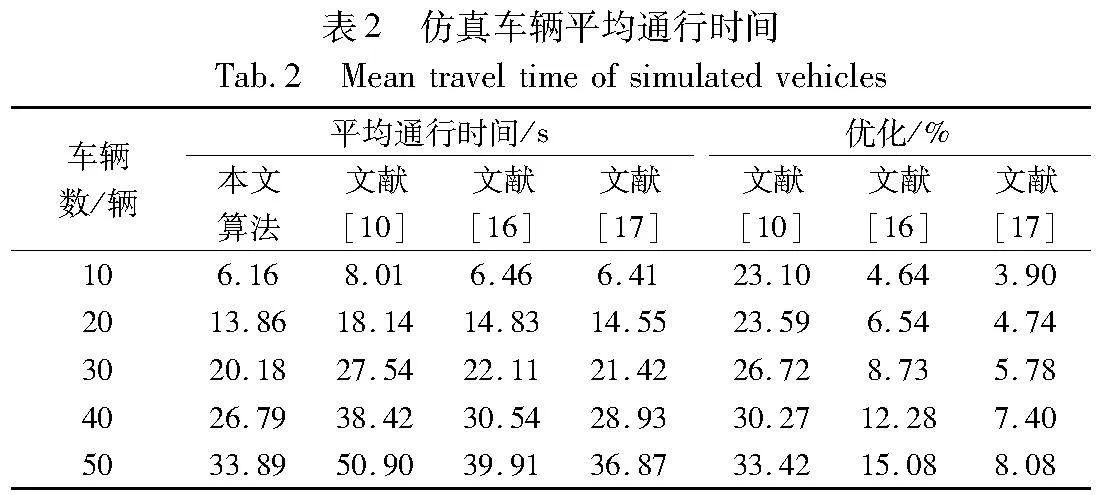
分别对五种车辆数时的场景进行仿真分析，结果如图7和表2所示。从图7可以看出，在车辆数较少时各算法的性能差异较小，这是由于车辆数较少，解空间较小，可以成组通行的车辆较少，进而算法间较难拉开差距。随着车辆数的增加，解空间增大，可成组通行的车辆增多，因而各算法的性能差距逐渐拉大。

在相同数量车辆的场景下，总体的通行时间是评价决策算法的重要指标，通行时间越短意味着算法对于交叉口冲突区的利用率越高。如表2所示，在不同车辆数场景下，本文算法相比文献［10］，通行时间分别缩短了23.1%、23.59%、26.72%、30.27%、33.42%；相比文献［16］，通行时间分别缩短了4.64%、6.54%、8.73%、12.28%、15.08%；相比文献［17］，通行时间分别缩短了3.9%、4.74%、5.78%、7.4%、8.08%。综上可得，本文算法相比于其他算法在不同车辆数情况下的通行效率均为最高，且随着车辆数的增加，通行效率的提升逐渐增大。

对优化的幅度进行分析，优化幅度随车辆数增加的增量在文献［10］上为0.49%、3.13%、3.55%、3.15%；在文献［16］上为1.9%、2.19%、3.55%、2.8%，在文献［17］上为0.84%、1.04%、1.62%、1.04%。车辆数较少时的优化涨幅呈增大趋势，当车辆数由40增加到50时，优化的增幅开始降低。分析可得，交叉口存在一个最大车辆通行能力上限，车辆数小于40时未达到该上限，随着车辆数增多本文算法相对于其他算法的缩短通行时间越多，当达到交叉口通行能力的瓶颈后继续增大车辆数，此时后方的车辆进入排队通行状态，本文算法相对于其他算法的优化程度开始降低。

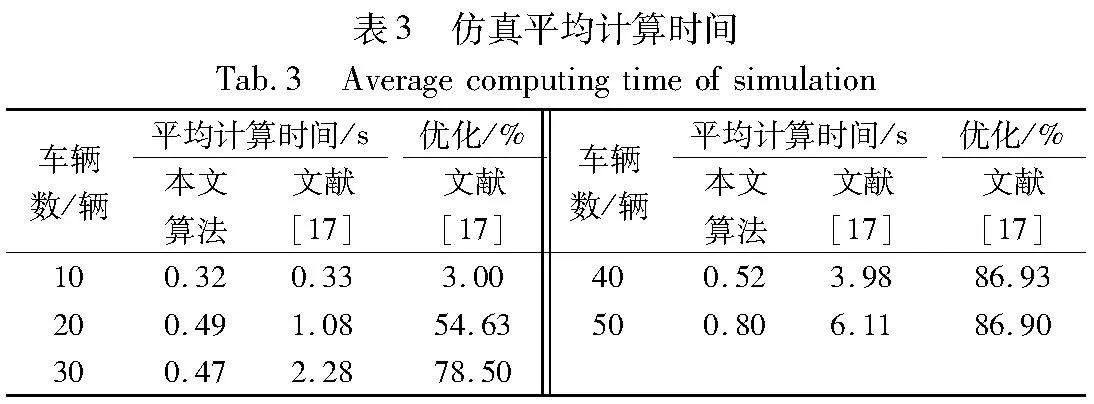
由于文献［10，16］的算法均为一次遍历便可获得结果，决策结果受车辆初始位置影响，在计算时间上不具备比较性。所以这里与同为启发式搜索算法的文献［17］进行比较，仿真计算时间如表3所示。可以看出文献［17］的计算时间随着车辆数增长呈现较大的增长趋势，车辆数为50时的计算时间超过6 s，本文算法仅为0.8 s，缩短了86.7%。

4.2 微缩平台实验

在微缩平台上进行进一步算法有效性验证。微缩平台基于机器人操作系统（robot operating system，ROS）开发，微缩车辆为搭载树莓派4B的阿克曼底盘小车，通过安装在顶部的相机对车辆进行定位，微缩车辆通过Wi-Fi与服务器进行通信，如图8所示。服务器配置为CPUi5-12600，内存16 GB，系统Ubuntu 20.6，编程语言为Python。微缩平台整体尺寸按照真实交叉口尺寸13∶1缩小，由于平台硬件性能限制，小车最高行驶速度为0.22 m/s，对应真实交通环境下的低速交通情况。

实验设计了五个不同的场景，尽可能包含不同的交叉口车辆分布情况，如图9所示。

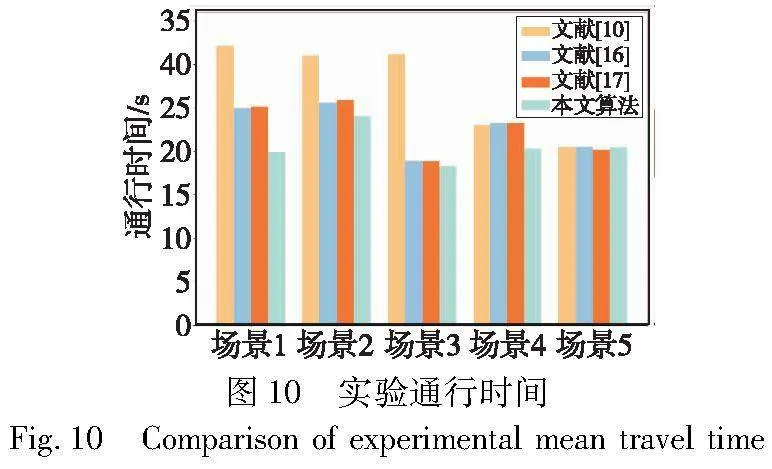
由于实验车辆数较少，各算法的计算时间均小于10 ms，在此情况下将着重对比车辆通行时间，结果如图10和表4所示。

由图10可以看出，本文算法在不同的场景下均能获得较低的通行时间。这是因为，文献［10，16］受车辆位置到冲突区距离的影响，在特定情况下也能获得较好的通行效率，但多数情况下的通行顺序与最优通行顺序差距较大。文献［17］虽然也是启发式搜索算法，但由于采用较为粗粒度的交叉口模型，限制了交叉口利用率的提高。由表4可以看出，本文算法相对于文献［10］的优化幅度从0.3%到41.18%不等，而在仿真中的优化幅度为23.1%到33.42%。分析可知，车辆数较少时文献［10］的性能受车辆分布影响较大，而本文算法在不同的车辆分布情况下均能获得接近最优解的通行顺序，体现在优化幅度上就是0.3%到41.18%的大跨度。随着车辆数的增多，结合不同车辆分布情况，一定程度上降低了不同车辆分布的极端情况，因此本文算法相对于文献［10］的优化幅度区间缩小为23.1%到33.42%。同样，文献［16，17］存在和文献［10］类似的缺点。

5 结束语

本文针对无信号交叉口车辆通行调度问题，建立基于冲突点的交叉口模型，提出一种自适应蒙特卡罗树搜索的顺序决策算法。首先将车辆通ac814468655d4be4abf56afdbd8919a1a863577205a998b4a39e20d4b029d207行顺序决策问题转换为树搜索问题，引入蒙特卡罗搜索思想并对超参数进行鲁棒性优化，获得通行顺序后计算各车到达冲突点的时间，建立最优控制命题求解车辆轨迹。经实验验证，本文算法相较于其他算法在不同车流量时均能有效提高交叉口通行效率，最高分别达到33.42%、15.08%、8.08%，并且在高车流量情况下同时求解50辆车时的平均计算时间低于0.8 s，为无信号交叉口车辆通行调度提供了一个有效解决方案。

参考文献：

［1］Guo Qiangqiang， Li Li， Ban Xuegang. Urban traffic signal control with connected and automated vehicles： a survey［J］. Transportation Research Part C： Emerging Technologies， 2019，101： 313-334.

［2］Bühm A. Delay-sensitive wireless communication for cooperative dri-ving applications［M］. Halmstad： Halmstad University Press， 2013.

［3］杨澜， 赵祥模， 吴国垣， 等. 智能网联汽车协同生态驾驶策略综述［J］. 交通运输工程学报， 2020， 20（5）： 58-72. （Yang Lan， Zhao Xiangmu， Wu Guoheng， et al. Review of collaborative ecological dri-ving strategies for intelligent networked vehicles［J］. Journal of Traffic and Transportation Engineering， 2020， 20（5）： 58-72.）

［4］Li Li， Wen Ding， Yao Danya. A survey of traffic control with vehicular communications［J］. IEEE Trans on Intelligent Transportation Systems， 2014， 15（1）： 425-432.

［5］Guler S I， Menendez M， Meier L. Using connected vehicle technology to improve the efficiency of intersections［J］. Transportation Research Part C： Emerging Technologies， 2014， 46： 121-131.

［6］Li Li， Wang Feiyue. Cooperative driving at blind crossings using intervehicle communication［J］. IEEE Trans on Vehicular Technology， 2006， 55（6）： 1712-1724.

［7］Rios-Torres J， Malikopoulos A A. A survey on the coordination of connected and automated vehicles at intersections and merging at highway on-ramps［J］. IEEE Trans on Intelligent Transportation Systems， 2017， 18（5）： 1066-1077.

［8］Li Shen， Shu Keqi， Chen Chaoyi， et al. Planning and decision-making for connected autonomous vehicles at road intersections： a review［J］. Chinese Journal of Mechanical Engineering， 2021， 34（1）： article No. 133.

［9］张毅， 裴华鑫， 姚丹亚. 车路协同环境下车辆群体协同决策研究综述［J］. 交通运输工程学报， 2022， 22（3）： 1-18. （Zhang Yi， Pei Huaxin， Yao Danya. Review on collaborative decision-making of vehicle groups in vehicle-road collaborative environment［J］. Journal of Traffic and Transportation Engineering， 2022， 22（3）： 1-18.）

［10］Dresner K， Stone P. Multiagent traffic management： a reservation-based intersection control mechanism［C］//Proc of the 3rd International Joint Conference on Autonomous Agents and Multiagent Systems.Piscataway， NJ： IEEE Press， 2004： 530-537.

［11］张毅， 姚丹亚， 李力， 等. 智能车路协同系统关键技术与应用［J］. 交通运输系统工程与信息， 2021， 21（5）： 40-51. （Zhang Yi， Yao Danya， Li Li， et al. Key technologies and applications of intelligent vehicle-road collaborative system［J］. Transportation System Engineering and Information， 2021， 21（5）： 40-51.）

［12］Meng Yue， Li Li， Wang Feiyue， et al. Analysis of cooperative dri-ving strategies for nonsignalized intersections［J］. IEEE Trans on Vehicular Technology， 2017，67（4）： 2900-2911.

［13］Carlino D， Boyles S D， Stone P. Auction-based autonomous intersection management［C］//Proc of the 16th International IEEE Conference on Intelligent Transportation Systems. Piscataway， NJ： IEEE Press， 2013： 529-534.

［14］Müller E R， Carlson R C， Junior W K. Intersection control for automated vehicles with MILP［J］. IFAC-PapersOnLine， 2016， 49（3）： 37-42.

［15］Ahn H， Del Vecchio D. Safety verification and control for collision avoidance at road intersections［J］. IEEE Trans on Automatic Control， 2017， 63（3）： 630-642.

［16］Chen Chaoyi， Xu Qing， Cai Mengchi， et al. A graph-based conflict-free cooperation method for intelligent electric vehicles at unsignalized intersections［C］//Proc of IEEE International Intelligent Transportation Systems Conference. Piscataway， NJ： IEEE Press， 2021： 52-57.

［17］Xu Huile， Zhang Yi， Li Li， et al. Cooperative driving at unsignalized intersections using tree search［J］. IEEE Trans on Intelligent Transportation Systems， 2019， 21（11）： 4563-4571.

［18］Pei Huaxin， Zhang Yuxiao， Zhang Yi， et al. Optimal cooperative driving at signal-free intersections with polynomial-time complexity［J］. IEEE Trans on Intelligent Transportation Systems， 2022， 23（8）： 12908-12920.

［19］李磊， 王文格， 彭景阳. 无信号交叉口网联车调度与分布式控制策略［J］. 计算机应用研究， 2022， 39（11）： 3346-3350. （Li Lei， Wang Wenge， Peng Jingyang. Combined vehicle scheduling and distributed control strategy at signalless intersection［J］. Application Research of Computers， 2022， 39（11）： 3346-3350.）

［20］Magnuson M. Monte Carlo tree search and its applications［J］. Scholarly Horizons： University of Minnesota， Morris Undergraduate Journal， 2015， 2（2）： article No.4.