增强学习标签相关性的多标签特征选择方法

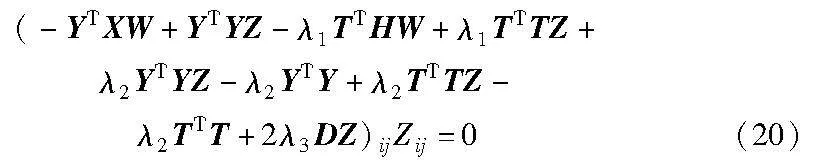
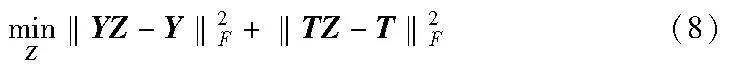
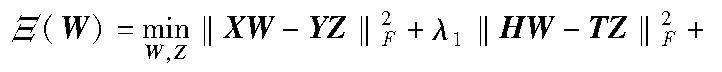
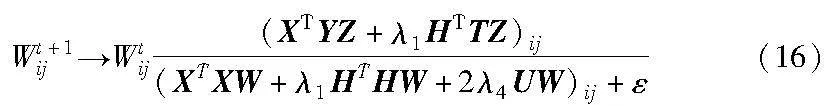
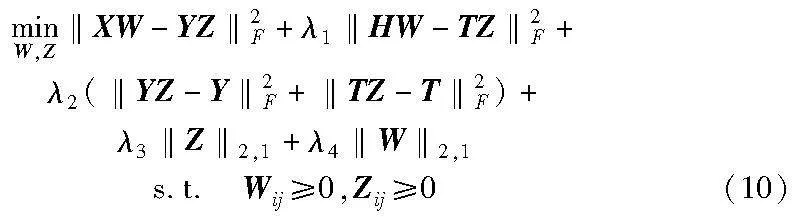
摘 要：针对现有多标签特征选择方法存在的两个问题：第一，忽略了学习标签相关性过程中噪声信息的影响；第二，忽略探索每个簇的综合标签信息，提出一种增强学习标签相关性的多标签特征选择方法。首先，对样本进行聚类，并将每个簇中心视为一个综合样本语义信息的代表性实例，同时计算其对应的标签向量，而这些标签向量体现了每个簇包含不同标签的重要程度；其次，通过原始样本和每个簇中心的标签级自表示，既捕获了原始标签空间中的标签相关性，又探索了每一个簇内的标签相关性；最后，对自表示系数矩阵进行稀疏处理，以减少噪声的影响，并将原始样本和每个簇代表性实例分别从特征空间映射到重构标签空间进行特征选择。在9个多标签数据集上的实验结果表明，所提算法与其他方法相比具有更好的性能。

关键词：多标签学习； 特征选择； 标签相关性； 聚类

中图分类号：TP391 文献标志码：A 文章编号：1001-3695（2024）07-022-2079-08

doi：10.19734/j.issn.1001-3695.2023.11.0550

Multi-label feature selection method with enhanced learning of label correlations

Abstract：Aiming at two problems of existing multi-label feature selection methods： first， ignoring the influence of noise information in the process of learning label correlations; second， neglecting to explore the comprehensive label information of each cluster， the paper proposed a multi-label feature selection method that enhanced label correlation learning. Initially， it clustered the samples and treated each cluster center as a representative instance of the comprehensive semantic information of the samples， while computing its corresponding label vectors which reflected the importance of different labels contained in each cluster. Then， through the label-level self-representation of the original samples and the center of each cluster， it both captured the label correlations in the original label space， and explored the label correlations within each cluster. Finally， the self-representation coefficient matrix was sparse to reduce the effect of noise， and the original sample and the representative instance of each cluster were mapped from the feature space to the reconstructed label space for feature selection. Experimental results on nine multi-labeled datasets show that the proposed algorithm has better performance compared with other methods.

Key words：multi-label learning; feature selection; label correlation; clustering

0 引言

随着计算机和通信技术的飞速发展，多标签数据集在不同领域有着广泛的应用，如文本挖掘［1］、图像识别［1，2］、蛋白质功能检测［3］和信息检索［4］等。这些数据集为机器学习和模式识别提供了丰富的研究数据源。在传统的单标签监督学习中，每个实例只与一个类标签相关联。然而，在真实世界的场景中，往往会涉及与多个语义相关联的实例［5］。例如，一份报告可能有多个主题，包括时尚、经济和体育；一首音乐可以表达多种情绪，包括悲伤、平静和孤独。因此，现有的多标签学习方法的目的是在训练实例和相应的标签集之间学习一个合适的映射函数，以便通过映射函数预测新实例中不可见的多个标签［6］。然而，在现实世界中，多标签数据集的特征表示通常具有高维性，并且容易受到噪声和冗余信息的影响［7］。这些因素不仅会增加计算和存储需求，还会对学习模型的分类性能产生不利影响，因此带来了巨大挑战［7］。

在高维数据处理领域，有特征提取和特征选择两种降维方法［8］。特征提取通常会产生新的特征，而特征选择不会改变数据的原始表示，其目的是获取一个特征子集来表示原始数据［9～11］。因此，本文将重点放在特征选择上。一般来说，关于特征选择的研究可分为基于过滤的、基于包装的和基于嵌入的方法三类［12，13］。基于过滤的方法用于生成特征子集，而不依赖于任何特定的学习算法。这些方法通过采用不同的评估标准来评估特征的相关性，包括卡方统计、互信息和样本距离［14］。然而，过滤的方法无法为特定的学习任务选择信息量最大的特征。基于包装的方法使用进化算法来搜索最佳特征子集，这种模型容易出现过拟合问题，还会产生巨大的计算成本［15］。基于嵌入的方法通过同时训练模型和选择特征，提供了一种独特的解决方案［16］。它们直接利用从模型训练中得到的特征系数矩阵来确定特征的排序，从而获得高效的执行和出色的分类性能［16］。因此，本文重点讨论嵌入式方法。

对于设计多标签特征选择方法，探索标签相关性是至关重要的，因为可以捕获非对称的标签关系［17］。在图1中，显示了一个非对称的标签关系例子。图（a）有“树”标签，也可能带有“天空”标签。然而，图（b）带有“天空”标签，但不一定带有“树”标签。因此，一些现有方法利用标签相关性设计多标签特征选择方法，取得不错的成果。例如，Li等人［18］提出了一种具有两种标签相关性的鲁棒多标签特征选择方法。Fan等人［19］提出了一种基于标签相关性和特征冗余的新的多标签特征选择方法，将低维嵌入用于挖掘标签相关性，这样可以保持原始标签空间的全局和局部标签结构。

然而，现有的多标签特征选择方法［10，13，18］在探索标签相关性时仍存在一些问题，进而导致模型学习效率降低。第一，忽略了学习标签相关性过程中噪声信息的影响。在原始标签空间中往往包含噪声信息，如果直接利用标签集中的数据来探索标签与标签之间的关系，会影响标签相关性的探索，导致产生一些不必要的依赖关系，降低模型的学习效率。在这里，通过一个例子说明在探索标签相关性时处理噪声影响的必要性。假设大部分实例都同时具有“标签1”与“标签2”，则本文认为“标签1”与“标签2”相关程度较高。由于人工过失，将个别实例的“标签2”标记为“标签3”，则本文认为“标签3”为噪声信息，“标签1”与“标签3”为不必要的标签依赖关系。如果不对上述情况作出处理，则会产生错误传播，即认为“标签1”与“标签3”存在相关性。第二，忽略探索每个簇的综合标签信息，仅在原始标签空间中探索标签相关性，无法挖掘更深层次的标签信息。直接利用原始标签数据，往往探索的是一个标签与其他所有标签的关系，无法描述一个局部区域内标签之间的关系。而高度相关的标签共用同一个特征子集，有利于提高特征选择的效率，因此，需要挖掘更深层次的标签信息，更好捕获标签与标签之间的关系。

为此，本文利用数据增强技术和标签级自表示模型，探索了不同标签之间的相关性。针对上述第二点问题，本文对样本进行聚类形成多个簇，则每个簇的中心可以看作是每个簇的综合信息实例，并假设其对应的特征向量和标签向量是簇中所有样本向量的平均值。每个簇中心的标签向量则反映了一个簇中每个标签的重要程度。然后，通过样本和每个簇的综合信息实例的标签级自表示，既可以探索原始标签空间中的标签相关性，又可以探索了每个簇内重要标签的相关性。此外，针对上述第一点问题，本文对自表达系数矩阵施加2，1范数约束，确保每个标签由与其最相关的标签表示，以减少噪声信息产生的不利影响。最后，设计了一种交替最小化方法来求解目标函数。综上所述，本文的主要贡献如下：

a）对样本聚类，并将每个簇的中心视为一个综合信息实例，以簇中所有样本向量的平均值作为综合信息实例的特征向量和标签向量。

b）引入样本和综合信息实例的标签级自表示，既捕获了原始标签空间中的标签相关性，又探索了每个簇内的标签相关性。

c）对标签级自表示系数矩阵施加2，1范数约束，增进每个标签与其最相关的标签之间的关系，以减少噪声信息产生的不利影响。

d）设计了一种具有收敛性证明的优化方案求解目标函数，并通过多重综合实验证明了该方法的优越性。

1 相关工作

1.1 多标签学习

近年来，许多成熟的多标签学习方法被提出。现有的多标签学习方法包括三种不同探索标签相关性的策略［19］。一阶策略是将多标签数据转换为单标签数据，从而利用传统的单标签算法，例如BR算法［20］可以对多标签分类问题进行变换。然而，这类方法忽略了标签相关性，而标签相关性对研究工作至关重要。因此，一些方法引入了二阶策略，主要侧重探索标签之间的成对相关性。例如，Huang等人［21］使用标签级正则化约束来考虑成对的标签相关性。尽管这些方法取得一些进步，但现实世界的多标签数据集往往包含的实例与多个标签相关联，显然标签之间的相关性超过成对关系。因此，一些方法引入了高阶策略，通过探索多个标签之间的相关性来解决这一问题。例如，分类器链（CC）［22］，另一种高阶方法LEAD利用标签依赖性，通过使用贝叶斯方法来学习多标签数据［18］。

此外，本文还回顾了一些通过探索标签相关性而设计的具有代表性和影响力的多标签特征选择方法。Hu等人［23］介绍了一种称为共享共模多标签特征选择（SCMFS）的方法，该方法利用耦合矩阵分解（CMF）来提取特征矩阵和标签矩阵之间的共享共模。这种方法结合了来自两个矩阵的综合数据信息，提高了特征选择性能。Fan等人［24］开发了一种名为基于局部判别模型和标签相关性的多标签特征选择的算法。该方法考虑实例的相邻实例，为实例构建局部聚类，并全局集成局部判别模型来评估所有实例的聚类性能。Li等人［25］提出了具有动态局部和全局结构保持的鲁棒稀疏和低冗余多标签特征选择方法，该特征选择方法使用图结构以保持全局标签相关性和动态局部标签关联。该方法的目标函数包括范数和内积正则化项，以实现高行稀疏性和低冗余特征选择。值得注意的是，上述大多方法局限于从给定的训练样本中探索标签相关性，无法探索每个簇蕴涵的标签信息。

1.2 数据增强

数据增强［26］是一种在机器学习任务中广泛使用的技术，它的目的是在原始训练集上应用一些转变，来综合创建新的样本，以扩大训练集。用于图像分类任务的传统数据增强技术通常通过翻转、扭曲、添加少量噪声或从原始图像中裁剪一个补丁，从原始训练数据中生成新的样本［26］。除了传统的数据增强技术之外，简单配对法也是一种数据增强方法［27］，随机选择两个样本（xa，ya）和（xb，yb），然后通过（（xa+xb）/2， ya）或者（（xa+xb）/2，yb）随机生成一个新的样例。这种方法通过关注两个实例来产生新的实例，虽然取得不错的效果，但如何从多个样本中产生新的实例，以及如何应用生成的新实例提高多标签学习的性能仍然具有挑战性。Shu等人［27］提出对原始样本进行聚类，并将聚类中心作为虚拟样本。然后，在同一聚类中的例子具有相同标签的假设下，他们提出了一个新的正则化术语来弥补实例和虚例之间的差距，从而提高学习函数的局部平滑性。然而，该方法忽略了探索标签相关性。因此，本文利用数据增强技术生成每个簇的综合代表实例，在探索原始样本的标签相关性之余，还探索了每个簇内的标签相关性，并用标签相关性重构标签空间，以提高多标签模型的学习性能。

2 研究方法

对于一个多标签数据集{（x1，y1），…，（xn，yn）}，假设特征

所提方法工作原理分为两个基本步骤，包括生成每个簇中心对应的特征向量、标签向量和多标签特征选择模型训练。因此，所提方法按照以下两个部分介绍：a）首先使用K-means方法对原始样本进行聚类，并将每个簇中心视为对应簇的综合代表实例。b）探索原始样本与每个簇中心的标签相关性，并重构标签空间，以进行特征选择。

2.1 生成每个簇中心对应的特征向量和标签向量

聚类技术被广泛应用于数据分析，本文采用常用的K-means算法。如图2所示，通过对原始样本聚类，并将每个簇的中心作为一个综合代表的实例。假设原始样本可以被划分为q个不相交的簇{C1，C2，…，Cq}，如果第j个实例被划分为第i个簇，则xj∈Ci。通常，每个簇的中心是簇的一个代表性实例，因此其语义可以是簇中所有样本的语义平均值。假设hi表示Ci簇中心对应的特征向量，可以表示为

其中：Ci表示第i个簇包含的样本个数。同样地，每个簇中心的标签语义可以是簇中所有实例的标签语义的平均值。假设ti表示Ci簇中心对应的标签信息，则ti应为Ci中所有样本的平均标签向量，可以表示为

这样可以得到一个簇中心集合{（hi，ti），…，（hq，tq）}，在这里，可以通过一个具体例子说明这种数据增强方法的优势。假设一个簇里面包含三个样本（xa，ya），（xb，yb）和（xc，yc），其

2.2 构建多标签特征选择模型

岭回归是一种无偏差的最小二乘法，通常用于处理机器学习的一些基本任务，包括分类、降噪、降维等［28］。将传统的岭回归应用于多标签特征选择，其一般形式如下：

其中：λ1是超参数，控制每个簇的综合代表实例（即簇中心）对特征选择W学习的贡献。由于簇中心是每个簇的综合代表实例，用其训练模型会增大每个簇对应特定特征的选择权值，从而提高模型学习性能。但是，式（5）在带有噪声和冗余信息的原始标签空间中进行特征选择，会降低了算法的学习性能。因此，需要利用标签相关性来重建标签空间，以更好进行特征选择。

从实例级的自表示模型得到启发，类似地，每个标签也可以用其他标签进行表示，从而探索一个标签和其他标签之间的关系。因此，可以得到改进后的标签级自表示模型如下：

从而探索一个标签和其他标签之间的关系），以互补原始数据探索的标签相关性。则其表达式为

结合式（6）（7），本文探索标签相关的表达式为

这样，既探索了原始标签空间中的标签相关性，又探索了每个簇内的标签相关性，充分捕获了标签信息。然而原始标签空间中往往包含噪声信息，会导致在探索标签相关性时，产生不必要的关系依赖。为此，本文通过对自表示系数矩阵施加2，1范数，确保每个标签由与其最相关的标签表示，以减少噪声信息的影响。则式（8）可以改写为

其中：λ3是正则化参数。结合式（5）（9），利用标签相关性重构原始标签空间，得到新的标签空间，然后通过特征矩阵投影到标签重构矩阵，以进行特征选择。另外，对W和Z施加非负约束，以保证数据的非负性。因此，最终的目标函数构造如下：

其中：‖XW-YZ‖2F为原始样本从特征空间映射到重建的标签空间以进行特征选择；‖HW-TZ‖2F为每个簇中心从特征映射到标签，以加强每个簇的标签对应特定特征的选择；‖YZ-Y‖2F和‖TZ-T‖2F为原始样本和簇中心的标签级自表达（即一个标签由其他标签进行表示，从而探索一个标签和其他标签之间的关系），分别探索了原始标签空间中的标签相关性和每个簇内的标签相关性；‖Z‖2，1为避免学习标签相关性过程中噪声信息的影响；λ1是超参数，控制每个簇的综合代表实例（即簇中心）对特征选择W学习的贡献；λ2正则化参数，调节原始样本和每个簇的综合代表实例的标签级自表示对多标签学习模型的影响；λ3与λ4是正则化参数。

2.3 优化模型

在本节中，给出关于目标函数式（10）的优化方案证明。目标函数有两个优化目标W和Z，以及对W和Z施加2，1范数的非光滑性，本文采用交替优化的方法来求解。

对于上述目标函数的迭代更新方法包含以下两个子问题。

子问题1 固定Z，更新W。

当固定Z时，获得只关于W的函数，可以表示为

根据拉格朗日定理，将约束条件Wij≥0整合到Θ（W），可以得到拉格朗日函数如下：

根据Karush-Kuhn-Tucker条件［18］，ΦijWij=0，可得

（XTXW-XTYZ+λ1HTHW-λ1HTTZ+2λ4UW）ijWij=0（15）

最后，得到W的更新规则：

子问题2 固定W，更新Z。

当固定W时，可以获得只关于Z的函数，可以表示为

同样地，根据拉格朗日定理，将约束条件Zij≥0整合到Θ（Z），可以得到拉格朗日函数如下：

根据Karush-Kuhn-Tucker条件，ΨijZij=0，可得

最后，得到Z的更新规则：

重复交替更新W和Z变量的值，直到目标函数收敛，最后计算‖Wi·‖2。本文算法流程如算法1所示。

算法1 所提方法的优化算法

算法1伪代码如下：

3 实验

将本文算法与其他五种先进的多标签特征选择方法进行比较，九个数据集的实验结果表明本文算法具有更好的学习性能，下面将描述实验详细过程。

3.1 实验数据

在本节中，将描述相关的实验数据集。采用从Mulan Library获取的九个不同领域的多标签数据集。 这些数据集包括各种领域，如音频、音乐、图像、生物学和文本，为评估提供了不同的数据。表2给出了关于所选数据集的详细信息。

3.2 实验设置

为了与其他方法进行比较，本文使用Hamming loss，ran-king loss，average precision，Macro-F1和Micro-F1来评估本文算法的性能。从解释上看，Hamming loss和ranking loss的值越小，说明分类性能越好，最佳值为0，意味着完美分类。相反，average precision，Macro-F1和Micro-F1的值越大，表示分类性能越好，最佳值为1，表示理想的分类结果。

为了确保公平性和可比性，本文在{0.01，0.1，0.3，…， 0.9，1.0}的范围内调整方法的正则化参数。

实验采用如下五种多标签特征选择方法作为对比算法：

a）MIFS［29］。基于流形框架探索标签相关性，以确保结构性。参数α，β和γ在{0.01，0.1，0.3，…，0.9，1.0}内进行调参。

b）SCMFS［23］。它通过耦合矩阵因式分解建立共享的共同模型。参数α，β和γ在{0.01，0.1，0.3，…，0.9，1.0}内进行调参。

c）MDFS［30］。它探索流形结构下的局部标签相关性和全局标签相关性。参数α设为1，其余参数β和γ在{0.01，0.1，1，…，10，100}内进行调参。

d）MRMD［28］。提出一种新的多标签特征选择方法，它有效地结合了流形正则化和依赖性最大化。参数α设为1，其余参数β和γ在{0.01，0.1，1，…，10，100}内进行调参。

e）LMFS［10］。结合逻辑回归、流形学习和稀疏正则化，构建了多标签特征选择的联合框架。参数α，β和γ在{0.001，0.01，0.1，1，10，100，1000}内进行调参。

为了评估所有竞争方法的性能，本文使用ML-KNN（K=10） 作为统一分类器来测试它们所选的特征，并采用五倍交叉验证来记录每个多标签数据集的平均性能。

3.3 实验结果与分析

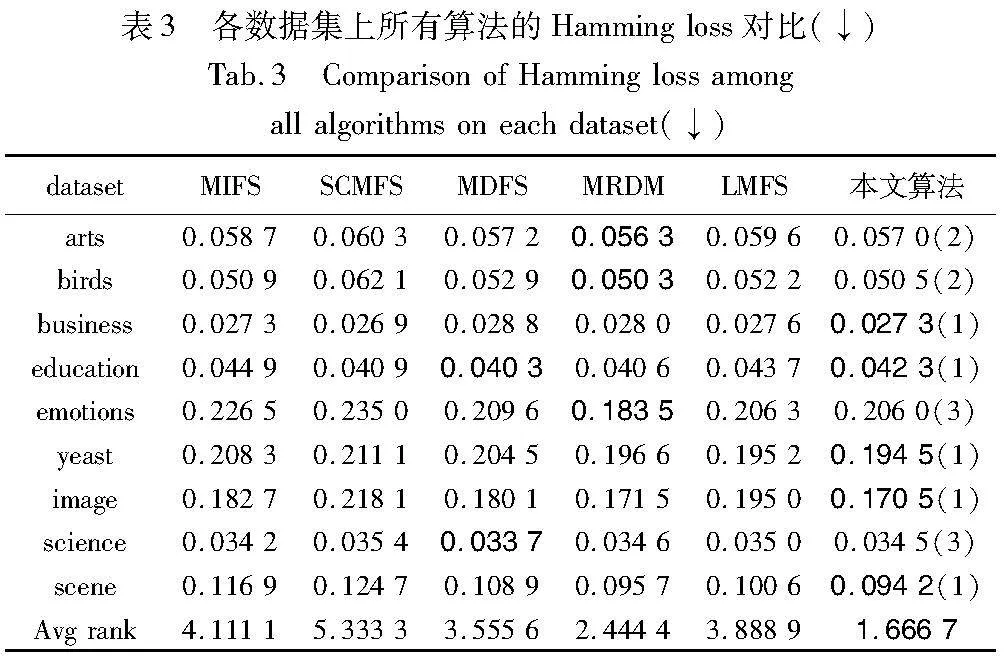
本节将展示和分析所有实验结果，在所有使用的数据集中使用了最优排序前20%的特征。表3～7描述了所有算法在每个评估指标下的结果。为了更清楚地突出实验结果，对每个数据集的最佳结果都采用了粗体字。此外，在最后一行中，计算了在数据集上的性能排名平均值。

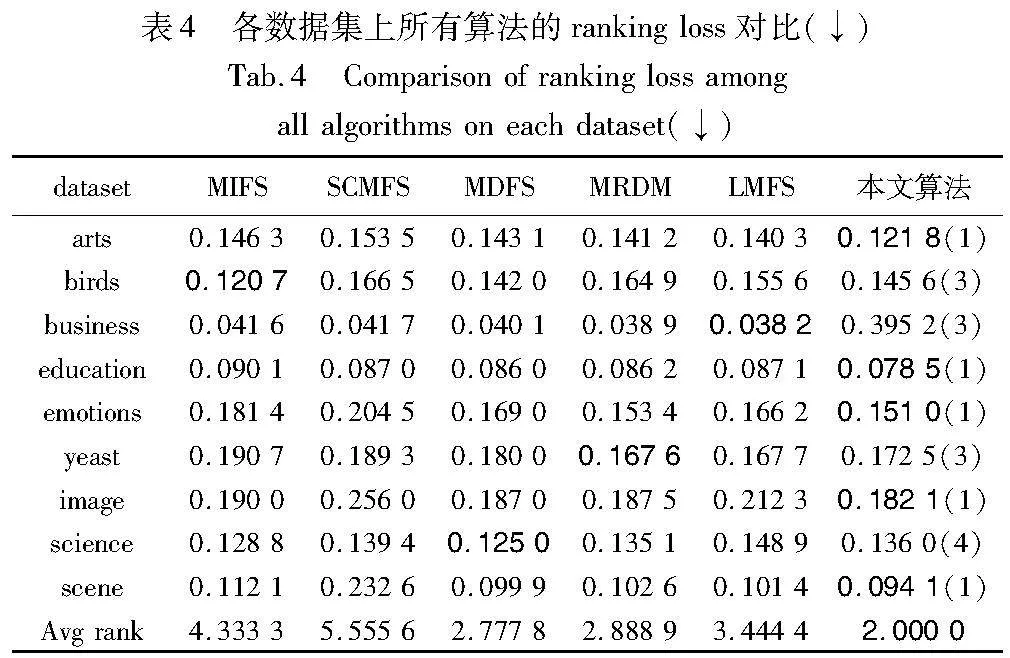
从表3～7可知，本文算法在各项评价指标上的表现总体优于其他比较算法。在表3中，本文算法在9个数据集中的6个数据集上获得了最佳结果，并且在所有数据集上都优于PUM、MIFS和SCMFS。在数据集arts和birds上，本文算法的性能仅次于MRMD。在表4中，本文算法在6个数据集上取得最佳结果，在其他数据集上也取得中等以上的排名。在表5中，除了数据集birds和business，本文算法在其他数据集上都取得最佳结果或次优结果。在表6中，除了数据集arts和yeast，本文算法在其他数据集上都取得最佳结果或次优结果。在表7中，本文算法在6个数据集上取得最佳结果，另外在数据集education上性能效果欠佳。

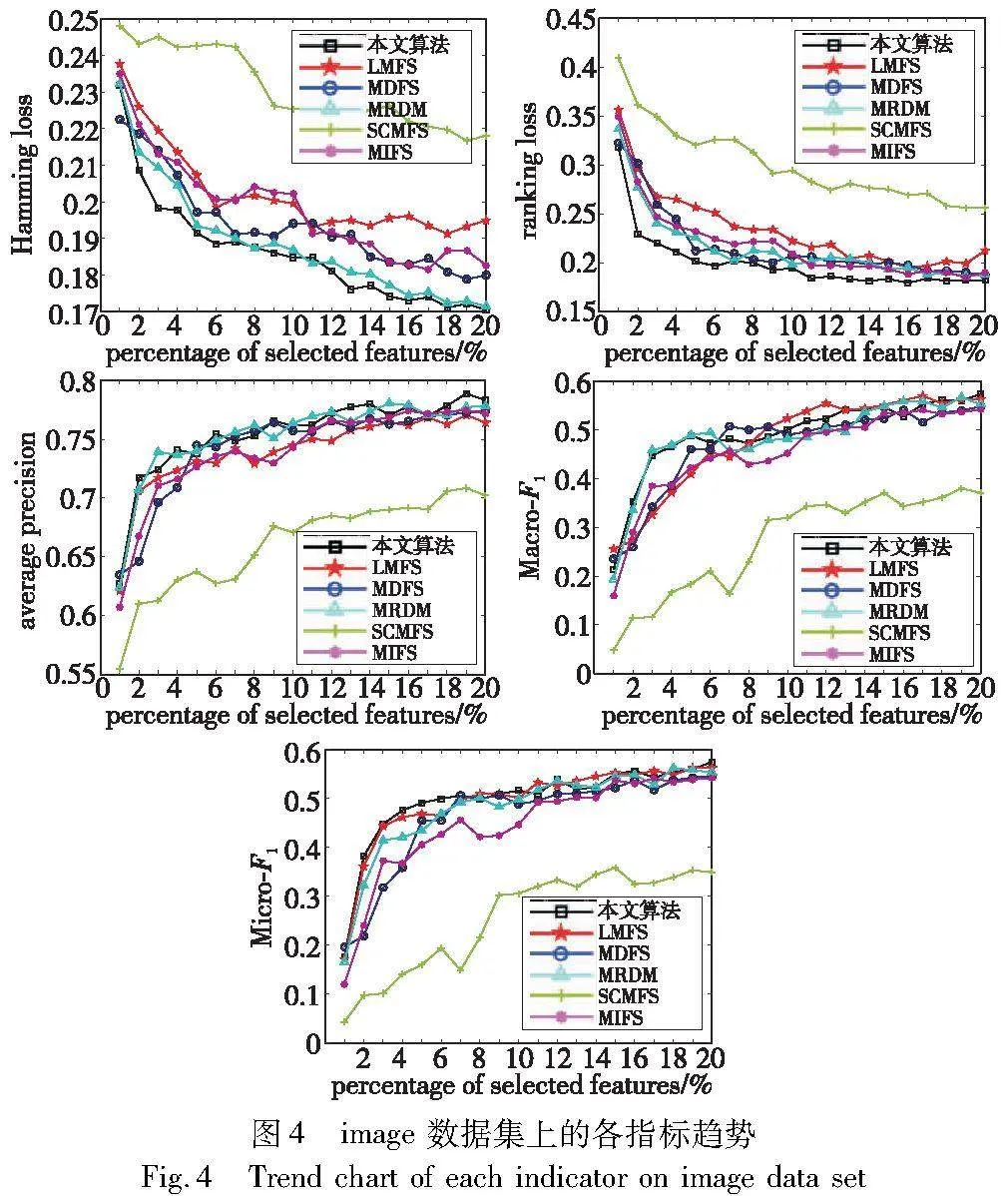
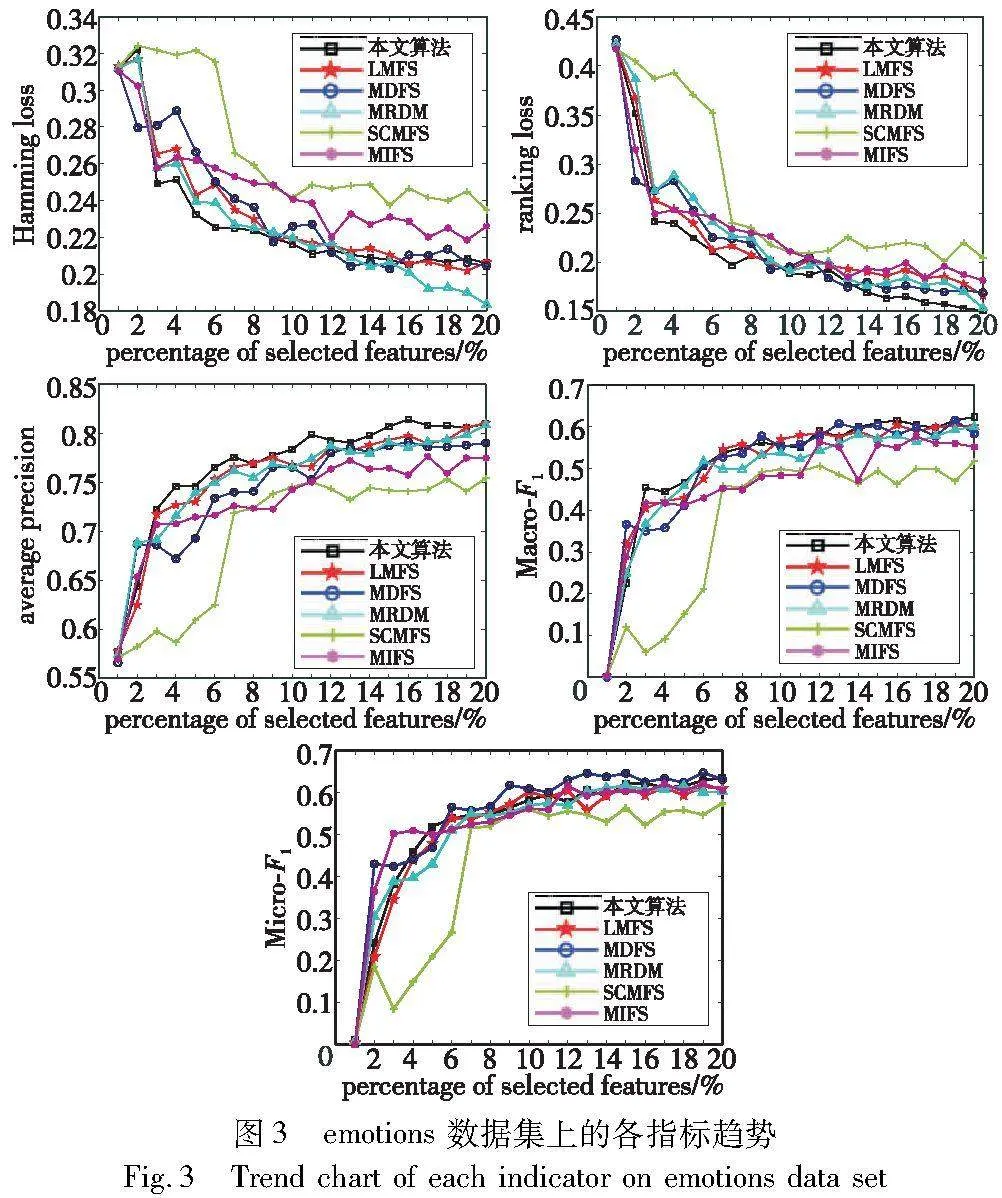
为了更好地观察各种多标签特征选择算法在Hamming loss、ranking loss、average precision、Macro-F1和Micro-F1指标下的性能曲线，本文给出emotions和image两个数据集的指标趋势图。对于每个数据集，所选特征的数量设置为前{1%，2%，3%，…，20%}个特征。如图3、4所示，随着所选特征数量的增加，所有算法的学习性能都会发生变化。

在所有数据集中，本文算法的学习性能首先随着所选特征的增加而提高，最后趋于稳定。这表明该算法是一种有效的多标签特征选择算法。总体而言，无论选择的特征数量如何，本文方法在所有数据集上都优于大多数比较算法。

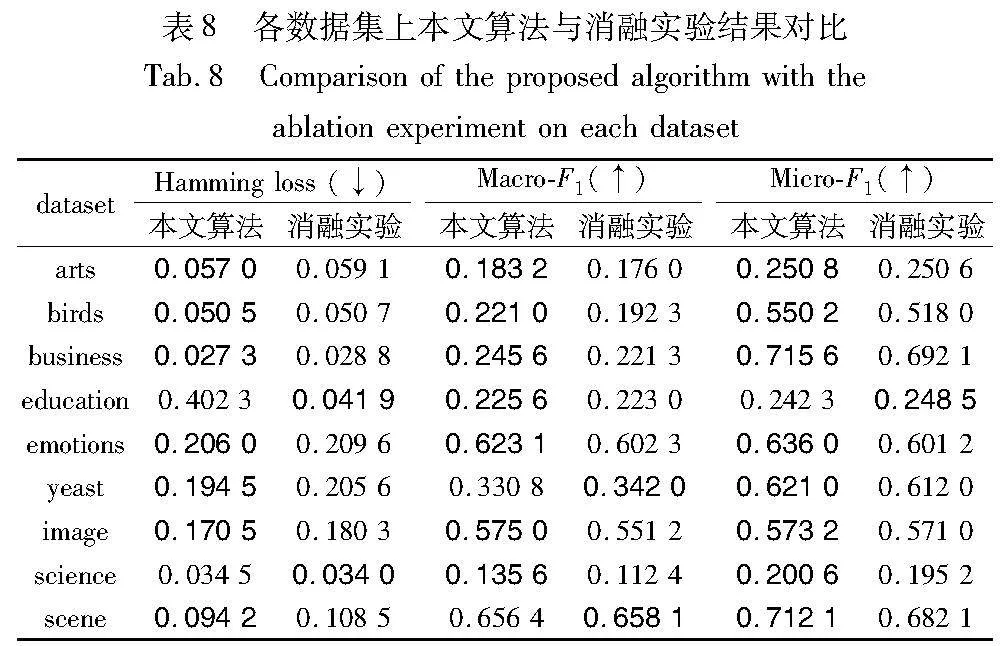
接下来，通过消融研究，分析本文算法引入簇中心探索标签相关性和增强模型学习的效果。通过目标函数式（10）去除有关簇中心部分，来验证该部分模型学习的性能。因此，可以得到消融实验的目标函数为

式（22）去除了簇中心特征选择和簇中心探索标签相关性部分，选取Hamming loss、Macro-F1和Micro-F1三个指标与本文算法进行对比。实验结果如表8所示，在三个指标下，本文算法在多数数据集上的结果都优于消融实验。这表明，引入簇中心探索标签相关性对训练多标签模型起着重要的作用。

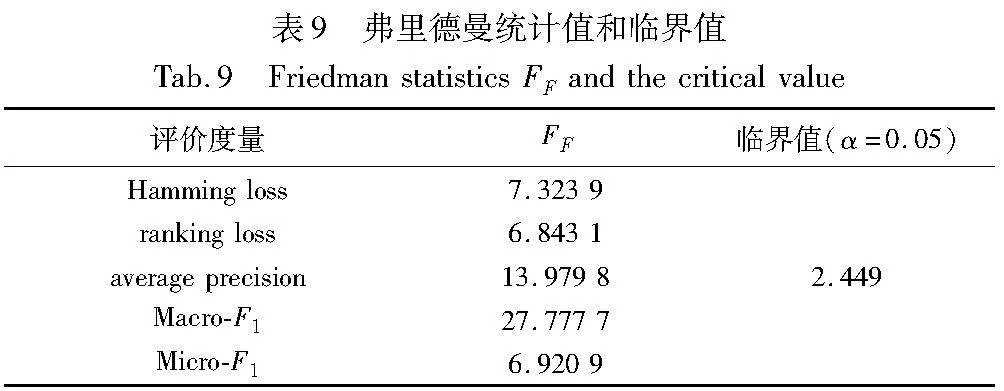
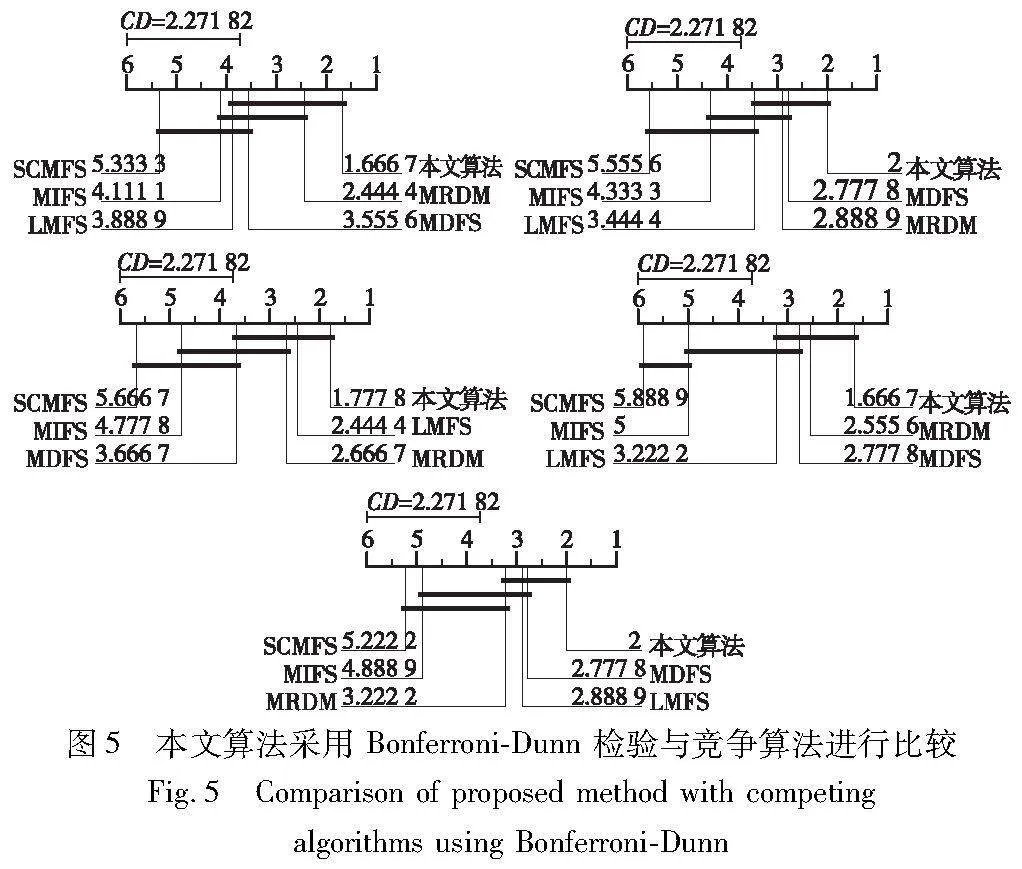
此外，本文还统一使用前20%的特征多标签学习的特征子集，系统分析本文算法与比较算法之间的相对性能。与其他算法类似，使用弗里德曼检验［31］进行相对性能分析。表9描述了每个评价度量的弗里德曼统计量FF和相应的临界值。可以看出，在显著水平α=0.05的情况下，每个度量都明确地否定了所有算法都具有相同性能的假设。因此，可以通过事后检验［32］来分析本文算法与比较算法之间的相对性能。

出，本文算法与MIFS、SCMFS这两种算法有显著的不同。在大部分评价度量下，与LMFS也有显著的差异。另外，本文算法与MDFS、MRDM没有显著的差异，但在每个评价指标中排名第一。

综合上述所有实验结果，本文算法具有比竞争方法更好的学习性能。从原理上看，本文算法与流形框架下探索标签相关性设计的算法（MIFS、MDFS、MRMD、LMFS）相比，避免使用低质量的图探索局部标签相关性，而是通过数据增强技术，对样本聚类，将每个簇的中心视为综合代表实例，而这些实例的标签向量恰恰能体现每个簇所包含标签的重要程度。通过原始样本和每个簇综合代表实例共同学习特征选择函数，又能增强每个簇对应特定特征的选择权重。其次，本文算法通过改进的自表示模型探索标签相关性，更重要的是，通过稀疏标签相关性矩阵，避免了原始空间中的噪声信息带来的影响，进而提高模型的精度。

最后，为了验证本文算法在实例上的应用结果，采用南京大学机器学习与数据挖掘研究所公开的自然图像数据集（https：//www.lamda.nju.edu.cn/data_MIMLimage.ashx），并利用分类指标评判本文算法的性能。该图像库共2 000张，分为desert（沙漠）、mountains（山脉）、sea（海洋）、sunset（日落）和trees（树木）五种类别。这些图像以单一标签、两个标签以及三个标签的形式存在，分别包含了1 543张、442张和15张。在图6，本文给出部分样本的分类结果，根据预测结果，除了图（k）（q）外，预测结果与图像的真实标签相匹配，表明本文算法是一种有效的多标签特征选择算法。对于一些无法准确预测真实标签的情况，如图（k）预测多了sea标签，原因可能是由于该图片包含mountains与sea或sunnet与sea共用特征子集中的特征，从而导致预测时关联的两个标签同时出现；而对于另一种情况，如图（q）未能预测到desert标签，原因可能是该类型的标记图像数量过少，模型没有很好地学习到该特征。

4 结束语

基于数据增强技术，本文提出标签相关性增强的特征选择算法。本文算法旨在利用数据增强技术生成每个簇的综合代表实例，扩充多标签数据集，进而用于探索标签相关性和优化模型学习。具体来说，通过原始样本聚类，将每个簇的中心作为综合代表实例，这些簇中心对应的标签向量自然体现了簇内包含不同标签的重要程度。将原始样本和每个簇综合代表实例同时进行标签级自表示，并对自表示系数矩阵进行稀疏处理，避免原始标签空间中噪声信息带来的影响。该算法既捕获了原始标签空间中的标签相关性，又探索了每个簇内标签相关性。同时，又处理了传统算法因为噪声信息而产生不必要的标签依赖问题。与近几年的五种算法在九个数据集上进行实验对比，实验结果表明本文算法的学习性能有优势。在未来将关注利用因果机制探索标签相关性，进而设计性能更好的特征选择方法。

参考文献：

［1］Tang Bo， Kay S， He Haibo. Toward optimal feature selection in naive Bayes for text categorization［J］. IEEE Trans on Knowledge and Data Engineering， 2016，28（9）： 2508-2521.

［2］Ma Zhigang， Nie Feiping， Yang Yi， et al. Web image annotation via subspace-sparsity collaborated feature selection［J］. IEEE Trans on Multimedia， 2012，14（4）： 1021-1030.

［3］Li Yonghao， Hu Liang， Gao Wanfu. Multi-label feature selection via robust flexible sparse regularization［J］. Pattern Recognition， 2023， 134： 109074.

［4］Miri M， Dowlatshahi M B， Hashemi A. Evaluation multi label feature selection for text classification using weighted borda count approach［C］//Proc of the 9th Iranian Joint Congress on Fuzzy and Intelligent Systems. Piscataway，NJ：IEEE Press， 2022： 1-6.

［5］Li Junlong， Li Peipei， Hu Xuegang， et al. Learning common and label-specific features for multi-label classification with correlation information［J］. Pattern Recognition， 2022，121： 108259.

［6］Siblini W， Kuntz P， Meyer F. A review on dimensionality reduction for multi-label classification［J］. IEEE Trans on Knowledge and Data Engineering， 2019， 33（3）： 839-857.

［7］潘敏澜， 孙占全， 王朝立，等. 结合标签集语义结构的多标签特征选择算法［J］. 小型微型计算机系统， 2023， 44（1）： 90-96. （Pan Minlan， Sun Zhanquan， Wang Chaoli， et al. Multi label feature selection algorithm based on semantic structure of label set［J］. Journal of Chinese Computer Systems， 2023， 44（1）： 90-96）.

［8］Liu Jinghua， Li Yuwen， Weng Wei， et al. Feature selection for multi-label learning with streaming label［J］. Neurocomputing， 2020， 387： 268-278.

［9］Fan Yuling， Liu Jinghua， Weng Wei， et al. Multi-label feature selection with constraint regression and adaptive spectral graph［J］. Knowledge-Based Systems， 2021， 212： 106621.

［10］Zhang Yao， Ma Yingcang， Yang Xiaofei. Multi-label feature selection based on logistic regression and manifold learning［J］. Applied Intelligence， 2022， 52：9256-9273.

［11］Cheng Yusheng， Zhang Chao， Pang Shufang. Multi-label space reshape for semantic-rich label-specific features learning［J］. International Journal of Machine Learning and Cybernetics， 2022，13（6）： 1-15.

［12］Teng Luyao， Feng Zhenye， Fang Xiaozhao， et al. Unsupervised feature selection with adaptive residual preserving［J］. Neurocompu-ting， 2019， 367： 259-272.

［13］Fan Yuling， Liu Jinghua， Liu Peizhong， et al. Manifold learning with structured subspace for multi-label feature selection［J］. Pattern Recognition， 2021， 120： 108169.

［14］Lim H， Kim D W. MFC： initialization method for multi-label feature selection based on conditional mutual information［J］. Neurocomputing， 2020， 382： 40-51.

［15］Tawhid M A， Ibrahim A M. Feature selection based on rough set approach， wrapper approach， and binary whale optimization algorithm［J］. International Journal of Machine Learning and Cyberne-tics， 2020， 11： 573-602.

［16］Hu Juncheng， Li Yonghao， Gao Wanfu， et al. Robust multi-label feature selection with dual-graph regularization［J］. Knowledge-Based Systems， 2020， 203： 106126.

［17］Kumar S， Rastogi R. Low rank label subspace transformation for multi-label learning with missing labels［J］. Information Sciences， 2022， 596： 53-72.

［18］Li Yonghao， Hu Liang， Gao Wanfu. Label correlations variation for robust multi-label feature selection［J］. Information Sciences， 2022， 609： 1075-1097.

［19］Fan Yuling， Chen Baihua， Huang Weiqin， et al. Multi-label feature selection based on label correlations and feature redundancy［J］. Knowledge-Based Systems， 2022， 241： 108256.

［20］Zhang Minling， Zhou Zhihua. A review on multi-label learning algorithms［J］. IEEE Trans on Knowledge and Data Engineering， 2013， 26（8）： 1819-1837.

［21］Huang Jun， Qin Feng， Zheng Xiao， et al. Learning label-specific features for multi-label classification with missing labels［C］//Proc of the 4th IEEE International Conference on Multimedia Big Data. Piscataway，NJ：IEEE Press， 2018： 1-5.

［22］Read J， Pfahringer B， Holmes G， et al. Classifier chains for multi-label classification［J］. Machine Learning， 2011， 85： 333-359.

［23］Hu Liang， Li Yonghao， Gao Wanfu， et al. Multi-label feature selection with shared common mode［J］. Pattern Recognition， 2020， 104： 107344.

［24］Fan Yuling， Liu Jinghua， Weng Wei， et al. Multi-label feature selection with local discriminant model and label correlations［J］. Neurocomputing， 2021， 442： 98-115.

［25］Li Yonghao，Hu Liang，Gao Wanfu. Robust sparse and low-redundancy multi-label feature selection with dynamic local and global structure preservation［J］. Pattern Recognition， 2023， 134： 109120.

［26］Inoue H. Data augmentation by pairing samples for images classification［EB/OL］. （2018-04-11）. https：//arxiv.org/abs/1801.02929.

［27］Shu Senlin， Lyu Fengmao， Yan Yan， et al. Incorporating multiple cluster centers for multi-label learning［J］. Information Sciences， 2022， 590： 60-73.

［28］Huang Rui， Wu Zhejun. Multi-label feature selection via manifold regularization and dependence maximization［J］. Pattern Recognition， 2021， 120： 108149.

［29］Jian Ling， Li Jundong， Shu Kai， et al. Multi-label informed feature selection［C］//Proc of International Joint Conference on Artificial Intelligence. San Francisco，CA： Morgan Kaufmann Publishers， 2016，16： 1627-1633.

［30］Zhang Jia， Luo Zhiming， Li Candong， et al. Manifold regularized discriminative feature selection for multi-label learning［J］. Pattern Recognition， 2019， 95： 136-150.

［31］Demar J. Statistical comparisons of classifiers over multiple data sets［J］. The Journal of Machine Learning Research， 2006， 7： 1-30.