面向在线率差异的SaaS订阅限额及资源配置组合优化

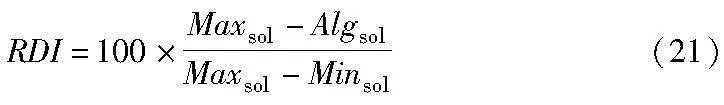
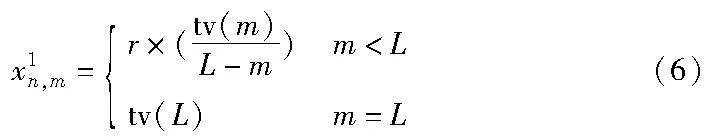
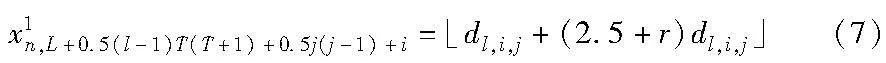
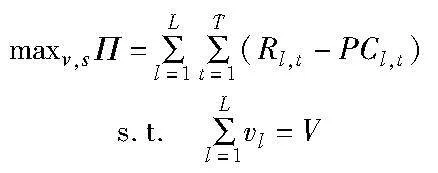
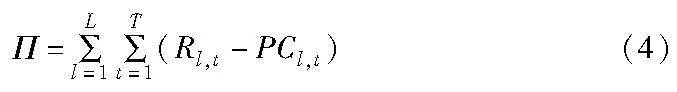
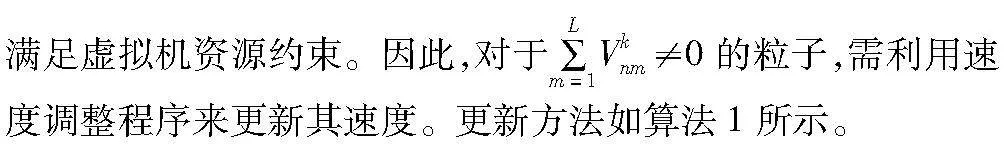
摘 要：软件即服务（softuare as a service，SaaS）是一种让用户通过支付订阅费来获得软件访问权的云服务模式。由于其业务的多样性，用户对不同软件的在线访问率存在很大差异，所以不同软件所消耗的云计算资源也存在差异。为避免违反服务等级协议（service level agreement，SLA）而产生违约赔付的风险，SaaS运营商不仅要优化各种软件的计算资源配置，还要对各类软件的订阅量加以限额。在考虑SLA限制的基础上，构建了一个以收益最大化为目标的有资源约束的非线性整数规划模型。由于模型计算的复杂性，其无法在多项式时间内求解，所以设计了基于Q学习-粒子群（particle swarm optimizoction，PSO）的融合算法来求解该NP难题。该算法将Q-学习嵌入到PSO中，动态调整PSO参数，从而避免直接使用PSO时会面临的局部最优陷阱和计算效率低下的问题。仿真实验验证了在不同场景下模型及算法的有效性，结果表明该算法可在云计算资源有限的条件下，以较高的求解效率获得收益更高的订阅限额及资源配置方案。其中，当处于需求波动大的情境下时，运营商应尽可能地降低软件的资源争用比，通过配置足量的虚拟机资源并设定严格的订阅限额来保障软件的服务质量，减少违约赔付成本；相反，当处于需求波动小的情境下时，运营商可以提高软件的资源争用比，通过放宽订阅限额来抢占更大的市场，实现收益最大化。

关键词：软件即服务； 订阅限额； 资源配置； 粒子群优化； Q-学习

中图分类号：TP391.9 文献标志码：A 文章编号：1001-3695（2024）07-021-2069-10

doi：10.19734/j.issn.1001-3695.2023.10.0542

Combination optimization of SaaS subscription limits andresource allocation considering online disparity

Abstract：SaaS is a cloud service model where users obtain software access rights by paying subscription fees. Due to the diversity of business operations， users exhibit significant variations in the online access rates for different software. Consequently， there are variations in the cloud computing resources consumed by different software applications. To avoid the risk of violating SLAs and incurring penalty payments， SaaS operators optimize the computational resource allocation for various software applications and impose subscription limits on each category of software. Considering SLA constraints， this paper formulated a resource-constrained nonlinear integer programming model with the objective of maximizing revenue. Due to the computational complexity of the model， it cannot be solved in polynomial time，and this paper proposed a Q-learning-PSO hybrid algorithm for this NP-hand problem. This algorithm embedded Q-learning into PSO to dynamically adjust PSO parameters， thereby avoiding the issues of local optima and low computational efficiency associated with direct PSO application. Simulation experiments validate the effectiveness of the model and algorithm in different scenarios. The results indicate that the algorithm can achieve higher revenue for subscription limits and resource allocation with superior solving efficiency under the condition of limited cloud computing resources. Specifically， in scenarios with significant demand fluctuations， operators should aim to reduce the resource contention ratio of software. This can be achieved by provisioning an ample amount of virtual machine resources and enforcing strict subscription limits to ensure the quality of service， consequently reducing penalty payments. Conversely， in scenarios with minimal demand fluctuations， operators have the flexibility to increase the resource contention ratio of software. By relaxing subscription limits， they can seize a larger market share， thus realizing revenue maximization.

Key words：software as a service; subscription limit; resource allocation; particle swarm optimization; Q-learning

0 引言

随着云计算技术带来巨大的商业模式变革，软件即服务（SaaS）模式获得了飞速发展。SaaS是将多租户应用部署在云中的软件交付模式。在该模式下，应用软件是一类可通过互联网进行远程访问的服务，用户无须构建IT基础设施或购买软件版权，而是根据自身需要向运营商支付订阅费来取得软件访问权，双方基于服务等级协议（SLA）来规范服务的提供与使用行为［1］。该模式为用户节省了大量IT投资，深受中小企业的欢迎。据Gartner预测，2023年全球SaaS市场规模将超两千亿美元［2］。近年来，国内外软件企业，如微软、SAP、ORACLE、阿里巴巴和用友等，都争先推出一系列SaaS产品［2］。

考虑到中小企业业务的多样性，用户对不同软件的服务时间需求以及在线访问率均有着显著差异，所谓在线率指的是任意时间内在线使用软件的用户数占该时间内订阅总人数的比例。由于在实际使用中，只有在线访问软件的用户才会消耗资源，所以不同软件所消耗的云计算资源存在很大差异。为保障SaaS服务的可用VnG8qZavw64AK2BA8ynlFQ==性，运营商需要提前为软件配置适量的虚拟机资源来满足用户的订阅需求。同时，在计算资源有限的条件下，运营商需要对不同软件的订阅限额加以限制来避免因违反SLA约束而产生违约赔付。资源配置和订阅限额均会对企业收益产生显著影响，且两者存在相互制约的关系，当运营商过度配置资源来放宽订阅限额时，其可以接受大量的订阅请求来占领市场，但由于不同用户对软件在线率的需求存在差异，这种策略容易导致虚拟机资源的浪费，造成资源利用率低下。相反，当运营商的资源配置不足时，则必须通过设定严格的订阅限额来保障服务质量，否则将面临因违反SLA约束而产生赔付的风险，从而影响收益。因此，如何对资源配置和订阅限额进行组合优化来实现SaaS运营商收益最大化，是一个亟待解决的问题。

本文研究的问题是基于收益管理的视角，收益管理作为一种通过控制消耗易逝资源产品的价格和可用性来提高收益的理论［3］，已经较为成熟地应用于航空、酒店和互联网等易逝产品领域。由于云计算资源具有无法长期存储且在销售期结束后其价值几乎为零的易逝品特点，所以可以将收益管理应用于SaaS云服务领域。当前对收益管理在SaaS领域的研究主要集中在定价策略上［4～6］，对资源配置和订阅限额控制的研究则相对较少。其中，Zhang等人［7］针对供需不确定的情景，设计了一种资源优化配置算法来实现SaaS运营商收益最大化的目标；Zhu等人［8］提出了一种基于深度强化学习的实时任务调度方法来智能地为不断达到的用户任务请求分配适当的资源，从而提高资源的利用率；Sikora等人［9］提出了自适应的准入控制框架来满足SLA约束，并将违反SLA的赔付纳入考量；Han等人［10］通过切片技术识别不耐烦用户，并设计准入控制系统来最大化云提供商的效用。

收益管理的各项策略在实际中都得到了应用，Pimentel等人［11］证明在一些行业中设置订阅限额能产生更多的收益。当前，许多行业都采用阈值控制的方法优化资源配置及订阅限额来提高收益或服务质量。王航臣等人［12］基于蒙特卡罗模拟来研究航空公司机票的预定限制；Luo等人［3］考虑设置嵌套预订限制来合理配置头等舱与经济舱的座位数量，从而避免因接受低票价预订而拒绝高票价预订的行为，并采用基于仿真的优化算法进行求解；邓连波等人［13］针对高铁列车的最大超售数量问题构建了基于随机规划的非线性整数规划超售模型，从而提高企业收益；Nababan等人［14］提出了适用于酒店行业的订阅限制模型，并利用机器学习算法预测用户的取消预订率来提高收益；You等人［15］构建了互联网行业中的带宽资源分配及订阅限额模型，解决了需求过载问题。这些领域的研究为本文提供了借鉴，然而相较于这些行业，SaaS云服务具有SLA约束的特点。越来越多的学者开始研究SaaS中提高SLA收益的优化方法［16］，SLA包括可用性、安全性与响应时间，本文重点关注软件的可用性，即保障用户的服务质量。当访问软件违约率超过合同限定值，用户将对服务提供商进行惩罚［17］，即SaaS供应商向用户进行赔付。Buyya等人［18］描述了通过避免过度使用资源来保证服务质量满足SLA的准入控制机制；Yuan等人［19］提出了运营商在违反SLA后的赔付算法来提高用户效用。为了实现收益最大化和用户满意度最大化的目标，SaaS运营商需要通过制定适当的准入控制策略来优化订阅限额。因此，为了满足客户差异化的需求以及更好地利用资源获得最大化收益，本文采用基于仿真的优化方法来解决随机需求下的资源配置及订阅限额问题。

本文对SaaS资源配置及订阅限额策略的优化研究属于大规模组合优化问题，云计算环境下的大规模服务组合优化问题被视为NP难题［20］，该类问题的求解复杂度会随着运营商提供软件类别的增加而呈指数级增长，因此无法使用传统的数学规划方法来精确地解决该类问题［21，22］。目前常用粒子群优化算法（PSO）对组合优化问题进行求解［3］，然而直接采用PSO求解本文模型会面临由于依赖先验知识而陷入局部最优以及计算效率低下的问题。针对这一问题，可参考其他领域中基于强化学习的融合算法。为解决可复用产品的最优经济订购批量难题，Fallahi等人［23］将强化学习算法分别与差分学习算法（differential evolution，DE）和粒子群优化算法相结合，并使用Q-学习来自适应DE和PSO中的控制参数，提高算法性能；在解决柔性作业车间调度难题时，Chen等人［24］提出了自学习遗传算法（self-learning genetic algorithm，SLGA），该算法以遗传算法（genetic algorithm，GA）为基本优化方法，并基于强化学习（reinforcement learning，RL）对关键参数进行智能调整，提高了算法优化水平。由此可见，利用强化学习动态调整元启发算法的关键参数，对提高算法性能有显著的作用。

本文在上述研究的基础上，对SaaS运营商有限时间内虚拟机资源配置及订阅限额进行研究，贡献表现为：a）在考虑SLA约束的基础上，为SaaS运营商构建了以收益最大化为目标的有资源约束的非线性整数规划模型，该模型考虑了用户对不同软件在线率的差异以及SLA违约赔付，从而对资源配置及订阅限额进行组合优化；b）由于模型计算的高复杂度，其无法在多项式时间内求解，所以在搜索解的过程中提出基于Q学习-粒子群的融合算法作为解决方法，通过在PSO中嵌入Q-学习算法来动态调整PSO关键参数，提高算法性能；c）通过仿真实验发现不同情景下的最优订阅限额及资源配置策略组合，为运营商的销售决策提供指导，实现收益最大化。

1 问题描述与模型构建

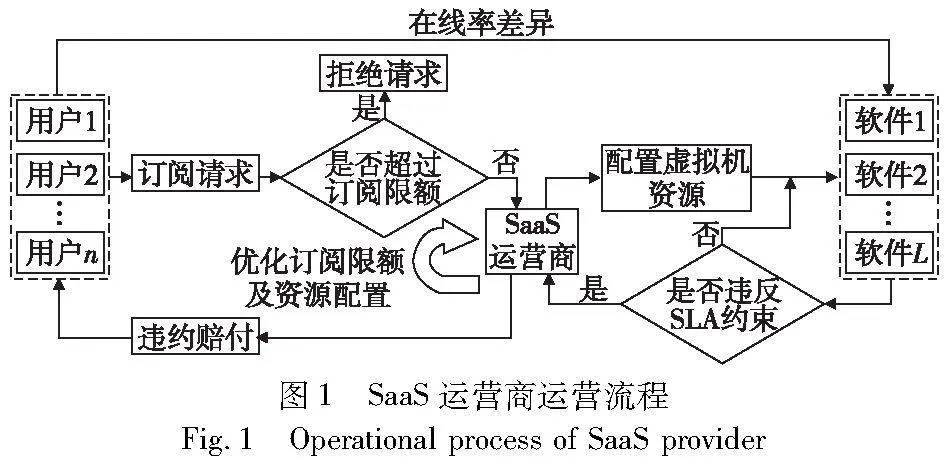
为保障软件可用性，SaaS运营商需要提前为各类软件配置虚拟机资源，同时确定订阅限额来管理用户的订阅请求，避免出现需求过载的情况。资源配置及订阅限额均对企业收益有较大的影响，资源配置过量或订阅限额设定过低会产生资源供过于求的情况，导致部分虚拟机资源浪费，影响企业收益；而资源配置不足或订阅限额设定过高则会产生资源供不应求的情况，导致虚拟机过载，从而出现用户访问请求被拒绝的现象，影响企业信誉的同时产生违约赔付，造成企业收益下降。因此，如何配置资源及优化订阅限额来提升企业收益是本文主要解决的问题。

1.1 问题描述

考虑一家提供L种软件订阅服务的SaaS运营商需要在限定服务时间内，利用有限的虚拟机资源来获得最大化收益。令l（l=1，2，…，L）表示软件类型的序列标识，t（t=1，2，…，T+1）表示时间段的序列标识，V表示虚拟机资源总量。假设在整段服务时间内运营商的虚拟机资源总量保持不变，用rl来描述单位时间内每位用户访问软件l所需要的虚拟机资源量。SaaS运营商通过与用户签订合约并收取订阅费来获得收益，合约中包含了用户所选择订阅的软件种类及订阅的服务时间范围。为此，将用户的订阅请求标记为（l，i，j），其中i和j（i，j=1，2，…，T+1，i ≤j）分别表示订阅的起始时间和终止时间，如果i=j则表示用户订阅一个时间周期的软件服务。为简化模型的复杂度，假设订阅请求需要在下一个时间段生效，即任何包含时间段t的订阅请求都应在时间段t-1之前进行订阅。因此，SaaS运营商的销售计划周期是从第1个到第T个时间段，而用户的有效订阅时长是从第2个到第T+1个时间段。

SaaS运营商的目的是将所有的虚拟机资源分配给各类软件，并在SLA约束下确定各种订阅需求的订阅限额，实现总收益最大化。因此，设定vl和sl，i，j为模型的决策变量，其中vl表示分配给软件l的虚拟机资源，sl，i，j表示订阅请求（l，i，j）的订阅限额。具体的符号说明如表1所示。

1.2 模型构建

设Rl，t表示考虑（l，i，j）的订阅限额为sl，i，j时，时间段t+1内软件l的订阅收益。由于在时间段t订阅的软件服务的起始时间i必须晚于t+1，即i≥t+1，所以时间段t内可供订阅的软件服务集合为{（l，i，j）|t≤i≤j≤T}，则Rl，t具体表示为

人数，即i≤t≤j。由于服务时间涵盖时间段t+1的订单只能在时间段t之前订阅，所以如果用户在时间段k（1≤k≤t）订阅了服务时间包含时间段t+1的软件服务，则该订阅的服务起始时间i和服务终止时间j必须分别满足k+1≤i≤t+1和t+1≤j≤T+1。因此，在时间段k提供的服务时间包含了时间段t+1的软件服务集合为{（l，i，j）|k≤i≤t，t≤j≤T}，则Wl，t表示为

由式（2）可知，软件l在时间段t+1内所需的虚拟机资源总量预计为Wl，tωlrl，其中Wl，tωl表示时间段t+1内在线访问软件的人数。在SLA约束下，SaaS运营商需对未达到服务质量水平的服务进行违约赔付，令Pel，t为软件l在时间段t内产生的违约率，其根据规定的服务水平αl与实际服务水平的差值来计算，若实际服务水平低于αl，则视为违约行为。其中软件l的实际服务水平用分配给软件l的虚拟机资源vl超过该类别实际所需的虚拟机资源Wl，tωlrl的概率来表示，违约率Pel，t具体表示为

Pel，t=max{αl-prob（vl≥Wl，tωlrl），0}

其中：prob（vl≥Wl，tωlrl）表示在时间段t内软件l的实际服务水平。令PCl，t表示在时间段t内软件l产生的违约赔付成本，其依赖赔付比例βl与违约率Pel，t，则赔付成本表示如下：

PCl，t=βlPel，tpl，t，t（3）

其中：pl，t，t表示订阅软件l一个时间周期的价格。设Π表示订阅限额为s时的总收益，由于l=1，2，…，L，i，j=1，2，…，T且i≤j，则i=1时，j=1，2，…，T，共T种服务时间组合；i=2时，j=2，3，…，T，共T-1种服务时间组合；i=T时，j=T，共1种服务时间组合，由此可知可能存在0.5LT（T+1）种不同的订阅需求，则s是维度为0.5LT（T+1）的向量，元素sl，i，j位于第0.5（l-1）T（T+1）+0.5j（j-1）+i个条目。总收益函数由订阅收益减去赔付成本构成，其为L类产品在整个收益周期下产生的收益总和，表示如下：

根据模型假设，SaaS运营商将有限的虚拟机资源全部分配给L类软件产品，则分配给各类软件的虚拟机资源vl之和等于总可用虚拟机资源V，因此该问题具有如下约束：

SaaS运营商的目标是通过确定向量v和s的值使收益最大化，其中v中包含了L个元素，是L维向量，元素vl位于第l个条目。因此，该问题建模如下：

1.3 模型求解难点分析

本文构建的SaaS资源配置及订阅限额模型属于大规模非线性整数规划模型，面临着求解难题，主要表现在以下方面：

a）大规模的决策空间。SaaS订阅问题面向众多用户，且运营商提供L种软件类型供用户选择，同时每个用户对于每种软件l都有不同的订阅时间需求，他们在订阅时根据需求自主选择订阅软件的起始时间i和终止时间j，这使得SaaS运营商会面临0.5LT（T+1）种不同的订阅请求组合，即订阅限额量sl，i，j是一个维度为0.5LT（T+1）的向量，资源配置量v是一个维度为L的向量。在实际应用中，决策空间会随着软件种类L和销售周期T的增加而呈指数级增加，导致求解的搜索空间规模很大，在实际求解过程中不能使用穷尽式搜索的方法对所有订阅组合进行尝试和计算。

因此，本文构建的模型具有非线性特性及大规模决策空间等特点，计算复杂度较高，是一个NP难题［26］。该模型无法利用分枝定界法等传统的数学规划方法在多项式时间内进行精确求解［27］，需采用元启发式算法来近似求解。当前粒子群优化算法是求解上述模型的主流算法之一［28］，PSO是一种基于群体优化的元启发式算法，可以有效地解决各种组合优化问题［3］，因此，本文利用PSO来解决多目标优化问题，并结合资源配置及订阅限额模型特性设计求解算法。

2 基于Q学习-粒子群融合算法的模型求解方法

针对模型求解难题，本章设计了基于Q学习-粒子群的融合算法（简记为Q-PSO），通过将Q学习算法嵌入到PSO中，动态调整PSO的参数来提高算法性能，确保求解的效率与质量。

2.1 问题求解的粒子群算法

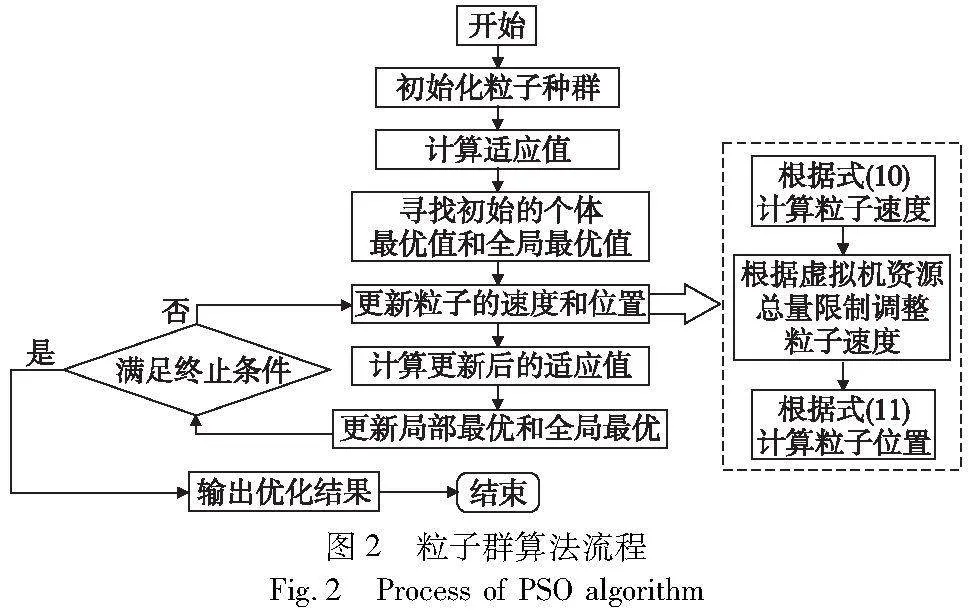
PSO是1995年提出的进化计算方法［29］，通过模仿鸟群觅食行为设计而来。群体中的个体称为粒子，每个粒子代表一个潜在的解决方案，粒子通过在搜索空间中运动来寻找最优解，粒子的运动由其位置和速度决定，其中位置代表一个可能的解，速度代表下一步要移动的距离。PSO利用随机解进行初始化，后续每个粒子依靠其自身历史最佳位置的信息、全局历史最佳位置的信息以及当前位置和速度来调整下一步的位置。在该算法中，粒子的局部最优与全局最优位置信息共享，将局部搜索与全局搜索相结合来搜索最优解。算法的具体步骤如图2所示。

2.1.1 粒子定义

在PSO中，粒子是算法的基本单元，可以看作是候选解在搜索解空间中的一个位置，因此为了将PSO应用到模型中，需要建立决策变量和PSO粒子之间的关系。当前模型中有L个虚拟机资源分配变量和0.5LT（T+1）个订阅限额变量，因此该问题的搜索空间需设定为L+0.5LT（T+1）维空间，粒子则设定为维度为L+0.5LT（T+1）的向量。为此，第n个粒子的位

2.1.2 种群初始化

PSO中每个粒子都代表了一个候选解，即一组资源配置量及订阅限额量，因此需要初始化PSO的粒子，使得每个粒子对应一个合法的候选解。PSO从一个种群大小为Npop的初始粒子群开始，初始化过程主要包括初始化粒子的位置和速度两个方面，具体创建方法如下。

1）位置初始化

为了保证每个粒子代表的候选解都是合法的，需要对初始位置向量进行限制，使其满足资源配置和订阅限额的约束条件，用式（6）构造初始种群中各粒子前L个元素的位置：

其中：r表示0～1的随机变量；tv（m）表示为前m种软件分配资源后，剩余的虚拟机资源，tv（1）=V。式（6）可以保证粒子前L个元素位置向量之和等于运营商总资源量，即满足模型的资源约束条件。粒子中其余元素的初始位置根据式（7）生成。

其中：dl，i，j为（l，i，j）的订阅需求所服从泊松分布的参数，符号·」表示向下取整。

2）速度初始化

其中：rb是一个二进制随机数；r是0～1的随机变量；Δa是一个预先确定的常数。速度向量中剩余的元素由式（9）生成。

其中：Δb是一个预先确定的常数。

2.1.3 速度更新

1）计算速度

在迭代过程中，粒子n在第k次迭代的速度及其到自身最佳位置pn和全局最佳位置g的距离决定了下一步的速度，该粒子在k+1次迭代时的速度Vk+1n计算公式如下：

Vk+1n=wVkn+c1r1（pn-Xkn）+c2r2（g-Xkn）（10）

其中：Vkn是粒子n在第k次迭代中的速度；Xkn是粒子n在第k次迭代中的位置；pn是粒子n的历史最佳位置；g是种群中所有粒子的历史最佳位置；w为惯性权重;r1和r2为0～1的随机值；c1和c2是控制粒子在搜索空间中运动的加速度因子。

2）速度调整程序

算法1 速度调整程序

2.1.4 位置更新

在速度调整后，将对粒子进行位置更新。粒子下一步迭代所处的位置取决于当前位置及其下一步的运动速度。因此，粒子n在第k+1次迭代中的位置更新公式为

Xk+1n=Xkn+Vk+1n（11）

在完成位置更新后，需对粒子的自身最佳位置和全局最佳位置进行更新，用于更新下一次迭代的速度。PSO通过比较粒子当前的位置和自身历史最佳位置来更新每个粒子的局部最佳位置pn，更新方法如下：

同时，如果粒子局部最佳位置的目标函数f（pn）大于全局最佳位置的目标函数f（g），则更新全局最佳位置。设置最大迭代次数kmax作为算法的停止条件，PSO的伪代码如算法2所示。

算法2 PSO

2.2 粒子群算法中的参数估计难题

运用经典粒子群算法可以完成对模型的求解，但是该算法的性能在很大程度上依赖于加速度因子参数的选择［28］，参数选择不当可能导致算法陷入局部最优解，同时在求解高维问题时计算效率较低。PSO中参数的最佳取值往往与模型特性有关，因此需要采用试错方法进行调参。然而，采用传统的试错方法需要耗费大量的经验和计算时间，在求解NP难题时面临极大的挑战。

在本文的问题背景下，运营商需要实时决定是否接受用户的订阅请求，考虑到SaaS运营商会面临SLA违约赔付的风险，这要求运营商必须在短时间内完成订阅限额和资源配置的决策，并相应地给出接受或拒绝请求的反馈，这对算法的求解效率提出了更高的要求。为了解决这一问题，本文将Q学习算法嵌入到PSO中来动态调整PSO的参数，提高粒子搜索能力，在避免算法陷入局部最优解的同时提高算法求解效率，提高算法性能。

2.3 Q学习-粒子群融合算法

2.3.1 强化学习

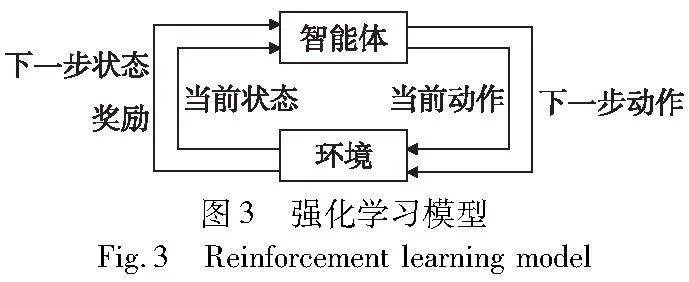
强化学习是机器学习的一种学习方式，主要由智能体、环境、状态、动作与奖励五个组件组成。在反复实验中智能体与环境进行交互，通过环境给予的奖励不断训练优化其状态与动作的对应关系，从而获得最大回报的学习机制。具体模型如图3所示。

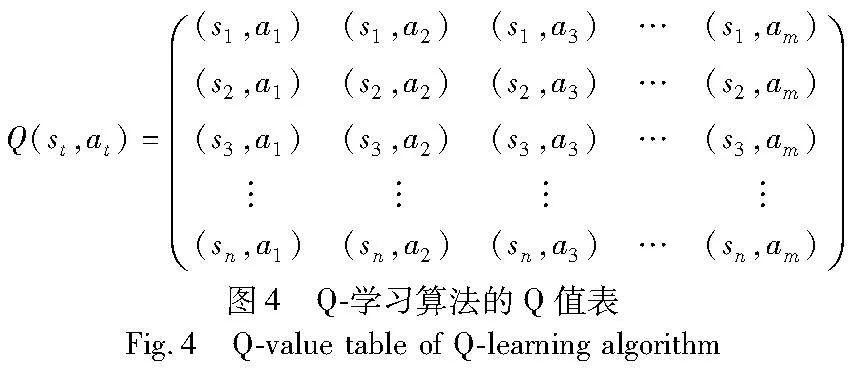
本文重点研究强化学习算法中带有Q值表的Q-学习算法，该算法将不同状态下的学习经验即状态与动作的对应关系存储在Q值表中，其中行代表状态，列代表动作，Q表的示意图如图4所示，然后根据Q值选取获得最大收益的动作。

在Q-学习算法中，智能体通过学习给定动作获得奖励来更新Q值表。初始Q值表中所有值都等于零，这表示智能体没有经验供算法使用。设S={s1，s2，…，sm}为系统的状态集合，A={a1，a2，…，am}为待执行的候选动作集合。智能体在不同的状态下，根据Q值表中提供的累积信息进行动作选择，此时环境给出奖励rt+1，状态变为st+1。Q表的值根据智能体的经验，通过贝尔曼方程进行更新，具体如下：

Q（st，at）=（1-α）Q（st，at）+α（rt+γmaxaQ（st+1，at+1））（13）

其中：Q（st，at）是在状态st下执行动作at获得的Q值；γ是折扣因子，α是Q-学习算法的学习因子，决定算法对于奖励的反映程度。该值越大，每次实验后Q值表的波动也越大。算法3中给出了Q-学习的伪代码。

算法3 Q-学习算法

2.3.2 Q学习调参

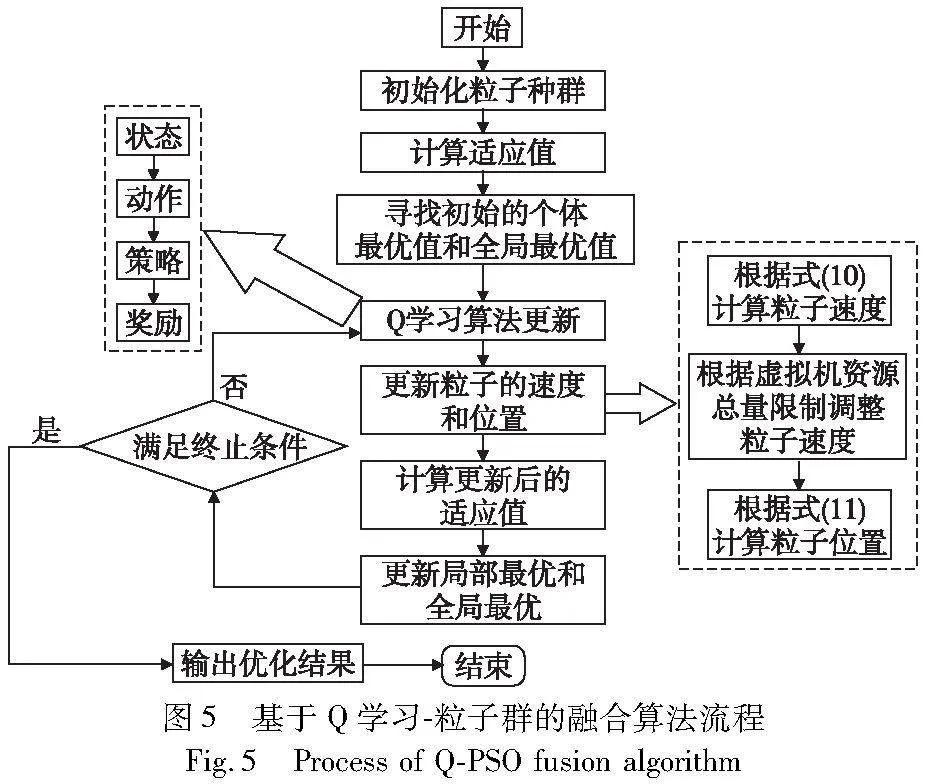
在利用PSO搜索解的过程中，加速度系数c1和c2是两个重要的参数，这些参数会极大影响算法的效率［30］。因此，本文将在PSO的基础上嵌入Q-学习算法，来帮助PSO在每次迭代中选择c1和c2最优对。Q学习-粒子群融合算法试图根据Q值表中的累积信息选择加速度系数c1和c2的最佳对。在该算法中，PSO被认为是一个环境，每次迭代都将该环境的状态从st更改为st+1。具体实现步骤如图5所示，算法中状态、动作、策略及奖励值定义如下。

1）状态

在这里环境状态被定义为一个加权函数，其包含平均种群适应度Z*1、总体方差Z*2和最佳个体适应度Z*3三个特征，具体表示为

s*=w1Z*1+w2Z*2+w3Z*3（14）

其中：w1、w2和w3是权重系数，w1+w2+w3=1。式（14）中的Z*1、Z*2和Z*3定义如下：

式（15）计算第k次迭代中种群的平均适应度，并通过除以第一次迭代的平均适应度对其进行归一化。式（16）表示第k次迭代中的总体方差，同样通过除以第一次迭代的方差进行归一化。最后根据式（17）计算归一化后的最佳个体适应度作为状态函数的第三个分量。

2）动作

算法中的动作集被定义为A={（c11，c12），（c21，c22），…，（ck1，ck2）}，表示PSO第k次迭代时用于更新速度向量的加速度系数c1和c2的值。加速度参数在限定范围内被划分为若干个离散值，并分别对应一个Q值，在算法执行过程中根据Q值的大小来选择动作。

3）策略

在Q学习-粒子群融合算法中使用ε-贪心策略作为动作选择策略［24］，其是一种基于随机性和贪心性的策略，在选择动作时会以1-ε的概率选择当前已知最优的行动，以ε的概率选择随机行动，其中ε∈（0，1），并通常会取一个较小的值。该策略可以平衡探索和利用之间的关系，保证算法在搜索过程中有机会尝试一些新的选择，不会陷入过于贪心的困境。ε-贪心策略具体如式（18）所示。

其中：ε为勘探率系数。

4）奖励

在每次迭代结束后需要计算奖励来反映算法当前所选择动作的优劣，该算法的奖励r*根据最佳个体适应度r1和平均群体适应度r2求取。

在这里，计算以上两个函数值并进行比较，选择其中较大值作为第k次迭代的奖励，即r*=max{r1，r2}。如果选择的奖励优于第k-1次迭代中的奖励，则说明当前选择的参数对是有效的，将计算得出的奖励r*作为反馈返回给算法，并据此对Q值表进行更新。算法4展示了Q学习-粒子群融合算法的伪代码。

算法4 Q学习-粒子群融合算法

3 数值实验

3.1 实验参数设定

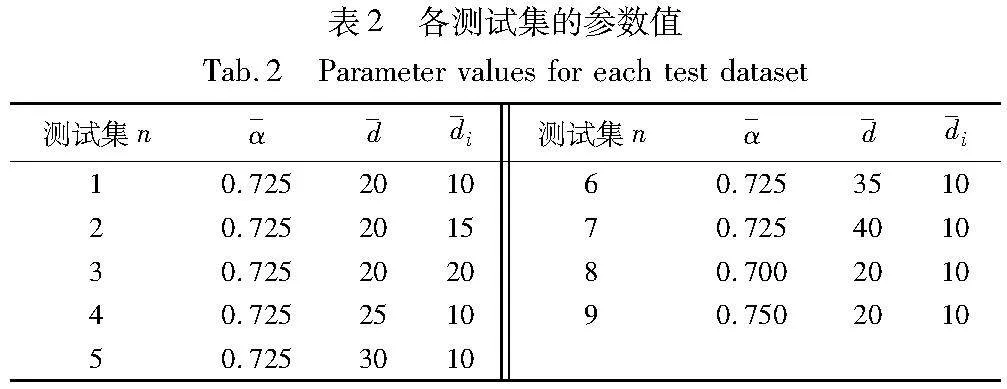
为了评价本文提出的Q学习-粒子群融合算法（Ｑ-PSO）在求解资源配置及订阅限额问题上的性能，本节开发了小型和大型两种规模问题集。问题集由商品类别数量L和规划周期T来区分。小型和大型两个问题集的（L，T）值分别固定为（3，3）和（4，6）。

本文利用PSO求解SaaS资源配置及订阅限额模型，其中算法中启发式参数描述为种群总体规模Npop，最大迭代次数kmax，惯性权重w，加速度系数c1和c2以及与粒子速度相关的跳步Δa和Δb。在实验中，通过下列方法控制参数值，将种群总体规模Npop设置为2L+T，最大迭代次数kmax设为5（L+T），惯性权重w设为0.85，Δa和Δb均设为10，加速度系数c1和c2通过Q-学习算法获得。算法均用Python编程软件编写，并在配置为2.7 GHz Intel Core i5处理器和8 GB内存的MacBook Pro个人笔记本电脑上运行。

3.2 模型及算法有效性验证

为验证本文算法在计算效率与决策效果上的表现，本节将Q-PSO与经典PSO以及目前广泛应用于求解资源配置问题的基于混沌映射的PSO算法（chaotic particle swarm optimization，CPSO）［31～33］进行比较。其中CPSO在PSO基础上引入混沌映射策略，对初始化种群和位置更新的计算方式进行改进，并通过对粒子位置进行变异更新来跳出局部最优解，从而提高了算法的求解准确性。因此本节将从算法的准确性和求解效率两个方面，对Q-PSO与CPSO进行对比来验证本文算法的有效性。

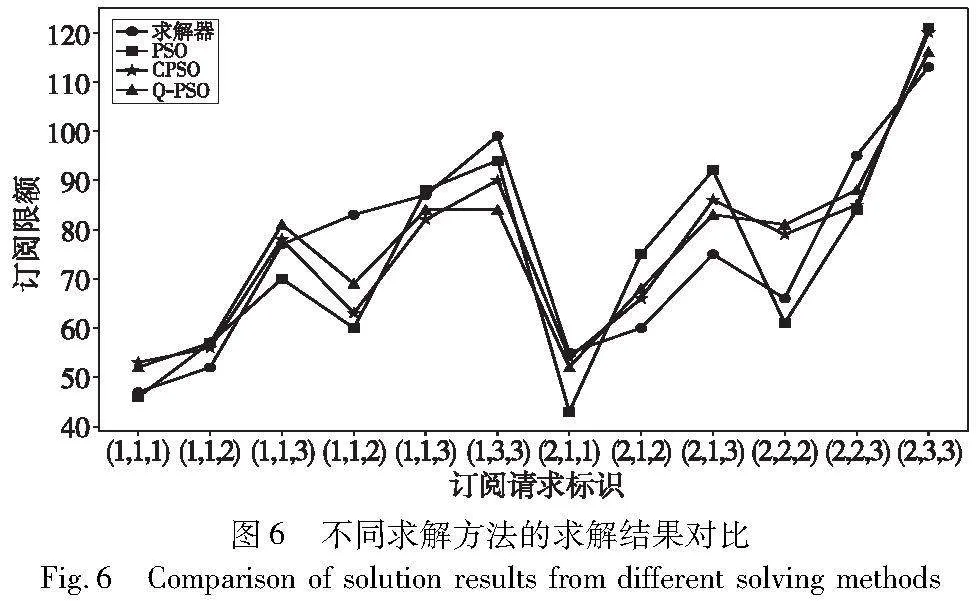
为了验证算法的准确性，本节对精确算法与近似算法对小型规模问题求解的结果进行比较，其中精确算法的结果利用CPLEX求解得到，而近似算法则为PSO、CPSO以及本文Q-PSO，求解的具体结果如图6所示。

图6分别展示了采用CPLEX求解器、PSO、CPSO以及Q-PSO的求解结果，其中横坐标为订阅请求标识，纵坐标为求解的订阅限额值。从图6可以发现采用四种方法的求解结果相似，说明本文算法求得的近似解与最优解的差距较小，算法的准确性较高。

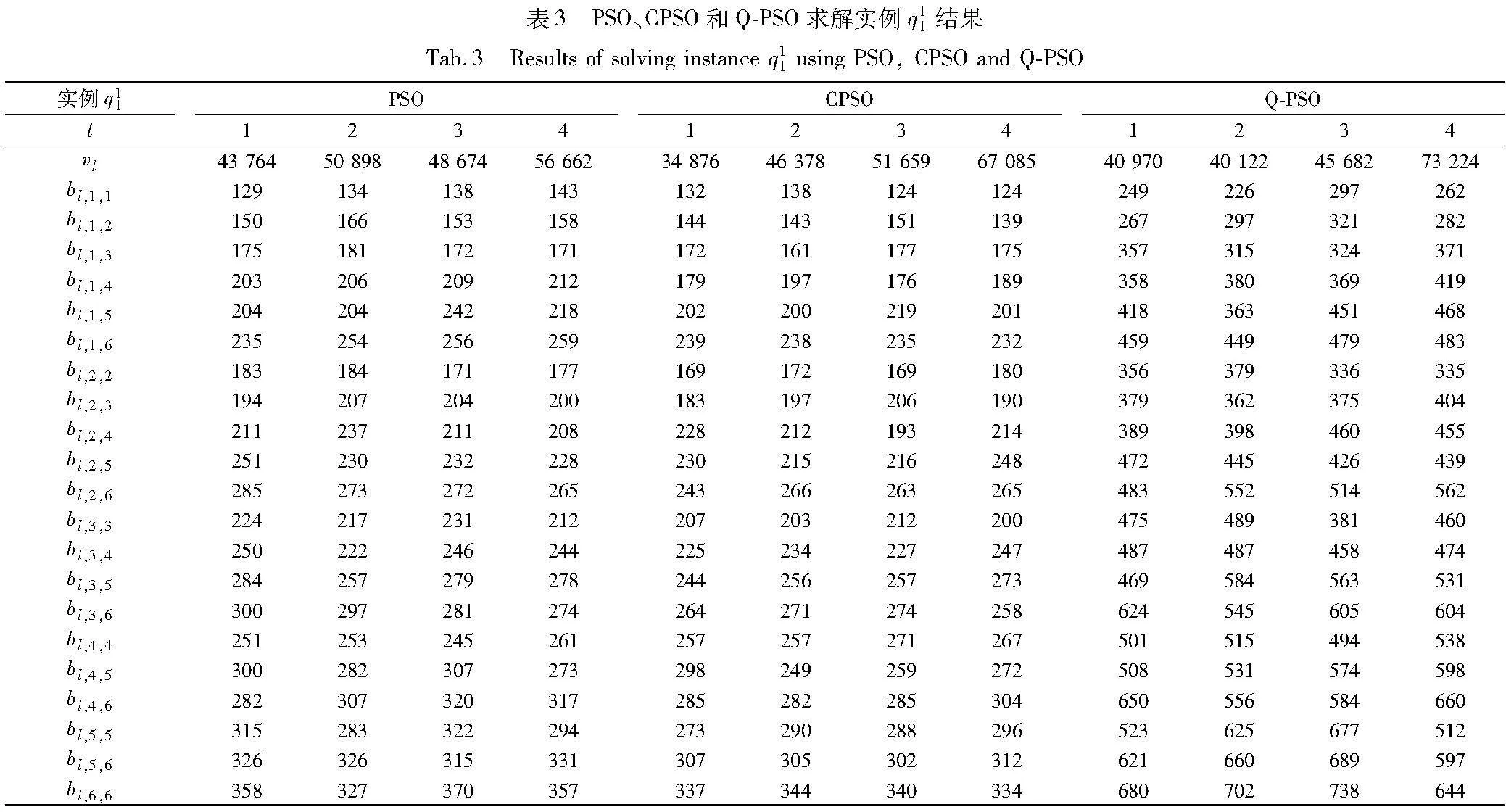
为了贴合实际，后续采用大规模问题数据集进行仿真。利用启发式算法求解资源配置及订阅限额模型，得到的可行解如表3所示，此处仅展示在大规模问题下第一个测试集q11的求解结果。

表3分别给出了利用PSO、CPSO和Q-PSO求解得到的结果，根据基于Q-PSO结果可知，SaaS运营商分配给各个产品类别的虚拟机资源量分别为40 970、40 122、45 682和73 224。由表3可知，当到达一个新的订阅需求为（1，2，3）时，需要判断当前系统中该订阅需求的订阅数量是否已达到379，只有当订阅数量未达到379时，SaaS运营商才能够接受该用户的订阅需求。同理可得，如果订阅（2，1，3）的数量已经达到了315，那么SaaS运营商将不再接受任何相同的订阅需求。

接下来利用平均目标函数、最佳目标函数、平均CPU时间和相对偏差指数（RDI）四个指标来评价解的质量并比较三种算法的有效性。其中RDI计算公式如下［34］：

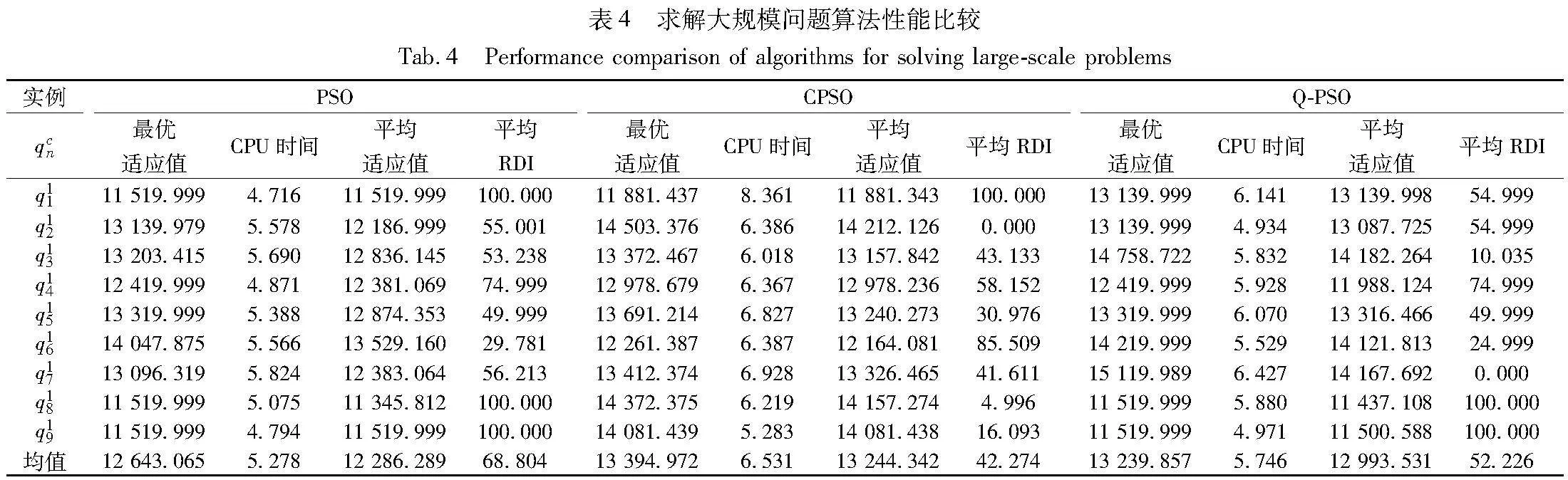
其中：Algsol表示当前算法的目标函数值；Maxsol表示算法中的最优函数值；Minsol表示所有实验中最小函数值。RDI值越小，表示算法性能越好。每种规模的问题利用9个测试集重复求解。大规模问题的求解结果如表4所示。

从表4可以发现，在对本文模型的求解中，利用Q-学习调参的方法能在不增加计算时间的情况下增强了PSO的性能，即Q-PSO求解不同规模的有约束非线性模型要比经典粒子群算法表现更好；相较于CPSO而言，Q-PSO的求解准确性较低，但是求解效率高，说明本文算法在不损失求解准确度的同时提高了求解效率。

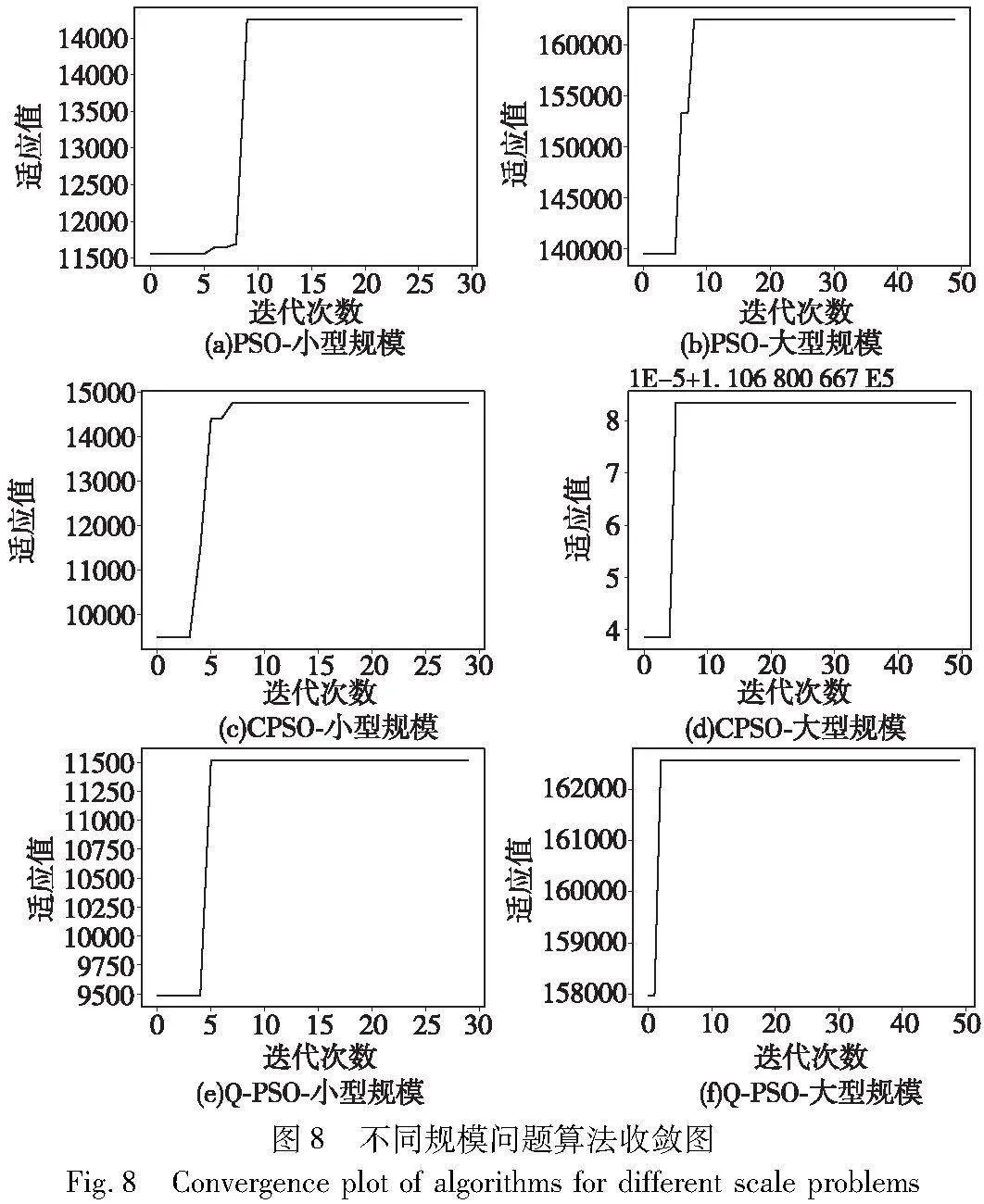
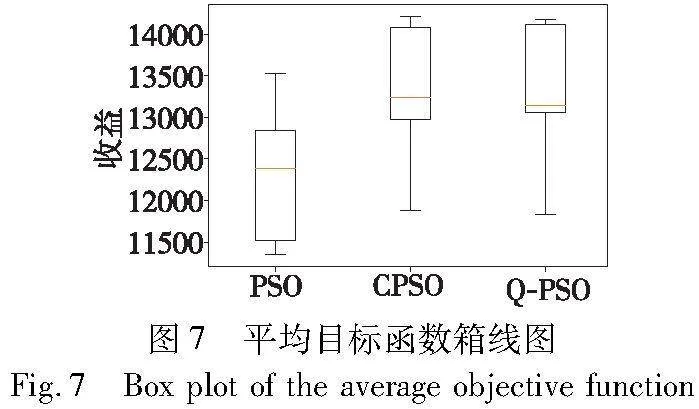
为了衡量算法的性能可靠性，本节绘制元启发式算法的平均目标函数箱线图，结果如图7所示。从图7可以看出，Q-PSO及CPSO的箱体均小于PSO求解结果的箱体，可以认为Q-PSO的嵌入成功地降低了算法求解的方差，即Q-PSO比PSO具备更高的可靠性和鲁棒性。三种算法的收敛图如图8所示。

从图8可以看出在不同规模下，Q-PSO都比PSO收敛得更快，并获得了更优解；对比CPSO和Q-PSO的收敛结果可以发现，在不同规模下Q-PSO收敛更快，且两者的求解结果相近，说明Q-PSO在不降低算法准确性的同时提高了求解效率。此外，为了了解Q-学习算法如何自适应PSO的参数，图9展示了算法在迭代过程中加速度参数的变化趋势。

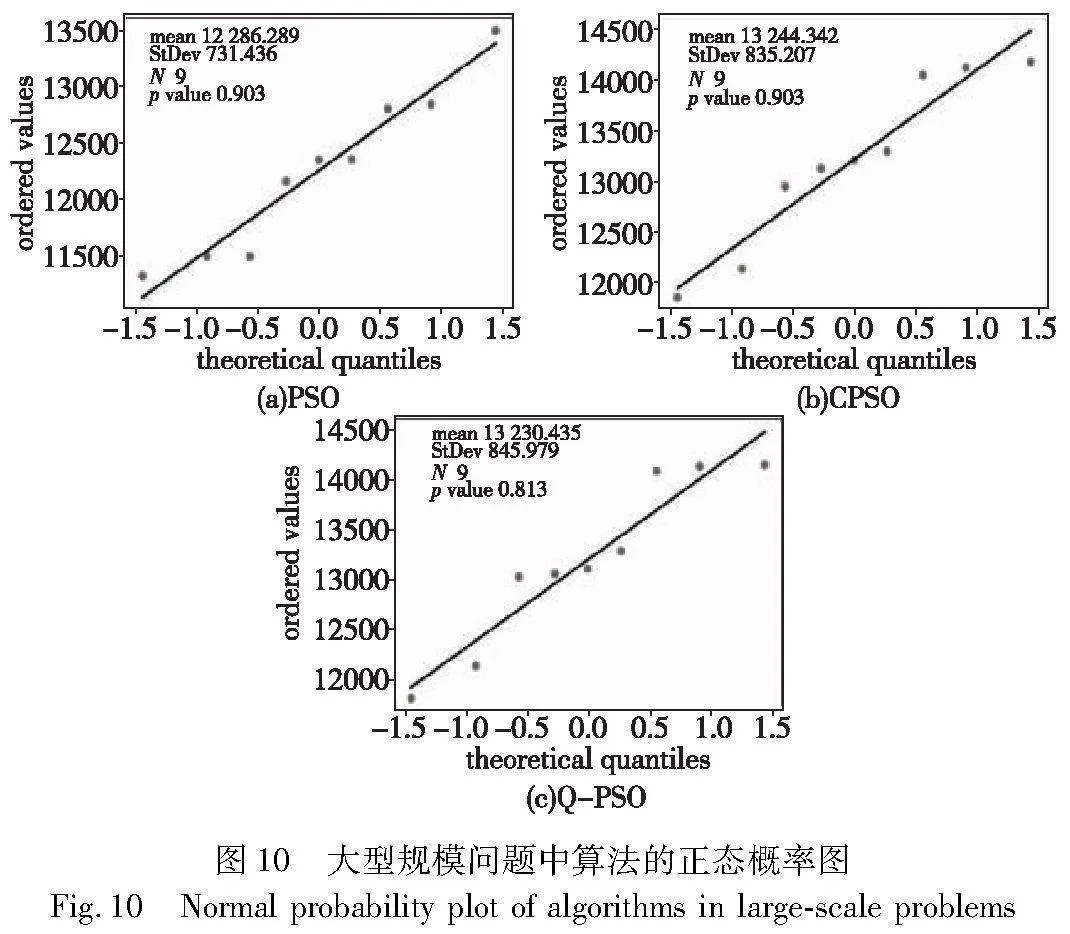
除了上述比较外，实验还对每种问题规模求解得到的平均目标函数进行统计比较。首先，根据表4的实验结果绘制大型规模问题的正态概率图，结果如图10所示。

从图10可以发现，三种算法所求结果的p值都大于0.05，说明三种算法所求得的平均目标函数都呈正态分布。接着根据单因素方差分析方法的流程假设三组数据两两之间的总体方差相等，即服从同一正态分布。其中，Q-PSO与经典PSO的检验结果如表5所示，发现p值小于0.05，因此可以拒绝原假设，即认为组间差异显著。由此可知，两种算法所求得的平均目标函数之间存在显著差异，即基于Q-PSO的性能高于PSO。Q-PSO与CPSO的检验结果如表6所示，发现p值大于0.05，说明利用两种算法所求得的结果无显著差异，即Q-PSO在提高求解效率的同时保证了求解的准确性。

综上，在解决订阅限额及资源配置问题上，本文Q-PSO具有更好的性能表现。Q-PSO通过自适应地调整PSO的参数，显著提高了算法的收敛速度，同时保证了求解的准确性，具备更高的稳定性和鲁棒性。

3.3 不同情境下实验结果分析

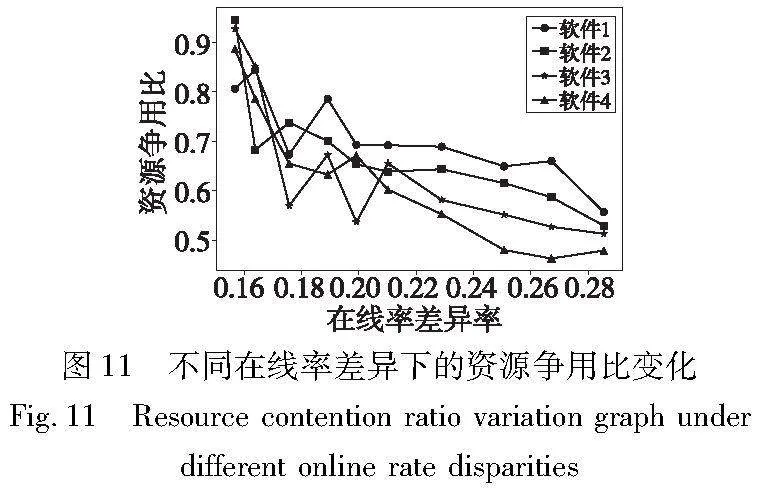
为了在不同在线率差异场景下，优化资源配置及订阅限额策略，本文引入了资源争用比来描述资源利用情况，资源争用比指的是某一软件的潜在用户数与分配给该软件的虚拟机资源之间的比例［35］，用c_rl来表示软件l在销售期内的资源争用比。资源争用比的具体计算方法为

图11展示了四种软件在不同在线率差异下的最优资源争用比变化情况，可以据此分析不同情境下最优资源配置及订阅限额策略。

图11反映出四种软件的资源争用比均随着在线率差异率的升高而降低，说明在需求波动大的情境下，即用户对不同软件的在线率差异率较大时，运营商应尽可能降低软件的资源争用比，通过配置足量的虚拟机资源并设定严格的订阅限额来保障软件的服务质量，从而减少违约赔付成本来提高收益；相反，在需求波动小的情境下，即用户对不同软件的在线率差异率较小时，运营商可以提高软件的资源争用比，通过放宽订阅限额来抢占更大的市场。此时由于在线率差异较小，该策略不会造成资源闲置，可以在保证资源利用率的同时提高运营商收益。此外，图11还反映了随着在线率差异率的升高，软件4的资源争用比下降幅度最大，并且一直低于其他软件。由参数设置可知，相较于其他软件，软件4的平均在线率最高且最稳定，因此运营商应尽可能为在线率高且稳定的软件配置更多的虚拟机资源，并相应地放宽订阅限额，从而增加收益。

4 结束语

为了保障软件可用性，在提供服务的过程中SaaS运营商需要提前为各种软件配置虚拟机资源，同时需要考虑各种订阅请求的订阅限额。本文针对该问题提出了一个以收益最大化为目标的有资源约束的非线性整数规划模型。模型考虑了用户对软件的在线率差异、用户订阅时间差异以及运营商的SLA违约赔付等实际因素，以此来研究SaaS运营商在不同的时间规划期内如何确定分配给各类软件的虚拟机资源量以及在SLA限制下每种订阅需求的订阅限额。由于求解所建立模型的计算复杂度较高，本文采用PSO进行求解，同时提出了一种基于Q-PSO的改进方法。该算法利用Q学习对PSO进行动态调参，能更好地避免陷入局部最优陷阱，提高PSO性能。借助仿真实验，本文针对需求波动大和需求波动小两种情境分别得出了最优资源配置及订阅限额策略。当处于需求波动大的情境下时，运营商应尽可能降低软件的资源争用比，通过配置足量的虚拟机资源并设定严格的订阅限额来保障软件的服务质量，减少违约赔付成本；相反，当处于需求波动小的情境下时，运营商可以提高软件的资源争用比，通过放宽订阅限额来抢占更大的市场，此时由于在线率差异较小，该策略不会造成资源闲置，可以在保证资源利用率的同时提高运营商收益。其中，针对在线率高且稳定的软件，运营商应为其配置更多的虚拟机资源，并相应地放宽订阅限额来增加收益。上述策略在实践中具有指导意义，可以帮助运营商在不同场景下进行更合理的销售决策，实现收益最大化。

本文只考虑了SaaS订阅模式下的资源配置及订阅限额组合优化问题，后续可以针对SaaS的其他定价策略，如按需付费及现货定价等模式展开研究。

参考文献：

［1］吴士亮， 仲琴. 云计算环境下应用软件服务定价策略研究——基于两阶段垄断模型的分析［J］. 价格理论与实践， 2017，21（8）： 144-147. （Wu Shiliang， Zhong Qin. Pricing strategy of application access service in cloud computing environment-based on the analysis of two-stage model of monopoly［J］. Price： Theory & Practice， 2017， 21（8）： 144-147.）

［2］Gartner Inc.. Gartner forecasts worldwide public cloud end-user spending to reach nearly SMonlam Uni Chouk|Ap 500 billion in 2022［EB/OL］. （2022-04-19） ［2023-07-11］. https：//www.gartner.com/en/newsroom/press-releases/2022-04-19-gartner-forecasts-worldwide-public-cloud-end-user-spending-to-reach-nearly-500-billion-in-2022.

［3］Luo Yongji， Yan Haifeng， Zhang Shoushuai. Simulation-based integrated optimization of nesting policy and booking limits for revenue management［J］. Computers & Industrial Engineering， 2020， 150（4）： 106864-106878.

［4］Lee I. Pricing and profit management models for SaaS providers and IaaS providers［J］. Journal of Theoretical and Applied Electronic Commerce Research， 2021，16（4）： 859-873.

［5］Ladas K， Kavadias S， Loch C. Product selling vs. pay-per-use ser-vice： a strategic analysis of competing business models［J］. Management Science， 2022， 68（7）： 4964-4982.

［6］Zhang Zan. Competitive pricing strategies for software and SaaS products［J］. Information & Management， 2020， 57（8）： 103367.

［7］Zhang Longchang， Bai Jing， Xu Jiajun. Optimal allocation strategy of cloud resources with uncertain supply and demand for SaaS providers［J］. IEEE Access， 2023， 11： 80997-81010.

［8］Zhu Jian， Li Qian， Ying Shi. SAAS parallel task scheduling based on cloud service flow load algorithm［J］. Computer Communications， 2022， 182（6）： 170-183.

［9］Sikora T D， Magoulas G D. Neural adaptive admission control framework： SLA-driven action termination for real-time application service management［J］. Enterprise Information Systems， 2021， 15（2）： 133-173.

［10］Han Bin， Sciancalepore V， Costa-Perez X， et al. Multiservice-based network slicing orchestration with impatient tenants［J］. IEEE Trans on Wireless Communications， 2020，19（7）： 5010-5024.

［11］Pimentel V， Aizezikali A， Baker T. An evaluation of the bid price and nested network revenue management allocation methods［J］. Computers & Industrial Engineering， 2018，115（1）： 100-108.

［12］王航臣， 曹宇露， 赵迪. 一种基于蒙特卡罗模拟的航空公司机票超售数量确定方法［J］. 民用飞机设计与研究， 2021，10（2）： 130-136. （Wang Hangchen， Cao Yulu， Zhao Di. A method to determine the overbooking quantity of airline tickets based on Monte Carlo simulation［J］. Civil Aircraft Design & Research， 2021，10（2）： 130-136.）

［13］邓连波， 许景， 彭齐， 等. 基于随机规划的高铁列车超售策略分析［J］. 铁道科学与工程学报， 2022，19（10）： 2813-2819. （Deng Lianbo， Xu Jing， Peng Qi， et al. Overbooking strategy analysis of high-speed train based on stochastic programming［J］. Journal of Railway Science and Engineering， 2022，19（10）： 2813-2819.）

［14］Nababan A A， Jannah M， Nababan A H. Prediction of hotel booking cancellation using K-nearest neighbors（K-NN） algorithm and synthe-tic minority over-sampling technique（SMOTE）［J］. INFOKUM， 2022， 10（3）： 50-56.

［15］You P S， Hsieh Y C， Huang C M. A particle swarm optimization based algorithm to the Internet subscription problem［J］. Expert Systems with Applications， 2009， 36（3）： 7093-7098.

［16］Chen Fuzan， Lu Aijun， Wu H， et al. Compensation and pricing strategies in cloud service SLAs： considering participants’ risk attitudes and consumer quality perception［J］. Electronic Commerce Research and Applications， 2022， 56（2）： 101215.

［17］Jain R， Sharma N. A quantum inspired hybrid SSA–GWO algorithm for SLA based task scheduling to improve QoS parameter in cloud computing［J］. Cluster Computing， 2023， 26（6）： 3587-3610.

［18］Buyya R， Garg S K， Calheiros R N. SLA-oriented resource provisioning for cloud computing： challenges， architecture， and solutions［C］//Proc of International Conference on Cloud and Service Computing. Piscataway， NJ： IEEE Press， 2011： 1-10.

［19］Yuan Shuai， Das S， Ramesh R， et al. Availability-aware virtual resource provisioning for infrastructure service agreements in the cloud［J］. Information Systems Frontiers， 2023， 25（4）： 1495-1512.

［20］Gabrel V， Manouvrier M， Moreau K， et al. QoS-aware automatic syntactic service composition problem： complexity and resolution［J］. Future Generation Computer Systems， 2018， 80（3）： 311-321.

［21］Kashani M H， Mahdipour E. Load balancing algorithms in fog computing［J］. IEEE Trans on Services Computing， 2022， 16（2）： 1505-1521.

［22］Ghafouri S H， Hashemi S M， Hung P C K. A survey on web service QoS prediction methods［J］. IEEE Trans on Services Computing， 2020， 15（4）： 2439-2454.

［23］Fallahi A， Bani E A， Niaki S T A. A constrained multi-item EOQ inventory model for reusable items： reinforcement learning-based differential evolution and particle swarm optimization［J］. Expert Systems with Applications， 2022， 207（11）： 118018-118038.

［24］Chen Ronghua， Yang Bo， Li Shi， et al. A self-learning genetic algorithm based on reinforcement learning for flexible job-shop scheduling problem［J］. Computers & Industrial Engineering， 2020， 149（11）： 106778.

［25］Chang Chenglin， Lin Qucheng， Liao Zuwei， et al. Globally optimal design of refinery hydrogen networks with pressure discretization［J］. Chemical Engineering Science， 2022， 247： 117021.

［26］郭文文， 计明军， 祝慧灵. 集装箱码头泊位与堆场协调分配模型与算法［J］. 系统工程， 2020，38（3）： 64-72. （Guo Wenwen， Ji Mingjun， Zhu Huiling. Model and algorithm of coordinated allocation for berth and yard in container terminals［J］. Systems Enginee-ring， 2020， 38（3）： 64-72.）

［27］Yin Lei， Liu Jin， Fang Yadong， et al. Two-stage hybrid genetic algorithm for robot cloud service selection［J］. Journal of Cloud Computing， 2023， 12（1）： 1-16.

［28］王纯子， 郭伟， 张斌. 求解非线性混合整数规划的算法设计与仿真［J］. 计算机科学与探索， 2013，7（9）： 854-864. （Wang Chunzi， Guo Wei， Zhang Bin. Algorithm design and simulation of solving nonlinear mixed integer programming problem［J］. Journal of Frontiers of Computer Science and Technology， 201jC1+kf5T2Byqo5Qd2mPTDA==3， 7（9）： 854-864.）

［29］Kennedy D D， Zhang Haibo， Rangaiah G P， et al. Particle swarm optimization with re-initialization strategies for continuous global optimization［M］. New York： Nova Science Publishers， 2013.

［30］Hou S， Gebreyesus G D， Fujimura S. Day-ahead multi-modal demand side management in microgrid via two-stage improved ring-topology particle swarm optimization［J］. Expert Systems with Applications， 2024， 238（2）： 122135.

［31］Zheng Qingshuai， Gu Yujiong， Liu Yuhang， et al. Chaotic particle swarm algorithm-based optimal scheduling of integrated energy systems［J］. Electric Power Systems Research， 2023， 216： 108979.

［32］刘陈伟， 孙鉴， 雷冰冰， 等. 基于改进粒子群算法的云数据中心能耗优化任务调度策略［J］. 计算机科学， 2023， 50（7）： 246-253. （Sun Chenwei， Sun Jian， Lei Bingbing， et al. Task scheduling strategy for energy consumption optimization of cloud data center based on improved particle swarm algorithm［J］. Computer Science， 2023， 50（7）： 246-253.）

［33］Zhang Feng. Intelligent task allocation method based on improved QPSO in multi-agent system［J］. Journal of Ambient Intelligence and Humanized Computing， 2020，11（2）： 655-662.

［34］Sadeghi J， Sadeghi S， Niaki S T A. Optimizing a hybrid vendor-managed inventory and transportation problem with fuzzy demand： an improved particle swarm optimization algorithm［J］. Information Sciences， 2014， 272（8）： 126-144.

［35］You P S， Hsieh Y C， Ikuta S. A heuristic to bandwidth allocation and sales limit setting for Internet service providers［J］. International Journal of Systems Science， 2012， 43（11）： 2135-2143.