增强型野马优化算法及其工程应用

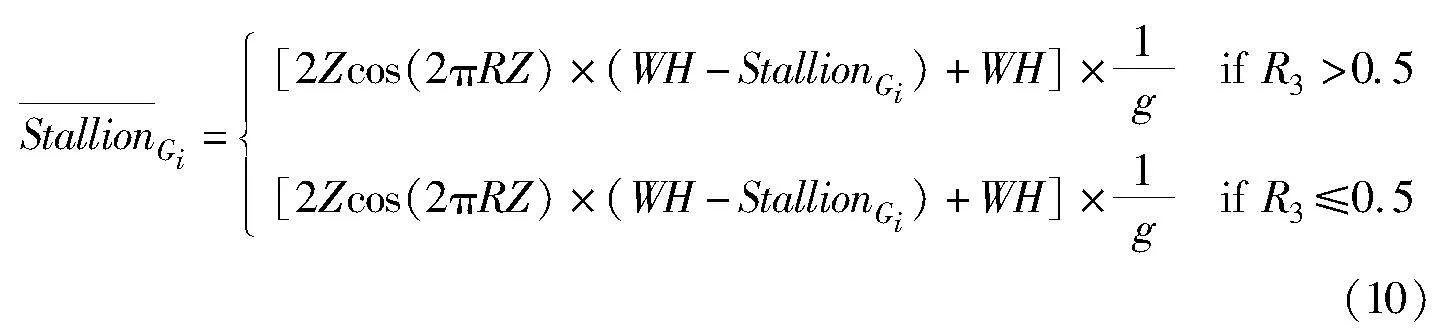
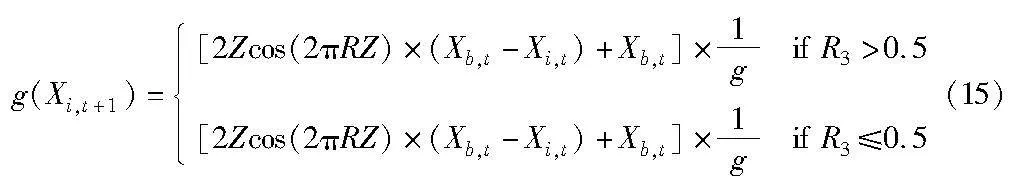
摘 要：针对野马优化算法易陷入局部最优、收敛速度慢等缺点，提出增强型野马优化算法。首先，在种群初始化阶段，采用Sinusoidal映射，增加种群的多样性；其次，在阶段更新过程中，设计出非线性收敛性更强的自适应权重，调节全局搜索和局部优化能力；然后，在更新领导者位置阶段加入扰动因子，平衡局部和全局探索能力；进一步，利用自适应t分布变异，对个体位置进行扰动，提高算法跳出局部最优的能力。通过在CEC2021测试竞赛进行测试优化比较，验证算法的有效性和稳健性，并利用Wilcoxon秩和检验和MAE排名，验证算法的有效性。最后将算法应用到工程难题问题中，验证了其在工程优化问题上的适用性与优越性。实验结果表明，与其他智能算法相比，增强型野马优化算法具有更强的寻优能力和更快的收敛速度。

关键词：野马优化算法； Sinusoidal映射； 自适应t分布； 工程优化

中图分类号：TP301.6 文献标志码：A 文章编号：1001-3695（2024）07-020-2061-08

doi：10.19734/j.issn.1001-3695.2023.10.0505

Enhanced wild horse optimization algorithm and its engineering application

Abstract：To overcome the weaknesses of wild horse optimization algorithm， such as easy to fall into local optima and slow convergence speed， this paper proposed an enhanced wild horse optimization algorithm. Firstly， in the population initialization stage， it utilized Sinusoidal mapping to increase the diversity of the population. Secondly， in the stage update process， it designed adaptive weights with stronge9Xjk1wlPuMDjFtZHAPcaIJvga+aWzTY8khYfD2oVPdE=r nonlinear convergence to adjust the abilities of global search and local optimization. Then， it introduced perturbation factors in the leader position update stage to balance local and global exploration capabilities. Furthermore， it utilized adaptive t-distribution mutation to perturb the individual positions and improve the algorithm’s ability to jump out of local optima. The effectiveness and robustness of the algorithm were validated by optimization comparisons in the CEC2021 competition test set， and the efficacy of the algorithm was verified through Wilcoxon rank sum test and MAE ranking. Finally， it applied the algorithm to two engineering problems， which verified the applicability and superiority of the algorithm for engineering optimization problems. The experimental results indicate that the enhanced wild horse optimization algorithm exhibits stronger optimization capabilities and faster convergence speed，which compared to other intelligent algorithms.

Key words：wild horse optimization algorithm; Sinusoidal mapping; adaptive t-distribution; engineering optimization

0 引言

随着人类社会的迅速发展，问题的规模和复杂度不断增加，因此需要更加通用和高效的算法来应对这些挑战。元启发式算法具有通用性强、计算效率高、问题规模可扩展等优点，被广泛应用于大量复杂的科学研究和工程应用问题。随着群智能算法的优点被大众熟知，越来越多新的群智能算法不断地被提出，如鲸鱼优化算法（whale optimization algorithm，WOA）［1］、正弦余弦算法（sine cosine algorithm，SCA）［2］、白骨顶鸡优化算法（coot optimization algorithm，COOT）［3］等。

野马优化器（wild horse optimization，WHO）是Naruei等人［4］提出的一种新的智能优化算法。该算法的灵感来源于野马的社会生活行为，主要包括小马驹的放牧行为、马的交配行为、领导种马群体，以及各种群领导者选拔行为等。该算法具有结构简单、时间复杂度低、控制参数少等特点，因此有广泛的应用前景。Ali等人［5］将改进WHO用于解决电力系统优化问题。Motwakel等人［6］将WHO用于电力数据中优化选择特征，最终实现了准确的负荷预测性能。Milovanovic＇等人［7］将WHO用于微电网多目标能量管理中。蔡延光等人［8］将改进WHO用于求解TS，相比原算法取得了很好的效果。

虽然野马优化算法优化能力具有一定的优势，但仍然存在一些缺陷。例如，在初始化阶段存在初始种群多样性差、全局搜索能力弱、易陷入局部最优等不足。针对上述问题，李高扬等人［9］首先引入tent映射初始化种群，提高算法的全局寻优能力，其次采用自适应领域搜索策略，改善算法的开发能力，最后利用高斯随机游走策略对个体的历史最优位置进行回溯搜索，改善算法的探索能力。然而tent映射可能导致种群中存在多个重复个体，并且初始种群分布不均，从而造成收敛速度慢以及容易陷入局部最优等问题。李一铭等人［10］首先利用非自适应因子，有效平衡了算法全局探索和局部挖掘能力，其次引入偏移进化策略增加个体多样性，然后引入黄金正弦分割系数，指引个体向全局最优位置方向移动。但是使用黄金正弦分割系数可能会导致引入的方向性过强，会使种群陷入局部最优解。

综上，本文提出一种增强型野马优化算法（enhanced wild horse optimization，EWHO），以解决WHO存在的不足。一方面，在野马种群初始化阶段进行Sinusoidal映射，Sinusoidal映射相比tent映射具有更加平滑、更广的映射范围和更好的分布性质等优点，能更好地提高种群多样性；另一方面，改进自适应因子以平衡全局探索和局部开发能力；然后，在更新种马位置时融入自适应扰动因子，相比黄金正弦分割系数，自适应扰动因子通过可调节的参数、自适应性和独立性，提供了更大的灵活性，能够使算法更好地适应不同的问题和优化目标；最后，引入自适应t分布和动态选择策略，进一步协调局部搜索和全局搜索的比重。

1 WHO算法

1.1 初始化种群

随机生成种群数为（x）={x1，x2，x3，…，xn}，接着对初始种群进行分组，如果总体成员数为N，则种马数量为G=N×PS。其中PS为种马在总群中所占的百分比，剩下的成员数量为N-G。根据种马数量G进行平均分组，从而保证每一个组别中都有一个种马。

1.2 小马驹放牧行为

小马驹通常大部分时间都在群体附近吃草，把种马视为放牧区域的中心，群体其他成员在不同半径的引线周围进行移动和探索的公式如式（1）所示。

xji，G=2Z cos（2πRZ）×（Stallionj-xji，G）+Stallionj（1）

其中：xji，G是群体成员当前位置；Stallionj是种马的位置；R是［-2，2］的随机数，可以使马驹以不同角度进行放牧；xji，G是群体成员在放牧时的新位置；Z是由式（2）计算出的自适应结构。

Z=R2·IDX+R3·（～IDX）（2）

其中：P=R1<TDR，IDX=（P==0），如果R1中的元素小于TDR，则返回逻辑值1，否则返回0；P是0和1组成的向量；R1和R3是在［0，1］均匀分布的随机向量；R2是在［0，1］均匀分布的随机数；IDX返回的是P向量中元素等于0的位置；TDR是自适应参数，从1开始，在算法执行过程中不断线性减小到0，表达公式如式（3）所示。

TDR=1-iter×（1/maxiter）（3）

其中：iter为当前迭代次数；maxiter为算法的最大迭代次数。

1.3 马的交配行为

当小马驹成熟后，会离开自己所在的群组进行交配行为，表达公式如式（4）所示。

XPG，K=Crossover（XqG，i，XzG，j） i≠j≠k，q=z=end（4）

其中：XPG，K表示群组k中的第p个个体的位置；Crossover表示取XqG，i和XzG，j的平均值；XqG，i表示群组i中的第q个个体的位置；XzG，j表示群组j中第z个个体的位置。

1.4 集体领导

群体领导者需要带领种群走向最佳栖息地，如果当前种群占主导地位，则可以使用栖息地，否则必须远离。这个过程可以用式（5）进行表示。

1.5 领导者的交流与选拔

随机选择领导者，确保算法的随机性质，后期如果成员有更好的适应度值则进行身份交换，如式（6）所示。

2 EWHO算法

2.1 Sinusoidal 映射

算法的初始化阶段对后期过程有很大影响。WHO算法的基本种群初始化是在整个空间内随机分布，具有较高的随机性和分布不均匀性，会导致种群多样性缺乏，搜索效率低等问题。许多学者利用混沌映射机制来增加种群的多样性，以改善算法的性能。常见的混沌模型包括Sinusoidal、Logistic和Circle映射。Sinusoidal映射是一种常用的混沌映射函数，它通过正弦函数生成非线性和周期性的数值序列。相对于Logistic和Circle映射，在某些区域产生更密集数值分布的情况下，Sinusoidal映射表现出更高的随机性。其非线性特性和周期性质使得它能够生成更复杂、更随机的序列，有助于增加种群的多样性，避免种群陷入局部最优解。

图1展示三种混沌映射方式所产生的混沌序列值的分布。可以看出，Logistic和Circle映射取值概率都不均匀，而均匀的混沌值范围可以促进种群在搜索空间内更均匀地分布，增加种群个体的多样性，Sinusoidal映射相对于Logistic和Circle映射分布更为均匀。

图2是在函数Griewangk’s function的测试下，WHO分别利用随机初始化、Sinusoidal映射初始化、Logistic映射初始化和Circle映射初始化得到的目标函数收敛曲线。由图可知，经过Sinusoidal映射初始化的WHO在收敛速度和求解精度上的表现都优于其他映射方法。这种初始化方式有助于增加初始化种群的多样性，使算法能够在更广泛的搜索空间内进行寻优，从而促进全局寻优过程。

同时Gandomi等人［11］证明了Sinusoidal映射比其他映射具有更好的优化效果，因此引入Sinusoidal映射改善种群分布，提高初始种群多样性。Sinusoidal混沌映射表达式如式（7）所示。

xk+1=ax2ksin（πxk）（7）

其中：a=2.3；xk为第k次迭代的值；xk+1为第k次迭代后得到的新值。

2.2 改进TDR

根据式（1）可知，小马驹的位置通过Z控制，所以自适应Z是协调全局探索和局部利用的关键，而TDR是用来控制变量的自适应参数，所以也是整个算法的关键。根据式（3），TDR的值随着算法迭代从1线性减小到0，虽然线性自适应参数可以平衡全局探索和局部优化，但比较有限，会降低算法的性能，受朱学敏等人［12］启发，提出将TDR改进为非线性自适应参数，表达公式为

TDR=［（1-iter/maxiter）（2iter/maxiter）］2iter/maxiter（8）

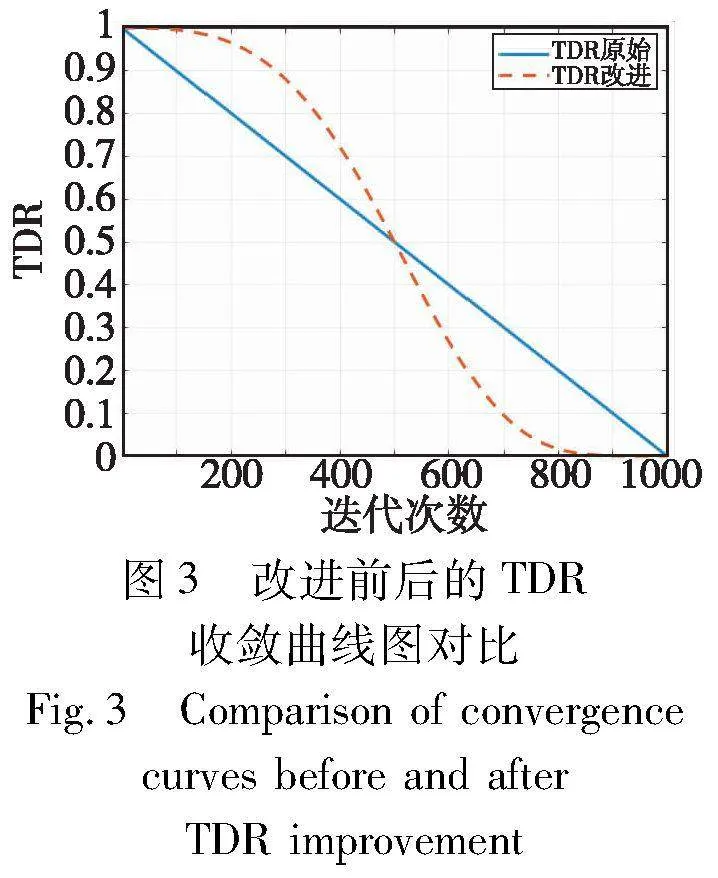
图3展示了改进后的TDR与原始TDR的对比。可以看出，重新设计的非线性自适应权重呈现出更为平滑的上、下界，有助于使算法在搜索空间中更为均匀地进行探索，有效减少了陷入局部最优解的风险。在迭代初期，改进后的TDR的数值保持在较高的位置，且表现相对平稳，促使算法进行更广泛地全局探索，避免过早收敛到次优解，提高对全局解的发现概率；迭代中期，其数值迅速减小，有助于加速从全局探索转变为局部开发的过程；在迭代后期，采用较小的自适应权重，使小马驹在探索空间中更为细致入微地寻找潜在解，增强了算法对局部最优解发现的概率。这一非线性自适应权重的改进方案使得算法更具平滑性和鲁棒性，有助于更有效地发现整个搜索空间中的最优解。

2.3 带扰动因子的领导者

整个寻优的过程中，领导者位置的变动关乎整个种群的动向。在StallionGi移动的过程中添加扰动因子，可以改变搜索范围，跳出局部最优，增加协调局部搜索和全局优化能力。扰动因子g定义为

g={cos［（1-iter/maxiter）2×π］+α}×β（9）

通过对α和β进行组合实验，当α=4，β=5，全局探索和局部寻优能力达到较好的平衡。改进后的领导者移动公式为

自适应性可以根据迭代的进程动态调整g的值，以适应不同的优化阶段。这样可以使算法在不同的迭代阶段表现更好。当StallionGi朝着最优位置移动时，勘探范围由大到小，可以增加局部搜索能力；远离最优位置时，搜索范围由小到大，能够增强全局探索能力，有效避免陷入局部最优。

2.4 自适应t分布与动态选择策略

t分布又称学生分布，含有参数自由度，t（n→∞）→N（0，1），t（n=1）=C（0，1），其中N（0，1）为高斯分布，C（0，1）为柯西分布，即标准高斯分布和柯西分布是t分布的两个边界特例分布［13］。三者分布如图4所示。

柯西变异的全局搜索能力较强，能够有效地保持种群的多样性；高斯变异的局部开发搜索能力较强，可以保证进化后期的收敛速度［14］。因此本文采用迭代次数iter为t分布自由度参数的t分布变异算子对小马驹的位置进行扰动，将迭代次数作为自由度参数的t分布，具有自适应性、平衡全局与局部搜索以及收敛速度优化的优点。通过动态调整自由度参数，算法能够在早期阶段促进全局搜索，发现更广阔的解空间；而在后期阶段加强局部搜索，收敛到更精确的解。这种方法能够提高算法的搜索效率和性能，使其在全局和局部搜索之间找到合适的平衡点，从而优化算法的探索能力、收敛速度和求解的精度。具体位置更新方式如式（11）所示。

虽然使用自适应t分布能够在很大程度上提升算法的寻优能力，但如果对所有个体使用，一方面会增加算法的计算时间，另一方面不能保留原始算法的优点。因此，小马驹个体是否采用自适应t分布，本文采用动态选择概率来调用自适应t分布变异算子的使用，具体公式如式（12）所示。

q=w1-w2×（maxiter-iter）/maxiter（12）

其中：w1=w2=0.8。动态选择q概率使得算法在迭代前期对小马驹位置进行扰动，改善迭代初期就存在收敛的倾向，在迭代后期，充分发挥原算法良好的局部开发能力，同时以小概率的t分布变异作为补充，提高算法的收敛速度。

2.5 EWHO实现步骤

综合以上针对WHO改进的策略，EWHO的伪代码如下。

2.6 时间复杂度分析

综上所述，EWHO时间复杂度为O（Nd）+O（NTd）+O（NTd）+O（NTd），与WHO时间复杂度一致。

2.7 收敛性分析

全局收敛性准则及定理［15］描述了算法满足全局收敛性需要的两个条件：

其中，f是适应度函数，D为随机搜索算法，x为解空间RN子集S中能使适应度函数取得最小值的点，ξ为算法D在迭代过程中得到的解， S为可行解空间。若满足该假设，则说明算法适应度值单调不增。

定理1 EWHO满足条件1。本文算法最优位置更新包括原始野马算法的位置更新和引入自适应t分布的位置更新，所以将EWHO定义为

其中：Xb，t为第t代时全局最优个体的位置；g（Xi，t）表示通过式（1）（4）（10）更新第t代的位置；h（Xi，t）为通过自适应t分布更新第t代位置。由式（13）（14）可知，Xb，t对应的全局最优适应度值单调不增，满足条件1。

定理2 EWHO满足条件2。对于EWHO中领导者位置更新机制，有

对于小马驹更新位置机制，有

由引理1可知，EWHO具有全局收敛性。

3 实验仿真与结果分析

3.1 仿真实验环境与参数设置

仿真实验所用软件为MATLAB R2021a，测试环境为操作系统Windows 10专业版64位（10.0，版本19042），处理器为Intel CoreTM i7-6820HQ CPU@2.70 GHz（8CPUs），内存为16 384 MB。

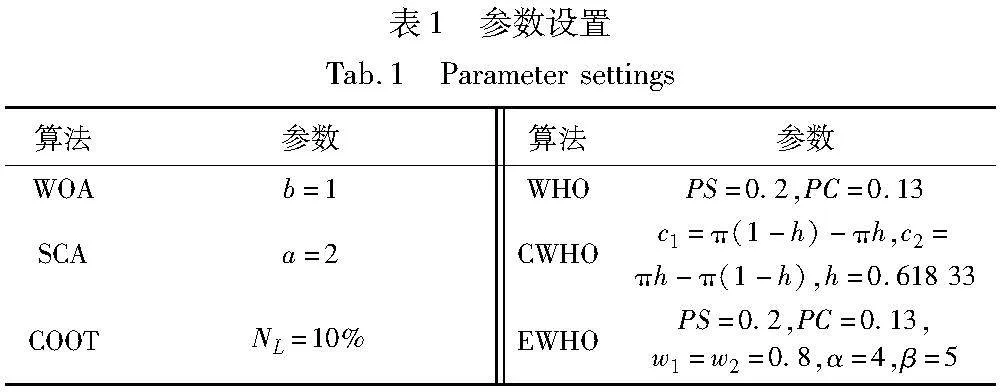
为验证EWHO的优越性能，选取鲸鱼优化算法（WOA）［1］ 、正弦余弦算法（SCA）［2］、白骨顶鸡优化算法（COOT）［3］、野马优化算法（WHO）［4］、改进野马优化算法（CWHO）［10］与EWHO进行对比。本文选取CEC2021的40个函数进行算法测试，以验证改进后算法的优越性。为保证实验的公平性，各个算法参数设置与原文献保持一致，如表1所示。同时，为保证仿真实验的有效性，其他运算参数均设置相同，种群规模设置为30，最大迭代次数为1 000，所有算法均进行30次独立重复实验。

3.2 CEC2021测试函数

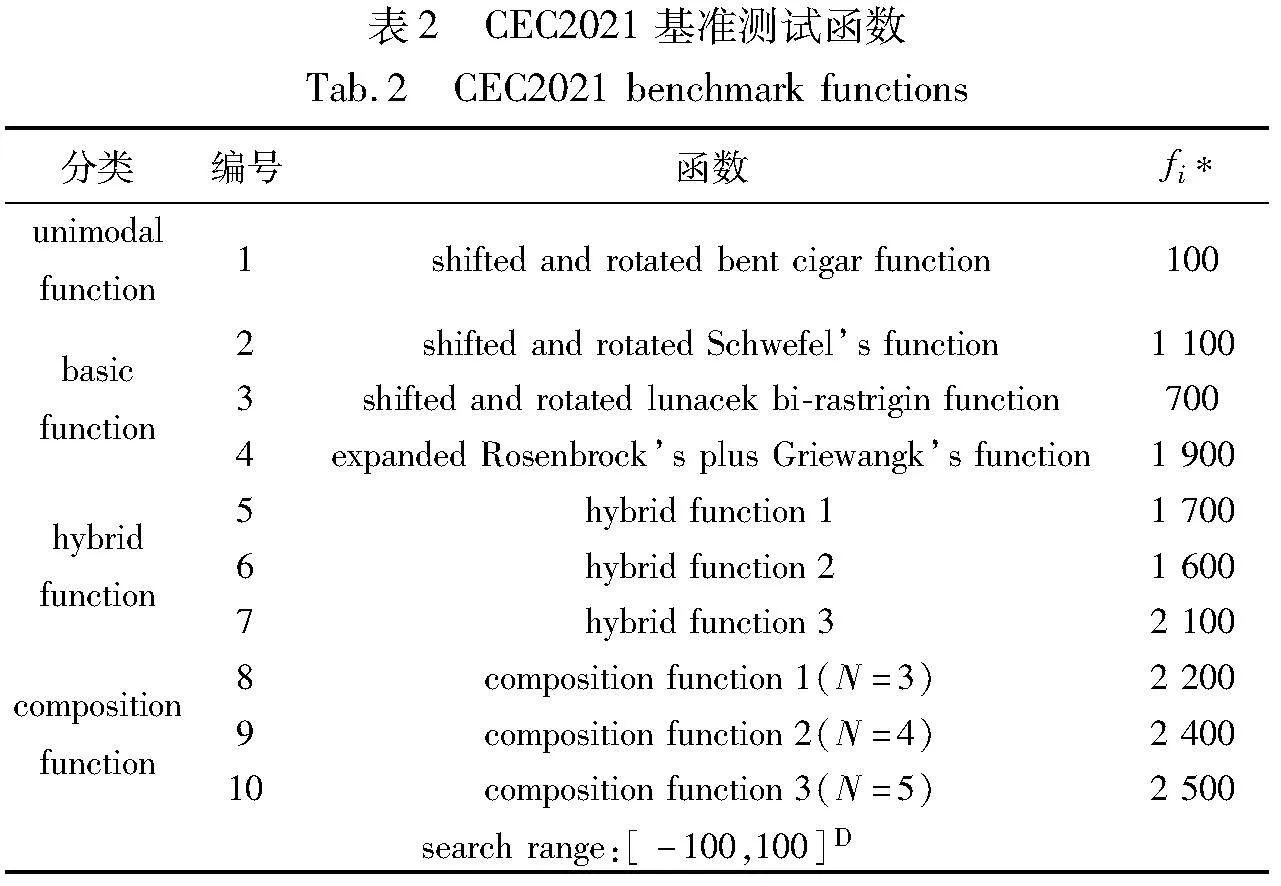
CEC2021测试函数是IEEE进化计算机大会单目标参数优化竞赛中提出的10个在10维、20维上可扩展的复杂测试函数，详细信息如表2所示。

本文在10个基准测试函数上扩展rotation和bias两种操作，1表示加入上述操作，0表示未加入上述操作，则基准函数可以得到00、01、10和11类型4种组合，共计40个测试函数，进行20维函数的测试实验。

3.3 灵敏性分析

在EWHO中动态选择概率q是决定是否采用自适应t分布变异的关键，为了使其性能达到最优，本节对参数w1和w2进行了灵敏性分析。

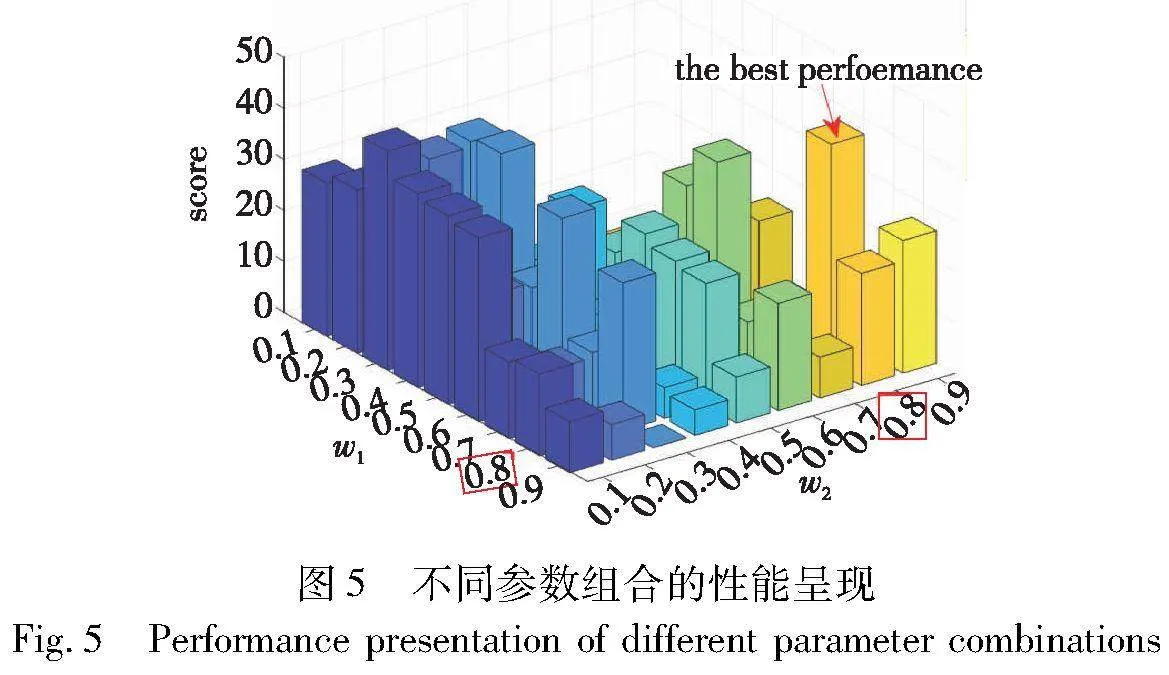
参数w1、w2和迭代次数决定了采用自适应t分布变异的时机，为了使得算法在迭代前期使用t分布变异对小马驹位置进行扰动，迭代后期以小概率的t分布变异作为补充，因此可以将［w1，w2］设为{［0.1，0.1］，［0.2，0.1］，［0.2，0.2］，［0.3，0.1］，［0.3，0.2］，［0.3，0.3］，［0.4，0.1］，…，［0.9，0.8］，［0.9，0.9］}（一共45组）。对于每个组合，计算在10个CEC2021测试函数上平均值的最终排名和得分（得分=45-最终排名），其中最大迭代次数为1 000，种群规模为30，分别进行独立30次运行。如图5所示，可以看到不同组合的得分情况，性能越好，得分越高，直方图越高。当［w1，w2］为［0.8，0.8］时，柱状图最高，本文将w1和w2均设为0.8。

为了验证有无动态选择概率是否会增加算法的运行时间以及是否会影响求解的精度，本文选择40个测试函数进行验证。由于篇幅有限，只选择有差异的部分进行呈现，结果如表3和4所示。通过表3可知，有无动态选择概率的求精精度相差不大，甚至在有选择动态概率时的求解精度要略胜于没有动态选择率的求解精度。表4展示了每种类型的函数独立运行30次所需的时间。可以看出，有动态选择概率的运行时间得到较大的提升，尤其是针对Rotation［10］类型，整体提升了139.4 s。

综上所述，通过参数灵敏性分析、求解精度以及运行时间对比，有动态选择概率的算法整体性能要优于无动态选择概率。

3.4 在测试函数上的算法性能分析

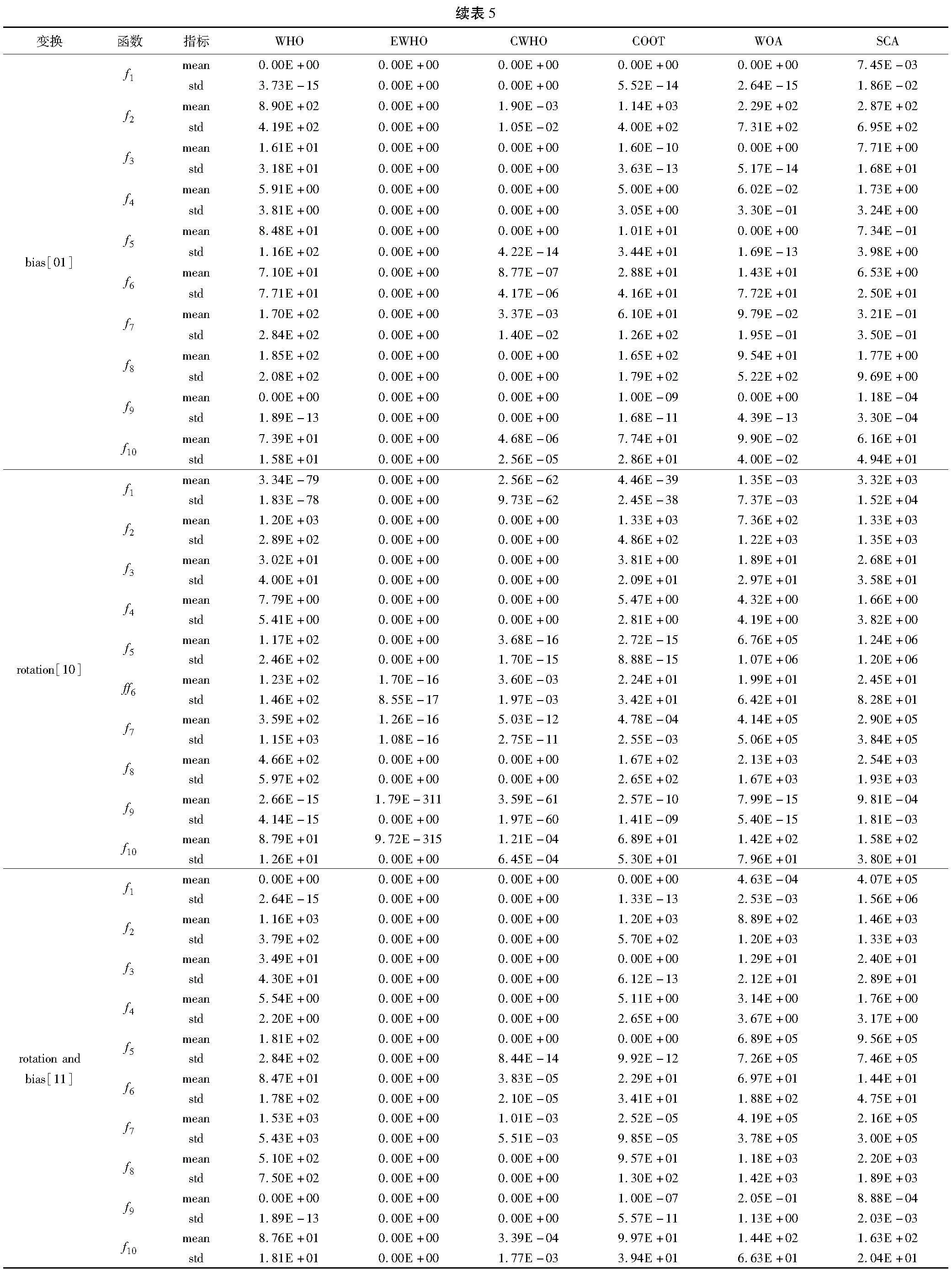
由于CEC2021的10个函数理论最优值各不相同，本文对各算法的寻优结果与理论最优值求差，以差值0作为各函数的最优值，以方便对比分析，表5为EWHO与各个算法在每个函数上运行30次的平均值和标准差。

根据表5，本文EWHO在40个测试函数中表现出最优的性能。在01类型的测试函数中，EWHO的求解平均值达到了函数理论最优值，标准差为0，而CWHO只找到了一半测试函数的理论最优值。在f2、f6、f7和f10函数中，只有EWHO的求解精度达到了函数理论最优值，而WOA在f1、f3和f5函数中也找到了最优值，这表明WOA在求解精度方面也表现出了较好的性能，而SCA的整体表现最差。

在11类型的测试函数中，EWHO找到了所有函数的理论最优值，标准差为0，是整体性能最优的算法。CWHO略逊一筹，对于其求解精度没有达到理论组最优值函数f6、f7和f10而言，EWHO求解精度达到了理论最优值。尽管CWHO相比WHO有一定的改进，但与EWHO相比仍存在较大差距。COOT在f1、f3和f5函数中也找到了最优值，而WHO和SCA的求解精度和稳定性表现较差。

在00和10测试函数中，EWHO在绝大多数函数的平均求解精度上达到了理论最优值，并且标准差为0。虽然在f6、f7、f9和f10函数中没有找到最优值，但相比其他算法，EWHO在这些函数上仍然表现出较好的性能，并且在f10函数中平均求解精度也达到了2.67E-315的数量级，远远高于CWHO的1.95E-07。尽管CWHO整体性能也较好，但仍稍逊于EWHO。WHO的平均求解精度均没有达到理论最优值，且标准差相对较大，整体表现较差。WOA在00类型中的f3和f8函数中也寻求到了理论最优值，整体性能优于SCA和WOA。

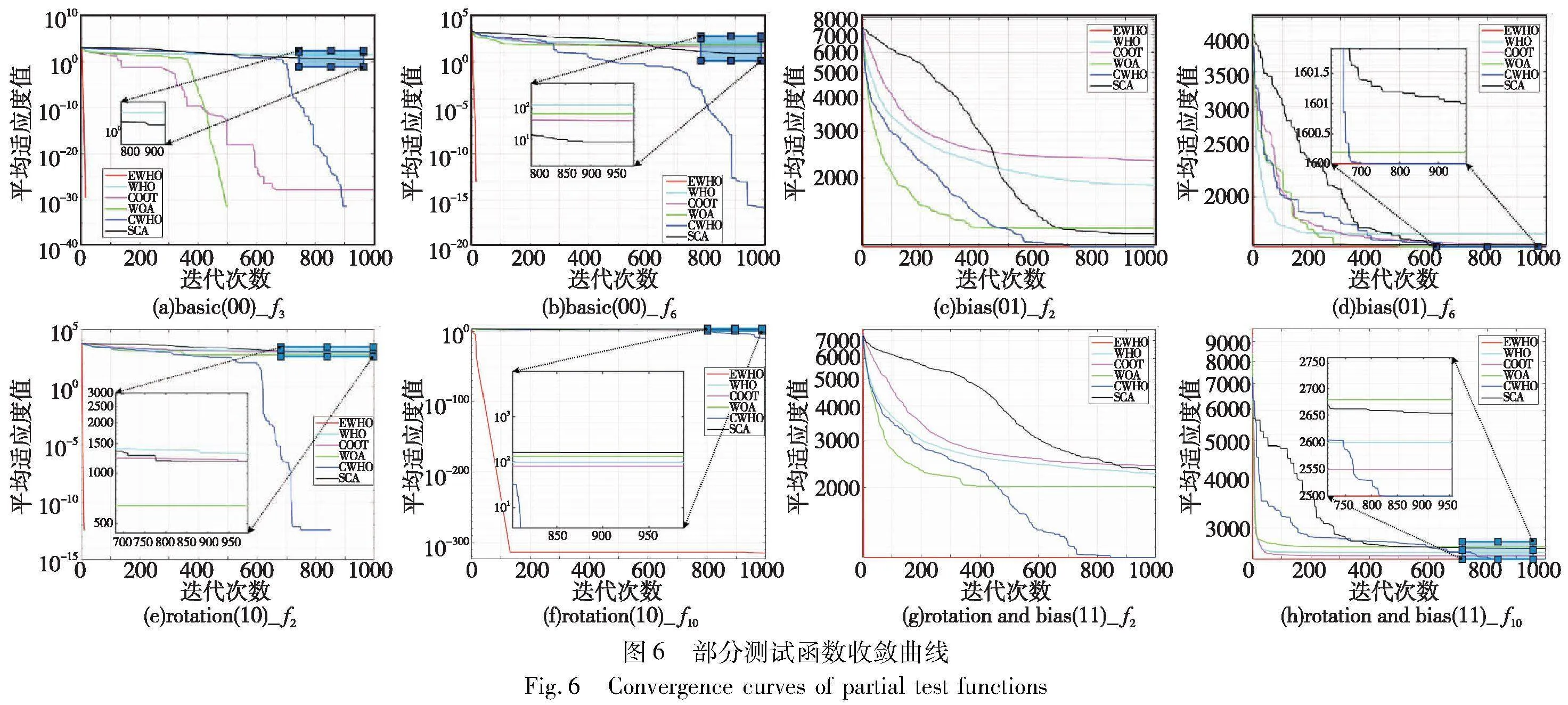
为了更直观地比较各个算法的收敛精度以及收敛速度，针对不同类型的组合函数，本文选取了部分收敛曲线，如图6所示。

从图6的收敛曲线可以看出，无论是在收敛速度还是求解精度上，EWHO都明显优于其他对比算法。虽然CWHO和EWHO在00类型的f3函数以及01、10和11类型的f2函数的平均求解精度都达到了理论最优值，但是EWHO的收敛速度要远远大于CWHO，甚至在迭代初期就达到了理论最优值，说明了EWHO在全局搜索和收敛性方面具有较好的性能。WOA在00类型的f3和01类型的f6上收敛速度仅次于EWHO，COOT和SCA的收敛速度较差。对于11类型的f2和f10函数来说，WHO的收敛速度和求解精度较差，CWHO优于WHO，EWHO不管是在收敛速度和求解精度上都是最优的。

本文提出的增强型野马优化算法，首先使用更加稳定的Sinusoidal映射初始化种群，扩大了种群的范围，提高种群多样性，为后续的全局探索奠定了良好的基础。在迭代前期，本文使用的非线性自适应参数替代传统线性参数的数值，保持在较高的位置，促进算法进行更为广泛的全局探索。此外，在领导者更新阶段加入扰动因子，在远离最优位置时，搜索范围由小到大，能够增强全局探索能力，同时有较大概率出现的自适应t分布在迭代前期接近柯西变异，具有较强的全局搜索能力。在迭代后期，非自适应参数保持在较低的数值，使得小马驹在迭代后期的局部探索时间增加，更好地进行局部寻优。通过在领导者位置更新阶段引入扰动因子，当朝着最优位置移动时，探勘范围由大到小，从而增加局部探索能力。此外，具有较小概率出现的自适应t分布在迭代后期接近高斯变异，局部开发探索能力较强，能够加快后期的收敛速度。

野马优化算法通过引入的策略，在迭代前期增强了全局探索能力，在后期增强了局部寻优的能力，实现了全局寻优和局部寻优的良好平衡。

3.5 Wilcoxon秩和检验

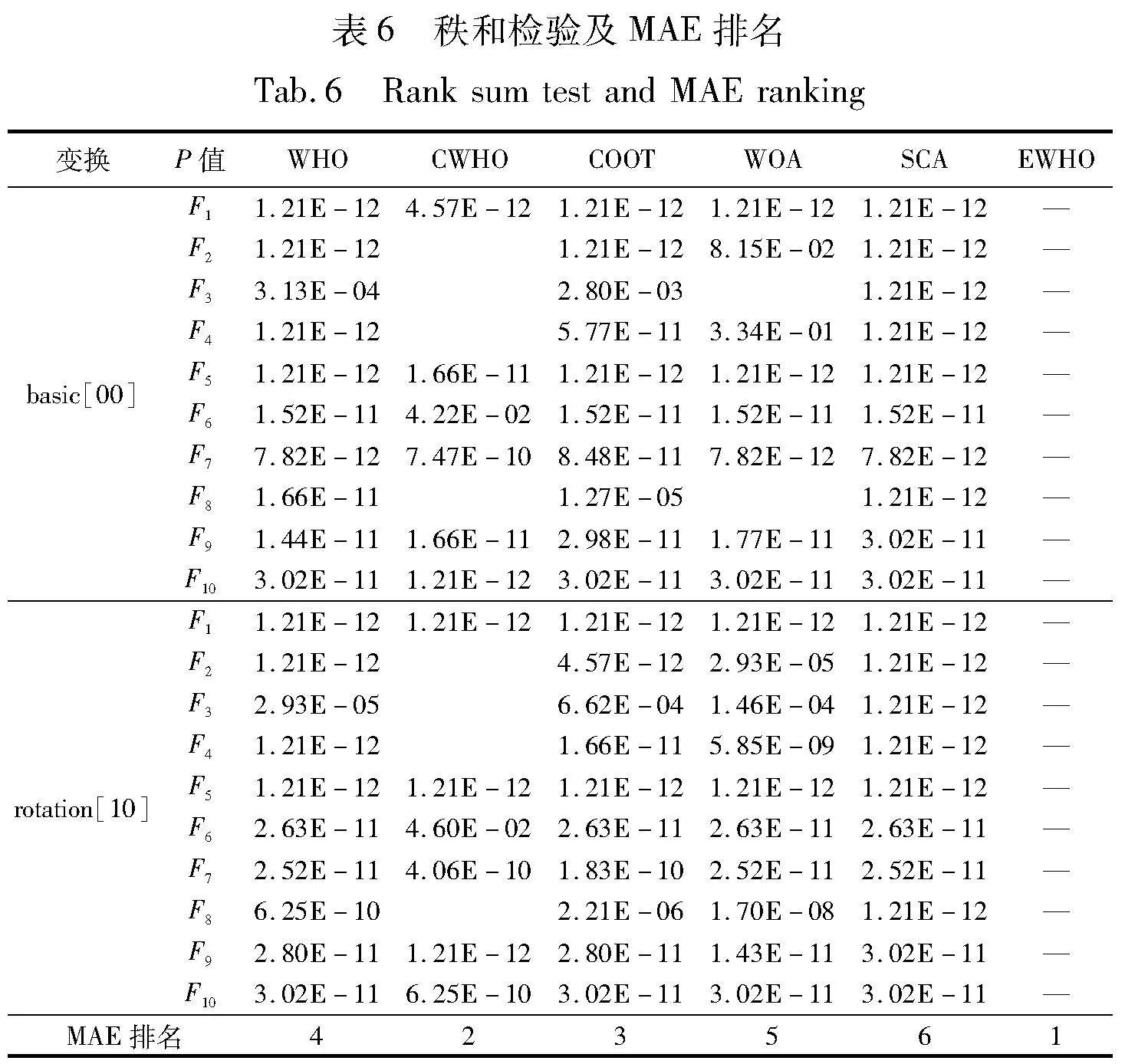
为了全面评估EWHO的可靠性和优越性，本文选取Wil-coxon秩和检验方法进一步验证各个算法实验结果的显著性差别。选取EWHO在CEC2021测试集函数上的运行结果与其他算法进行Wilcoxon秩和检验，并计算P值检验结果，同时为了综合评估EWHO与其他算法的竞争性，使用MAE对上述算法进行排序。由于篇幅有限，仅列出部分20维函数的实验结果，如表6所示。当P值小于5%时，说明两种算法的差异性显著，否则，不显著。由表6可知，大部分的P值都是小于5%的，说明改进后的EWHO与其他算法相比差异性明显，且经过MAE排名可知，EWHO排名第一，由此可以认为EWHO在CEC2021测试函数上的整体性能强于其他算法，进一步证明了本文算法的有效性。

4 EWHO算法的工程优化应用研究

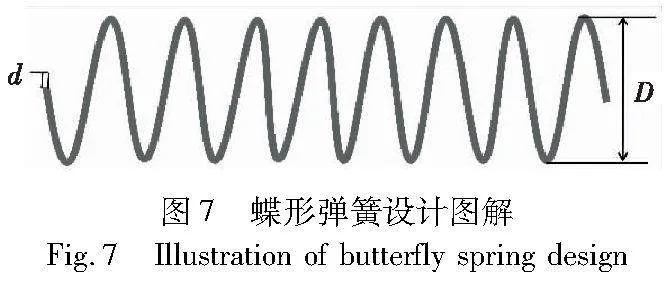
蝶形弹簧设计问题的目标是满足剪应力、浪涌频率、翘曲度等相关指标标准的约束下，使图7所示的拉伸/压缩弹簧的质量最小化。

该问题包括弹簧线圈直径d、弹簧线圈平均直径D和弹簧线圈数量N三个设计变量。该问题的数学模型为

x=［x1，x2，x3］=［d D N］

min f（x）=（x3+2）x2x21

表7为各个算法求解蝴蝶弹簧设计问题的实验结果。从表7可以看出，EWHO求解的最优值优于WHO以及其他对比算法，达到了0.012 665 233，此时d=0.051 685 08、D=0.356 621 99、N=11.294 582 09，总体平均值和标准差也都优于其他算法。可见对于蝶形弹簧设计问题，EWHO具有良好的寻优能力和稳定性，充分说明了该算法良好的性能。

5 结束语

野马优化算法是近年来提出的一种新颖的群智能算法，针对其易陷入局部最优、收敛速度慢等不足，本文提出了融入Sinusoidal映射、扰动因子和自适应t分布的EWHO。将EWHO与五个算法通过CEC2021的40个函数、Wilcoxon检验以及MAE排名测试的实验，验证了改进后的算法具有更强的寻优能力和鲁棒性。最后将其应用于蝶形弹簧设计问题，EWHO求解得到的结果精度和稳定性更好，从而证实了EWHO在实际问题应用中的实用性。因此下一步研究重点是将其应用于解决大规模、复杂的多目标优化和实际工程应用等问题中。

参考文献：

［1］Mirjalili S， Lewis A. The whale optimization algorithm［J］. Advances in Engineering Software， 2016， 95（5）： 51-67.

［2］Mirjalili S. SCA： a sine cosine algorithm for solving optimization problems［J］. Knowledge-Based Systems， 2016， 96（5）： 120-133.

［3］Naruei I， Keynia F. A new optimization method based on coot bird natural life model［J］. Expert Systems with Applications， 2021，183（2）： 115352.

［4］Naruei I， Keynia F. Wild horse optimizer： a new meta-heuristic algorithm for solving engineering optimization problems［J］. Enginee-ring with Computers， 2021，38（S4）： 3025-3056.

［5］Ali M H， Kamel S， Hassan M H， et al. An improved wild horse optimization algorithm for reliability based optimal DG planning of radial distribution networks［J］. Energy Reports， 2022，8： 582-604.

［6］Motwakel A， Alabdulkreem E， Gaddah A， et al. Wild horse optimization with deep learning-driven short-term load forecasting scheme for smart grids［J］. Sustainability， 2023，15（2）： 1524.

［7］Milovanovic＇ M， Klimenta D， Panic＇ M， et al. An application of wild horse optimizer to multi-objective energy management in a micro-grid［J］. Electrical Engineering， 2022，104（6）： 4521-4541.

［8］蔡延光， 方春城， 吴艳林，等. 求解TSP的离散野马优化算法［J］. 计算机工程与应用， 2024，60（1）：145-153. （Cai Yanguang， Fang Chuncheng， Wu Yanlin， et al. Discrete wild horse optimization algorithm for solving TSP［J］. Computer Engineering and Applications， 2024，60（1）：145-153.）

［9］李高扬， 黎向锋， 赵康，等. 全粒子推动野马优化算法的无人机三维路径规划［J］. 系统仿真学报， 2024，36（3）：595-607. （Li Gaoyang， Li Xiangfeng， Zhao Kang， et al. UAV three-dimensional path planning based on all-particle driven mustang optimization algorithm［J］. Journal of System Simulation， 2024，36（3）：595-607.）

［10］李一铭， 王跟成. 基于改进野马优化算法的AGV路径规划［J］. 组合机床与自动化加工技术， 2023（1）： 11-14. （Li Yiming， Wang Hecheng. AGV path planning based on improved mustang optimization algorithm［J］. Combined Machine Tool and Automatic Processing Technology， 2023（1）： 11-14.）

［11］Gandomi A H， Yang Xinshe， Talatahari S， et al. Firefly algorithm with chaos［J］. Communications in Nonlinear Science and Numerical Simulation， 2013，18（1）： 89-98.

［12］朱学敏， 刘升， 朱学林，等. 多策略混合改进的海洋捕食者算法及其工程应用［J］. 国外电子测量技术， 2023，42（5）： 125-134. （Zhu Xuemin， Liu Sheng， Zhu Xuelin， et al. Improved marine predator algorithm and its engineering application with multi-strategy mixing［J］. Foreign Electronic Measurement Technology， 2023，42（5）： 125-134.）

［13］郑婷婷， 刘升， 叶旭. 自适应t分布与动态边界策略改进的算术优化算法［J］. 计算机应用研究， 2022，39（5）： 1410-1414. （Zheng Tingting， Liu Sheng， Ye Xu. Arithmetic optimization algorithm for improved adaptive t-distribution and dynamic boundary strategy［J］. Application Research of Computers， 2022，39（5）： 1410-1414.）

［14］Lan K T， Lan C H. Notes on the distinction of Gaussian and Cauchy mutations［C］//Proc of the 8th International Conference on Intelligent Systems Design and Applications. Piscataway， NJ： IEEE Press， 2008： 272-277.

［15］Solis F J， Wets R J B. Minimization by random search techniques［J］. Mathematics of Operations Research， 1981，6（1）： 19-30.