基于二阶价值梯度模型强化学习的工业过程控制方法
2024-08-15张博潘福成周晓锋李帅












摘 要:为了实现对高延时、非线性和强耦合的复杂工业过程稳定准确的连续控制,提出了一种基于二阶价值梯度模型强化学习的控制方法。首先,该方法在模型训练过程中加入了状态价值函数的二阶梯度信息,具备更精确的函数逼近能力和更高的鲁棒性,学习迭代效率更高;其次,通过采用新的状态采样策略,可以更高效地利用模型进行策略学习。最后,通过在OpenAI的Gym公共实验环境和两个工业场景的仿真环境的实验表明:基于二阶价值梯度模型对比传统的基于最大似然估计模型,环境模型预测误差显著降低;基于二阶价值梯度模型的强化学习方法学习效率优于现有的基于模型的策略优化方法,具备更好的控制性能,并减小了控制过程中的振荡现象。可见该方法能有效地提升训练效率,同时提高工业过程控制的稳定性和准确性。
关键词:工业过程控制; 模型强化学习; 二阶价值梯度; 状态价值函数; 状态采样策略
中图分类号:TP391 文献标志码:A
文章编号:1001-3695(2024)08-026-2434-07
doi:10.19734/j.issn.1001-3695.2023.11.0580
Industrial process control method based on second-ordervalue gradient model reinforcement learning
Zhang Bo1,2,3,4, Pan Fucheng1,2,3, Zhou Xiaofeng1,2,3, Li Shuai1,2,3
(1.Key Laboratory of Networked Control Systems, Chinese Academy of Sciences, Shenyang 110016, China; 2.Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016, China; 3.Institutes for Robotics Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China; 4.University of Chinese Academy of Sciences, Beijing 100049, China)
Abstract:To achieve stable and accurate control of complex industrial processes with high latency, nonlinearity, and strong coupling, this paper proposed a control method based on second-order value function gradient model reinforcement learning. Firstly, during the model training process, the method incorporated second-order gradient information of the state-value function, enabling more accurate function approximation and higher robustness, resulting in improving learning iteration efficiency. Secondly, by adopting a new state sampling strategy, this method facilitated more effective utilization of the model for policy learning. Lastly, experiments conducted in the OpenAI Gym public environments and simulated environments of two industrial scenarios demonstrate that compared to traditional maximum likelihood estimation models, the second-order value gradient model significantly reduces the prediction error of the environment model. In addition, the reinforcement learning method based on the second-order value gradient model exhibits higher learning efficiency than existing model-based policy optimization methods, showcasing better control performance and mitigating oscillation phenomena during the control process. In conclusion, the proposed method effectively enhances training efficiency while improving the stability and accuracy of industrial process control.
Key words:industrial process control; model-based reinforcement learning; second-order value gradient; state value function; state sampling strategy
0 引言
随着现代工业的不断发展,过程控制技术逐渐成为工业过程中不可或缺的一部分。准确、稳定可靠、能够快速响应和适应复杂变化的控制方法可以提高产品质量、生产效率和安全性,创造更好的经济效益。然而,在大多数工业过程中,比如青霉素发酵生产过程、食品生产加工过程等,控制方法面临诸多挑战,如工业过程系统的复杂动态特性、高延时和变量之间的非线性强耦合等[1,2]。因此,面对这些挑战,需要研究合理的控制方法。
为了提高复杂工业过程系统的控制性能,研究者们提出利用强化学习方法对工业过程进行控制。针对非线性强耦合系统,罗傲等人[3]将强化学习中的执行-评价结构应用到控制策略中,取得了较好的控制效果,但是面对多输入约束情况时,存在控制性能下降的问题。针对复杂滞后的工业过程,张丹阳[4]将基于内在好奇心奖励生成方法改进DDPG(deep deterministic policy gradient)方法应用于啤酒发酵过程控制上,得到了最优控制方法,该方法使用的仿真实验环境虽然比较理想,但是需要在更多的工业过程场景下进行验证。针对冷机的负荷分配、冷却塔风机频率以及冷却水泵频率的组合优化控制,马帅等人[5]提出一种能够有效降低能耗的改进的双池DQN算法,但是该方法只能进行离散控制,不能进行连续型动作控制。针对复杂工艺环境下,具有序列相关设置时间的纺机制造车间调度问题,纪志勇等人[6]提出了一种具有多动作空间的强化学习训练算法,但是忽略了多因素对调度目标的影响。任安妮等人[7]利用基于注意力机制的强化学习方法优化交通信号控制,但是该方法依赖大量的训练数据。宋江帆等人[8]使用策略函数输出的改变量计算动作重复的概率,并根据该概率随机地重复或改变动作,提高策略梯度法在连续时间问题中的训练效率,但是该方法在复杂工业场景下工况频繁变化时,控制性能表现较差。
上述方法都是针对复杂工业过程系统提出的无模型强化学习的控制方法,这些方法需要智能体与环境交互产生的大量数据来训练策略网络,这限制了它们在复杂的现实场景中的适用性。基于模型的强化学习控制方法可以解决无模型强化学习控制方法中数据利用低效的问题[9],基于模型的强化学习控制方法构建了环境的显式模型,利用学习到的环境模型[10],即使在高维状态空间下[11],智能体也可以与环境模型交互并优化其策略,从而减少所需的真实环境交互次数,提高数据利用率。
Janner等人[12]提出基于前向预测模型的策略优化,使用概率集成方法学习得到环境模型,并利用模型进行短分支推演得到的数据来训练策略网络,有效减少了智能体与真实环境的交互次数。为了减少环境模型的预测误差,Lai等人[13]提出基于双向模型的策略优化,显著提高了环境模型的预测性能。Shen等人[14]利用无监督学习方法学习真实环境与环境模型的特征不变性,减少环境模型的预测误差。
这些方法都在不同程度上减少了基于模型强化学习中环境模型的预测误差,但是现有的基于模型的强化学习方法主要将模型学习和模型利用分开处理,这可能导致模型和策略之间的学习目标不匹配,即一个在训练数据集上具有较小预测误差的模型并不能得到一个具有高累积奖励的策略[15]。为了解决这个问题,Farahmand等人[15]提出价值感知模型,在模型学习阶段加入状态价值信息。在价值感知模型的基础上,针对在训练过程中的状态价值误差问题,Voelcker等人[16]提出价值梯度模型。
针对强化学习工业过程控制方法的数据利用低效、不能进行连续型动作控制、应用场景有限等问题,本文在价值梯度模型的基础上,提出基于二阶价值梯度模型强化学习方法。在模型损失函数中加入了状态价值函数的二阶梯度信息,在模型利用阶段采用新的状态采样策略。通过在多个强化学习标准实验环境和工业仿真环境的实验表明,本文方法在性能上优于现有的基于强化学习的工业过程控制方法。
1 基于价值感知模型的强化学习
1.1 基于模型的强化学习
强化学习解决的问题是长时决策问题。长时决策问题可以建模成马尔可夫决策过程(Markov 7izO7p6Thns2eaMvp8tv+g==decision process,MDP)[17],MDP使用一个五元组(S,A,P,r,γ)表示。其中:S为状态空间,是环境状态构成的集合;A为动作空间,是智能体动作构成的集合;P(s′|s,a)为状态转移概率,对智能体是未知的;r(s,a)为奖励函数,此时奖励同时取决于状态和动作;γ为折扣因子。在一个马尔可夫决策过程中,从第一个时刻开始,直到终止状态时,智能体与环境交互产生了一条轨迹,即τ=(s0,a0,…,st,at…),并获得一系列的奖励(r0,r1,…,rt,…),那么,所有折扣奖励之和称为累积折扣奖励η。
η=r(s0,a0)+γr(s1,a1)+…+γtr(st,at)+…=
∑∞t=0γtr(st,at)(1)
强化学习的目标是智能体通过与环境交互,学习一个与环境相适应的最优策略π*,使得智能体在与环境交互的过程中最大化累积折扣奖励η。
π*=arg maxπEuclid Math TwoEApπ[η]=arg maxπEuclid Math TwoEApπ[∑∞t=0γtr(st,at)](2)
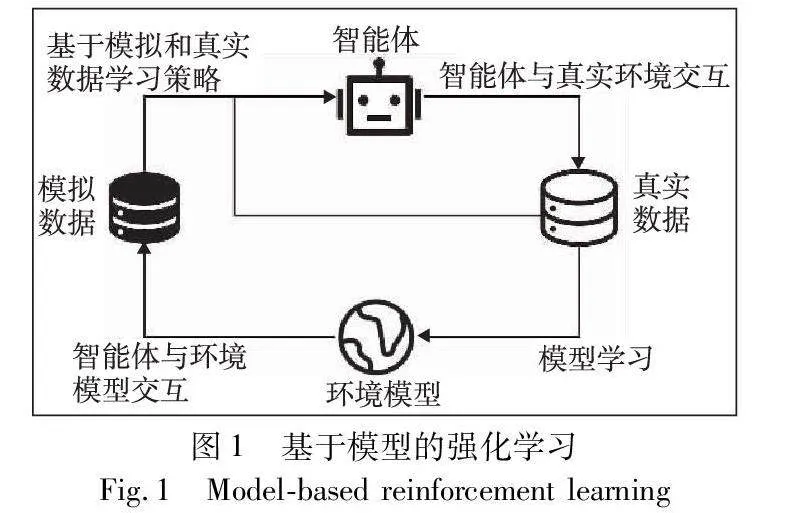
基于模型的强化学习(model-based reinforcement learning,MBRL)[9]通常用神经网络学习一个环境模型Pθ(s′|s,a),其中θ是神经网络参数,然后利用该环境模型来帮助智能体训练和决策,从而求解MDP,如图1所示。
由于基于模型的强化学习算法具有一个环境模型,智能体可以额外与环境模型进行交互,对真实环境中样本的需求量往往会减少,所以通常会比无模型的强化学习算法具有更低的样本复杂度。
1.2 价值感知模型
以往基于模型的强化学习(MBRL)的研究主要将模型学习和模型利用视为两个独立的过程。比如,基于模型的策略优化(model-based policy optimization,MBPO)[12]是深度强化学习中一种热门的基于模型的强化学习,该方法中的策略学习使用了SAC(soft actor-critic)方法[18],具体算法如下:
算法1 基于模型的策略优化
输入:智能体策略π的初始网络,智能体交互的真实环境,环境模型pθ的初始网络。
输出:学习到的智能体策略π*网络。
a)初始化环境模型参数pθ,真实环境数据集合Denv,模型数据集合Dmod
b)循环
c) 通过环境数据来训练模型参数pθ
d) 循环时间步T次
e) 根据策略π与环境交互,并将交互的轨迹添加到Denv中
f) 循环E步 //E为模型推演次数
g) 从Denv中均匀随机采样一个状态st
h) 以st为初始状态,在模型中使用策略π进行k步的推演,并将产生的轨迹添加到Dmod中
i) 循环结束
j) 循环
k) 基于模型数据Dmod和真实环境数据Denv使用SAC算法来更新策略参数π
l) 直到策略参数π收敛
m) 循环结束
n)直到模型参数pθ收敛
算法1中,环境模型的学习过程,即步骤c)的优化目标是利用真实环境数据Denv训练得到预测更精确的环境模型,在方法上采用最大似然估计方法训练环境模型;模型的利用过程,即步骤j)~ l)的优化目标是得到高累积奖励的策略。由于两者的优化目标不一致,导致即使环境模型在训练数据机上预测误差较小,也不能总是得到具有高累积奖励的最优策略[15]。
为了解决目标不匹配问题,Farahmand等人[15]提出了价值感知模型学习(value-aware model learning,VAML),设计新的损失函数,在环境模型学习过程中加入状态价值信息,如下所示。
lossV(,p,μ)=Euclid SymbolrCpμ(s,a)|Euclid SymbolrCpp(s′|s,a)V(s′)ds′-Euclid SymbolrCp(s′|s,a)V(s′)ds′ |2dsda(3)
式(3)表明,VAML的损失函数是最小化真实环境和模型环境的单步价值估计,μ表示状态-动作对的分布,V(s)表示状态价值函数,Euclid SymbolrCpp(s′|s,a)V(s′)ds′表示真实环境下的价值估计,Euclid SymbolrCp(s′|s,a)V(s′)ds′表示模型环境下的价值估计。可以看出,VAML的损失函数取决于价值函数V(s)的确切值,但是在实践中则是通过深度神经网络进行估计,导致损失函数产生偏差。
1.3 基于价值梯度模型的强化学习
Voelcker等人[16]进一步改进了VAML,考虑价值函数的梯度,提出了基于价值梯度模型(value-gradient weighted model,VaGraM)。假设模型预测的下一个时刻的状态和真实环境的下一时刻状态s′接近,值函数可以通过泰勒展开来近似,用V^s′表示围绕参考点s′展开的值函数的泰勒展开,得到
V^s′(s)≈V(s′)+(sV(s)|s′)T(s-s′)(4)
代入到式(3)中,化简后得到VaGraM的损失函数:
lossV^=∑{si,ai,s′i}∈D(Euclid SymbolrCpθ(s′|si,ai)((sV(s)|s′i)T(s′-s′i))ds′)2(5)
VaGraM的损失函数与VAML的损失函数不同,式(5)不依赖于未知状态样本的价值的具体数值,只需要在训练过程中知道价值网络的梯度信息。通过将价值信息融入模型学习中,环境模型可以更合理地迭代更新参数,比传统的最大似然方法更具鲁棒性,特别是当模型能力不足以完全表征环境特征时。如果使用确定性环境模型,即s′m=fθ(s,a),那么VaGraM的损失函数可以进一步化简成
∑i((sV(s)|s′i)T(fθ(si,ai)-s′i))2(6)
2 基于二阶价值梯度模型的强化学习
在基于价值梯度模型的强化学习基础上,为了加快环境模型训练的收敛速度,进一步提升算法的学习效率,本文提出基于二阶价值梯度模型,并采取新的状态采样策略。
2.1 二阶价值梯度模型
VaGraM方法基于一个前提,即模型预测的下一个时刻的状态和真实环境的下一个时刻状态s′接近,使用一阶泰勒展开公式。现使用二阶泰勒展开公式,写成向量的形式,如下:
f(x)≈f(x0)+f(x0)(x-x0)+12(x-x0)TH(x0)(x-x0)(7)
其中:H(x)为海森矩阵。令s=x,s′=x0,V(s)=f(x)得到
V^s′(s)≈V(s′)+(sV(s)|s′)T(s-s′)+12(s-s′)TH(s′)(s-s′)(8)
其中:s是状态向量;V^s′表示围绕参考点s′展开的值函数的二阶泰勒展开。那么,新的损失函数可以表示为
loss=∑i((sV(s)|s′i)T(fθ(si,ai)-s′i)+12(fθ(si,ai)-si)TH(s′i)(fθ(si,ai)-si))2(9)
改进的损失函数,即式(9)与VaGraM的损失函数相比,VaGraM方法采用一阶泰勒展开,仅考虑价值函数在给定点的一阶梯度信息,因此只能线性近似;而改进后的损失函数通过引入二阶泰勒展开,考虑了价值函数在给定点的二阶梯度信息,能够提供更准确的函数逼近,尤其当状态空间S是高维度时(在复杂工业过程控制场景下,观测到的状态空间往往是高维度空间),这种更精确的函数逼近能力在基于模型的强化学习中对于准确环境建模至关重要。在基于强化学习的工业过程控制中,真实环境中常常存在噪声和不确定性,当噪声或不确定性引起环境动态发生剧烈变化时,一阶泰勒展开表现较差,因为它只能提供线性的估计,无法近似更复杂的价值函数(欠拟合);相比之下,二阶泰勒展开考虑了价值函数的二阶梯度信息,能够更好地适应噪声和不确定性,从而得到更鲁棒的环境模型。
在实际的深度神经网络训练时,如果直接计算海森,会带来不必要的复杂性。这里采用海森矩阵的快速乘法[19],只需要O(W)次操作就可以直接算出xTH,并且能够快速进行反向传播,大大加快了深度神经网络的训练速度。
2.2 状态采样策略
为了更好地利用环境模型,受到Goyal等人[20]的启发,本文希望更多地从高价值的状态而不是随机选择的状态作为起点,利用环境模型展开推演。如此,智能体可以更大几率地学习快速到达高价值状态的策略;同时,为了兼顾智能体也能学习低价值状态下的策略,本文采用Boltzmann概率分布[21]:
p(s)∝eβV(s)(10)
其中:β是控制高价值状态比例的超参数;V(s)是通过智能体的价值网络对状态价值的估计值。
2.3 算法流程
结合二阶价值梯度模型和状态采样策略,本文提出的基于二阶价值梯度模型的强化学习算法整体流程如算法2所示。
算法2 基于二阶价值梯度模型的强化学习
输入:智能体策略π的初始网络,价值函数vψ的初始网络,智能体交互的真实环境,环境模型pθ的初始网络。
输出:学习到的智能体策略π*网络。
a)初始化真实环境数据集合Denv、模型数据集合Dmod
b)循环N步 //N为训练轮数,超参数
c) 循环
d) 从环境数据集合Denv中取一批次训练数据(s,a,r,s′),通过式(9)计算环境模型的损失函数值lossvψ
e) 更新环境模型的网络pθ参数:θ←θ-αdlossvψdθ
f) 直到pθ收敛
g) 循环时间步T次 //T为智能体与真实环境交互回合数
h) 根据策略πφ与环境交互,并将交互的轨迹添加到Denv中
i) 循环E步 /*E为模型推演次数,即智能体与模拟环境交互回合数*/
j) 从Denv中根据式(10)的概率分布,随机采样一个状态st
k) 以st为初始状态,在模型中使用策略π进行k步的推演,并将生产的轨迹添加到Dmod中
l) 循环结束
m) 循环
n) 基于模型数据Dmod和真实环境数据Denv的并集,使用SAC算法来更新策略参数π,同时更新价值网络vψ
o) 直到策略参数π收敛
p) 循环结束
q) 结束循环
算法2的步骤c)~ f)是改进的二阶价值梯度模型的训练过程,步骤j)是基于Boltzmann概率分布的采样方法。整个算法的框架是基于MBPO算法,步骤i)~l)是MBPO算法的短分支推演[12],比如参数k可以取值1~5,这样做可以使模型的累积误差不至于过大,从而保证最后的采样效率和策略表现,如图2所示。
3 应用实例研究
为了充分验证基于二阶价值梯度模型强化学习的有效性,本文选择来自OpenAI Gym[22]的公共强化学习实验环境以及两个工业场景的仿真环境进行实验。
3.1 公共强化学习实验环境
OpenAI Gym是一个用于开发和比较强化学习算法的公共的开源工具包。它提供了一系列标准化的环境,供研究人员和开发者测试和评估强化学习算法的性能。OpenAI Gym[22]提供统一的接口,使得不同的强化学习算法可以在相同的环境下进行比较。
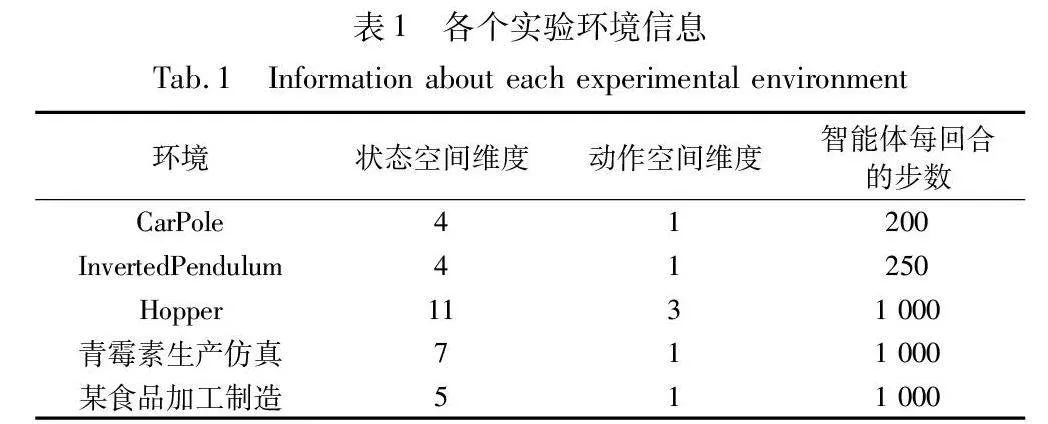
本文从OpenAI Gym中选取3个MuJoCo[23]实验环境,分别是CarPole、InvertedPendulum和Hopper。其中:CarPole是一个经典的控制实验环境,模拟小车上的杆子,任务目标是通过控制小车的水平位置使得杆子保持平衡并防止倒下;InvertedPendulum(倒立摆)也是一个经典的控制实验环境,模拟了一个倒立的摆杆,摆杆通过一个关节与支撑物相连,任务目标是通过控制关节的力矩使得摆杆保持垂直和平衡;Hopper模拟了一个单腿跳跃机器人,用于测试强化学习算法在控制单腿机器人上的表现。CarPole、InvertedPendulum和Hopper的环境参数如表1前3行所示。
3.2 工业场景仿真环境
3.2.1 青霉素生产仿真环境
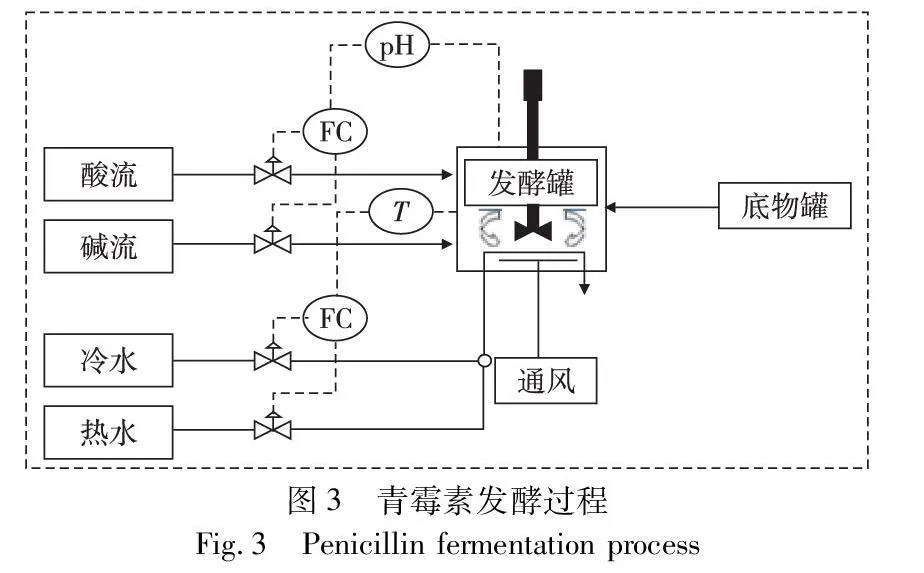
在适宜的培养基、pH值、温度和通气搅拌等发酵条件下,青霉素菌种进行生长和合成青霉素的代谢活动。青霉素仿真过程是通过模拟一系列步骤来模拟青霉素的发酵过程[24]。为了实现这一过程,使用了多种设备和工具,包括发酵罐、冷水调节器、热水调节器、搅拌器和酸碱液调节器。图3展示了青霉素生产发酵的整体流程[25]。
青霉素发酵过程是一个非线性、多输入和强耦合的过程,涉及到9个初始变量和7个过程变量。在青霉素合成过程中,最佳温度为298 K,最佳pH值为6.5~6.9。本文选择青霉素合成期作为实验背景,并以温度控制为实验内容。为了进行青霉素生产仿真,本文采用了基于MATLAB/Simulink环境的仿真平台[26],并将其转换为Python语言的Gym框架下的青霉素生产仿真环境。
建立青霉素生产仿真过程的MDP模型如下:
a)状态空间S。在确保pH稳定控制的条件下,考虑到生化反应中各个状态值之间的紧密关系和密切相关性,选择了当前时刻的氧气浓度、菌体浓度、青霉素浓度(单位为g/L)、培养基体积(单位为L)、二氧化碳浓度、发酵器反映温度以及温度差七个变量作为构成状态空间的重要参数。这些参数的选择是基于它们在青霉素生产过程中的关键作用,并且它们的变化可以直接反映出发酵过程中的动态变化和效果。
b)动作空间A。基于实际控制原则的考虑,选取冷水值作为实际控制过程中的被控变量,并将其作为主要的控制动作。这样的选择是基于对系统稳定性和性能优化的追求,同时也考虑到冷水值在控制过程中的重要作用。
c)状态转移概率P。假设在青霉素生产仿真过程中,状态转移概率是固定且未知的。
d)奖励函数r。控制的目标是将温度保持在297.5 K。因此,奖励函数如下:
reward=50 if |err|<σ1100if σ1≤|err|<σ2-errif σ2≤|err|<σ3-1000if |err|≥σ3(11)
其中:err是当前温度与297.5 K的差值;σ1、σ2、σ3是温度差的阈值。
e)折扣因子γ。实验中折扣因子保持不变,γ=0.99。
3.2.2 某食品加工制造仿真环境
某食品加工制造的控制是根据出口含水率的波动实时调整运行指标中的动作,以适应不同的工况条件[27, 28]。具体的过程是,原料在滚筒的轴向倾角作用下进入系统,滚筒的旋转带动原料不断翻滚、松散搅拌,并持续向出料端滚动。在蒸汽的作用下,使用双介质喷嘴进行增湿水的雾化喷射,以促进原料均匀吸收水分。图4展示了完整的工艺流程[27]。
选取某品牌食品加工制造过程作为验证环境,在实际控制过程中,加水量作为控制动作被选为受控变量。原料中的含水率是控制干燥过程的关键指标,18.5%是控制目标。
建立某食品加工制造仿真过程的MDP模型如下:
a)状态空间S。采用过去5个时间步的出口含水率的5个变量作为构成状态空间的重要参数。
b)动作空间A。因为工艺要求,在获取5个时间步的出口含水率后,加水实际值作为控制动作。
c)状态转移概率P。假设在某食品加工制造仿真过程中,状态转移概率是固定且未知的。
d)奖励函数r。针对本实验中某个品牌的食品原料,笔者的控制目标是含水率为一个定值,即18.5%,在合理范围内,两者的误差要尽可能小。同时,为了避免因大动作调控导致过程振荡,将动作值限定在[-0.2,0.2],奖励函数为
reward=-∑5i=1abs(yi-18.5)(12)
其中:y是5个时间步的出口含水率,是5×1维的向量,即y=(y1,y2,y3,y4,y5)T。
e)折扣因子γ。实验中折扣因子保持不变,γ=0.99。
3.3 对比方法
为了验证基于二阶价值梯度模型的强化学习方法的有效性,与四种主流的控制领域的方法作对比,这些方法包括预测控制方法、无模型强化学习方法、有模型强化学习方法,是近几年比较先进的深度强化学习方法。
a)PETS概率集成(probabilistic ensembles with trajectory sampling,PETS)[29],一种经典的模型预测控制(model predictive control,MPC)方法,它没有显式构建一个策略(即一个从状态到动作的映射函数)。
b)SAC[18]是一种经典的无模型强化学习算法。在无模型的强化学习算法中,SAC是非常高效的算法,它学习一个随机性策略,在不少标准环境中取得了领先的成绩。
c)MBPO[12]是深度强化学习领域中最重要的基于模型的强化学习算法之一,它已经成为基于模型的强化学习算法的基本框架。
d)VaGraM[16]是一种结合了状态价值函数梯度的基于模型的强化学习。
上述方法中,PETS是传统的基于模型的预测控制方法,SAC是无模型强化学习方法的代表,MBPO是基于模型的强化学习方法的代表,以VaGraM为代表的方法改进了MBPO方法的模型损失函数。选择这些方法进行对比,可以充分验证基于二阶价值梯度模型的强化学习方法的有效性。本文的所有实验、所有对比方法的超参数都根据原论文的建议调整至最优。
同时,本文采用累积奖励、均方误差(mean squared error, MSE)、平均绝对误差(mean absolute error, MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)、均方根误差(root mean squared error,RMSE)作为评价指标。
3.4 公共强化学习实验环境对比实验
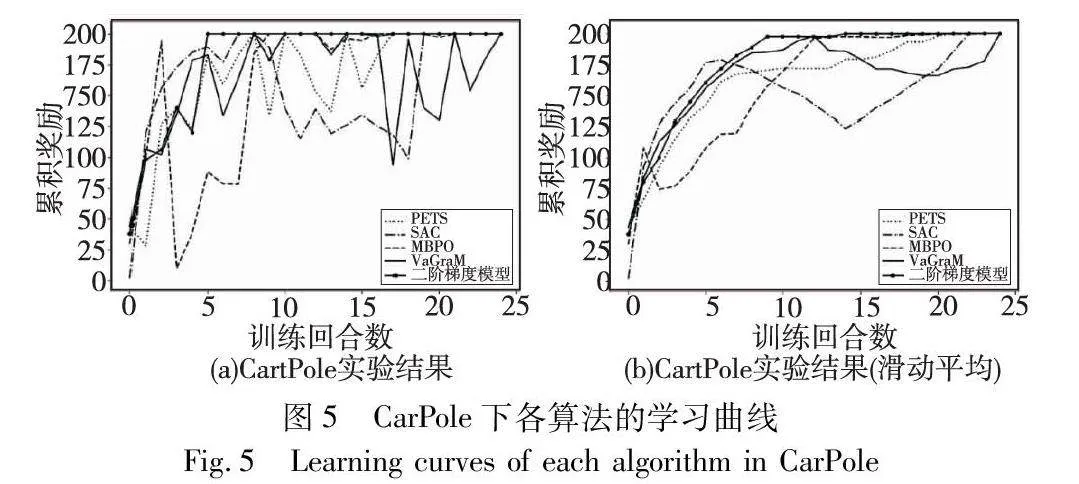
在公共强化学习实验环境中,将基于二阶价值梯度模型的强化学习方法和上述四种方法进行实验,得到实验结果并进行比较,结果如图5~7所示,分别对应CarPole、InvertedPendulum和Hopper三个实验环境。三个实验环境的学习曲线显示,与其他算法相比,基于二阶价值梯度模型的强化学习方法在达到最大奖励值方面表现出快速收敛,并始终保持较高的累积奖励曲线,波动起伏不大。这表明在学习效率方面,基于二阶价值梯度模型优于其他方法,在学习速度和渐近性能方面,优于先前的基于模型和无模型算法。
Hopper实验状态空间和动作空间维度比较高,并且动作变量是连续型变量,Hopper属于复杂控制任务,比较容易区分各个算法的性能。图7显示,基于二阶价值梯度模型的强化学习方法比VaGraM方法更加稳定、收敛速度更快,分析原因,这是因为二阶梯度方法对于曲率较大或变化较快的函数,能够表征更多的梯度信息,在同一次训练回合内更新效率更高;同时由于采用了状态采样策略,智能体在高价值状态时能更大概率学习到更好的控制策略。
此外,从模型预测性能上比较各个方法的性能。如表2所示,VaGraM和基于二阶价值梯度模型的方法在模型误差上明显强于其他方法,模型的误差减少40%以上,基于二阶价值梯度模型的方法比VaGraM方法模型性能上略有提高,提高10%左右。这说明价值感知模型的损失函数在加入了状态价值函数的信息后,要比单纯使用似然损失函数更具鲁棒性,尤其是模型容量不足以表达真实环境时;二阶价值梯度模型相比于一阶价值梯度模型,虽然收敛速度快,但是最终的模型误差相差不是很大。
3.5 工业场景仿真环境对比实验
为了进一步验证基于二阶价值梯度模型强化学习的有效性,本文在两个工业场景的仿真环境下进行对比实验,一个是青霉素生产仿真环境,另一个是某食品加工制造仿真环境。
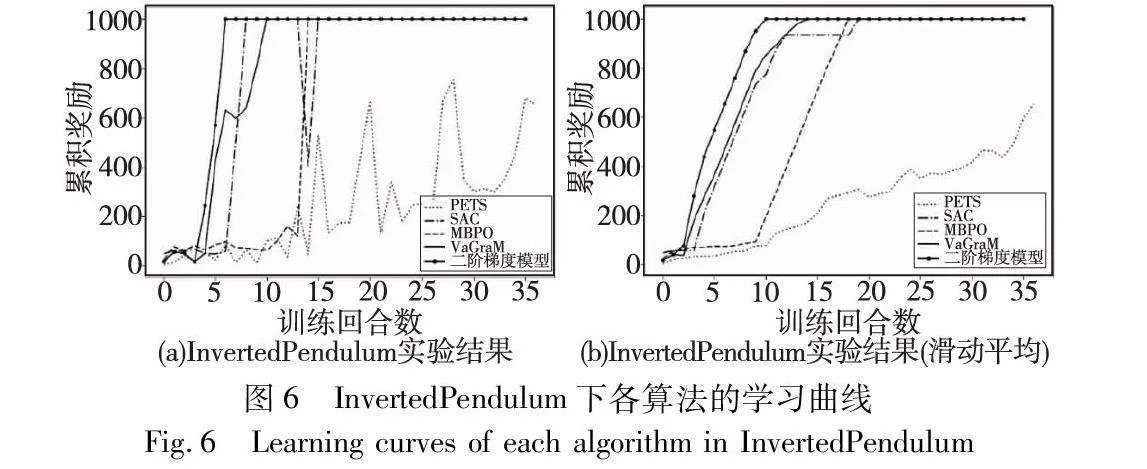
3.5.1 学习曲线对比
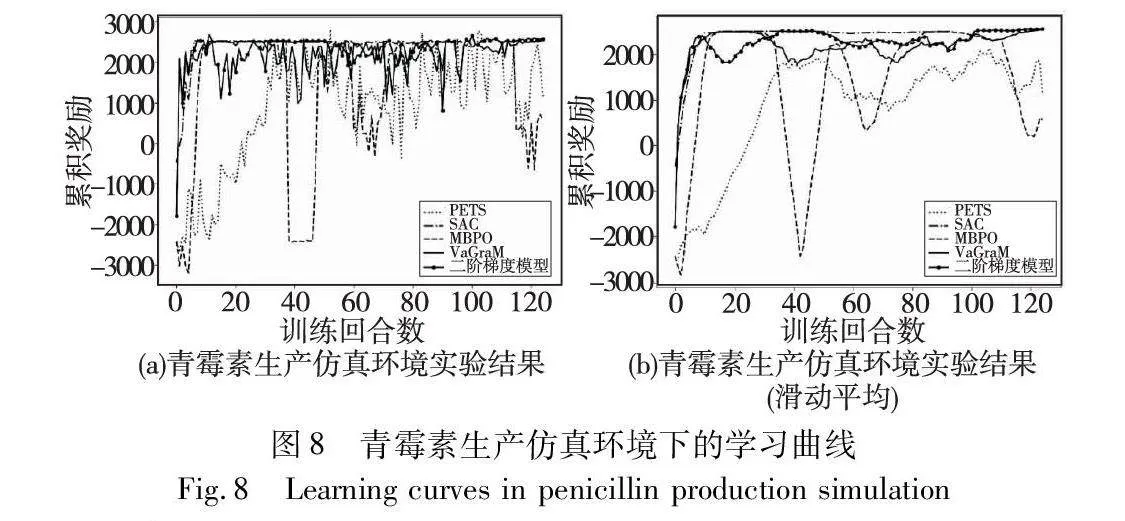
学习曲线如图8、9所示,从实验结果上来看,经典的基于模型的控制方法如PETS,虽然最终能够达到最大的累积奖励,但是学习效率最差、收敛速度最慢;经典的无模型强化学习算法如SAC,由于采样效率低,导致策略学习速度慢于基于模型的强化学习方法,尤其是在复杂环境,比如高维度状态下;MBPO作为典型的基于模型的强化学习方法,学习效率低于基于价值感知模型的方法;在某食品加工制造仿真中VaGraM方法和基于二阶价值梯度模型的方法比较接近,在青霉素生产仿真中,性能低于后者;无论是在青霉素仿真还是某食品加工制造仿真中,基于二阶价值梯度模型的强化学习方法都能最快到达累积奖励,并保持稳定,说明该方法在VaGraM基础上改进后具备更好的鲁棒性。
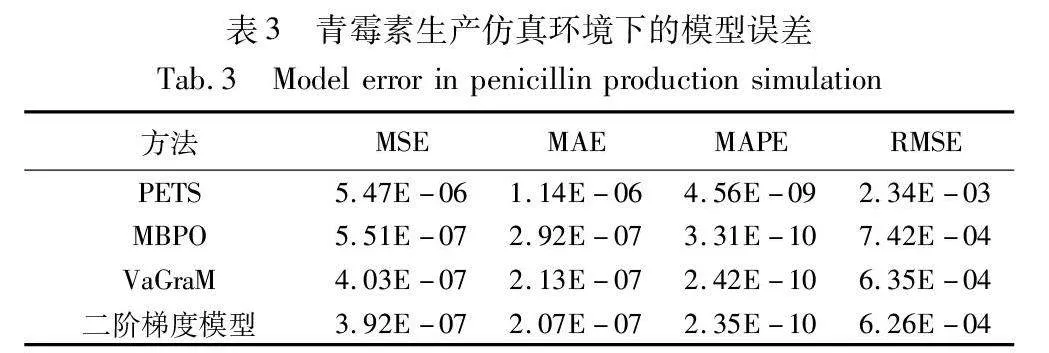
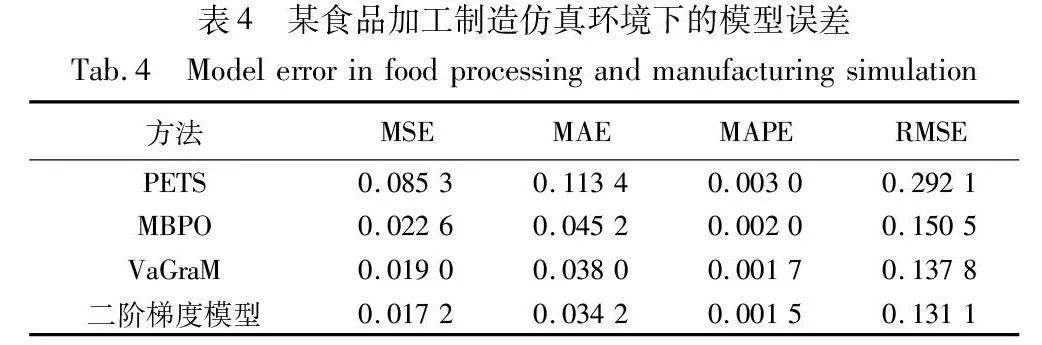
3.5.2 模型误差对比
训练结束后,利用环境模型与真实环境作对比,统计模型误差,统计结果如表3、4所示。在青霉素生产仿真中,价值感知模型比MBPO误差减少20%以上,二阶价值梯度模型比VaGraM提升3%,提升效果不明显。分析原因是,前者使用二阶价值梯度,在训练过程中可以加快模型的收敛速度,但是不影响最终收敛后的模型误差,两者模型误差接近。在某食品加工制造仿真中,价值感知模型性能提升显著。
3.5.3 控制效果对比
在训练完成后,使用策略网络在工业过程仿真环境中进行控制实验。对于青霉素生产仿真实验,初始发酵温度设定为298.35 K,并使用经过PETS、SAC、MBPO、VaGraM和基于二阶价值梯度模型方法得到的策略网络来分别控制冷水流量值,目标是使青霉素发酵环境更加适宜和稳定,温度调整目标是297.5 K。实验结果如图10所示,VaGraM方法和基于二阶价值梯度模型方法首先到达297.5 K附近,并能保持稳定,其中基于二阶价值梯度模型方法在接近297.5 K后,比VaGraM更加稳定,没有出现波动。
对于某食品加工制造仿真实验,初始含水率为18.5%,目标设定也为18.5%,使用经过PETS、SAC、MBPO、VaGraM和基于二阶价值梯度模型方法得到的策略网络来分别控制加水值。实验结果如图11所示,VaGraM方法和基于二阶价值梯度模型方法能够稳定在18.5%附近,振动幅度接近,使用其他三种方法训练出的智能体控制效果偏差较大。基于二阶价值梯度模型方法的调节粒度更加精细,相比于PETS、SAC和MBPO等经典的强化学习方法,无论是偏差量还是整体的平稳性都有显著提升。以上两个工业过程仿真实验说明,基于二阶价值梯度模型方法在工业过程控制中具备良好的控制性能。
4 结束语
针对工业控制过程的非线性、强耦合、高延时等特点,本文在基于价值梯度模型的强化学习基础上,提出了基于二阶价值梯度模型的方法,旨在加快环境模型训练的收敛速度,提高算法的学习效率。同时尝试采用新的状态采样策略,以高价值的状态作为起点,利用环境模型展开推演。
为了验证基于二阶价值梯度模型强化学习的有效性,本文选择了OpenAI Gym公共强化学习实验环境以及两个工业场景的仿真环境进行实验。实验结果显示,与其他算法相比,基于二阶价值梯度模型的强化学习方法在达到最大奖励值方面表现出快速收敛,并始终保持较高的累积奖励的特点。两个工业过程仿真实验也进一步证明了该方法在工业过程控制中具备良好的控制性能。
综上所述,基于二阶价值梯度模型的强化学习方法在加快环境模型训练收敛速度、提高学习效率以及实现工业过程控制方面表现出了良好的性能。这些发现为进一步研究和应用基于二阶价值梯度模型的强化学习算法提供了有力支持。未来的工作将侧重于进一步提升价值感知模型的性能,如引入注意力机制模块等,并探索该方法在其他领域的应用。
参考文献:
[1]柴天佑, 程思宇, 李平, 等. 端边云协同的复杂工业过程运行控制智能系统[J]. 控制与决策, 2023, 38(8): 2051-2062. (Chai Tianyou, Cheng Siyu, Li Ping, et al. Intelligent system for operation-al control of complex industrial process based on end-edge-cloud collaboration[J]. Control and Decision, 2023, 38(8): 2051-2062.)
[2]乔俊飞, 黄卫民, 丁海旭, 等. 复杂工业过程特征建模方法及应用研究[J]. 控制与决策, 2023, 38(8): 2063-2078. (Qiao Junfei, Huang Weimin, Ding Haixu, et al. Research on feature modeling method for complex industrial process and its application[J]. Control and Decision, 2023, 38(8): 2063-2078.)
[3]罗傲, 肖文彬, 周琪, 等. 基于强化学习的一类具有输入约束非线性系统最优控制[J]. 控制理论与应用, 2022, 39(1): 154-164. (Luo Ao, Xiao Wenbin, Zhou Qi, et al. Optimal control for a class of nonlinear systems with input constraints based on reinforcement learning[J]. Control Theory & Applications, 2022, 39(1): 154-164.)
[4]张丹阳. 一种基于改进好奇心机制的深度强化学习方法及其在过程控制中的应用[D]. 北京:北京化工大学, 2023. (Zhang Danyang. A deep reinforcement learning method based on improved curiosity mechanism and its application in process control[D]. Beijing: Beijing University of Chemical Technology, 2023.)
[5]马帅, 傅启明, 陈建平, 等. 基于双池DQN的HVAC无模型优化控制方法[J]. 智能科学与技术学报, 2022, 4(3): 426-444. (Ma Shuai, Fu Qiming, Chen Jianping, et al. HVAC model-free optimal control method based on double-pools DQN[J]. Chinese Journal of Intelligent Science and Technology, 2022, 4(3): 426-444.)
[6]纪志勇, 袁逸萍, 巴智勇, 等. 基于多动作深度强化学习的纺机制造车间调度方法[J]. 计算机应用研究, 2023, 40(11): 3247-3253. (Ji Zhiyong, Yuan Yiping, Ba Zhiyong, et al. Multi-action deep reinforcement learning based scheduling method for spinning machine manufacturing shop floor[J]. Application Research of Computers, 2023, 40(11): 3247-3253.)
[7]任安妮, 周大可, 冯锦浩, 等. 基于注意力机制的深度强化学习交通信号控制[J]. 计算机应用研究, 2023, 40(2): 430-434. (Ren Anni, Zhou Dake, Feng Jinhao, et al. Attention mechanism based deep reinforcement learning for traffic signal control[J]. Application Research of Computers, 2023, 40(2): 430-434.)
[8]宋江帆, 李金龙. 用于连续时间中策略梯度算法的动作稳定更新算法[J]. 计算机应用研究, 2023, 40(10): 2928-2932,2944. (Song Jiangfan, Li Jinlong. Action stable updating algorithm for policy gradient methods in continuous time[J]. Application Research of Computers, 2023, 40(10): 2928-2932,2944.)
[9]Moerland T M, Broekens J, Plaat A, et al. Model-based reinforcement learning: a survey[J]. Foundations and Trends in Machine Learning, 2023, 16(1): 111-118.
[10]Nagabandi A, Kahn G, Fearing R S, et al. Neural network dynamics for model-based deep reinforcement learning with model-free fine-tuning[C]//Proc of IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE Press, 2018: 7559-7566.
[11]Campbell R H, Czechowski K, Erhan D, et al. Model-based reinforcement learning for Atari[C]//Proc of International Conference on Learning Representations. 2019: 6-9.
[12]Janner M, Fu J, Zhang M, et al. When to trust your model: model-based policy optimization[C]//Proc of the 33rd International Confe-rence on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc., 2019:12519-12530.
[13]Lai Hang, Shen Jian, Zhang Weinan, et al. Bidirectional model-based policy optimization[C]//Proc of the 37th International Conference on Machine Learning.[S.l.]: ML Research Press, 2020: 5618-5627.
[14]Shen Jian, Zhao Han, Zhang Weinan, et al. Model-based policy optimization with unsupervised model adaptation[C]//Proc of the 34th International Conference on Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc.,2020: 2823-2834.
[15]Farahmand A, Barreto A, Nikovski D. Value-aware loss function for model-based reinforcement learning[C]//Proc of International Conference on Artificial Intelligence and Statistics.[S.l.]: ML Research Press, 2017: 1486-1494.
[16]Voelcker C, Liao V, Garg A, et al. Value gradient weighted model-based reinforcement learning[C]//Proc of International Conference on Learning Representations. 2022.
[17]Puterman M L. Markov decision processes[M]//Simulation-Based Algorithms for Markov Decision Processes. London :Springer, 1990: 331-434.
[18]Haarnoja T, Zhou A, Abbeel P, et al. Soft actor-critic: off-policy maximum entropy deep reinforcement learning with a stochastic actor[C]//Proc of International Conference on Machine Learning.[S.l.]: ML Research Press, 2018: 1861-1870.
[19]Pearlmutter B A. Fast exact multiplication by the Hessian[J]. Neural Computation, 1994, 6(1): 147-160.
[20]Goyal A, Brakel P, Fedus W, et al. Recall traces: backtracking models for efficient reinforcement learning[C]//Proc of International Conference on Learning Representations. 2018.
[21]Zhang Nan, Ding Shifei, Zhang Jian, et al. An overview on restricted Boltzmann machines[J]. Neurocomputing, 2018, 275: 1186-1199.
[22]Palanisamy P. Hands-on intelligent agents with OpenAI Gym: your guide to developing AI agents using deep reinforcement learning[M].[S.l.]: Packt Publishing Ltd., 2018.
[23]Todorov E, Erez T, Tassa Y. MuJoCo: a physics engine for model-based control[C]//Proc of IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ: IEEE Press, 2012: 5026-5033.
[24]李云龙, 唐文俊, 白成海, 等. 青霉素生产工艺优化及代谢分析提高产量[J]. 中国抗生素杂志, 2019, 44(6): 679-686. (Li Yunlong, Tang Wenjun, Bai Chenghai, et al. Optimization of the feeding process and metabolism analysis to improve the yield of penicillin[J]. Chinese Journal of Antibiotics, 2019, 44(6): 679-686.)
[25]邓绍斌, 朱军, 周晓锋, 等. 基于局部策略交互探索的深度确定性策略梯度的工业过程控制方法[J]. 计算机应用, 2022, 42(5): 1642-1648. (Deng Shaobin, Zhu Jun, Zhou Xiaofeng, et al. Industrial process control method based on local policy interaction exploration-based deep deterministic policy gradient[J]. Journal of Computer Applications, 2022, 42(5): 1642-1648.)
[26]叶凌箭, 程江华. 基于MATLAB/Simulink的青霉素发酵过程仿真平台[J]. 系统仿真学报, 2015, 27(3): 515-520. (Ye Lingjian, Cheng Jianghua. Simulator of penicillin fermentation process in MATLAB/Simulink environment[J]. Journal of System Simulation, 2015, 27(3): 515-520.)
[27]彭慧, 朱雪靖, 周晓锋, 等. 基于TVA-TCN的制造过程关键参数多步预测方法[J]. 控制与决策, 2022, 37(12): 3321-3328. (Peng Hui, Zhu Xuejing, Zhou Xiaofeng, et al. Multi-step prediction method for key parameters of manufacturing process based on TVA-TCN[J]. Control and Decision, 2022, 37(12): 3321-3328.)
[28]Bi Suhuan, Zhang Bin, Mu Liangliang, et al. Optimization of tobacco drying process control based on reinforcement learning[J]. Drying Technology, 2020, 38(10): 1291-1299.
[29]Chua K, Calandra R, McAllister R, et al. Deep reinforcement lear-ning in a handful of trials using probabilistic dynamics models[C]//Proc of the 32nd International Conference onNeural Information Processing Systems. Red Hook, NY: Curran Associates Inc., 2018:4759-4770.
