精英引导和信息交互的多目标狼群算法
2024-08-15陈福军吴润秀肖人彬王晖赵嘉










摘 要:鉴于狼群算法在单目标优化问题上的优越表现,结合狼群的生物习性将其运用到多目标优化问题上,提出一种精英引导和信息交互的多目标狼群算法(MOWPA-EGII)。首先,提出精英引导策略,利用外部档案中的精英狼和当前子种群的头狼共同引导种群移动,让人工狼均匀地分布在整个搜索空间,增强算法的全局搜索能力;其次,设计信息交互机制,模拟狼群捕猎过程中的信息传递,具有不同优势的个体可以相互传递信息,保证狼群的捕猎效率,提高算法勘探Pareto最优解的能力;最后,加入变异算子,扰动人工狼的移动方向,让算法跳出局部最优,增强算法的局部搜索能力。为了验证MOWPA-EGII的有效性,将其与5种经典算法和10种新近算法进行比较,结果表明MOWPA-EGII拥有良好的收敛性和多样性,证明了所提算法具有较好的优化性能。
关键词:狼群算法; 多目标优化; 精英引导; 信息交互; 变异算子
中图分类号:TP18 文献标志码:A
文章编号:1001-3695(2024)08-022-2404-08
doi:10.19734/j.issn.1001-3695.2023.12.0587
Multi-objective wolf pack algorithm with elite guidance and information interaction
Chen Fujun1a,1b, Wu Runxiu1a,1b, Xiao Renbin2, Wang Hui1a,1b, Zhao Jia1a,1b
(1. a.School of Information Engineering, b.Nanchang Key Laboratory of IoT Perception & Collaborative Computing for Smart City, Nanchang Institute of Technology, Nanchang 330099, China; 2.School of Artificial Intelligence & Automation, Huazhong University of Science & Techno-logy, Wuhan 430074, China)
Abstract:In consideration of the superior performance of the wolf pack algorithm on single-objective optimization problems, combining with the biological habits of wolves to apply it to multi-objective optimization problems, this paper proposed a multi-objective wolf pack algorithm with elite guidance and information interaction(MOWPA-EGII) . Firstly, MOWPA-EGII proposed an elite guidance strategy, using the elite wolf in the external file and the head wolf of the current sub-population to jointly guide the population movement, so that the artificial wolves uniformly distributed in the whole search space, and the strategy enhanced the global search ability of the algorithm; Secondly, it designed the information interaction mechanism to simulate the information transfer in the wolf hunting process, so that individuals with different advantages could transfer information to each other to ensure the hunting efficiency of the wolves and improved the ability of the algorithm to explore the optimal solution of the Pareto; Finally, it added the mutation operator to perturb the moving direction of the artificial wolves, so as to let the algorithm jump out of the local optimum and enhance the local search ability of the algorithm. In order to verify the effectiveness of MOWPA-EGII, comparing it with 5 classical algorithms and 10 recent algorithms, and the results show that MOWPA-EGII possesses good convergence and diversity, which proves that the present algorithm has a better optimization performance.
Key words:wolf pack algorithm; multi-objective optimization; elite guidance; information interaction; variational operator
0 引言
目前工程应用中存在大量需要同时优化多个目标的问题,这些问题被称为多目标优化问题(multi-objective optimization problem,MOP)[1]。MOP中不同的目标之间相互冲突或竞争,即改善一个目标会导致其余的几个目标退化,这使得难以找到全局最优解。因此,需要对各个目标进行权衡,找到一组非劣解的集合,即Pareto最优解集[2]。
在处理多目标优化问题时,尽管有混合整数线性规划法、ε约束法和凸优化法等[3],但这些方法通常需要目标函数满足一些特定的条件,而且这些数学优化方法面对复杂MOP时往往无法建立精确的数学表达式,即使建立了精确表达式计算的代价也十分昂贵。为了解决这类问题,出现了许多受生物启发的多目标进化算法(multi-objective evolutionary algorithm,MOEA)[4]。Coello等人[5]提出多目标粒子群算法(multi-objective particle swarm optimization,MOPSO),通过不断更新粒子的速度和位置以及最优解的信息,寻找Pareto最优解集,从而解决多目标优化问题。Hedayatzadeh等人[6]提出多目标人工蜂群算法(multi-objective artificial bee colony,MOABC),模拟蜜蜂的搜索和交流行为,将优秀的解信息传递给其他个体,使整个种群逐步向全局最优解靠近。Cheng等人[7]提出一种基于分解的多目标蚁群算法(multi-objective ant colony optimization based on decomposition,MoACO/D),利用切比雪夫法将一个大问题分解为多个子问题,并将蚁群分解为多个重叠的子种群,每个子种群分别对应一个子问题进行寻优,同时维护聚合信息素轨迹和聚合启发式矩阵。Deb等人[8]提出基于参考点的非支配排序方法的多目标进化优化算法(evolutionary many-objective optimization algorithm using reference point based nondominated sorting approach,NSGA-Ⅲ),利用参考点引导非支配个体寻优,更好地反映个体在多目标函数下的性能,并使用快速非支配排序和特殊拥挤度距离来维护种群的多样性。Yang等人[9]提出了多目标萤火虫算法(multi-objective firefly algorithm,MOFA),模拟自然界中萤火虫的发光行为和相互作用,通过优化搜索过程来搜索多个目标解的集合。Mirjalili等人[10]提出了多目标灰狼算法(multi-objective grey wolf optimizer,MOGWO),模拟灰狼群体的追逐和领导行为,将问题的解空间映射为灰狼个体的搜索空间,领导者引领狼群进行位置更新,寻找Pareto最优解。这些经典的多目标优化算法,因其创造性设计和优异性能在多目标优化领域稳步发展,为解决工程中的MOP提供了很多思路,也激励了新算法的诞生。
吴虎胜等人[11]通过分析狼群的捕猎与分工,提出了一种新的狼群算法(wolf pack algorithm,WPA)。该算法由于在全局搜索和局部开发上具有较强的能力,被广泛应用于各种工程实践。如:张鸿运等人[12]利用狼群算法解决多无人机协同任务规划问题;徐祐民等人[13]利用狼群算法优化支持向量神经网络;She等人[14]利用改进的狼群算法提高求解高度非线性黑箱函数结构可靠度问题的精度和效率;贾光耀等人[15]利用改进的狼群算法提出一种交通子区边界控制方案。此外还应用于最大熵图像分割问题、路径规划问题和船舶避碰问题等。上述算法在各自的工程应用中都取得了较好的优化结果,充分体现了狼群算法较好的全局收敛性和计算鲁棒性,以及在函数优化领域表现出广阔的应用前景。虽然狼群算法在处理单目标优化问题上的发展与应用非常成熟,但在处理多目标优化问题上却很少表现。鉴于狼群算法在单目标优化问题上的突出表现,它在多目标优化问题上丰富与发展就非常有意义,于是有学者将狼群算法应用到多目标优化领域中。如:荀洪凯等人[16]提出一种多目标启发式狼群算法用于解决不相关并行机分批调度问题;陶翼飞等人[17]将多目标狼群算法应用于机场行李导入问题;李小川等人[18]提出了一种文化狼群算法用于解决多目标带时间窗的车辆路径问题。上述算法为狼群算法求解多目标优化问题提供了解决方案,优化结果较好,但它们都是用于解决离散问题,并不能用于解决连续优化问题。为此,对于狼群算法在多目标连续优化问题上的应用,本文结合狼群的生物习性提出一种精英引导和信息交互的多目标狼群算法(multi-objective wolf pack algorithm based on elite guidance and information interaction,MOWPA-EGII)。MOWPA-EGII具有如下特点:a)精英引导[19]策略,子种群中的头狼和档案中的精英狼共同引导人工狼,可以扩大种群搜索范围,防止算法陷入局部最优;b)信息交互机制,模拟捕猎过程中的信息传递,人工狼之间进行信息交互,让优良信息在种群中传递,保证算法搜索效率的同时维持种群多样性;c)变异算子[20],前期可以减弱人工狼对头狼的盲目跟从,后期增强算法的局部搜索能力。在上述三种策略的相互作用下,避免了算法在寻优过程中陷入局部最优,增强了算法的勘探能力,提高了算法的收敛性和分布性。
1 相关基础知识
1.1 多目标优化问题
对于一个具有n个决策变量和m个目标的多目标优化函数,以最小化问题为例,可建立多目标优化问题的模型:
min y=F(x)=(f1(x),f2(x),…,fm(x))
s.t.gi(X)≤0 i=1,…,p
hj(X)=0 j=1,…,q
x=(x1,x2,…,xn)∈X∈Rny=(y1,y2,…,ym)∈Y∈Rm(1)
其中:x表示决策向量;X表示n维决策空间;y表示目标向量,Y表示m维目标空间;g*(X)表示有p个不等式约束;h(X)表示有q个等式约束。对于xi,xj∈X,若xj的目标函数都不大于且至少存在一个小于xi的目标函数,则xi Pareto支配xj,记为xixj。若x*∈X且x*不受任意个体xi支配,则称x*为非支配个体。决策空间中所有非支配个体的集合称为Pareto最优解集(Pareto set,PS),该解集构成目标空间中的Pareto前沿(Pareto front,PF)。
1.2 狼群算法
狼群算法是模拟自然界中狼群捕食行为而提出的一种新的群智能算法。该算法模拟狼群捕猎并抽象出三种行为:游走行为、召唤行为和围攻行为。狼群中有明确的分工,探狼负责游走探寻猎物,猛狼负责围攻捕猎,头狼负责决策指挥。按照“强者生存”的机制,保证种群的生存与发展。
WPA的规则和行为描述如下:
a)头狼产生规则:将目标空间中适应度值最优的人工狼视为头狼。头狼不参与人工狼的捕食行为,直至更加优秀的人工狼取代它。若存在适应度值相同的头狼则随机选择一匹人工狼为头狼。
b)游走行为:探狼i在解空间Xi=(x1,x2,x3,…,xN)中进行游走,选择其探索的h个方向中猎物气味浓度Yip最大的方向前进,重复游走行为,直至探狼i感知的气味浓度Yi优于头狼Ylead,或者游走次数T>Tmax。探狼i的游走位置更新公式如下:
xpid=xid+stepda×sin(2π×p/h)(2)
其中:xid为探狼i在d(d=1,2,3,…,D)为空间中的初始位置,stepda为游走步长,h∈[hmin,hmax]且为整数,p(p=1,2,3,…,h),xpid为第p个方向上的空间位置。
c)召唤行为:游走之后,头狼会召唤N-S-1匹猛狼,猛狼i收到头狼的召唤会迅速按照向头狼奔袭。猛狼i的奔袭公式如下:
xk+1id=xkid+stepdb×gkd-xkid|gkd-xkid|(3)
其中:xkid为猛狼i在第k次迭代时的空间位置;gkd为第k次迭代头狼的空间位置;stepdb为奔袭步长。
在奔袭的过程中,猛狼i若未能取代头狼,则会继续奔袭,直至它们之间的距离d<dnear,此时转入围攻行为。头狼与猛狼之间的距离判定如下:
dnear=1D·ω·∑Dd=1|maxd-mind|(4)
其中:ω为距离判定因子;mind和maxd为第d个维度变量的下界和上界。
d)围攻行为:在头狼召唤,猛狼奔袭后,把头狼位置视为猎物位置,狼群进行捕猎。围攻的位置更新公式如下:
xk+1id=xkid+λ×stepdc×|gkd-xkid|(5)
其中:λ∈[-1,1]的随机数;stepdc为人工狼的围攻步长。
e)三种步长之间的关系:探狼的游走步长stepda、猛狼的奔袭步长stepdb以及人工狼的攻击步长stepdc,在d为空间中的关系如下:
stepda=stepdb2=2×stepdc=|maxd-mind|S(6)
其中:S为步长因子,表示人工狼在搜寻猎物过程的精细程度。
f)更新机制:采用“强者生存”的更新机制,保证种群的生存与发展。将适应度值较差的R匹人工狼进行淘汰,然后再随机生成R匹人工狼,其中,R∈[N/2γ,N/γ]且为整数,γ为种群的更新比例因子。
2 精英引导和信息交互的多目标狼群算法
WPA虽然在单目标优化问题上表现出良好的收敛性和计算鲁棒性,但应用于求解多目标优化问题时还存在如下问题:a)人工狼和头狼易出现聚集现象;由于WPA本质是头狼引导人工狼朝其所在的方向进行搜索,在求解多目标优化问题时人工狼和头狼易聚集在某一区域,使算法陷入局部最优;b)种群中的优良信息易流失;WPA在狼群捕猎过程中未涉及内部的信息交互,易使种群中的优良信息无法传递,最终导致种群优良信息流失和多样性较差;c)种群进化停滞;随着种群的不断进化,个体之间的差异逐渐变小,使得种群进化停滞。针对上述问题,本文提出一种精英引导和信息交互的多目标狼群算法(MOWPA-EGII)。
2.1 精英引导策略
WPA中人工狼会向当前种群的头狼学习,在求解单目标优化问题时,这种学习方式会加速算法收敛,快速寻找到最优解,但在求解多目标优化问题时,种群的快速收敛往往会导致算法陷入局部最优,出现人工狼和头狼聚集现象,即问题a)。通过分析发现,出现这种聚集现象是由于WPA在执行围攻行为和召唤行为后人工狼总会直线朝头狼所在方向移动,最终导致算法陷入局部最优。针对于此,提出一种精英引导策略:首先,种群通过快速非支配排序[21]选出非支配等级为1的人工狼为头狼,将头狼所支配的人工狼划分为一个子种群,面对多匹头狼支配同一人工狼问题,按照欧氏距离就近分配;其次,引入外部档案,让外部档案中的精英狼和当前子种群的头狼共同引导狼群前进捕猎,让狼群前期均匀分布在搜索空间,防止产生聚集现象,增强算法的全局搜索能力。经过精英引导策略改进后,召唤行为中式(3)更新为
xk+1id=xkid+ω1×stepdb×gkSub-xkid|gkSub-xkid|+ω2×stepdb×gkElite-xkid|gkElite-xkid|(7)
围攻行为中式(5)更新为
xk+1id=xkid+ω3×λ×stepdc×|gkSub-xkid|+
ω4×λ×stepdc×|gkElite-xkid|(8)
其中:gkSub为子种群中的头狼,gkElite为外部档案中任意一匹精英狼,ω1,ω2∈[0,1]且∑2i=1ωi=1,ω3,ω4∈[0,1]且∑4i=3ωi=1;其余变量含义和式(3)(5)中一致。
为了验证提出的精英引导策略的有效性,对采用精英引导策略前后的实验结果进行比较。图1展示了算法采用头狼引导策略和精英引导策略,获得ZDT1问题的Pareto前沿,图中红色圆圈表示算法求得的Pareto前沿,黑色线条表示ZDT1的真实Pareto前沿(见电子版)。图1(a)为初始种群;(b)为采用头狼引导策略的算法在ZDT1问题上迭代20次的Pareto前沿;(c)为采用精英引导策略的算法在ZDT1问题上迭代20次的Pareto前沿。由图1可知,采用头狼引导策略时种群出现了严重的聚集现象,通过观察发现算法得到前沿主要集中在真实Pareto前沿的左半部分,算法的收敛性与分布性较差;采用精英引导策略后,种群中的聚集现象得到了较大改善,算法得到的前沿较为均匀地分布在真实Pareto前沿上,该策略虽然在增加全局搜索能力时牺牲了一定的精细搜索能力,但种群的分布性得到了较大的改善。
2.2 信息交互机制
在生物界中,狼群会使用嗅觉和视觉来追踪猎物的位置,一旦发现猎物,它们会发出特定的叫声向同伴传递信息,其他狼会迅速向其靠拢。狼群会一起追逐猎物,相互合作,采取不同的位置来包围猎物,阻止猎物逃跑,最终在狼群的相互协作与信息传递下成功捕猎。基于这一生物学原理,本文在狼群算法的基础上设计信息交互机制。WPA的每一次迭代视为一次捕猎,但狼群实际并未捕获到猎物,即没有寻找到最优解,也就不存在“强者生存,弱者淘汰”。事实上,算法的每次迭代是向猎物靠近的过程,狼群中不同的个体会相互传递信息,最终捕获到猎物。所以针对问题b),重视不同个体相互传递的优势信息,设计信息交互机制。该机制可以让优良信息在种群中传递,防止因为淘汰造成的优良信息流失,维护了种群多样性。狼群的信息交互如下:
xk+1id=xkid+t×rand×(xk(n-i+1)d-xkid)+α×ε(9)
其中:i∈[1,N]且为整数。t为抖动因子,取值为式(10)。rand∈[0,1]。xk(n-i+1)d为狼群中编号n-i+1的人工狼。α×ε为扰动项,α是扰动步长因子,α∈[0,1],ε是服从高斯分布、均匀分布或其他分布中提取的随机数向量。α×ε扰动项,一方面,可以防止t=1时导致学习与被学习人工狼之间过于相似,陷入局部最优;另一方面,可以扩大搜索范围。
t=rand×(ubb-1)+1 rand≤0.5rand×(-1+ubb)-ubbrand>0.5(10)
其中:ubb=1.5-(k-1)×1.5/Maxit,k为迭代次数,Maxit为最大迭代次数,rand∈[0,1]。
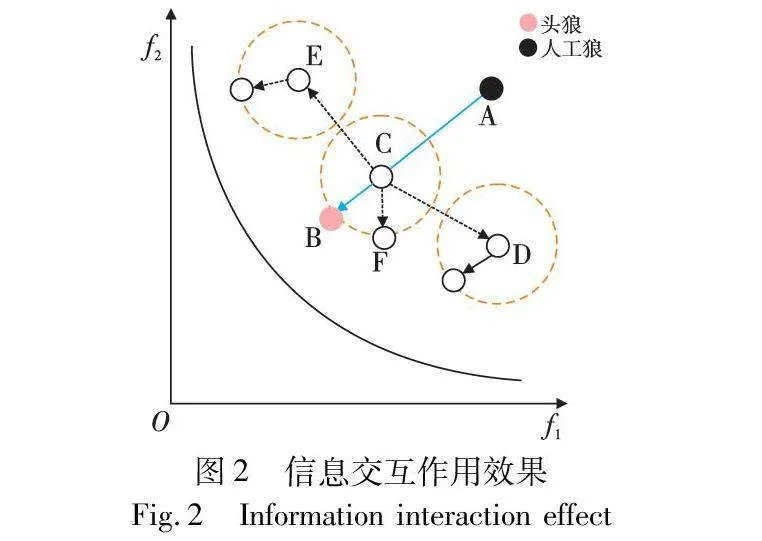
以二目标为例,图2展示了采用信息交互机制的模型简化图,黑球为人工狼,红球为头狼,白球为移动后可能的位置。在学习和被学习人工狼相同的情况下,当不加入抖动因子和扰动项时,搜索后可能位于线段AB上的某一点C;当加入抖动因子和扰动项时,在抖动因子的作用下,点C可能会位于线段AB上方E点或线段AB下方的D点。在扰动项的作用下,点C可能会出现在以C为圆心的橙色圆内的某一点F,点D和E扰动后的可能位置如图所示(见电子版)。由图2可以看出,搜索范围显著增大,在保留各人工狼优良信息的同时有效提升算法探索到真实Pareto前沿的概率。
按照上述更新式(9),会产生与原种群P大小N一样的新种群Q,将新旧种群合并,然后按照快速非支配排序,先选择前n个非支配层Zi(i=1,2,3,…)的人工狼,使得Z1+Z2+Z3+…+Zn<N,当Z1+Z2+Z3+…+Zn+Zn+1>N,对于第Zn+1层的人工狼进行拥挤度距离排序,选择拥挤度大的前N-(Z1+Z2+…+Zn)匹人工狼。这样可以很好保留人工狼身上的优良信息,避免优秀人工狼被淘汰,从而增加搜索效率。
2.3 变异算子
针对问题c),随着种群的不断进化,人工狼之间的差异逐渐变小,种群中可用信息变少,这时会使种群进化停滞。此时,通常会引入变异算子,变异算子是对种群的父代个体进行随机变化来形成子代,其目的是保持种群的多样性和避免过早收敛。因此本文加入单维选择变异算子,人工狼i每次进行完游走行为、召唤行为和围攻行为后,按照一种随迭代次数动态递减的变异概率Pm随机对人工狼i的某一维进行变异,这里Pm=1-k/Maxit,若选中第d维分量,变异可定义为
xd′i=rand×(ud-ld)+ud rand≤Pmxdirand>Pm(11)
其中:d为人工狼i的第d维分量;ud和ld分别为人工狼i第d维分量的上限和下限;k为迭代次数;Maxit为最大迭代次数,式中的ud和ld定义如下:
ud=xdi+(1-kMaxit)×(u-l)
ld=xdi-(1-kMaxit)×(u-l)(12)
通过对变异前后进行比较,若xd′i支配xdi则进行替换;若xdi支配xd′i则不进行替换;若xdi和xd′i互不支配,是否替换判断如下:
xdi=xd′i rand≤0.5xdirand>0.5(13)
算法前期,迭代次数k较小,可以使人工狼有较大的位置波动,变异算子和精英引导策略相互作用,可以减弱人工狼对于头狼的盲目跟从,使人工狼较为均匀地搜索决策空间,增强算法的全局搜索能力,改善种群的分布性,有效避免种群进化停滞,维护种群的多样性;算法后期,人工狼之间的差异变小,即种群通过非支配排序后非支配等级都为1,种群中的人工狼都变为头狼,精英引导策略会失效。此时变异算子随着迭代次数k增大,可以使人工狼有较小的位置波动,该算子使人工狼注重局部搜索,使变异后产生的新解以更大的概率逼近真实的Pareto前沿,保证了算法的收敛性。
2.4 算法流程
输入:决策变量的维度D;区间为[U,L];种群的大小N;最大迭代次数Maxit;最大游走次数Tmax;距离判定因子ω;步长因子S。
输出:Pareto最优解集。
结合前文描述的多个策略,给出MOWPA-EGII算法步骤。
a)种群和参数初始化。初始化决策变量的维度D,区间为[U,L],种群的大小N,最大迭代次数Maxit,最大游走次数Tmax,距离判定因子ω,步长因子S,生成N匹人工狼xi。
b)计算每匹人工狼的适应度值。
c)对种群进行预处理。找到位于非支配等级为1的头狼各自所支配的人工狼,每匹头狼和它支配的人工狼划为一个子种群,并将非支配等级为1的人工狼存于外部档案。
d)游走行为。对于除头狼外的人工狼按照式(2)执行游走行为,直至人工狼在解空间中的位置优于支配它的头狼,或达到最大游走次数T>Tmax,则转步骤e)。
e)召唤行为。头狼发起召唤,人工狼按照式(7)进行奔袭,若在奔袭的过程中人工狼在解空间中的位置优于其所在子种群的头狼,则取代该头狼,替代它并发起召唤行为;若劣于其所在子种群的头狼,人工狼继续奔袭,直至d<dnear,则转步骤f)。
f)围攻行为。人工狼按照式(8)对猎物发起攻击。
g)种群变异。对执行完上述三种行为的人工狼按照式(11)进行变异,若变异后的人工狼,支配变异前的人工狼,则进行替换;若互不支配,则按照式(13)判断是否替换;否则不进行替换。
h)外部档案的更新与维护。将种群中的精英解存入外部档案,若档案的大小超过规定的大小N,则先对档案进行去重,然后按照拥挤度距离进行删除。
i)判断是否达到最大迭代次数Maxit,若达到则转至步骤j),否则转至步骤c)。
j)输出Pareto最优解集。
2.5 算法时间复杂度分析
N为种群大小,NA为外部档案大小,m为目标空间维数。WPA中游走、召唤和围攻行为以及更新机制都是串行,所以WPA的时间复杂度近似为O(N)。MOWPA-EGII基于狼群算法,对N匹人工狼在m个目标空间进行预处理,确定支配关系、存写档案和划分子种群,此过程通过快速非支配排序并行处理,故间复杂度近似为O(m×NlogN)。精英引导策略,对N匹人工狼执行式(7)(8),时间复杂度为O(N)。信息交互机制,对2N匹人工狼进行快速非支配排序,对超过种群大小N的个体按照拥挤距离淘汰,时间复杂度为O(2Nlog2N)+O(m×N)。变异算子,对N匹人工狼的某一维度进行变异,时间复杂度为O(N)。档案维护,采用拥挤距离对档案进行维护,NA的大小通常与种群大小N相等,最大时间复杂度为O(m×2N),综上,MOWPA-EGII的时间复杂度为O(mNlogN)。
3 实验结果与分析
3.1 多目标测试函数集
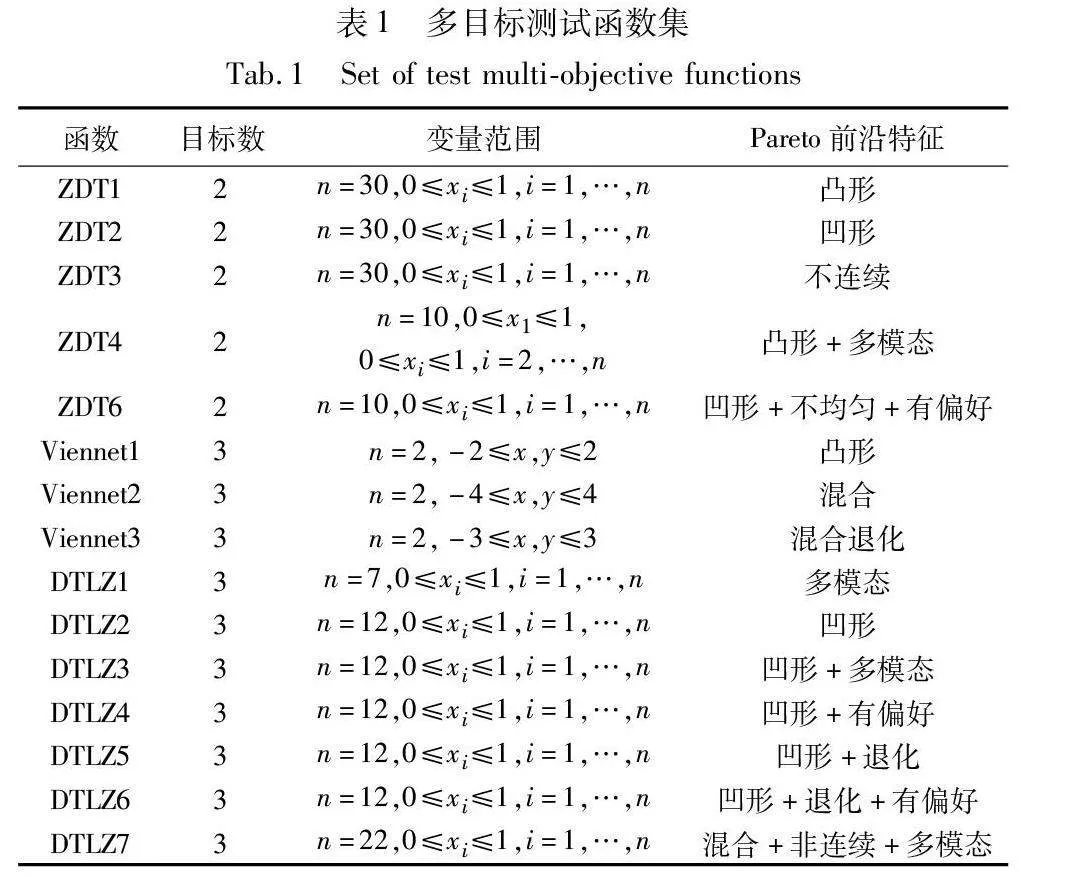
多目标测试函数集选择。为了验证MOWPA-EGII的有效性,本文选取了15个基准MOP测试函数,测试MOWPA-EGII面对不同类型MOP问题时算法的性能。测试函数集包括5个2-目标ZDT系列的测试函数,3个3-目标Viennet系列测试函数,以及7个3-目标DTLZ系列测试函数。多目标测试函数集的特征和性质如表1所示。
3.2 性能指标
性能指标选择。反世代距离IGD(inverted generational distance),反映真实Pareto前沿到算法得到的近似Pareto前沿的距离。通过计算真实Pareto前沿和近似Pareto前沿之间的距离可以反映一个算法收敛性和多样性。一般情况下,某算法的IGD值越小说明该算法获得的Pareto前沿收敛性和多样性越好。IGD可以通过式(14)计算得到。
IGD(X,P*)=min∑x*∈P*d(x*,X)|P*|(14)
其中:P*表示真实Pareto前沿上均匀分布的点集,|P*|表示P*内真实点集的个数,d(x*,X)表示x*∈P*的解到X中解的最小欧氏距离。
3.3 信息交互机制的有效性分析
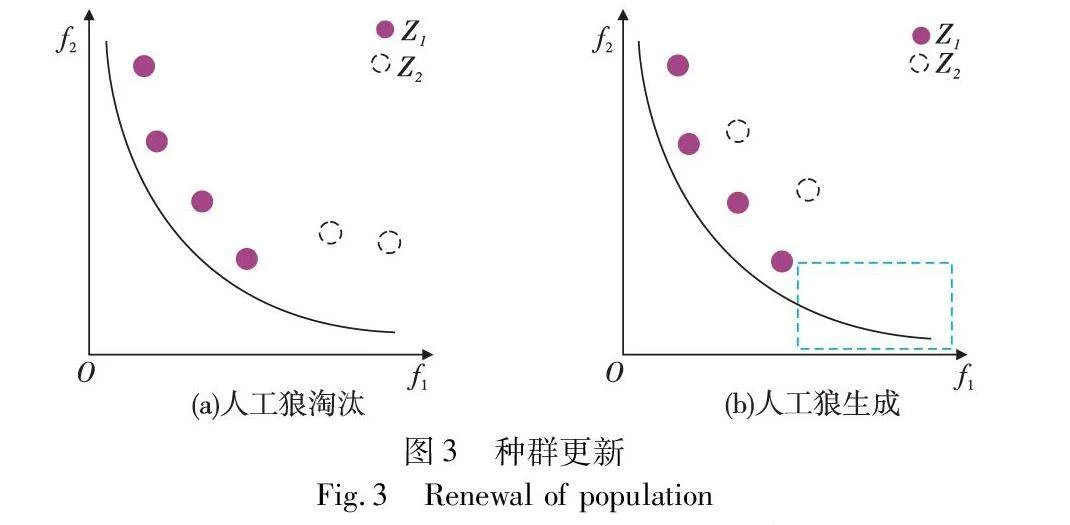
信息交互机制比强者生存机制具有更好的寻优效率和算法多样性,是因为强者生存机制是直接淘汰种群中较差的R匹人工狼,然后再随机生存R匹人工狼,这种随机很有可能使种群的优良信息流失,使种群进化变得缓慢和多样性缺失,最终会导致算法在目标空间中的分布为图3(b)所示状况。信息交互机制不会直接淘汰,而是按照式(9)重新生成和原种群大小相等的新种群,最后在目标空间中按照拥挤距离[21]淘汰,最终种群的分布状况会和图3(a)类似。因此信息交互机制可以较好地保持种群多样性。图3中Z1和Z2为非支配序后的非支配等级。
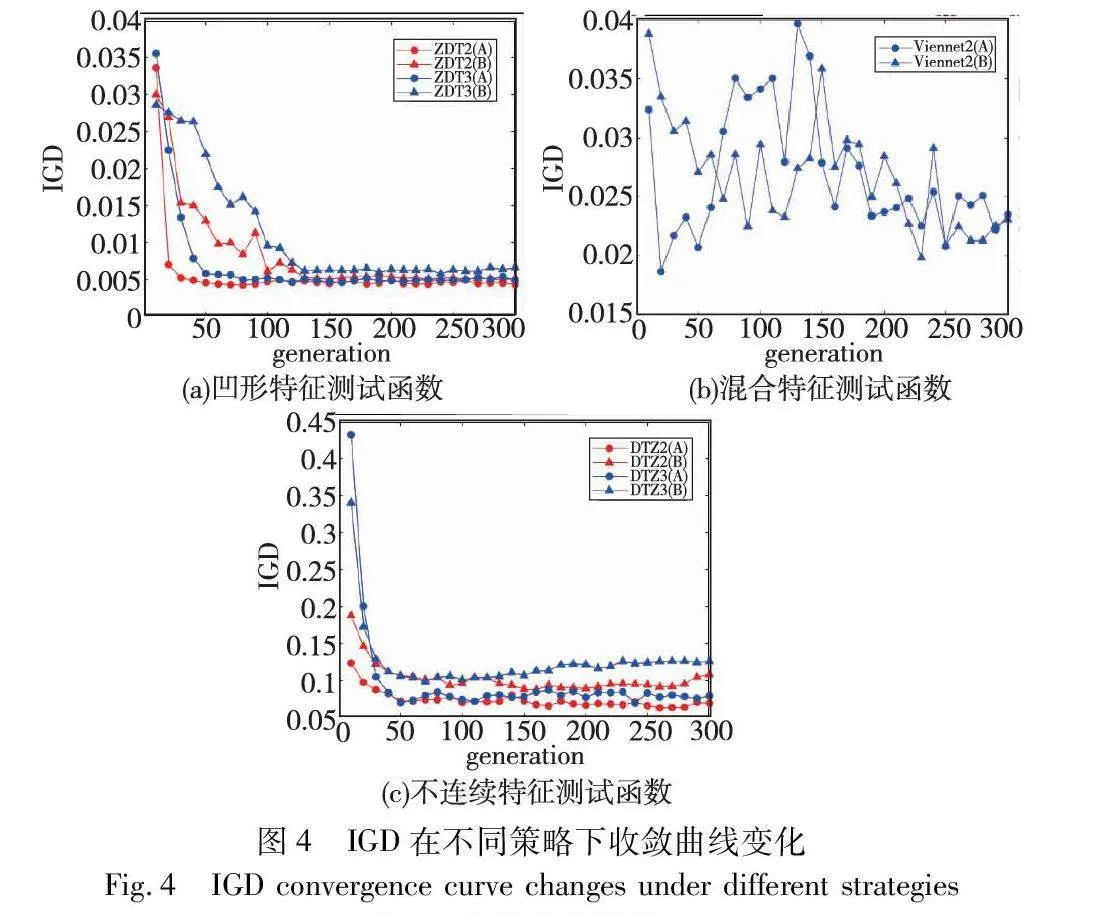
算法的多样性和寻优效率验证如下:实验将采用信息交互机制的算法命名为A,采用强者生存机制的算法命名为B,其他策略保持不变,画出算法A和B的IGD随迭代次数增加的收敛曲线图。选择不同Pareto前沿特征测试函数,凹形:ZDT2(二目标)和DTLZ2(三目标),不连续:ZDT3(二目标)和DTLZ7(三目标),混合:Viennet2。为了防止偶然性,在算法运行30次结果中,每间隔10迭代次数取一次IGD的平均值,总共取30组数据。算法随迭代次数增加IGD收敛曲线变化,如图4所示。从图4(a)可得出:算法A在ZDT2和ZDT3上迭代到80次左右IGD趋于平稳,而算法B在迭代到120次左右IGD趋于平稳,算法A比B收敛速度快且精度更高;从图4(b)可得出:算法A在迭代约180次时IGD趋于0.24左右,而算法B在迭代200次后IGD仍然有较大的波动,说明算法A比B收敛速度快且稳定;从图4(c)可得出:算法A和B在DTLZ2和DTLZ7上,虽然在迭代到大约50次后IGD都趋于稳定,但算法A的精度比B高。综上所述,算法采用信息交互机制能够较好地保留种群中的优良信息,取得了更快的收敛速度和更好的IGD值,说明算法采用信息交互机制可以拥有更好的多样性与寻优效率。
3.4 与经典多目标优化算法比较
为了测试MOWPA-EGII算法的性能,本节将MOWPA-EGII与5种经典多目标优化算法在ZDT、Viennet和DTLZ系列函数上进行比较,比较算法包括MOEA/D[22]、MOPSO[5]、NSGA-Ⅱ[21]、PSEA-Ⅱ[23]以及MOFA[9]。除MOFA算法参数取自原文献,其余算法参数与实验数据均来自PlatEMO平台,版本为PlatEMO4.1,如表2所示。表3给出了5种经典算法和MOWPA-EGII获得的IGD的平均值(mean)和标准差(std),每种算法最优值的总数(total),Friedman检验对各个算法进行秩(ranking)排名,以及各个多目标优化算法的最终排名(final rank)。其中,Friedman检验的秩均值越小表示算法的性能越好,表3中加黑数据为每种算法在同一种测试函数上的最优结果。为了保证实验的公平性,每种算法的种群规模设置为100,外部档案设置为100,对二目标测试函数评估10 000次,三目标测试函数评估20 000。为了防止偶然性的出现,对每个测试函数在每个算法独立运行30次取IGD均值。
根据表3,对算法的综合性能进行评估,在15个测试函数上,MOWPA-EGII取得9次最好的优化结果,MOEA/D和NSGA-Ⅱ取得1次最好的优化结果,PSEA-Ⅱ取得4次最好的优化结果,MOPSO和MOFA未取得最好的优化结果。其中,MOWP-EGII在ZDT系列测试函数上全部占优,Viennet3、DTLZ3、DTLZ6和DTLZ7优化结果占优;在Viennet1和Viennet2测试函数上虽然未取得最好的优化结果,但与优化结果最好的算法属于同一个数量级并且相差较小;在DTLZ2、DTLZ4和DTLZ5与取得最优结果的算法属于同一个数量级;在DTLZ1上优化结果较差。根据表3,所有算法的均值和方差结果表明MOWPA-EGII比其他5种经典算法具有更好的IGD性能。从Friedman检验结果可以看出,MOWPA-EGII的秩均值最小,NSGA-Ⅱ的秩均值次之,MOFA的秩均值最大,本文算法稳定性更好。综合上述分析,MOWPA-EGII的最优值总数(total)、秩均值(ranking)和最终排名(final rank)均位列第一,所以本文算法与其他5种经典多目标优化算法对比,表现出更好的优化结果,在收敛性和分布性上具有较好的性能,在不同的测试问题上具有更强的稳定性。为了直观地表现出MOWPA-EGII的性能,表4列出各算法在6个典型的测试函数上的Pareto前沿拟合图,二目标选取了Pareto前沿特征为连续(ZDT2)和非连续(ZDT3),三目标选取了Pareto前沿特征为混合(Viennet2)、面(DTLZ2)、线(DTLZ6)和非连续(DTLZ7)。拟合图中红色圆圈代表各算法求解到的Pareto前沿,黑灰色的点线和面表示该测试函数的真实Pareto前沿面。从表4中可以看出,MOWPA-EGII在二目标测试函数上收敛性和分布性具有较大的优势,在三目标测试函数上也具有较强的竞争力。
3.5 与新兴多目标优化算法比较
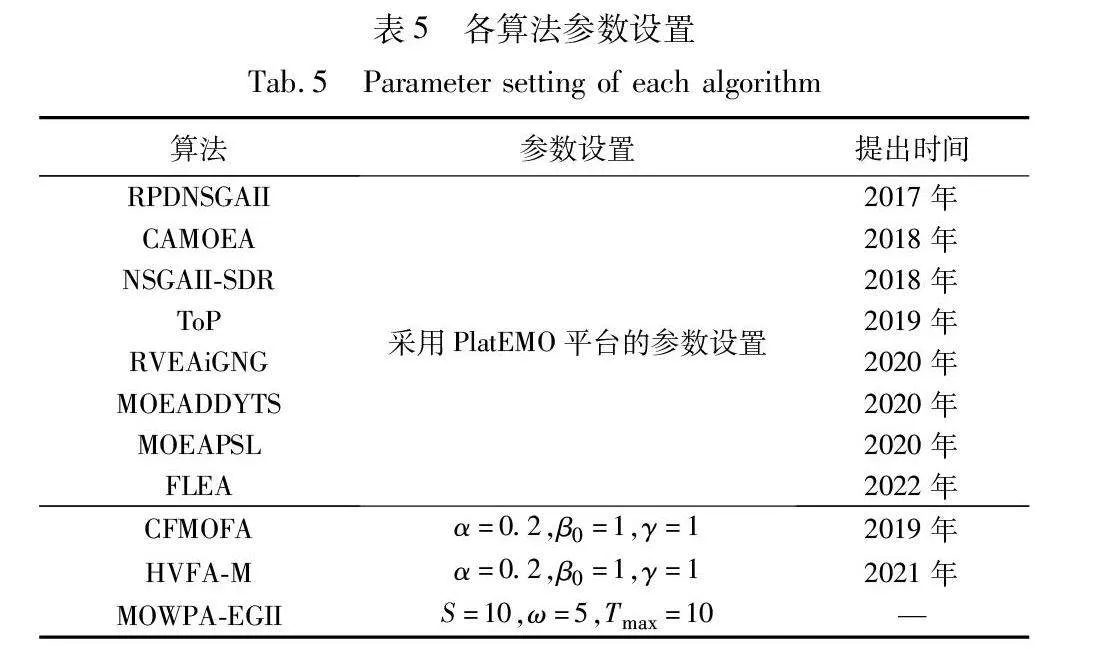
为了进一步测试MOWPA-EGII性能,本节将MOWPA-EGII与9种新兴算法作比较,比较算法包括:CAMOEA[24]、FLEA[25]、MOEADDYTS[26]、RPDNSGAII[27]、RVEAiGNG[28]、ToP[29]、NSGAII-SDR[30]、MOEAPSL[31]、CFMOFA[32]、HVFA-M[19],除CFMOFA和HVFA-M算法参数取自原文献,其余比较算法的参数和实验数据均来自PlatEMO平台,版本为PlatEMO4.1,算法的参数设置如表5所示。
本节测试函数选择如表6所示,评价指标、种群大小、外部档案大小和测试函数评估次数的设置上与3.3节相同。为了保证公平性,所有算法独立运行30次取IGD的均值。
根据表6可知,MOWPA-EGII在15个测试函数上取得7次最好的优化结果,CAMOEA取得4次最好优化结果,RPDNSGAII和RVEAiGNG分别取得2次最好的优化结果,TOP、NSGAIISDR、MOEAPSL、CFMOFA、HVFA-M、FLEA和MOEADDYTS未取得最好优化结果。
其中,MOWPA-EGII在ZDT系列测试函数、DTLZ3和DTLZ6上取得了最好的优化结果;在Viennet1、Viennet2、Viennet3、DTLZ2、DTLZ4、DTLZ5和DTLZ7上虽然未取得最好的优化结果,但与优化结果最好的算法属于同一数量级,且相差较小;在DTLZ1上的优化结果较差。根据表6,所有算法的均值和方差结果表明,MOWPA-EGII比其他10种新兴算法具有更好的IGD性能。从Friedman检验结果可以看出,MOWPA-EGII的秩平均值最小,CAMOEA秩均值次之,FLEA的秩均值最大,本算法稳定性更好。综合上述分析,MOWPA-EGII的最优值总数(total)、秩均值(ranking)和最终排名(final rank)均位列第一,所以本文算法与其他10种新兴多目标优化算法对比,表现出更好的优化结果,体现出其在求解MOPs时有较好的收敛性、多样性和稳定性。
综上,MOWPA-EGII在面对多数测试函数时,在收敛性和分布性上表现较好,获得较好Pareto前沿拟合效果,表现出较强的竞争力,是一种可靠的多目标优化算法。
4 结束语
优化问题在计算机领域一直是研究热点之一,本文鉴于狼群算法在求解单目标优化问题时的优越性,将狼群算法应用于多目标优化问题,提出一种精英引导和信息交互的多目标狼群算法(MOWPA-EGII)。MOWPA-EGII提出精英引导策略,通过快速非支配排序,选出非支配等级为1的人工狼视为头狼并存入外部档案,再将每匹头狼所支配的人工狼划为同一个子种群,人工狼在支配它的头狼和外部档案中的精英狼共同引导下在解空间中进行搜索,能够有效防止算法陷入局部最优;设计信息交互的机制,模拟狼群捕猎过程中的信息交流并向猎物一次次靠近的过程,该更新机制凸显人工狼个体之间的优势差异,它们可以相互学习,防止种群中的优良信息流失,保持种群的多样性;加入变异算子,能够有效帮助种群跳出局部,增强局部搜索的能力。将MOWPA-EGII与5种经典算法和10种新兴算法比较,通过在多目标领域的测试函数上作对比,并将实验结果进行Friedman检验,证明了MOWPA-RGII是解决多目标优化问题的一种行之有效的方法。然而在实验过程中发现,在处理多模态问题时,与其他算法对比略失竞争力。未来将进一步提高算法在多模态问题上的优化能力,并将算法应用于高维超多目标优化问题[33,34]和实际的工程应用[35]当中。
参考文献:
[1]Hua Yicun, Liu Qiqi, Hao Kuangrong, et al. A survey of evolutio-nary algorithms for multi-objective optimization problems with irregular Pareto fronts[J]. IEEE/CAA Journal of Automatica Sinica, 2021, 8(2): 303-318.
[2]Wang Liping, Pan Xiaotian, Shen Xiao, et al. Balancing convergence and diversity in resource allocation strategy for decomposition-based multi-objective evolutionary algorithm[J]. Applied Soft Computing, 2021, 100: 106968.
[3]刘佳, 王先甲. 系统工程优化决策理论及其发展战略[J]. 系统工程理论与实践, 2020, 40(8): 1945-1960. (Liu Jia, Wang Xianjia. The development of optimization and decision theory in systems engineering[J]. Systems Engineering-Theory & Practice, 2020, 40(8): 1945-1960.)
[4]胡智勇, 于千城, 王之赐, 等. 基于多目标优化的联邦学习进化算法[J]. 计算机应用研究, 2024, 41(2):415-420,437. (Hu Zhiyong, Yu Qiancheng, Wang Zhici, et al. Federated learning evolutionary algorithm based on multi-objective optimization[J]. Application Research of Computers, 2024, 41(2) :415-420,437.)
[5]Coello C A C, Pulido G T, Lechuga M S. Handling multiple objectives with particle swarm optimization[J]. IEEE Trans on Evolutionary Computation, 2004, 8(3): 256-279.
[6]Hedayatzadeh R, Hasanizadeh B, Akbari R, et al. A multi-objective artificial bee colony for optimizing multi-objective problems[C]//Proc of the 3rd International Conference on Advanced Computer Theory and Engineering. Piscataway,NJ:IEEE Press, 2010: 275-281.
[7]Cheng Jixang, Zhang Gexiang, Li Zhidan, et al. Multi-objective ant colony optimization based on decomposition for bi-objective traveling salesman problems[J]. Soft Computing, 2012, 16: 597-614.
[8]Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints[J]. IEEE Trans on Evolutio-nary Computation, 2013, 18(4): 577-601.
[9]Yang Xinshe. Multiobjective firefly algorithm for continuous optimization[J]. Engineering with Computers, 2013, 29: 175-184.
[10]Mirjalili S, Saremi S, Mirjalili S M, et al. Multi-objective grey wolf optimizer: a novel algorithm for multi-criterion optimization[J]. Expert Systems With Applications, 2016, 47: 106-119.
[11]吴虎胜, 张凤鸣, 吴庐山. 一种新的群体智能算法-狼群算法[J]. 系统工程与电子技术, 2013, 35(11): 2430-2438. (Wu Husheng, Zhang Fengming, Wu Lushan. New swam intelligence algorithm-wolf pack algorithm[J]. Systems Engineering and Electronics, 2013, 35(11): 2430-2438.)
[12]张鸿运, 王磊, 张旭,等. 考虑子系统执行能力的多无人机协同任务规划[J]. 系统工程与电子技术, 2023, 45(1): 127-138. (Zhang Hongyun, Wang Lei, Zhang Xu, et al. Multi-UAV cooperative mission planning considering subsystem execution capability[J]. Systems Engineering and Electronics, 2023, 45(1): 127-138.)
[13]徐祐民, 陈秀梅, 彭宝营, 等. 变负载直驱力矩电机位置误差预测模型研究[J]. 传感器与微系统, 2024, 43(1): 69-71,83. (Xu Youmin, Chen Xiumei, Peng Baoying, et al. Position error prediction models for variable load direct drive torque motors[J]. Transducer and Microsystem Technologies, 2024, 43(1): 69-71,83.)
[14]She Aiqing, Wang Linjun, Li Jiahao, et al. Structural reliability analysis based on improved wolf pack algorithm AK-SS[J].Structures, 2023,57: 105289.
[15]贾光耀, 闫飞, 张添翼. 改进狼群算法的交通子区迭代学习边界控制方法[J]. 计算机应用研究, 2023, 40(9): 2775-2780. (Jia Guangyao, Yan Fei, Zhang Tianyi. Iterative learning boundary control method for traffic subregion based on improved wolf pack algorithm[J]. Application Research of Computers, 2023, 40(9): 2775-2780.)
[16]荀洪凯, 陶翼飞, 张源, 等. 多目标启发式狼群算法求解不相关并行机分批调度问题[J]. 信息与控制, 2023, 52(1): 93-103,114. (Xun Hongkai, Tao Yifei, Zhang Yuan, et al. Multi-objective heuristic wolf pack algorithm for unrelated parallel machine batch Scheduling problem[J]. Information and Control, 2023, 52(1): 93-103,114.)
[17]陶翼飞, 丁小鹏, 罗俊斌, 等. 基于多目标狼群算法的机场行李导入系统仿真优化研究[J/OL]. 系统仿真学报. (2024-02-01) . https://doi. org/10.16182/j. issn1004731x. joss.23-0437. (Tao Yifei, Ding Xiaopeng, Luo Junbin, et al. Research on simulation optimization of airport baggage import system based on multi-objective wolf pack algorithm[J/OL]. Journal of System Simulation. (2024-02-01) . https://doi.org/10.16182/j. issn1004731x.joss. 23-0437.)
[18]李小川, 刘媛华, 王影歌. 求解多目标带时间窗VRP的文化狼群算法[J]. 计算机应用研究, 2020, 37(4): 1025-1029. (Li Xiaochuan, Liu Yuanhua, Wang Yingge. Cultural wolf pack algorithm for solving multi-objective VRP with time window[J]. Application Research of Computers, 2020, 37(4): 1025-1029.)
[19]赵嘉, 陈丹丹, 肖人彬, 等. 一种基于最大最小策略和非均匀变异的萤火虫算法[J]. 智能系统学报, 2021, 17(1): 116-130. (Zhao Jia, Chen Danan, Xiao Renbin, et al. A heterogeneous variation firefly algorithm with maximin strategy[J]. CAAI Trans on Intelligent Systems, 2021, 17(1): 116-130.)
[20]Zhao Jia, Chen Wenping, Xiao Renbing, et al. Firefly algorithm based on self-learning for multi-peak optization problem[J]. Frontiers of Information Technology & Electronic Engineering, 2021, 22(10): 1311-1334.
[21]Kalyanmoy D. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Trans on Evolutionary Computation, 2002, 6(2): 182-197.
[22]Qi Yutao, Ma Xiaoliang, Liu Fang, et al. MOEA/D with adaptive weight adjustment[J]. Evolutionary Computation, 2014, 22(2): 231-264.
[23]Gadhvi B, Savsani V, Patel V. Multi-objective optimization of vehicle passive suspension system using NSGA-II, SPEA2 and PESA-II[J]. Procedia Technology, 2016, 23: 361-368.
[24]Hua Yicun, Jin Yaochu, Hao Kuangrong. A clustering-based adaptive evolutionary algorithm for multiobjective optimization with irregular Pareto fronts[J]. IEEE Trans on Cybernetics, 2018, 49(7): 2758-2770.
[25]Li Lianghao, He Cheng, Cheng Ran, et al. A fast sampling based evolutionary algorithm for million-dimensional multiobjective optimization[J]. Swarm and Evolutionary Computation, 2022, 75: 101181.
[26]Sun Lei, Li Ke. Adaptive operator selection based on dynamic Thompson sampling for MOEA/D[C]//Proc of International Conference on Pa-rallel Problem Solving from Nature. Cham: Springer, 2020: 271-284.
[27]Elarbi M, Bechikh S, Gupta A, et al. A new decomposition-based NSGA-Ⅱ for many-objective optimization[J]. IEEE Trans on Systems Man and Cybernetics: Systems, 2017, 48(7): 1191-1210.
[28]Liu Qiqi,Jin Yaochu,Heiderich M,et al. An adaptive reference vector-guided evolutionary algorithm using growing neural gas for many-objective optimization of irregular problems[J]. IEEE Trans on Cybernetics, 2020, 52(5): 2698-2711.
[29]Liu Zhizhong, Wang Yong. Handling constrained multiobjective optimization problems with constraints in both the decision and objective spaces[J]. IEEE Trans on Evolutionary Computation, 2019, 23(5): 870-884.
[30]Tian Ye, Cheng Ran, Zhang Xingyi, et al. A strengthened dominance relation considering convergence and diversity for evolutionary many-objective optimization[J]. IEEE Trans on Evolutionary Computation, 2018, 23(2): 331-345.
[31]Tian Ye, Lu Chang, Zhang Xingyi, et al. Solving large-scale multiobjective optimization problems with sparse optimal solutions via unsupervised neural networks[J]. IEEE Trans on Cybernetics, 2020, 51(6): 3115-3128.
[32]Lyu Li, Zhao Jia, Wang Jiayuan, et al. Multi-objective firefly algorithm based on compensation factor and elite learning[J]. Future Generation Computer Systems, 2019, 91: 37-47.
[33]肖人彬, 李贵, 陈峙臻. 进化超多目标优化研究进展及展望[J]. 控制与决策, 2023, 38(7): 1761-1788. (Xiao Renbin, Li Gui, Chen Zhizhen. Research progress and prospect of evolutionary many-objective optimization[J]. Control and Decision, 2023, 38(7): 1761-1788.)
[34]赵嘉, 谢智峰, 吕莉,等. 深度学习萤火虫算法[J]. 电子学报, 2018, 46(11): 2633-2641. (Zhao Jia, Xie Zhifeng, Lyu li, et al. Firefly algorithm with deep learning[J]. Acta Electronica Sinica, 2018, 46(11): 2633-2641.)
[35]肖人彬, 冯振辉, 王甲海. 群体智能的概念辨析与研究进展及应用分析[J]. 南昌工程学院学报, 2022, 41(1): 1-21. (Xiao Renbin, Feng Zhenhui, Wang Jiahai. Collective intelligence: conception research progress and application analyses[J]. Journal of Nanchang Institute of Technology, 2022, 41(1): 1-21.)
