结合对抗互信息的多变量时间序列抗噪异常检测

摘 要：近年来，对多变量时间序列的异常检测在各领域中逐渐突显出其重要性。然而，由于多变量时间序列的时空依赖性以及采集所存在的噪声干扰，使得模型学习到的分布与真实分布存在一定的偏差，进而影响检测性能。为了解决以上问题，提出一种结合对抗互信息的多变量时间序列抗噪异常检测模型（RADAM）。通过设计对比学习机制来达到多变量时间序列全局信息和局部信息的互信息最大化，以此来学习多变量时间序列的时间与空间依赖性；利用自适应权重和过滤器模块减少噪声样本对于训练过程的干扰，使模型在训练过程中具备较高的抗噪能力。在五个真实数据集上与六个先进的同类异常检测方法进行了对比实验，实验结果证明RADAM性能明显优于其他基线模型，说明RADAM能显著提升在包含噪声的多变量时间序列数据集上异常检测的准确度。

关键词：多变量时间序列； 抗噪异常检测； 生成对抗学习； 对比学习； 互信息最大化

中图分类号：TP391 文献标志码：A

文章编号：1001-3695（2024）08-019-2384-08

doi：10.19734/j.issn.1001-3695.2023.11.0579

Robust anomaly detection for multivariate time series based onadversarial mutual information

Zhang Benchu， Qiao Yan， Hu Rongyao

（Anhui Province Key Laboratory of Industry Safety and Emergency Technology， Hefei University of Technology， Hefei 230601， China）

Abstract：In recent years， anomaly detection for multivariate time series has gradually highlighted its importance in various fields. However， due to the spatiotemporal correlation of the multivariate time series distribution and the inevitable noise in the multivariate time series collected， there exists a non-negligible deviation between the distribution learned by the model and the real distribution， which will affect the detection performance. To tackle the above problems， this paper proposed a new robust anomaly detection model （RADAM） for multivariate time series. The new model used contrastive learning to maximize the mutual information of global and local information of multivariate time series to learn the spatiotemporal correlation among time series. It also used the adaptive weights and a sample filter module to reduce the interference of abnormal samples on the training process， which enabled the model to have high noise resistance ability during training. Finally， through comparing the new model with the-state-of-the-art anomaly detection models on five real-world multivariate time series datasets， the experimental results show that RADAM performs better than other baseline models， which demonstrate that RADAM can significantly improve the performance of anomaly detection on polluted multivariate time series datasets.

Key words：multivariable time series; robust anomaly detection; generative adversarial learning; contrastive learning; mutual information maximization

0 引言

多变量时间序列是由多个随时间变化的时间序列所组成的，每个时间序列描述了被监测对象的不同属性值。如航天器的遥感通道在连续时间内对温度、辐射、动力等属性的测量值［1］，云服务器内部节点的CPU利用率、内存利用率等性能值［2］。相对单变量时间序列数据，多变量时间序列能更全面地呈现对象特征。对多变量时间序列的异常检测是指检测出时间序列中不符合现实变化规律的数据片段，这些异常的数据段通常表明被监测对象正处于一种异常的工作状态，有时也代表某类异常事件的发生。若监测中的异常数据没有被及时发现并处理，则可能会导致巨大的经济损失甚至人员伤亡。因此，及时、准确地检测出多变量时间序列中的异常数据具有重要的现实意义。

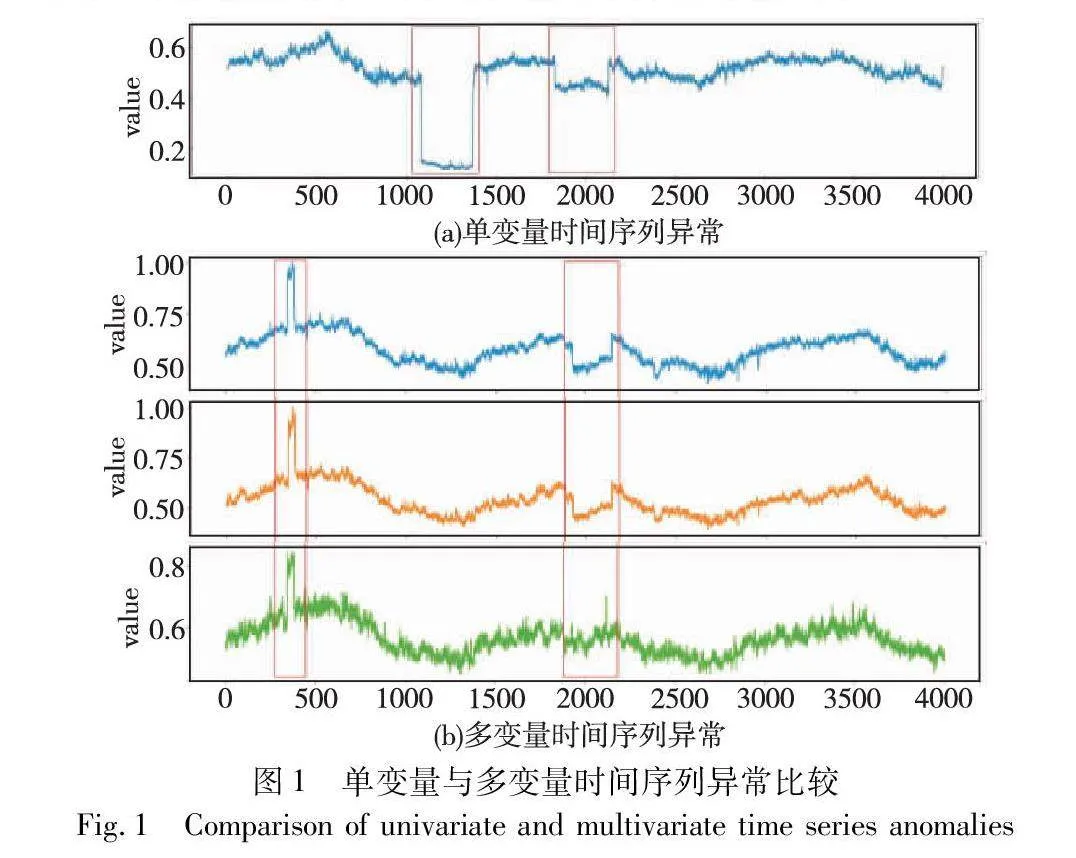
传统的异常检测方法一般通过建立静态阈值来判断数据是否出现异常［3］。然而，该类方法仅能应用于单变量时间序列（如图1（a）所示）的异常检测。多变量时间序列（如图1（b）所示）不仅具有时间依赖性（即每个序列在相邻时间的相关性），还具有空间依赖性（即同一时间所有序列之间的相关性）。因而无法用传统的阈值法来界定多变量时间序列异常。

随着机器学习技术的发展，基于机器学习的异常检测方法迅速涌现。这些方法主要分为基于聚类的异常检测方法、基于单分类的异常检测方法和基于重构的异常检测方法。其中基于聚类的方法（如K均值聚类算法［4］和密度聚类算法［5］）将远离任何聚类中心的观测值视为异常。基于单分类的方法（如单分类支持向量机（one-class SVM，OCSVM）［6］和孤立森林算法（isolation forest，IF）［7］）只对正常数据进行分布建模，将不符合此分布的观测值视为异常。以上两类方法在检测高维度时间序列时存在较高的时间复杂度，且无法保证检测准确度。近年来，基于重构的异常检测方法逐渐成为研究热点。此类方法大多采用自编码器（autoencoder，AE）模型，利用数据的重构误差进行检测。并且通过引入长短期记忆网络（long short term memory，LSTM）［8］、门控循环单元（gate recurrent unit，GRU）［9］来捕捉时间维度的动态变化，但却忽略了不同时间序列之间空间依赖性。为了解决这一问题，一些研究者引入了图神经网络（graphic nuaral network，GNN）［10，11］来更好地建模空间依赖关系。然而，此类模型通常应用于图像和视频等依赖关系存在于相邻区域的样本数据，对于具有较长片段及复杂空间依赖关系的多变量时间序列样本无法到达较好的检测效果。

随着生成对抗网络（generative adversarial network，GAN）［12］的提出，基于GAN的异常检测方法在复杂数据的异常检测问题中表现出更优的性能。AnoGAN［13］首先将GAN应用于医学图像的异常检测中。Zenati等人［14］提出基于Bidirectional GAN（BiGAN）架构的异常检测方法，提高了AnoGAN的检测准确度。然而以上方法仅适用于图像领域的异常检测问题，且基于GAN的异常检测模型需要无噪声的纯净数据集才能学习到准确的样本特征，而现实世界中的多变量时间序列在采集过程中不可避免地存在噪声［1］，这更加大了GAN模型的学习难度。

综上所述，对于多变量时间序列异常检测，本文的核心思想是在消除数据中噪声影响的同时，对多变量时间序列的时间依赖性和空间依赖性进行建模，以更好地捕获多变量时间序列的正常模式。对于多变量时间序列中复杂的时空依赖性，通过利用门控循环单元作为模型的基本网络来捕获时序数据的长期依赖，并引入对比学习机制来学习数据的局部特征和全局特征，从而构建更加丰富的重构信息；此外，为消除数据中噪声的影响，应用对抗训练中不断放大重构误差的原理，设计了自适应权重和噪声过滤模块，有助于防止潜在噪声导致的模型过拟合。本文的主要贡献如下：a）提出了结合对抗互信息的多变量时间序列异常检测模型（RADAM），通过引入对比学习机制来促进鉴别器特征编码之间的互信息最大化，从而有效地学习多变量时间序列样本的时间与空间依赖性，提高模型在多变量时间序列数据上的特征学习和重构能力;b）设计了基于重构误差的样本自适应权重与噪声过滤模块，自适应权重可在训练过程中动态调整样本重构损失，过滤模块可根据时间序列样本的重构误差区分样本质量，过滤疑似噪声，从而使模型能够在受污染训练集中更准确地学习正常样本分布特征;c）在五个真实多变量时间序列数据集上对RADAM方法进行实验评估，并与同类算法进行对比，验证了本文模型的优越性。

1 相关工作

目前基于机器学习的异常检测方法主要可以分为基于聚类的异常检测方法518a1a327c916ee632180c0fe11f97d3、基于单类分类的异常检测方法和基于重构的异常检测方法三类。

基于聚类的异常检测方法将样本到聚类中心点的距离作为异常评分。例如K均值聚类算法［4］和密度聚类算法［5］，将远离聚类中心的样本点视为异常样本。Saeedi等人［15］提出基于密度的聚类算法（DBSCAN）来检测无线传感器网络中的异常数据。基于聚类的异常检测方法的模型复杂度低，易于实现，然而对于复杂分布的数据会产生较高的检测误差。基于单分类的异常检测方法首先学习样本中大多数数据分布，再将不符合此分布的样本视为异常。Tax等人［16］提出的SVDD模型通过建立超球体来囊括尽可能多的数据，将超球体外的样本点视为异常样本。Shen等人［17］提出的THOC通过建立多个超球体将正常数据包围起来，通过评估观察值与超球体所代表的正常模式的偏离程度来进行异常点的检测。Khreich等人［18］提出了一种基于OCSVM的异常检测方法（ADS），该方法将样本的时间信息与OCSVM相结合，以此来降低异常检测的误差。基于单分类的异常检测方法对于低维度数据有较好的检测性能，但对于高维度的多变量时间序列同样会出现检测时间过长及准确度欠佳的情况。基于重构的异常检测方法首先学习正常的样本分布，再通过重构样本来检测异常。例如基于自编码器的异常检测方法［19，20］在训练过程中通过编码器和解码器对训练样本进行重构，在异常检测时通过判断样本的重构误差来鉴别异常。周小晖等人［20］采用自编码器模型，通过在编码器的时域卷积模块和自注意力模块间加入信息共享机制来实现信息融合，实现对多维时序更好地重构。InterFusion［21］采用分层的VAE学习多变量时间序列的样本重构，每一层的潜在变量均参与学习多变量时间序列的空间相关性和时间相关性，以此提高异常检测效果。Adformer［22］通过两个阶段的训练使Transformer能够放大重建误差，并充分捕捉时间序列中的短期趋势，以此增强了模型的异常检测能力。杨超城等人［23］提出了一种融合双重注意力机制的单变量时间序列异常检测方法，通过设计两个注意力机制来挖掘子序列的局部特征和捕获时间序列的长期依赖关系。伍冠潮等人［24］则是提出了一种全局自适应融合与交互学习的网络结构来保留时间序列的依赖关系。近年来随着生成对抗网络（GAN）的出现，基于GAN的异常检测算法［25，26］显示出比自编码器更优异的检测性能，尤其适用于具有复杂分布的高维样本的异常检测问题。尹春勇等人［27］提出使用多个生成器来保证生成样本的多样性，通过堆叠式LSTM捕获时间序列的时间相关性。然而大多数基于GAN的异常检测方法对训练样本有较高的要求，在受噪声污染训练集中很难学习到准确的数据分布。FGANomaly［28］则是提出了用于噪声数据集的异常检测方法，通过设计过滤模块处理数据集中的噪声样本。然而该模型未考虑时间序列样本的时空特征，导致异常检测效果也难以达到最优。

针对现有异常检测方法在应用于真实多变量时间序列异常检测问题时出现的问题，本文设计了一种新的多变量时间序列异常检测模型，能通过自适应权重和样本过滤有效地剔除噪声样本对于训练的干扰，并设计对比学习机制来充分捕获时间与空间重构信息，从而提升模型对于多变量时间序列样本的重构能力，提高多变量时间序列中异常检测的准确度。

2 结合对抗互信息的多变量时间序列抗噪异常检测

2.1 数据处理

多变量时间序列数据是在固定时间间隔采样的，由多维时间变量形成的时间序列Xr={x1，x2，…，xR}。每个观测点xr都是在时间戳r下获得的多维数据，xr∈Rm，r∈{1，2，…，R}。由于不同维度数据的量纲不同，特征向量的取值范围也不同。为了提升模型的收敛速度以及检测性能，在模型训练前，对多变量时间序列进行归一化处理：

xi=xr-Min（Xr）Max（Xr）-Min（Xr）（1）

其中：xi是归一化后的向量；Max（Xr）和Min（Xr）分别表示该特征数据在多变量时间序列Xr中的最大值和最小值。原始数据Xr经过归一化处理后得到时间序列X。考虑到时间序列存在时间相关性，构建长度为n的时间窗口W（t）={xt1，xt2，…，xtn}，其中t代表当前时间窗口的序列号，为了简单起见，在下文中将省略t进行描述。给定一个多变量时间序列X，将其转换为时间窗口数据W={W（1），W（2），…，W（T）}，然后用时间窗口数据W作为模型的输入。这样，模型的异常检测将不只是关注观测值本身，而是根据观测值的时间依赖信息来判断该观测值是否异常。

2.2 RADAM异常检测模型

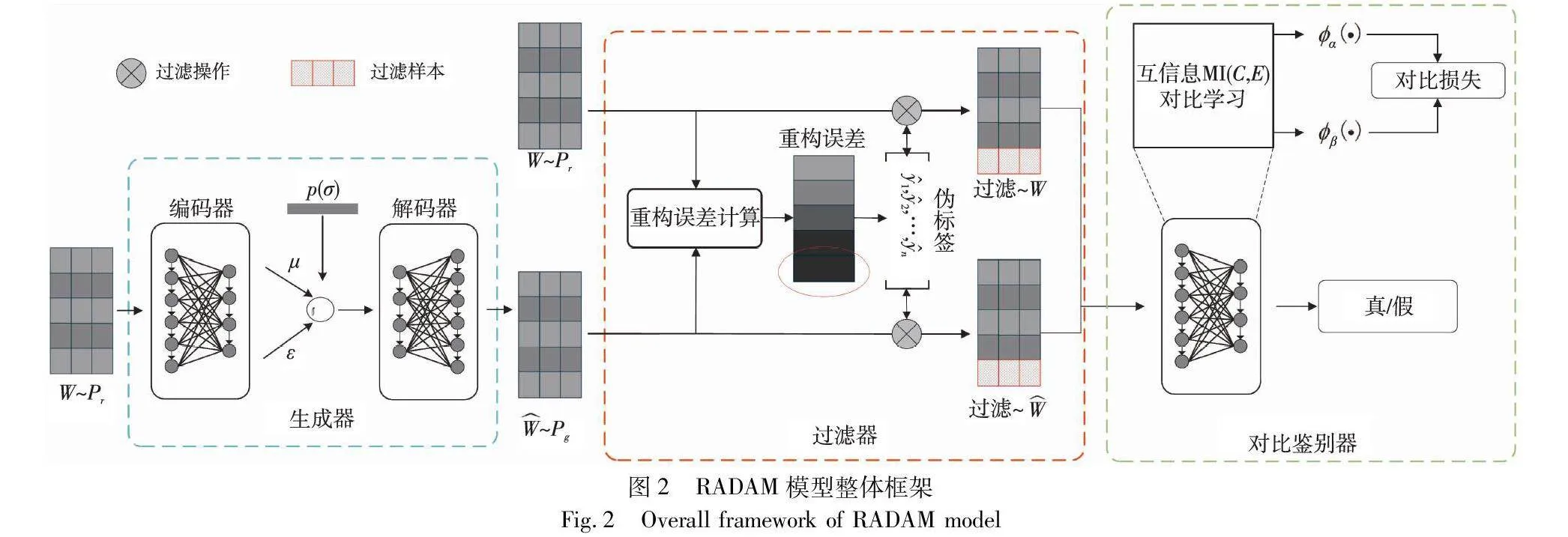
RADAM模型的整体框架如图2所示。该模型由生成器模块、过滤器模块和对比鉴别器模块三个模块组成。在该框架中，多变量时间序列经过数据处理得到时间窗口数据。生成器模块G为输入数据生成重构数据。过滤器模块首先计算两个时间窗口数据W和W^的重构误差，再依据重构误差为每个观测值计算伪标签和生成器模块中的自适应权重，最后将疑似为噪声的样本舍弃。在对比鉴别器中，构造了基于局部特征和全局特征的对比学习机制，鉴别器模块D对过滤后的样本进行对比学习：首先将鉴别器网络中不同层的编码特征进行配对，再对配对后的编码特征进行正负样本划分，最后利用正负样本的对比损失对生成器和鉴别器网络进行优化。通过对比学习，可学习到时间序列样本的时间与空间依赖性，从而更准确地重构时间序列样本。以下将分别对模型中的生成器、过滤器与对比鉴别器模块做详细介绍。

2.2.1 生成器

生成器模块采用变分自编码器（VAE）网络结构，VAE中的编码器网络和解码网络均由门控循环单元（GRU）组成。编码器的作用是将输入数据xi编码到潜在空间，并学习从输入xi到潜在空间变量σi的后验分布q（σi|xi）。该分布的学习可转换为对潜在变量σi的均值μi与方差εi的学习。为了约束潜在空间的分布，将潜在空间变量的先验分布p（σ）用正态分布N（0，1）建模，并在模型训练过程中最小化潜在变量先验分布和后验分布之间的KL散度。解码器的功能是从后验分布q（σi|xi）中采样，并最大化对数似然logp（xi|σi）来生成重构数据xi。从重构的角度，定义生成器的重构损失为

Lirec=Eq（σi|xi）［logp（xi|σi）］-DKL（q（σi|xi）‖p（σ））=

‖xi-i‖-1/2（μ2i+ε2i-2log（εi）-1）（2）

其中：重构损失Lirec是由输入xi与生成i的重构差异和KL散度正则项组成。KL正则项的作用是使编码器生成的潜在变量σi更加连续和有序，确保在该空间中均匀采样的点能够生成具有多样性的样本。

当训练集中包含噪声或异常数据时，模型在学习正常样本特征的同时也会学习到噪声或异常的样本特征，从而产生过拟合现象。“噪声”与“异常”均指数据集中所出现的非正常数据， 当异常数据出现在训练数据集中时会对模型的训练效果产生影响，因此本文将训练集中的异常数据称之为“噪声”。RADAM在重构损失中增加自适应权重来引导生成器网络尽可能学习正常的样本分布。由于噪声样本往往具有较大的重构误差［13］，且随着训练次数的增加，噪声样本的重构误差与正常样本的差异在不断扩大。所以，可利用样本的重构误差来估计样本质量。假设输入样本W={x1，x2，…，xn}与重构样本W^={1，2，…，n}的重构误差为d={d1，d2，…，dn}，其中di=‖xi-i‖，1≤i≤n，根据所有样本重构误差，定义观测值xi的偏离分值为zi，其计算公式为

zi=di-δ（3）

其中：和δ分别为重构误差d的均值和方差。重构误差越大，观测值xi为噪声的可能性越大。因此根据偏离分数，为每个观测值xi的重构损失Lirec乘上自适应权重Δi，其计算公式为

Δi=1Z×eziezi+e-zi×N-1×ezi+e-ziN×ezi（4）

其中：Z为归一化因子；N为训练的总迭代次数；为0～1的小数。分配的权重越大，样本质量越高。训练刚刚开始时，N=1且Δi=1/n，意味着每个观测值都有相同的权重值，贡献了相同的重构损失。随着训练次数的增加，观测值的权重差异会越来越大。当zi＞0，即重构误差di大于平均值时，样本会被分配较小的权重；相反，当zi＜0，即重构误差di小于平均值时，样本会被分配较大的权重。通过为样本的重构损失Lirec分配自适应权重，生成器可更倾向于学习正常数据分布。

2.2.2 过滤器

模型在鉴别器之前添加过滤器，将训练数据中疑似为噪声的样本筛除。通过在每一轮的训练过程中对训练样本动态添加伪标签n（n∈{0，1}） ：当n 为0时，表示样本为高质量样本，可用于鉴别器训练；当n为1时，表示该样本为低质量样本，不参与鉴别器训练。与生成器的自适应权重类似，样本伪标签的计算同样与重构误差和训练迭代次数两个因素相关。重构误差越大，则样本为噪声的概率越大；训练次数越高重构误差的可信度越高。

给定输入数据W={x1，x2，…，xn}，首先将样本xi的异常信度定义为

B^（xi）=eziezi+e-zi（5）

其中：zi如式（3）所定义。式（5）根据重构误差的不同，将异常信度置于0～1。当样本重构误差等于均值时，其异常信度为0.5；当样本重构误差大于均值时，该样本异常信度大于0.5；反之，样本的异常信度小于0.5。

然而，B^（xi）拥有效果的前提是模型有效地学习到多变量时间序列数据的特征。但在训练刚刚开始时，生成器与鉴别器还未能充分地学习到时间序列特征分布，仅依靠重构损失并不能准确地反映异常概率。因此，设计了能随着训练迭代次数的增加，不断优化过滤器过滤效果的平衡因子（1-1/N），观测值xi的异常概率最终被定义为

P^（xi）=eziezi+e-zi×（1-1N）（6）

其中：N为训练的迭代次数。根据上式，异常概率会随着训练的迭代次数动态调整。得到异常概率P^={P^（x1），P^（x2），…，P^（xn）}。并采用四分位法为每个样本生成伪标签：假设ρ为P^从小到大排列第（n+1）×0.75位置的数值。随着训练的进行，观测值xi的异常概率P^（xi）若小于ρ则被分为正常样本（i=0），大于ρ则被分为疑似噪声样本（i=1），以此生成伪标签={1，2，…，n}。

2.2.3 对比鉴别器

多变量时间序列不仅有着时间依赖性，还具有空间依赖性。传统的生成对抗网络很难同时学习时间与空间依赖性，因而对于多变量时间序列特征的学习往往不够充分，从而导致重构误差作为异常评分的效果并不显著。因此，模型RADAM添加对比鉴别器模块，通过对比学习对生成器网络和鉴别器网络进行训练。对比学习目前多应用于视觉特征提取领域，通过最大化样本与特征之间的互信息来提取更精细的样本特征。对于两个离散随机变量X和Y，其互信息定义如下：

I（X;Y）=∑x∈X∑y∈Yp（x，y）log（p（x，y）p（x）p（y））（7）

其中：p（x，y）是X和Y的联合概率密度函数，而p（x）和p（y）分别是X和Y的边缘概率密度函数。对于包含参数ψ的编码网络Eψ，通过最大化输入数据X和编码器数据Eψ（X）之间的互信息MI（X;Eψ（X）），可使编码网络Eψ提取更深层次的样本特征［29］。考虑到MI（X;Eψ（X））计算的复杂性，文献［30］提出了MI（X;Eψ（X））的下界：

MI（Cψ（X）;Eψ（X））≤MI（X;Eψ（X））（8）

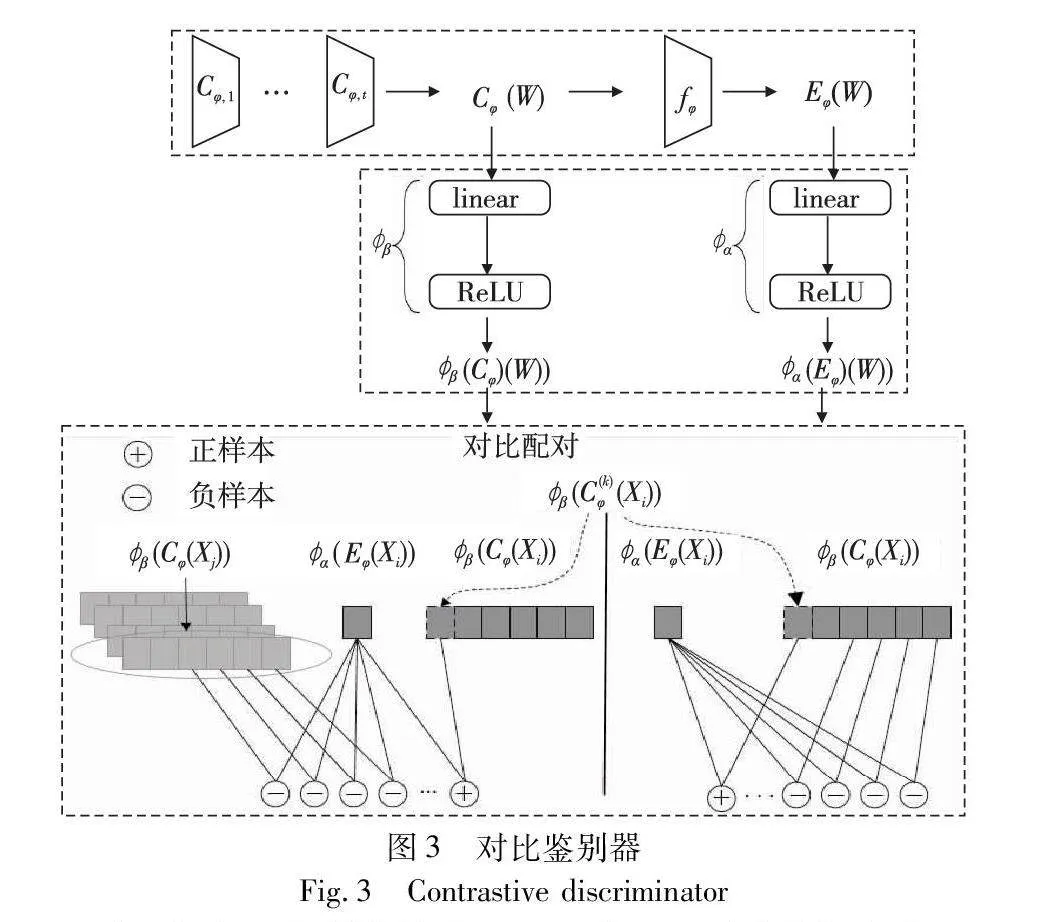
其中：Cψ（X）和Eψ（X）是同一编码器在网络参数ψ下的不同层输出特征，通过最大化MI（Cψ（X）;Eψ（X））可以间接最大化MI（X;Eψ（X））。RADAM通过将鉴别网络中间层特征与输出层的输出作为样本的局部特征与全局特征，最大化样本间的局部特征与全局特征的互信息来间接最大化时间序列样本与鉴别网络输出之间的互信息，从而更全面地学习多变量时间序列样本的时间与空间依赖性。对比鉴别器内部结构如图3所示。

对于包含n个样本的窗口W，对比鉴别器为每个窗口W生成中间局部特征Cφ（W）和中间全局特征Eφ（W）：

Cφ（W）=Cφ，t（Cφ，t-1（…Cφ，1（W））（9）

EXENghV0Gsh+Jl4xn1FXAJW5ckCOfxG/XKtA8L15vAyI=φ（W）=fφ（Cφ（W））（10）

其中：Cφ=Cφ，1，…，Cφ，t是鉴别器网络的一系列中间层，用以生成中间局部特征Cφ（W）∈Rn×m，而fφ则是鉴别器的最后一层全连接层，用于将中间局部特征Cφ（W）编码压缩为中间全局特征Eφ（W）∈Rn×1。生成的中间全局特征和中间局部特征通过线性评价网络α：Rn×1→Rn×1和β：Rn×m→Rn×M分别映射到空间Rn×1和Rn×M，其中M>m，两个线性评价网络分别为

α（Eφ（W））=ReLU（linear（Eφ（W）））（11）

β（Cφ（W））=ReLU（linear（Cφ（W）））（12）

其中：linear（.）为全连接网络；ReLU（.）为激活函数，得到全局特征α（Eφ（W））和局部特征β（Cφ（W））。局部特征映射到Rn×M空间后，窗口W中的一个样本xi局部特征可表示为β（Cφ（xi））={β（C（1）φ（xi）），β（C（2）φ（xi）），…，β（C（M）φ（xi））}，其中β（C（k）φ（xi））称为样本xi的第k个局部特征，1≤k≤M。在获取线性评价后的全局特征α（Eφ（xi））和局部特征β（Cφ（xi））后，模型对局部特征和全局特征进行配对，并划分正负样本。如图3所示，一个正样本对是由α（Eφ（xi））和β（C（k）φ（xi）） 配对而成，构成正样本对（α（Eφ（xi）），β（C（k）φ（xi））），其中k∈Euclid Math OneMAp={1，2，…，M}是样本局部特征的索引。对应负样本对的构成可从两方面考虑：a）负样本可由同一时间窗口的另一时间序列xj的局部特征来构成，表示为（α（Eφ（xi）），β（C（k）φ（xj））），xj∈W，j≠i，该样本能使模型学习到样本间的时间依赖关系；b）负样本可由相同样本的另一局部特征来构成，记作（α（Eφ（xi）），β（C（z）φ（xi））），z∈Euclid Math OneMAp，z≠k，该样本能使模型学习到样本间的空间依赖关系。根据以上规则，在一个时间窗口的n个多维时间序列数据中，对正样本进行n×m次配对，每产生一个正样本，会产生n×m-1个负样本。

在得到所有的正负样本后，模型通过InfoNCE对比损失［31］来最大化局部特征和全局特征的互信息MI（Cφ（xi）;Eφ（xi））：

Linfo（W）=-Ex∈WEk∈Euclid Math OneMAp［θ］

θ=logexp（α（Eφ（xi））β（C（k）φ（xi））T）∑（xj，k）∈W×Euclid Math OneMApexp（α（Eφ（xi））β（C（k）φ（xj））T）（13）

其中：W={x1，…，xn}为包含n个多变量时间序列的窗口样本；Euclid Math OneMAp={1，…，M}代表每个样本M维局部特征的索引。在训练中，模型通过不断区分正样本和负样本，能够逐步理解多变量时间序列数据中的关联性和特征表达，让模型学习到样本的时间依赖性和空间依赖性，从而提高模型在多变量时间序列数据上的特征学习和重构能力。

2.3 模型训练

为了让模型的训练更加稳定，实验中使用Wassertein loss［32］作模型的对抗损失：

Lgan_D（D，G^）=-Ex～pr［D（x）］+Ez～pz［D（G^（z））］（14）

Lgan_G（D^，G）=-Ez～pz［D^（G（z））］（15）

其中：x表示输入数据；z表示潜空间向量；G^代表训练鉴别器D时，参数固定的生成器；D^代表训练生成器G时，参数固定的鉴别器。

在生成器G的训练过程中，除了考虑对抗损失外，还增加了生成数据的对比损失Linfo（W^）和重构损失Lrec，将重构损失Lrec与自适应权重Δ相结合能极大降低噪声样本的影响。因此，生成器的损失函数为

Ltotal_G=Lgan_G（D^，G）+∑ni=1Lirec·［Δi］+λgLinfo（W^）（16）

其中：λg为超参数。

在对比鉴别器D的训练过程中，训练目标为最小化对抗损失与真实样本W的对比损失。为了消除样本中噪声数据对训练的影响，根据过滤器对样本添加的伪标签来过滤疑似噪声样本。因此，对比鉴别器的损失函数可表示为

Ltotal_D=-1K∑ni=1（1-i）［Lgan_D（D，

G^）+λdLinfo（W）］（17）

其中：K表示过滤器过滤后样本的数量;i为过滤器生成的伪标签;λd为超参数。

RADAM异常检测模型训练过程如算法1所示。

算法1 RADAM模型训练算法

输入：多变量时间序列W={W（1），W（2），…，W（T）}；模型迭代次数N;超参数λg，λd，。

输出：训练后的生成器G和对比鉴别器D。

for epoch=1，2，…，N do

for t=1，2，…，T do

重构样本数据W^←G（W）

for all xi∈W（t） do

计算重构误差d←{d1，d2，…，dn}

根据式（4）计算得到自适应权重Δ

根据式（6）为每个观测值xi计算异常概率P^（xi）

ρ←P^的上四分位数

if P^（xi）<ρ then

i←0

else

i←1

end if

end for

←{1，2，…，n}

将重构样本送入对比鉴别器得到对比损失Linfo（W^），并使用式（16）计算生成器损失，更新生成器G参数wG

将过滤后的真实样本送入对比鉴别器得到对比损失Linfo（W），并使用式（17）计算鉴别器损失，更新对比鉴别器D参数wD

end for

end for

return 训练后的生成器G和对比鉴别器D

2.4 异常检测

训练后的RADAM模型可检测样本是否为异常。首先，测试样本X′={x′1，x′2，…，x′J}，被转换为一系列滑动窗口W′={W′（1），W′（2），…，W′（T）}。其次，RADAM的生成器G针对样本窗口W′生成重构数据。最后，对于每个窗口数据计算输入数据和重构数据的重构误差，并以此计算测试样本的异常分值：

A（x′i）=softmax（d′i-d′δ′）（18）

其中，d′i为测试样本x′i与相应重构样本′i的重构误差；d′和δ′分别为当前窗口数据重构误差的均值和方差，异常评分越高表明该测试样本点越异常。

3 实验

3.1 数据集

本实验使用了五个真实的多变量时间序列数据集。表1列出了五个数据集的统计信息。

a）MSL和SMAP［1］。MSL是由探测器本身的传感器数据和执行器数据组合而成。SWAP则是探测器收集的土壤样本和遥感信息组成的数据集。MSL和SMAP的每个数据分别由55和25维数据组成。两个数据集均由一个训练集和一个测试集组成，其中测试集中的异常均已被标记。

b）SMD［9］。SMD由文献［9］收集的一家大型互联网公司连续5周的服务器性能数据。SMD包含28台服务器数据，每台服务器数据均包含38维性能指标，如内存使用率、CPU负载等。

c）PSM［2］。PSM是从eBay的多个应用程序服务器节点内部收集的性能数据。数据集中的时间序列分别描述了服务器的26个不同性能指标。训练集包含13周的服务器数据，测试集包含8周的服务器数据。

d）SWaT［33］。SWaT是从水处理实验设备上收集的多变量时间序列数据。SWaT数据集中包含51个特征，如压强变化，水位信息等。本实验将数据集前7天正常场景下的数据作为训练集，后4天受攻击场景下的数据作为测试集。

3.2 基准模型

本实验将具有代表性的六种异常检测模型作为实验基准模型：

a）isolation forest（IF）［7］。其为最具有代表性的机器学习异常检测方法之一，通过将分布稀疏且远离高密度群体的点作为异常点。

b）BeatGAN［25］。其为一种基于GAN模型的异常检测方法，采用自编码器结构和鉴别器作对抗正则化来缓解过拟合，通过比较输入时间序列和反向生成的时间序列来定位时间序列异常。

c）OmniAnomaly［9］。其为一种基于VAE模型的异常检测方法，利用随机变量连接、平面归一化流等技术同时考虑多变量时间序列的时间依赖性。

d）InterFusion［21］。其为一种基于VAE的模型，通过分层VAE在两个潜在空间中学习多变量时间序列低维的时空嵌入。

e）GDN［10］。其为一种基于图神经网络的异常检测方法，通过使用图注意力机制学习多变量时间序列数据之间的关系图，以此来捕获变量间的依赖性。

f）Adformer［22］。其是一种基于AE与对抗学习的异常检测方法。通过将第一阶段的重构误差作为第二阶段编码器的先验知识，再经过两阶段对抗性训练使变换器放大重构误差，同时能捕捉时间序列中的短期变化趋势。

3.3 实验设置

参照已有的多变量时间序列特征学习模型［9，21］，本文实验中样本的滑动窗口大小和步长分别设置为100和1。生成器的编码器和解码器均由三层GRU网络组成，对比鉴别器的Cφ中间层数t设置为3，GRU层的维度选取范围为{64，128，256}。在模型训练阶段，设置样本批量batch大小为256，训练迭代次数N为100，采用初始学习率为0.000 1的ADAM优化器对模型进行优化。生成器潜在空间维度设置为128，高维局部特征的M设置为256。式（4）（16）和（17）的超参数 、λg和λd分别设置为0.8、0.1和0.1。在实验中，所有数据集均使用原始的划分得到训练集和测试集。

在计算异常分值时，考虑到时间序列中的异常存在时间连续性，参照文献［34］，对检测出的异常进行点调整策略，将时间序列中每个不连续的异常时间段作为一个异常。依据文献［9］将每个异常分值逐一设置为阈值来评估分数，从中选出最佳的F1分数。

3.4 实验结果及分析

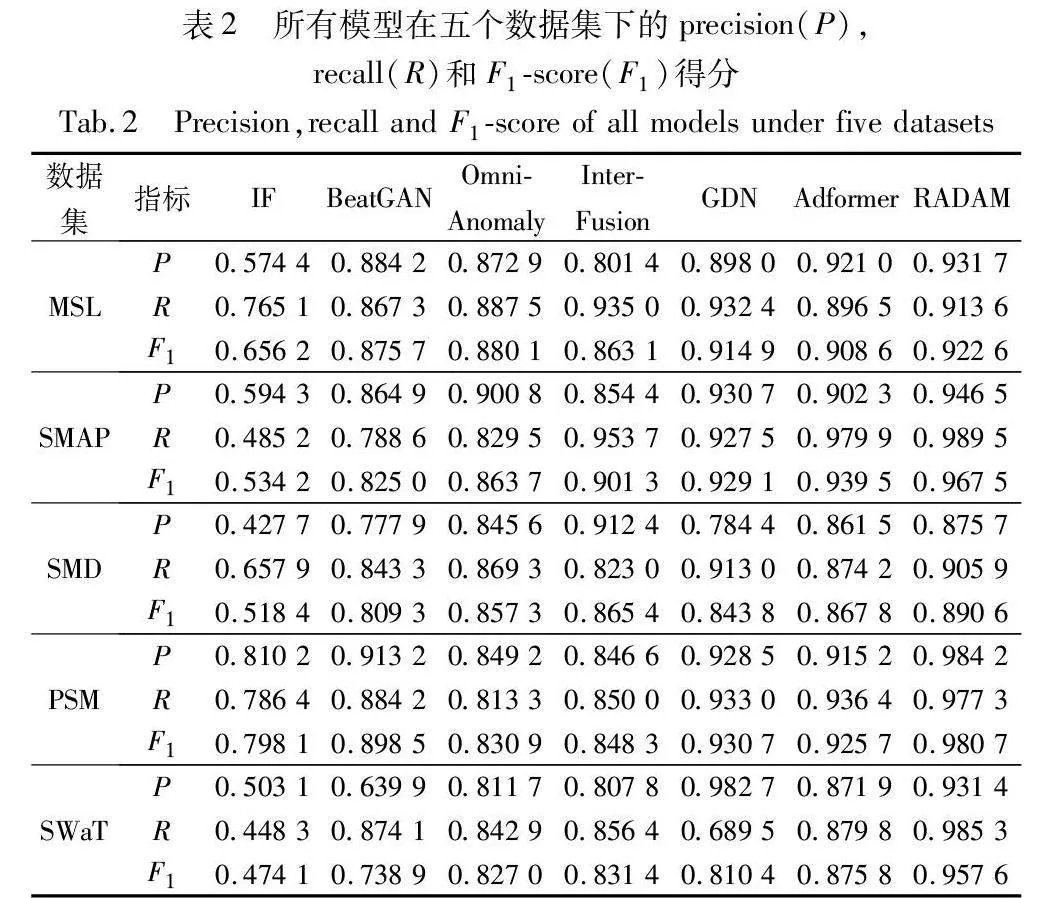
七个模型在五个不同数据集下的准确度（P），召回率（R）和F1分数如表2所示。

从表2可看出，RADAM在五个数据集中均优于基准模型。IF把每个样本点作为独立个体来考虑，忽略了样本点的分布规律，呈现出最低的检测性能。BeatGAN在整体则表现出较低的性能，虽然BeatGAN在对抗训练中加入正则化机制来缓解过拟合，但是缺乏对时间和空间依赖性的充分考虑，很难学习到多变量时间序列数据的复杂分布。InterFusion的性能在整体上优于OmniAnomaly，因为相对于OmniAnomaly，InterFusion不仅考虑了样本自身的时间相关性，同时也考虑了样本之间的空间相关性。GDN通过基于图模型的结构来学习多变量时间序列的空间依赖特征，而未充分学习序列的时间依赖关系。Adformer的两阶段训练则更加注重捕捉时间序列中的短期趋势，而且缺少对多变量空间依赖性的学习。本文RADAM在五个数据集中均获得了最高的F1值，超过了所有的基准模型。

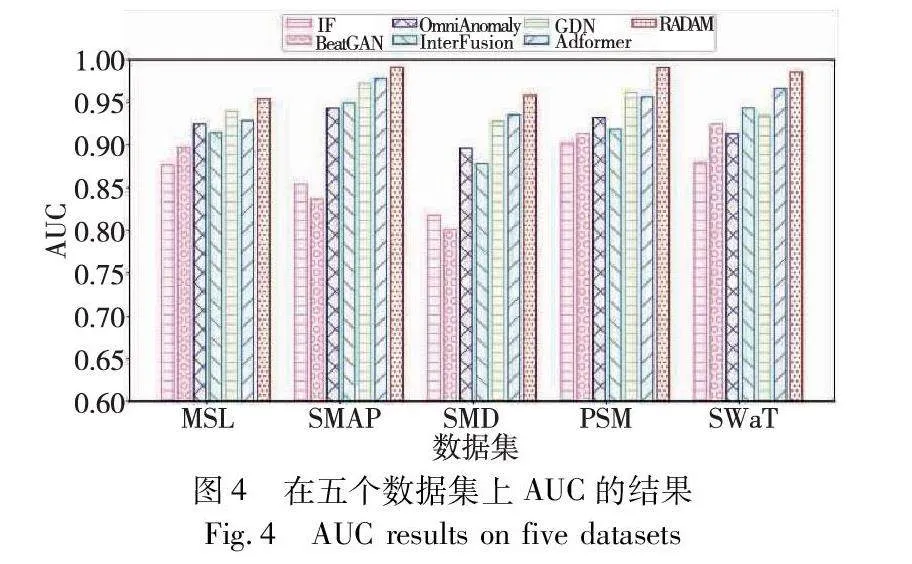
图4展示了五个数据集下各模型的AUC。AUC被定义为ROC曲线下的面积，ROC曲线则是以误报率为横轴，正报率为纵轴绘制的曲线。更高的AUC代表模型具有更低的误报率和更高的正报率。从图4可看出，RADAM的AUC优于所有的基准模型。这也表明，RADAM在多变量时间序列异常检测中能更精准地识别出样本异常。

3.5 消融实验

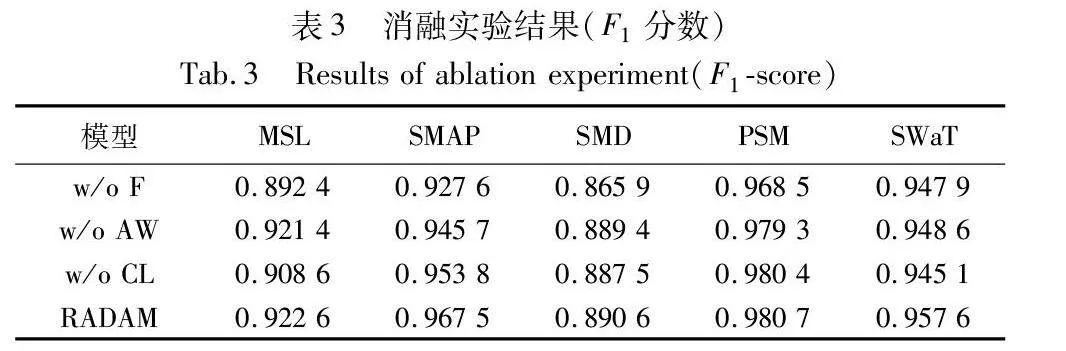
本小节对RADAM中的过滤器模块、生成器中的自适应权重以及模型的对比学习机制分别进行了消融实验，以验证各个部分的重要性与RADAM模型结构的合理性。实验方法如下：

a）w/o （without） F。在RADAM中去除过滤器模块，将所有数据直接送入鉴别器中进行训练，从而验证过滤器在模型中的作用。

b）w/o （without） AW。在RADAM中去除生成器中的自适应权重，令生成器直接使用重构损失，以验证自适应权重的作用。

c）w/o （without） CL。在RADAM中去除模型中的对比学习机制，以验证对比学习对于模型的作用。

d）RADAM。本文提出的原始模型，采用了过滤器、自适应权重和对比机制。

表3列出了三种消融实验的实验结果。可以看出，RADAM在分别去除过滤器、自适应权重及对比学习机制后异常检测性能均有不同程度下降。其中，去除过滤器后模型性能下降幅度最大，这表明受到噪声数据的影响，RADAM很难学习到准确的数据分布。从自适应权重消融实验可看出，通过在生成器中增加样本自适应权重，能够进一步消除噪声对于模型训练的影响。对比学习消融实验结果可看出，对比学习能够使模型更全面地学习多变量时间序列的时间依赖性和空间依赖性，从而提升了RADAM异常检测的性能。

3.6 鲁棒性验证

本节实验通过在训练集中加入不同比例的噪声样本，验证模型在不同噪声比例下的鲁棒性。所有噪声样本从高斯分布（μ=0，δ=1）数据集中随机取样，并注入训练集中。

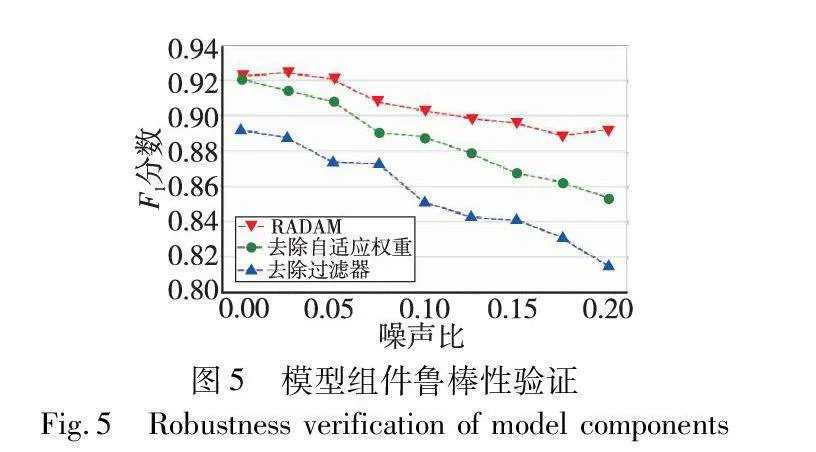
为了验证模型的鲁棒性，实验在训练集中加入了0%～20%的噪声样本，并对比未使用过滤器与未使用自适应权重的性能。以MSL数据集为例，三种模型在注入异常后的F1分数对比如图5所示。从图5可看出，RADAM的F1虽然随着噪声比的增加有一定的下降，但都维持在0.9左右。这证明了RADAM具有较高的鲁棒性。在去除过滤器和去除自适应权重两种情况下，F1随着噪声比例的增加而迅速下降。且随着噪声比例的增加，两个模型与原始模型的F1分数差异越来越大。

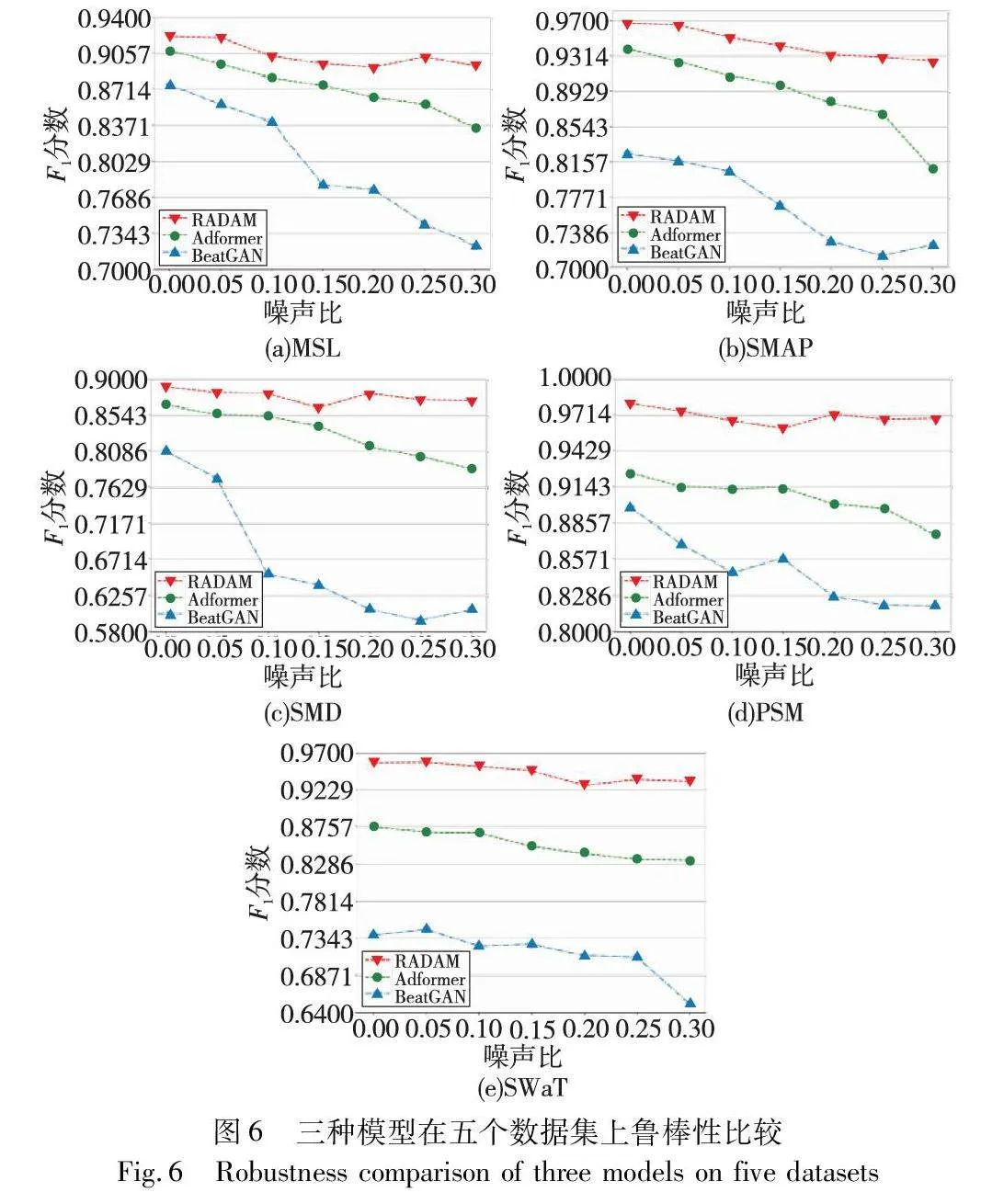
图6比较了RADAM、BeatGAN和Adformer三种基于对抗方法的模型在五个数据集上的鲁棒性。注入的噪声比为0%～30%。从图中可看出，BeatGAN的鲁棒性最差，其随着噪声比率的增加，F1分数迅速下降。尤其在SMD数据集上，F1下降到0.6以下。这是因为BeatGAN仅能应用于纯净的训练集，当训练集中包含噪声时会学习到有偏差的样本分布。由于Adformer提出的融合异常策略在训练中能更加清晰地分出正常和异常之间的区别，其相较于BeatGAN具有更好的鲁棒性。RADAM不仅加入了样本过滤模块，同时融入了对比损失和自适应权重损失，从而具有更优的鲁棒性和更强的特征学习能力。在PSM数据集上，RADAM的F1分数随着噪声比例的增加而略有提升，这是因为模型采用对比学习，将注入训练集的噪声作为新的对抗样本，并利用互信息最大化捕捉更多的样本的特征，从而增加提升了模型的整体性能。

3.7 案例研究

现阶段，随着我国企事业单位信息技术程度的不断加深，信息系统运营的规模也在逐步扩大。为了维护系统的稳定运行，一般需对大量监测模块收集到的多维时序数据进行检测分析，以及时发现系统中的异常状态。随着在线服务系统的部署和更改日渐频繁（如上线新功能、修复错误和更改配置等），导致系统出现异常的概率也在不断升高。因此，采用稳定且准确的异常检测方法，及时检测出多维时序数据中的异常对于维护系统的稳定至关重要。

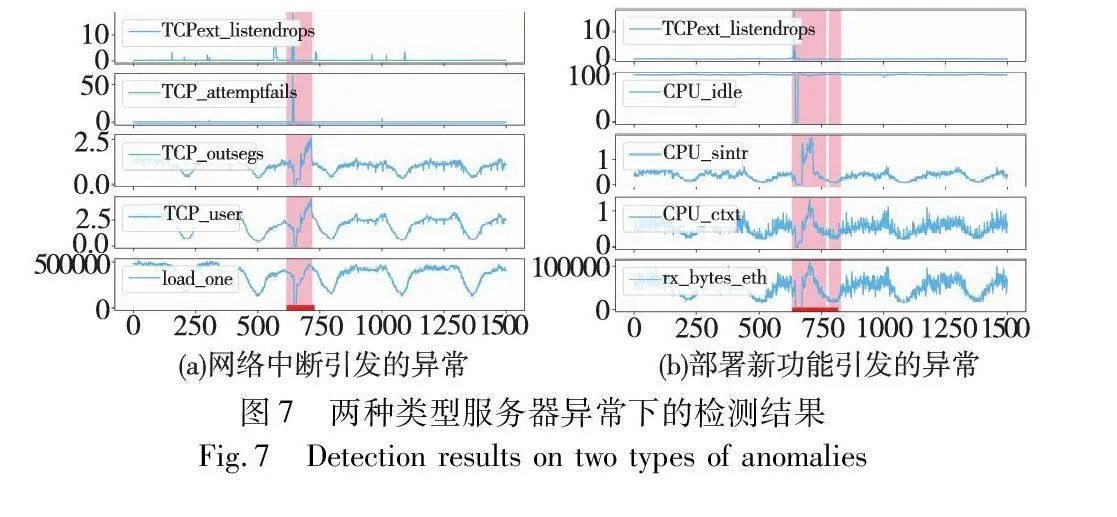
为了直观地验证RADAM的异常检测能力，本小节使用GCP［35］数据集进行案例研究。该数据集由一家国际互联网内容平台发布，该平台每日为超过8亿的活跃用户提供搜索、排序和数据处理等服务。GCP数据集记录了其在七周时间内从30个在线服务系统上收集而来的服务指标数据。数据集维度为19，收集频率为每五分钟取样一次。通过实验结果表明，RADAM在GCP数据集上的准确度（P）达到了0.966 5、召回率（R）达到了0.987 1以及F1分数达到了0.976 7。图7展示了TCP连接状态以及CPU运行指标等属性的时间序列曲线，图底部的红线表示测试集中标记的异常段，红色阴影表示被检测到的异常数据。图7（a）是由于网络中断问题导致服务响应时间过长从而引发的异常，图7（b）是由于上线新功能而引发的服务中断。从图中可看出RADAM能够有效地检测出两种异常。

4 结束语

本文提出了用于多变量时间序列的抗噪异常检测模型RADAM，可在有噪声的数据集中学习正常的时间序列样本分布，并在测试阶段准确地检测出异常样本。RADAM利用对比学习达到互信息最大化的同时学习多变量时间序列的时间依赖性与空间依赖性，提高模型在多变量时间序列数据上的特征学习和重构能力。为了降低噪声样本对模型训练的影响， RADAM加入了自适应权重和过滤器模块。自适应权重能促使生成器学习正常的样本分布，而过滤器模块能在训练鉴别器之前过滤训练集中的噪声及异常样本，提高鉴别器的训练准确度。最后，通过五个真实数据集上的实验将RADAM与六个具有代表性的异常检测模型做了对比，实验结果表明，RADAM在噪声数据集中具有显著的优越性。在以后的工作中，本文将进一步探究多变量时间序列的周期与频率信息，以实现更好的多变量时间序列异常检测效果。

参考文献：

［1］Hundman K， Constantinou V， Laporte C， et al. Detecting spacecraft anomalies using LSTMs and nonparametric dynamic thresholding［C］//Proc of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM Press， 2018：387-395.

［2］Abdulaal A， Liu Zhuanghua， Lancewicki T. Practical approach to asynchronous multivariate time series anomaly detection and localization［C］//Proc of the 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. New York： ACM Press， 2021： 2485-2494.

［3］Roy J. Rule-based expert system for maritime anomaly detection［C］//Proc of Sensors， and Command， Control， Communications， and Intelligence（C3I） Technologies for Homeland Security and Homeland Defense IX. 2010： 597-608.

［4］Candelieri A. Clustering and support vector regression for water demand forecasting and anomaly detection［J］. Water， 2017， 9（3）： 224.

［5］Sharma R， Chaurasia S. An enhanced approach to fuzzy C-means clustering for anomaly detection［C］//Proc of the 1st International Conference on Smart System， Innovations and Computing. Berlin： Springer， 2018： 623-636.

［6］Scholkopf B， Platt J C， Shawe-Taylor J， et al. Estimating the support of a high-dimensional distribution［J］. Neural Computation， 2001， 13（7）： 1443-1471.

［7］Liu Feitong， Ting Kaiming， Zhou Zhihua. Isolation forest［C］//Proc of the 8th IEEE International Conference on Data Mining. Pisca-taway，NJ： IEEE Press， 2008： 413-422.

［8］Park D， Hoshi Y， Kemp C C. A multimodal anomaly detector for robot-assisted feeding using an lstm-based variational autoencoder［J］. IEEE Robotics and Automation Letters， 2018， 3（3）： 1544-1551.

［9］Su Ya， Zhao Youjian， Niu Chenhao， et al. Robust anomaly detection for multivariate time series through stochastic recurrent neural network［C］//Proc of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM Press， 2019： 2828-2837.

［10］Deng A， Hooi B. Graph neural network-based anomaly detection in multivariate time series［C］//Proc of AAAI Conference on Artificial Intelligence. Palo Alto，CA： AAAI Press， 2021： 4027-4035.

［11］李怀翱， 周晓锋， 房灵申， 等. 基于时空图卷积网络的多变量时间序列预测方法［J］. 计算机应用研究， 2022， 39（12）： 3568-3573. （Li Huaiao， Zhou Xiaofeng， Fang Lingshen， et al. Multivaria-te time series forecasting with spatio-temporal graph convolutional network［J］. Application Research of Computers， 2022， 39（12）： 3568-3573.）

［12］Goodfellow I， Pouget-Abadie J， Mirza M， et al. Generative Adversarial Nets［C］//Proc of the 27th International Conference on Neural Information Processing Systems. Cambridge，MA：MIT Press， 2014： 2672-2680.

［13］Schlegl T， Seebock P， Waldstein S M， et al. Unsupervised anomaly detection with generative adversarial networks to guide marker disco-very［C］//Proc of International conference on information processing in medical imaging. Berlin： Springer， 2017： 146-157.

［14］Zenati H， Romain M， Foo C S， et al. Adversarially learned anomaly detection［C］//Proc of IEEE International conference on data mi-ning. Piscataway，NJ： IEEE Press， 2018： 727-736.

［15］Saeedi E H， Mazinani S M. A novel anomaly detection algorithm using DBSCAN and SVM in wireless sensor networks［J］.BIpf/cYsHVNipd/GzpxAkA== Wireless Personal Communications， 2018， 98： 2025-2035.

［16］Tax D M J， Duin R P W. Support vector data description［J］. Machine Learning， 2004， 54： 45-66.

［17］Shen Lifeng， Li Zhuocong， Kwok J. Timeseries anomaly detection using temporal hierarchical one-class networks［C］//Proc of the 33th International Conference on Neural Information Processing Systems. Red Hook，NY： Curran Associates Inc.， 2020： 13016-13026.

［18］Khreich W， Khosravifar B， Hamou-Lhadj A， et al. An anomaly detection system based on variable N-gram features and one-class SVM［J］. Information and Software Technology， 2017， 91： 186-197.

［19］张月， 唐伦， 王恺， 等. 基于GB-AENet-FL网络的物联网设备异常检测［J］. 计算机应用研究， 2022， 39（11）： 3410-3416. （Zhang Yue， Tang Lun， Wang Kai， et al. Anomaly detction algorithm of IoT devices based on GB-AENet-FL network［J］. Application Research of Computers， 2022， 39（11）： 3410-3416.）

［20］周小晖， 王意洁， 徐鸿祚， 等. 基于融合学习的无监督多维时间序列异常检测［J］. 计算机研究与发展， 2023， 60（3）： 496-508. （Zhou Xiaohui， Wang Yijie， Xu Hongzuo， et al. Fusion learning based unsupervised anomaly detection for multi-dimensional［J］. Journal of Computer Research and Development， 2023， 60（3）： 496-508.）

［21］Li Zhihan， Zhao Youjian， Han Jiaqi， et al. Multivariate time series anomaly detection and interpretation using hierarchical inter-metric and temporal embedding［C］//Proc of the 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining， Singapore. New York： ACM Press， 2021： 3220-3230.

［22］Zeng Fanyu， Chen Mengdong， Qian Cheng， et al. Multivariate time series anomaly detection with adversarial Transformer architecture in the Internet of Things［J］. Future Generation Computer Systems， 2023， 144： 244-255.

［23］杨超城， 严宣辉， 陈容均， 等. 融合双重注意力机制的时间序列异常检测模型［J］. 计算机科学与探索， 2024，18（3）： 740-754. （Yang Chaocheng， Yan Xuanhui， Chen Rongjun， et al. A time series anomaly detection model with dual attention mechanism［J］. Journal of Frontiers of Computer Science and Technology， 2024，18（3）： 740-754.

［24］伍冠潮， 凌捷. 基于自适应交互学习的CPS时间序列异常检测［J］. 计算机应用研究， 2023， 40（10）： 2933-2938. （Wu Guanchao， Ling Jie. Time series anomaly detection for cyber physical systems based on adaptive interactive learning［J］. Application Research of Computers， 2023， 40（10）： 2933-2938.）

［25］Zhou Bin， Liu Shenghua， Hooi B， et al. BeatGAN： anomalous rhythm detection using adversarially generated time series［C］//Proc of International Joint Conference on Artificial Intelligence. Palo Alto，CA： AAAI Press， 2019： 4433-4439.

［26］段雪源， 付钰， 王坤. 基于VAE-WGAN的多维时间序列异常检测方法［J］. 通信学报， 2022， 43（3）： 1-13. （Fu Xueyuan， Fu Yu， Wang Kun. Multi-dimensional time series anomaly detection method based on VAEWGAN［J］. Journal on Communications， 2022， 43（3）： 1-13.）

［27］尹春勇， 周立文. 基于再编码的无监督时间序列异常检测模型［J］. 计算机应用， 2023， 43（3）： 804-811. （Yin Chunyong， Zhou Liwen. Unsupervised time series anomaly detection model based on re-encoding［J］. Journal of Computer Applications， 2023， 43（3）： 804-811.）

［28］Du Bowen， Sun Xuanxuan， Ye Junchen， et al. GAN-based anomaly detection for multivariate time series using polluted training set［J］. IEEE Trans on Knowledge and Data Engineering， 2023， 35（12）： 12208-12219.

［29］Linsker R. Self-organization in a perceptual network［J］. Compu-ter， 1988， 21（3）： 105-117.

［30］Tschannen M， Djolonga J， Rubenstein P K， et al. On mutual information maximzation for representation learning［EB/OL］. （2020-01-23） . https：//arxiv.org/abs/1907.13625.

［31］Oord A， Li Yazhe， Vinyals O. Representation learning with contrastive predictive coding［EB/OL］. （2019-01-22） . https：//arxiv.org/abs/1807.03748.

［32］Gulrajani I， Ahmed F， Arjovsky M， et al. Improved training of Wasserstein GANs［C］//Proc of the 31st International Conference on Neural Information Processing Systems. Red Hook，NY： Curran Associates Inc.， 2017： 5769-5779.

［33］Mathur A P， Tippenhauer N O. SWaT： a water treatment testbed for research and training on ICS security［C］//Proc of International Workshop on Cyber-physical Systems for Smart Water Networks. Piscataway，NJ： IEEE Press， 2016： 31-36.

［34］Xu Haowen， Chen Wenxiao， Zhao Nengwen， et al. Unsupervised anomaly detection via variational autoencoder for seasonal KPIs in Web applications［C］//Proc of World Wide Web Conference. New York： ACM Press， 2018： 187-196.

［35］Ma Minghua， Zhang Shenglin， Chen Junjie， et al. Jump-starting multivariate time series anomaly detection for online service systems［C］//Proc of USENIX Annual Technical Conference. Berkeley，CA： USENIX， 2021： 413-426.