考虑负载量均衡的自动拣货系统AGV任务分配优化

摘 要：为提高AGV自动拣货系统作业效率、降低作业成本，在剖析造成系统拥堵的关键影响因素基础上，提出考虑负载量均衡的AGV任务分配双层规划模型，上层考虑总成本最小，下层通过构建多目标函数来最小化系统负载量标准差和AGV空闲率。针对传统GA求解任务分配问题效率低、易陷入局部最优等问题，提出了一种改进自适应遗传算法（SAGA），引入sigmoid函数用于适应度值的转换，并参与到自适应调整交叉变异算子的操作中，加入灾变策略防止算法出现早熟的情况。最后将该算法对不同规模算例进行仿真，结果证明，相比遗传算法、自适应遗传算法、自适应灾变遗传算法、蚁群算法，该改进算法在不同规模算例实验结果中均有明显优化，表明改进算法能更好地避免早熟、提升求解质量与收敛稳定性，有效地均衡了路网负载量，降低了作业总成本。

关键词：任务分配； 负载量均衡； 自动拣货系统； 双层规划； 遗传算法

中图分类号：TP391.9;TP11 文献标志码：A

文章编号：1001-3695（2024）08-017-2366-08

doi：10.19734/j.issn.1001-3695.2023.11.0576

Optimization of AGV task assignment considering load balancing in RMFS

Tian Shuaihui， Shen Yifan， Ou Liying， Fan Lue

（School of Modern Posts， Chongqing University of Posts & Telecommunications， Chongqing 400065， China）

Abstract：To enhance the efficiency of RMFS and reduce operating costs， this paper proposed a double-layer planning model for AGV task allocation considering load balancing， following an analysis of key factors causing congestion in RMFS. The upper layer sought to minimize the total cost， while the lower layer addressed the minimization of the system load standard deviation and AGV idle rate through a multi-objective function. It introduced a modified adaptive genetic algorithm（SAGA） to overcome the challenges of low efficiency and susceptibility to local optima in solving task allocation problems using traditional GA. It integrated the sigmoid function was to transform fitness values and participates in the adaptive adjustment of cross-mutation operators. Additionally， it incorporated catastrophic strategies to prevent premature convergence of the algorithm. Finally， it simulated the proposed algorithm on different scale cases， and the results demonstrate that， in comparison to the genetic algorithm， adaptive genetic algorithm， adaptive disaster genetic algorithm， and ant colony algorithm， the improved algorithm exhibits substantial optimization in the experimental results of various scale cases. This suggests that the enhanced algorithm effectively avoids premature convergence， enhances solution quality and convergence stability， actively balances road network load， and reduces total operating costs.

Key words：task allocation; load balancing; robotic mobile fulfillment systems（RMFS）; bi-level programming; genetic algorithm

0 引言

我国电子商务逆势增长，订单量不断增加，客户对订单的配送时效性和服务质量需求持续增高，这对电子商务仓库拣货作业效率及准确率提出更高要求。以AGV为代表的AGV自动拣货系统（RMFS）应运而生，自动拣货系统拣选效率是传统拣货系统的 2～3倍，相比较传统仓库的拣货作业模式拣货效率有了很大的提升。

基于每天数以万计的大规模电子商务订单，自动拣货系统对高效率、低成本的拣货解决方案需求大幅上升。然而，不断增长的订单业务，导致自动拣选系统拥堵问题日益严重，降低了拣选效率［1］。多台AGV同时在同一地点进行作业，可能导致节点负载量（节点在当前AGV作业策略下的实际吞吐量）不均衡，进而引起系统拥堵［2］。系统节点在单位时间内的累计负载超过一定阈值时，节点就会陷入拥堵状态［3］。在这种状态下，不同路段之间的负载不均衡问题会变得更加严重［4］。解决拥塞问题的关键，在于防止拣货系统中每个节点的负载超过合理范围。AGV任务分配直接影响多AGV作业中的拥堵情况以及任务完成的效率等，是自动拣货系统降本增效的关键环节。

多AGV任务分配（multi-robot task allocation，MRTA）一直以来都是学者关注的热点问题。任务分配的优化目标在于将任务分配给适当的AGV，并确定作业顺序。当多AGV同时完成订单拣选任务时，研究如何在满足多约束条件的前提下，寻求最优任务分配方案使AGV能同时满足多种目标，对提升拣货系统的作业性能具有重要意义。

目前国内外学者关于任务分配的研究主要是从模型构建到求解方法的探讨。MRTA问题的模型主要有多旅行商问题、车辆路由问题和混合整数线性规划模型等，其目标函数可以是单目标函数，也可以是多目标融合函数。大量学者集中于以作业成本、作业时间和行驶距离为研究目标来优化MRTA问题。许丽丽等人［5］为解决四向穿梭车仓储系统的任务分配问题，构建作业时间最短为目标的数学模型，并使用遗传算法求解得到最优任务分配方案；周航等人［6］研究了仓储多机器人任务分配问题，以成本最小化为目标函数建立数学模型，使用混合遗传禁忌搜索算法优化任务分配结果；李腾等人［7］为提高移动机器人履约系统拣选效率，以作业成本最小为优化目标，并建立了考虑移动机器人重载和空载成本差异的数学模型，得到协同优化的任务分配和货架储位再指派策略；李缘［8］针对多AGV多任务分配问题，提出周期任务分配策略，考虑总成本最优建立模型，使用改进粒子群遗传算法求解，实现总成本最小化；于佳乔等人［9］以AGV完成任务行走总距离最短为优化目标，采用双层编码的方式，解决AGV在多任务下的分配问题。也有部分学者优化其他目标函数来研究MRTA问题，Zou等人［10］以能耗、AGV数量和客户满意度三个目标建立多目标优化模型，并使用多目标贪婪算法解决了多AGV任务分配问题；王子意［11］将多AGV任务分配问题拆分为任务组合和任务派发两个问题，构建以优化剩余电量与AGV疲劳程度的任务分配模型，解决了任务分配存在的不均衡问题。

对于MRTA问题模型的求解方法，从较早期的匈牙利算法到拍卖算法、博弈论等，再到后来引入智能优化算法，国内外学者的相关研究都致力于探索如何提高MRTA问题的求解效率。孟宪福等人［12］考虑任务执行时间、节点间的通信时间和任务调度费用等因素建立目标模型，使用了匈牙利算法求解任务分配问题。Zlot等人［13］基于动态变化的任务分配问题，提出了一种基于市场拍卖机制算法，结果表明该方法能克服环境信息的不确定性，有效优化任务分配。Das等人［14］提出了一种基于分布式拍卖算法，用于解决多个异构自主机器人系统中的任务分配问题。Garapati等人［15］研究了博弈论算法在解决多机器人任务分配问题的有效性，寻找无人机之间的冲突平衡，再利用投票系统来确定最终的任务分配方案。对于求解任务分配的常用智能优化算法有遗传算法、蚁群算法、模拟退火算法和粒子群算法等。秦新立等人［16］将MRTA 问题转换为 MTSP模型，改进了蚁群算法求解机器人任务分配问题，提升了收敛速度且避免陷入局部极小问题。Wei等人［17］改进了多目标粒子群优化算法求解多机器人任务分配问题，在算法设计上提出了帕累托前沿细化策略和基于概率的领导者选择策略，仿真结果验证了算法的有效性。丁一等人［18］考虑AGV任务分配与路径优化问题，建立了两阶段模型，并设计改进的模拟退火算法求解第一阶段模型。张子迎等人［19］提出了一种基于启发式深度Q学习的多机器人多任务分配算法，解决多机器人任务分配方法在环境复杂性增加时出现的维度灾难问题，证明了所改进算法的实用性和鲁棒性。邓辅秦等人［20］提出一种结合遗传算法和滚动调度的MRTA算法，优化现有算法在求解大规模多约束的MRTA问题时存在的不足。

基于以上研究内容，将系统负载量作为任务分配优化考虑因素的研究较为罕见，同时现有求解任务分配问题方法的效率仍有待提升。本文以移动AGV自动拣货系统为研究对象，考虑造成系统拥堵的关键影响因素，将AGV任务分配与AGV数量配置结合建立双层规划模型，运用A*算法进行自动拣货系统AGV路径仿真实验，针对传统GA求解MRTA问题效率低、易陷入局部最优等问题，提出了一种基于sigmoid改进的自适应遗传算法，避免早熟问题的发生，增强了算法全局的搜索能力。

1 问题描述

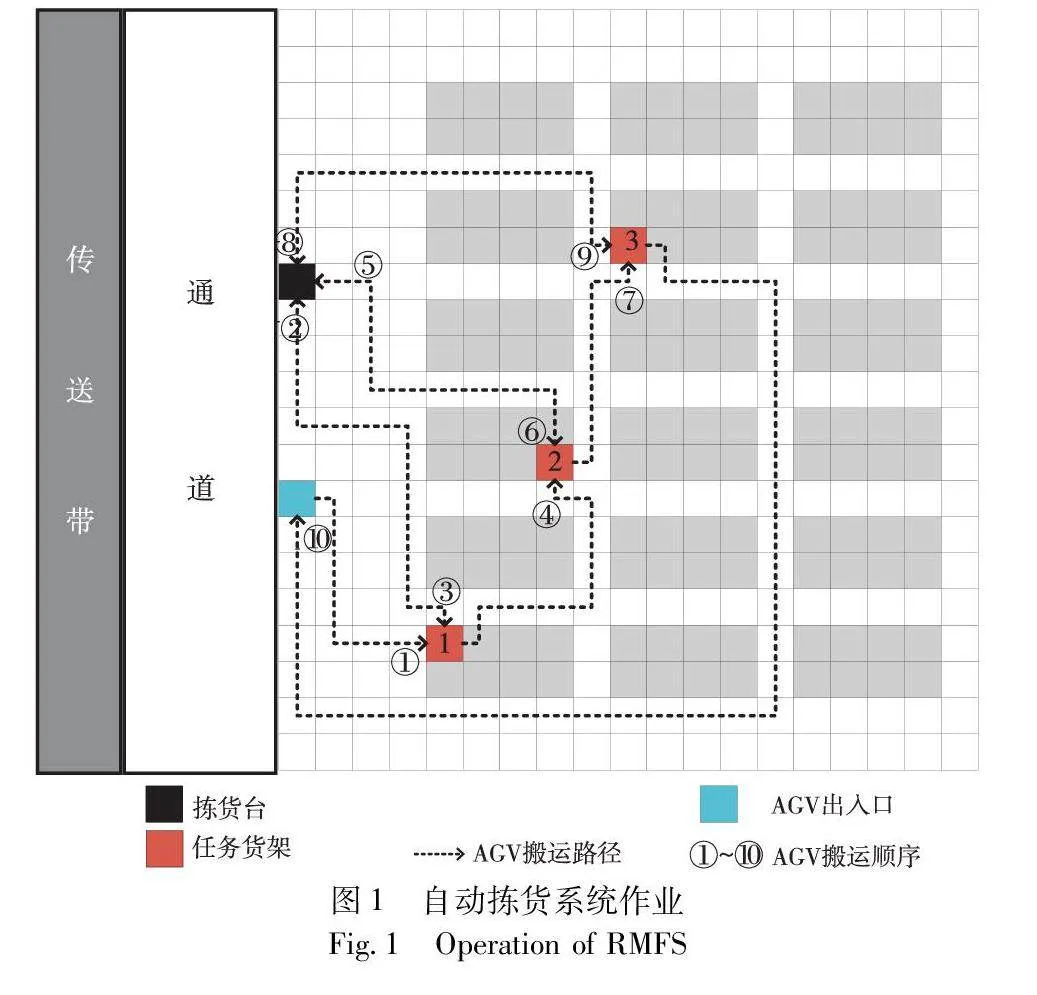
多AGV自动拣货系统采用分布式智能的思想，其作业顺序为：系统根据任务订单信息，调度AGV去拣取货物货架，AGV运至拣选台取出货物，再将空货架运回后进行下一个任务的拣选。AGV作为自动拣货系统的关键设备，不同的任务分配方式影响AGV行走距离和系统负载量均衡，从而影响拣货速度。从图1可以观察到，自动拣货系统中，AGV作业连续性强，AGV数量与任务分配的决策将直接影响作业场景的拥堵情况、完成订单拣选的效率等，是提升系统作业性能的重要因素。

本文采用栅格法进行环境建模。栅格法易于算法实现，且能清楚地表示拣货系统中的实物，每个栅格代表相应系统单位节点，便于计算节点负载量。如图1所示，表示一个AGV完成三个任务的作业流程。以完成第一个任务为例，首先该AGV从AGV出入口沿路径①出发前往第一个任务位置，取出货架之后再沿路径②前往拣货台取出货物，接着沿路径③运载空货架返回该任务位置，最后沿路径④前往下一任务位置，该AGV在完成所有任务之后原地等待下一批订单的执行命令。自动拣货系统AGV完成一组任务序列包含四个步骤：

a）AGV从初始入口位置到第一个任务位置。

b）AGV搬运任务货架至拣货台取出货物。

c）AGV搬运空货架从拣货台返回当前任务位置。

d）AGV从当前任务位置到下一任务位置。

2 参数设定与模型构建

2.1 条件假设及参数定义

为了便于模型的构建，作出以下假设（参数设定如表1所示）：

a）每个AGV同时只可以搬运一个货架，每个货架同时只能由一个AGV进行搬运。

b）每个AGV作业能力相同，均能独立完成搬运任务。

c）不考虑AGV电量问题，作业AGV不考虑充电情况。

d）每个AGV速度相同且运行过程中速度保持不变。

e）不同的任务分布在不同的货架，不存在缺货情况。

f）待拣选任务的位置随机，不考虑货位影响负载均衡的因素。

参数如表1所示。

2.2 模型建立

双层规划具有层次性、制约性等特点，上层的决策影响下层的执行，而下层的反馈影响上层的决策。针对自动拣货系统场景，考虑AGV数量与任务分配优化问题为一个层次性较强的问题。由于在确定AGV调度数量的前提下才能考虑后续的任务分配问题，而后续作业过程中产生的各项成本又对AGV数量和任务分配的决策产生影响，这一特性符合双层规划模型的应用特征，所以提出运用双层规划模型解决该系统优化问题。上层模型以考虑完成任务的AGV行驶距离成本、负载量不均衡产生的延误时间成本、AGV空闲成本以及AGV固定成本为目标函数，决策变量为AGV数量；下层模型考虑系统节点负载量标准差和AGV空闲率最小为目标函数，以任务分配为决策变量，刻画系统负载量均衡程度和AGV损耗程度。

2.2.1 基于AGV数量的上层模型

基于上述问题描述、假设条件及参数变量，构建上层数学模型：

min Z=∑ni=1Di×Yi×Cr+t×Cd+lavg×n×Cf+n×Cp（1）

s.t. Yi∈{0，1}（2）

Nmin≤n≤Nmax，n∈Euclid ExtraeBp+（3）

上层模型中式（1）表示最小化AGV完成任务的总成本，其目标函数的成本由以下四部分构成：Cr表示所有AGV完成所有任务的行驶距离成本；Cd表示由节点负载量不均衡导致的拥堵产生的延误时间成本；Cf表示AGV的空闲成本；Cp表示AGV运行的固定成本。Cr、Cf和Cd均由下层目标函数结果决定。约束条件式（2）中，Yi为0则不调用此AGV，Yi为1则调用。式（3）表示AGV的配置数量n要在设定的范围之内，且n必须为正整数。

2.2.2 基于AGV任务分配的下层模型

下层模型：

f1=θ=f（Ngh）=min∑g∈G，h∈H（Ngh-∑g∈G，h∈HNghNG×NH）2NG×NH（4）

f2=min lavg=1n×∑ni=1li=1n×∑ni=1{1-（∑mj=1Tij×XijT）}=

∑ni=11-∑mj=1∑pk=1{［（d1ioj+d2ijk+d3ikj）/Vi］×Xij}Tn（5）

根据实际作业场景中的重要性程度，设置f1和f2的权重为ω1和ω2，∑ωα=1。因此，多目标函数计算方法如式（6）所示，其中μα为调整系数。

f=∑ωα（μαfα）（6）

s.t Xij∈{0，1} i=1，2，3，…，n;j=1，2，3，…，m（7）

∑ni=1Xij=1 j=1，2，3，…，m（8）

∑mj=1Xij×Yi≥Yi i=1，2，3，…，n（9）

Ngh≥0，Ngh∈N，g∈G，h∈H（10）

下层目标函数为多目标函数。式（4）为最小化系统的负载量标准差，其反映自动拣货系统的拥堵程度，通过转换系数β将负载量标准差转换为负载量不均衡导致的延误时间t，并计算相应成本，Ngh表示第g行第h列子区域负载量，NG×NH表示拣货系统总节点数；式（5）表示AGV在完成单批订单完成的时间内，最小化AGV的平均空闲率；式（7）表示决策变量Xij，表示AGV Ri是否完成任务Zj；式（8）表示一个任务只允许由一个AGV完成；式（9）表示被调度的AGV至少完成一个任务；式（10）表示负载量的非负约束与整数约束。

3 模型求解

多AGV任务分配问题是典型的NP-hard 问题，解决此类问题常使用遗传算法，其编码规则简单有效，具有高度并发性和全局搜索能力。而传统GA易早熟、计算效率低，导致计算结果易陷入局部最优。因此为了得到更优的任务分配方案，本文提出基于sigmoid改进的自适应遗传算法。其中，在交叉与变异过程中引入sigmoid函数计算个体的值，提高个体较多、个体间差异较小时自适应遗传算法的优越性；交叉操作考虑了一种快速判断个体是否交叉的方法，避免相同个体间的无效交叉；引入灾变算子，当最优个体重复出现一定次数以后增加变异基因，以寻求更优秀的个体。

3.1 改进遗传算法设计

3.1.1 初始化种群

确定AGV数量初始配置、批量订单任务数量，对任务分配问题进行随机生成初始种群pop。

3.1.2 编码

采用整数编码方式进行编码，染色体长度为待搬运任务的数量，第i个位置的编号j表示第i个任务由第j台AGV完成，并保证所调度AGV的序号在染色体中至少出现一次，如图2所示，为10个任务由3台AGV分配完成的染色体编码。

3.1.3 选择

使用二元锦标赛与精英保留策略进行选择操作，从种群pop中以同一概率随机选择两个个体，根据每个个体的适应度值，选择其中适应度值最好的个体进入下一代种群，直到新的种群规模达到原来的种群规模。

3.1.4 基于sigmoid函数的自适应交叉与变异算子

1）交叉算子

采用随机交叉位置的单点交叉法。交叉操作是为了产生更多可选择的AGV任务分配方案，可以增大任务分配解空间的搜索范围。按照交叉概率Pc将染色体随机一段基因进行交叉，产生新个体。重复此操作直到所有个体都被访问，用所有产生的新的个体替换掉newPop中的原个体。

由于选择操作将适应度值最好的个体加入下一代种群，随着迭代次数增加，个体相同的情况变多，此时个体交叉是无效的。本文考虑了一种快速判断个体是否交叉的方法，采用行驶距离长度和AGV序号的累加值作为判断依据进行快速筛选，若相似度100%，则不进行交叉，提高算法的计算效率。

S（Ii，Ij）=λ1×dis（Ii）+λ2×∑QUANim=1Ii（m）λ1×dis（Ij）+λ2×∑QUANjn=1Ij（n）（11）

i≠j∈pop（12）

其中：S（Ii，Ij）为两个个体相似度评价函数，如果其比值为1，则这两个个体不进行交叉；Ii和Ij表示个体i和j；λ1和λ2为行驶距离长度与AGV序号累加值的权重，λ1=0.1，λ2=2；dis（Ii）、dis（Ij）分别为两个个体的行驶距离长度；m、n为个体i、j中的某一个AGV编号，QUANi为QUANj为两个个体的AGV编码总量。

2）变异算子

采用随机位置染色体单点变异方式，按照变异概率Pm进行变异，生成新的个体。重复操作直至所有个体都被访问，变异时染色体的某个基因变异成某个AGV的序号。

3）基于sigmoid的自适应策略

sigmoid 函数是最常用的激活函数之一，其具有指数函数形状，常用于二分类问题中，将输出映射到［0，1］，表示某个事件发生的概率。其可导性好的特性使得sigmoid函数在神经网络中得到广泛应用［21］。sigmoid函数的数学表达式为

f（x）=11+e-x（13）

为了保证当前种群中最优个体的Pc和Pm不为零，防止进化初期种群最高适应度停滞不前的可能性，降低算法陷入局部最优解的可能，使优质个体更有机会传递到下一代，引入sigmoid函数。由sigmoid函数计算某一代种群pop中，N个个体中的某一个体的适应度值fk对应的sigmoid值，其计算公式为

Sk=efkefk+1（14）

本文基于sigmoid函数思想建立了交叉概率Pc和变异概率Pm调节公式：当个体较优时，交叉率和变异率会减小，反之则增大。由于某一代种群中的最优个体未必是全局最优解，不应设定最优个体的交叉概率和变异概率为0。为避免早熟，交叉概率和变异概率不应过小。

Pc=Pc1×Sbest-SselectedSbest-Save fs≥fave

Pc2fs＜fave（15）

Pc=Pc1×efbestefbest+1-efsefs+1efbestefbest+1-1N fs≥favePc2fs<fave（16）

Pm=Pm1×Sbest-SindividualSbest-Save fs′≥favePm2fs′<fave（17）

Pm=Pm1×efbestefbest+1-efsefs+1efbestefbest+1-1N fs′≥favePm2fs′<fave（18）

其中：fs为某一代种群中参与交叉的两个个体中较大的适应度值；fs′为某一代种群中变异个体的适应度值； fave为某一代种群适应度平均值；Sbest为适应度最优个体的sigmoid值；Save为某一代种群平均适应度的sigmoid值；Sselected为fs对应的sigmoid值；Sindividual为fs′对应sigmoid值。改进的自适应交叉率由式（15）（16）计算得出，自适应变异率由式（17）（18）计算得出。

3.1.5 灾变策略

遗传算法的演化过程中常常会出现早熟现象，导致算法无法找到全局最优解或者最优解的质量较差。为了避免遗传算法早熟，本文引入了改进的灾变操作，以增加算法的全局搜索能力和局部搜索能力。

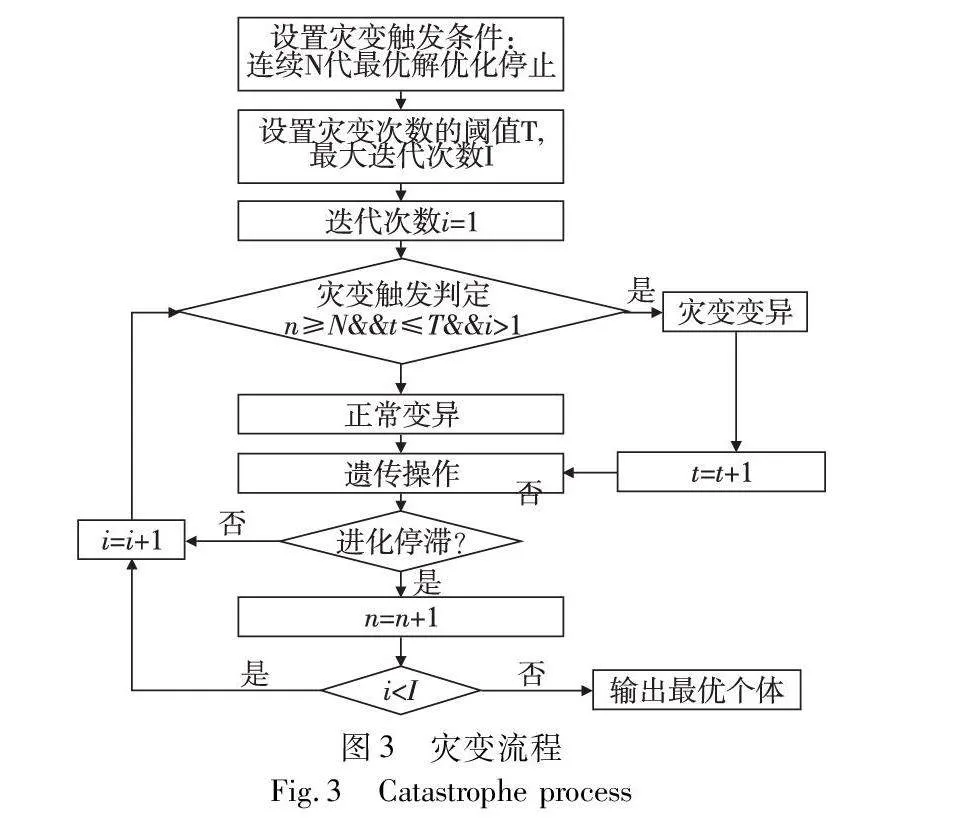
灾变策略的实施步骤为：在种群经过n代进化后，若未能生成更优个体，且连续出现达到阈值次数的情况，即触发灾变操作，保留最优个体的同时增加一个变异位进行变异；如果执行灾变次数达到设定范围，停止灾变，若此时局部最优个体无变化，则认为此个体为全局最优个体，算法结束，如图3所示。

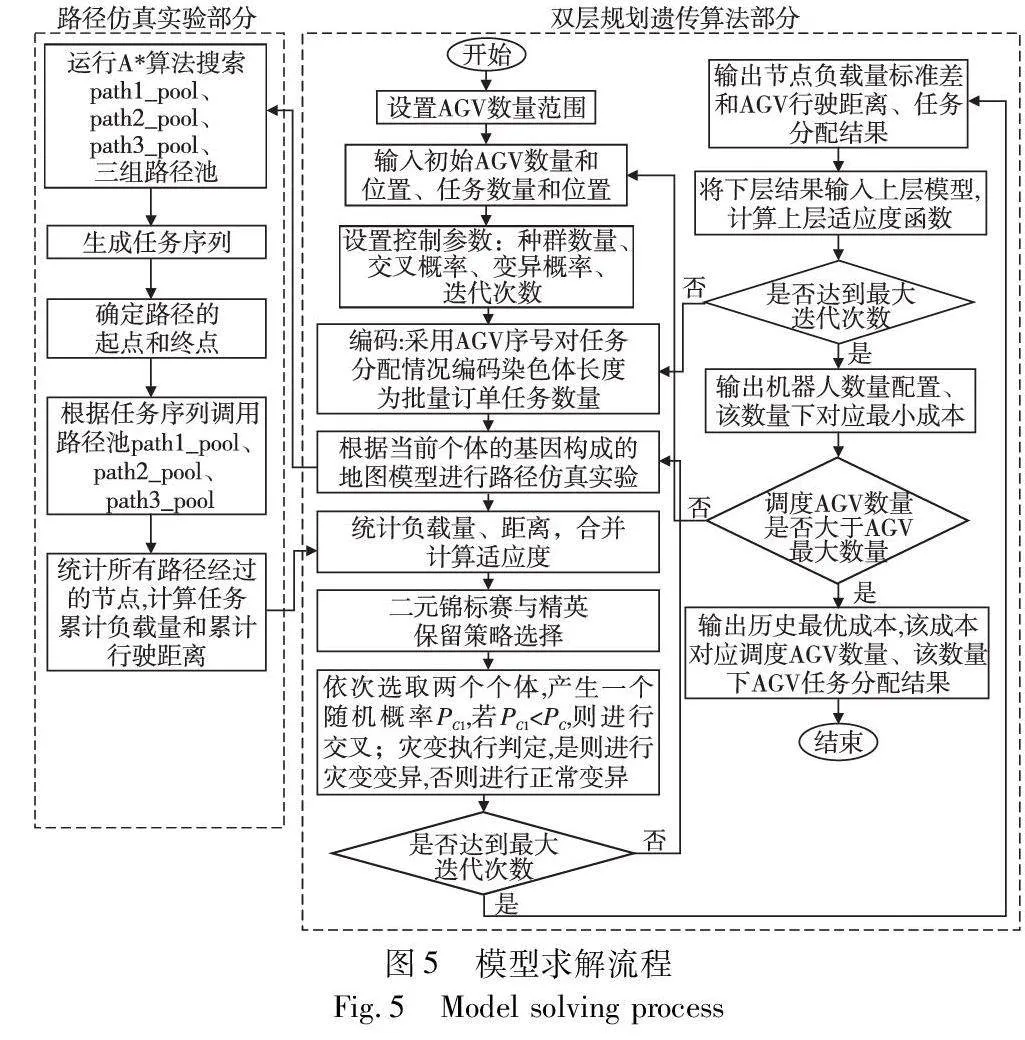
3.2 模型求解流程

A*算法是一种常用的启发式搜索算法，用于解决路径规划和图搜索等问题，它在找到最短路径时能够具有较好的效率和准确性，因此本文采用A*算法进行AGV路径仿真实验。使用改进的自适应遗传算法对不同数量AGV完成批量订单任务的任务分配进行优化。具体步骤如下：

a）设置上层模型中AGV的最大数量和最小数量。

b）以最小AGV数量为初始配置，确定批量订单任务数量，对任务分配问题进行随机生成初始种群pop；设置种群规模N，交叉概率Pc，变异概率Pm，迭代次数I。

c）编码。

d）仿真路径实验：遍历当前种群中的染色体，构成对应的图模型路径进行仿真实验。

（a）确定货架位置、拣选台位置、AGV初始位置、任务位置，形成相应的地图模型。

（b）设置AGV出入口到任务序列的第一个任务为第一段路径、设置当前任务到拣货台为第二段路径、设置拣货台到当前任务为第三段路径、设置当前任务到下一任务为第四段路径。

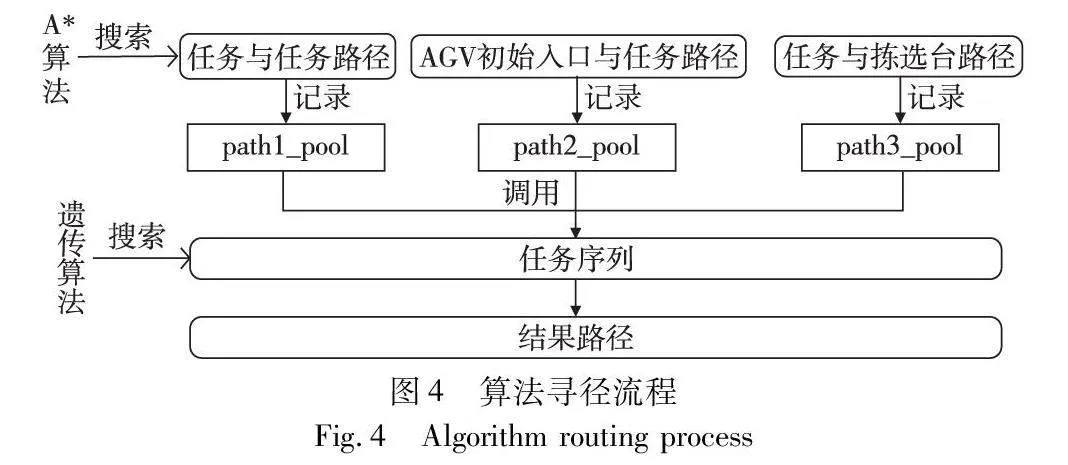
（c）行驶路径寻优。使用A*算法搜索AGV完成任务的最优路径。考虑到实际场景遍历式迭代搜索路径的复杂性，仿真路径实验思路为：设置路径池，记录所有任务与任务之间的路径、拣选台与任务之间的路径、AGV初始入口与任务之间的路径；根据待搜索路径的任务序列调用此路径池，其中第一段路径调用path2_pool、第二与三段路径调用path3_pool、第四段路径调用path1_pool；记录路径。算法寻径流程如图4所示。

（d）计算值。计算AGV完成任务经过节点的节点负载量与行驶距离。

（e）实验终止条件。判断AGV是否完成所有任务的拣选，若完成则输出负载量和行驶距离，实验结束。

e）适应度函数。下层考虑的目标函数为多目标函数，因此在计算适应度函数时，采用将多目标函数转换为单目标函数的方法计算适应度值，适应度值为AGV完成任务的节点负载量标准差、AGV行驶总距离的倒数（AGV行驶距离由运行A*算法寻径得到），将两个适应函数值分别赋予权重，并相加作为适应度评价指标。为保证AGV任务分配结果不被多目标函数其中某一个目标函数过度影响，因此设置合理的调整系数值。

f）选择。

g）交叉。

h）变异。

i）收敛判断。如果Inter>I，迭代终止，否则pop（Inter）=newPop（Inter），Inter=Inter+1，返回步骤e）。

j）将下层计算结果输入上层模型，计算AGV完成所有任务所花费的总成本。找到调度该数量AGV下的最小总成本，并得到任务分配结果。

k）将AGV的调度数量增加一个，返回步骤b）。

l）若AGV的调度数量达到AGV数量设置上限，则停止计算，输出历史最优成本、调度AGV的数量与任务分配结果。模型求解流程如图5所示。

4 算例仿真

为验证SAGA的有效性，使用MATLAB 2019a完成各项仿真实验，分别对GA［22］、AGA［23］、IAGA［24］以及文献［16］的蚁群算法部分进行仿真，设置小规模算例和大规模算例实验。仿真环境设定为某32 m×42 m的电子商务仓库，以32×42的栅格刻画仿真环境。每台AGV的固定成本为6 万元，按照每台AGV的功率为100 W/h，电费为0．86 元/kW·h计算得出，其行走单位距离所花费的成本为0.000 83 元/m，考虑每台AGV的折旧费用为2万/年计算得出，一台AGV在单位时间内负载量不均衡造成的延误时间成本和空闲成本为0.000 6 元/s，转换系数β为40，由于AGV的固定成本相同，以下仿真结果只包括AGV的运行成本、延误时间成本以及空闲成本。下层多目标函数设置如下：

f=0.5×75.5×f1+0.5×0.3×f2

算法参数中，SAGA、GA、AGA、IAGA设置如下：初始化种群个数设为100个，交叉概率Pc=0.8，变异概率Pm=0.07，小规模迭代400次，大规模迭代700次。蚁群算法参数设置如下：小规模算例蚂蚁数antNum1=20，大规模算例蚂蚁数antNum2=40，信息挥发因子为0.1，信息素重要程度为1，启发因子重要程度为5，信息素增加强度系数为50，小规模迭代400次，大规模迭代700次。为了保证测试的公平性，实验中所有的数据都是运行20次的均值。

4.1 小规模算例

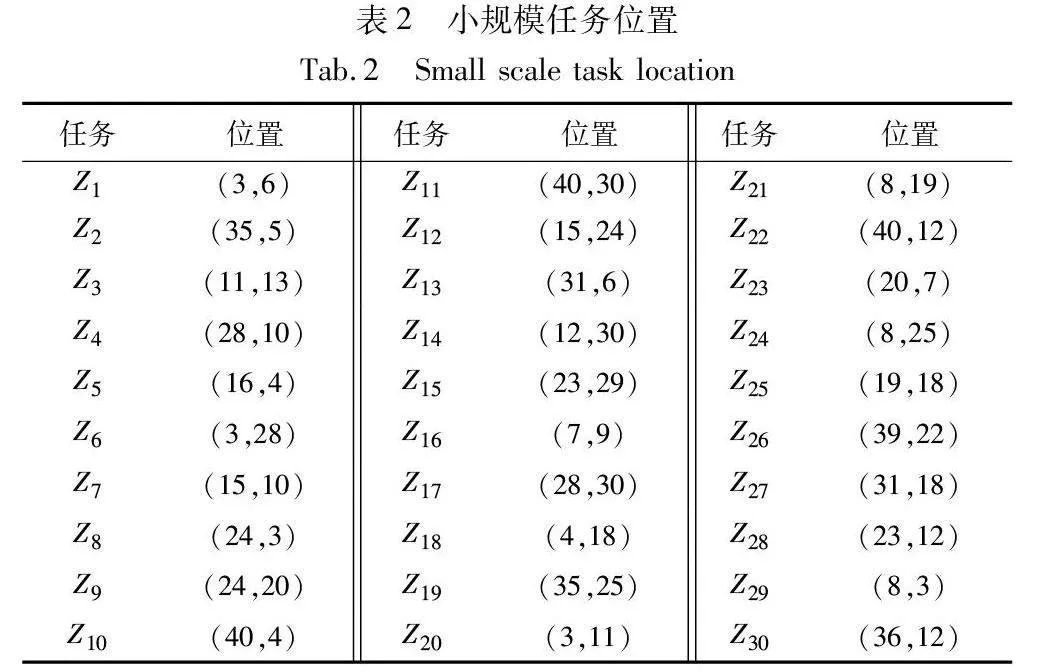
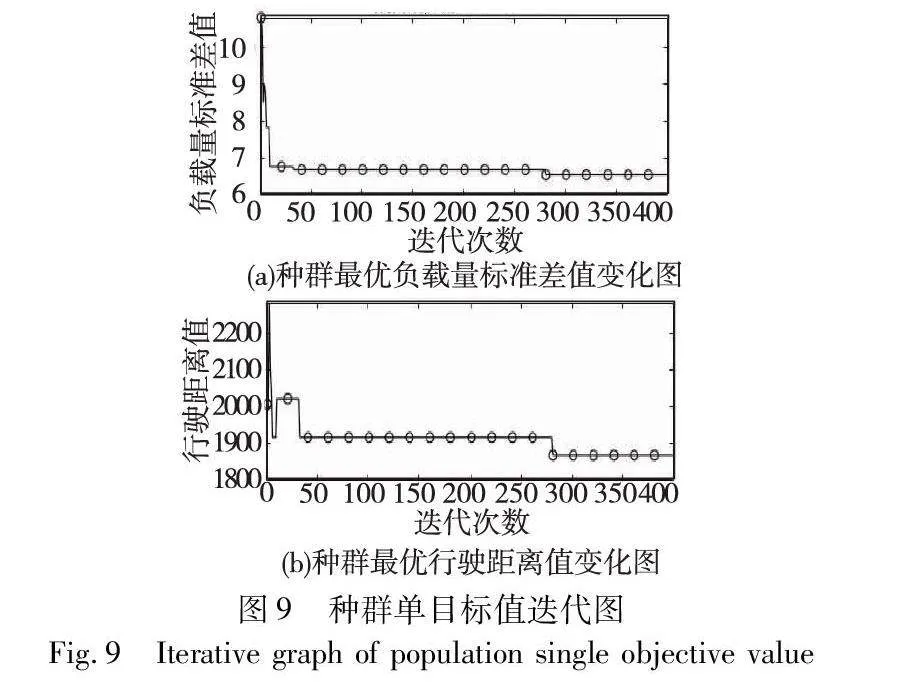
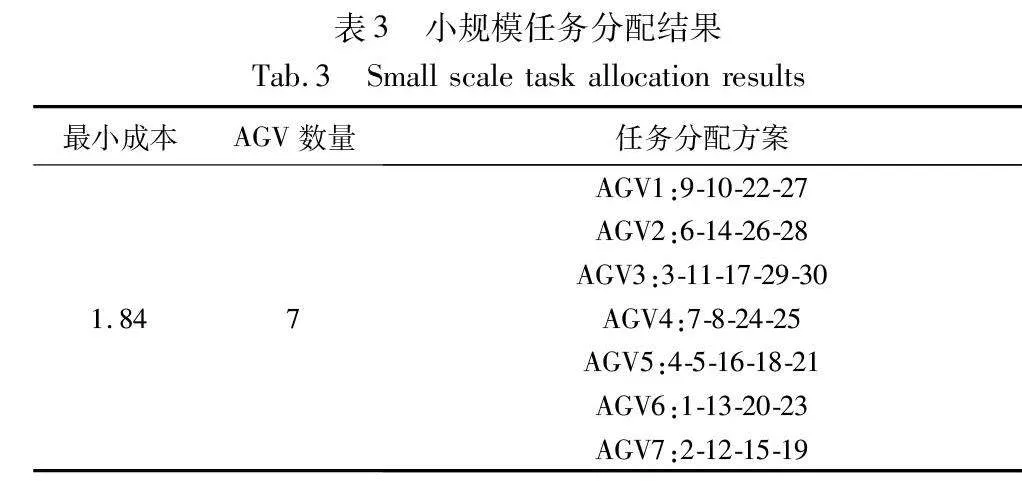
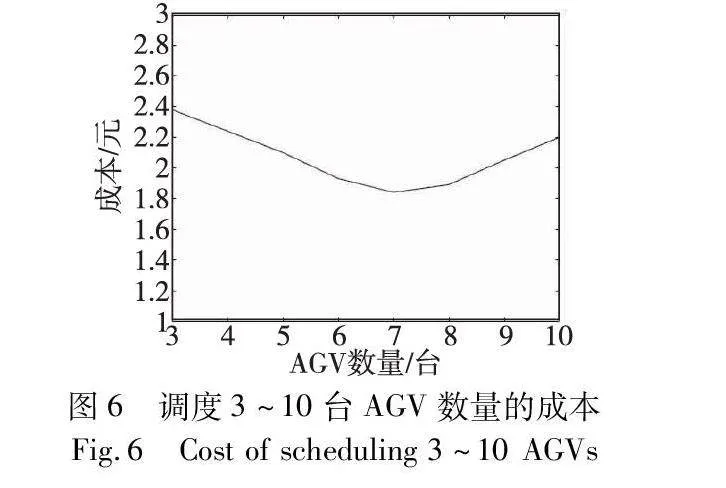
小规模实验参数中，设置3～10个AGV完成任务数量为30个的单批订单，拣选台的位置为（20，1） ，由于AGV在进行一批订单的拣选前都在一个AGV出入口排队等待，故指定AGV的初始位置都为（29，1），任务坐标位置如表2所示。仿真结果如图6～9、表3所示。

4.2 大规模算例

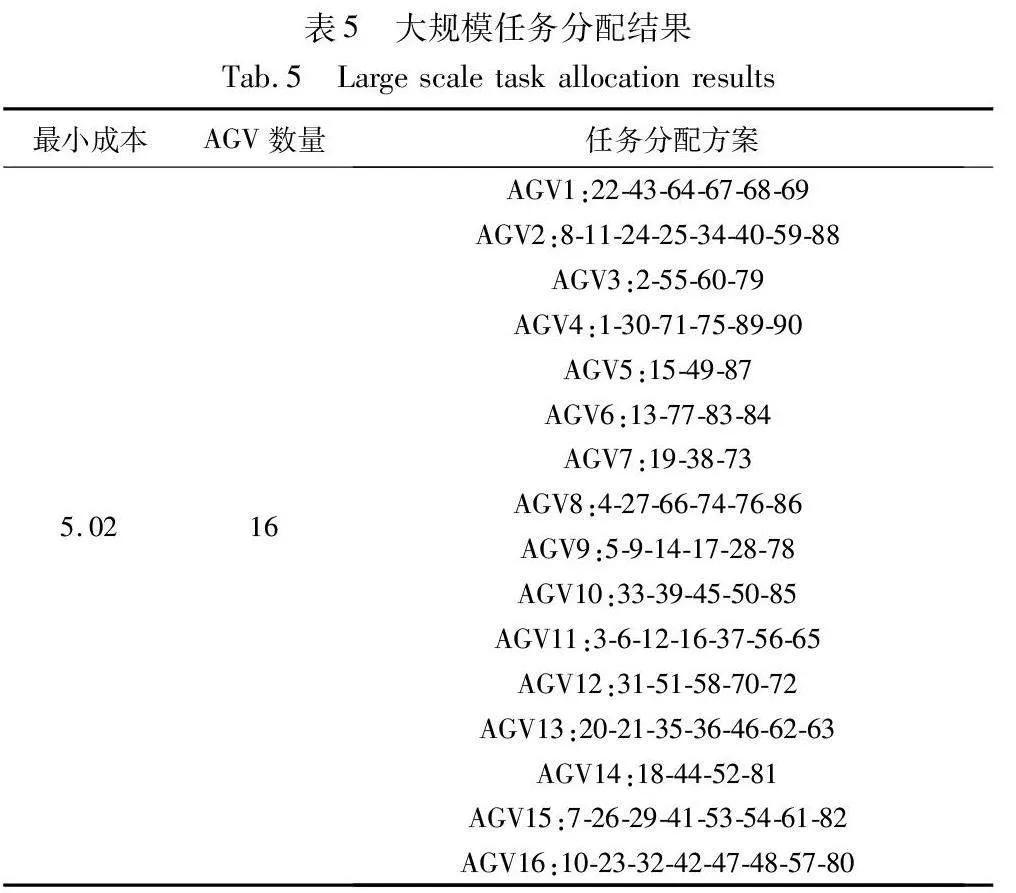
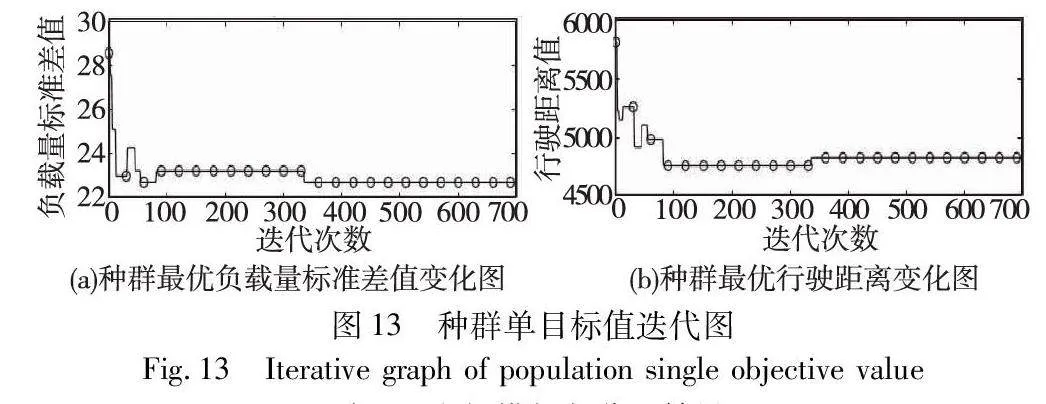
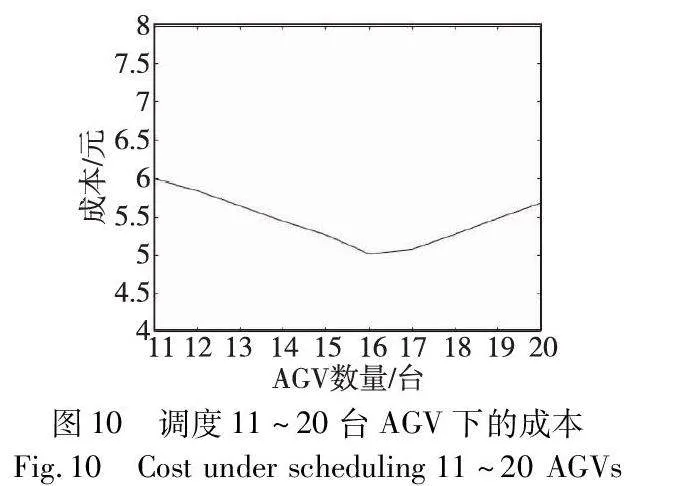
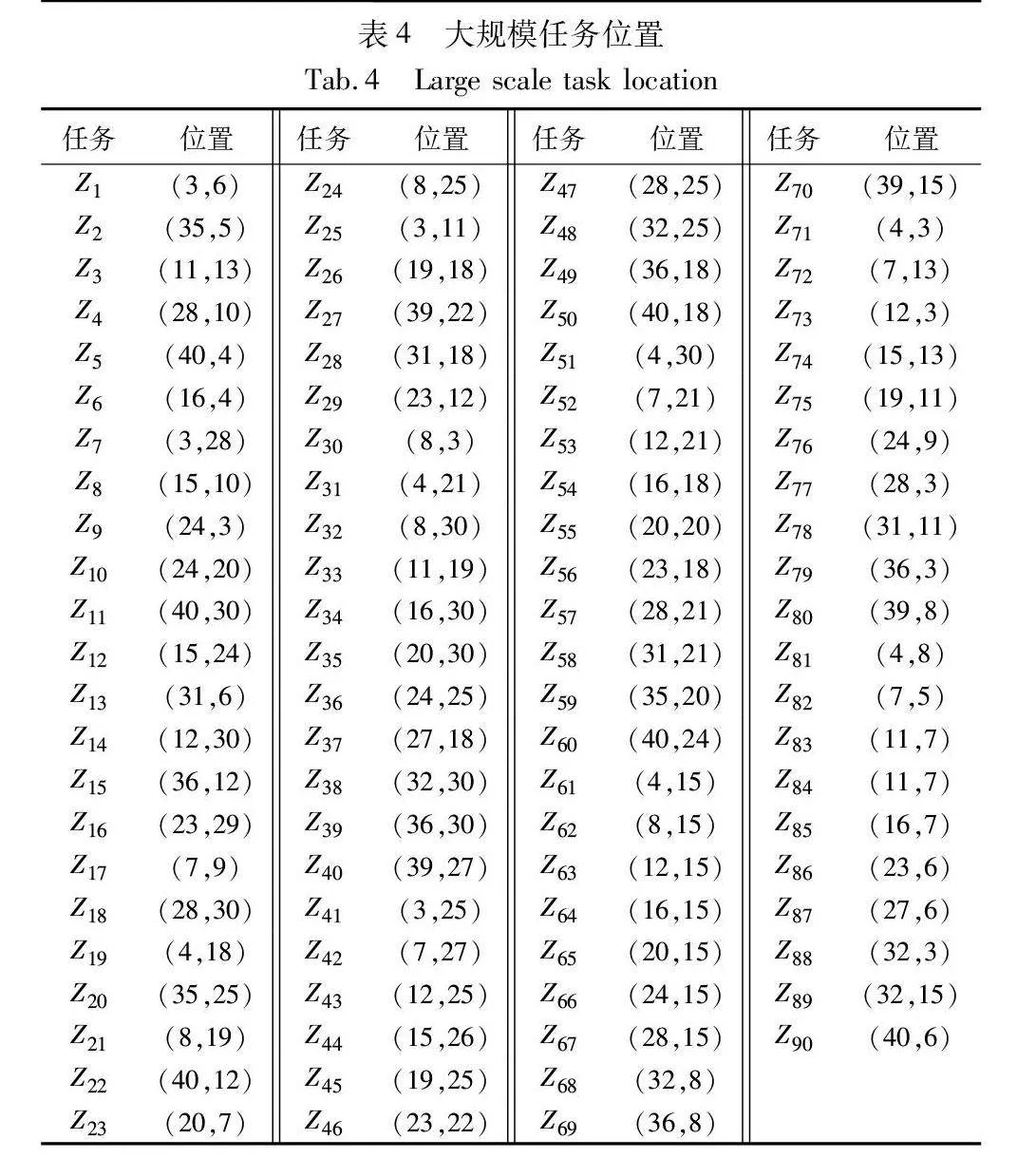
为验证本文方法能有效解决大规模AGV的任务分配问题，在大规模算例中仓库环境设置与小规模相同，AGV初始位置为（29，1），大规模任务位置如表4所示。AGV的数量为11～20个，模拟三批订单，其任务数量为90个，仿真结果如图10～13、表5所示。

4.3 实验结果分析

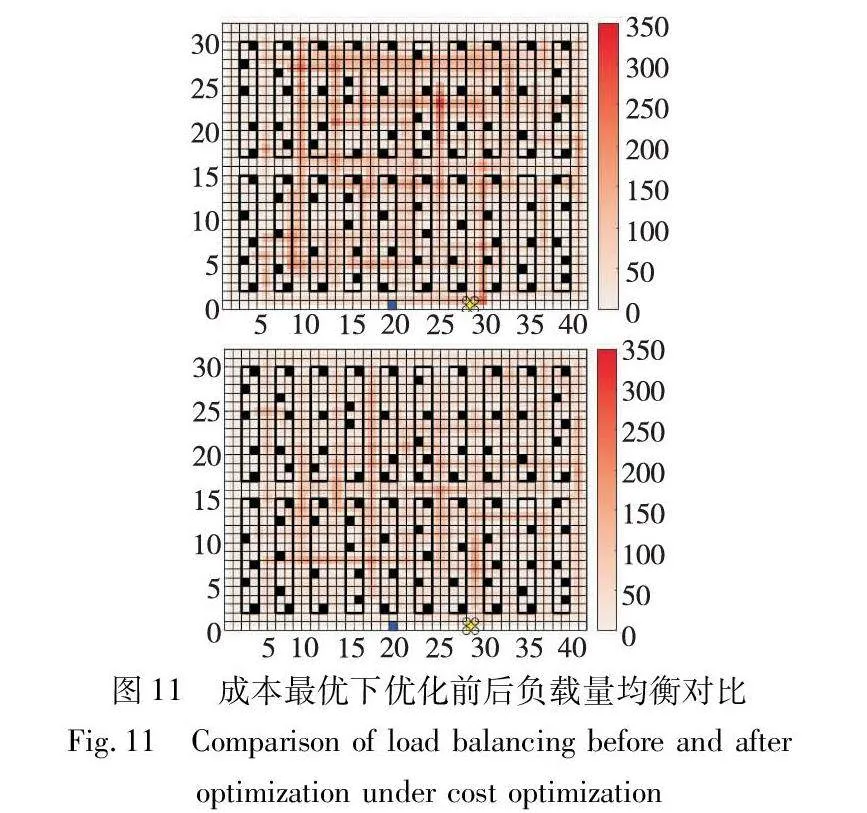
如图6、10所示，对于小规模算例和大规模算例，皆存在一个最佳AGV数量使得系统作业成本最小，当调度7个、16个AGV时，此时作业总成本最小。调用高于7个、16个AGV的成本更高，是由于随着AGV调度的数量增加，AGV空闲率增加，进而使得成本增加。

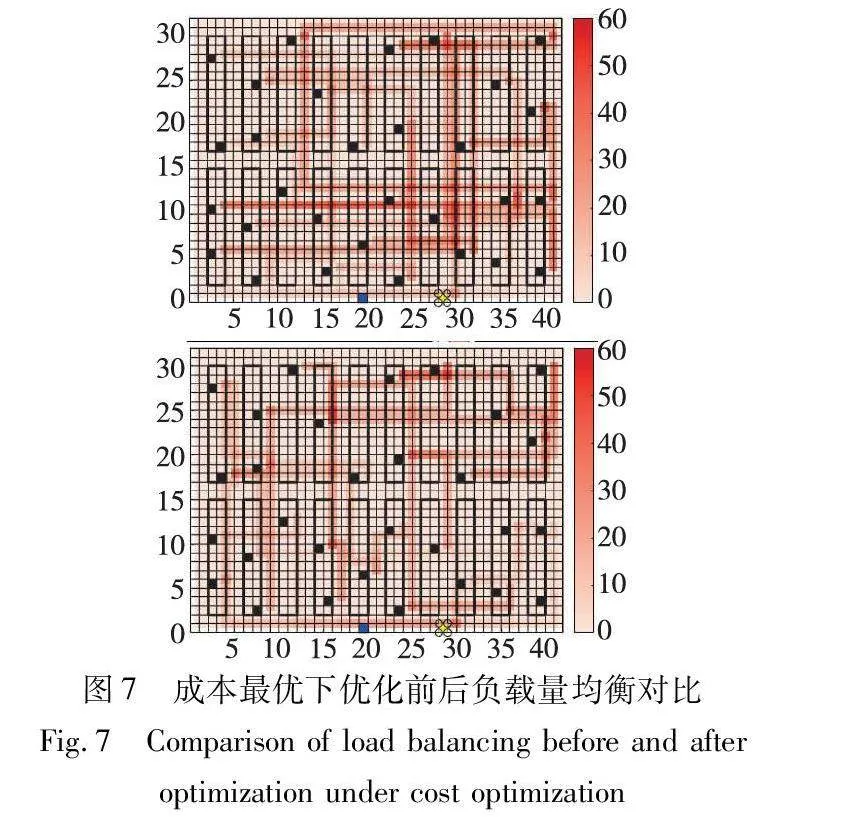
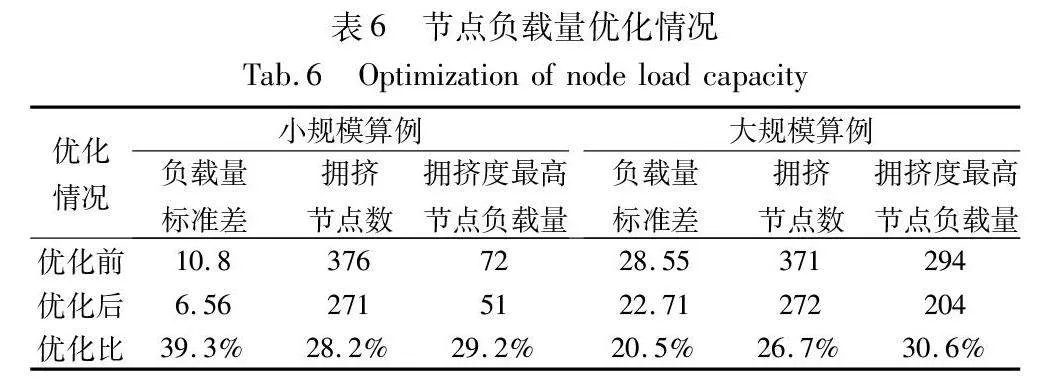
对调度成本最优下的AGV数量进行任务分配优化，仿真结果如图7、11所示，表示调度7个、16个AGV时，AGV任务分配优化前后的系统节点负载量对比情况，由于任务到拣选台之间的路径行走产生的负载情况不受任务分配的影响，所以仿真未记录此部分路径负载图。使用改进的SAGA算法分别就大小规模算例进行优化，节点负载量优化结果如表6所示，优化后负载量标准差分别优化了20.5%和39.3%。将节点负载量高于平均节点负载量2倍定义为拥挤节点，优化后拥挤节点数分别下降了26.7%和28.2%。由于任务分配的优化，AGV在完成当前任务后分配下一任务时，前往下一任务需经过的节点可能存在拥挤节点数多，而对于另一个AGV从上一任务前往此任务位置，可能经过的拥挤节点相对较少，则会在算法迭代时不断寻优，寻找全局负载量标准差相对最优的任务分配方案。综合来说，优化之后的节点负载量明显均衡提升，大小规模算例中拥挤度最高节点负载量分别降低了30.6%和29.2%。

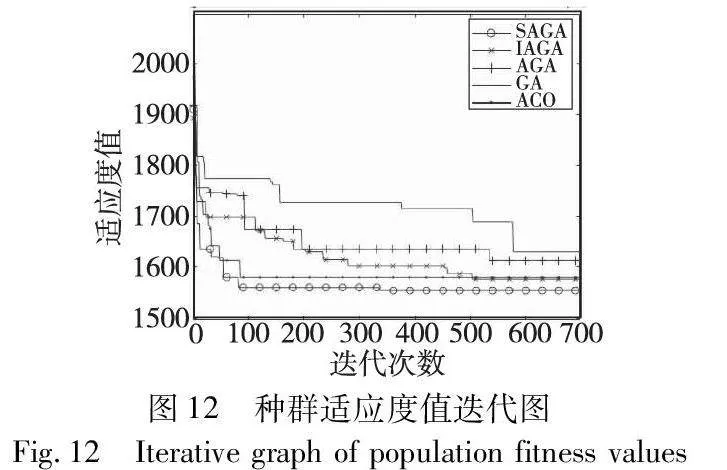
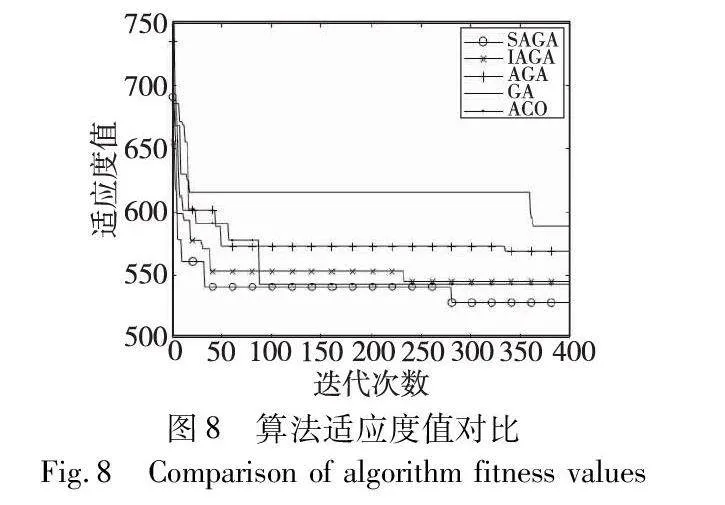
图9和13为单目标适应度迭代情况，如图8、12显示，相比较GA、AGA、IAGA、蚁群算法，本文基于sigmoid函数改进的自适应遗传算法所计算的总适应度、单目标都有较好的收敛效果，并得到AGV任务分配方案。

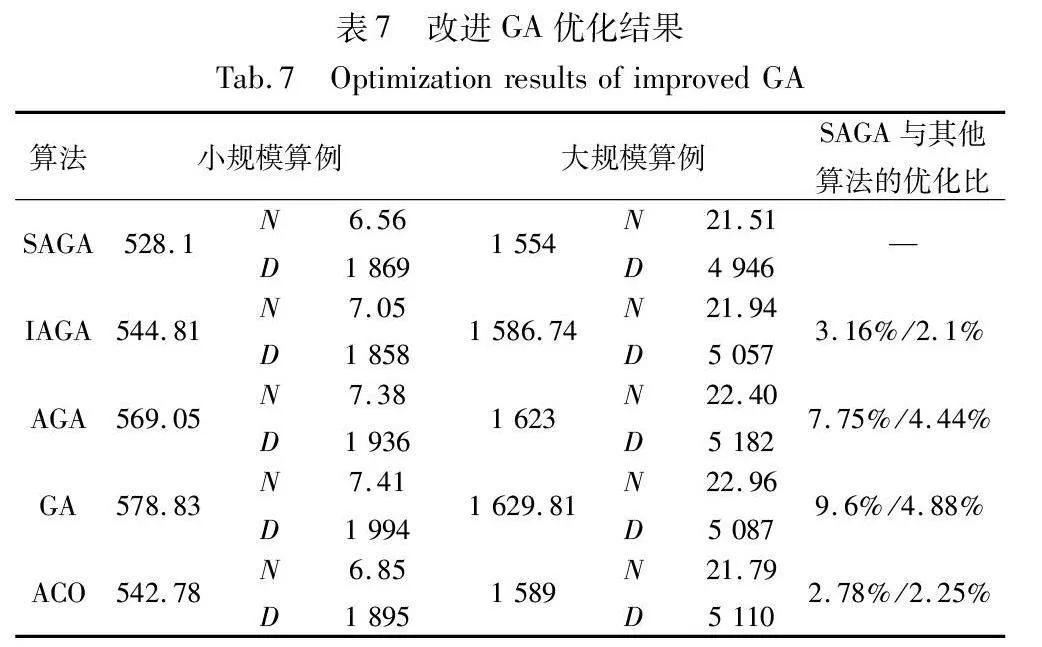
从五种算法的收敛结果来看，GA收敛速度最慢，且收敛平滑度较差，而AGA与IAGA两种算法相较于传统GA，收敛速度和平滑度有所改善，但都较容易早熟。蚁群算法收敛速度最快，但其早熟概率也比较高，容易导致任务分配质量下降，是由于蚂蚁在搜索过程中依赖于其他蚂蚁的信息，可能会导致算法陷入局部最优解，特别是在搜索进行到一定程度后，所有个体所发现的解完全一致，不能对解空间进一步搜索，不利于发现更好的解。而SAGA在收敛平滑的同时，避免了陷入局部最优解而导致的早熟，其原因在于：使用sigmoid函数来转换适应度值，在一定程度上增强了算法的自适应性，sigmoid函数的特点是将值域映射到0～1，对适应度值进行了归一化处理，每个个体被选中的概率就与其适应度值成比例，增加了适应度值相对较小的个体在算法中的生存机会。并且函数值变化较为平滑，防止适应度值在遗传算法迭代过程中发生剧烈的变化，避免算法的震荡和陷入局部最优，这样增强了算法的探索能力，使其更有可能跳出局部最优解，找到更优的解决方案。此外，在算法的初期阶段，由于适应度值差异较大，一些个体的操作概率过高，导致算法收敛速度缓慢，使用sigmoid函数转换适应度值，降低了个体操作概率的差异性，加入快速判断个体是否交叉的方法，减少了无效交叉操作，从而加速算法的收敛速度。同时为防止算法跳出局部最优，加入了改进的灾变策略。改进GA优化结果如表7所示。

5 结束语

为提高自动拣货系统作业效率、降低作业成本，本文考虑了造成自动拣货系统拥堵的关键因素，提出一种基于AGV数量与任务分配的双层规划模型，上层以最小化运行成本、延误时间成本、AGV空闲成本和AGV固定成本为目标函数，以AGV数量为决策变量，下层构建最小化节点负载量标准差和AGV空闲率的多目标函数，以任务分配为决策变量。运用A*算法对AGV完成任务所行驶的路径进行仿真实验，并设计改进的自适应遗传算法对模型求解。仿真结果显示，通过此模型，提升了系统的负载量均衡水平，降低了AGV完成任务的行驶距离，考虑成本因素优化了AGV数量配置。

本文针对现有任务分配算法计算低效、易早熟等问题：a）在自适应遗传算法的基础上，加入sigmoid函数，增强自适应性、探索能力和收敛速度，并且增加算法的鲁棒性；b）改进交叉算子通过引入快速判别步骤防止了相同个体之间的无效交叉，减少计算资源；c）加入并改进了灾变策略，执行灾变时在变异环节增加变异位进行变异，帮助遗传算法跳出局部最优解，增加算法的搜索范围，从而提高搜索效率和优化结果的质量。通过不同规模仿真实验证明，SAGA的收敛效果均优于其他算法，验证了模型和算法对于自动拣货系统AGV任务分配优化问题具有良好的效果，帮助自动拣货系统降低作业成本。对于后续的研究，由于路径优化也是降低系统拥堵与AGV作业行驶距离的关键决策，未来还需加入AGV路径优化与任务分配进行协同优化，这有待进一步研究。

参考文献：

［1］Zhong Meisu， Yang Yongsheng， Sun Shu， et al. Priority-based speed control strategy for automated guided vehicle path planning in automated container terminals［J］. Trans of the Institute of Measurement and Control， 2020， 42（16）： 3079-3090.

［2］Suman P P， Reddy P， Chenna R P. Energy and congestion-aware load balanced multi-path routing for wireless sensor networks in am-bient environments［J］. Computer Communications， 2022， 195（5）： 217-226.

［3］宋海权. 基于复杂网络理论的网络交通拥堵问题研究［D］. 成都： 西南交通大学， 2016. （Song Haiquan. Research of network traffic congestion based on complex networks theory［D］. Chengdu： Southwest Jiaotong University， 2016.）

［4］项俊平. 城市道路交通信号区域均衡控制方法及应用研究［D］. 合肥： 中国科学技术大学， 2018. （Xiang Junping. Study on the method and application for urban road traffic signal regional equilibri-um control［D］. Hefei： University of Science and Technology of China， 2018.）

［5］许丽丽， 詹燕， 鲁建厦，等. 四向穿梭车仓储系统复合作业调度优化［J］. 浙江大学学报：工学版， 2023， 57（11）： 2188-2199. （Xu Lili， Zhan Yan， Lu Jianxia， et al. Optimization of composite job scheduling for four way shuttle warehouse system［J］. Journal of Zhejiang University： Engineering Edition， 2023， 57（11）： 2188-2199.）

［6］周航， 秦实宏， 方泾丞. 基于混合遗传禁忌搜索算法的多机器人任务分配［J］. 自动化与仪表， 2023， 38（11）： 35-39. （Zhou Hang， Qin Shihong， Fang Jingcheng. Multi robot task allocation based on hybrid genetic taboo search algorithm［J］. Automation and Instrumentation， 2023， 38（11）： 35-39.）

［7］李腾， 张茹兰， 丁佩佩. 机器人履约系统任务分配与货架储位再指派联合优化［J］. 科学技术与工程， 2023， 23（26）： 11271-11281. （Li Teng， Zhang Rulan， Ding Peipei. Joint optimization of task allocation and shelf storage reassignment in robot fulfillment systems［J］. Science， Technology and Engineering， 2023， 23（26）： 11271-11281.）

［8］李缘. 多AGV路径规划算法与任务分配调度策略研究［D］. 杭州：浙江大学， 2022. （Li Yuan. Research on multi AGV path planning algorithm and task allocation and scheduling strategy［D］. Hangzhou： Zhejiang University， 2022.）

［9］于佳乔， 李岩. 基于改进遗传算法的自动导航小车路径规划调度［J］. 机床与液压， 2022， 50（5）： 16-20. （Yu Jiaqiao， Li Yan. Path planning and scheduling of automatic navigation vehicles based on improved genetic algorithm［J］. Machine Tool and Hydraulic， 2022， 50（5）： 16-20.）

［10］Zou Wenqiang， Pan Quanke， Wang Ling， et al. Efficient multiobjective optimization for an AGV energy-efficient scheduling problem with release time［J］. Knowledge-Based Systems， 2022， 242（2）： 45-56.

［11］王子意. 多AGV系统的路径规划与调度算法的研究［D］. 北京：北京邮电大学， 2019. （Wang Ziyi. Research on path planning and scheduling algorithms for multi AGV systems［D］. Beijing ：Beijing University of Posts and Telecommunications， 2019.）

［12］孟宪福， 张晓燕. 对等网络环境下多目标约束的并行任务调度策略研究［J］. 计算机集成制造系统， 2008（4）： 761-766. （Meng Xianfu， Zhang Xiaoyan. Research on parallel task scheduling strategy with multi-objective constraints in peer-to-peer network environment［J］. Computer Integrated Manufacturing System， 2008（4）： 761-766.）

［13］Zlot R A， Stentz A T， Dias A B， et al. Multi-robot exploration controlled by a market economy［C］//Proc of IEEE International Confe-rence on Robotics and Automation. Piscataway， NJ： IEEE Press， 2002： 3016-3023.

［14］Das G P， McGinnity T M， Coleman S A， et al. A distributed task allocation algorithm for a multi-robot system in healthcare facilities［J］. Journal of Intelligent & Robotic Systems， 2015， 80（1）： 33-58.

［15］Garapati K， Roldan J J， Gatron M， et al. A game of drones： game theoretic approaches for multi-robot task allocation in security missions［C］//Proc of the 3rd Iberian Robotics Conference. Cham： Springer， 2017： 855-866.

［16］秦新立， 宗群， 李晓瑜，等. 基于改进蚁群算法的多机器人任务分配［J］. 空间控制技术与应用， 2018， 44（5）： 55-59. （Qin Xinli， Zong Qun， Li Xiaoyu， et al. Multi robot task allocation based on improved ant colony algorithm［J］. Space Control Technology and Applications， 2018， 44（5）： 55-59.）

［17］Wei Changyun， Ji Ze， Cai Boliang. Particle swarm optimization for cooperative multi-robot task allocation： a multi-objective approach［J］. IEEE Robotics and Automation Letters， 2020， 5（2）： 2530-2537.

［18］丁一， 袁浩， 方怀瑾，等. 考虑冲突规避的自动化集装箱码头AGV优化调度方法［J］. 交通信息与安全， 2022， 40（3）： 96-107. （Ding Yi， Yuan Hao， Fang Huaijin， et al. Optimization sche-duling method for automated container terminal AGV considering conflict avoidance［J］. Traffic Information and Safety， 2022， 40（3）： 96-107.）

［19］张子迎， 陈云飞， 王宇华，等. 基于启发式深度Q学习的多机器人任务分配算法［J］. 哈尔滨工程大学学报， 2022， 43（6）： 857-864. （Zhang Ziying， Chen Yunfei， Wang Yuhua， et al. Multi robot task allocation algorithm based on heuristic deep Q-learning［J］. Journal of Harbin Engineering University， 2022， 43（6）： 857-864.）

［20］邓辅秦， 黄焕钊， 谭朝恩，等. 结合遗传算法和滚动调度的多机器人任务分配算法［J］. 计算机应用， 2023， 43 （12）： 3833-3839. （Deng Fuqin， Huang Huanzhao， Tan Chaoen， et al. Multi robot task allocation algorithm combining genetic algorithm and rolling scheduling［J］. Journal of Computer Applications， 2023， 43（12）： 3833-3839.）

［21］方耀宁， 郭云飞， 扈红超，等. 一种基于sigmoid函数的改进协同过滤推荐算法［J］. 计算机应用研究， 2013，30（6）： 1688-1691. （Fang Yaoning， Guo Yunfei， Hu Hongchao， et al. An improved collaborative filtering recommendation algorithm based on sigmoid function［J］. Application Research of Computers， 2013， 30（6）： 1688-1691.）

［22］张远春， 范秀敏， 驹田邦久. 基于仿真优化的多种类型AGV数量配置优化方法［J］. 中国机械工程， 2011， 22（14）： 1680-1685. （Zhang Yuanchun， Fan Xiumin， Kota Bangjiu. Optimization method for multiple types of AGV quantity allocation based on simulation optimization［J］. China Mechanical Engineering， 2011， 22（14）： 1680-1685.）

［23］张京钊， 江涛. 改进的自适应遗传算法［J］. 计算机工程与应用， 2010， 46（11）： 53-55. （Zhang Jingzhao， Jiang Tao. Improved adaptive genetic algorithm［J］. Computer Engineering and Application， 2010， 46（11）： 53-55.）

［24］刘畅， 张承瑞， 孙玉玺. 改进自适应遗传算法在多载AGV调度的应用研究［J］. 小型微型计算机系统， 2021， 42（11）： 2241-2245. （Liu Chang， Zhang Chengrui， Sun Yuxi. Research on the app-lication of improved adaptive genetic algorithm in multi load AGV scheduling［J］. Journal of Chinese Micro Computer System， 2021， 42（11）： 2241-2245.）