考虑模糊质检时间的柔性作业车间动态调度问题

摘 要：为解决更符合现实情形的模糊质检时间柔性作业车间动态调度问题，以最小化完工时间为目标，立足紧急插单、机器在空载运行时发生故障和机器在加工工件时发生故障的三种故障情形，建立了带模糊质检时间的机器故障、紧急插单重调度模型。设计了基于元胞自动机邻域搜索和随机重启爬坡算法的改进遗传算法求解模型，即针对车间调度问题中存在的订单排序和机器选择双决策问题特征，设计包含工序码和机器码的双层编码方案，并基于遗传算法思想对工序码和机器码设计相应的交叉、变异等遗传操作。同时，将遗传操作应用于基于元胞自动机的邻域搜索算法框架中以增强算法全局搜索能力，整合基于关键工序的随机重启爬坡算法以提高算法局部开发能力。实验选取10个柔性车间调度算例验证了所提算法的有效性，同时，测试1个模糊质检时间柔性车间调度算例验证了模型的有效性。另外，实验也测试了不同故障场景，得出该动态调度方法优于实际场景中常使用的“工件后移”调度策略。

关键词：柔性作业车间调度问题； 模糊质检时间； 重调度； 遗传算法

中图分类号：TP306.1;TH186 文献标志码：A

文章编号：1001-3695（2024）08-015-2351-09

doi：10.19734/j.issn.1001-3695.2023.11.0575

Flexible job shop dynamic scheduling problem withfuzzy quality control time

Zhang Xiaonan1， Gong Jialong1， Jiang Shuai1， Wang Luyu1， Li Yang2

（1.School of Mechanical & Electrical Engineering， Shaanxi University of Science & Technology， Xi’an 710021， China; 2.School of Economics & Management， Liaoning Petrochemical University， Fushun Liaoning 113001， China）

Abstract：To solve the flexible job shop dynamic scheduling problem with fuzzy quality control time， which is more realistic， this paper established two rescheduling models for machine breakdown and urgent order insertion with the objective of minimizing completion time. Two models were for three failure scenarios： emergency order insertion， machine failure during no-load operation， and machine failure during work-piece processing. To solve this model， this paper designed a novel genetic-neighborhood search algorithm that integrated cellular-automata-based neighborhood search and random restart hill-climbing. Aiming at the characteristics of dual sub-decisions involving order sequencing and machine selection， this paper designed a two-layer coding scheme including process code and machine code， and designed corresponding genetic operations such as crossover and mutation for them. After that， this paper applied the genetic operations into the framework of cellular-automata-based neighborhood search to enhance the algorithm’s global search capability， and integrated the random restart hill-climbing algorithm based on key operations to improve the algorithm’s local development capability. Experiments tested 10 flexible job shop scheduling instances and one flexible job shop scheduling instance with fuzzy quality control time to verify the effectiveness of the proposed algorithm and models. In addition， the test results under different failure scenarios show the proposed method outperforms the backward-based scheduling strategy used in practice.

Key words：flexible job shop scheduling problem; fuzzy quality test time; rescheduling; genetic algorithm

0 引言

柔性作业车间调度问题（flexible job shop scheduling problem，FJSP）是指有m台机器和n个工件，每个工件存在L道工序，每道工序可以选择任意一台机器进行加工的生产调度问题［1］。然而，在FJSP实际执行期间可能会发生机器故障、紧急插单等多种干扰事件，这些干扰事件使得原有调度方案失效，若不及时处理会造成生产紊乱或生产中断，导致工件无法如期完成。为避免此类情况发生，决策者必须在有限的时间内作出代价小、响应迅速的方案变更以保证生产系统稳定运行。另外，为防止出现大批不合格品，同时避免上道工序的不合格品流入下道工序，生产者通常会在每道工序后增设质检环节，然而，工序的质检时间依赖产品的不合格程度，呈现出不确定特性［2］。举个例子，一个合格产品正常流入下一工序，质检时间小且固定；一个轻微不合格产品通过少量修正流入下一道工序，质检时间轻微增加；一个严重不合格产品通过大量修正后流入下一道工序，质检时间增加显著。本文针对考虑模糊质检时间的柔性作业车间动态调度问题（slexible job shop dynamic scheduling problem with fuzzy quality control time，FJDSP-FQC）展开研究。相较于常规FJSP，该问题同时具有模糊性和动态性特征，更符合实际车间作业过程，但也更复杂、更难解决。

现有文献多集中于研究常规动态FJSP问题（flexible job shop dynamic scheduling problem，FJDSP），而考虑模糊质检时间的FJDSP研究几乎没有。例如：Luo［3］以最小化最大完工时间为目标，研究了紧急插单事件干扰的FJDSP；裴小兵等人［4］以订单延期交货为目标，研究了紧急插单的FJDSP；张祥等人［5］考虑全局任务最大生产完成时间、机器负载和能耗等多优化目标，研究了紧急插单的多目标FJDSP；包博等人［6］研究了考虑设备故障干扰的FJDSP； 文献［7，8］研究了考虑机器故障的多目标FJDSP。在算法应用方面，众多算法已被广泛应用于动态FJDSP。侯娅楠等人［9］在传统遗传算法中融入了混合故障矩阵对机器混合故障下的FJDSP进行求解； Sajadi等人［10］设计了“求解单目标→求解多目标”的二阶遗传算法求解机器故障的多目标FJDSP；苗志鸿等人［11］等在遗传算法中融合锦标赛与精英选择，求解紧急插单的FJDSP；金鹏博等人［12］将遗传算法与BP神经网络相结合，求解机器故障的FJDSP；李瑞等人［13］将遗传算法与人工群峰算法融合，并在探索蜂阶段引入了六种变邻域方法，提高算法局部开发能力。此外，Caldeira等人［14］提出改进Jaya算法求解FJDSP，利用涉及三点交换和关键工序块随机交换的两种局部搜索策略改善解质量；Alzaqebah等人［15］整合头脑风暴算法、自适应多选择法和邻域搜索算法； Baykasogˇlu等人［16］提出随机贪婪自适应搜索算法求解，并采用贪婪局部搜索进行二次深化；Zarrouk等人［17］针对FJSP包含的订单排序和机器选择双决策问题，设计了面向工序顺序和机器分配的两级粒子群优化算法； Serna等人［18］将禁忌搜索算法扩展应用于元胞自动机邻域搜索框架中，将可行解扩展至其更大邻域集合中来选择最优解，以提高全局搜索能力。

通过梳理可知：a）现有FJDSP的研究主要涉及“紧急插单”“机器故障”等干扰事件［3～8］，且其在考虑机器故障时多默认机器在空载时发生故障，实际上，机器可能在加工工件时发生故障，这种场景下，加工中断的工件需要重新流转到其他机器上完成剩余部分的加工;b）遗传算法［9～13］、改进Jaya算法［14］、随机贪婪自适应搜索算法［16］等各类算法已被广泛应用于求解FJDSP，然而，寻求具有更高求解效率和质量的改进手段还需进一步探索。另外，本文也发现，在应用遗传算法求解的文献中，如文献［9～13］，将遗传算法与其他算法融合以保持算法全局搜索能力和改善算法局部开发能力，是改进的主流手段。

基于此，本文扩展FJDSP的故障情形为“紧急插单”“机器在空载运行时发生故障”和“机器在加工工件时发生故障”三种干扰情况，同时考虑模糊质检时间，以最小化完工时间为目标，建立考虑模糊质检时间的FJDSP初始调度模型，并将其进一步修正为带模糊质检时间的机器故障和紧急插单重调度模型。为求解模型，将遗传算法与元胞自动机邻域搜索算法、随机重启爬坡算法融合，设计了基于元胞自动机邻域搜索和随机重启爬坡算法的改进遗传算法（genetic algorithm with cellular automata-inspired neighborhood and random-restart hill-climbing，GA-CARRHCNS）。针对FJDSP包含的订单排序和机器选择双决策问题，设计包含工序码和机器码的双层编码方案，并分别对双层编码段设计相应的交叉、变异等遗传操作；将交叉、变异等遗传操作置于元胞自动机邻域搜索算法框架中以增强算法全局搜索能力，同时，开发基于关键工序的随机重启爬坡算法以提高算法局部开发能力；在满足迭代次数后，继续采用带插入和逆序的常规邻域搜索算法深化最优解的求解质量。实验选取10个FJSP标准算例和1个考虑模糊质检时间的FJSP算例进行测试，验证了本文算法的有效性，同时，测试1个考虑模糊质检时间的FJDSP算例，验证了模型和重调度策略的有效性。

需要说明的是，本文问题具有模糊性和动态性特征，以往FJSP文献中同时考虑模糊性和动态性的仅有文献［19］，然而，两者研究问题和求解技术均不相同。文献［19］考虑模糊交货期，研究了机器故障扰动下的柔性作业车间动态调度问题，并设计改进的自适应免疫遗传算法求解；本文考虑模糊质检时间，考虑故障情形为“紧急插单”“机器在空载运行时发生故障”和“机器在加工工件时发生故障”三种干扰情况，设计GA-CARRHCNS求解。另外，在算法设计方面，元胞自动机邻域搜索思想来源于文献［17］，然而与文献［17］将元胞自动机邻域搜索与禁忌搜索算法融合不同，本文将元胞自动机邻域搜索与遗传算法、随机重启爬坡算法整合；在算例验证部分，也证明了本文算法优于文献［17］。

1 问题描述和模型建立

1.1 问题描述

FJSP可定义为：有n个工件，每个工件i=1，…，n有工序Oij。每道工序Oij都可以在m台机器中选择其中一台进行加工，且工序Oij在机器k上的加工时间为Pijk。研究目标是通过为每道工序选择一台加工机器，并合理安排工序的加工顺序，使总完工时间最小。

本文研究的考虑模糊质检时间的FJDSP是在FJSP基础上进一步考虑模糊质检时间，即同一个工件的两道工序之间存在质检，且质检时间是模糊的，并基于这一问题研究决策者在应对故障干扰事件时（这里考虑“紧急插单”、同时存在“机器在空载运行时发生故障”和“机器在加工工件时发生故障”的机器故障情形），如何在有限的时间内作出代价小、响应迅速的动态变更方案以减少动态事件的影响。

1.2 模糊质检时间和故障场景的说明

1）关于模糊质检时间的说明

本文采用模糊数表示模糊质检时间，即ij=［a，b］，其表示工序Oij的质检时间为模糊数［a，b］的模糊数。

2）关于故障场景的说明

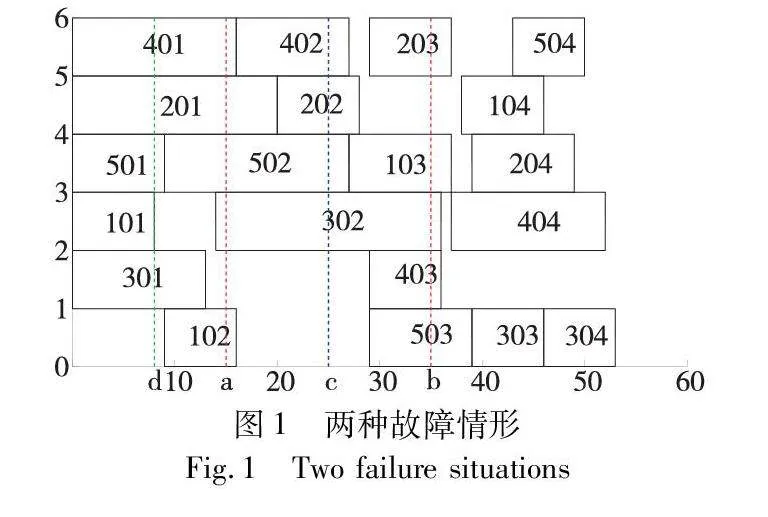
本文考虑了机器故障和紧急插单两种动态事件。为便于理解这两种情况及其相应的重调度模型构建逻辑，这里以图1为例展示了5个工件、6台机器的机器故障和紧急插单情形及其相应的处理策略。图中横坐标为时间，纵坐标为机器号，数字为工件与工序编号，如301表示工件3的第1道工序，虚线a、b表示机器故障发生与修复的时间节点，c对应紧急插单情况的发生节点。

a）在发生机器故障时（如线a时间节点所示），所有工序包括已完工工序101、301、501，正在加工工序201、401、102、302、502，以及未加工工序202、402、103、203、303、403、503、104、204、304、404、504。针对此情况，将故障机器上的正在加工工序及未加工工序定义为新的工序集，其中故障机器上的正在加工工序的加工时间从b点开始计算，其余机器上的正在加工工序的加工时间从a点开始刻画当前状态，建立重调度模型。

b）在发生紧急插单时（如线c时间节点所示），已开始加工工序101、201、301、401、501、102、202、302、402、502，未开始加工工序103、203、303、403、503、104、204、304、404、504。针对此场景，当有新工件插入时，新工件的工序与未开始加工工序定义为新的工序集，加工时间从c点开始刻画当前状态，构建重调度模型。

1.3 假设条件和参数设置

为建立模型，本文考虑以下假设条件：a）初始方案加工从零时刻开始；b）同一时刻下，每个工件只能由一台机器进行加工，且每台机器只能加工一个工件；c）每道工序须在前一工序完成质检后才可加工；d）同一时刻，每道工序只能由一台机器加工；e）当动态事件发生后，保留已完工工序，对剩余工序进行重调度，并从动态事件发生时刻开始。表1列举了模型所需的参数和符号说明。

1.4 模型的建立

建立初始模型如下：

目标函数：

f=min（Cmax）（1）

s.t.

Cijk=Sijk+Pijk×xijk（2）

Sijk≥Ci（j-1）k（3）

Sijk≥Ci（j-1）k+ij（4）

Sijk≥Ci′j′k（5）

Cijk≤Si′j′k（6）

其中：式（1）为最小化最大完工时间；式（2）表示工件在加工过程中不会中断；式（3）表示每道工序需等前一工序完工后才能加工；式（4）表示每道工序都需等到前一道工序质检完成后才可加工；式（5）和（6）表示每台机器在同一时刻只能加工一道工序。

1.4.1 机器故障下的重调度模型

当机器故障事件发生时，定义机器故障发生时的未加工工件数为n′，可用机器为m′，工件集合为J={Ji|（i1=1，2，3，…，n）}，每个工件有hi1={hi1|（i1=1，2，3，…，l）}道工序。目标函数不变，则考虑模糊质检时间的FJDSP在处理机器故障时需要在常规约束式（2）～（6）的基础上，增加约束条件式（7）～（10）。

l=breaktime-Si1j1k1Pi1j1k1（7）

P′i1j1k1′=（1-l）Pi1j1k1′（8）

Ci1j1k1=Si1j1k1+l×Pi1j1k1×xi1j1k1（9）

S故障i1j1k1≥max（endtime，Si1j1k1+ij）（10）

其中：式（7）为机器发生故障时正在该机器上加工工件的已完工部分的比例；式（8）为加工中断工件转移到新机器上所需的加工时间；式（9）表示机器在加工工件过程中发生故障导致加工中断；式（10）表示分配到故障机器上的工件需等质检结束后才可加工。

1.4.2 紧急插单下的重调度模型

当紧急插单事件到来时，定义生产加工过程中有新订单插入时的新工件与未加工工件总数为n，可用机器为m，工件集合为J={Ji2|（i2=1，2，3，…，n）}，每个工件有hi2={hi2|（i2=1，2，3，…，l）}道工序。目标函数不变，则考虑模糊质检时间的FJDSP在处理紧急插单时需要在常规约束式（2）～（6）的基础上增加约束式（11）。

Snewi2j2k2≥max（insertime，Si2′，j2′，k2′）（11）

式（11）表示新插入工件只能在插入时间后开始加工，并且需要等到相应机器的前面工序完工后开始。

2 GA-CARRHCNS算法设计

本文设计基于元胞自动机邻域搜索和随机重启爬坡算法的改进遗传算法（GA-CARRHCNS）求解模型。该算法是遗传算法、元胞自动机邻域搜索算法、随机重启爬坡算法的融合，即：首先，针对车间调度问题中存在的订单排序和机器选择双决策问题特征，设计包含工序码和机器码的双层编码方案，并基于遗传算法思想对工序码和机器码设计相应的交叉、变异等遗传操作；其次，将遗传操作应用于基于元胞自动机的邻域搜索算法框架中，通过将种群扩展为带邻域解的大规模种群，从而增强算法的全局搜索能力；再次，针对元胞自动机邻域搜索算法更新得到的新种群，设计基于关键工序的随机重启爬坡算法以进一步改善解质量，从而增强算法的局部开发能力；最后，在满足迭代次数后，继续采用带插入和逆序的常规邻域搜索算法以深化搜索到的最优解。

2.1 编码和解码

针对车间调度问题中订单排序和机器选择的双决策问题特征，采用包含工序码和机器码的双层编码方式，第一层对工序排序子决策进行编码，第二层对机器选择子决策进行编码。工序码表示每道工序的顺序，机器码表示每道工序选择的机器。工序码长度与机器码长度一致［13］。

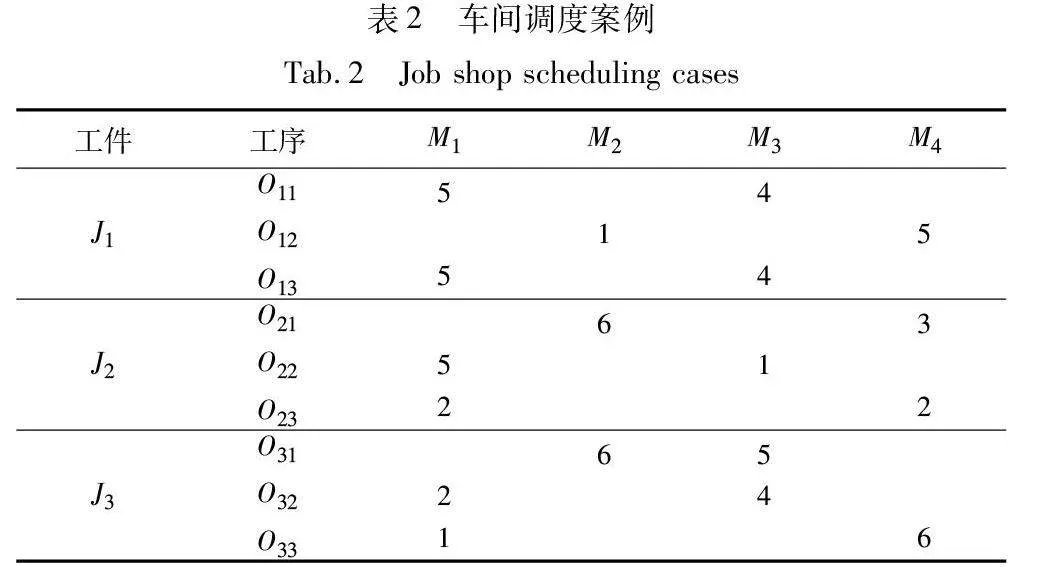
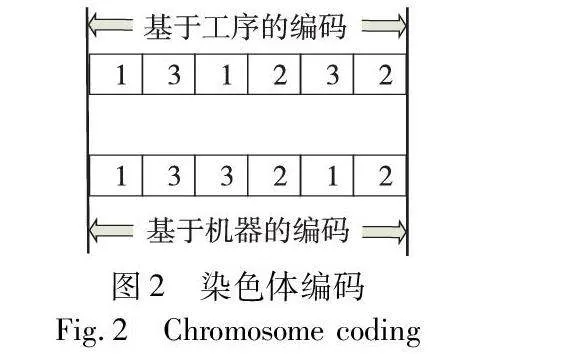
图2以简单FJSP问题（如表2）为例展示了相应的可能编码示例。图中，工序码“1 3 1 2 3 2”表示（O11，O31，O12，O21，O32，O22），机器码“1 3 3 2 1 2 ”表示（M1，M3，M3，M2，M1，M2）。该编码表示：工序O31在M3上加工，工序O21对应的加工机器为M2，依次类推。

解码过程采用贪婪解码方法，即对每道工序，找到该工序在所选机器上能够加工的最早时间。

2.2 初始化种群

考虑到问题的订单排序和机器选择双决策特征，立足双层编码方式，采用随机生成方法，随机产生工件的加工顺序生成工序码，随机选择工序的可选择加工机器生成机器码，最终将工序码和机器码组成一个解个体。NIND个个体组成初始种群。

2.3 遗传操作

2.3.1 选择操作

采用精英选择及锦标赛双选择方式。精英选择为：设置精英解概率Ep，精英解数量为En=Ep×NIND。将所有解从小到大排列，则前En个为精英解。锦标赛选择为：取第En+l到第NIND个解，在这些解中随机抽取两个解比较大小，将两个解中更小的保留，此过程进行NIND-（En+l）次，将第En+l到第NIND个解依次替换。

2.3.2 交叉操作

同样考虑到所研究问题的订单排序和机器选择双决策特征，本文立足双层编码方式，分别针对工序码和机器码设计相应的交叉操作。

1）面向工序码的交叉操作

在面向工序码的交叉操作中，设计了工序优先交叉和工序常规交叉两种方法。两种交叉方法任意选择执行。下面以两个父代n1和n2中的工序码OS1和OS2交叉生成两个子代OS′1和OS′2为例。两种交叉方法具体描述如下：

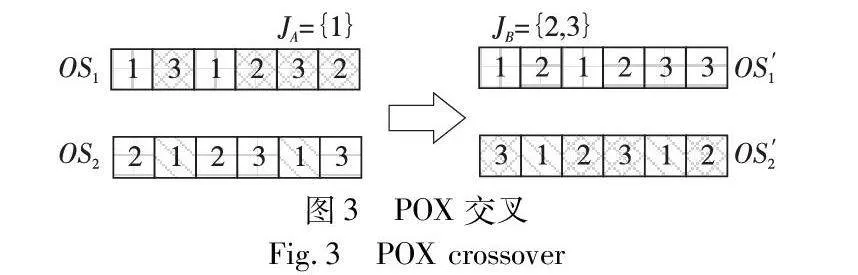
a）工序优先交叉。将工序J随机分成两JA和JB部分，满足JA∩JB=和JA∪JB=J。在OS′1生成时，工件JA的工序参照OS1位置放置在OS′1的相同位置，而JB的工序按照OS2的加工顺序依次填补OS′1的空位置。在生成OS′2时，工件JA的工序参照OS2位置放置在OS′2的相同位置，而JB的工序按照OS1的加工顺序依次填补OS′2的空位置。图3展示了一个有3个工件和6个工序的交叉示例。

b）工序常规交叉。将工序J随机分成JA和JB两部分，满足JA∩JB=和JA∪JB=J。OS′1生成方式与上述“工序优先交叉”相同。而在生成OS′2时，先将工件JB的工序参照OS2位置放置在OS′2的相同位置，然后将JA工序按照OS1的加工顺序依次填补OS′2的空位置。图4展示了一个有3个工件和6个工序的交叉示例。

2）面向机器码的交叉操作

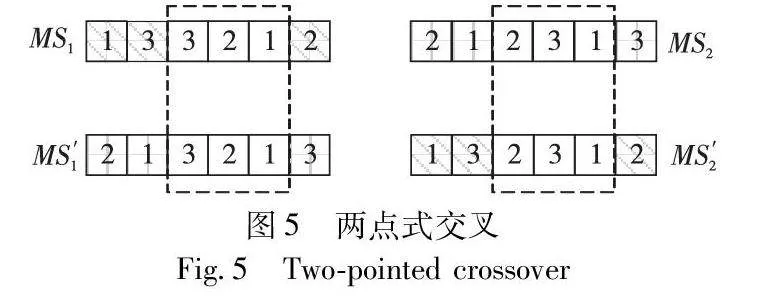
采用两点式交叉执行面向机器码的交叉操作。同样以两个父代n1和n2中的工序码MS1和MS2交叉生成两个子代MS′1和MS′2为例。具体为：随机选择两个位置p1和p2（0<p1<p2<pmax），将MS1的位置［1，p1-1］和［p2+1，pmax］编码和MS2的位置［p1，p2］编码结合，得到一个新的序列MS′1。同样地，将MS1的位置［p1，p2］编码和MS2的位置［1，p1-1］和［p2+1，pmax］编码结合，生成新序列MS′2。图5展示了一个有3台机器和6个工序的交叉示例。

2.3.3 变异操作

同样考虑到所研究问题的订单排序和机器选择双决策特征，这里也立足双层编码方式，分别针对工序码和机器码设计相应的变异操作。

1）面向工序码的变异操作

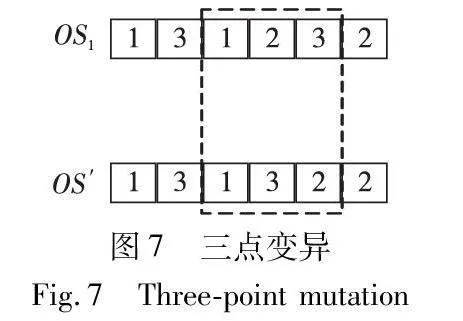
设计了交换变异和三点变异两种方法执行面向工序码的变异操作。两种变异方法任意选择执行。两种变异方法具体描述如下：

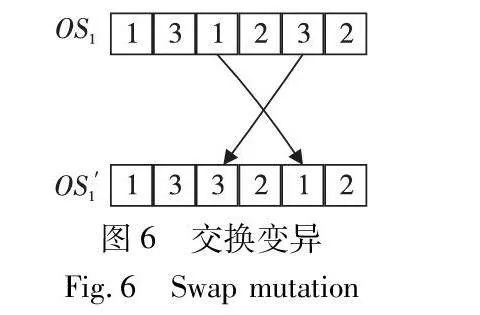
a）交换变异。即在一个解的序列上随机选取两个位置的编码进行交换得到新解，如图6所示。

b）三点变异。随机改变三个不同编码的位置，随机交换三个编码的位置得到子代，如图7所示。通过此步骤，可使解的多样性增加，从而可以使解以一定概率跳出局部最优解。

2）面向机器码的交叉操作

机器码采用随机指定机器突变的变异方式，即选择任意随机位置，将此位置上的机器号变为与初始机器不同的可行机器，如图8所示。

2.4 基于元胞自动机的邻域搜索算法框架

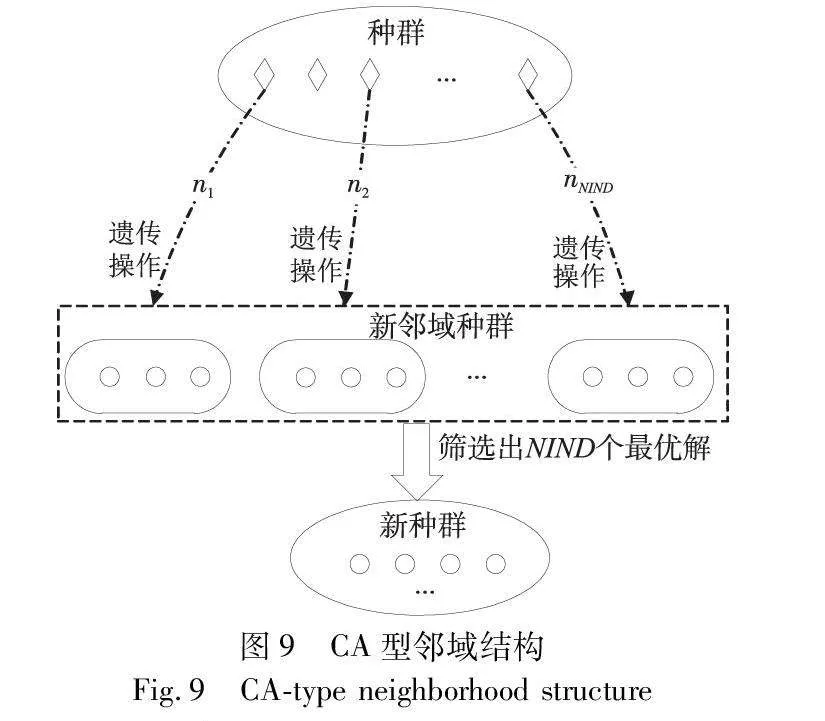
为改善求解质量，将2.3节的遗传操作置于基于元胞自动机（cellular automata，CA）［20］的邻域搜索算法框架中，以改善种群解质量。算法流程可以描述为：通过选择、交叉和变异操作使种群中的每个解产生l个新型邻域解，从而组成了种群规模为l×NIND的新邻域种群，继而在种群规模为l×NIND的邻域种群中选择最好的NIND个解组成新种群。

图9展示了整合遗传操作和基于元胞自动机邻域搜索算法的示意图，图中种群中的每个解n1～nNIND通过选择、交叉、变异生成l个新型邻域解。

2.5 随机重启爬坡算法

针对基于元胞自动机的邻域搜索算法框架整合遗传操作后得到的新种群，本文将进一步对新种群中的每个解执行基于关键工序的随机重启爬坡操作，以进一步改善解质量。

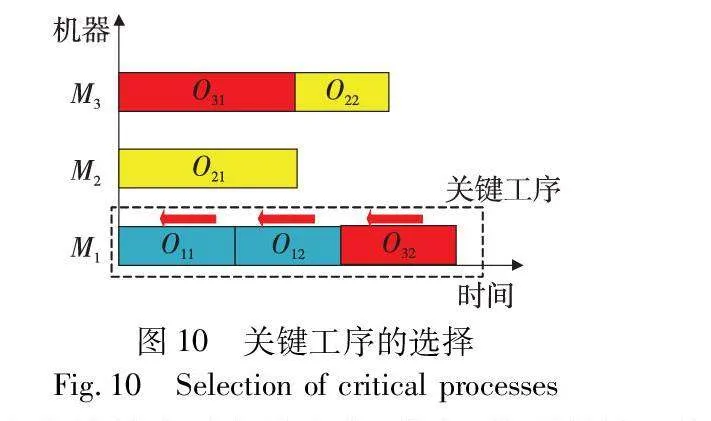
随机重启爬坡算法的核心在于找到关键工序集。本文采用基于空闲时间的方法确定关键工序，具体描述为：从最后一个工序中选择一个与最大完工时间相同的工序，从机器角度或工件角度检查同一台机器或同一作业的前一工序，若前一工序的加工完成时间等于当前工序的开始时间，则将其定义为关键工序。注意，若多个前工序均满足加工完成时间等于当前工序的开始时间，则随机选择。重复上述步骤，直到没有前序工序为止。图10展示了关键工序的选择示例，图中按照O32、O12和O11的顺序找到关键工序集。

随机重启爬坡算法可以描述为：首先，找到关键工序集，并任意选择某一关键工序，将其分配给与先前方案不同的可行的机器加工，以此产生一个新机器序列MS′。然后，以概率αc选择其他关键工序，并随机选择一个非关键工序与之配对，将两者执行交换操作，以获得一个新的工序序列OS′。新的MS′和OS′生成一个新个体n′。若产生的新解n′优于原解n，则新解n′替换原解n，否则，重新对原解n进行随机重启爬坡。随机重启爬坡算法的终止条件为：满足最大迭代次数Hn后退出迭代。图11展示了随机重启爬坡的操作示例。图中，随机选择关键工序O21，将其加工机器从M1更新为M2，生成新机器序列MS′；然后，对于其他关键工序O11和O12，以概率αc选中O11，将其与非关键工序O21交换，生成新工序序列OS′。图11中左子图为执行随机重启爬坡算法的流程示例，右子图为执行随机重启爬坡算法后的新方案。

2.6 邻域搜索

重复执行整合遗传操作的元胞自动机邻域搜索算法框架和随机重启爬坡算法，当迭代次数超过最大迭代次数MAXGEN时，针对输出的最优解继续采用常规邻域搜索算法深化其解质量。邻域搜索包含插入和逆序两种邻域操作：

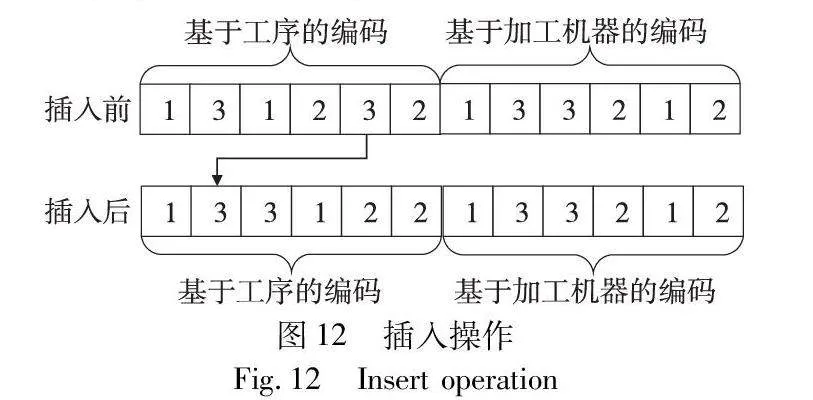
a）插入。随机在该解上选择两个位置，将后面位置的编码插入到前面位置，将前面位置及其后面位置的编码后移，如图12所示，得到新解。

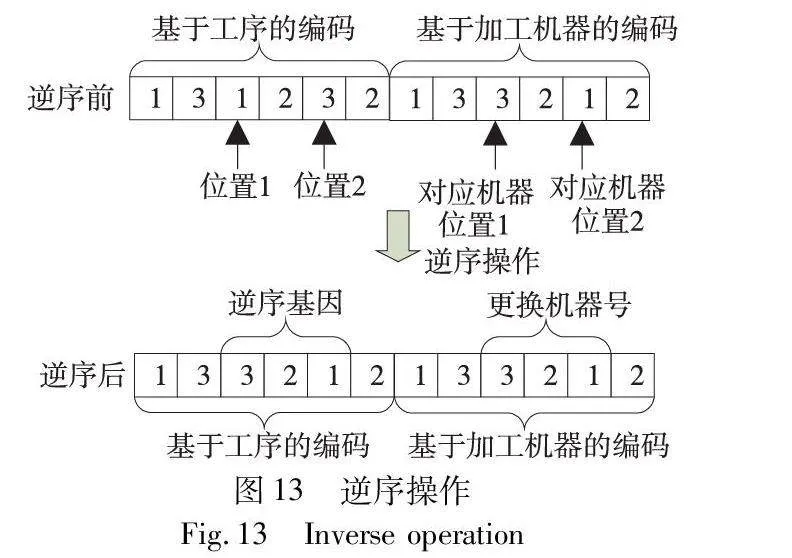
b）逆序。随机选择两基因位，截取两基因位之间的基因片段，将所有基因位上的工序号顺序逆置，再将对应位置的机器号进行更换，如图13所示。

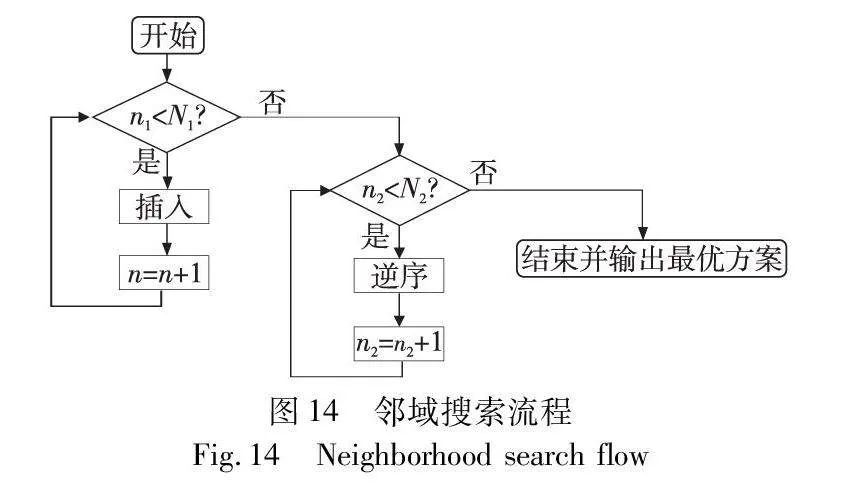
图14给出了邻域搜索算法的流程。具体步骤如下：

a）设最大迭代次数为N1。当插入操作次数达到最大迭代次数N1时，转入步骤b）；

b）将步骤a）得到的当前最优解进行逆序操作，当达到最大迭代次数N2时，输出最优方案。

2.7 整体算法流程

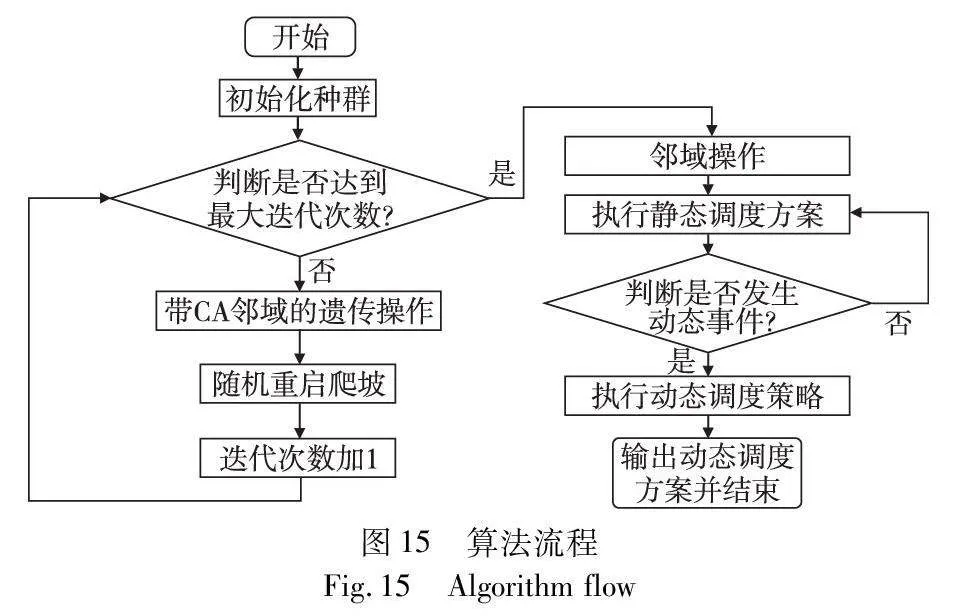
图15是GA-CARRHCNS的整体算法流程。

具体算法步骤为：

a）设当前迭代次数gen=0，种群规模NIND，最大迭代次数MAXGEN，精英解概率Ep、交叉概率XOVR和变异概率MUTR；

b）初始化种群；

c）采用精英筛选及锦标赛的方式对种群进行筛选；

d）将新种群进行交叉操作和变异操作；

e）将交叉变异后的新种群执行基于元胞自动机的邻域搜索算法；

f）随机重启爬坡；

g）迭代次数n=n+1；

h）判断是否达到最大迭代次数，若达到，则输出最优解，并对最优解执行带N次插入和逆序的常规邻域搜索，否则，转回步骤b）。

i）输出静态调度方案；

j）判断是否发生动态事件，若是，对受影响工序用本文算法重新求解，求出重调度方案，否则，输出静态调度方案。

3 算例验证和结果分析

3.1 算法有效性验证

由于目前没有FJDSP-FQC的标准测试算例，所以本文通过以下两个层面测试算法性能：a）FJDSP-FQC属于FJSP的扩展，学术界虽无FJDSP-FQC标准测试算例，但有FJSP标准算例，故本文求解FJSP标准算例，并将求解结果与已有文献求解结果进行比较，以验证算法性能；b）为了证明本文算法适用于求解考虑模糊质检时间的FJSP，进一步改进生成一个6×6的考虑模糊质检时间的FJSP算例，采用样本平均近似（SAA）方法处理模糊性，对比本文算法与基本遗传算法（即不带元胞自动机邻域搜索和随机重启爬坡算法的遗传算法）的求解结果，从而验证本文算法对求解考虑模糊质检时间FJSP的适用性，以及所设计的元胞自动机邻域搜索和随机重启爬坡算法的有效性。

3.1.1 标准FJSP算例测试

这里选取标准FJSP算例库中的MK01～MK10共10个案例进行测试。其中，MK01～MK02为小规模案例，MK03～MK07为中规模算例，MK08～MK10为大规模算例。上述算例可以在网址http：//www.dsia.ch/monaldo下载［21］。

采用MATLAB 2018b编程，运行环境为Windows 10 家庭版64位操作系统，Intel Core i5-7200U @ 2.50 GHz双核处理器，8 GB RAM。算法参数设置：种群规模NIND=200、迭代次数MAXGEN=1000、交叉率0.5、变异率0.5，精英解概率为0.02，CA型邻域解数量为3，其他关键工序选择概率αc=0.05。

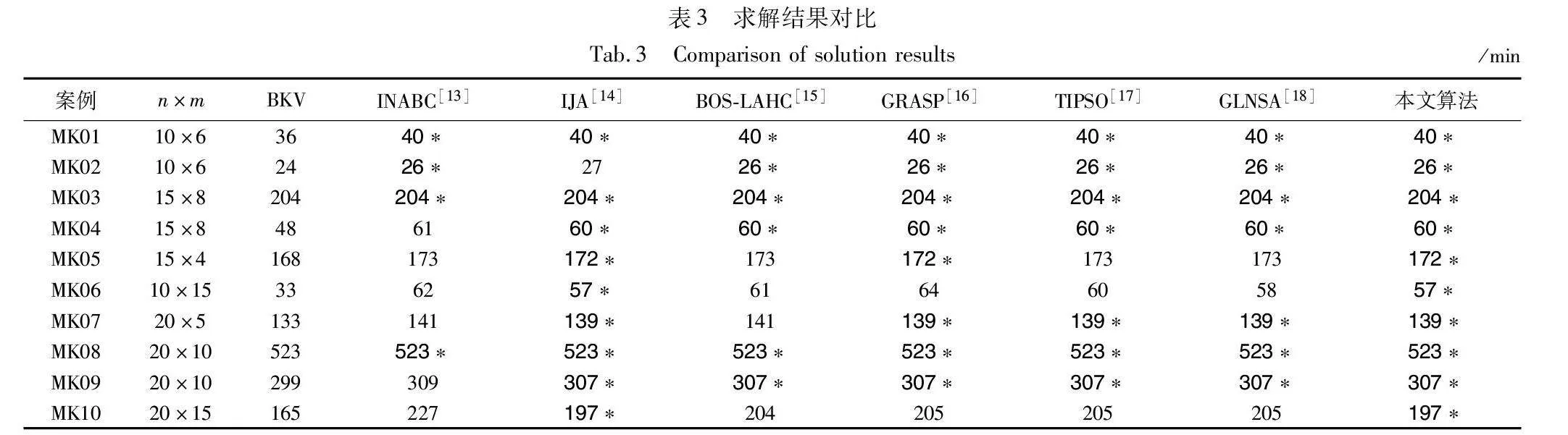
表3是GA-RHHCNS与INABC［13］、IJA［14］、BOS-LAHC［15］、GRASP［16］、TIPSO［17］、GLNSA［18］的求解结果对比。每个测试算例被重复求解10次，表中展示的是10次中的最优解，BKV为已知最优解。另外，*标记最大完工时间的最优值，加粗表示算法达到了已知最优解BKV。从中可以看出：本文算法在MK01～MK10共10个算例中均能找到对比算法能搜索到的最好值，如对于MK10算例来说，本文算法求解结果为197 min，优于INABC的227 min、BOS-LAHC的204 min、GRASP的205 min、TIPSO的205 min、GLNSA的205 min，其他算例类似。综合可见，本文算法适用于求解FJSP问题，算法合理有效。

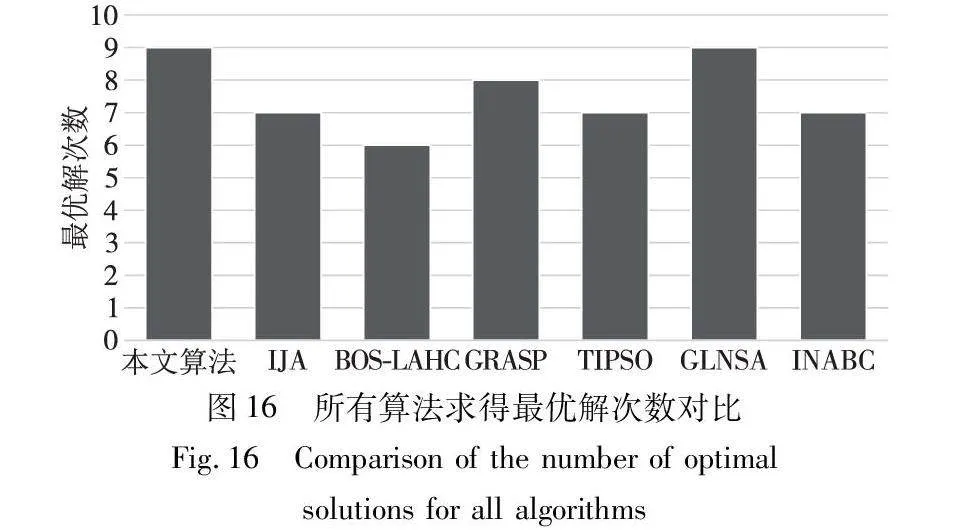
为测试展示算法的稳定性，参考文献［22］，本文进一步采用每种对比算法在运行10次时求解出最优解的次数和相对百分比偏差（RPD）两个指标来检验算法稳定性。

a）每种对比算法在运行10次时求解出最优解的次数指标。图16展示了每种对比算法在运行10次时求解出最优解的次数，可见本文算法与GLNSA算法求解出最优解的次数为9，数量多余其他算法。

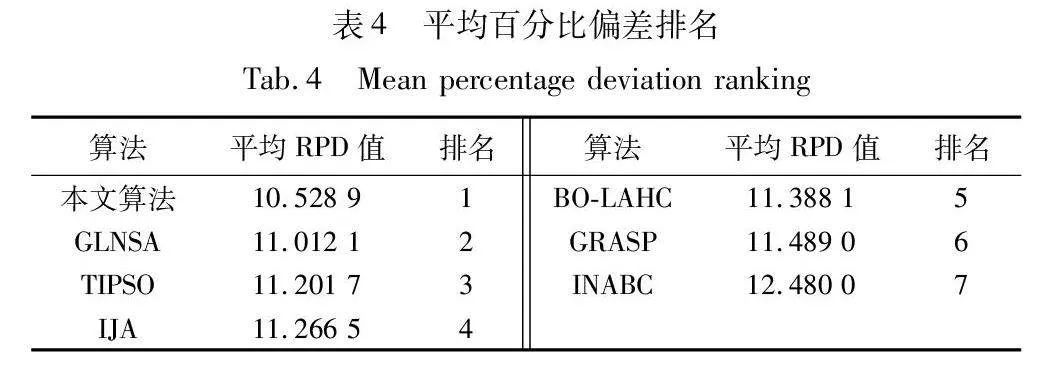
b）相对百分比偏差（RPD）指标。RPD计算如式（12）所示，式中，BOV是每个算法得到的最大完工时间值。RPD越小表示所得结果越接近BKV，算法性能越好。表4展示了每种对比算法的平均RPD值及排名，可知本文算法的平均RPD值最小。

RPD=BOV-BKVBOV×100（12）

综上可见，本文算法较INABC、IJA、BOS-LAHC、GRASP、TIPSO、GLNSA算法稳定性良好。

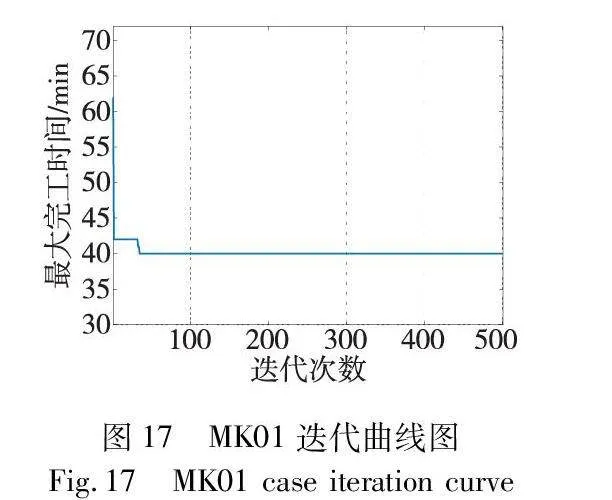
另外，图17以MK01为例展示了本文算法求解该算例的算法迭代曲线。可知，本文算法在迭代至第35次时已经收敛到最优解，说明算法稳定有效。

3.1.2 考虑模糊质检时间的FJSP算例测试

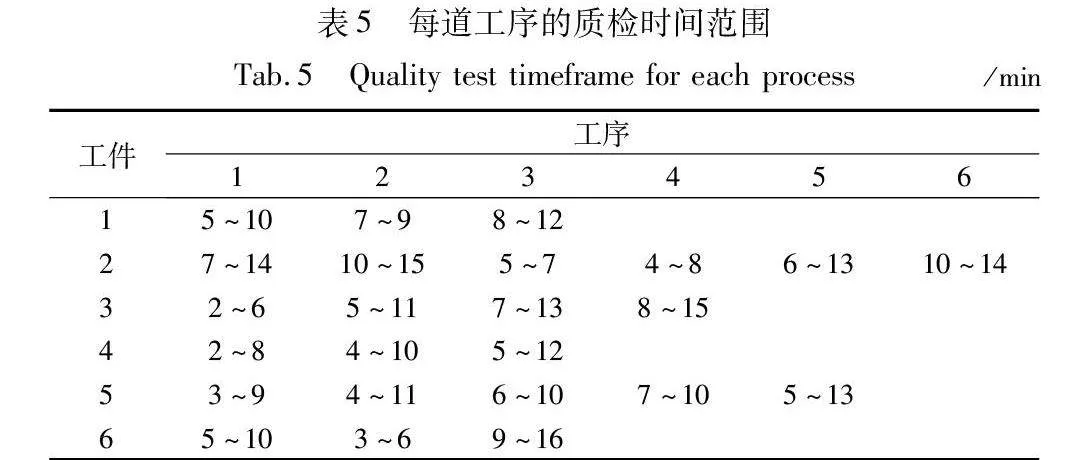
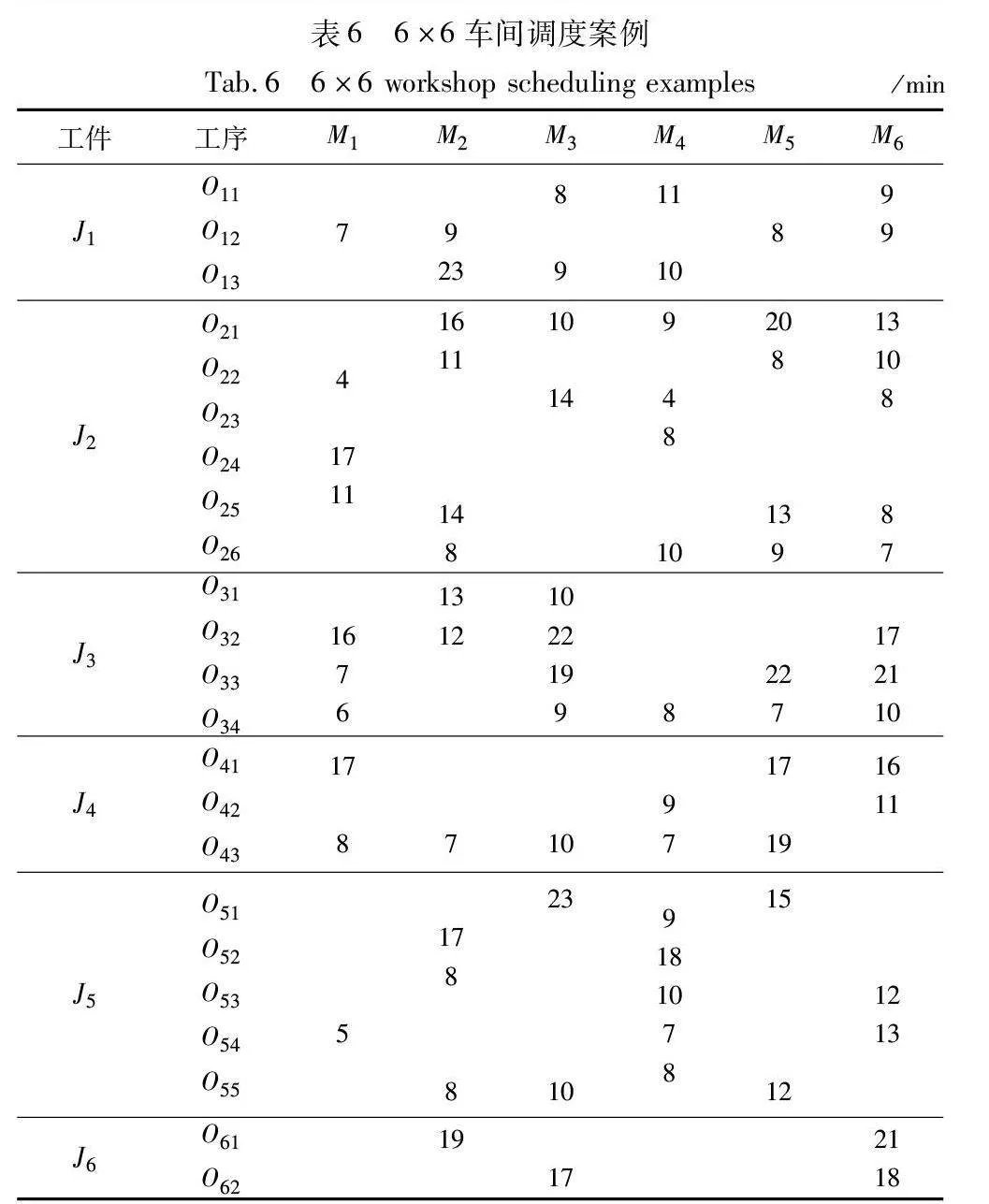
进一步生成一个6×6的模糊质检时间FJSP算例，表5展示了该算例的模糊质检时间范围，另外， 表6给出了生成算例的具体数据。

采用GA-CARHHCNS求解，同时，采用样本平均近似（SAA）方法处理模糊质检时间属性，即预期目标函数由随机样本的样本平均估计来近似。样本规模取200，其他算法参数同3.1.1节，则本文算法的求解结果为：应对不同质检时间场景，综合性能最优的调度方案的平均最大完工时间为90 min。表7是本文算法和基本遗传算法（即不带元胞自动机邻域搜索和随机重启爬坡算法的遗传算法）的求解结果对比，从表7中可以看出，本文算法结果相较于基本遗传算法缩短了21.8 min，改进率为19.5%。

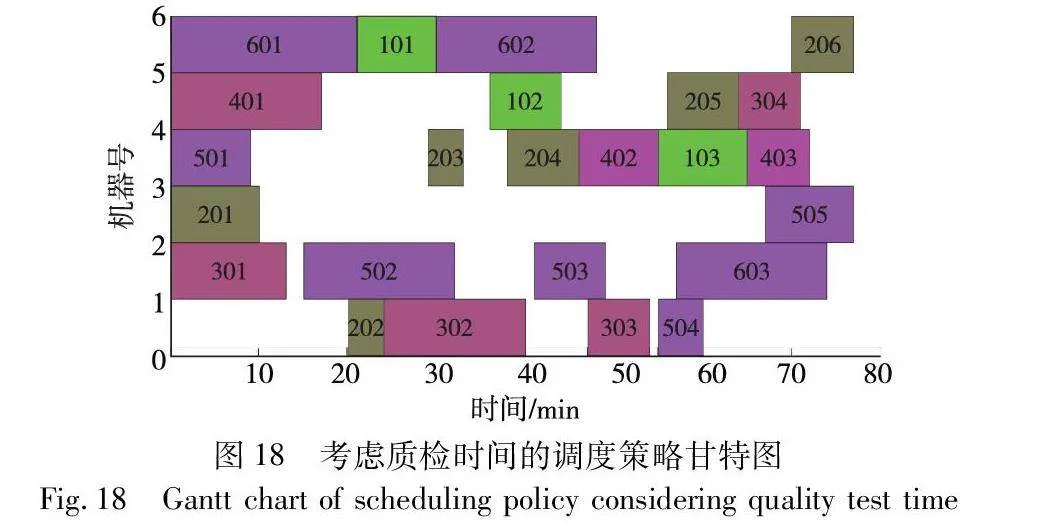
另外，图18展示了最优方案下的某一随机样本的调度方案甘特图。图中，纵坐标表示机器号，横坐标表示时间，相同颜色表示同一工件，数字表示工件与工序编号，如204表示工件2的第4道工序。需要注意的是，虽然图中显示所有工体的最大完成时间为77 min，但实际完工时间是89 min，原因在于：最后一道工序206质检之后整个生产任务才算完成。

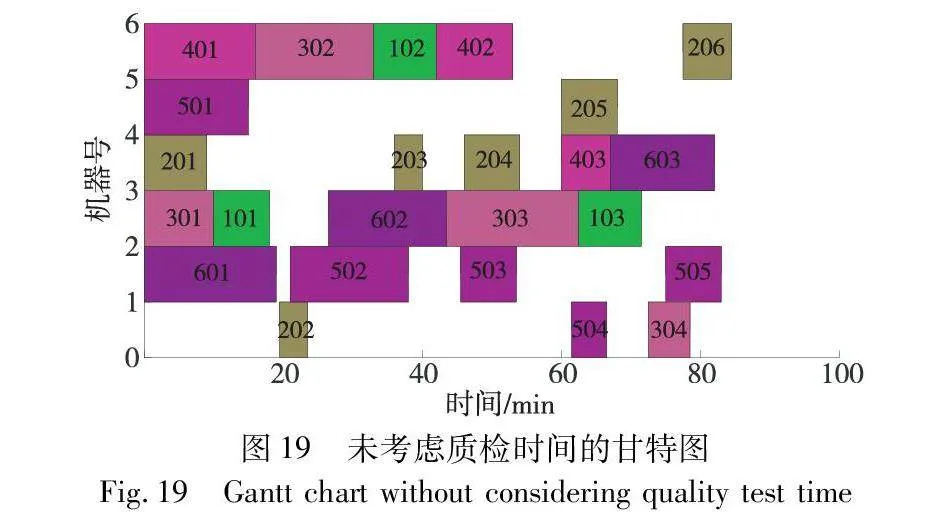
为进一步讨论模糊质检时间的刻画对调度结果的影响，本文进一步对比了“采用模糊数刻画不确定质检时间”以及“采用平均值刻画不确定质检时间”的求解结果。“采用平均值刻画不确定质检时间”的最大完工时间甘特图如图19所示。从中可以看出，“采用模糊数刻画不确定质检时间”的最大完工时间平均期望值为90 min，而“采用平均值刻画不确定质检时间”的最大完工时间为96.5 min，验证了模型的有效性。需要注意的是，与图18同理，图19虽然显示所有工件的最大完工时间为84.5 min，但实际完成时间应是96.5 min。

3.2 考虑模糊质检时间的FJDSP算例测试

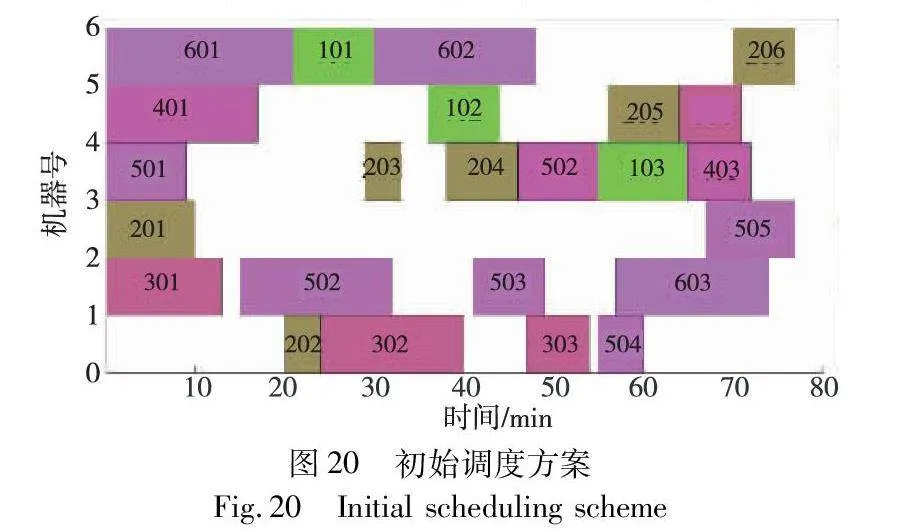
以3.1.2节中求解得到的综合性能最优的调度方案为对象，以其应对某一随机场景下的调度甘特图为例，进一步探讨机器故障、订单插入等干扰事件下的重调度策略和方案。图20是某一随机场景下的调度甘特图，最大完工时间为77 min。

1）机器故障的动态调度

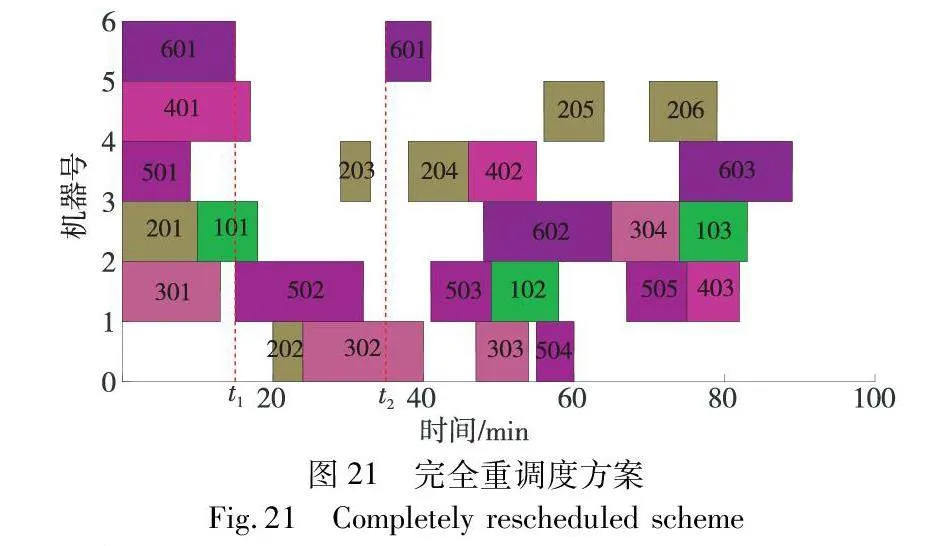
在图20的基础上，假设发生故障的机器为M6，故障发生时间t1=15 min，故障修复时间t2=35 min。根据图20可看出，在机器M6发生故障时工序601正在M6上加工。经过重调度后生成的重调度方案如图21所示，最大完工时间89 min。

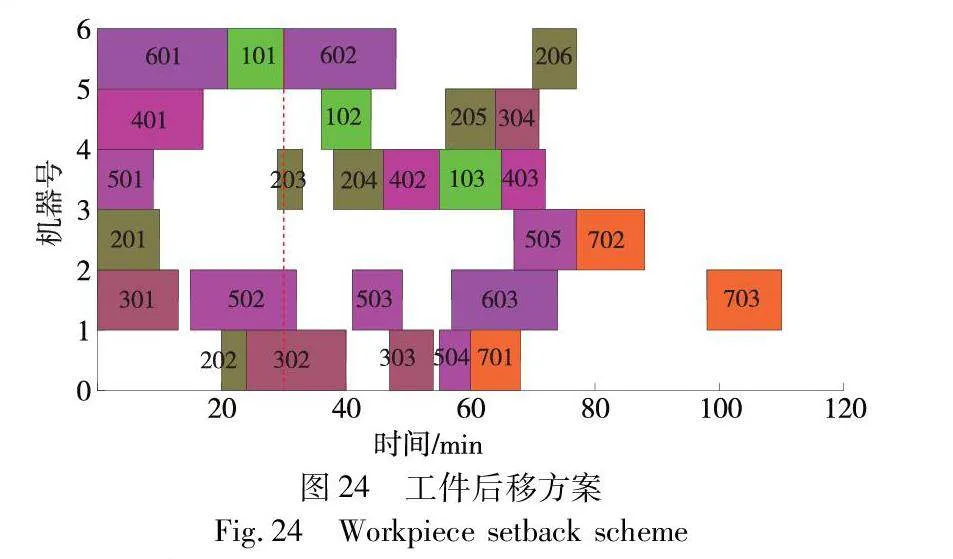
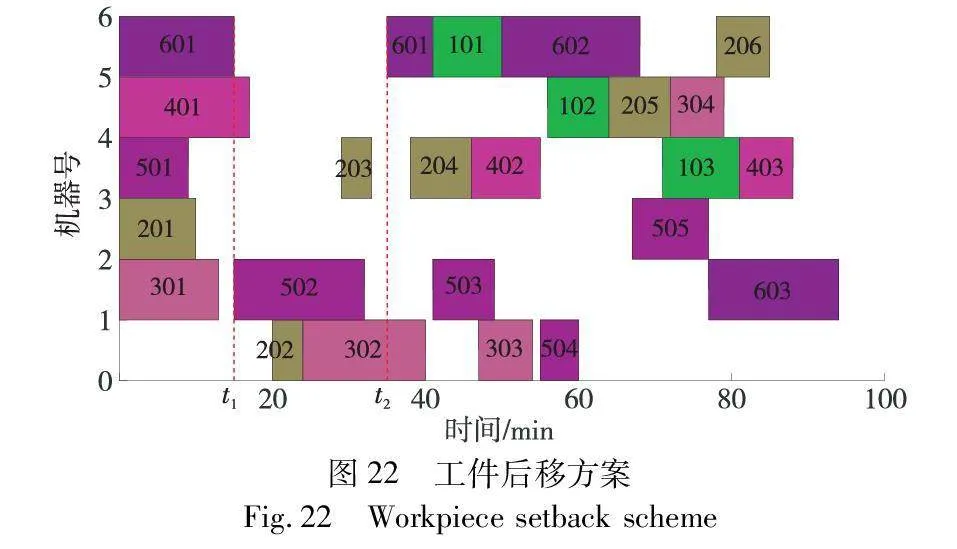
为验证该重调度方案的有效性，图22展示了“工件后移策略”的调度甘特图，最大完工时间为94 min。将其与本文结果对比，可知本文重调度方法下的最大完工时间远远少于“工件后移策略”，证明了该重调度方案的有效性。

2）订单插入的动态调度

在图20的基础上，假设初始方案开始后第30 min有紧急订单插入并且需要优先加工，定义工件7为紧急订单，工件7包含3道工序，每道工序的可选机器及加工时间如表8所示。

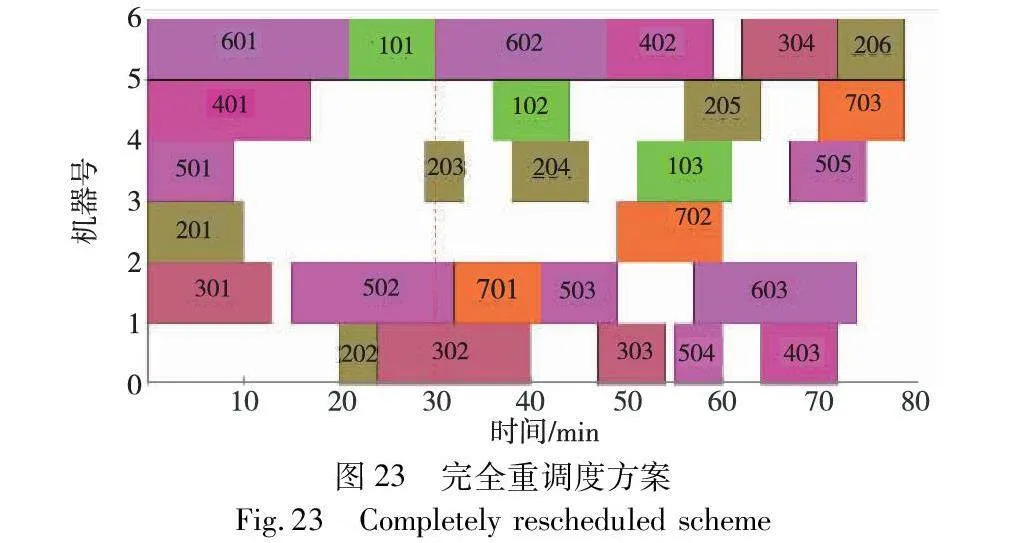
图23是新插入工件与未加工工件共同进行完全重调度方案，最大完工时间为79 min，图中橙色部分为新插入订单，其余颜色部分为原有订单。同理，在不进行重调度的情形下，新订单需等待所有工件完工后才可加工。

图24展示了“工件后移策略”调度方案，经计算得出最大完工时间为110 min。对比两种方案可以看出，采用完全重调度花费的时间更短，验证了本文重调度方案应对紧急插单干扰事件的有效性。

4 结束语

本文扩展FJSP中的动态调度故障情形为紧急插单、机器在空载运行时发生故障和机器在加工工件时发生故障三种情况，同时将模糊质检时间考虑在内，研究了考虑模糊质检时间的柔性作业车间动态调度问题。首先，以最小化完工时间为目标，建立考虑模糊质检时间的初始调度模型，并基于初始调度模型，立足紧急插单、机器在空载运行时发生故障和机器在加工工件时发生故障的三种故障情形，进一步修正为带模糊质检时间的机器故障、紧急插单重调度模型。然后，设计带元胞自动机邻域搜索和随机重启爬坡算法的改进遗传算法（GA-CARRHCNS）求解模型，即针对FJDSP包含的订单排序和机器选择双决策问题，设计包含工序码和机器码的双层编码方案，并分别对双层编码段设计相应的交叉、变异等遗传操作，同时，将遗传操作应用于基于元胞自动机的邻域搜索算法框架中以增强算法全局搜索能力，并整合基于关键工序的随机重启爬坡算法以提高算法局部开发能力。最后，实验选取10个FJSP标准算例和1个考虑模糊质检时间的FJSP算例进行测试，验证了本文算法的有效性，同时，测试1个考虑模糊质检时间的FJDSP算例验证了模型和重调度策略的有效性。实验结果如下：

a）本文算法较INABC、IJA、BOS-LAHC、GRASP、TIPSO、GLNSA算法而言，求解结果更优，算法性能更有效，且算法稳定性也更良好。

b）在求解考虑模糊质检时间的FJSP算例时，采用模糊数刻画不确定质检时间的最大完工时间平均值为90 min，而采用平均值刻画不确定质检时间的最大完工时间为96.5 min，本文所建模型是有效的。

c）在求解考虑模糊质检时间的FJDSP算例时，当遭遇机器故障，相较于工件后移策略，本文的重调度策略能将最大完工时间从94 min缩减至89 min，效率提高了5.3%；当遭遇紧急插单，本文的重调度策略能将最大完工时间从110 min缩减至79 min，效率提高了28.2%。

未来研究可结合问题特点进一步优化算法的全局搜索与局部搜索能力，或者进一步考虑其他生产条件，研究多种因素的柔性作业车间调度问题。

参考文献：

［1］米恬怡， 唐秋华， 成丽新， 等. 融合强化学习与变邻域搜索的柔性作业车间调度研究［J］. 工业工程与管理， 2023， 28（5）： 101-107. （Mi Tianyi， Tang Qiuhua， Cheng Lixin， et al. Research on flexible job shop scheduling by integrating reinforcement learning and variable neighborhood search［J］. Industrial Engineering and Management， 2023， 28（5）： 101-107.）

［2］卫少鹏， 王婷， 周彤. 考虑多时间因素的绿色柔性作业车间动态调度［J］. 组合机床与自动化加工技术， 2021（1）： 164-168. （Wei Shaopeng， Wang Ting， Zhou Tong. Dynamic scheduling of green flexible job shop considering multiple time factors［J］. Combined Machine Tools and Automated Machining Technology， 2021（1）： 164-168.）

［3］Luo Shu. Dynamic scheduling for flexible job shop with new job insertions by deep reinforcement learning［J］. Applied Soft Computing， 2020， 91： 106208.

［4］裴小兵， 杨景霞. 一种解决带有紧急插单问题的果蝇优化算法［J］. 系统工程， 2020， 38（6）： 139-146. （Pei Xiaobing， Yang Jingxia. A fruit fly optimization algorithm for solving the problem with urgent insertion orders［J］. Systems Engineering， 2020， 38（6）： 139-146.）

［5］张祥， 王艳， 纪志成. 基于动态交互层的柔性作业车间动态调度问题研究［J］. 系统仿真学报， 2020， 32（11）： 2129-2137. （Zhang Xiang， Wang Yan， Ji Zhicheng. Research on dynamic scheduling problem of flexible job shop based on dynamic interaction layer［J］. Journal of System Simulation， 2020， 32（11）： 2129-2137.）

［6］包博， 张琳， 张搏. 设备故障条件下柔性作业车间重调度方法［J］. 计算机工程与应用， 2018， 54（19）： 248-253. （Bao Bo， Zhang Lin， Zhang Bo. A flexible job shop rescheduling method under equipment failure conditions［J］. Computer Engineering and App-lications， 2018， 54（19）： 248-253.）

［7］Ahmadi E， Zandieh M， Farrokh M， et al. A multi objective optimization approach for flexible job shop scheduling problem under random machine breakdown by evolutionary algorithms［J］. Computers & Operations Research， 2016， 73： 56-66.

［8］Salama S， Toshiya K， Nobutada F， et al. Evolving dispatching rules using genetic programming for multi-objective dynamic job shop scheduling with machine breakdowns［J］. Procedia CIRP， 2021， 104： 411-416.

［9］侯娅楠， 袁逸萍， 巴智勇， 等. 机器混合故障下柔性作业车间鲁棒调度方法［J］. 机械设计与制造， 2022（4）： 1-4，9. （Hou Yanan， Yuan Yiping， Ba Zhiyong， et al. Robust scheduling method for flexible job shop under mixed machine breakdown［J］. Machine Design and Manufacturing， 2022（4）： 1-4，9.）

［10］Sajadi S M， Alizadeh A， Zandieh M， et al. Robust and stable flexible job shop scheduling with random machine breakdowns： multi-objectives genetic algorithm approach［J］. International Journal of Mathematics in Operational Research， 2019， 14（2）： 268-289.

［11］苗志鸿， 杨明顺， 王雪峰， 等. 考虑优先级的IPPS紧急订单处理问题研究［J］. 西安理工大学学报， 2019， 35（4）： 434-442. （Miao Zhihong， Yang Mingshun， Wang Xuefeng， et al. Research on IPPS emergency order processing problem considering priority［J］. Journal of Xi’an University of Technology， 2019， 35（4）： 434-442.）

［12］金鹏博， 唐秋华， 成丽新， 等. 机器故障下柔性作业车间的生产重调度方式决策模型［J］. 计算机集成制造系统， 2023， 29（11）： 3750-3761. （Jin Pengbo， Tang Qiuhua， Cheng Lixin， et al. A decision model for production rescheduling approach in flexible job shops under machine failure［J］. Computer Integrated Manufacturing Systems， 2023， 29（11）： 3750-3761.）

［13］李瑞， 徐华， 杨金峰， 等. 改进近邻人工蜂群算法求解柔性作业车间调度问题［J］. 计算机应用研究， 2024， 41（2）： 438-443. （Li Rui， Xu Hua， Yang Jinfeng， et al. Improved algorithm of near-neighbor artificial bee colony for flexible job-shop scheduling［J］. Application Research of Computers， 2024， 41（2）： 438-443.）

［14］Caldeira R H， Gnanavelbabu A. Solving the flexible job shop scheduling problem using an improved Jaya algorithm［J］. Computers & Industrial Engineering， 2019， 137： 106064.

［15］Alzaqebah M， Jawarneh S， Alwohaibi M， et al. Hybrid brain storm optimization algorithm and late acceptance hill climbing to solve the flexible job-shop scheduling problem［J］. Journal of King Saud University-Computer and Information Sciences， 2022， 34（6）： 2926-2937.

［16］Baykasogˇlu A， Madenogˇlu F S， Hamzaday A. Greedy randomized adaptive search for dynamic flexible job-shop scheduling［J］. Journal of Manufacturing Systems， 2020， 56： 425-451.

［17］Zarrouk R， Bennour I E， Jemai A. A two-level particle swarm optimization algorithm for the flexible job shop scheduling problem［J］. Swarm Intelligence， 2019， 13（2）： 145-168.

［18］Serna N J E， Seck-Tuoh-Mora J C， Medina-Marin J， et al. A global-local neighborhood search algorithm and Tabu search for flexible job shop scheduling problem［J］. PeerJ Computer Science， 2021， 7： e574.

［19］曹庆奎， 张晓丽， 任向阳. 考虑模糊交货期的柔性作业车间动态调度研究［J］. 数学的实践与认识， 2019， 49（22）： 65-78. （Cao Qingkui， Zhang Xiaoli， Ren Xiangyang. Research on dynamic scheduling of flexible job shop considering fuzzy delivery date［J］. Practice and Understanding of Mathematics， 2019， 49（22）： 65-78.）

［20］Hernández-Gress E S， Seck-Tuoh-Mora J C， Hernández-Romero N， et al. The solution of the concurrent layout scheduling problem in the job-shop environment through a local neighborhood search algorithm［J］. Expert Systems with Applications， 2020， 144： 113096.

［21］刘琼， 张超勇， 饶运清， 等. 改进遗传算法解决柔性作业车间调度问题［J］. 工业工程与管理， 2009， 14（2）： 59-66. （Liu Qiong， Zhang Chaoyong， Rao Yunqing， et al. Improved genetic algorithm to solve flexible job shop scheduling problem［J］. Industrial Enginee-ring and Management， 2009， 14（2）： 59-66.）

［22］Derrac J， García S， Molina D， et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms［J］. Swarm and Evolutionary Computation， 2011， 1（1）： 3-18.