考虑强制同机并行作业的广义作业车间调度优化

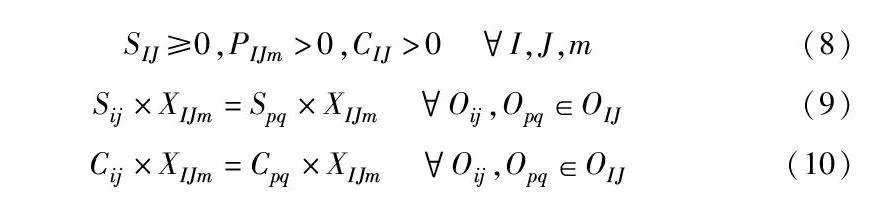
摘 要：模具组合加工、电子产品合检等带来不同工件强制同机并行作业，这打破了作业车间调度同一机器不能在同一时刻处理不同工件的约束。为解决该类作业车间调度问题，提出一种自适应混合初始化遗传算法对其进行求解。首先，将该问题定义为考虑强制同机并行作业的广义作业车间调度；利用混合整数规划法以最小化最大完工时间为优化目标建立优化模型。然后，新设计了相应的编码、解码以支持同机并行作业约束下可行调度方案的表达和约束解析；建立了种群混合初始化方法，以支持新约束下高质量可行解的生成；设计了新的交叉、变异操作方法，保证了同机并行作业约束下新生解的可行性；构建了交叉、变异自适应算子，实现了子代的自适应更新，提高了算法全局搜索能力。最后，基于作业车间调度基准算例构建了40个测试算例，对该测试算例和电子产品分组合检实例开展实验。结果表明，所构建模型和算法可以有效求解强制同机并行作业的广义作业车间调度问题，提出的改进策略均有效提升了解的质量，验证了模型的可行性和算法的优越性。

关键词：强制同机并行作业； 广义作业车间调度； 自适应； 混合初始化； 遗传算法

中图分类号：TP18 文献标志码：A

文章编号：1001-3695（2024）08-014-2343-08

doi：10.19734/j.issn.1001-3695.2023.12.0609

General job shop scheduling optimization considering mandatoryconcurrent operations on same machine

Jin Hong， Zhang Hucheng， Xin Dequan， Lyu Shengping

（School of Engineering， South China Agricultural University， Guangzhou 510642， China）

Abstract：The combination processing of molds and electronic product joint inspection introduce the mandatory concurrent operations on the same machine（MCDSM）， which breaks the constraint that the same machine cannot process different jobs at the same time in the job shop scheduling（JSP） . To solve this type of job shop scheduling problem， this paper proposed an adaptive hybrid initialization genetic algorithm（AHIGA）. Firstly， this paper defined the problem as a generalized JSP considering mandatory concurrent operations on the same machine（GJSPMCO） problem， and established an optimization model using mixed integer programming with the objective of minimizing the maximum completion time. Next， it designed corresponding encoding and decoding techniques to support the representation and resolution of feasible scheduling plans within the constraints of MCOSM. Meanwhile， it established a population hybrid initialization method to generate high-quality feasible solutions. This paper also designed novel crossover and mutation operation methods to ensure the feasibility of newly generated solutions under the constraint of MCOSM. Additionally， it constructed an adaptive crossover and mutation operators to enable the adaptive updating of offspring， thereby enhancing the algorithm’s global search capability. Finally， it constructed 40 test cases based on JSP benchmark， and used these test cases and an example of joint inspection of electronic products for experiments. The results show that the proposed model and algorithm can effectively solve GJSPMCO problem， and the improvement strategies can enhance the quality of solutions， demonstrating the feasibility of the model and the superiority of AHIGA.

Key words：mandatory concurrent operations on the same machine; generalized job shop scheduling; adaptive; hybrid initiali-zation; genetic algorithm

0 引言

模具生产中的部分工序需要进行组合加工，使得车间运行优化时需要考虑不同工件强制同机并行作业的特殊约束。比如，模具型腔结构复杂，经常设计成由多个镶块组成的型腔，为保证模具型腔成型精度和外观的美观，在进行型腔加工之前应先将镶块正确地镶拼在相应位置，而各镶块上的其他特征单独进行加工。类似，在电子产品检测过程中，检测车间对同种产品样机设计总工艺路线，并将样机划分为不同组，各分组样机按照其工艺路线指定子路线串行完成各工序的检测。但部分检测样机需要跨组组合检测经历不同前置检测工序的多个组件或功能，形成强制同机并行作业约束。无论是型腔加工还是电子产品检测，都要确保强制同机并行作业工序的所有前驱工序全部完成，才能开始进行强制同机并行作业。

模具组合加工、电子产品检测车间同种产品不同样机合检等带来了不同工件强制同机并行作业，这打破了作业车间调度（job shop scheduling，JSP）同一机器不能在同一时刻处理多个不同工件的约束。这种新约束给车间的智能调度优化带来了新的挑战，解决带强制同机并行作业约束的作业调度是模具生产和电子产品检测车间亟待突破的瓶颈。为此，本研究将其定义为考虑强制同机并行作业的广义作业车间调度（general JSP considering mandatory concurrent operations on the same machine，GJSPMCO）。

JSP是车间运行优化的核心，是优化利用车间生产资源、提高生产效率、减少车间运行成本、缩短生产周期的重要手段［1］。国内外学者对其已开展了大量研究。从模型约束角度看，相关研究者主要考虑了车间不确定性［2］、搬运和货物托盘影响（如AGV联动）［3］、人机双资源约束［4］等。这些约束给JSP模型构建和优化求解带来了新的挑战，但其更符合车间生产实际。同时，JSP研究扩展考虑了工艺柔性（如机器可选、工艺路线可选以及工序顺序无关）［5～7］，形成了柔性作业车间调度（flexible job shop scheduling，FJSP）。无论是JSP还是FJSP，其所考虑的核心约束为单一工件作业时独占其所选机器，未涉及本研究所考虑强制同机并行作业约束。

从（F）JSP优化方法角度看，现有研究主要经历了三个主要阶段。20世纪60年代，混合整数规划、动态规划等运筹学方法以及一些寻找近似优化解的启发式算法被提出来［8，9］；70年代，JSP被相关学者证实为NP-Complete问题［10］，难以在多项式时间内得到精确最优结果，故大量启发式规则不断涌现；80年代以来，大量智能优化方法不断应用于（F）JSP［11～16］，这些方法能快速获得近似最优甚至最优化结果，大大扩展了（F）JSP的求解范围与规模，是当前深受欢迎的方法。近年来，候鸟算法［17］、蛙跳算法［18］、灰狼算法［19］、樽海鞘群算法［20］、强化学习算法［21］等智能优化算法被广泛应用于该类问题。

上述研究推动了（F）JSP约束模型构建和优化求解，但是所建立的约束模型和相应优化机制难以直接应用于GJSPMCO。因为GJSPMCO不同于传统的（F）JSP，（F）JSP中的工件之间相互独立，作业遵循各自的加工路径，在可行方案表达、生成、解析、迭代操作时只需考虑各自工件的前驱工序约束；GJSPMCO中的某些工件之间存在强制同机并行作业约束，导致工件之间并不相互独立，在可行方案表达、生成、解析、迭代操作每一步都需要联合考虑强制同机并行作业工序的前驱工序约束，从而保证每一步生成的个体都为可行个体。将（F）JSP中的可行方案表达、生成、解析、迭代操作应用于GJSPMCO，打破强制同机并行作业工序的前驱工序约束，从而生成不可行解。因此强制同机并行作业约束给问题建模、优化求解时可行方案的表达、生成、解析、迭代操作等带来挑战。遗传算法因自身具有并行性、灵活性、适应性、可拓展性等特点，在求解（F）JSP时能取得不错的效果，所以当前大量学者在求解（F）JSP时会选择在遗传算法的基础上进行改进［22］。而且遗传算法的求解过程是基于个体的基因编码，可以对问题进行灵活的建模和表达，所以可以根据实际问题的需要定义适当的编码方式和操作，以便更好地表达问题的约束和目标，并且遗传算法的可拓展性可以使遗传算法与其他优化方法结合，形成混合算法，从而进一步提高求解效果。为简单高效地求解GJSPMCO，本文将在遗传算法的基础上对GJSPMCO开展研究。创新工作如下：a）定义了GJSPMCO新问题，并利用混合整数规划法建立了GJSPMCO优化模型；b）以最小化最大完工时间为优化目标，根据GJSPMCO问题特性提出一种自适应混合初始化遗传算法（adaptive hybrid initialization genetic algorithm，AHIGA），具体包括针对强制同机并行作业约束设计了相应编码、解码、混合初始化种群以及交叉、变异操作方法，并引入了自适应算子提高了算法全局搜索能力；c）基于JSP基准算例，通过随机引入强制组合作业构建了GJSPMCO测试算例，基于该测试算例和电子产品分组合检实例开展测试和对比分析，验证了AHIGA的可行性和优越性。

1 GJSPMCO问题描述

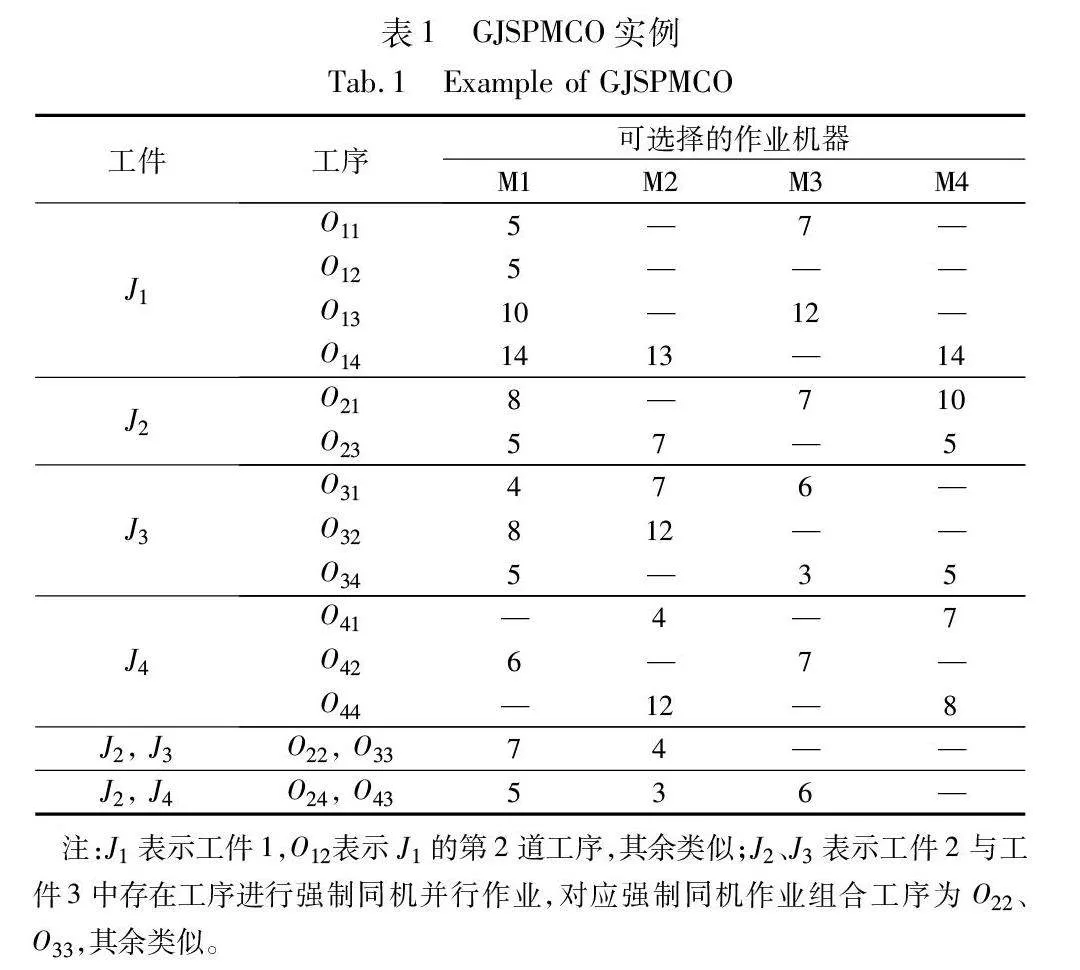
GJSPMCO问题描述如下：N个工件{1，2，…，N}在M台机器{1，2，…，M}上作业；各工件具有确定的工艺路线，但存在不同工件的多个工序形成组合工序的同时，在同一机器上并行完成作业；为提高泛化性并满足车间生产实际，同时考虑机器柔性即每道工序可能在多台不同机器上作业，各工件工序的作业时间由所在机器确定。调度目标是在满足机器可用、工序顺序和强制同机并行作业约束条件下，为各工序选择最合适的机器，确定每台机器上各工序的最佳作业顺序，使系统的某些性能指标达到最优。表1给出了四个工件四台机器的GJSPMCO实例，机器下面对应的数字表示工序在该机器上的作业时间。

为此，GJSPMCO还需要满足如下约束条件：

a）一台机器在同一时刻只能处理一个工序或指定组合工序；

b）一个工件同一时刻只能在一台机器上作业；

c）同一工件的工序之间存在先后顺序约束，不同工件的工序之间受到强制同机并行作业约束影响；

d）所有工件的优先级相同；

e）某道（组合）工序一旦在某台机器上开始作业就不能中断，直到该工件作业完成；

f）所有工件在零时刻可以对其进行作业。

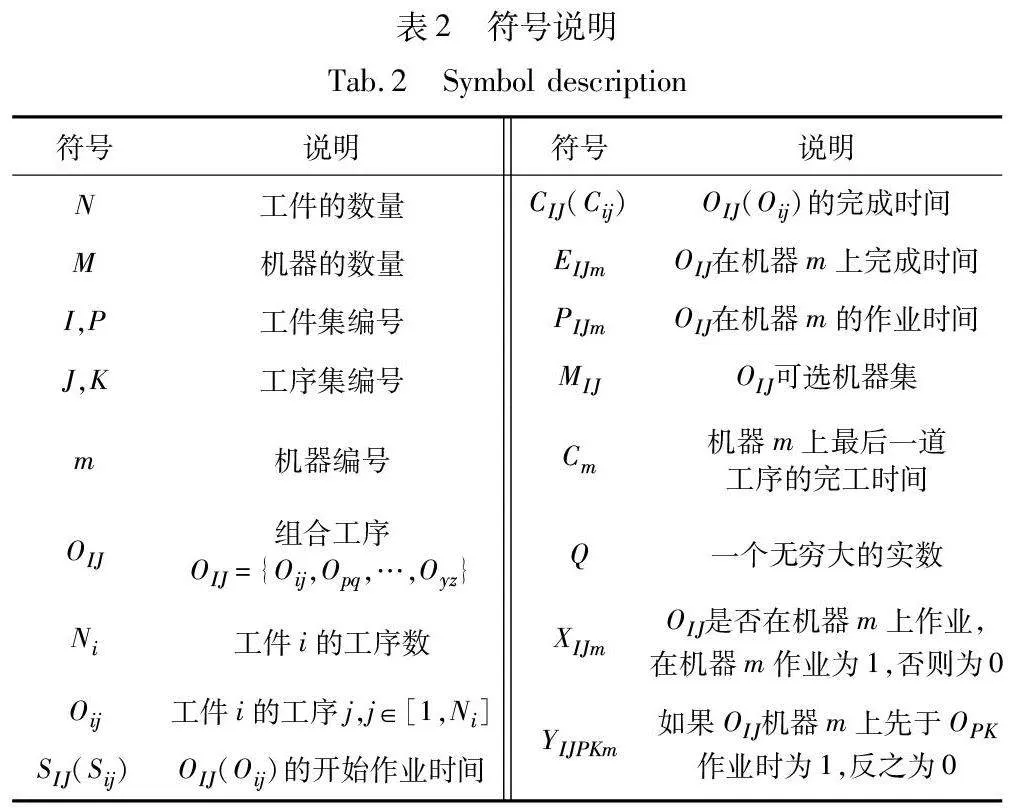
现有的（F）JSP模型无法准确描述GJSPMCO问题：一是强制同机并行作业的多个工序形成组合工序，组合工序中组成元素对应工件紧前工序耦合影响该组合工序的可开始时间，该组合工序的结束时间影响组成元素的所有工件紧后工序的可开始时间，但现有（F）JSP模型中并未引入该约束；二是现有（F）JSP模型无法约束构成组合工序的多个工序元素之间的关系。为解决上述问题，建模时先将各工件的工序Oij统一抽象为只包含一个元素的组合工序OIJ，并将Oij和OIJ统称为工序。在此基础上构建优化模型，模型涉及的符号定义如表2所示。

在此，基于混合整数规划法构建其优化模型，以最小化最大完工时间为优化目标。

Cmax=min（max（Cm）） 1≤m≤M（1）

约束：CIJ-SIJ=PIJm I，J，m（2）

∑Mm=1XIJm=1 I，J（3）

SIJ+XIJmPIJm≤CIJ I，J，m（4）

CIJ≤Cmax I，J（5）

CIJ+Q（YIJPKm-1）≤SPK I，J，P，K，m（6）

Ci（j-1）≤SIJ I，J，Oij∈OIJ（7）

SIJ≥0，PIJm>0，CIJ>0 I，J，m（8）

Sij×XIJm=Spq×XIJm Oij，Opq∈OIJ（9）

Cij×XIJm=Cpq×XIJm Oij，Opq∈OIJ（10）

上述模型约束关系主体基于OIJ构建，如无特别说明，这里的工序均指OIJ；具体组成元素Oij以工件工序进行说明。式（1）为优化目标函数；式（2）表示工序进行作业后中途不能中断；式（3）表示任意工序在机器上只作业一次；式（4）表示任意工序的开始作业时间都不大于其完工时间；式（5）表示任意工序完工时间都不大于最大完工时间；式（6）表示每台机器在同一时刻只能有一道工序在作业；式（7）表示任意工件工序开始作业时间不小于该工序工件紧前工序的完工时间，同时约束了组合工序的开始时间大于等于其所有组成元素的工件紧前工序的结束时间；式（8）表示任意工序的开始作业时间非负，作业时间和完工时间大于0；式（9）和（10）表示组合工序OIJ的各元素Oij∈OIJ必须同时开始和同时完工。

2 自适应混合初始化遗传算法

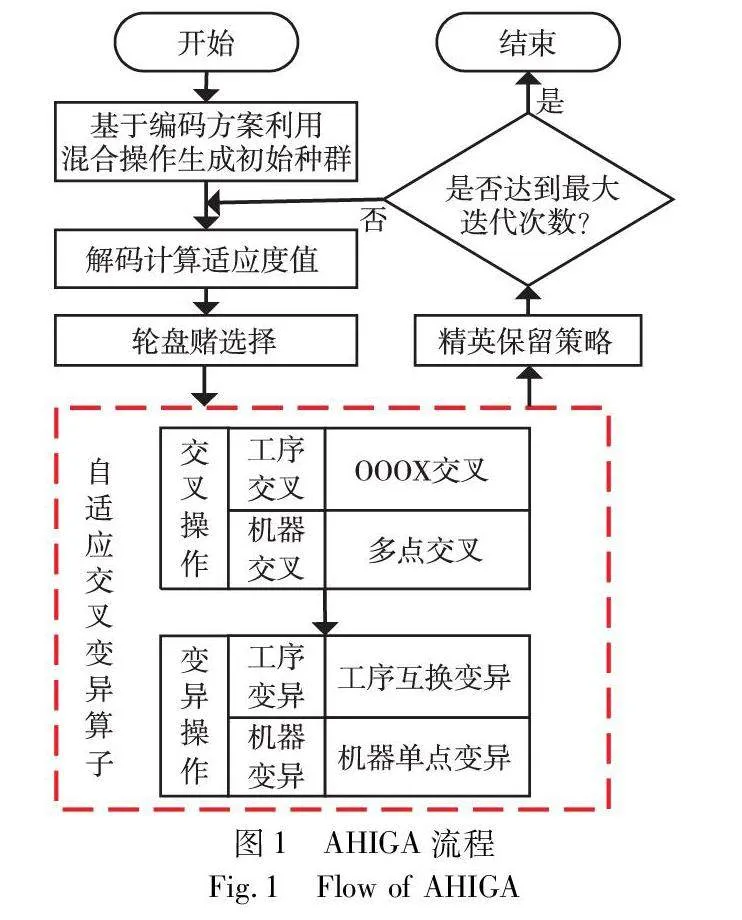
为满足强制同机并行作业约束要求，设计新的编码、解码以及初始可行方案生成机制，在此基础上研究相应的优化迭代操作方法，为此提出AHIGA机制，具体流程如图1所示。

2.1 编码和解码

GJSPMCO考虑工序排序和机器QWvpp9oxu09JF/Ac27srPzqgaFZufewoSbkC9kQw6eU=选择，在此采用工序编码，编码由三段整数编码序列组成，表1对应的编码实例如图2所示。

第一段为工序编码序列，每个基因用工件集序号表示，为了保证各基因位的一致性，每个基因位的元素数量设为l=max{|OIJ|}，I，J;对于|OIJ|<l，在该基因位用虚拟工件0进行补位，具体如图2第一行所示。每个基因位中非0元素i，i∈［1，N］出现频次j∈［1，Ni］代表工件i对应工序Oij，如图2中第二行所示。第二段为机器编码，其可选范围为［1，M］，机器编码顺序与工序编码相对应，表示该工序编码序列对应（组合）工序所指定作业机器。第三段为作业时间编码，表示其对应工序在指定机器上作业所需要时间。

基于编码方案设计的顺序解码方法如算法1所示。

算法1 顺序解码方法

a）设置AO（1，1：ON）、AO（2，1：ON）分别存储各工序的开始时间和完工时间，ON=|OPlan|；用JP={JP［1］，JP［2］，…，JP［N］}、MP={MP［1］，MP［2］，…，MP［M］}分别记录各工件和机器紧前工序的工序结束时间。初始化AO、MP、JP元素为0，k=1。

b）从左往右顺序读取工序编码序列OPlan［k］，1≤k≤|OPlan|中各基因位非0元素（工件编号），确定其工序OIJ，并从MPlan和TmPlan中分别获取OIJ作业机器m和作业时间PIJm。

c）OIJ的开始和完工时间分别为SIJ=maxi∈I{JP［i］，MP［m］}，CIJ=SIJ+PIJm。

d）更新JP［i］=CIJ，i∈I，MP［m］=CIJ，AO（1，k）=SIJ，AO（2，k）=CIJ。

e）若k<ON，k=k+1，转b），否则转f）。

f）结束。

2.2 混合初始化种群

初始种群的质量决定遗传算法求解质量和收敛速度。为增强初始解的质量，在此采用混合初始化方式［23］，其中一半种群采用贪婪初始化方式生成，另一半种群采用随机初始化方式生成。基于编码方式设计混合初始化种群生成算法，如算法2所示。

算法2 混合初始化种群

a）初始化种群规模NP，定义NP×3的数组Pop，计数器np=1，k=max{|OIJ|}，I，J。

b）生成新的空的基于工件表示的工序序列OPlan、机器序列MPlan和作业时间序列TmPlan，设置［1，N］所有数为未标状态。

c）如果［1，N］全部被标记，转f）；反之，随机选取［1，N］中未标记的数i，判断OPlan中i出现频次j，如果j=Ni，标记工件i，转c）；如果j<Ni，从不同工件工艺路线PPlank，1≤k≤N中获取Oij，如果Oij为常规工序，将i加入OPlan尾部，并在该基因位补l－1个0；如果Oij为组合工序元素，转d）。

d）获取Oij∈OIJ={Oij，Opq，…，Oyz}对应工件集I，将I中各工件编号绑定放入到OPlan尾部，并在该基因位补l－|OIJ|个0。

e）获取OIJ未放入调度序列的前驱工序集JP［OIJ］，判断OIJ中i∈I是否有前驱组合工序，如果工件i无前驱组合工序，依次将Oij∈JP［OIJ］对应工件编号i随机插入在OPlan中I之前；反之将其随机插入在最靠近i的前驱组合工序和I之间，转c）；并在插入的基因位补l－1个0。

f）生成（0，1）的随机数r，若r<0.5，对于OPlan［k］，1≤k≤|OPlan|中工序OIJ，根据顺序解码选择m=argmin{EIJm1，EIJm2，…，EIJmj}，m1，m2，…，mj∈MIJ作为作业机器；反之从MIJ中随机选择m作为OIJ作业机器；最后形成机器序列MPlan。进一步确定各工序作业时间，生成作业时间序列TmPlan。存储Pop（np，1）=OPlan、Pop（np，2）=MPlan、Pop（np，3）=TmPlan。

g）如果np<NP，np=np+1，转b）；反之结束。

利用算法2和表1中的数据生成一个初始可行方案的示意，如图3所示。假设算法2中步骤c）随机生成了（3，0）（1，0）（4，0）（2，0）（1，0）（1，0）工件集序号表示的工序序列（如图3中第一行），对应工序分别为O31、O11、O41、O21、O12、O13。然后基于步骤c）随机选取工件2，对应工序O22、O22和O33形成组合工序，基于步骤d）在序列尾部放入O22、O33，对应工件（2，3）（如图3中第三行），但O33前驱工序O32未插入工序序列且O22、O33无前驱组合工序，基于步骤e）将O32对应工件集编号3插入到（2，3）之前，并采用0补位（如图3中的第四行），网格框为工件3随机插入位置。在已生成工序序列基础上基于步骤c）生成工件编号3的工序序列，对应工序为O34。继续基于步骤c）随机生成工件编号4，对应工序O43，因为O24和O43为组合工序O24、O43，基于步骤d）在序列尾部放入O24、O43，对应工件（2，4）。但O24前驱工序中O23未进行插入且O24、O43工件2存在前驱组合工序O22、O33，基于步骤e）将O23对应工件编号2插入（2，4）和（2，3）之间，并采用0补位。根据步骤c）继续选取未标记的工件编号连同补位0一起加入工序序列尾部，直至1～4中所有数都被标记，此时工序序列编码完成，最终工序编码序列如图3中第五行所示。进一步基于步骤f）生成对应机器和作业时间序列，如图中第六、七行所示。

2.3 自适应遗传操作

迭代过程中的遗传操作包括选择、交叉、变异和精英保留等。选择操作是为了挑选出种群中优秀的个体作为后续交叉变异的对象，本研究以目标函数的倒数为适应度函数f，采用轮盘赌方式进行选择。对于种群规模为NP的种群，基于各个体概率Pi=fi/∑NPj=1fj，1≤i≤NP计算相应累计概率Qq=∑qi=1Pi，1≤q≤NP，然后生成（0，1）之间的随机数r，当r≤Q1，选择第一个个体；当Qq－1≤r≤Qq，选择第q个个体，当选择NP数量个体时选择操作结束。

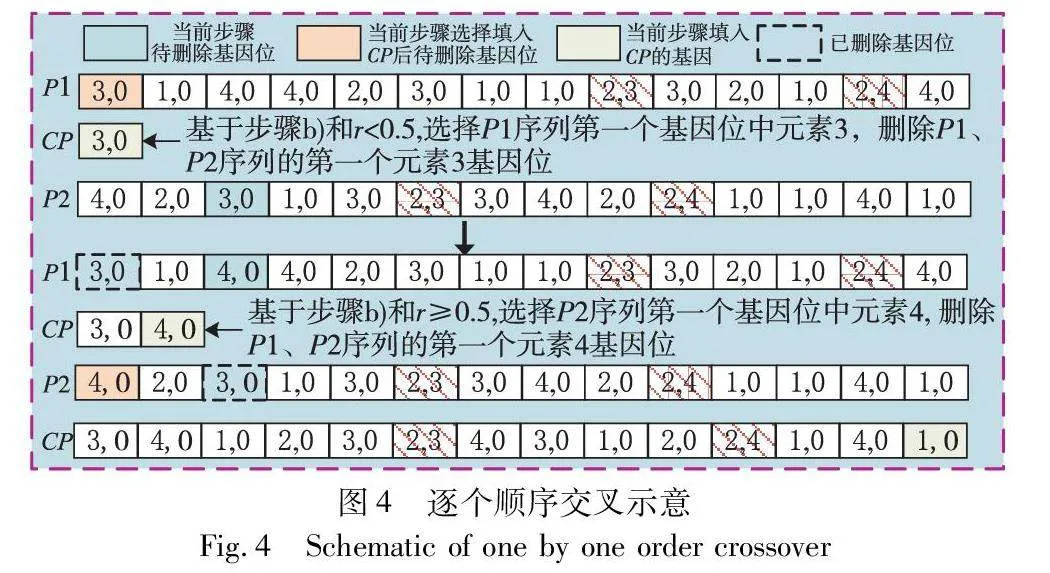
交叉是产生具有更优基因组合后代的重要操作。常见的交叉操作有单点交叉、多点交叉、均匀交叉、次序交叉、工序顺序交叉和扩展顺序交叉等［24］。但这些交叉操作无法处理同机并行作业工序带来的耦合影响，无法避免在子代中产生不可行解。为满足同机并行作业约束，需设计新的交叉机制，对工序序列设计逐个顺序交叉方法（one by one order crossover，OOOX），具体步骤如下：

a）选择父代工序序列P1和P2，设置工序序列子代CP=、设备序列子代CM=和作业时间序列子代CT=。

b）生成（0，1）的随机数r，若r<0.5，则选择P1工序序列第一个基因位元素，否则选择P2工序序列第一个基因位元素。

c）将所选元素添放在CP末尾，并将该元素对应机器和时间分别放入CM和CT末尾。在P1和P2中删除第一次出现该元素的基因。

d）重复b）和c），直到父代P1和P2中元素为空，则工序交叉完成。

以表1数据为例，OOOX示意如图4所示。首先通过随机数r<0.5选择P1工序序列第一个基因位元素3，将元素3添放入子代CP首位，并删除P1和P2中第一次出现元素3的基因位；然后继续生成随机数r≥0.5，选择P2第一个基因位元素4，将元素4添放入子代CP末尾，并删除P1和P2中第一次出现元素4的基因位；依此类推，直到P1和P2中元素为空则交叉完成，生成子代工序序列CP。

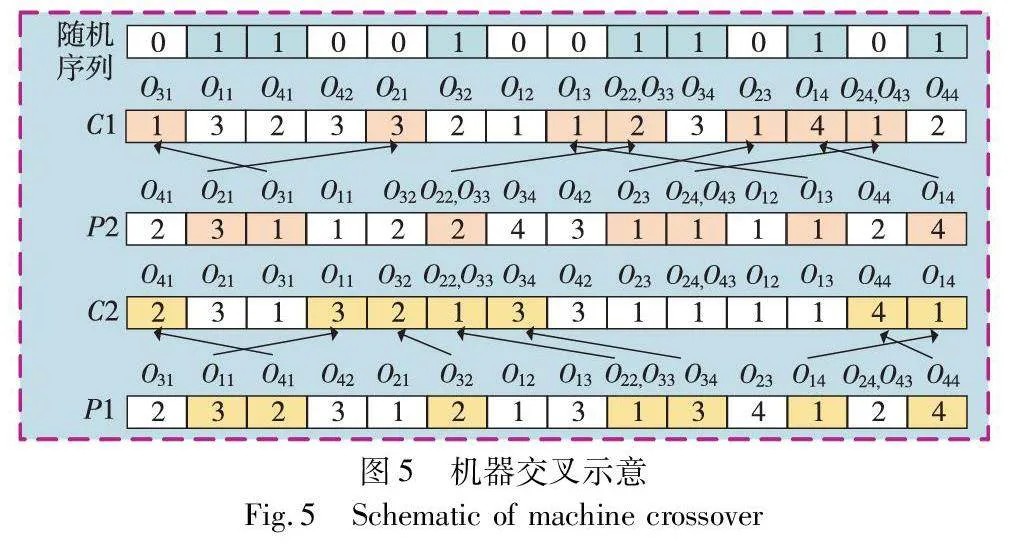
为使交叉更加充分，在完成工序交叉后进一步对机器编码序列进行多点交叉，具体步骤如下：

a）随机生成一段长度等于机器编码序列长度的0-1序列，序列中元素1对应机器编码位置即为进行机器交叉的位置。

b）将父代P1编码序列复制给子代C1，父代P2编码序列复制给子代C2。

c）将父代P1机器交叉位置的机器更新到子代C2对应工序的机器编码位置，将父代P2机器交叉位置的机器更新到子代C1对应工序的机器编码位置。

d）P1机器交叉位置的机器对应的作业时间更新到子代C2对应工序的作业时间编码位，P2机器交叉位的机器对应的作业时间更新到子代C1对应工序的作业时间编码位。

机器交叉示意如图5所示。首先将父代P1编码序列复制给子代C1，父代P2编码序列复制给子代C2，机器编码上方为该机器对应的工序；然后根据产生的随机序列中元素1的位置进行机器交叉，父代P1机器序列中工序O11、O41、O32、O22，O33、O34、O14、O44对应机器3、2、2、1、3、1、4更新到子代C2工序O11、O41、O32、O22，O33、O34、O14、O44对应的机器码位，父代P2机器序列中工序O21、O31、O22，O33、O23、O24，O43、O13、O14对应机器3、1、2、1、1、1、4更新到子代C1工序O21、O31、O22，O33、O23、O24，O43、O13、O14对应的机器码位。

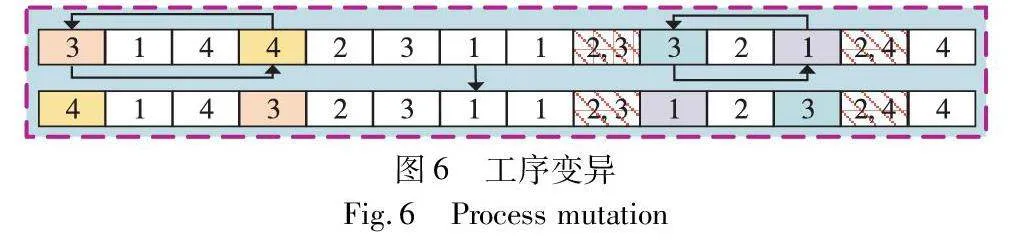
变异操作可增加种群的多样性并防止早熟，影响着算法的局部搜索能力。对于（F）JSP，常见的变异操作有互换变异、逆序变异、插入变异和单点变异。但是这些变异操作应用于本研究问题的工序序列变异时，因其随机性，不可避免地打破了同机并行作业的工件前驱工序约束。为确保组合工序在变异后能够满足工序前后作业约束，对于工序变异，将以组合工序为节点进行分段变异。先以组合工序为分段点，依次判断各分段工序编码序列长度。若分段工序编码序列长度大于等于2，则在分段工序编码序列中随机选择两个工序进行工序互换变异，否则不进行变异操作。为得到可行解，变异完成后需更新机器序列和作业时间序列，使得各工序对应的作业机器和作业时间与变异之前相同。工序变异操作如图6所示。

对于机器编码序列的变异操作采用单点变异方式进行变异，将该位置上的机器随机替换成该工序可选作业机器集中其他一台机器。为得到可行解，与机器编码变异位置对应的作业时间需更新为该工序在替换机器上的作业时间。

为获得更优种群并加速收敛，在此提出一种自适应交叉变异算子。将种群中的个体分为三类：适应度值f前20%的个体为优良个体，应降低交叉率和变异率来保留自身优良基因；f倒数20%的个体为拙劣个体，应提高交叉率和变异率以增加生成优良个体的概率；其余个体称为普通个体，以一个适中的交叉率和变异率进行交叉和变异。分段函数描述的自适应交叉率和变异率如式（11）（12）所示。

Pc=-arctan（50（fi-fminfmax-fmin+s-0.2））5π+0.9 fmin≤fi≤fmax+4fmin5

-2arctan（20（fi-fminfmax-fmin+s-0.2））5π+0.9

fmax+4fmin5<fi≤4fmax+fmin5

-3arctan（100（fi-fminfmax-fmin+s-0.8））5π+0.74fmax+fmin5<fi≤fmax（11）

Pm=-arctan（50（fi-fminfmax-fmin+s-0.2））5π+0.3 fmin≤fi≤fmax+4fmin5

-arctan（20（fi-fminfmax-fmin+s-0.2））5π+0.3fmax+4fmin5<fi≤ 4fmax+fmin5-arctan（50（fi-fminfmax-fmin+s-0.8））5π+0.24fmax+fmin5<fi≤fmax（12）

其中：fmax、fmin分别表示种群中最大和最小的适应度值；fi表示个体i的适应度值；s为极小的正实数。

采取精英保留策略保留具有优良基因的个体到下一代。将经过遗传操作的种群与上一代种群合并形成新的种群，计算新种群中个体的适应度值，取新种群中适应度值大的50%个体作为下一代的初始种群，精英保留可以将历代种群中具有优良基因的个体保留下来，防止优良个体遗失。

设N为种群规模，L表示一个染色体的位数，P表示一个染色体中的组合工序数。上述混合初始化、轮盘赌选择、交叉、变异和精英保留等在最坏情况下操作的时间复杂度分别为O（N×L）、O（N）、O（N×L）、O（N×（P+1））、O（2×N），整体时间复杂度为O（N×L），由此推断本文算法的时间复杂度并不高。

3 实验结果与分析

因缺乏GJSPMCO问题相关基准实例，本文在MK01-MK15［25］和SFJS6-SFJS10［26］基准算例基础上，通过随机引入一、两个组合工序生成测试算例，组合工序的作业时间信息如表3所示，其中由于MK01-MK15和SFJS6-SFJS10国际基准算例并未说明单位，所以本研究中基于这两个算例生成的GJSPMCD测试算例也无具体单位。以SFJS6为例：O12和O22为第一个组合工序，可在机器1和2上作业，作业时间分别为150和160；O13和O23为第二个组合工序，可在机器3上作业，作业时间为70。同时将对电子产品分组合检实例进行进一步验证。基于上述数据开展实验，所有实验均在Windows 10操作系统、主频3.5 GHz、内存16 GB的个人计算机上完成。

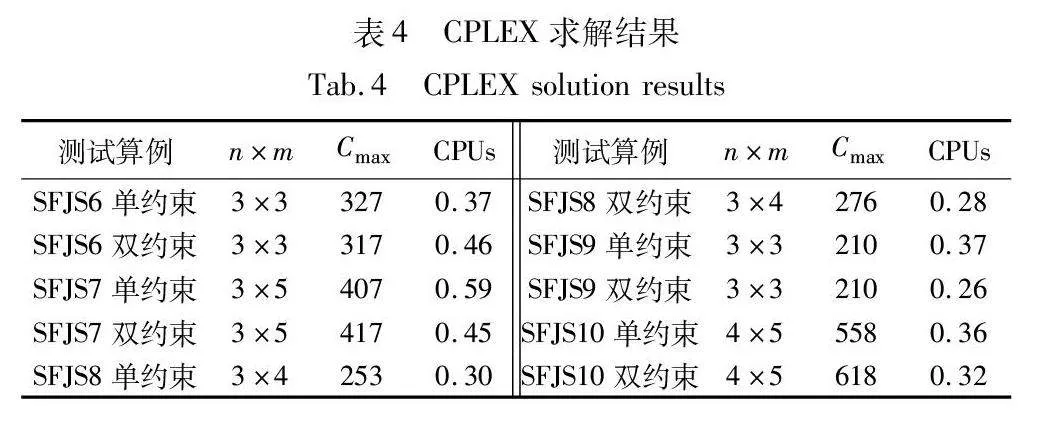
为验证所构建的GJSPMCO混合整数规划模型的有效性，基于引入组合工序的SFJS6-SFJS10算例，利用IBM ILOG CPLEX 12.10进行求解，运行时间上限设置为360 s。CPLEX所得结果如表4所示。

表4中单约束为只考虑表3中对应算例的第一个组合工序，双约束为考虑各算例中两个组合工序，更多组合工序在原理上与双约束场景相似。n×m表示测试算例问题规模，Cmax为最小化最大完工时间，CPUs表示CPLEX实际求解时间，单位为秒（s）。可以看出，CPLEX能获得这些小规模GJSPMCO问题的可行解，证明了模型的可行性。

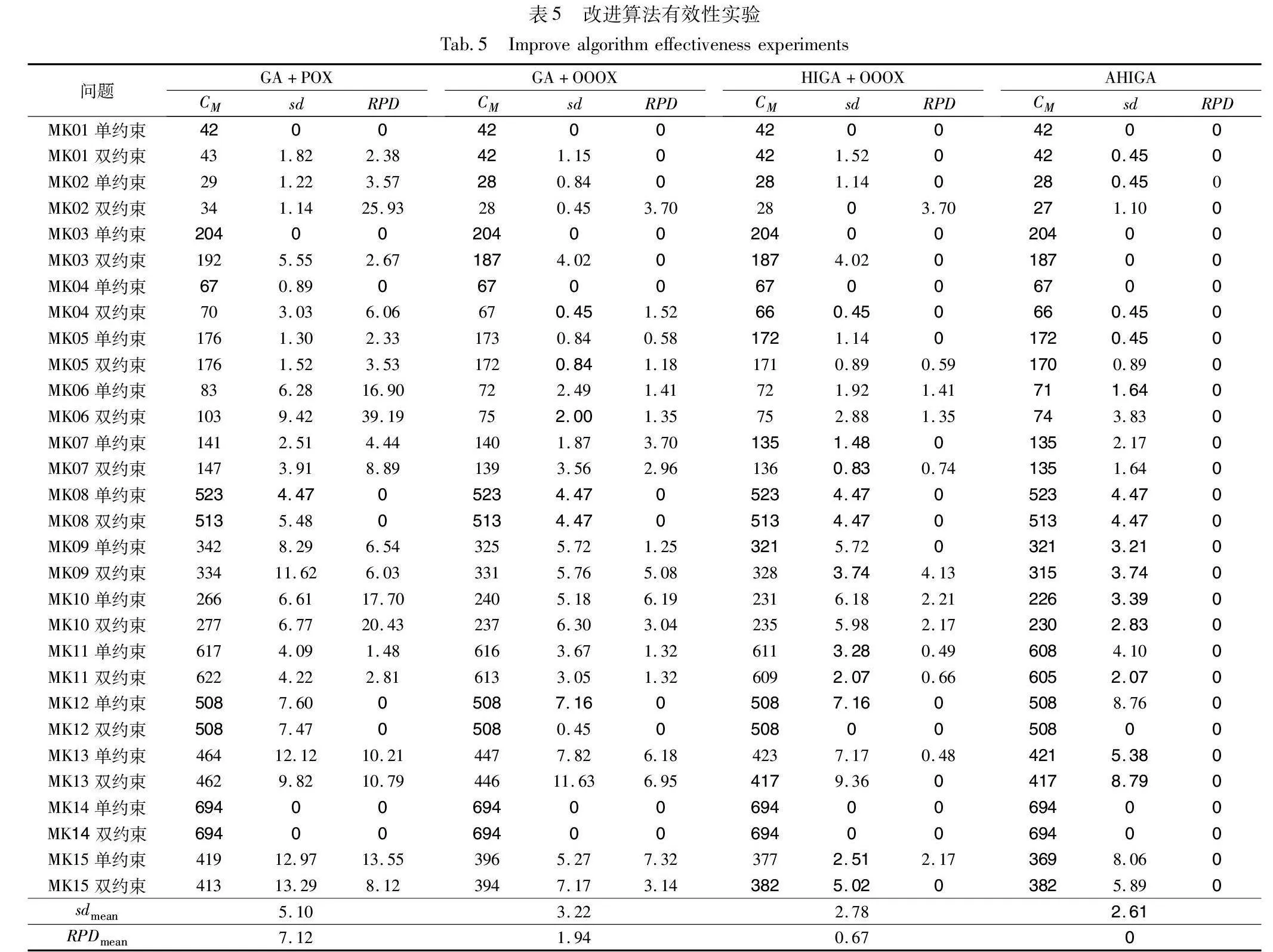
进一步通过对比实验验证OOOX、混合初始化策略以及自适应算子的效果。在此，将GA+OOOX与常规的GA+工序顺序交叉（POX）进行实验对比。因直接应用POX到GJSPMCO将得到不可行子代，所以在此限定POX只能对不涉及组合工序的工件进行交叉。在GA+OOOX基础上，引入混合初始化，形成HIGA+OOOX；进一步增加自适应算子，形成最终算法AHIGA。本研究选取文献中常见的实验参数进行初步实验并选取效果最好的一组实验参数：种群规模为200，交叉率和变异率为0.8和0.3，最大迭代次数为300，并采用MATLAB 2021a软件实现。实验结果如表5所示，表中CM为各算法运行10次所得Cmax的最小值；sd为算法10次运行所得Cmax的标准差，用来评估算法在求解各算例的稳定性，sd越小，算法的稳定性越高；sdmean为30个算例下各算法sd的平均值，用来评估算法面对不同规模算例时的综合稳定性；RPD表示相对百分比差异，用于评估当前算法与最优算法之间的差距，计算公式为RPD=100×（CM-Min）/Min，其中Min表示各算法最优结果的最小值，RPD越小，算法的搜索能力越强；RPDmean为30个算例下所求解得到RPD的平均值，用来评估算法面对不同规模算例时的综合搜索能力。加粗数字为所有算法中的最优值。

从表中可知，在所有30个测试算例中，引入OOOX的GA+OOOX得到的CM和RPD，有21个算例优于GA+POX所得结果，其余9个算例中，两者得到相同的CM和RPD，且RPDmean降低了72.8%，表明OOOX可以大幅度提升算法全局搜索能力。同时可以看出，GA+OOOX得到的sd有24个算例优于GA+POX所得结果，5个算例中，两者得到相同的sd，仅1个算例GA+OOOX的sd劣于GA+POX，且GA+OOOX与GA+POX相比将sdmean降低了36.9%，说明OOOX可以显著提高GA的稳定性。对比HIGA+OOOX和GA+OOOX可知，引入混合初始化策略的HIGA+OOOX在GA+OOOX基础上进一步改进了15个算例的CM和RPD，其余15个算例中，两者得到相同的CM和RPD，且RPDmean降低了65.5%，表明混合初始化策略进一步增强了算法的全局搜索能力。而HIGA+OOOX得到的sd有13个算例优于GA+OOOX所得结果，11个算例中，两者得到相同的sd，6个算例HIGA+OOOX的sd劣于GA+OOOX，且HIGA+OOOX与 GA+OOOX相比，将sdmean降低了13.7%，说明混合初始化策略也可以有效提高算法的稳定性。引入自适应算子的AHIGA在HIGA+OOOX基础上进一步改进了12个算例的CM和RPD，其余18个算例，两者得到相同的CM和RPD，且RPDmean降低至0，表现出自适应算子对提高算法全局搜索能力的有效性。而AHIGA得到的sd有10个算例优于HIGA+OOX所得结果，12个算例中，两者得到相同的sd，8个算例中，AHIGA的sd劣于HIGA+OOOX，且AHIGA与HIGA+OOOX相比将sdmean降低了6.1%，表明自适应算子进一步提升了算法的稳定性。上述对比结果证明了OOOX、混合初始化以及自适应算子均有利于提升算法全局搜索能力和维持算法稳定性，所提出的优化策略具有可行性和有效性。

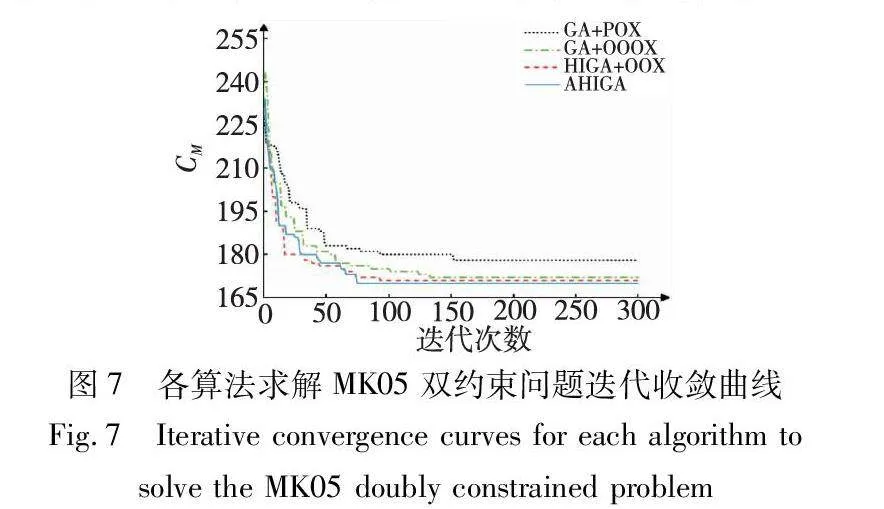
各优化策略算法求解10次MK05双约束问题获得最优结果的迭代过程收敛曲线对比如图7所示。可以看出，OOOX、混合初始化以及自适应算子均有利于减少GA的迭代次数，获得更好的优化结果，证明了本文方法能快速获得高质量解。

图8为针对MK05双约束问题AHIGA所得最优调度方案的甘特图。可以看出，图中所有工序均满足工序作业顺序约束、不同工序在同一机器上作业先后顺序与强制同机并行作业约束等要求。

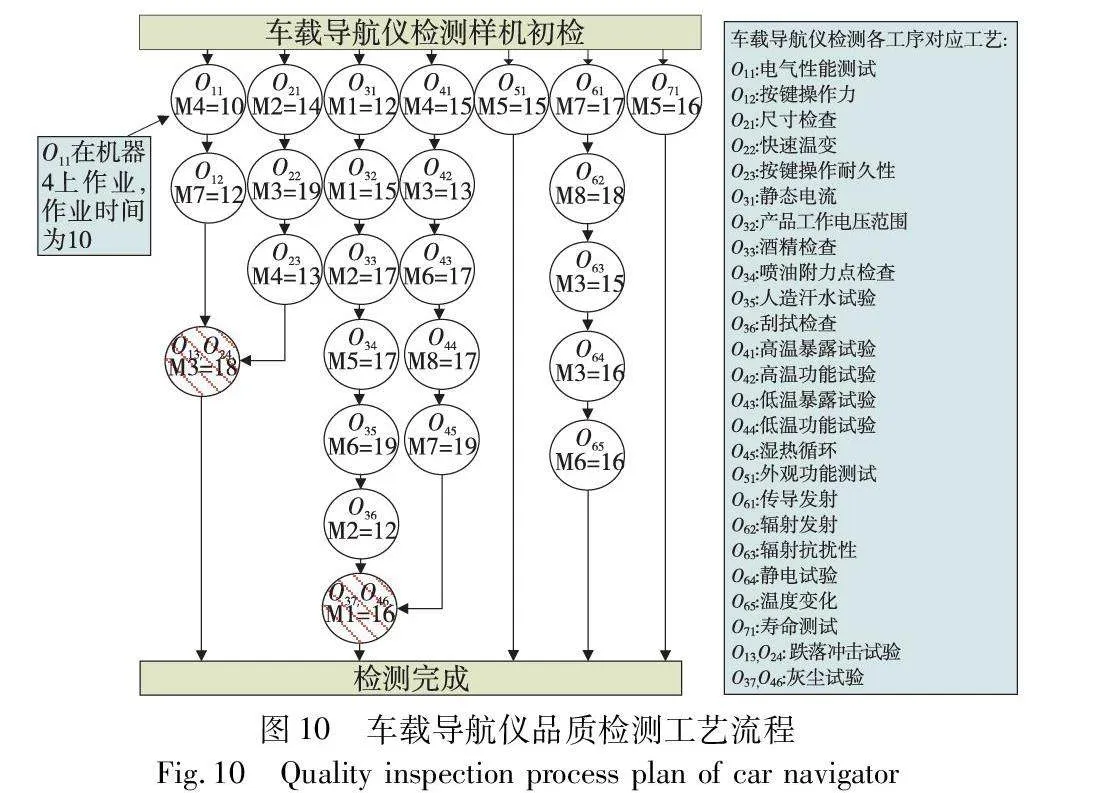
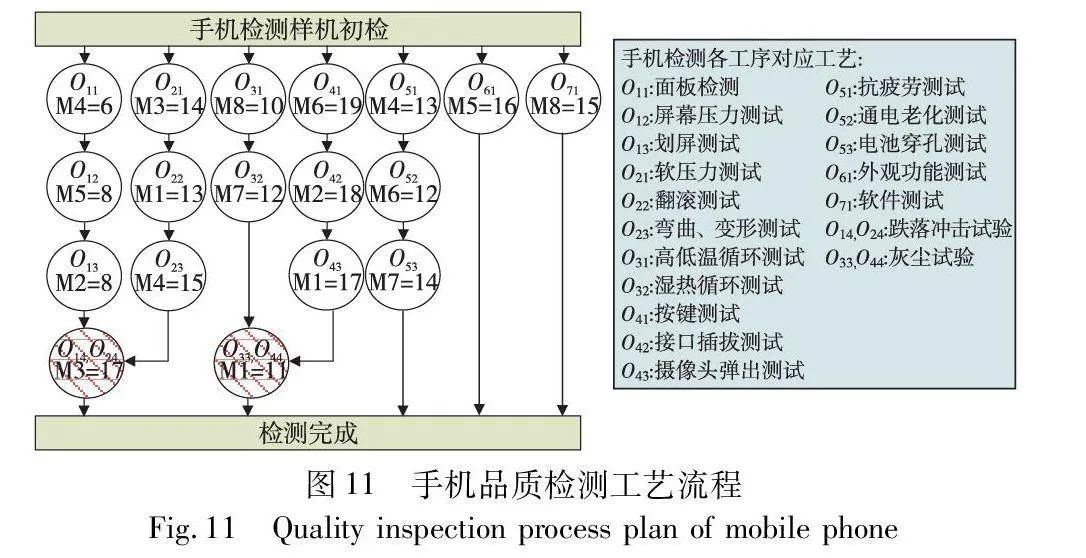
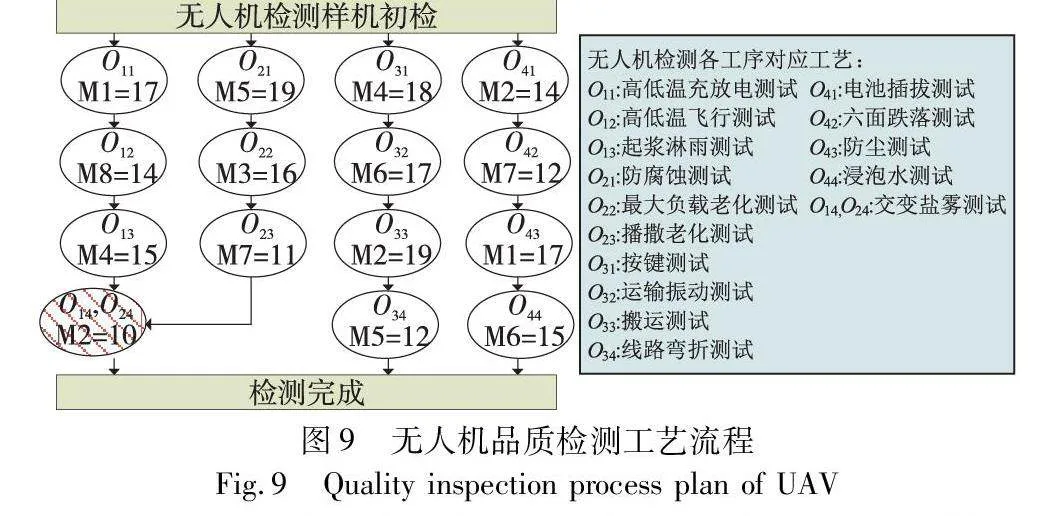
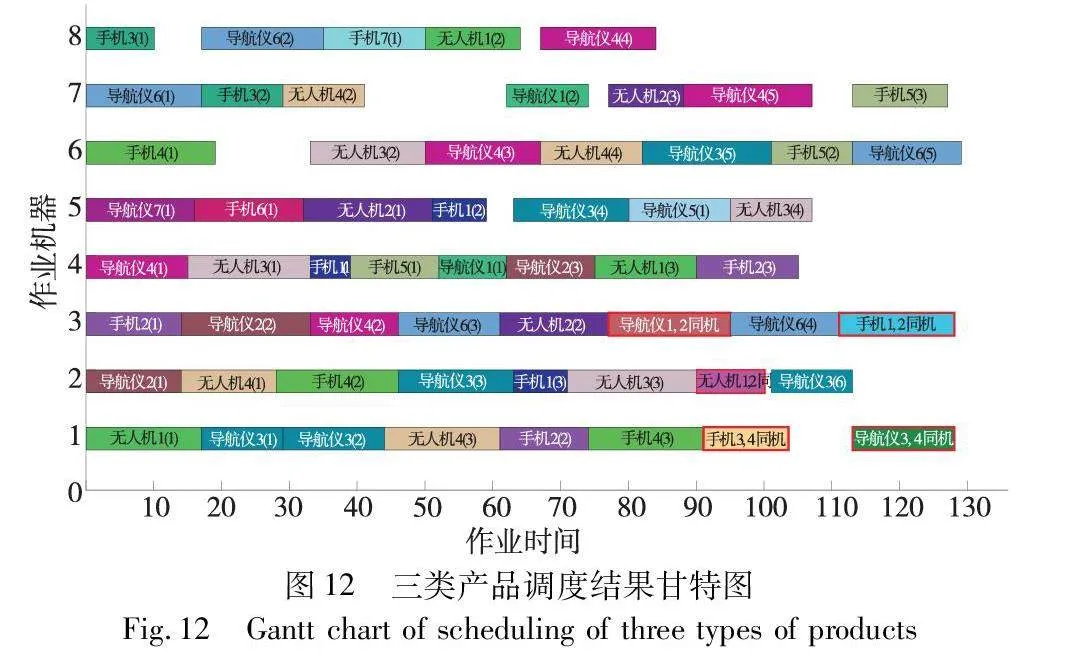
进一步以电子产品检测车间中的无人机、手机和车载导航仪三类产品的检测实例来验证本文模型和所提出的AHIGA。其中无人机、导航仪和手机相应的待检样机分别被划分为4、7、7组（每组视为一个工件），为各工件分别设计相应工艺路线，具体工艺路线及产品检测信息分别如图9～11所示，工序下方为该工序的作业机器及对应作业时间，作业时间单位为小时（h）。其中车载导航仪和手机的强制同机并行作业约束工序均为其分组后工件1、2的跌落冲击测试和工件3、4的灰尘实验；无人机的强制同机并行作业约束工序为工件1、2的交变盐雾测试。

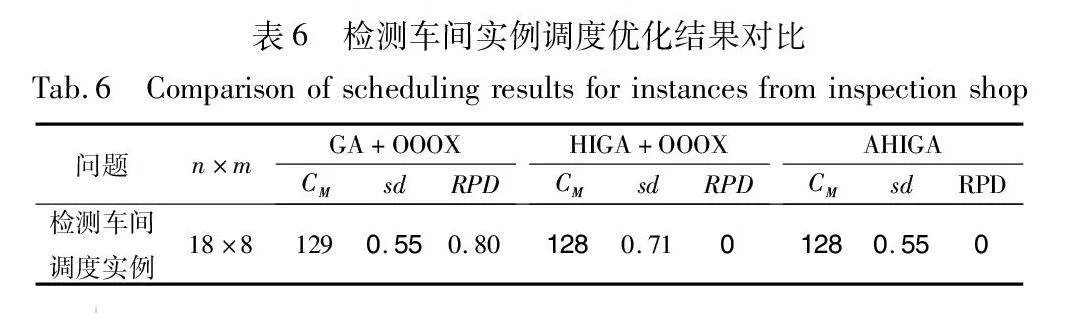
针对这三类产品检测作业的调度，表6给出了各优化策略运行10次的求解结果对比，其中CM单位为小时（h）。可以看出，AHIGA与HIGA+OOOX获得最优CM，AHIGA与GA+OOOX获得最优sd。进一步说明AHIGA具有较强的全局搜索能力和较好的解的稳定性。图12为AHIGA运行10次得到的最优调度结果甘特图，其中进行强制同机并行作业的组合工序用红色框图标注（参见电子版），横坐标单位为小时（h）。从图中可以看出，进行强制同机并行作业的组合工序依旧满足工序顺序、作业机器和作业时间约束，再一次验证了AHIGA求解GJSPMCO问题的可行性。

4 结束语

本文探究利用自适应混合初始化遗传算法（AHIGA）求解考虑强制同机并行作业的广义作业车间调度（GJSPMCO）问题。但在实际生产应用中，存在强制同机并行作业、柔性同机并行作业和设备与工人耦合等多种约束影响，接下来将研究更符合车间实际情况的多约束广义作业车间调度问题。

参考文献：

［1］张洁， 秦威. 智能制造调度为先—《制造系统智能调度方法与云服务》导读［J］. 中国机械工程， 2019，30（8）： 1002-1007. （Zhang Jie， Qin Wei. Intelligent manufacturing scheduling first：a guide of manufacturing system intelligent scheduling method and cloud service［J］. China Mechanical Engineering， 2019， 30（8）： 1002-1007.）

［2］Gao Liang， Pan Quanke. A shuffled multi-swarm micro-migrating birds optimizer for a multi-resource-constrained flexible job shop scheduling problem［J］. Information Sciences， 2016， 372： 655-676.

［3］Zhang Fayong， Li Rui， Gong Wenyin， et al. Deep reinforcement learning-based memetic algorithm for energy-aware flexible job shop scheduling with multi-AGV［J］. Computers & Industrial Enginee-ring， 2024， 189： 109917.

［4］郭鹏， 郝东辉， 郑鹏， 等. 考虑工人疲劳的双资源柔性作业车间调度优化［J］. 浙江大学学报： 工学版， 2023， 57（9）： 1-10. （Guo Peng， Hao Donghui， Zheng Peng， et al. Scheduling optimization of dual resource-constrained flexible job shop considering worker fatigue［J］. Journal of Zhejiang University： Engineering Science， 2023， 57（9）： 1-10.）

［5］刘琼， 梅侦. 面向低碳的工艺规划与车间调度集成优化［J］. 机械工程学报， 2017， 53（11）： 164-174. （Liu Qiong， Mei Zhen. Integrated optimization of process planning and shop scheduling for reducing manufacturing carbon emissions［J］. Journal of Mechanical Engineering， 2017， 53（11）： 164-174.）

［6］Li Yufeng， He Yan， Wang Yulin， et al. An optimization method for energy-conscious production in flexible machining job shops with dynamic job arrivals and machine breakdowns［J］. Journal of Cleaner Production， 2020， 254： 120009.

［7］Gong Xu ， Pessemier T D， Martens L， et al. Energy and labor-aware flexible job shop scheduling under dynamic electricity pricing： a many-objective optimization investigation［J］. Journal of Cleaner Production， 2019， 209： 1078-1094.

［8］Ku Wenyang， Beck J C. Mixed integer programming models for job shop scheduling： a computational analysis［J］. Computer & Operations Research， 2016， 73： 165-173.

［9］Ozolins A. Bounded dynamic programming algorithm for the job shop problem with sequence dependent setup times［J］. Operational Research， 2020， 20： 1701-1728.

［10］Meng Leilei， Duan Peng， Gao Kaizhou， et al. MIP modeling of energy-conscious FJSP and its extended problems： from simplicity to complexity［J］. Expert Systems with Applications， 2024， 241： 122594.

［11］李佳磊， 顾幸生. 双种群混合遗传算法求解具有预防性维护的分布式柔性作业车间调度问题［J］. 控制与决策， 2023， 38（2）： 475-482. （Li Jialei， Gu Xingsheng. Two-population hybrid genetic algorithm for distributed flexible job-shop scheduling problem with preventive maintenance［J］. Control and Decision， 2023， 38（2）： 475-482.）

［12］张国辉， 闫少峰， 陆熙熙， 等. 改进混合多目标蚁群算法求解带运输时间和调整时间的柔性作业车间调度问题［J］. 计算机应用研究， 2023， 40（12）： 3690-3695. （Zhang Guohui， Yan Shaofeng， Lu Xixi， et al. Improved hybrid multi-objective ant colony optimization for flexible job-shop scheduling problem with transportation time and setup time［J］. Application Research of Computers， 2023， 40（12）： 3690-3695.）

［13］董君， 叶春明. 新型教与同伴学习粒子群算法求解作业车间调度问题［J］. 计算机应用研究， 2019， 36（12）： 3764-3768. （Dong Jun， Ye Chunming. Novel teaching and peer-learning-based particle swarm optimization for job-shop scheduling problem［J］ . Application Research of Computers， 2019， 36（12）： 3764-3768.）

［14］Zhang Pengyu， Song Shiji， Niu Shengsheng， et al. A hybrid artificial immune-simulated annealing algorithm for multiroute job shop scheduling problem with continuous limited output buffers［J］. IEEE Trans on Cybernetics， 2022， 52（11）： 12112-12125.

［15］王雷， 邹新. 基于改进免疫克隆选择算法的柔性作业车间调度［J］. 南京理工大学学报， 2018， 42（3）： 345-351. （Wang Lei， Zou Xin. Flexible job-shop scheduling based on improved immune clone selection algorithm［J］. Journal of Nanjing University of Science and Technology， 2018， 42（3）： 345-351.）

［16］吴锐， 郭顺生， 李益兵， 等. 改进人工蜂群算法求解分布式柔性作业车间调度问题［J］. 控制与决策， 2019， 34（12）： 2527-2536. （Wu Rui， Guo Shunsheng， Li Yibing， et al. Improved artificial bee colony algorithm for distributed and flexible job-shop scheduling problem［J］. Control and Decision， 2019， 34（12）： 2527-2536.）

［17］杜凌浩， 向凤红. 改进多邻域候鸟优化算法的柔性作业车间调度研究［J］. 兵器装备工程学报， 2022， 43（12）： 299-306. （Du Linghao， Xiang Fenghong. Research on flexible job shop scheduling based on improved multi-neighborhood migratory bird optimization algorithm［J］. Journal of Ordnance Equipment Engineering， 2022， 43（12）： 299-306.）

［18］杨冬婧， 雷德明. 新型蛙跳算法求解总能耗约束FJSP［J］. 中国机械工程， 2018， 29（22）： 2682-2689. （Yang Dongjing， Lei Deming. A novel shuffled frog-leaping algorithm for FJSP with total energy consumption constraints［J］. China Mechanical Engineering， 2018， 29（22）： 2682-2689.）

［19］Jiang Tianhua， Zhang Chao. Application of grey wolf optimization for solving combinatorial problems： job shop and flexible job shop schedu-ling cases［J］. IEEE Access， 2018， 6： 26231-26240.

［20］牛昊一， 吴维敏， 章庭棋， 等. 自适应樽海鞘群算法求解考虑运输时间的柔性作业车间调度［J］. 浙江大学学报： 工学版， 2023， 57（7）： 1267-1277. （Niu Haoyi， Wu Weimin， Zhang Tingqi， et al. Adaptive salp swarm algorithm for solving flexible job shop scheduling problem with transportation time［J］. Journal of Zhejiang Univer-sity： Engineering Science， 2023， 57（7）： 1267-1277.）

［21］王无双， 骆淑云. 基于强化学习的智能车间调度策略研究综述［J］. 计算机应用研究， 2022， 39（6）： 1608-1614. （Wang Wu-shuang， Luo Shuyun. Research on intelligent shop scheduling strategies based on reinforcement learning［J］. Application Research of Computers， 2022， 39（6）： 1608-1614.）

［22］Chen Ronghua， Yang Bo， Li Shi， et al. A self-learning genetic algorithm based on reinforcement learning for flexible job-shop scheduling problem［J］. Computers & Industrial Engineering， 2020， 149： 106778.

［23］屈新怀， 王娇， 丁必荣， 等. 贪婪初始种群的遗传算法求解柔性作业车间调度［J］. 合肥工业大学学报： 自然294a220038706dc2bb88ce1a66a85b639fdd1bd212e61d3c4d685b4045a1560a科学版， 2021， 44（9）： 1153-1156，1171. （Qu Xinhuai， Wang Jiao， Ding Birong， et al. Genetic algorithm of greedy initial population to solve flexible job-shop scheduling［J］. Journal of Hefei University of Technology： Natural Science， 2021， 44（9）： 1153-1156，1171.）

［24］黄学文， 陈绍芬， 周阗玉， 等. 求解柔性作业车间调度的遗传算法综述［J］. 计算机集成制造系统， 2022， 28（2）： 536-551. （Huang Xuewen， Chen Shaofen， Zhou Tianyu， et al. Survey on genetic algorithms for solving flexible job-shop scheduling problem［J］. Computer Integrated Manufacturing Systems， 2022， 28（2）： 536-551.）

［25］Brandimarte P. Routing and scheduling in a flexible job shop by Tabu search［J］. Annual Operation Research， 1993， 41： 157-183.

［26］Bagheri A， Zandieh M， Mahdavi I， et al. An artificial immune algorithm for the flexible job-shop scheduling problem［J］. Future Gene-ration Computer Systems， 2010， 26（4）： 533-541.