多样性约束和高阶信息挖掘的多视图聚类
2024-08-15赵振廷赵旭俊
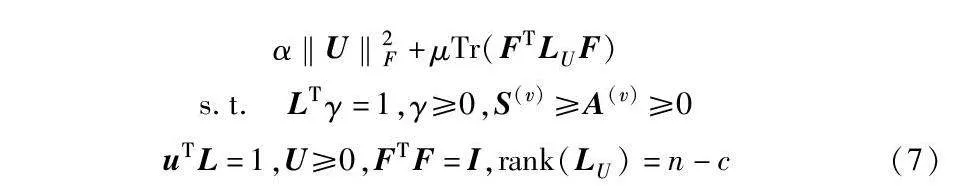








摘 要:在现有的多视图聚类研究中,大多数方法没有考虑多视图的多样性,也没有关注数据的高阶邻域信息,导致聚类结果不够准确,难以挖掘数据集的底层信息。为了解决这些问题,提出了基于多样性约束和高阶信息挖掘的多视图聚类算法(MVCDCHO)。首先设计了视图间多样性测量的方法,利用多样性的约束保留数据的交集特征,同时去除多视图的差异特征;然后提出了一种挖掘视图高阶信息的方法,要求多视图的交集特征接近混合相似图,以挖掘数据间相关性所没有关注到的高阶信息;最后将多视图的交集特征融合成共识图,通过谱聚类来获取聚类目标图;另外,设计了一种交替迭代的方法来迭代学习优化目标函数。实验结果表明,MVCDCHO在归一化互信息(NMI)、调整后的兰德指数(ARI)、聚类精度(ACC)多个聚类评价指标上表现出优异的性能。理论分析和实验研究验证了MVCDCHO中多视图多样性和高阶信息的关键作用,证明了MVCDCHO的优越性。
关键词:多视图聚类; 多样性; 一致性; 高阶信息
中图分类号:TP399 文献标志码:A
文章编号:1001-3695(2024)08-009-2309-06
doi:10.19734/j.issn.1001-3695.2023.12.0615
Multi-view clustering with diversity constraints and high-order information mining
Zhao Zhenting, Zhao Xujun
(School of Computer Science & Technology, Taiyuan University of Science & Technology, Taiyuan 030024, China)
Abstract:In the current research on multi-view clustering, the majority of methods have not adequately considered the diversity of multiple views nor focused on the high-order neighborhood information of the data, which leds to clustering results that lack accuracy and struggle to uncover the underlying information in datasets. To address these issues, this paper proposed a multi-view clustering method based on diversity constraints and high-order information mining(MVCDCHO). Firstly, it designed a method for measuring diversity between views, utilizing diversity constraints to preserve the intersection features of the data while eliminating differing features across multiple views. Subsequently, it introduced a method for mining high-order information in views, requiring the intersection features of multiple views to approximate a mixed similarity graph, thereby extracting high-order information in data correlations that has been overlooked. Finally, it fused the intersection features of multiple views into a consensus graph and employ spectral clustering to obtain the clustering target graph. Additionally, it designed an alternating iterative method, iteratively learning to optimize the objective function. The experimental results show that MVCDCHO has excellent performance on the normalized mutual information(NMI), the adjusted Rand index(ARI), and the clustering accuracy(ACC). Theoretical analysis and experimental study underscore the crucial role of multi-view diversity and high-order information in the MVCDCHO algorithm, providing evidence for its superiority.
Key words:multi-view clustering; diversity; consistency; high-order information
0 引言
近些年来,随着人们获取和处理信息的方式日益多样化,已经可以从现实世界的各个应用领域中获取大量的数据。这些数据是多视图数据,通常包含来自多种模态或多个视角的异构特征。随着多视图数据的不断涌现,单一视图的分析方法在处理多模态数据时显得力不从心,多视图聚类就成为了应对复杂多模态数据分析的重要工具。例如,在生物医学研究中,一种药物,自己的化学结构和在与不同细胞中的化学反应可以被看作不同的视图;一种蛋白质,自己的序列和在不同细胞中的基因表达值可以被看作不同的特征[1]。利用多视图聚类有助于发现新的药物结构、预测药物在不同细胞中的活性,优化药物设计,以及提高疾病分类和诊断的准确性。在金融领域,面临着从多个角度收集的数据,如客户的交易历史、行为模式和信用评分等。这些信息可以被看作是不同的视图,反映了客户在金融系统中的多个方面。通过采用多视图聚类算法,可以更好地理解客户群体的行为模式,并检测异常交易模式或潜在的欺诈行为。这种综合多视图的方法有助于提高金融风险管理的效果,为金融机构提供更精确的风险评估和预测工具。多视图聚类旨在整合来自不同视图或数据源的信息,以更全面和准确地揭示数据之间的关系,为数据挖掘和知识发现提供更强大的工具。与传统的单视图聚类方法相比,多视图聚类能够更好地处理异构特征,充分利用多模态数据的信息,从而提高聚类结果的质量和可解释性。多视图聚类在许多领域都有着广泛的应用,包括图像分析、生物医学研究、金融风险评估、文本挖掘、社交网络分析等。
尽管现有算法已经从各方面提高了聚类的性能,但大多数方法仍有一定的局限性。首先,现有很多方法严重依赖视图之间的一致性信息,忽视了多视图的多样性信息,这导致了它们容易受到低质量或带有噪声的数据集的干扰,从而影响了聚类结果的质量。其次,主要关注样本之间的直接关系,即样本间的相似性。但是,样本不仅与它的邻居相似,而且还与其邻居的邻居相似。所以,直接关系中的信息并不完全,导致了未能准确地提取隐藏在高阶邻近中有价值的信息。最后,现有聚类方法通常使用分多个阶段进行的策略,这导致了协同处理不同阶段之间的挑战,限制了聚类性能的提升。
针对上述问题,本文提出了一种基于多样性约束和高阶信息挖掘的多视图聚类(multi-view clustering with diversity constraints and high-order information mining,MVCDCHO),将多视图的多样性学习、高阶信息的挖掘、一致性学习以及谱聚类集成到一个框架中进行联合优化学习,有效减少了信息的丢失,避免了多步策略带来的次优结果。首先,本文设计了数据间多样性测量的方法,将多个视图的数据分离成交集特征和差异特征,通过对多样性的约束保留数据的交集特征,同时去除差异特征;其次,提出了一种挖掘视图高阶信息的方法,通过要求多视图的交集特征接近混合相似图,准确地提取数据间相关性所没有关注到的高阶信息;最后,在将交集特征进行图融合后,对共识图进行谱聚类操作实现多视图聚类;此外,设计了一种有效的交替迭代方法,用于优化聚类的目标函数。
1 相关工作
1.1 多视图聚类
近年来,多视图聚类受到学术界以及工业界的广泛关注,从不同的角度开发了很多的多视图聚类算法。
协同训练的思想是将多个独立的模型组合在一起,并让它们相互学习和提供反馈,以改进每个模型的性能。Zhou等人[2]提出了一种半监督回归算法,采用协同训练风格。该算法利用两个回归量去相互标记未标记数据,通过均方误差减少量估计置信度,以有效地利用未标记数据来改进回归估计。Zhang等人[3]提出一种新的协同训练算法,通过数据编辑技术估计分类器对未标记示例的预测置信度,并在不同视图之间传递高置信度的预测标签。然而,当不同视图之间的相关性较低时,协同训练可能面临一些限制。首先,不同视图提供的信息可能差异较大,使得协同训练难以有效整合多视图信息,因为模型通常通过共享信息来提高性能,但当不同视图之间缺乏明显关联时,模型之间的协同学习可能受到限制;其次,协同训练通常依赖于共享参数或交替训练的方式,以最大程度地利用各个视图的信息,在不同视图相关性较低的情况下,这可能导致优化问题的复杂性增加,使得模型难以收敛或陷入局部最优。因此,协同训练可能无法有效利用多视图信息,导致性能下降。在设计协同训练方法时需要认识到这些局限性,并寻求解决方案以提高在复杂多视图数据下的性能。
多视图的图聚类是一种利用多个不同视角或特征表示的数据进行聚类分析的方法。通过综合多个视图的信息,以获得更准确和全面的聚类结果。AWP方法[4]对单视点光谱聚类的光谱旋转技术进行多视点扩展,提出了自适应加权方法以克服权重平均在多视图任务中的局限。Tang等人[1]提出了一种统一的一步多视点光谱聚类方法,通过整合光谱嵌入和K-means到一个统一的框架中,直接从统一图中获取离散聚类标签,避免了信息丢失。刘金花等人[5]在谱嵌入阶段实施多视图信息的融合,以减少噪声和数据差异的影响,并在联合优化学习中整合了图学习和谱聚类,有效提高了模型的性能。GMC[6]的学习方法是能够相互学习每个视图的图矩阵和统一图矩阵的一体化框架,自动加权每个数据图矩阵并自然地划分数据点为所需数量的聚类。Chen等人[7]提出的基于低秩张量的接近学习方法,通过将多个低秩概率亲和矩阵叠加在一个低秩约束张量中,综合考虑多个视图间的全面性和高阶相关性,并将特定视图表示的自适应置信度与共识指标图结合起来。
多视图子空间是用于处理多视图数据的一种数据表示和分析方法,通过结合不同视图的子空间来获得更全面、更准确的数据描述和分析结果。Lin等人[8]通过对不同特征赋予权重,并在特定于视图的自表示特征空间中捕获数据的局部信息,以提高视图聚类的性能。该方法采用了聚类分配正则化来保持多视图的一致性,并通过增广拉格朗日乘子的交替迭代算法进行优化。DiMSC[9]扩展了现有的子空间聚类方法,以适用于多视图数据。它不仅考虑了数据的子空间结构,还考虑了不同视图之间的互补性。CSMSC方法[10]将一致性和特异性结合起来用于子空间表示学习,部署了一个通用的一致表示和一组特定的表示来制定多视图设置中的自表达属性。赵兴旺等人[11]提出一种基于二部图的联合谱嵌入多视图聚类算法,通过考虑多视图数据的邻域关系和重要性,以及引入聚类指示矩阵的方式,实现了更准确和鲁棒的聚类。
1.2 高阶信息
高阶的邻域关系已经被开发出了很多方法。L-MSC[12]利用多个视图的互补信息,同时寻找底层潜在表示,考虑具有低秩约束的展开张量来捕获高阶相关性。Wang等人[13]探索多视图数据中的高阶统计量来增强多视图聚类,将高阶相似性和高阶相关性整合到自适应学习模型中,更加全面地挖掘内在的聚类结构。李理等人[14]通过将高维多视图数据投影到低维嵌入空间,学习到干净字典以消除冗余信息和噪声对聚类性能的影响。将低秩投影融入基于张量学习的多视图子空间聚类框架,充分挖掘多视图数据的高阶信息。SCMV-3DT[15]基于三阶张量空间的t积来处理多视图聚类问题,通过考虑多个视图之间的高阶统计信息,增强了对多视图数据的潜在子空间结构的恢复,从而提高了聚类性能。
上述方法中仍然存在一些缺点:a)这些方法中大多数只是处理多视图的一致性信息,忽视了多视图的多样性信息;b)大多数方法只是考虑数据的一阶相似度信息,没有考虑多数据的高阶相似度信息。这些方法由于在数据处理中对这些信息的忽视,可能会影响聚类的效果。相反,MVCDCHO模型可以利用多视图的多样性信息以及挖掘多视图的高阶信息。
2 相关理论基础
本章回顾了多视图的多样性以及高阶信息探索的知识。主要使用的符号如表1所示。
2.1 视图间的多样性测量
为了测量多视图的多样性,将初始图S(v)分解为交集特征A(v)和差异特征E(v),表示为
S(v)=A(v)+E(v)(1)
其中:A(v),E(v)∈Euclid Math TwoRApn×n≥0。这里的关键是找到矩阵A(v)、E(v)。这种差异特征可以被视为一个更普遍的概念,它不仅可能是由噪声引起,还可能是由各个视图特定的不同类型特征引发的。在相似图上,噪声通常被认为是稀疏的,但差异特征不是稀疏的。因此,在相似图上处处可能出现差异。这样,图内的稀疏性不再是检测多样性的合理考虑因素,并且差异特征应该是彼此有差异的,因为没有差异就等于是交集特征而不是差异特征了。文献[16]假设差异部分在视图之间稀疏,将多视图的差异特征E(v)乘积,如果视图之间的多样性稀疏,则差异特征的乘积之和应较小,文献[16]中有
η∑Vv,u=1v≠usum((E(v))☉(E(u)))(2)
其中:η是一个权衡参数。式(2)明确地衡量了不同观点之间的多样性。同时,因为还希望每个视图内的差异特征较小,设θ也表示一个权衡参数,可以表述为
θ∑Vv=1sum((E(v))☉(E(v)))(3)
2.2 高阶信息探索
在这里进一步探索特征空间中的相似信息。相似度是数据点之间的基本关系,利用高阶关系学习有价值的信息。文献[17]定义n阶图是Wnv=Wn-1v×W1v,Wnv是相似图。为了挖掘高阶邻域关系的信息,将混合相似图定义为
fv(W)=W1v+W2v+…+Wnv(4)
其中:一阶邻近关系是节点间最直观的关系,而无穷级相互作用关系是移动无穷步后的稳定关系。假设一阶和无穷阶相似图包含了大部分信息,则定义n→∞时代价最小的混合相似图为
fv(W)=W1v+Wnv(5)
为了结合多视图的高阶信息,要求A(v)接近混合相似图,用数学公式表示为
minγv,A(1)…A(V)∑Vv=1γv‖A(v)-fv(W)‖2F(6)
3 多样性约束和高阶信息挖掘的多视图聚类
为了解决大多数多视图聚类的方法没有考虑到多视图的多样性以及没有充分考虑到高阶邻域信息的问题,提出了MVCDCHO的多视图聚类方法,并展示了方法的优化求解过程。
3.1 多样性约束和高阶信息挖掘的多视图聚类
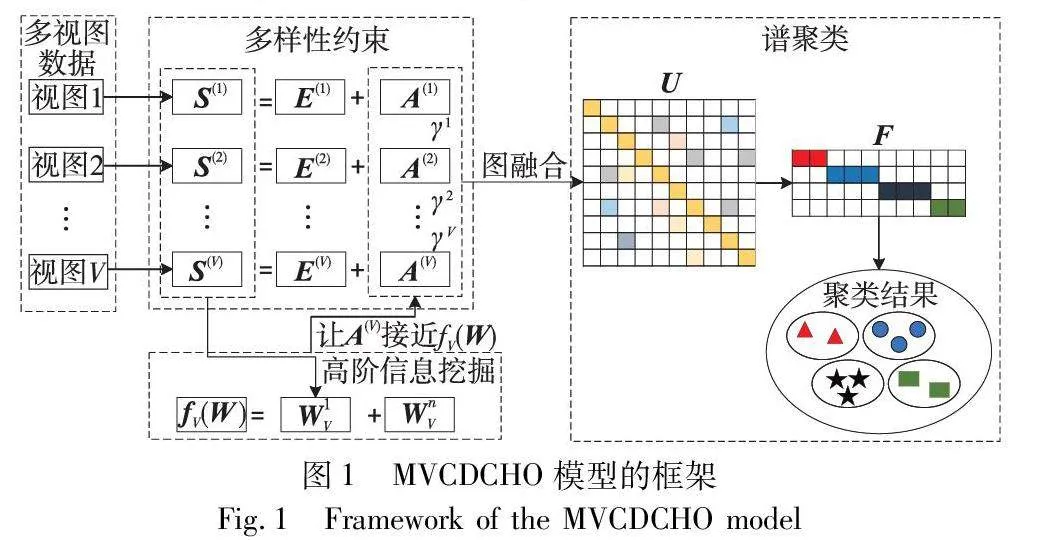
为了提高多视图聚类的性能,提出了一个将多视图的一致性学习、多样性学习以及挖掘多视图的高阶信息联合学习的框架。图1给出了MVCDCHO模型的框架图,主要分为多样性约束和高阶信息挖掘两部分。在进行数据处理后,通过图融合得到共识图U,对共识图U进行谱聚类操作得到F指标矩阵,获得聚类结果。在目标函数中,利用多样性约束以及挖掘到的高阶信息之后的交集特征来构建目标图,而非依赖最初的相似图,从而提高适应真实世界数据集的性能。利用E(v)=S(v)-A(v)和sum((E(v))☉(E(u)))=Tr(E(v)(E(u))T),将式(3)(6)合并得到目标函数:
minγv,A(1)…A(V),U,F∑Vv,u=1wvuγvγuTr((S(v)-A(v))(S(u)-A(u))T)+
∑Vv=1γv‖A(v)-fv(W)‖2F+∑Vv=1γv‖A(v)-U‖2F+α‖U‖2F+μTr(FTLUF)
s.t. LTγ=1,γ≥0,S(v)≥A(v)≥0
uTL=1,U≥0,FTF=I,rank(LU)=n-c(7)
其中:第一项是测量视图间的多样性,使视图中的多样性稀疏,目的是统一视图中的多样性;第二项是探索视图中的高阶信息,挖掘视图间的高阶信息,利用高阶关系学习有价值的信息;第三、四项是图融合,它是通过将各个视图的交集特征A(v)线性组合,最终获得共识图U;第五项是用谱聚类求解共识图,引入U的拉普拉斯矩阵LU,通过谱聚类实现图聚类,将得到的k个连通分量组成最终的特征矩阵F,使用K-means聚类来对数据进行最终的聚类,这里的α、μ是权衡参数。
3.2 优化过程
为了求解式(7),采用交替迭代最小化优化方案。分别固定U,A(1),…,A(V),F求解γv,固定γv,A(1),…,A(V),F求解U,固定U,γv,F求解A(1),…,A(V),固定γv,A(1),…,A(V),U求解F,将优化分成四个部分,每次优化一个问题,通过迭代这个过程不断优化,直至目标函数收敛即完成优化方案。在优化方案中,对于γv,A(1),…,A(V),因为不好求解,将其转换成求解二次规划问题,为了获得二次规划中的P、q,将目标函数式(7)转换成不同的形式,如式(9)(10)所示。
f(γv,A(1),…,A(V),U,F)=
∑Vv,u=1wvuγvγu∑i,j((S(v)ij-A(v)ij)(S(u)ij-A(u)ij)T)+∑Vv=1γv∑i,j(A(v)ij-Uij)2+∑Vv=1γv∑i,j(A(v)-fv(W))2+
α∑i,jU2ij+μTr(FTLUF)=(8)
∑i,j∑Vv,u=1wvuTr((S(v)-A(v))(S(u)-A(u))T)γvγu+
∑Vv=1(‖A(v)-fv(W)‖2F+‖A(v)-U‖2F)γv+C1=(9)
∑i,j∑Vv=1(2γv(A(v)ij)2+∑Vu=1wvuγvγuA(v)ijA(u)ij)-
2∑Vv=1γv(fv(W)+Uij+∑Vu=1γuwvuS(v)ij)A(v)ij+C2(10)
1)固定U,A(1),…,A(V),F求解γv
定义γ=(γ1,γ2,…,γv),将目标函数表示为二次规划问题
minγ12γTPγ+qTγ s.t. γ>0,l·γ=1(11)
根据式(9)可以知道,这里的P∈Euclid Math TwoRApV×V并且由公式中的二次项以及一次项可得
q=∑Vv=1(‖A(v)-fv(W)‖2F+‖A(v)-U‖2F)(12)
P=∑Vv,u=1wvuTr((S(v)-A(v))(S(u)-A(u))T)(13)
2)固定γv,A(1),…,A(V),F求解U
当固定γv,A(1),…,A(V),F时,式(7)可以简化成
∑Vv=1γv‖A(v)-U‖2F+α‖U‖2F(14)
对其进行求导,令导数等于零,则有
U=∑Vv=1γvA(v)α+1(15)
3)固定U,γv,F求解A(1),…,A(V)
对于一对固定的(i,j),设x=[A(1)ij,…,A(v)ij]T是A的对应列,所以通过式(10)可以看出,公式是关于x的二次函数,所以可以将目标函数表示为一个有上界和下界的二次规划问题:
minγ12xTPx+qTx s.t. 0≤x≤u(16)
其中:u=[S(1)ij,…,S(v)ij]T,要对每一个(i,j)求解二次规划,容易知道这些QP问题中的下界为0,上界为S。由式(10)中的二次项以及一次项可知
P=∑Vv=1(2γv+∑Vu=1wvuγvγu)(17)
q=-2∑Vv=1γv(fv(W)+Uij+∑Vu=1γuwvuS(v)ij)(18)
4)固定γv,A(1),…,A(V),U求解F
当固定γv,A(1),…,A(V),U,式(7)可以简化成minF μTr(FTLUF)(19)
最优解F可由LU的c个最小特征值对应的c个特征向量得到。在迭代优化的方案中,变量γv,A(1),…,A(V),U和F可以以相互作用的方式迭代更新,直到收敛。
优化过程的每次迭代都会减小目标函数式(7)的目标函数值。在这里根据文献[17],确定定义下界是10-5。在实验过程中,监测目标函数的变化情况,观察到在算法不断迭代中,所有的目标函数值都是不断下降并趋近于10-5时,算法收敛,因此定义下界是10-5。基于多样性约束和高阶信息探索的多视图聚类算法(MVCDCHO)的详细步骤如算法1所示。
算法1 MVCDCHO
输入:算法最大迭代次数N;数据点X1,…,XV ;参数θ,η,α,μ。
输出:聚类的结果,聚类指标ACC,NMI,ARI。
a)初始化相似图S并且设每个视图的权重γv=1V
b)通过式(4)求出混合高阶相似图fv(W)
c)while 目标函数值>10-5 do
通过式(12)(13)更新γv,式(9)对目标函数进行计算推导,用求解二次规划的方法更新γv
通过式(15)更新U,将目标函数化简成式(14),通过求导更新U
通过式(17)(18)更新A1,…,AV,式(10)对目标函数进行计算推导,用求解二次规划的方法更新A1,…,AV
通过式(19)对共识图U进行谱聚类操作,先获得特征矩阵F,再对特征矩阵F中的k个连通分量使用K-means聚类处理
end while
d)获得聚类指标ACC,NMI,ARI,U上的聚类结果
4 实验分析
4.1 实验设置
为了评估提出的基于多样性约束和高阶信息挖掘的多视图聚类(MVCDCHO)方法的效果,实验中采用了如下的几个基准的多视图数据集进行对比分析。
a)Yale。该数据集是一个广泛用于计算机视觉和模式识别研究的人脸图像数据集。这个数据集以耶鲁大学的名字命名,包含来自15个不同人的165张人脸图像。每个人都提供了11个不同的表情或姿势,以及各种光照条件下的图像。
b)ORL。该数据集是一个用于人脸识别研究的常用数据集。它由意大利Pentland实验室的研究人员创建,包含了40个不同人的400张灰度人脸图像。每个人提供了10张不同姿势和表情的图像,这些图像在相机中以不同的光照条件捕获。
c)BBCSport。该数据集包含来自BBCSport网站的体育新闻文章,总共包含大约544条新闻文章样本。这些样本被分为五个不同的体育主题类别,通常包括足球、网球、篮球、田径和汽车赛车等。
d)UCI。该数据集是一个用于机器学习和模式识别研究的手写数字识别数据集。该数据集包含了手写数字0~9的图像样本。每个数字类别都有200个不同的样本,共有2 000个样本。
用于对比的11种方法分别是AASC[18]、GMC[6]、AWP[5]、RMSC[19]、CSMSC[10]、L-MSC[12]、DiMSC[9]、WMSC[20]、SCMV-3DT[15]、SGMF-GS[21]和SGMF-KO[21] 。通过归一化互信息(NMI)、调整后的兰德指数(ARI)、聚类精度(ACC)三个广泛使用的指标来衡量聚类性能。
4.2 参数敏感性分析
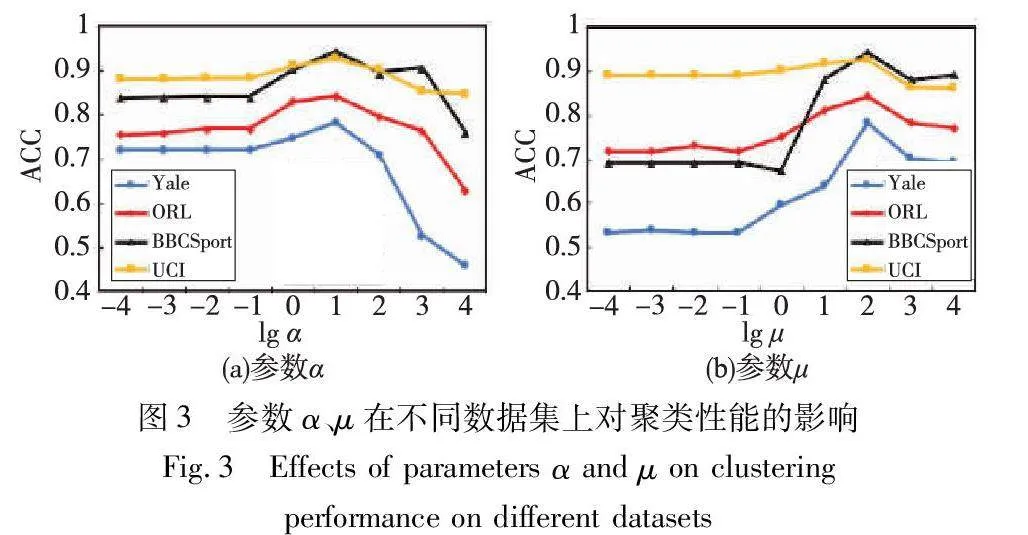
本文方法有四个自由参数需要调优,分别是θ、η、α、μ。设置这些参数在相同的范围{10-4,10-3,10-2,…,104}。在图2、3中展示了这些参数在不同数据集上的聚类性能。
从图2可以看出,参数θ、η在一定的范围内是稳定的,表明该参数没有那么敏感。由于参数θ、η在取值为103、10时各数据集的聚类都能取得较好结果,最终固定参数θ=103,η=10。从图3(a)分析可知,当参数α的值过小时,它带来的影响并不明显,然而若取值α过大,则会引起强烈的约束,导致聚类性能的下降,也表明α对调节目标函数还是很重要的。从图3(b)可以发现,参数η会影响谱聚类的性能,可以看出随着参数的增大,准确率跟着上升,直到峰值随着参数的继续增大准确率会逐渐下降。这两者都在这个范围内显示出峰值,说明模型对参数α、μ是鲁棒的。因此,为了提高模型参数调整的效率,在比较实验中选择参数α=10,μ=102。
4.3 实验对比与分析
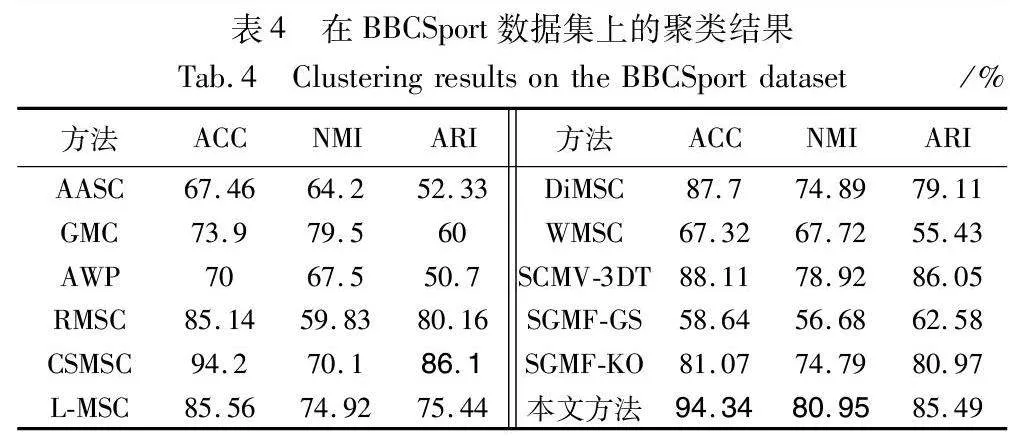
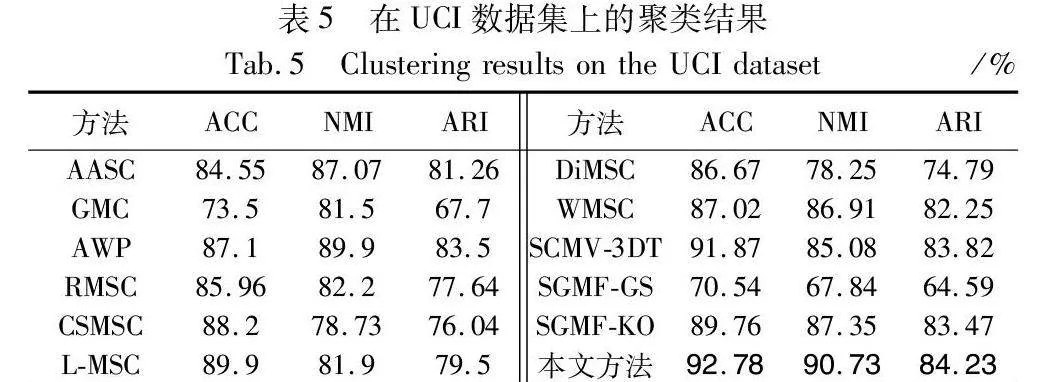
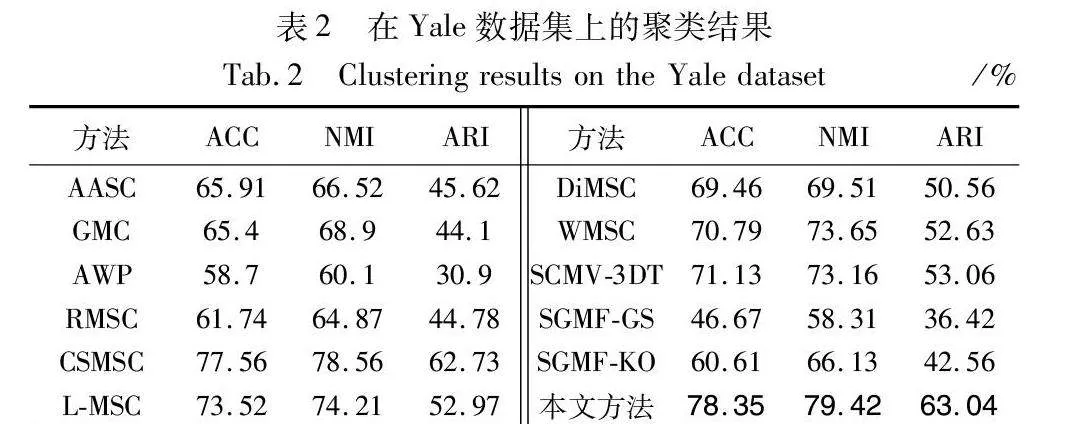
将MVCDCHO与11种聚类算法进行了对比实验,表2~5以及图4分别报告了在不同数据集下,用不同方法得到的ACC、NMI、ARI的详细聚类结果。在每个表的不同数据集中,采用粗体强调了各个度量方面的最佳性能。从这几个表中可以观察到:
a)MVCDCHO几乎在所有的数据集上都取得了最佳的聚类性能结果,证明了该方法在所有数据集上的鲁棒性。例如,在Yale数据集上,其在ACC和NMI方面比次优方法大约提高了0.8和0.9百分点。
b)MVCDCHO通过将多视图的交集特征融合后再进行联合聚类优化,不但去除了多视图中的噪点与损失,而且挖掘了多视图中的高阶信息,还通过谱聚类直接获得聚类结果,防止分步策略带来的次优结果。不同于RMSC通过标准马尔可夫链进行谱聚类,不同于DiMSC挖掘互补信息来增强多视图聚类,也不同于L-MSC、SCMV-3DT通过使用张量来挖掘高阶信息,MVCDCHO引入混合相似图,让交集特征接近混合相似图来挖掘高阶信息,通过使用拉普拉斯矩阵求解特征向量实现多视图聚类。从实验结果可以看出,MVCDCHO可以更合理地挖掘多视图数据中隐藏的高阶信息,使聚类效果更加准确和可靠。
c)MVCDCHO优于AASC、RMSC以及对每个视图进行自适应加权的GMC、AWP、WMSC,这可以解释为对比方法没有考虑多视图间的不一致性。然而,MVCDCHO充分考虑了多视图间的不一致性,从而获得了更好的聚类结果。
d)对于DiMSC、CSMSC,与MVCDCHO相似,都是选择融合的方法来寻求一致的类簇结构,CSMSC将一致性和特异性结合起来用于子空间表示学习,DiMSC探索多视图表示的互补性,与MVCDCHO不同的是,用不同的方法去除噪声以及挖掘高阶信息,不同的操作必然会对最终结果造成影响。从实验结果可以看出,MVCDCHO优于DiMSC、CSMSC,只有在BBCSport数据集下,ARI指标略低于CSMSC,因为MVCDCHO主要针对的是聚类的准确性,而且ARI的差距不大,可以忽略。
e)与L-MSC、SGMF-GS、SGMF-KO等相比,它们的性能不如MVCDCHO,可能是忽略了多视图数据的高阶相似度信息。而MVCDCHO挖掘了多视图数据之间更深层次的信息,获得多视图数据的高阶相似度信息,所以在聚类性能的提升上取得了突破。
f)图4进一步分析了本文方法在直观上优越的潜在原因,展示了不同方法在UCI数据集上的可视化,从图中可以看出,每个方法都使数据得到了很好的恢复。MVCDCHO的聚类结果优于其他算法,尤其是GMC、DiMSC,其中GMC忽略了多视图的多样性,DiMSC没有考虑隐藏在多视图的高阶信息。相比SCMV-3DT,MVCDCHO有更好的数据结构,即块对角结构,验证了MVCDCHO的有效性和鲁棒性。
4.4 收敛性分析
对四个数据集上的收敛性进行实验研究,图5展示了MVCDCHO在四个不同数据集上的收敛曲线,从图中可以看出,目标函数值的曲线是收敛的,随着迭代次数的增加,目标函数值逐渐下降后保持稳定,并且都可以在20次迭代中收敛,证明了MVCDCHO收敛稳定。
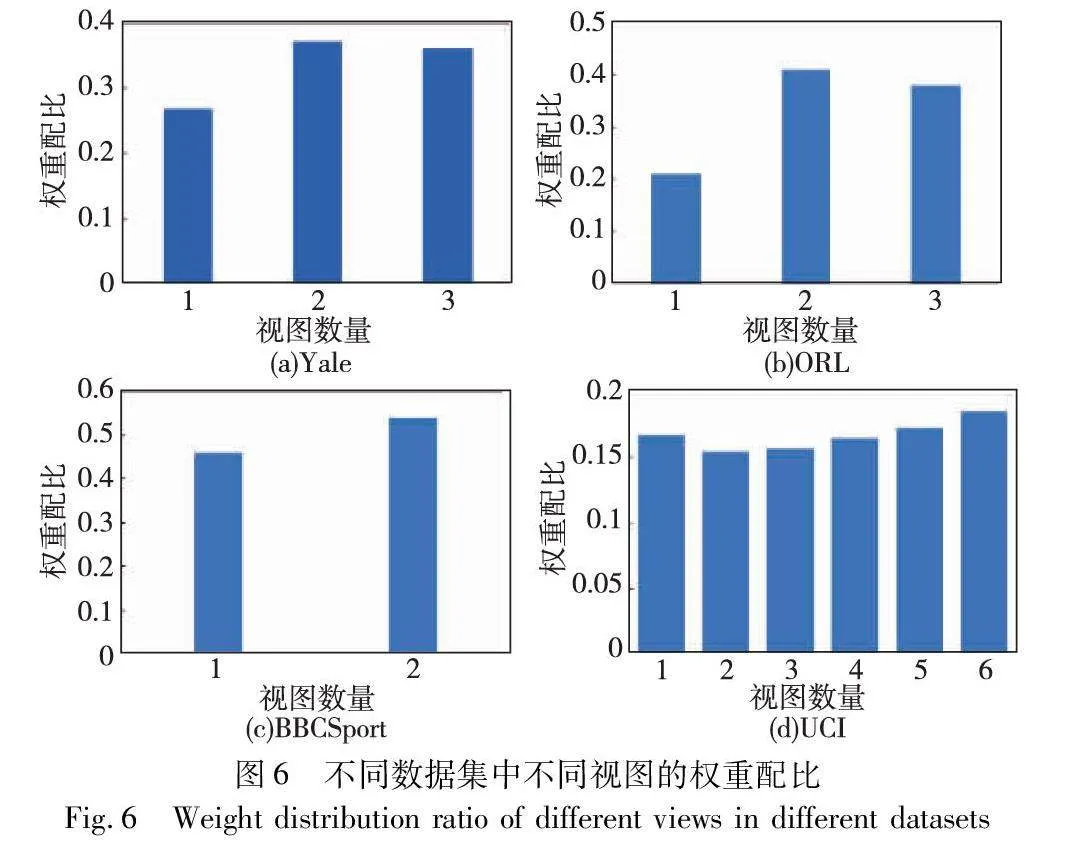
4.5 权重分析
在MVCDCHO达到收敛后,确定了多视图聚类中的每个视图的权重,图6展示了MVCDCHO在不同数据集中不同视图的权重配比。从图中可以看出,该算法在权重分配时并未使用极化或零权重的策略,而是基于每个视图在算法中的重要性进行自适应分配。实验结果显示了MVCDCHO在处理多视图数据时的有效性,通过迭代学习调整权重配比,提高了聚类性能。
5 结束语
本文主要提出了一种基于多样性约束和高阶信息挖掘的多视图聚类算法(MVCDCHO),该算法同时利用了多视图的一致性部分、多样性部分以及高阶信息探索。具体地说,该算法利用多视图的多样性去除视图间的噪声,然后通过要求交集特征等于混合相似图探索高阶信息,在将多视图的交集特征融合成共识图后,用谱聚类实现图聚类,先获得特征矩阵F,再对特征矩阵F中的k个连通分量使用K-means进行聚类处理。采用交替迭代优化方案,分别优化多视图的权重、多视图的交集特征和多视图的共识图,每个子任务可以通过协同优化其他子任务的结果来达到更好的性能。理论分析和实验结果均强调了多视图多样性和高阶信息的关键作用。
参考文献:
[1]Tang Chang, Liu Xinwang, Zhu Xinzhong, et al. CGD: multi-view clustering via cross-view graph diffusion[C]//Proc of AAAI Confe-rence on Artificial Intelligence. Palo Alto, CA: AAAI Press, 2020: 5924-5931.
[2]Zhou Zhihua, Li Ming. Semisupervised regression with cotraining-style algorithms[J]. IEEE Trans on Knowledge and Data Engineering, 2007,19(11): 1479-1493.
[3]Zhang Mingling, Zhou Zhihua. CoTrade: confident co-training with data editing[J]. IEEE Trans on Systems, Man, and Cyberne-tics, Part B, 2011, 41(6): 1612-1626.
[4]Nie Feiping, Lai Tian, Li Xuelong. Multiview clustering via adaptively weighted procrustes[C]//Proc of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM Press, 2018: 2022-2030.
[5]刘金花, 汪洋, 钱宇华. 基于谱结构融合的多视图聚类[J]. 计算机研究与发展, 2022, 59(4): 922-935. (Liu Jinhua, Wang Yang, Qian Yuhua. Multi-view clustering based on spectral structure fusion[J]. Journal of Computer Research and Development, 2022, 59(4): 922-935.)
[6]Wang Hao, Yang Yan, Liu Bin. GMC: graph-based multi-view clustering[J]. IEEE Trans on Knowledge and Data Engineering, 2019, 32(6): 1116-1129.
[7]Chen Mansheng, Wang Changdong, Lai Jianhuang. Low-rank tensor based proximity learning for multi-view clustering[J]. IEEE Trans on Knowledge and Data Engineering, 2022,35(5): 5076-5090.
[8]Lin Shixun, Zhong Guo, Shu Ting. Simultaneously learning feature-wise weights and local structures for multi-view subspace clustering[J]. Knowledge-Based Systems, 2020, 205: 106280.
[9]Cao Xiaochun, Zhang Changqing, Fu Huazhu, et al. Diversity-induced multi-view subspace clustering[C]//Proc of IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE Press, 2015: 586-594.
[10]Luo Shirui, Zhang Changqing, Zhang Wei, et al. Consistent and specific multi-view subspace clustering[C]//Proc of AAAI Conference on Artificial Intelligence. Palo Alto, CA: AAAI Press, 2018: 3730-3737.
[11]赵兴旺, 王淑君, 刘晓琳, 等. 基于二部图的联合谱嵌入多视图聚类算法[J/OL]. 软件学报. (2023-11-16). https://kns.cnki.net/kcms/detail/11.2560.TP.20231115.1508.009.html. (Zhao Xingwang, Wang Shujun, Liu Xiaolin, et al. Joint spectral embedding multi-view clustering algorithm based on bipartite graphs[J/OL]. Journal of Software. (2023-11-16). https://kns.cnki.net/kcms/detail/11.2560.TP.20231115.1508.009.html.)
[12]Zhang Changqing, Fu Huazhu, Hu Qinghua, et al. Generalized latent multi-view subspace clustering[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2018, 42(1): 86-99.
[13]Wang Haiyan, Chen Jiazhou, Zhang Bin, et al. Accurate multi-view clustering by exploiting within-view high-order affinities through tensor self-representation[C]//Proc of IEEE International Conference on Bioinformatics and Biomedicine. Piscataway, NJ: IEEE Press, 2022: 595-600.
[14]李理, 李敬豪, 张小乾. 基于张量学习的潜在多视图子空间聚类[J]. 西南科技大学学报, 2022, 37(3): 52-59. (Li Li, Li Jinghao, Zhang Xiaoqian. Tensor learning-based for latent multi-view subspace clustering[J]. Journal of Southwest University of Science and Technology, 2022, 37(3): 52-59.)
[15]Yin Ming, Gao Junbin, Xie Shengli, et al. Multiview subspace clustering via tensorial t-product representation[J]. IEEE Trans on Neural Networks and Learning Systems, 2019, 30(3): 851-864.
[16]Liang Youwei, Huang Dong, Wang C D, et al. Multi-view graph learning by joint modeling of consistency and inconsistency[J]. IEEE Trans on Neural Networks and Learning Systems, 2024, 35(2): 2848-2862.
[17]Pan Erlin, Zhao Kang. High-order multi-view clustering for generic data[J]. Information Fusion, 2023, 100: 101947.
[18]Huang H C, Chuang Y Y, Chen C S. Affinity aggregation for spectral clustering[C]//Proc of IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE Press, 2012: 773-780.
[19]Xia Rongkai, Pan Yan, Du Lei, et al. Robust multi-view spectral clustering via low rank and sparse decomposition[C]//Proc of the 28th AAAI Conference on Artificial Intelligence. Palo Alto, CA: AAAI Press, 2014: 2149-2155.
[20]Zong Linlin, Zhang Xianchao, Liu Xinyue, et al. Weighted multi-view spectral clustering based on spectral perturbation[C]//Proc of the 32nd AAAI Conference on Artificial Intelligence. Palo Alto, CA: AAAI Press, 2018: 4621-4629.
[21]He Yanfang, Yusof U K. Self-weighted graph-based framework for multi-view clustering[J]. IEEE Access, 2023, 11: 30197-30207.
