基于最大联盟粗糙集的三支聚类
2024-08-15陈之琪万仁霞岳晓冬陈瑞典


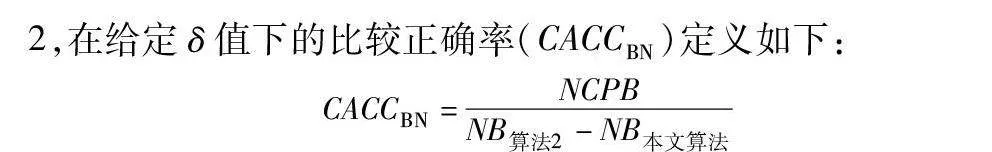













摘 要:针对邻域粗糙集模型受邻域参数影响大、刻画样本信息时不够精细等问题,提出了一种基于最大联盟理论的粗糙集模型。在标准化邻域信息系统后,引入最大联盟集来描述邻域颗粒信息,使得邻域粗糙集模型对信息的划分更加精细,从而显著降低了边界域的不确定性。将该模型与三支聚类相结合,设计了一种基于最大联盟粗糙集的三支聚类算法。在6个UCI公共数据集上进行对比实验,结果表明,所提算法相较于对比算法具有更好的聚类质量,在处理边界域样本时具有更高的比较正确率。
关键词:标准化邻域信息系统; 最大联盟集; 领域粗糙集; 边界域; 三支聚类; 比较正确率
中图分类号:TP391 文献标志码:A
文章编号:1001-3695(2024)08-007-2292-09
doi:10.19734/j.issn.1001-3695.2023.12.0582
Three-way clustering algorithm based on maximum coalition rough set
Chen Zhiqi1, Wan Renxia1, Yue Xiaodong2, Chen Ruidian3
(1.College of Mathematics & Information Science, North Minzu University, Yinchuan 750021, China; 2.School of Computer Engineering & Science, Shanghai University, Shanghai 200444, China; 3.Hongyang Institute for Big Data in Health, Fuzhou 350002, China)
Abstract:In order to address the limnK9/OI5+92Gg3hqxzIj3st+kscQHWd+Vpo2yVP+X3yw=itations of the neighborhood rough set model caused by neighborhood parameters and inadequate sample information representation, this paper proposed a rough set model based on the maximum coalition theory. By normalizing the neighborhood information system and utilizing the maximum coalition set to describe neighborhood granular information, the proposed model enabled finer information division and significant reduction of uncertainty in the boundary region. Combining the model with three-way clustering, this paper designed a three-way clustering algorithm based on maximum coalition rough set. Comparative experiments on six UCI public data sets show that the proposed algorithm has better clustering quality than the comparison algorithms, and has higher comparison accuracy when dealing with boundary region samples.
Key words:standardized neighborhood information system; maximum coalition set; neighborhood rough sets; boundary region; three-way clustering; comparison accuracy
0 引言
粗糙集理论是在1982年由波兰数学家Pawlak教授[1]提出的一种用于处理不确定性知识或不一致信息的数据推理方法。经典Pawlak粗糙集模型是以等价关系和等价类为基础的一种粒度计算模型,用于处理名义型数据,而无法直接处理数值型数据。为了突破这种限制,一些学者延伸拓展出了更多其他类型的粗糙集模型。Yao等人[2]通过引入条件概率提出了决策粗糙集模型。Azam等人[3]通过权衡策略将边界域内的样本划分给正域或负域时的不确定性,使之达到最佳平衡,提出了博弈粗糙集模型。Lin[4]结合拓扑学中内点和闭包的知识,提出了邻域模型的概念,该模型将空间中点的邻域作为基本信息粒子对论域进行粒化。文献[5,6]分别提出了1-step邻域和k-step邻域,并对邻域信息系统的性质进行了详细讨论。胡清华等人[7]将邻域的概念引入到粗糙集理论中,用邻域关系代替严格的等价关系,提出了能够处理混合型数据的邻域粗糙集模型。Lin等人[8]将邻域粗糙集和多粒度粗糙集相结合,构造了邻域多粒度粗糙集模型。Wang等人[9]基于邻域的思想,定义了局部近似集,提出了局部邻域粗糙集模型。Wang等人[10]结合了δ邻域和k近邻颗粒的优点,提出了k最近邻域粗糙集模型。当前,邻域粗糙集已成为处理数值数据被广泛使用的粗糙集模型之一。
聚类分析[11]是数据挖掘中的一项重要技术,是一种无监督的机器学习技术,已经广泛地应用于多个领域,如模式识别、图像处理、统计学、生物信息学、信息粒化等。所谓聚类,就是将数据集中相似度高的样本划分到相同类簇,相似度低的样本划分到不同类簇。大多数的传统聚类算法都是硬聚类算法,要求聚类结果具有清晰的边界,即元素要么属于一个类,要么不属于一个类。然而,在处理不确定信息时,考虑到当前可用信息的不充分性,若强制将元素划分到某个类中,通常会导致较高的错误率或决策风险。
目前,已经有许多新的聚类策略被提出,用来解决传统聚类方法存在的问题。Yao[12]于2010年提出了一种符合人类认知能力的三支决策模型,为粗糙集的正域、负域、边界域提供了合理的语义解释。钱文彬等人[13]针对不完备混合决策系统构造了三种决策风险下的三支决策模型。吕艳娜等人[14]通过改变粒度选择方式重新构建多粒度空间,提出了基于深度置信网络的代价敏感多粒度三支决策模型。于洪[15]将三支决策思想融入到传统聚类中,提出了一种基于K-means的三支决策聚类算法,用核心域、边界域和琐碎域来表示一个类簇。刘强等人[16]利用元素的邻域在二支聚类的结果上进行收缩和扩张,提出了一种基于ε邻域的三支聚类算法。万仁霞等人[17]考虑分类错误的风险代价,将数据对象属于各个类簇的后验概率作为决策评价函数,提出了基于三支决策的高斯混合聚类算法。花遇春等人[18]利用朴素贝叶斯确定两样本的共现概率,提出了基于共现概率的三支聚类模型。申秋萍等人[19]通过考虑近邻的标签,对二支聚类结果的临界点和噪声点进行重新划分,提出了基于局部半径的三支DBSCAN算法。相比于传统的聚类方法,三支聚类在处理不确定性和模糊性较高的数据时更具优势,更能适应实际情况中存在的多样性和交叉性。
Pawlak[20]定义了具有支持、中立、反对评价的三值信息系统,给出了三值信息系统中计算辅助函数和距离函数的方法,用于确定不同代理间的冲突、中立和联盟关系。然而,在任意联盟集中,给定代理与其他代理之间都存在联盟关系,但并非所有代理之间都是两两联盟的。为此,Lang等人[21]在决策粗糙集理论的基础上,提出了动态信息系统中的概率冲突集、中立集和联盟集的增量构造方法,并给出了最大联盟集的概念,使得最大联盟集中任意两代理之间都满足联盟关系。郭淑蓉[22]针对计算最大联盟集时运算量较大的问题,通过将参数β区间化,把无限多个最大联盟集的计算问题减少为有限多个,从而提高了计算效率。罗珺方等人[23]在不完备异构冲突信息系统中,定义了极大一致联盟区间集族,并利用极大团的枚举算法进行获取。
使用粗糙集模型刻画样本信息时,本文希望通过压缩边界域来减少信息的不确定性,以提高分类精度。而最大联盟集使得数据对象之间的关系更加紧密,且相较于δ邻域颗粒信息,可以更为细致地刻画样本信息,为解决不确定性问题提供了新的思路。本文通过引入最大联盟集的相关概念,提出了基于最大联盟的邻域粗糙集模型,并基于该模型设计了一种新的三支聚类算法。
1 预备知识
1.1 邻域粗糙集
在决策分析中,通常各指标间的计量单位和数量级不尽相同,从而使得各指标之间不具备综合性,数据标准化旨在消除各指标量纲之间的影响,有助于确保数据的质量和一致性。
定义1 设NS=(U,A,V,f,δ)为一个邻域信息系统,其中论域U={x1,x2,…,xn},属性集A=C∪D,C是条件属性,D是决策属性,值域V={Va|a∈A},f:U×A→V为信息函数,f(x,a)表示对象x在属性a上的值,δ为邻域半径。对于任意实数p∈[1,+∞),ak∈A,xiU,映射函数(xi,ak)定义如下:
(xi,ak)=f(xi,ak)-fmin(x,ak)fmax(x,ak)-fmin(x,ak)×1pn
其中:fmax(x,ak)和fmin(x,ak)分别为对象x在属性ak上的最大值和最小值。
映射函数将所有数据信息缩放到区间[0,1/pn]上,起到了标准化作用。后文中,本文用NSnorm=(U,A,V,f,δ)表示NS=(U,A,V,f,δ)标准化后的邻域信息系统。
定义2[7] 设邻域信息系统NSnorm=(U,A,V,f,δ),对于ak∈A,xi,xj∈U,则xi和xj之间的距离函数Δ(xi,xj)为
Δ(xi,xj)=(∑nk=1(xi,ak)-(xj,ak)p)1p
其中:当p=1时,为曼哈顿距离;当p=2时,为欧氏距离;当p=3时,为切比雪夫距离。
性质1 设邻域信息系统NSnorm=(U,A,V,f,δ),对于xi,xj∈U,有0≤Δ(xi,xj)≤1。
证明 由定义1可知,0≤f(xi,ak)≤1/pn≤1,则0≤f(xi,ak)-f(xj,ak)≤1/pn。对于p∈[1,+∞),有0≤f(xi,ak)-f(xj,ak)p≤1/n,则0≤∑nk=1f(xi,ak)-f(xj,ak)p≤1,故而0≤(∑nk=1f(xi,ak)-f(xj,ak)p)1p≤1。
定义3[7] 设邻域信息系统NS=(U,A,V,f,δ),对于xi∈U,特征子集BA,xi在B上的δ邻域定义如下:δB(xi)={xj|xj∈U,ΔB(xi,xj)≤δ}
其中:ΔB(xi,xj)表示在特征子集B上xi和xj之间的距离,样本xi的邻域是由距离函数Δ、邻域半径δ和属性集合B共同决定的。
定义4[7] 设邻域信息系统NS=(U,A,V,f,δ),对于BA,XU,则X关于B的邻域下近似集、上近似集、正域、负域和边界域分别为
下近似集:NB(X)={xi|δB(xi)X,xi∈U}
上近似集:B(X)={xi|δB(xi)∩X≠,xi∈U}
正域:POSB(X)=N(X)
负域:NEGB(X)=U-(X)
边界域:BNB(X)=(X)-N(X)
其中:(NB(X),B(X))称为δ邻域粗糙集。
1.2 最大联盟集
定义5[21] 设邻域信息系统NS=(U,A,V,f,δ),阈值α、β满足0≤β<α≤1,对于BA,xU,x的概率冲突集、中立集和联盟集分别为
a)冲突集:COαβ(x)={y∈U|ΔB(x,y)>α};
b)中立集:NEαβ(x)={y∈U|α≥ΔB(x,y)≥β};
c)联盟集:ALαβ(x)={y∈U|ΔB(x,y)<β}。
由定义5可得,若β=δ,则ALαβ(x)=δ(x),即x的概率联盟集就是x的δ邻域。
定义6[21] 设邻域信息系统NS=(U,A,V,f,δ),阈值α、β满足0≤β<α≤1,BA,XU:
a)若x,y∈X,ΔB(x,y)<β,则称X为一个联盟集;
b)若X为一个联盟集,并且不存在联盟集Y,使得XY,则称X为一个最大联盟集。
定理1[21] 设邻域信息系统NS=(U,A,V,f,δ),XU且0≤β≤α≤1,则X为最大联盟集的充要条件为
∩x∈XALαβ(x)=X
命题1[21] 设邻域信息系统NS=(U,A,V,f,δ),MC={MC1,MC2,…,MCp}是论域U中全体最大联盟集的集合,则
∩1≤i≤pMCi=U
1.3 三支聚类
Yu等人将三支决策引入到聚类算法中,提出了三支聚类方法。给定一个数据集U={x1,x2,…,xn},可获得聚类结果C={C1,C2,…,Ck}。三支聚类在传统的二支聚类结果中加入了边界域的概念,用三个互不相交的集合表示一个类,即Co(Ci)、Fr(Ci)与Tr(Ci),分别称为类Ci的核心域、边界域和琐碎域。其中,核心域中的对象确定属于这个类,边界域中的对象可能属于这个类,琐碎域中的元素肯定不属于这个类,它们满足如下性质:
a)Co(Ci)≠,i=1,2,…,k。
b)∪ki=1(Co(Ci)∪Fr(Ci))=U。
c)Co(Ci)∩Co(Cj)=,i≠j。
其中:性质a)要求每个类簇的核心域不能为空;性质b)确保所有对象都能被有效划分;性质c)要求不同类簇的核心域之间没有交集。
三支聚类的结果表示如下:
TC={(Co(C1),Fr(C1)),(Co(C2),Fr(C2)),…,(Co(Ck),Fr(Ck))}
刘强等人[16]利用每个类中元素的δ邻域进行收缩和扩张,提出了一种基于动态邻域的三支聚类算法。该算法的大致流程如下:
a)利用硬聚类算法对U进行聚类,得到聚类结果C={C1,C2,…,Ck};
b)对于每一类Ci,任取xj∈Ci,若δ(xj)Ci,则xj∈Co(Ci),否则xj∈Fr(Ci);
c)对于每一类Ci,任取xjCi,若δ(xj)∩Ci≠,则xj∈Fr(Ci);
d)得到最终聚类结果为
TC={(Co(C1),Fr(C1)),(Co(C2),Fr(C2)),…,(Co(Ck),Fr(Ck))}
2 基于最大联盟粗糙集的三支聚类
本章定义了最大联盟集的紧致度公式,用于确定每个对象最紧致的最大联盟集,并将其作为一种新的邻域颗粒信息与粗糙集模型相结合,构造了最大联盟粗糙集模型,然后将该模型应用于聚类分析中,提出了基于最大联盟的三支聚类算法。
2.1 基于最大联盟的粗糙集模型
给定邻域信息系统NSnorm=(U,A,V,f,δ),MC={MC1,MC2,…,MCp}是论域U中全体最大联盟集的集合,MC(xi)={MC1(xi),MC2(xi),…,MCt(xi)}是论域U中包含xi的所有最大联盟集的集合,其中t≤p。
定义7 样本点xi的局部密度为
ρ(xi)=MCk(xi)∑xj∈MCk(xi)exp(-dij) if MCk(xi)>10if MCk(xi)=1
其中:|MCk(xi)|表示xi的最大联盟集中的样本点数量;dij表示样本点xi与xj之间的距离,样本点xi的局部密度是由集合的样本数量和各点到该样本点的距离共同决定的。
定义8 x,y∈MCk(xi),最大联盟集MCk(xi)的紧致度定义如下:
Euclid Math OneTAp(MCk(xi))=ρ(xi)+12∑x∑yexp(-d(x,y))
分析上式可知,Euclid Math OneTAp反映了最大联盟集MCk(xi)在空间中的紧密程度。将MC(xi)按紧致度从大到小依次排列{MC1′(xi),MC2′(xi),…,MCt′(xi)},得到与xi紧密程度最高的最大联盟集MCbest(xi)=MC1′(xi)。
定义9 设NSnorm=(U,A,V,f,δ)是邻域信息系统,XU,定义X基于最大联盟集的下近似集、上近似集、正域、负域和边界域分别为
下近似集:M(X)={xi|MCbest(xi)X,xi∈U}
上近似集:(X)={xi|MCbest(xi)∩X≠,xi∈U}
正域:MPOS(X)=M(X)
负域:MNEG(X)=U-(X)
边界域:BM(X)=(X)-M(X)
称(M(X),(X))为最大联盟粗糙集。
如图1所示,采用δ邻域和最大联盟集分别刻画样本x的邻域信息,其中,实心圆形和实心三角形分别代表两类样本,实线圆圈表示x的δ邻域,虚线圆圈表示x的3个最大联盟集,红色虚线圆则表示与x紧密程度最高的最大联盟集(参见电子版)。观察x的δ邻域,可以发现两种类型的样本都包含其中,根据δ邻域粗糙集的定义,样本x将被划分到边界域中。再分别观察x的三个最大联盟集,根据最大联盟粗糙集的定义,在邻域粒度MC1(x)下,样本x将被错误地划分到实心圆类别中;在邻域粒度MC2(x)下,样本x将被划分到边界域中;而在邻域粒度MCbest(x)下,样本x将被划分到实心三角形类别中,从而得到最正确的划分。
关于最大联盟粗糙集,本文有以下一些重要性质。
性质2 设邻域信息系统NSnorm=(U,A,V,f,δ),对于XU,有:
a)M(X)X(X);
b)M()=()=,M(U)=(U)=U;
c)M(X∩Y)=M(X)∩M(Y),(X∪Y)=(X)∪(Y);
d)若XY,则M(X)M(Y),(X)(Y);
e)M(X∩Y)M(X)∩M(Y),(X∩Y)(X)∩(Y);
f)M(~X)=~(X),(~X)=~M(X)。
证明 a)设xi∈M(X)MCbest(xi)X,因为xi∈MCbest(xi),所以xi∈X,故M(X)X;设xi∈XMCbest(xi)∩X≠xi∈(X),故X(X)。
b)由a)知,M(),而M(),所以M()=;假设()≠,则存在xi使得xi∈(),即MCbest(xi)∩≠,而MCbest(xi)∩=与假设矛盾,因此()=;xi∈UMCbest(xi)Uxi∈M(U)UM(U),由a)知,M(U)U,故M(U)=U;由a)知,U(U),但(U)U,因此(U)=U。
c)对于xi∈M(X∩Y)MCbest(xi)X∩YMCbest(xi)X∧MCbest(xi)Yxi∈M(X)∩M(Y),因此M(X∩Y)=M(X)∩M(Y);xi∈(X∪Y)MCbest(xi)∩(X∪Y)≠(MCbest(xi)∩X)∪(MCbest(xi)∩Y)≠MCbest(xi)∩X≠∨MCbest(xi)∩Y≠xi∈(X)∨xi∈(Y)xi∈(X)∪(Y),因此(X∪Y)=(X)∪(Y)。
d)设XY,则X∩Y=X,X∪Y=Y,所以M(X∩Y)=M(X),(X∪Y)=(Y),由c)知,M(X)∩M(Y)=M(X),(X)∪(Y)=(Y),故M(X)M(Y),(X)(Y)。
e)因XX∪Y,YX∪Y,所有M(X)M(X∪Y),M(Y)M(X∪Y),故M(X)∩M(Y)M(X∩Y);因为X∩YX,X∩YY,所以(X∩Y)(X),(X∩Y)(Y),故(X∩Y)(X)∩(Y)。
f)对于xi∈M(X)MCbest(xi)XMCbest(xi)∩~X=xi(~X)xi∈~(~X),因此M(X)=~(~X),故而M(~X)=~(X)。
性质3 设NSnorm=(U,A,V,f,δ)是邻域信息系统,0≤β<α≤1且β=δ,XU,有:
a)MCbest(xi)δ(xi),xi∈U;
b)N(X)M(X);
c)(X)(X);
d)BM(X)BN(X)。
证明 a)由定理1可知,MC(xi)AL(xi)。又当β=δ时,AL(xi)=δ(xi),故MC(xi)δ(xi)。因为MCbest(xi)MC(xi),所以MCbest(xi)δ(xi)。
b)因为xi∈N(X)δ(xi)XMCbest(xi)X,则有xi∈M(X),所以N(X)M(X)。
c)因为xi∈(X)MCbest(xi)∩X≠δ(xi)∩X≠,则有xi∈(X),所以(X)(X)。
d)由b)和c)的证明可知,BM(X)=(X)-M(X)(X)-N(X)=BN(X)。
定义10 设NSnorm=(U,A,V,f,δ)是邻域信息系统,属性集A=C∪D,C是条件属性,D是决策属性,U/D={D1,D2,…,Dr}为论域U在决策特征D上的等价划分。决策相对应的属性子集的正域、负域和边界域分别定义如下:
正域:MPOS(D)=∪rj=1M(Dj)
负域:MNEG(D)=U-∪rj=1(Dj)
边界域:BM(D)=∪rj=1(Dj)-∪rj=1M(Dj)
显然,正域和边界域是互补的,正域是由所有决策类下近似的并集构成。
2.2 基于最大联盟粗糙集的三支聚类算法
相对于经典粗糙集,最大联盟粗糙集为数据对象提供了更加丰富的邻域颗粒信息,将最大联盟粗糙集模型与三支决策理论相结合,用产生的三支聚类结果代替传统的二支聚类结果,有效规避了直接作出属于某一类或不属于某一类决策所带来的潜在风险,将为分析数据对象间的关系提供更可靠的信息支持。
设对象集U的k个聚类结果是C={C1,C2,…,Ck},则Ci的核心域Co(Ci)和边界域Fr(Ci)分别表示为Co(Ci)=M(Ci),Fr(Ci)=(Ci)-M(Ci)。三支聚类结果可以表示为
TC={(Co(C1),Fr(C1)),(Co(C2),Fr(C2)),…,(Co(Ck),Fr(Ck))}
基于最大联盟粗糙集的三支聚类算法具体步骤如下:
输入:数据集U={x1,x2,…,xn},参数k、q。
输出:聚类结果{(Co(C1),Fr(C1)),(Co(C2),Fr(C2)),…,(Co(Ck),Fr(Ck))}。
a)利用硬聚类算法对U进行聚类,得到C={C1,C2,…,Ck};
b)对于任意xi,xj∈U,根据定义2计算任意两点之间的距离Δ(xi,xj),找到每个样本点xi的δ邻域集δ(xi)={xj|xj≤q};
c)确定U中满足条件∩x∈MCkδ(x)=MCk的所有最大联盟集MC={MC1,MC2,…,MCp};
d)对于任意xi∈U,依次遍历U中所有的最大联盟MC,筛选出xi的所有最大联盟集的集合MC(xi)={MC1(xi),MC2(xi),…,MCt(xi)},根据定义8中的紧致度公式,找到与xi紧密程度最高的最大联盟集MCbest(xi);
e)对于每一类Ci,任取xj∈Ci,若MCbest(xi)Ci,则xj∈Co(Ci),否则xj∈Fr(Ci);
f)对于每一类Ci,任取xjCi,若MCbest(xi)∩Ci≠,则xj∈Fr(Ci);
g)通过步骤e)和f)得到Co(Ci)和Fr(Ci)(i=1,2,…,k),返回最终聚类结果{(Co(C1),Fr(C1)),(Co(C2),Fr(C2)),…,(Co(Ck),Fr(Ck))}。
其中,步骤c)可以简化为:(a)如果δ(x)={x},则{x}是一个最大联盟集,接下来仅需考虑U/{x|δ(x)={x}};(b)假设δ(x)=X,且X>1,取y∈X/{x},计算δ(x)∩δ(y)。若δ(x)∩δ(y)={x,y},则{x,y}是一个最大联盟集,否则,取z∈{δ(x)∩δ(y)}/{x,y}。若δ(x)∩δ(y)∩δ(z)={x,y,z},则{x,y,z}是一个最大联盟集,否则,重复上述直至满足对于YX,∪x∈Yδ(x)=Y。
3 评价指标
3.1 不确定性评价
粗糙集理论中的不确定性度量是评价系统分类能力及提高分类精度的重要工具,国内外众多学者对此进行了研究。设邻域信息系统NS=(U,A,V,f,δ), C是条件属性,D是决策属性,A=C∪D,U/D={D1,D2,…,Dm}是对象集U在决策特征D上的等价划分,本文采取以下三个指标进行评价:
a)邻域近似精度[24]:
αδB(D)=∑mi=1Di∑mi=1Di
b)邻域信息熵[24]:
Hδ(B)=1+1U∑|U|i=1nδB(xi)U lgUlg1|nδB(xi)|
c)加权邻域信息熵[24]:
αH(d,B)=αδB(d)*Hδ(B)
3.2 聚类效果评价
本文选取三个经典的聚类指标准确率(ACC)、戴维森堡丁指数(DBI)和宏平均(Macro_F1)作为评估聚类算法的标准。
a)准确率(accuracy,ACC):
ACC=1N∑ki=1Ci
其中:数据集的大小为N,被成功划分到类i的样本数记为Ci,聚类数为k,ACC的取值为[0,1]。ACC值越大,表示聚类效果越好。本文通过计算核心域的样本数据获得ACC的取值。
b)戴维森堡丁指数(Davies-Bouldin index,DBI):
DBI=1k∑ki=1maxi≠j(S(Ci)+S(Cj)‖wi-wj‖2)
其中:S(Ci)表示第i类中的所有样本元素到聚类中心wi的平均距离;‖wi-wj‖2表示类i与j之间的欧氏距离;k表示聚类数。DBI评价一个聚类结果好坏的依据是:要求类内元素相似度高,类间元素相似度低。DBI值越小,表示聚类结果越好,意味着簇内数据点更加紧密地聚集在一起,而簇与簇之间的区别更加明显。
c)宏平均(Macro_F1)[25]:
Macro_F1=2MacroP×MacroRMacroP+MacroR
其中:MacroP=1k∑ki=1TPCiTPCi+FPCi,MacroR=1k∑ki=1TPCiTPCi+FNCi。TPCi表示core(Ci)中对象被正确分类为该类的数量,FPCi表示非core(Ci)中对象被错误分类为该类的数量,FNCi表示非core(Ci)中对象被正确分类为不属于该类的数量。宏平均F1值综合了精确率和召回率,用于衡量聚类结果的准确性和完整性。它是通过计算每个簇的F1值并求其平均值得到的,该值越大表示聚类结果越好。
由于三支聚类结果是由两个区域近似表示的,所以仅使用硬聚类指标评价无法评估类簇的核心域和边界域之间的关系,会导致评估结果不够客观和全面。因此,本文除选取上述三个常用的评价指标外,还选取了三个软聚类评价指标对三支聚类效果进行评价:
d)所有正域的平均质量[26]:
γ=1n∑ki=1|Co(Ci)|
e)c个类簇的平均质量[27]:
α=1c∑ki=1|Co(Ci)||Co(Ci)|+|Fr(Ci)|
f)c个类簇的整体质量[27]:
α*=∑cj=1|Co(Ci)|∑cj=1|Co(Ci)|+|Fr(Ci)|
第一个软聚类评价指标γ是由Maji提出的,用于衡量所有正域的平均质量,该值越大,表示聚类效果越好。在Maji的启示下,Zhang提出了另外两个软聚类评价指标α和α*,分别用于衡量c个类簇的平均质量和整体质量。对于特定的类簇而言,核心域中的数据点越多,意味着有更多数据点被明确地归属于该类簇。也就是说,下近似与上近似中数据点数量的比率可以显示聚类结果的质量。这两个指标的数值越大,表示聚类效果越好。
4 实例分析与实验验证
4.1 实例分析
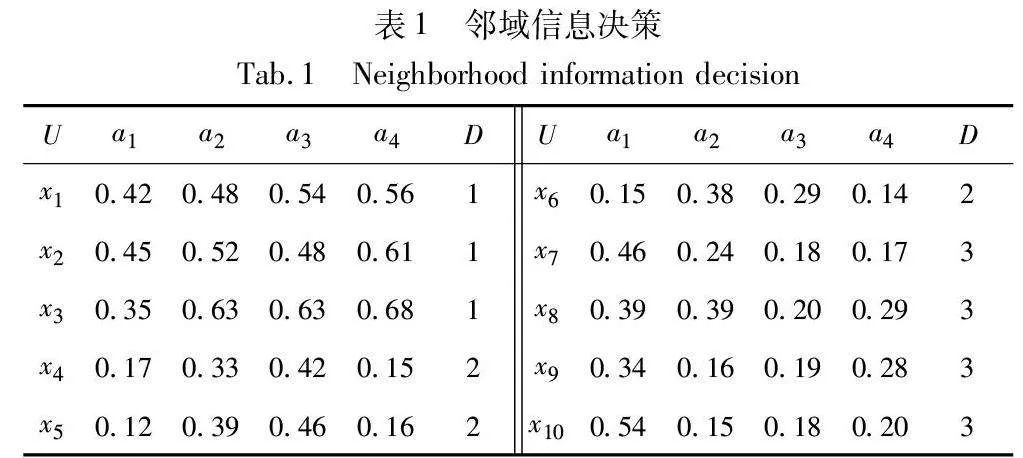
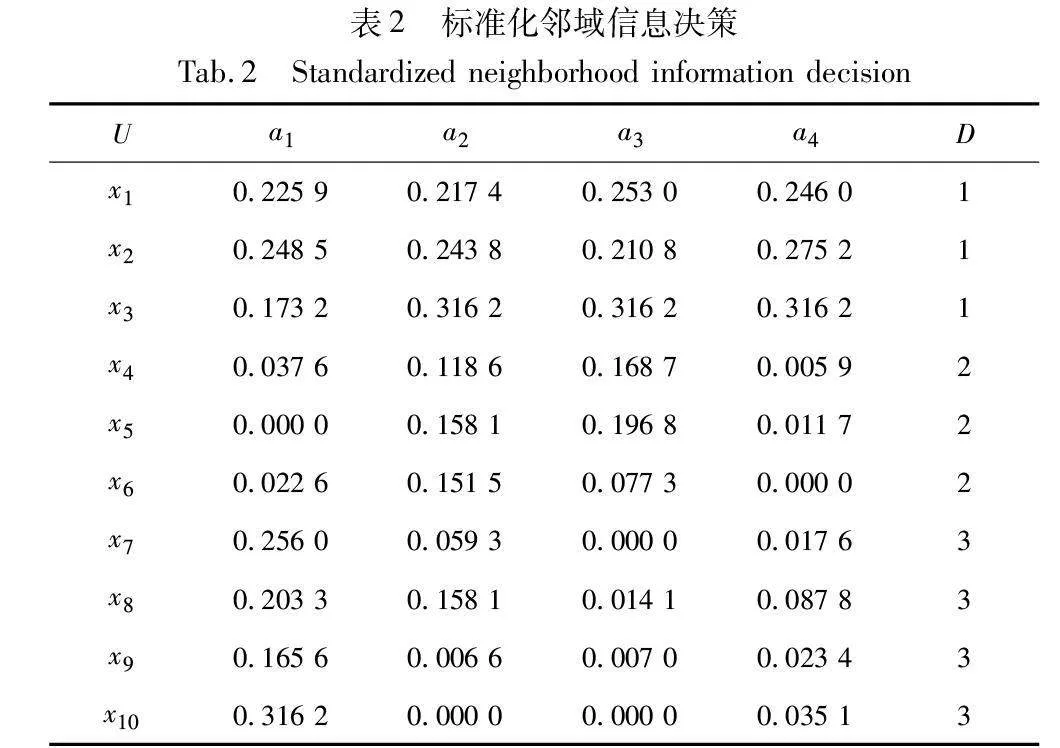
给定一个邻域信息决策系统NS=(U,A,V,f,δ)[28],其中对象集U={x1,x2,x3,x4,x5,x6,x7,x8,x9,x10};条件特征集C={a1,a2,a3,a4};D为决策特征集,论域U在决策特征上等价划分为U/D={D1,D2,D3},即D1={x1,x2,x3},D2={x4,x5,x6},D3={x7,x8,x9,x10},邻域参数δ=β=0.25。通过邻域信息决策表1对邻域粗糙集模型和最大联盟粗糙集模型进行不确定性度量。本文中的样本(对象)的距离均采用欧氏距离进行计算。
a)根据定义1中的映射函数,对该邻域信息系统进行标准化处理,结果如表2所示。
b)找到每个对象的邻域类δ(xi)和最优最大联盟集MCbest(xi),结果如表3所示。
c)确定决策特征上等价划分的上下近似集合,结果如表4所示。
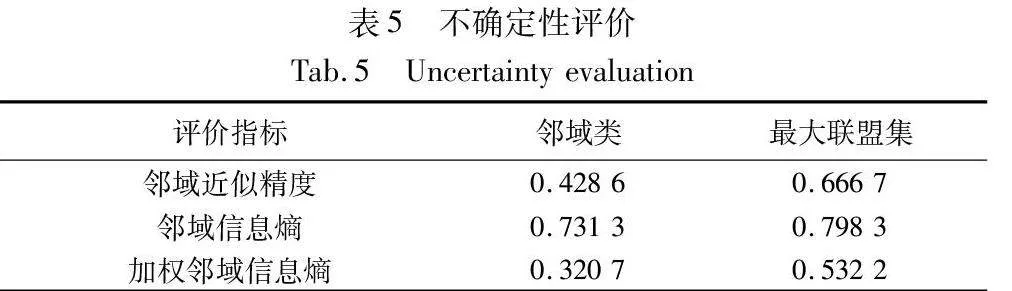
d)不确定性评价的结果如表5所示。
由表5的评价结果可知,最大联盟粗糙集的邻域近似精度、领域信息熵、加权邻域信息熵均优于邻域粗糙集模型。可以看出,相较于邻域粗糙集模型,基于最大联盟粗糙集提供了更精细的划分信息,从而有效降低了边界域的不确定性。
4.2 数据集上的实验分析
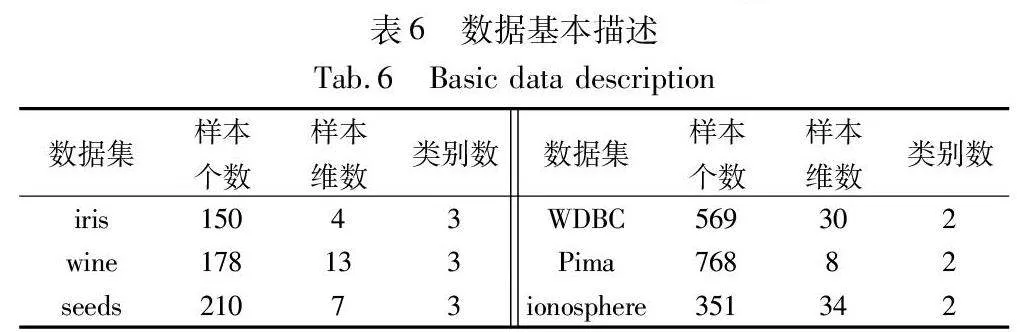
为验证基于最大联盟粗糙集的三支聚类算法的有效性,本文选取了6组UCI数据集进行实验,数据集的一些基本描述如表6所示。本次实验采用Python编写,在Windows 10企业版操作系统上运行,计算机配置为Intel CoreTM i5-4200U CPU,内存容量为16 GB,编码环境选用Anaconda Spyder。
下面将本文所提出的基于最大联盟粗糙集的三支聚类方法与基于k近邻粗糙集的三支聚类方法[12](算法1)、基于δ邻域粗糙集的三支聚类方法[16](算法2)、基于k最近邻域粗糙集的三支聚类方法[10](算法3)进行比较。其中,算法3是将文献[10]提出的k最近邻域粗糙集模型引入三支聚类框架所得到的聚类算法。本实验根据映射函数对数据进行标准化处理,针对部分实验数据集特征维度较多的问题,采取PCA方法降维之后,选用传统K-means算法进行初始聚类,算法1和3所用到的近邻参数k取值为3,算法2和本文算法中所需邻域参数δ取值相同,且取值在0~1。
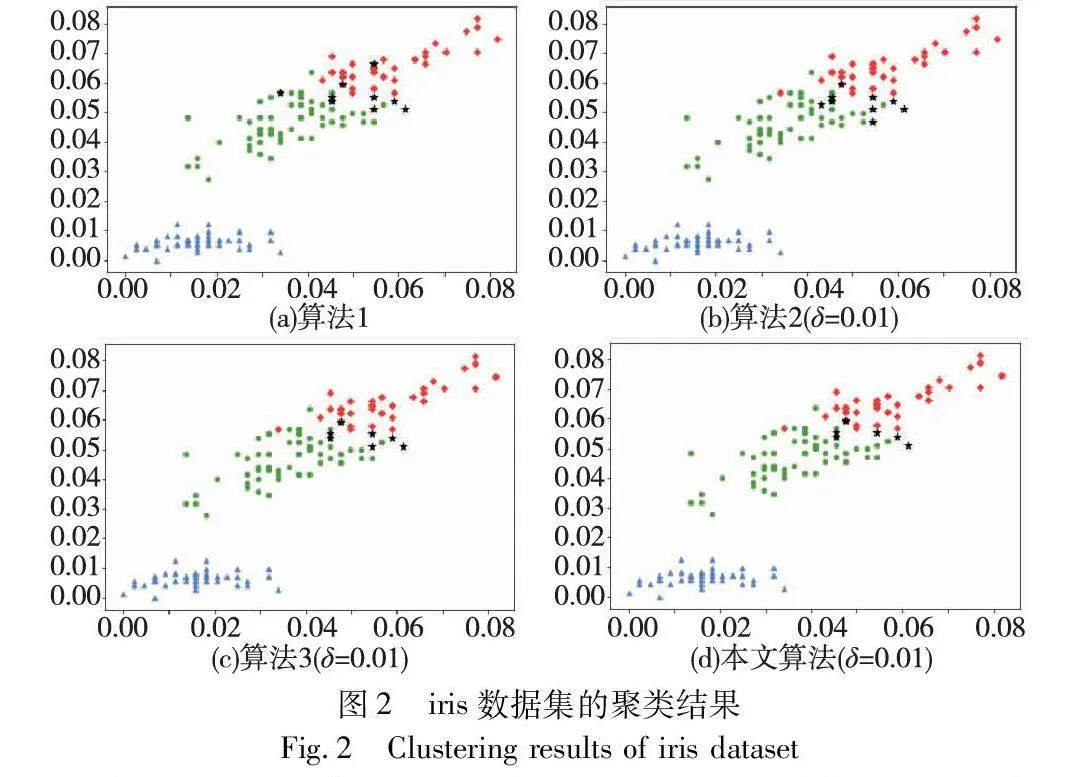
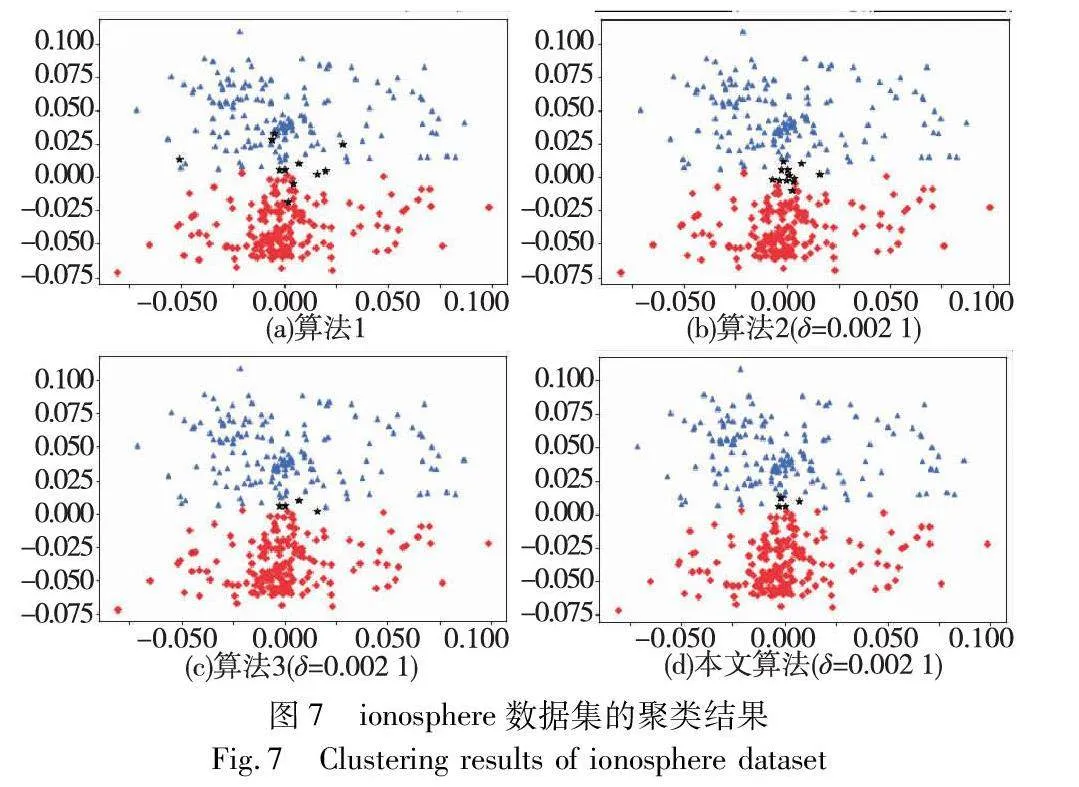
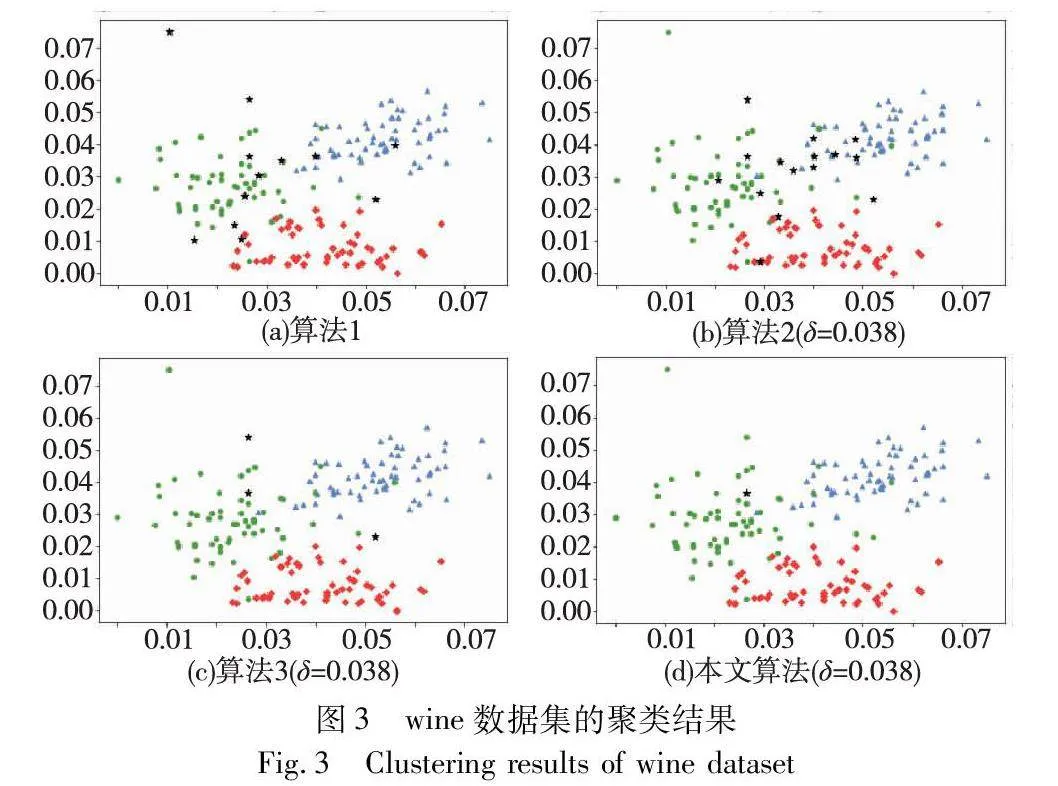
对实验数据集分别进行三支聚类分析,得到如图2~7所示的聚类结果对比图。其中,每种颜色代表一个类簇,黑色五角星表示被划分在边界域的对象。在算法1~3和本文算法下,iris数据集边界域内的样本数量分别为9个、9个、7个和6个;wine数据集边界域内的样本数量分别为12个、15个、3个和1个;seeds数据集边界域内的样本数量分别为28个、15个、13个和8个;WDBC数据集边界域内的样本数量分别为17个、11个、7个和2个;Pima数据集边界域内的样本数量分别为23个、10个、10个和9个;ionosphere数据集边界域内的样本数量分别为11个、12个、4个和4个。可见,采用本文提出的聚类算法处理各个实验数据集时,都能成功地将边界域的样本数量减至最少,可以更精确地划分类与类的边界域。
基于实验所得的聚类结果,将本文算法与其他三种算法的评价指标进行对比,评价结果如表7所示。本文提出的基于最大联盟粗糙集的三支聚类算法在wine、seed、WDBC和Pima数据集上的各个评价指标都有所提升,说明本文算法在这些数据集上的聚类效果明显优于其他三种聚类算法。在ACC评价指标方面,本文算法在wine和WDBC数据集上表现最为突出,聚类准确率分别为94.94%和92.44%,同时,在其他数据集上本文算法的准确率也都是最高的。在DBI评价指标方面,本文算法在wine、seed、WDBC和Pima数据集上都具有最小的DBI值,说明对于这四种数据集,本文算法所得到的聚类结果相同,簇内数据点更加紧密,而不同簇之间的距离更远,聚类效果更好,然而,本文算法在iris数据集上的DBI值略逊于算法3,在ionosphere数据集上的DBI值略逊于算法2,但由于差值较小,对聚类效果的影响有限。在宏平均F1评价指标方面,本文算法的F1值都是最高的,表明本文算法相较于其他三种算法在不同类别上的分类性能最好。
在γ评价指标方面,本文算法也表现出极佳的效果,在各个数据集上该指标值均达到95%以上,说明本文算法对数据集中大部分数据点都进行了明确划分,仅保留较少部分数据点于边界域中,得到的聚类结果中所有正域的平均质量更高。在α和α*评价指标方面,相较于其他三种算法,本文算法在各个数据集上的指标值均最高,并且都大于90%,说明本文算法所得到的类簇平均质量和整体质量都更高,聚类效果更好。
4.3 参数δ分析
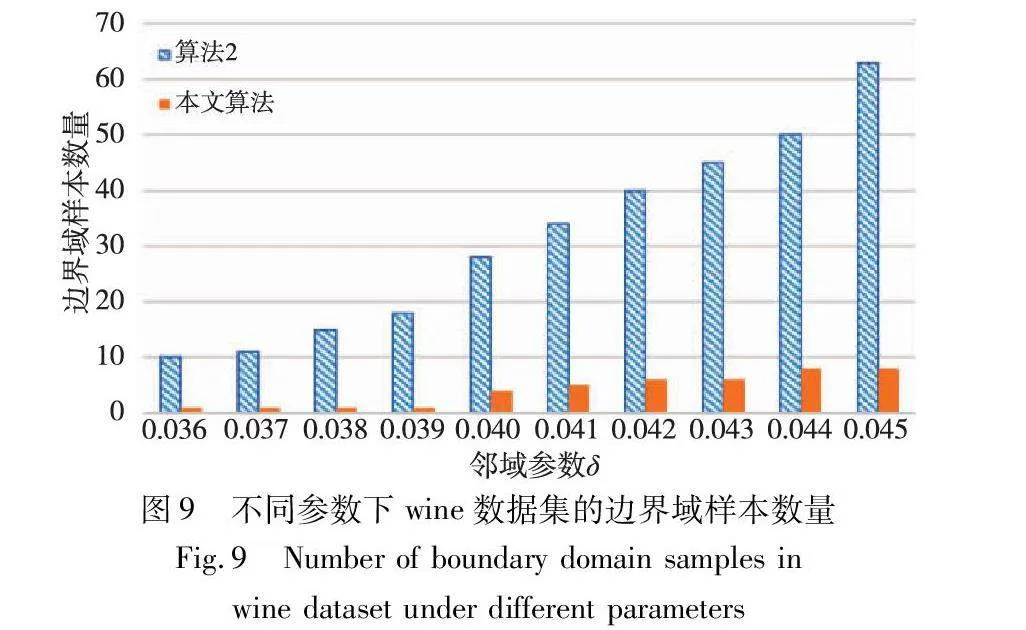
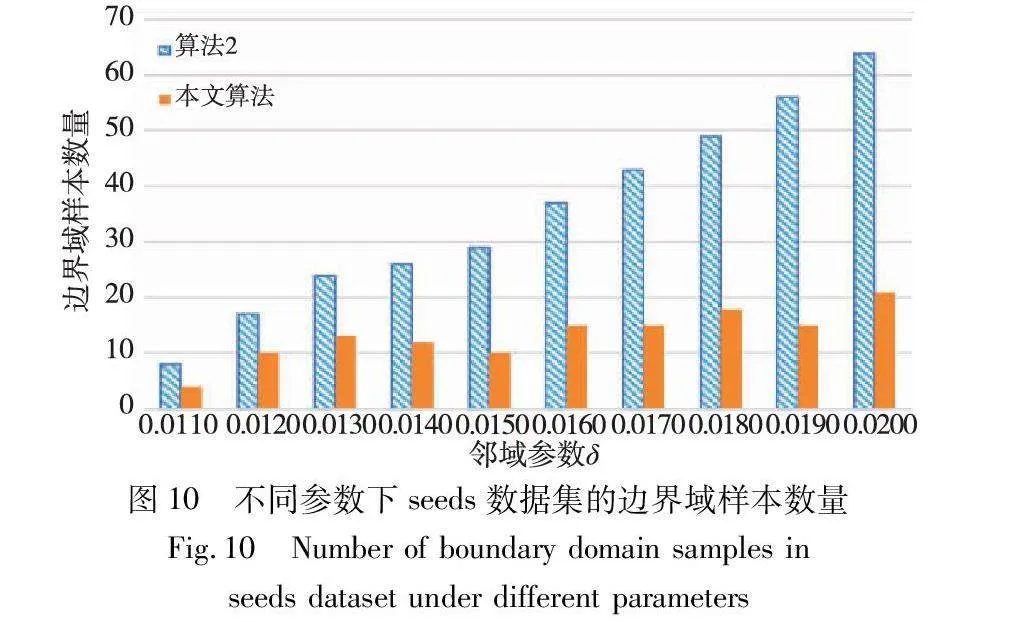
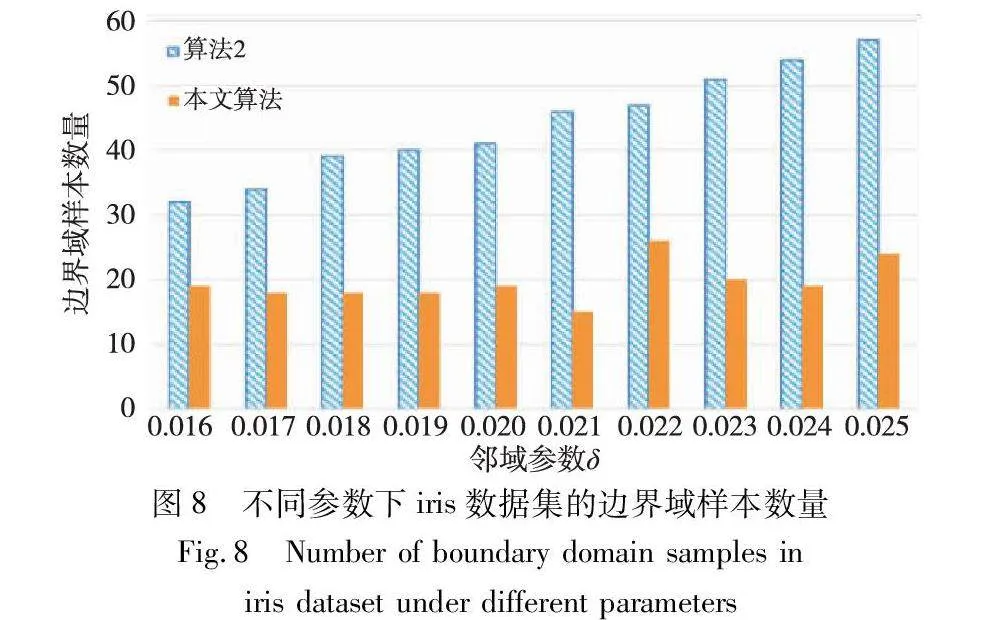
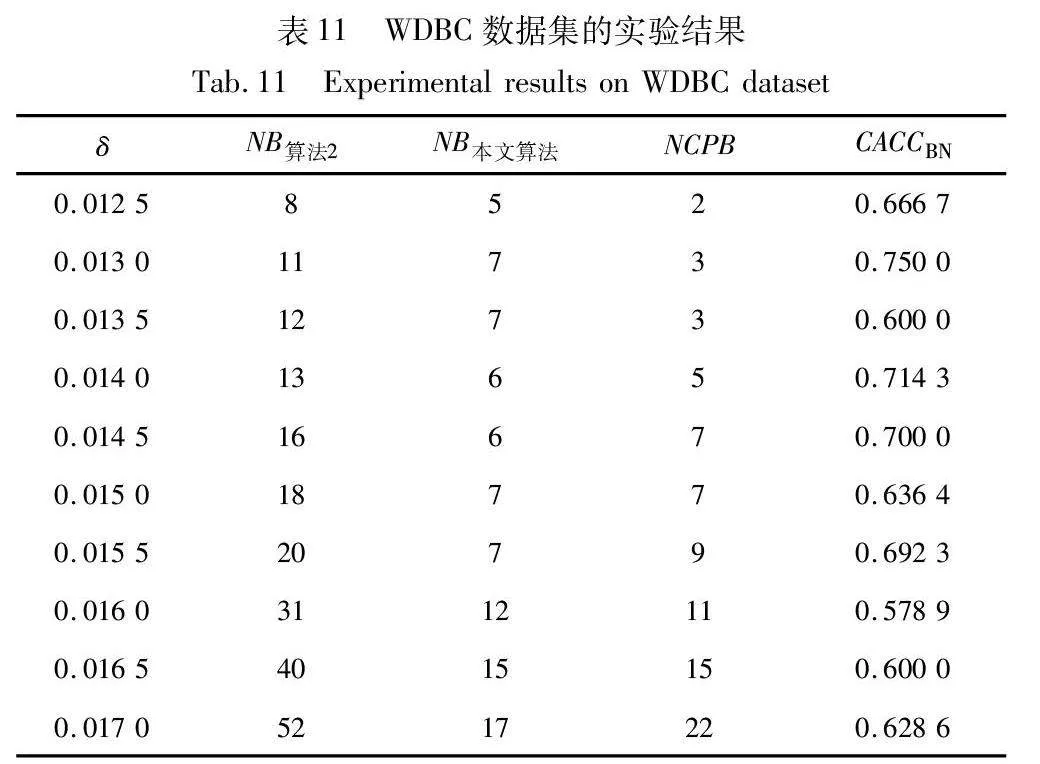
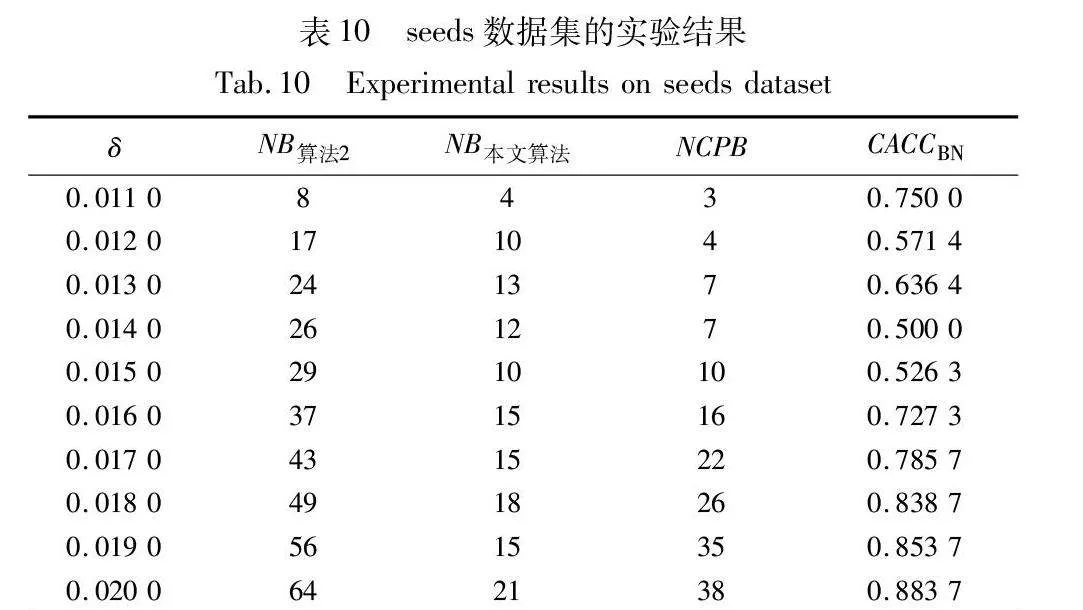
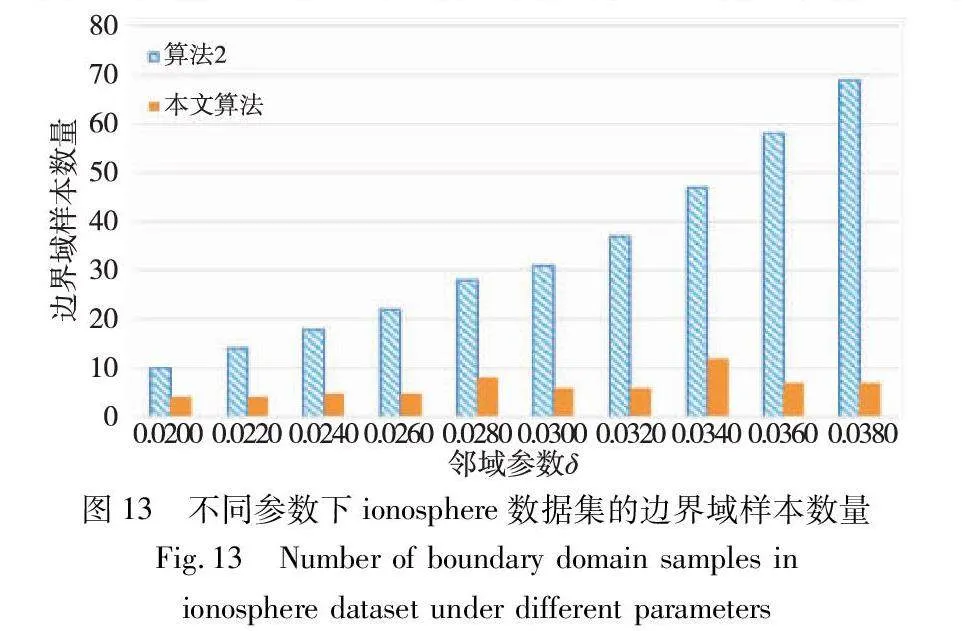
边界域的划分,是三支聚类效果和质量最直接的反映。本文算法中,邻域半径δ的取值直接影响三支聚类边界域的划分,在不同的δ取值下,算法得到的边界域不同,从而影响三支聚类的精度。为了分析参数δ对边界域产生的影响,本文针对各个实验数据集,分别考察了邻域参数δ在给定取值区间上产生边界域对象的情况,并与同为基于δ邻域技术的算法2进行对比,实验结果如图8~13所示。
随着δ值的增加,算法2中的δ邻域颗粒信息不断扩大,使得该算法在三支划分阶段将较多的样本归于边界域中,增大了聚类结果的不确定性。然而,本文算法所使用的邻域颗粒信息MCbest,相对于邻域参数δ的取值大小并不呈现单调关系,受参数影响较小,从而产生相对稳定的三支聚类结果。从图8~13可以看出,随着δ值的增加,算法2得到的边界域样本个数呈明显的上升趋势,而本文算法得到的边界域样本个数保持相对稳定,这表明本文算法在不同邻域参数δ下可以得到较为稳定的聚类结果,相较于算法2受邻域参数δ的影响较小。
为进一步观测同一类型算法在给定相同参数下的性能差异,本文给出了比较划分正确率的概念。针对本文算法和算法2,在给定δ值下的比较正确率(CACCBN)定义如下:
CACCBN=NCPBNB算法2-NB本文算法
其中:NB表示算法产生的边界域中包含的样本数;NCPB表示两比较算法的边界域相对补集中被正确划分到正域的样本数。
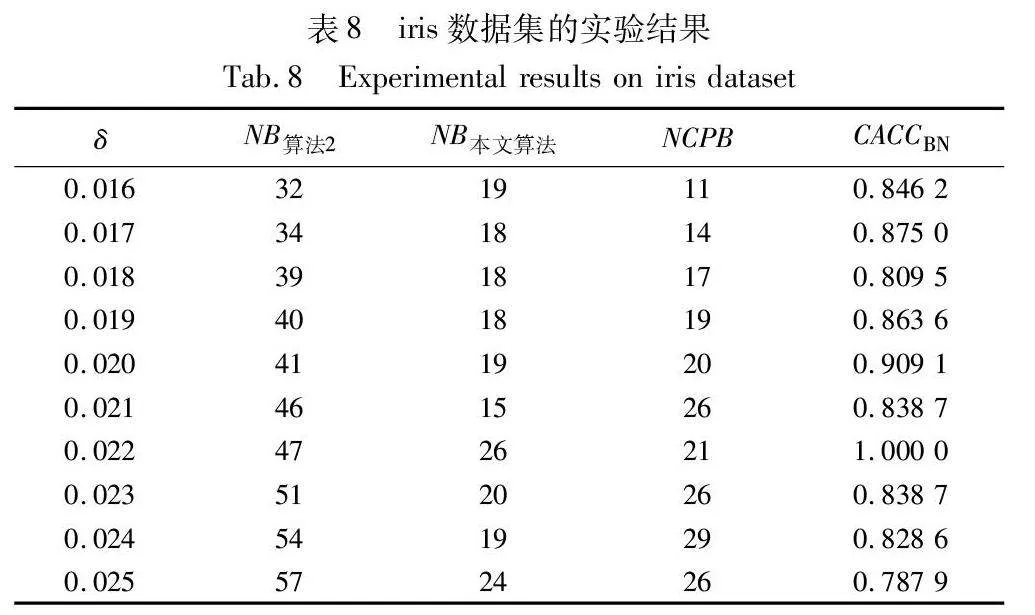
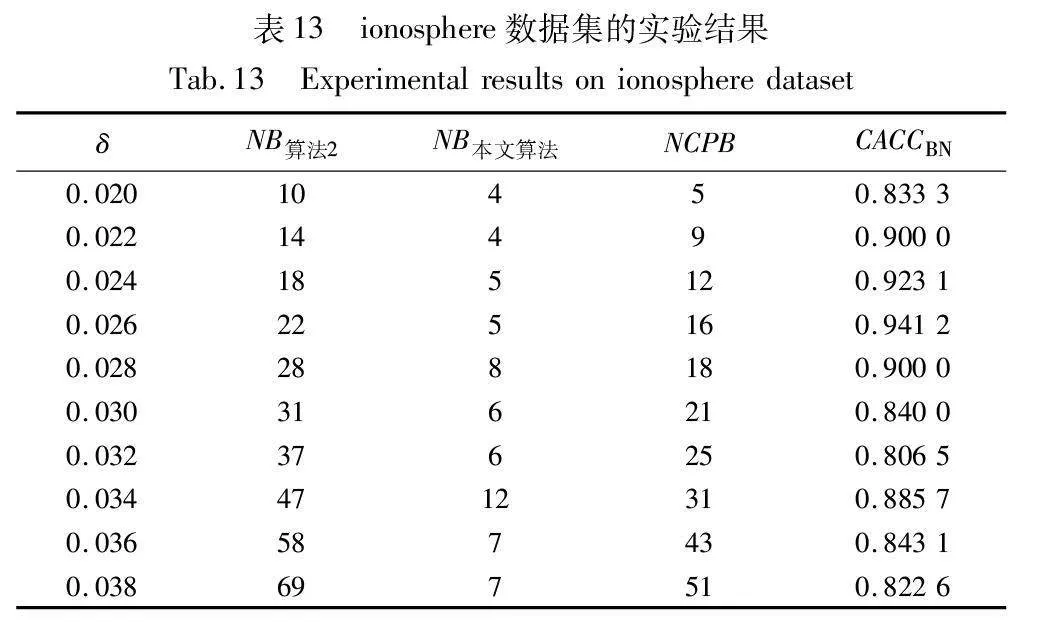
当CACCBN<0时,表明本文算法的边界域包含更多样本,本文算法性能低于算法2;当CACCBN>0时,表明本文算法的边界域包含更少样本,本文算法性能优于算法2。CACCBN的绝对值越大,说明两个算法差异性越大。当NB算法2=NB本文算法时,表明两个算法产生的边界域包含的样本一样多,算法性能接近,这时计算比较正确率CACCBN失去意义。结果如表8~13所示。
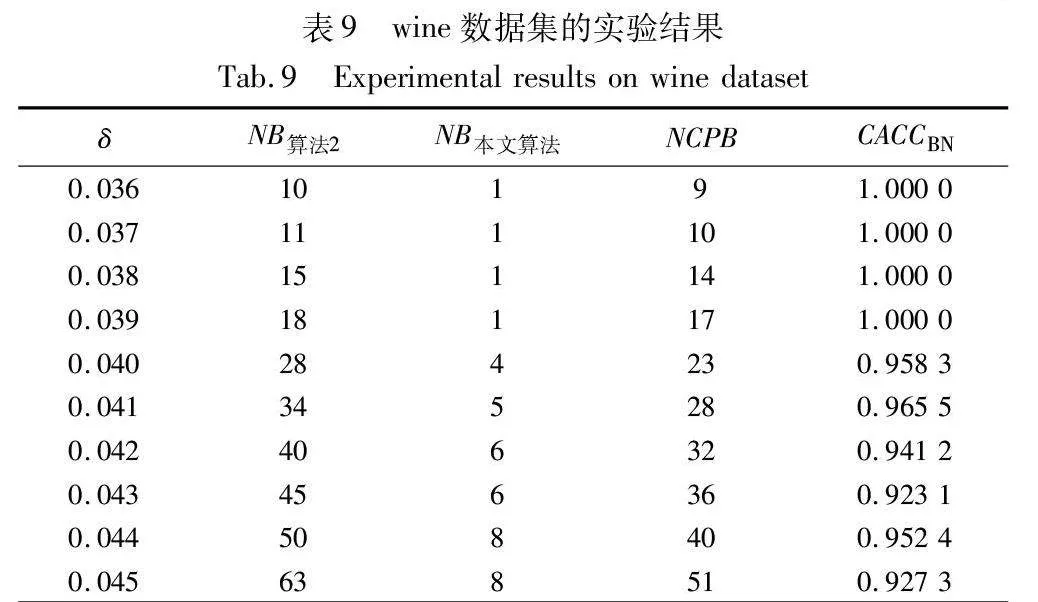
由表8~13的实验结果可知,对于iris数据集,本文算法比较正确率整体较高,且当δ取值为0.022时,所有被处理的样本均得到了正确的划分,比较正确率达到100%;对于wine数据集,本文算法比较正确率均达到90%以上,且当δ取值为0.036、0.037、0.038和0.039时,比较正确率均达到100%;对于seeds数据集,除δ取值为0.012、0.013、0.014和0.015时比较正确率相对较低外,在其余六个取值上比较正确率均达到70%以上;对于WDBC数据集,本文算法比较正确率大多稳定在60%~70%;对于Pima数据集,当δ取值为0.058时,比较正确率最高,达到90%;对于ionosphere数据集,本文算法的比较正确率最小值为80.65%,最大值为94.12%。因此,本文算法在处理边界域样本时,可以较大程度地将样本划分到正确类别。
综上所述,本文基于最大联盟粗糙集的三支聚类算法的聚类效果普遍更好,在保留边界域信息的同时,有效提高了核心域的精度。
5 结束语
本文在给出标准化邻域信息系统的定义基础上,通过引入最大联盟集的概念,定义了一种新的邻域颗粒信息,使得样本邻域信息的刻画更为细致。将该邻域颗粒信息与粗糙集理论相结合,构造了最大联盟粗糙集模型,该模型在一定程度上提高了正域的分类精度,降低了边界域的不确定性。将最大联盟粗糙集模型应用于三支聚类分析中,提出了基于最大联盟粗糙集的三支聚类算法。在6个UCI数据集上进行对比实验的结果表明,本文算法有效提高了聚类结果的准确率,所有正域的平均质量均超过95%,类簇的整体质量和平均质量均超过90%。本文算法在不同邻域参数δ下边界域样本的比较正确率相对较高,可以较大程度地将边界域样本划分到正确类别。
粗糙集理论为解决多属性决策和不确定性问题提供了重要思路,然而在实际决策中,决策任务通常呈现出多视角、多粒度、多层次等复杂特性,单一结构化的决策方法有时无法应对这类复杂的决策问题。为此,下一步工作将考虑从粒计算的角度出发,从不同粒度层次中提取有效信息,探索更适用于解决实际决策问题的粗糙集模型和聚类方法。
参考文献:
[1]Pawlak Z. Rough sets[J]. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356.
[2]Yao Yiyu, Yan Zhao. Attribute reduction in decision-theoretic rough set models[J]. Information Sciences, 2008, 178(17): 3356-3373.
[3]Azam N, Yao Jingtao. Interpretation of equilibria in game-theoretic rough sets[J]. Information Sciences, 2015, 295: 586-599.
[4]Lin T Y. Neighborhood systems:a qualitative theory for fuzzy and rough sets[J]. Advances in Machine Intelligence and Soft Computing, 1997, 4: 132-155.
[5]Yao Yiyu. Relational interpretations of neighborhood operators and rough set approximation operators[J]. Information Sciences, 1998, 111(1-4): 239-259.
[6]Wu Weizhi, Zhang Wenxiu. Neighborhood operator systems and approximations[J]. Information Sciences, 2002, 144(1-4): 201-217.
[7]胡清华, 于达仁, 谢宗霞. 基于邻域粒化和粗糙逼近的数值属性约简[J]. 软件学报, 2008,19(3): 640-649. (Hu Qinghua, Yu Daren, Xie Zongxia. Numerical attribute reduction based on neighborhood granulation and rough approximation[J]. Journal of Software, 2008,19(3): 640-649.)
[8]Lin Guoping, Qian Yuhua, Li Jinjin. NMGRS: neighborhood-based multigranulation rough sets[J]. International Journal of Approximate Reasoning, 2012, 53(7): 1080-1093.
[9]Wang Qi, Qian Yuhua, Liang Xinyan, et al. Local neighborhood rough set[J]. Knowledge-Based Systems, 2018, 153: 53-64.
[10]Wang Changzhong, Shi Yunpeng, Fan Xiaodong, et al. Attribute reduction based on k-nearest neighborhood rough sets[J]. Internatio-nal Journal of Approximate Reasoning, 2019, 106: 18-31.
[11]贺玲, 吴玲达, 蔡益朝. 数据挖掘中的聚类算法综述[J]. 计算机应用研究, 2007, 24(1): 10-13. (He Ling, Wu Lingda, Cai Yichao. Survey of clustering algorithms in data mining[J]. Application Research of Computers, 2007, 24(1): 10-13.)
[12]Yao Yiyu. Three-way decisions with probabilistic rough sets[J]. Information Sciences, 2010, 180 (3): 341-353.
[13]钱文彬, 彭莉莎, 王映龙, 等. 不完备混合决策系统的三支决策模型与规则获取方法[J]. 计算机应用研究, 2020, 37(5): 1421-1427. (Qian Wenbin, Peng Lisha, Wang Yinglong, et al. Three-way decisions model and rule acquisition method for incomplete decision systems[J]. Application Research of Computers, 2020, 37(5): 1421-1427.)
[14]吕艳娜, 苟光磊, 张里博, 等. 深度置信网络的代价敏感多粒度三支决策模型研究[J]. 计算机应用研究, 2023, 40(3): 833-838. (Lyu Yanna, Gou Guanglei, Zhang Libo, et al. Research on cost-sensitive multi-granularity three-way decision model for deep belief network[J]. Application Research of Computers, 2023, 40(3): 833-838.)
[15]于洪. 三支聚类分析[J]. 数码设计, 2016, 5(1): 31-35. (Yu Hong. Three-way cluster analysis[J]. Peak Data Science, 2016, 5(1): 31-35.)
[16]刘强, 施虹, 王平心, 等. 基于邻域的三支决策聚类分析[J]. 计算机工程与应用, 2019, 55(6): 140-144. (Liu Qiang, Shi Hong, Wang Pingxin, et al. Three-way clustering analysis based on neighborhood[J]. Computer Engineering and Applications, 2019, 55(6): 140-144.)
[17]万仁霞, 王大庆, 苗夺谦. 基于三支决策的高斯混合聚类研究[J]. 重庆邮电大学学报:自然科学版, 2021, 33(5): 806-815. (Wan Renxia, Wang Daqing, Miao Duoqian. Gaussian mixture clustering based on three-way decision[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2021, 33(5): 806-815.)
[18]花遇春, 赵燕, 马建敏. 基于共现概率的三支聚类模型[J]. 西北大学学报:自然科学版, 2022, 52(5): 797-804. (Hua Yuchun, Zhao Yan, Ma Jianmin. Three-way clustering model based on co-occurrence probability[J]. Journal of Northwest University:Natural Science Edition, 2022, 52(5): 797-804.)
[19]申秋萍, 张清华, 高满, 等. 基于局部半径的三支DBSCAN算法[J]. 计算机科学, 2023, 50(6): 100-108.(Shen Qiuping, Zhang Qinghua, Gao Man, et al. Three-way DBSCAN algorithm based on local eps[J]. Computer Science, 2023, 50(6): 100-108.)
[20]Pawlak Z. An inquiry into anatomy of conflicts[J]. Information Sciences, 1998, 109(1-4): 65-78.
[21]Lang Guoming, Miao Duoqian, Cai Mingjie. Three-way decision app-roaches to conflict analysis using decision-theoretic rough set theory[J]. Information Sciences, 2017, 406: 185-207.
[22]郭淑蓉. 基于区间直觉模糊信息系统的三支冲突分析[D]. 太原: 山西师范大学, 2022. (Guo Shurong. Three-way conflict analysis based on interval-valued intuitionistic fuzzy information system[D]. Taiyuan: Shanxi Normal University, 2022.)
[23]罗珺方, 张硕, 胡梦君. 不完备异构冲突信息系统中的极大一致联盟区间集族[J]. 计算机科学与探索, 2023, 11(3): 1-12. (Luo Junfang, Zhang Shuo, Hu Mengjun. A family of maximum consistent alliances interval sets in an incomplete heterogeneous conflict information systems[J]. Computer Science and Exploration, 2023, 11(3): 1-12.)
[24]陈玉明, 曾志强, 田翠华. 邻域粗糙集中不确定性的熵度量方法[J]. 计算机科学与探索, 2016,10(12): 1793-1800. (Chen Yuming, Zeng Zhiqiang, Tian Cuihua. Uncertainty measures using entropy and neighborhood rough sets[J]. Computer Science and Technology, 2016, 10(12): 1793-1800.)
[25]Uysal A K. On two-stage feature selection methods for text classification[J]. IEEE Access, 2018, 6: 43233-43251.
[26]Maji P, Pal S K. RFCM: a hybrid clustering algorithm using rough and fuzzy sets[J]. Fundamenta Informaticae, 2007, 80(4): 475-496.
[27]Zhang Kai. A three-way C-means algorithm[J]. Applied Soft Computing Journal, 2019, 82: 105536.
[28]梁海龙, 谢珺, 续欣莹, 等. 新的基于区分对象集的邻域粗糙集属性约简算法[J]. 计算机应用, 2015,35(8): 2366-2370. (Liang Hailong, Xie Jun, Xu Xinying, et al. New attribute reduction algorithm of neighborhood rough set based on distinguished object set[J]. Journal of Computer Applications, 2015,35(8): 2366-2370.)
