大规模图计算在社区发现中的应用研究

摘要：为更好地布局和展示社交网络数据，降低图计算和布局难度，本文提出了一种改进的社区发现算法，旨在解决现有社区发现算法存在的社区质量低和图计算效率低等问题。该算法以Louvain算法为基础，针对大规模社交网络数据进行了优化和改进。最后，采用实验验证的方式分析和对比了本文算法的有效性和可靠性。实验结果表明，与Louvain算法、吴祖峰算法等相比，本文算法在提高社区划分质量和效率方面具有显著优势。

关键词：图计算；社区发现

引言

针对当前社区发现算法在处理大规模社交网络数据时存在的诸多不足，如社区划分质量较差、计算效率低下等问题，本文提出了一种改良版本的社区发现算法，沿用了Louvain算法第一阶段的做法，但在第二阶段采取了一系列优化策略。该算法经过优化和改进，能够更加贴合大规模社交网络的特性和实际需求。根据社交网络特点，预先选取最大度数的节点，并将该节点设置为种子节点，实现小社区的及时合并，使得该算法迭代次数降到最低。

1. Louvain算法概述

Louvain算法是一种经典的社区发现算法，其核心思想是基于模块度优化，通过不断地将节点聚集并适当划分，从而得到最终的社区划分结果。具体来说，该算法会反复地将网络中的节点合并到不同的社区中，同时根据一定的模块度计算公式，评估合并前后社区质量的变化，选择能够最大程度提高模块度的方案，直至模块度不再有提升为止[1]。其目标函数为

（1）

式（1）中cin项表示该社区内部所有边的权重之和；ctot项体现了社区C与外部世界的联系程度；ki项展示了节点i作为个体，与其所有邻居节点之间连接的总强度；ki，in代表各个节点i与社区中节点邻接边权重之和；m项代表整个社交网络中所有边的权重总和。通过优化这些权重相关的变量，Louvain算法可以得到较优的社区划分结果。Louvain算法的执行过程分为两个阶段。在阶段1中，算法将网络中的节点划分到不同的社t。具体来说，对于每个节点，如果其邻居节点可以归入一个不同的社区，则需要按照一定顺序，将节点依次尝试添加到这个社区中。在每次添加时，根据公式（1）计算添加前后模块度的变化量，选择使模块度提升最大的社区作为节点的所属社区。

将最大值设置为max△Q，如果max△Q大于0，将节点i加入该社区后模块度有所提升，在Louvain算法的执行过程中，阶段1会将网络中的节点初步划分到不同社区，根据模块度公式计算；如果将某个节点加入某个社区能使模块度提高，则将其归入该社区，否则保持原社区归属。阶段1完成后，可获得一个初步的社区划分结果和对应的模块度值。

阶段2则对阶段1的结果进行迭代优化。每轮迭代都会重新计算模块度，当模块度函数在给定的迭代步骤下无法获得进一步提升时，算法的迭代过程终止。

2. 结合种子节点的社区发现算法

2.1 问题征集与创新方案

在现有Louvain算法中，阶段2会多次执行迭代环节，当模块Q度停止变化时，迭代环节执行结束。当处理大规模网络数据时，Louvain算法会存在迭代次数多、运行效率低、大社区合并过度、小社区数量过多等问题，为提高社交网络数据信息的展示效率和清晰度，要适当地减少社区发现算法运行时间和小社区数量。因此，Louvain算法不适用于大规模社交网络数据图计算和可视化处理需求[2]。

在社交网络中，通常表现出无标度、小世界效应等特点，因此，整个社交网络节点度数主要呈现幂率分布特点，导致社交网络中含有较多的低度数节点和少量的高度数节点。其中，高度数节点通常对附近的低度数节点产生较高的吸引力，从而形成一个完整的社区。当Louvain算法阶段1执行完毕后，会产生大量的小社区和少量的大社区。在Louvain算法阶段2中，可以完成对新网络图G'的构建。在Louvain算法阶段1中，借助各个社区，可以压缩出若干个节点，这些节点经过组合，形成新网络图G'。根据社交网络特点，本文基于Louvain算法，提出一种改进的社区发现算法，该算法可以对大社区之间的合并操作进行有效抑制，同时，还能实现对小社区的有效合并处理，有效解决Louvain算法存在的缺陷问题。

2.2 改进的社区发现算法

本文所提出的改进社区发现算法在保留Louvain算法阶段1的基础上，重点改进了Louvain算法阶段2，同时，该阶段2无须进行迭代执行。在整个网络图G节点中，含有若干个社区集合C，由于阶段1存在过多的小社区，因此，在阶段2中，要不断地划分社区。

在改进社区发现算法阶段2中，进一步压缩处理阶段1所对应的划分结果，从而完成对新网络图G'的构建。在构建好的新网络图G'中，选取多个种子节点，该种子节点集合如下所示：

（2）

式（2）中的deg（ν）代表节点ν的度数；g代表节点平均度数；p代表节点度数所对应的标准方差。在划分社区时，算法将所有节点分配到不同的社区中。对于网络中的每个非种子节点i，算法会检查其邻居节点所属的社区情况。如果该节点的邻居节点分属于多个不同的社区，那么算法会按照一定的顺序，尝试将该节点逐一加入这些社区中。每次加入时，算法利用公式（1）计算该节点加入前后模块度的变化量，以评估该节点加入该社区对模块度（即社区质量）的影响程度，以评估将节点△Qj（j=1，2，…，t）划分到不同社区的优劣。如果该社区含有若干个种子节点，需要将该社区自动添加到所设置好的集合D1中，反之，则自动添加到集合D2中。然后，对集合D1中的△Qj最大值设置为max△Q，如果该△Qj最大值大于0，需要将节点i自动分配△Qj到最大值所对应的社区中，反之，须对集合D2中的△Qj最大值设置为max△Q，如果该△Qj最大值大于0，需要将节点i自动分配到△Qj最大值所对应的社区中，对于那些既不属于种子节点集合，也不适合并入任何一个含有种子节点的社区的节点，算法将保留其原有的社区归属，不对其进行重新分配[3]。

本文提出的改进社区发现算法具体步骤如下：

步骤1：通过对Louvain算法的阶段 1进行执行，初步获得相应的社区划分结果，该结果用C表示。

步骤2：对所获得的社区划分结果C进行初步压缩处理，获得G'（V'，E'）。

步骤3：运用式（2），计算出种子节点集合S。

步骤4：将非种子节点i直接分配到所构建好的新社区中。

步骤5：重复操作步骤4，将所有非种子节点i分配到相应的新社区中。

步骤6：输出最终社区划分结果C，此时，整个算法全部结束。

3. 实验和结果分析

3.1 社区发现算法实验方案

本文主要选用了模块度值Q、社区数量、算法运行时间三种评价指标，模块度值Q和社区划分效果之间存在正相关关系，后者随着前者的变大而变得越来越好，算法运行时间和算法运行效率存在反相关关系，后者随着前者的变短而变得越来越高。

3.2 社区发现算法实验及分析

3.2.1 不同数据集实验的统计对比

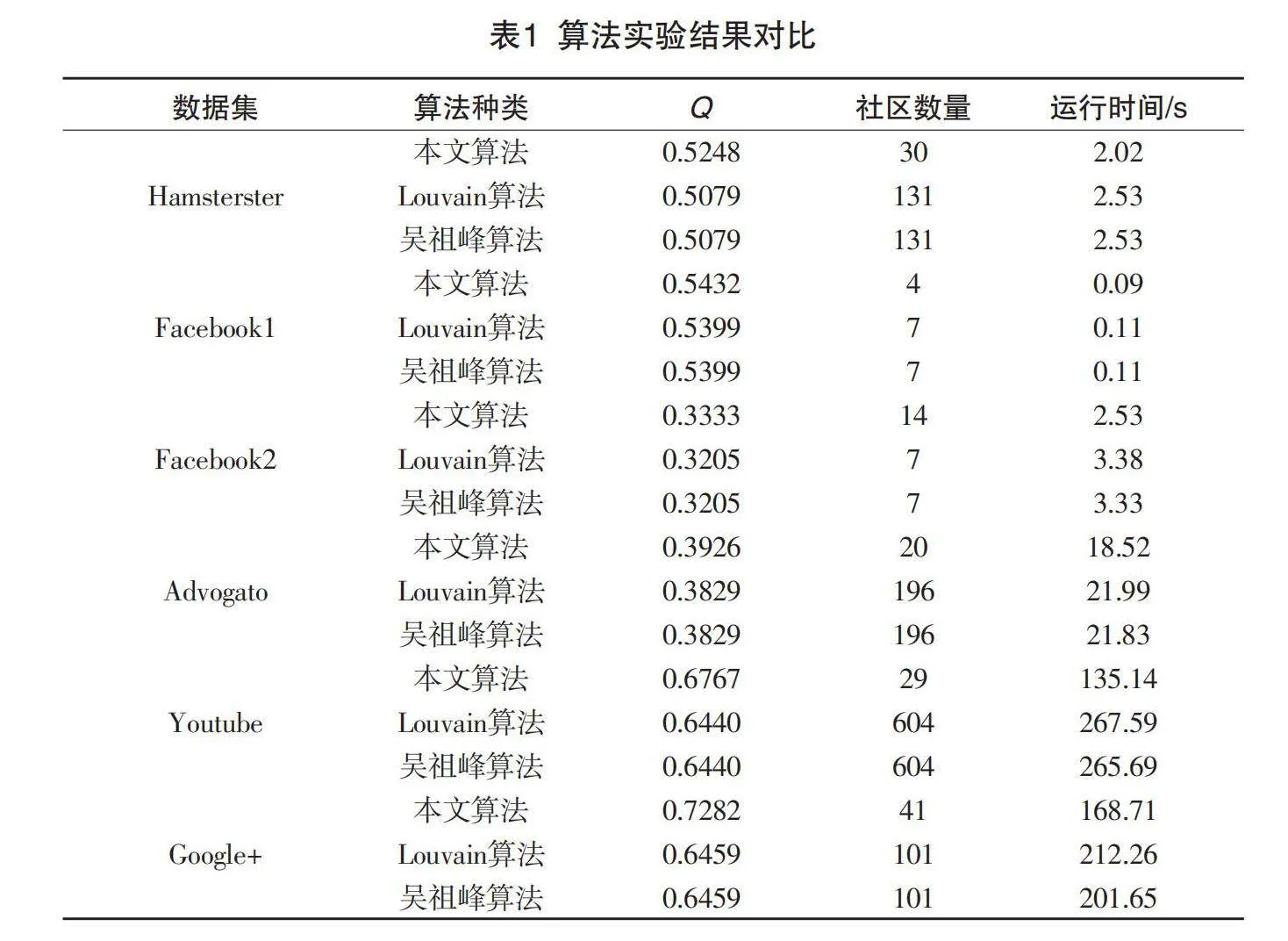
为全面评测本文提出算法的社区划分质量和计算效率，开展了与Louvain算法和吴祖峰算法的对比实验。实验结果如表1所示，选取了模块度Q、社区数量和算法运行时间三个指标作为评估标准。其中，模块度Q可以用来衡量社区划分的质量和合理性，模块度越高，表明社区划分结果越好。通过比较不同算法在这三个指标上的表现，可以全面评价本文算法的优劣和改进效果。从表1可以看出，与Louvain算法、吴祖峰算法等相比，本文算法的模块度Q更大，社区数量更小，这说明运用本文算法可以获得较高的社区划分质量。此外，本文算法运行效率明显高于其他两种算法。实验结果表明：本文所提出的改进社区发现算法具有社区划分质量高、算法运行效率高等特点。

3.2.2 典型数据集的可视化结果对比

为直观对比本文算法与Louvain算法在社区划分效果上的差异，对部分数据集进行了可视化处理，结果分别呈现在图1和图2中。由于吴祖峰算法和Louvain算法在本数据集上产生了相同的社区划分，因此分别与本文算法进行对比，其实质含义是一致的，无须重复展示。通过将改进算法与经典算法的输出结果并列比对，能够更加直观地反映出两种算法在处理同一数据时的差异表现，有助于凸显本文算法的创新之处。在这些可视化图中，使用不同颜色代表不同的社区，同一颜色的节点表示它们被划分到了同一个社区。通过对比不同算法产生的社区划分结果，可以直观评估算法的优劣及改进效果。

Hamsterster数据集社区划分结果可视化对比如图2所示。从图2中可以看出，运用Louvain算法所划分的社区数量为131个，运用本文算法所划分的社区数量为30个，这说明运用本文算法所划分的小社区数量相对较少，有效地解决了Louvain算法存在的小社区数量过多问题。

在数据集中可以发现，本文算法所获得的模块度Q远远超过Louvain算法，这说明本文算法可以缓解Louvain算法存在的过度合并大社区问题。

结语

在社交网络中，含有无尺度、小世界特性的社区结构，应用该社区结构，可以降低图计算复杂度，通过应用图计算技术，可以实现对网络数据的计算和获得。本文在参照Louvain算法的基础上，提出一种改进社区发现算法，该算法满足图计算、图可视化相关标准和要求。在本文算法的设计中，主要采取了以下策略：选取度数较大的节点作为种子节点，避免了使用Louvain算法时大社区过度合并的问题。优先合并小社区，将小社区数量降至最小。在第二阶段无须进行迭代执行，减少了计算开销。实验结果表明：与Louvain算法、吴祖峰算法相比，本文算法在提高社区划分质量和效率方面具有显著优势。

参考文献：

[1]欧朋成.大规模网络表示学习和结构发现算法研究[D].石家庄：河北地质大学，2020.

[2]王晨旭，周俊铭，姜佩京.基于拓扑结构表示学习的大规模无监督图对齐方法研究[J].计算机学报，2023，46（7）：1350-1365.

[3]赵鹏.大规模图计算系统优化技术研究[D].北京：中国科学院大学，2019.

作者简介：王延楠，本科，研究方向：大数据、图计算。