反比例函数的奇妙世界

反比例函数，用简洁而优美的形式表达着两个变量之间的反比例关系。它告诉我们，在某些情况下，当一个量增加时，另一个量则会相应地减少，两者之间存在一种微妙的平衡。它的图像，是一条双曲线，无限延伸却永不相交，展现了数学的对称之美，也让我们感受到了规律的严谨与奇妙。

今天我给大家分享一下反比例函数的三条常用性质和六个模型，简称“三头六臂”。

“三头”包括反比例函数的不变性，即一“乘”不变，xy=k，|k|越大，函数图像离原点越远；增减性，即同一象限用增减，不同象限看符号；对称性，即关于原点中心对称，关于直线y=±x对称。

“六臂”，即有6种模型，具体如下：

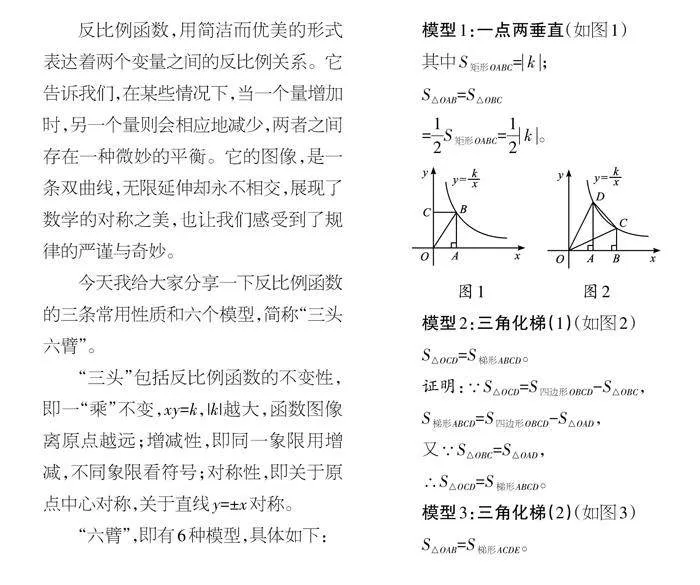
模型1：一点两垂直（如图1）

其中S矩形OABC=[k]；

S△OAB=S△OBC

=[12]S矩形OABC=[12][k]。

模型2：三角化梯（1）（如图2）

S△OCD=S梯形ABCD。

证明：∵S△OCD=S四边形OBCD-S△OBC，

S梯形ABCD=S四边形OBCD-S△OAD，

又∵S△OBC=S△OAD，

∴S△OCD=S梯形ABCD。

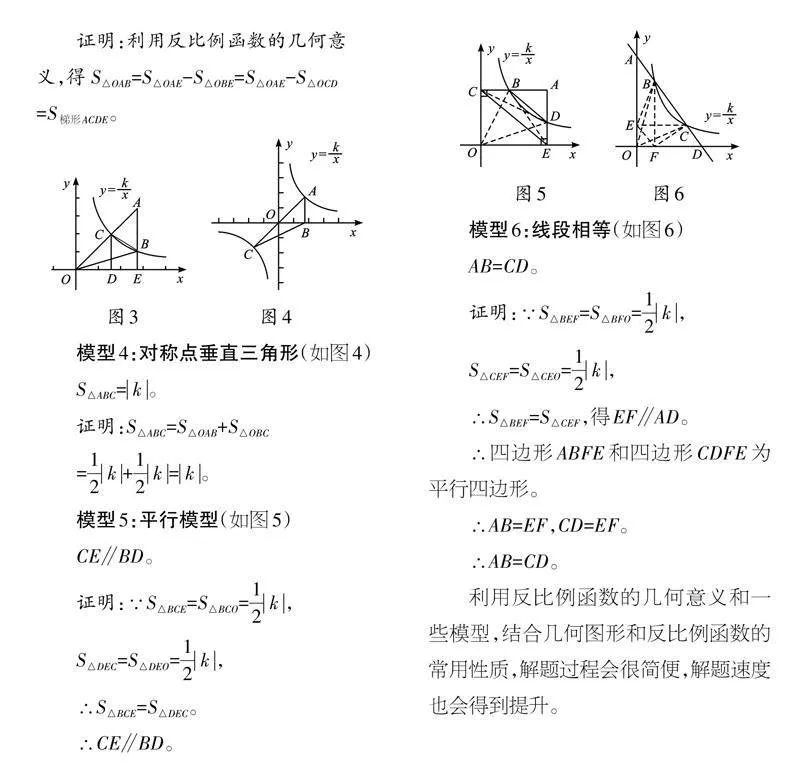
模型3：三角化梯（2）（如图3）

S△OAB=S梯形ACDE。

证明：利用反比例函数的几何意

义，得S△OAB=S△OAE-S△OBE=S△OAE-S△OCD

=S梯形ACDE。

模型4：对称点垂直三角形（如图4）

S△ABC=[k]。

证明：S△ABC=S△OAB+S△OBC

=[12][k]+[12][k]=[k]。

模型5：平行模型（如图5）

CE∥BD。

证明：∵S△BCE=S△BCO=[12][k]，

S△DEC=S△DEO=[12][k]，

∴S△BCE=S△DEC。

∴CE∥BD。

模型6：线段相等（如图6）

AB=CD。

证明：∵S△BEF=S△BFO=[12][k]，

S△CEF=S△CEO=[12][k]，

∴S△BEF=S△CEF，得EF∥AD。

∴四边形ABFE和四边形CDFE为平行四边形。

∴AB=EF，CD=EF。

∴AB=CD。

利用反比例函数的几何意义和一些模型，结合几何图形和反比例函数的常用性质，解题过程会很简便，解题速度也会得到提升。

教师点评

王瑞琦同学在解决反比例函数问题后总结了三条常用性质和六个模型。模型是对某类题系统地简化和概括得到的，可见该同学在学习过程中渗透了模型思想。总结模型是对解题的进一步深化，是透过现象看到本质的过程。

（指导教师：崔建平）