梯度隐藏的安全聚类与隐私保护联邦学习

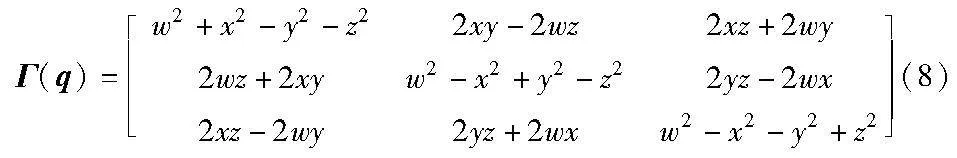
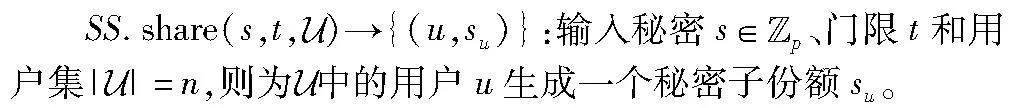
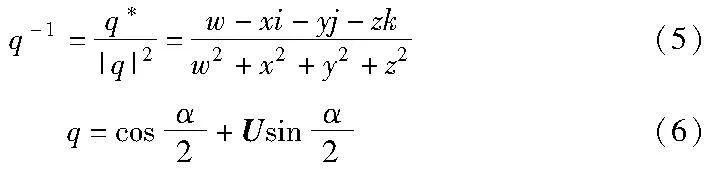
摘 要：联邦学习是一种前沿的分布式机器学习算法，它在保障用户对数据控制权的同时实现了多方协同训练。然而，现有的联邦学习算法在处理Non-IID数据、梯度信息泄露和动态用户离线等方面存在诸多问题。为了解决这些问题，基于四元数、零共享与秘密共享等技术，提出了一种梯度隐藏的安全聚类与隐私保护联邦学习SCFL。首先，借助四元数旋转技术隐藏首轮模型梯度，并且在确保梯度特征分布不变的情况下实现安全的聚类分层，从而解决Non-IID数据导致的性能下降问题；其次，设计了一种链式零共享算法，采用单掩码策略保护用户模型梯度；然后，通过门限秘密共享来提升对用户离线情况的鲁棒性。与其他现有算法进行多维度比较表明，SCFL在Non-IID数据分布下准确度提高3.13%～16.03%，整体运行时间提高3～6倍。同时，任何阶段均能保证信息传输的安全性，满足了精确性、安全性和高效性的设计目标。

关键词：联邦学习； 隐私保护； 聚类； 四元数； 零共享； 秘密共享

中图分类号：TP390 文献标志码：A

文章编号：1001-3695（2024）06-037-1851-11

doi：10.19734/j.issn.1001-3695.2023.09.0403

Gradient-hiding secure clustering and privacy-preserving federated learning

Abstract：Federated learning is a kind of advanced distributed machine learning algorithm， which realizes multi-party cooperative training while ensuring the user’s control over the data. However， the existing federated learning algorithms have many problems in dealing with Non-IID data， gradient information leakage and dynamic user offline. To solve these problems， this paper proposed a gradient hidden safe clustering and privacy-protecting federated learning based on quaternion， zero sharing and secret sharing techniques. Firstly，it used quaternion rotation technology to hide the first-round model gradient and achieve secure clustering stratification without altering the gradient feature distribution， so as to solve the performance degradation issue caused by Non-IID data. Secondly， this paper designed a chain zero sharing algorithm， using single strategy to protect the user model gradient mask. Then，it used the threshold secret sharing to improve the robustness against offline users. Multi-dimensional comparison with other existing algorithms shows that the accuracy of SCFL is improved by about 3.13%～16.03% under the Non-IID data distribution， and the overall running time is improved by about 3～6 times. Mean while， the security of information transmission is guaranteed at any stage， satisfying the design goals of accuracy， security and efficiency.

Key words：federated learning; privacy-preserving; clustering; quaternion; zero-sharing; secret sharing

0 引言

随着机器学习、人工智能的广泛应用，全球产业不断向智能化发展。传统的集中式机器学习算法通常要求用户将自己的本地数据上传至中央服务器，以换取高质量的机器学习模型。用户的数据一旦脱离本地，将不再享有对数据的控制权。数据安全和隐私边界将不可避免地遭到侵犯，危害用户的个人利益与信息安全。随着欧盟2018年正式执行《通用数据保护法案》，信息技术行为逐渐规范，构建安全的网络空间环境成为大数据发展与实施的基石。机器学习领域也随之演化出了一种不需要用户披露的私有数据，也能实现模型训练的分布式学习框架，即联邦学习（FL）［1］。该技术实现了数据隐私保护和数据协同分析的平衡，它只需要用户在本地数据集上进行模型训练，上传梯度更新到服务器，服务器聚合得到全局梯度即可。FL用模型梯度保护了终端与个人数据的隐私，在合法合规的前提下，开展高效率的机器学习，实现了“数据可用不可见，数据不动模型动”的预想。经过多年的发展，FL逐渐为5G自动驾驶［2］、智慧医疗管理［3］、边缘联合计算［4］等多个领域带来了高效的资源利用与价值提供，传统集中式学习框架逐渐过度到分布式安全智能终端体系。

FL参与用户拥有的高质量数据是机器学习模型实现高精度的基础。多数情况下，各领域企业或个人所拥有数据往往是异构的，即数据满足非独立同分布（Non-IID）。该情况在物联网（IoT）场景中尤为明显，物联网设备的多样性影响着数据的种类，使用者的个性化决定了数据的差异［5］。物联网设备在使用过程中，可能会由于处理能力、存储电量或网络带宽差异，导致设备无法对模型训练作出响应。这种情况即为设备离线，当其环境改变后可重新参与训练。在Non-IID分布下与动态的训练环境下，不同用户本地模型梯度更新偏差较大，全局模型发生偏移，进而获得理想模型的概率降低［6］。此外，FL还面临着来自敌手服务器的隐私威胁。服务器对用户的本地数据感到好奇，可能会从接收到的本地模型梯度进行反向攻击。利用重构攻击［7，8］从模型梯度中重建出隐私数据，或利用推理攻击［9，10］推断隐私数据的敏感信息。

目前，研究人员针对Non-IID数据和隐私保护问题分别提出了各自的解决方案。首先，为了提高FL在数据样本分布倾斜情况下的训练准确度，本地梯度正则化、个性化训练和聚类分簇成为主流解决策略。文献［11］通过对目标函数添加修正项来解决异构问题。文献［12～14］将元学习、迁移学习和多任务学习应用在FL中，但要求所有用户必须完整地参与训练，并不适用于动态的训练环境。文献［15，16］发现模型梯度的偏差由数据差异性决定。当两个用户之间数据越相似时，它们的训练结果越接近。为此，他们对模型梯度进行特征统计，使用聚类算法把梯度特征相似的用户分到一个簇中进行训练。簇内训练、簇间聚合，减轻因数据异构造成的差异。事实上，以上方案虽能改善FL性能，但均忽略了隐私泄露问题。为了保护系统安全性和个人数据隐私性，差分隐私、同态加密和安全多方计算成为解决该问题的多种可能［17］。具体来说，文献［18，19］研究了差分隐私方案，向本地梯度中加入适当噪声使敏感数据失真，防御由先验背景知识所进行的攻击。在差分隐私中，隐私预算的分配将直接影响数据隐私性与安全性之间的平衡。隐私预算越小，加入的噪声越多，数据隐私性越高，FL模型可用性越差。文献［20，21］使用同态加密算法，加密明文信息，保证数据的安全性和完整性。然而，同态加密往往需要巨大的计算与通信开销，且没有考虑动态环境用户离线问题。文献［22，23］将多方安全计算应用与FL之中，实现了对模型梯度的保护，但可扩展性较差。如何在不泄露用户隐私的前提下，设计一种既解决Non-IID数据，又保护模型梯度安全的FL算法势在必行。

本文提出了一个安全、高效的聚类隐私保护方案SCFL（secure clustering and privacy-preserving federated learning）以解决上述问题。为了实现这一目标，本文将SCFL划分为聚类阶段（初始化阶段）和聚合阶段（训练阶段）两个关键阶段。这两个阶段均以保护模型梯度隐私为基础，解决Non-IID数据导致的偏离问题和用户离线导致的聚合失败问题为子目标，旨在为动态训练场景提供一种有效的解决方案。在聚类阶段和聚合阶段，本文分别采用旋转缩放和新型零共享技术，来满足不同阶段对梯度隐私保护的需求，确保结果的可用性和准确性。此外，分别采用K-means聚类和门限秘密共享应对剩余问题。实际上，这一方案能够显著降低通信和计算成本。本文的主要贡献如下：

a）借助四元数旋转技术，提出了一种混淆梯度聚类分层算法。通过旋转和缩放将真实梯度信息转变为与之不可区分的混淆梯度，并保证梯度间的余弦相似性不变，实现并行分簇训练。进而提高模型准确度、提升聚合阶段训练效率。

b）设计了一种零共享链式可消除扰动算法来保护单个用户的模型梯度。簇内用户通过零共享算法得到各自的随机数，将随机数作为掩码保护模型梯度，防御推理攻击。

c）采用门限秘密共享技术解决用户动态离线，全局模型无法聚合的问题。只有簇内在线用户数量大于或等于秘密共享重构的门限值，才能正确消除离线用户的随机数，保持模型的准确度与可用性。

SCFL是首个将聚类与隐私保护相结合的解决方案。主要改进依据是基于旋转缩放不改变向量间余弦相似度的数学理论，保证聚类阶段模型梯度统计分布的不变性；结合零共享算法生成掩码的可抵消性、秘密共享的可还原性来保证聚合结果的正确性，其合理性在后续的实验中得到了充分的验证。

1 相关工作

1.1 聚类联邦学习

聚类FL是用来解决Non-IID数据导致模型精度下降的一个新兴研究热点，该方案将参与训练的用户分成多个簇。在相同的簇中，近似数据有利于模型训练，改善模型梯度偏离现象。Sattler等人［15］通过贪心算法将用余弦相似度计算出的相似矩阵分为两组，组内用户数据分布相同。Briggs等人［16］通过计算用户本地模型更新相较于全局模型更新间的欧几里德距离，使用层次聚类的方式分离用户集群。Zhang等人［24］通过衡量用户间梯度的余弦相似度和模型更新延迟，构建相似度关联矩阵，把数据量和计算能力相似的用户分成一组。Morafah等人［25］假设服务器本身拥有一些真实或合成的数据，进而对用户模型进行推理。Shu等人［26］提出了使用移动搬土距离测量模型相似性的聚类FMTL，来实现对Non-IID数据进行多任务学习。Chen等人［27］设计了一个分层聚合联邦学习HAFL方案，通过引入子聚合器和聚合器提高训练效率。文献［28］通过Deep Sets模型提取本地数据特征，利用不同节点之间数据分布的欧氏距离实现了聚类FL框架。然而，以梯度相似性衡量数据相似性的分层聚类方法均未考虑隐私泄露的风险，模型梯度极易受到对数据安全有威胁的重构攻击，从而暴露用户的隐私信息。

1.2 隐私保护联邦学习

隐私保护技术旨在保护信息的安全性，降低数据泄露的风险。具体来说，隐私保护分为信息扰动机制和过程加密机制［29］。信息扰动机制以模糊原始信息为目的，通过掩码或差分隐私等技术隐藏信息。Bonawitz等人［30］通过Diffie-Hellman密钥交换协商生成掩码，对模型梯度加以扰动，使用秘密共享技术分享密钥，使其方案对用户离线具有鲁棒性。Hu等人［19］为了解决联邦知识图谱中的隐私信息泄露问题，利用差分隐私的随机梯度下降（DP-SGD）技术对梯度进行裁剪并添加高斯噪声，更改隐私水平来权衡隐私与性能。过程加密机制以改变信息形式为目的，通过同态加密、秘密共享等技术使信息不可读。文献［20］提出使用Paillier加密来保护模型梯度安全。Ma等人［21］使用多密钥加密方案xMK_CKKS，梯度信息被隐含在密文中，在聚合阶段，需要每个用户提供部分解密信息辅助服务器进行聚合，能够解决因私钥泄露引发的公共信息安全问题。Wang等人［22］提出了一个基于秘密共享的随机掩码的轻量级隐私保护协议，使用数字签名实现消息完整性和一致性认证。加密策略与秘密共享技术对模型梯度具有较强的保护效果，但应用在高维的神经网络上，势必会消耗大量的计算与通信资源，影响训练效率。

2 基础知识

2.1 联邦学习

联邦学习通常是服务器-用户架构，即一个服务器S和n个用户Euclid Math OneUAp={u1，u2，…，un}。在第e轮训练中，服务器负责将最新的全局模型weg分发给用户集合Euclid Math OneUAp，用户ui使用m维本地数据Di={（x1，y1），（x2，y2），…，（xm，ym）}，进行随机梯度下降（SGD）训练，得到模型梯度：

we+1i=weg-ηfi（Di，weg）（1）

其中：x表示输入样本；y表示样本标签；η表示学习率。用户ui的目标损失函数如下：

然后，用户ui将本地模型梯度we+1i发给服务器；服务器由式（3）更新得到全局模型we+1g并分发给用户集合Euclid Math OneUAp。重复迭代执行，直到达到预期精度或预定时间。

2.2 四元数旋转

爱尔兰数学家William Rowan Hamilton在1843年首次提出四元数［31］的概念，它可以用来实现空间中的旋转。四元数q由一个实数与三个虚数组成，其复数形式如下

q=w+xi+yj+zk（4）

其中：w，x，y，z为实数;i，j，k为虚数单位。i，j，k具有如下性质：i2=j2=k2=-1，ij=-ji=k，jk=-kj=i，ki=-ik=j。四元数q的逆和其三角式如式（5）（6）所示。

其中：α为实数;U为单位向量。

四元数可以实现比旋转矩阵更高效的旋转，还能避免使用欧拉角旋转过程中的万向节锁现象。若将模型梯度视为一个三维向量A，其绕单位向量U=（1，1，1）旋转α度得到新向量A′的过程可分为两步：a）将单位向量U和旋转角度α代入式（6）求得四元数q；b）根据式（7）计算旋转后的向量A′：

A′=q·A·q-1（7）

实际上，向量A的旋转过程也可以写成A′=Γ（q）·A，Γ（q）为四元数q生成的旋转矩阵：

向量A的缩放：一个数乘以向量A以改变向量A的大小，即=ζ×A，ζ为缩放因子。

2.3 双线性聚合签名

BLS双线性聚合签名方案［32］能够处理n个不同私钥对不同信息进行签名的结果，将其合并为一个聚合签名。相应地，验证者根据n个公钥与签名信息对聚合签名进行验证。若验证通过，其效果等同于对n个签名进行单独验证且全部通过。由此可见，当所有签名均正确时，聚合签名可以有效降低存储空间和验证过程中的流量成本。双线性映射为e：G1×G2→G3，哈希函数h：{0，1}*→G2，满足e（a·P，b·Q）=e（P，Q）ab。下面介绍BLS聚合签名的构造细节。

SIG.gen（g）→（pk，sk）：密钥初始化过程。g是乘法循环群G的生成元。用户选择随机数sk作为私钥，计算公钥pk=gsk。

SIG.sign（sk，m）→σ：签名产生过程。输入用户私钥sk和消息m，输出签名σ←（h（m））sk。

SIG.ver（pk，h（m），σ）→0/1：签名验证过程。将用户公钥pk、对消息m的哈希值h（m）和签名σ作为输入，验证者验证等式e（pk，h（m））=e（g，σ）是否成立，如果返回1，则表示签名验证通过，否则返回0。

2.4 门限秘密共享

Shamir等人［33］在1970年首次提出基于拉格朗日插值的（t，n）门限秘密共享。该方案的核心思想是参与方Pi将自己的秘密s拆成n份子秘密，分发给其他n-1个参与方。当收集到的秘密份额数量大于门限t时，能够恢复出原始秘密s，该技术可以抵御t-1个参与方合谋。共包含以下两个阶段。

SS.share（s，t，Euclid Math OneUAp）→{（u，su）}：输入秘密s∈Euclid ExtrabBpp、门限t和用户集|Euclid Math OneUAp|=n，则为Euclid Math OneUAp中的用户u生成一个秘密子份额su。

Shamir秘密共享满足加法同态［34］，即参与方Pi拥有秘密x和y的子份额xi，yi，能够得到子份额之和zi=xi+yi。当收集超过t个子份额之和z1，z2，…，zt时可通过秘密重构算法SS.recon（{z1，z2，…，zt}）恢复秘密s=x+y。

3 SCFL模型架构

3.1 设计目标

在分布式FL训练场景中，由于参与用户的多样性和差异性，整体训练过程中可能出现以下情况：a）用户间的Non-IID数据；b）云服务器计算与通信压力大；c）模型梯度隐私泄露风险；d）用户因网络或环境问题脱离训练。SCFL初始化阶段以解决以上问题为导向，制定了如下目标：

a）同构性。通过聚类分簇的思想将数据异构的用户分到不同的簇中，保证簇内同构、簇间异构以提升训练性能。

b）高效性。为每个簇分配近端边缘服务器，分摊通信和计算开销，减少传输时间，提高系统训练效率。

c）安全性。敌手就算得到用户上传的信息，也无法从中获取用户的隐私数据。保证各个阶段用户所上传的混淆梯度与真实梯度不可区分。

d）正确性。在部分用户离线的情况下，SCFL同样能够保证聚合结果的正确性、完整性和真实性。

3.2 安全聚类分层

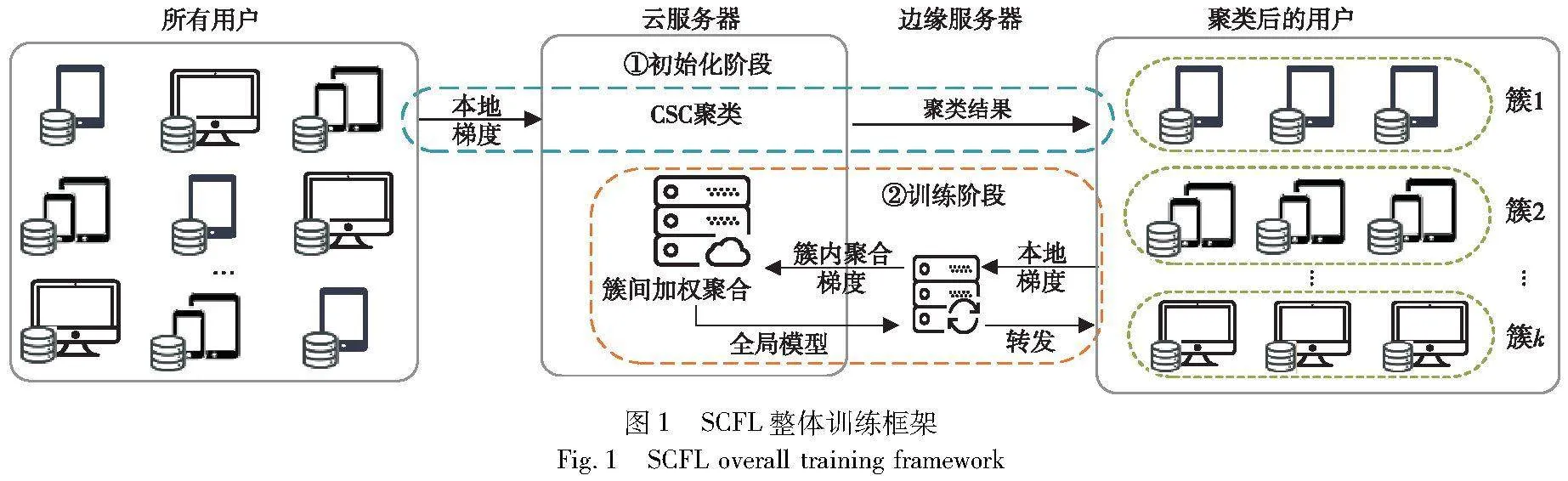
根据以上设计目标，本文将SCFL分为初始化阶段（安全聚类分层阶段）和训练阶段（安全掩码聚合阶段）两个阶段，如图1所示。首先介绍聚类分层的实现过程，值得注意的是，初始化阶段仅在首轮训练结束后执行一次。

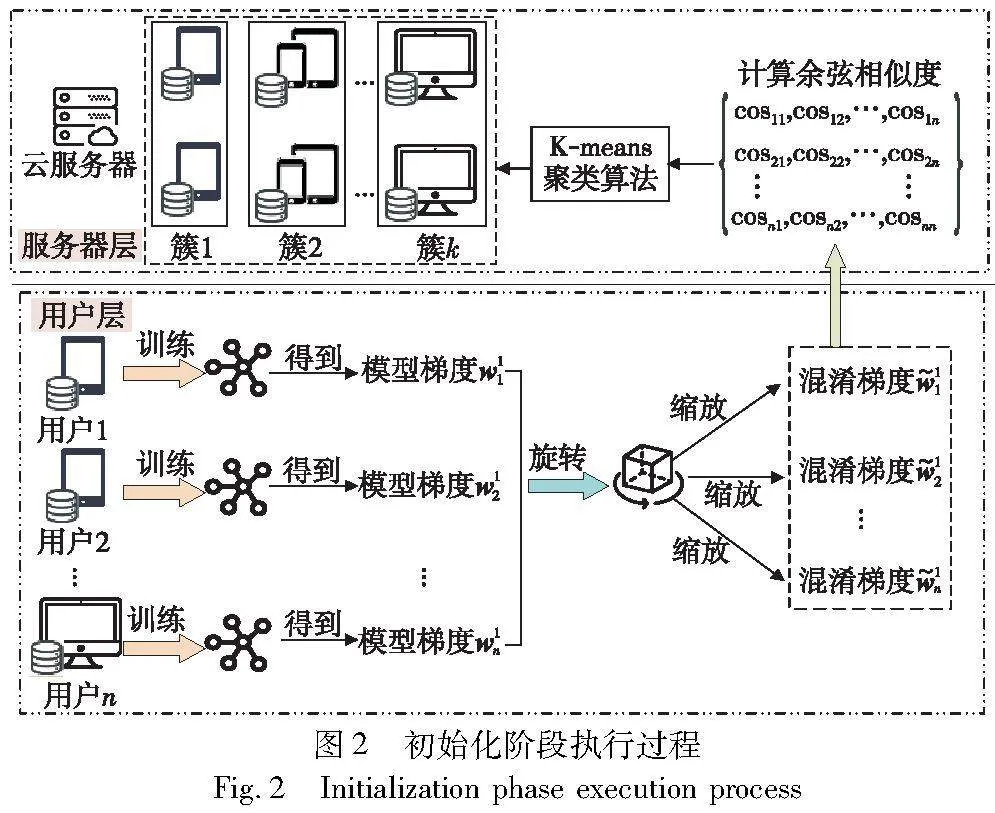
该阶段包括本地训练、安全聚类分层和簇内密钥广播三个组件，大致执行过程如图2所示。为了同时保证用户梯度的相似性和隐私性，本文提出了一种基于四元数旋转的余弦相似度聚类算法CSC。具体细节如算法1所示。

算法1 余弦相似度聚类CSC

其中：w1·w2表示梯度w1和w2的内积；‖w1‖表示梯度w1的模。

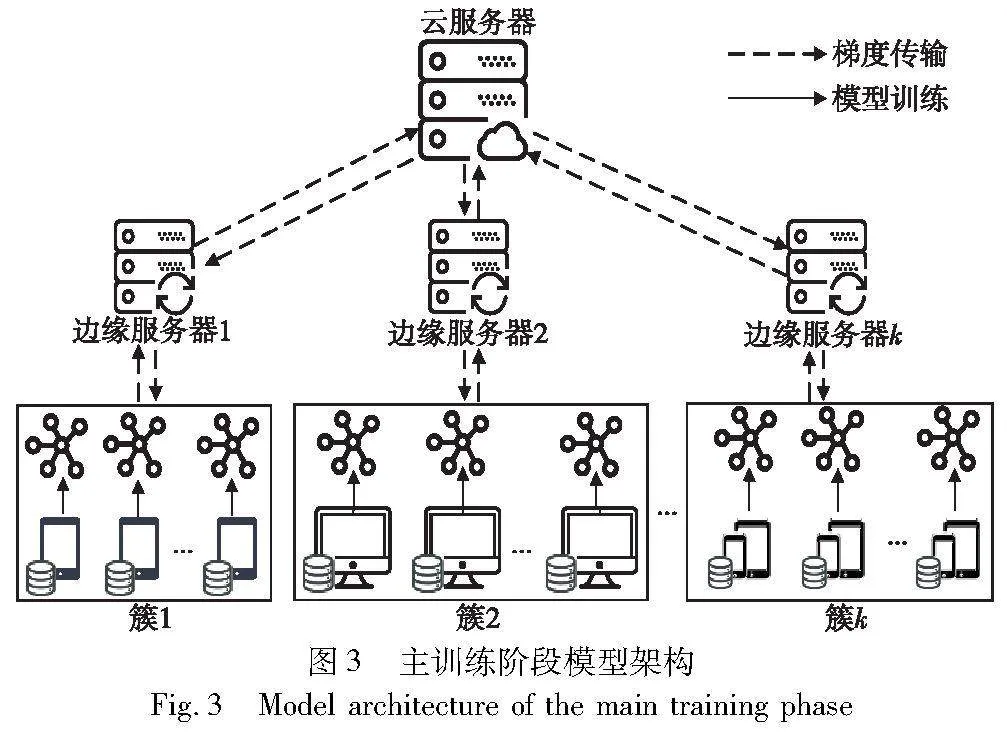
CSC算法以实现簇内同构、簇间异构为目的，利用旋转缩放不改变梯度间余弦相似度的特性，达到了在保护隐私的同时，实现准确聚类的想法。其中，本文借助具有强可解释性和收敛速度快的无监督K-means算法实现聚类过程。分簇结束后，为了简单起见，本文假设任意一个用户都有一个公钥加密系统。即簇Euclid Math OneCApj内用户u生成一对公私钥（cpku，csku），并对公钥cpku进行签名，将{u，cpku，σu}发送给ESj。ESj转发给簇Euclid Math OneCApj内其他用户，簇内用户验证所接收的信息。在此后的信息传输过程中，用户u使用Enc（cpku，msg）和Dec（csku，Enc（cpku，msg））对消息msg进行加密和解密，保证信息的安全性。通过CSC算法将两层“云端”架构转变为图3所示的三层“云边端”架构。其中，云服务器、边缘服务器和用户更详细的定义与行为定义如下。

CS：云服务器作为训练任务的承包者，负责初始化训练模型、聚类分层和聚合全局模型。

ESj∈［1，k］：k个边缘服务器作为训练任务的辅助者，管理簇Cj∈［1，k］内的Euclid Math OneUApj个用户，成为云服务器和用户通信的桥梁。主要负责簇内信息转发、接收与聚合。所有的边缘服务器都具备实时处理能力，不会主动退出训练。云服务器和边缘服务器之间不存在合谋行为，并且会诚实地执行协议，但他们可能会试图学习更多的知识，推理用户非公开的隐私信息。

Users：n个用户作为训练任务的参与者，都被赋予一个唯一的ID。他们利用自身私有数据参与FL训练，以提升全局模型最终性能。所有用户遵守方案流程，但对服务器或其他用户发送的信息感到好奇。个别用户可能在利益的驱动下，泄露信息给边缘服务器或其他用户，从而危害目标用户隐私。

3.3 SCFL安全聚合

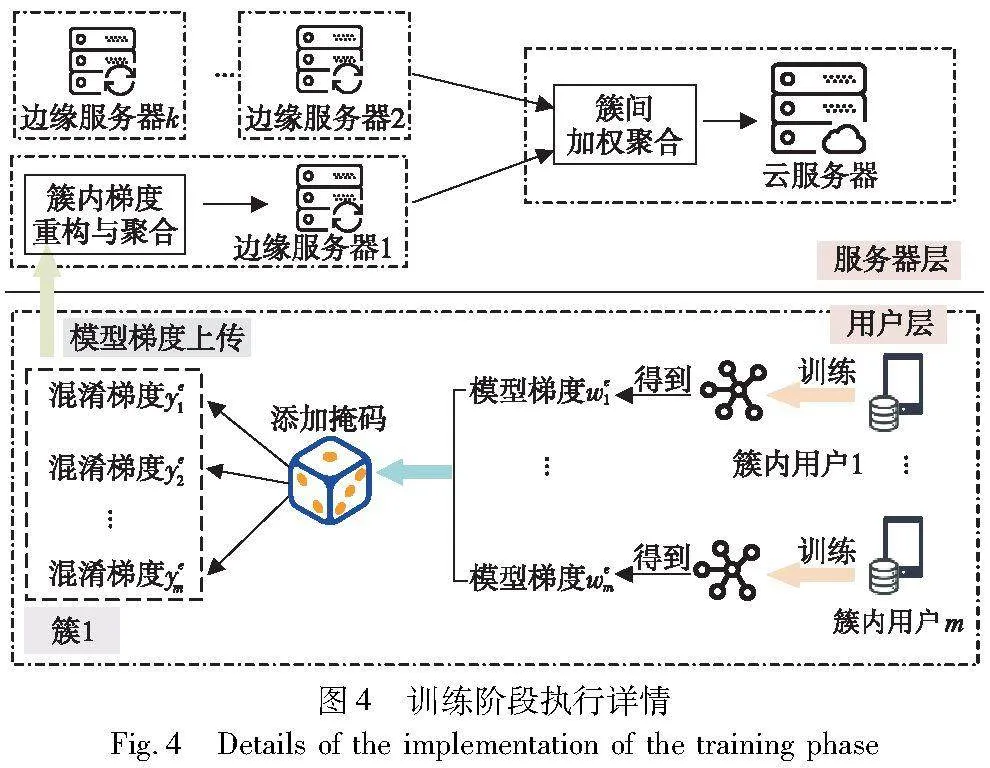
当三层“云边端”架构形成后，SCFL将进入训练阶段。该阶段包括本地训练、梯度信息保护、簇内簇间安全聚合三个组件。如图4所示，假设簇1中有m个用户，簇1中用户i∈［1，m］在得到第e轮本地模型梯度wei后，将添加过掩码的混淆梯度上传给边缘服务器，进而保护模型梯度安全。在有用户离线的状况下，边缘服务器ES1对梯度进行重构并聚合出簇内用户梯度之和。其他簇并行执行同样的操作。ES1，ES2，…，ESk将簇内梯度之和上传给CS，CS加权聚合得到全局梯度。

3.4 在线场景安全聚合协议

为了实现簇内用户随机数的选取，本文设计了一种链式零共享算法，按照簇Euclid Math OneCApj内用户ID大小构建首尾相连的链式结构。用户u生成|Euclid Math OneUApj|/2个随机种子κu，v，并将κu，v分别发给链式结构中位于自己后方的|Euclid Math OneUApj|/2个用户v。同时，接收链式结构中位于自己前方的|Euclid Math OneUApj|/2个用户z分别发送的随机种子κz，u。|Euclid Math OneUApj|为簇Euclid Math OneCApj内用户个数。此后，用户u根据式（13）生成随机数ru。

链式零共享算法有以下三个优势：a）通信与存储开销低。假设某个簇内用户数量为m。每个用户每轮只需要存储m个（m为偶数）或者m+1个（m为奇数）随机种子，相较于文献［36］存储2m个随机种子来说，存储与计算开销降低约50%。b）抗m-2个用户合谋。随机种子个数x∈［1，m］越小，通信与存储开销越小，抗合谋能力越弱。x取「m/2在降低开销的情况下，使安全性达到最优。当敌手想要恢复目标用户的随机数时，他必须与簇内剩下的m-1个用户合谋。c）正确性。随机数之和为0，不影响模型梯度聚合。借助链式零共享算法本文设计了协议1，该协议可简单安全地保护模型梯度，避免隐私泄露问题。

从式（14）可以看出，用户数量越小的簇，在聚合过程中将占有更高的权重。CS根据式（14）得到新一轮的全局聚合后，通过ESj将wg转发给簇内所有用户。

协议1 ：SPFL簇内在线安全聚合方案

3.5 离线场景安全聚合协议

最后，ESj将模型梯度总和ws，j上传至云服务器CS，CS执行与3.1节相同的反向簇间加权聚合策略，以获得新一轮的全局模型wg。

协议2 SPFL簇内离线安全聚合方案

4 安全分析

4.1 安全性

首先，本文采用满足语义安全的公钥加密技术，对于任意的加密密文，具有概率多项式计算能力的恶意敌手，就算拥有密文信息Enc（cpku，m），也不能根据密文信息和公钥cpku推断出明文信息m。由此，在诚实用户私钥不泄露的前提下，信息传输是安全的。其次，本文要证明添加随机数后的掩码梯度是安全的，此时的安全性依赖于引理1，即将随机数添加到梯度中所得梯度与原始梯度看起来是一致随机的。

证明 为了证明定理2，本文使用标准混合论证。这种证明方法主要是从真实视图出发，构造中间一系列满足不可区分性的实验，进而最终归纳出真实视图与模拟视图是不可区分的。

可以观察到，根据式（18），xu+ru的分布与wu+ru的分布相同。所以半诚实敌手的联合视图SIM在计算上与实际执行REAL的视图没有区别，定理2得证。

4.2 完整性

5 实验分析

5.1 实验设置

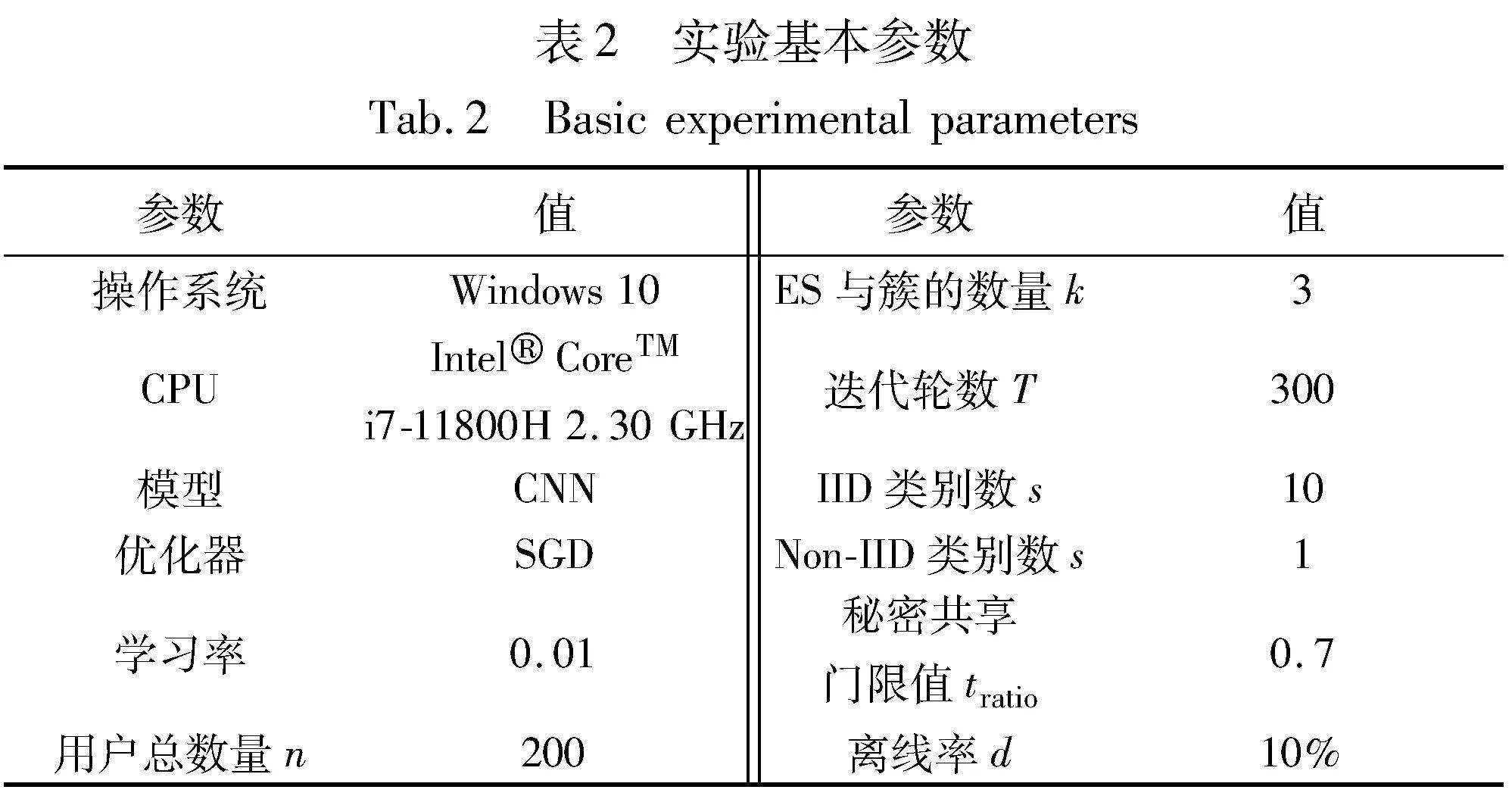
为了更好地衡量性能，本文方案主要是在Python环境下使用gmpy2、密码学库和其他几个标准库实现的。利用BLS库实现签名与验证，加密方案选择了Paillier同态加密库， Shamir秘密共享来完成随机数分发与恢复。实验过程中默认参数设置如表2所示。

SCFL基于MNIST和Fashion-MNIST数据集在卷积神经网络（CNN）上进行了评估。其中，MNIST数据集由手写0～9数字图像组成，包含6万个训练样本和1万个测试样本。Fashion-MNIST数据集由10种类型的灰色衣服图像构成，相较于MNIST来说，图片内容更加多样化、信息更加复杂化、模型训练更具挑战性。每个用户拥有的训练数据集种类记为s，s∈［1，10］。如果s=10，则用户能从MNIST数据集中拿到相同的数据，用户数据分布满足独立同分布（IID），否则，用户数据是Non-IID的。同时，采用文献［7］中提出的深度梯度泄露算法DLG模拟重构攻击，检测梯度的安全性。为了消除结果随机性，进行了多次重复实验并取平均值作为最终结果。为了更好地表现本文方案的准确性与高效性，依次选取联邦平均FedAvg［1］、聚类分层FLHC［16］、FedDK［28］、掩码保护PPML［30］和PVFL［36］五个方案进行比对。

5.2 准确度

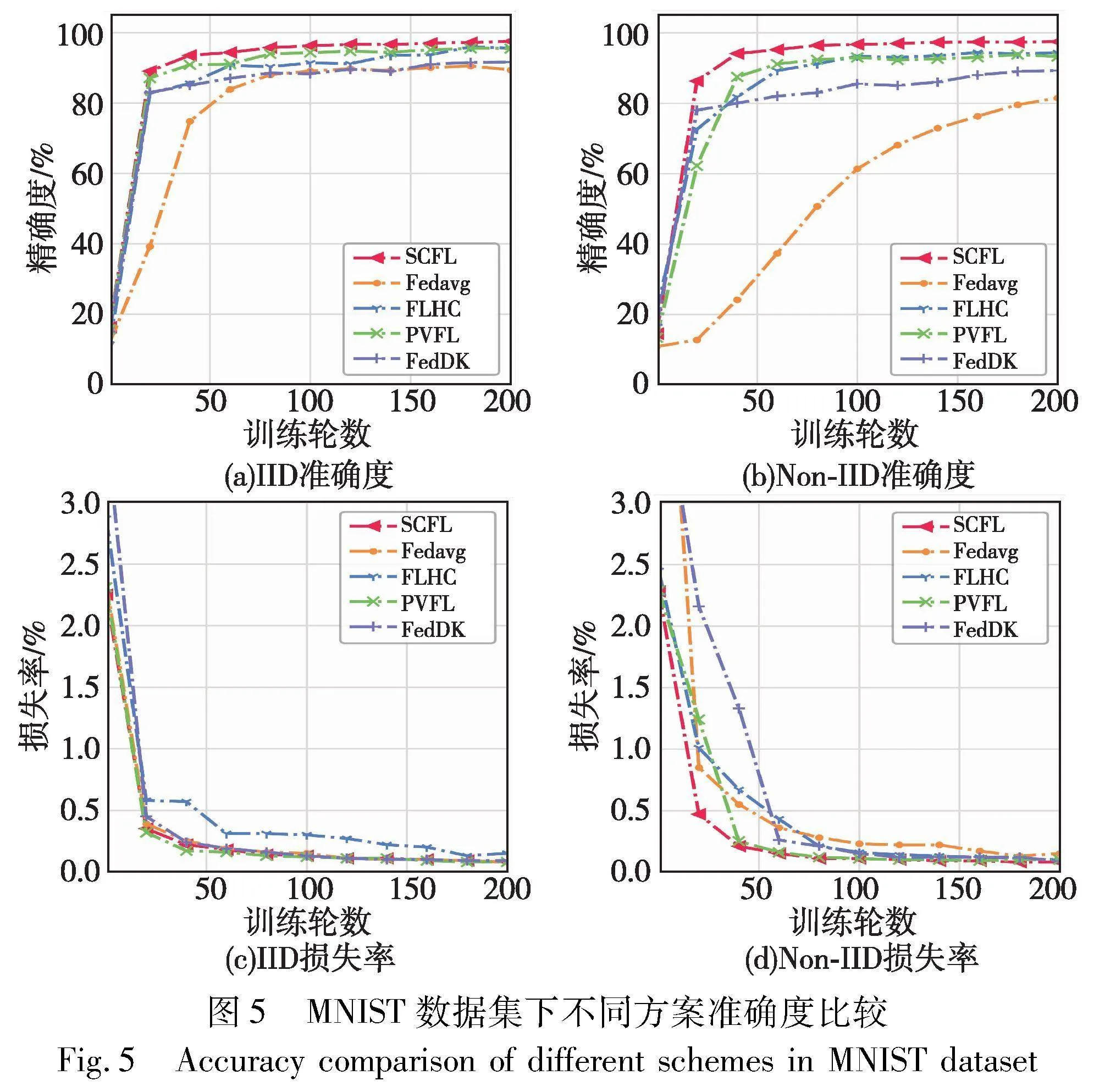
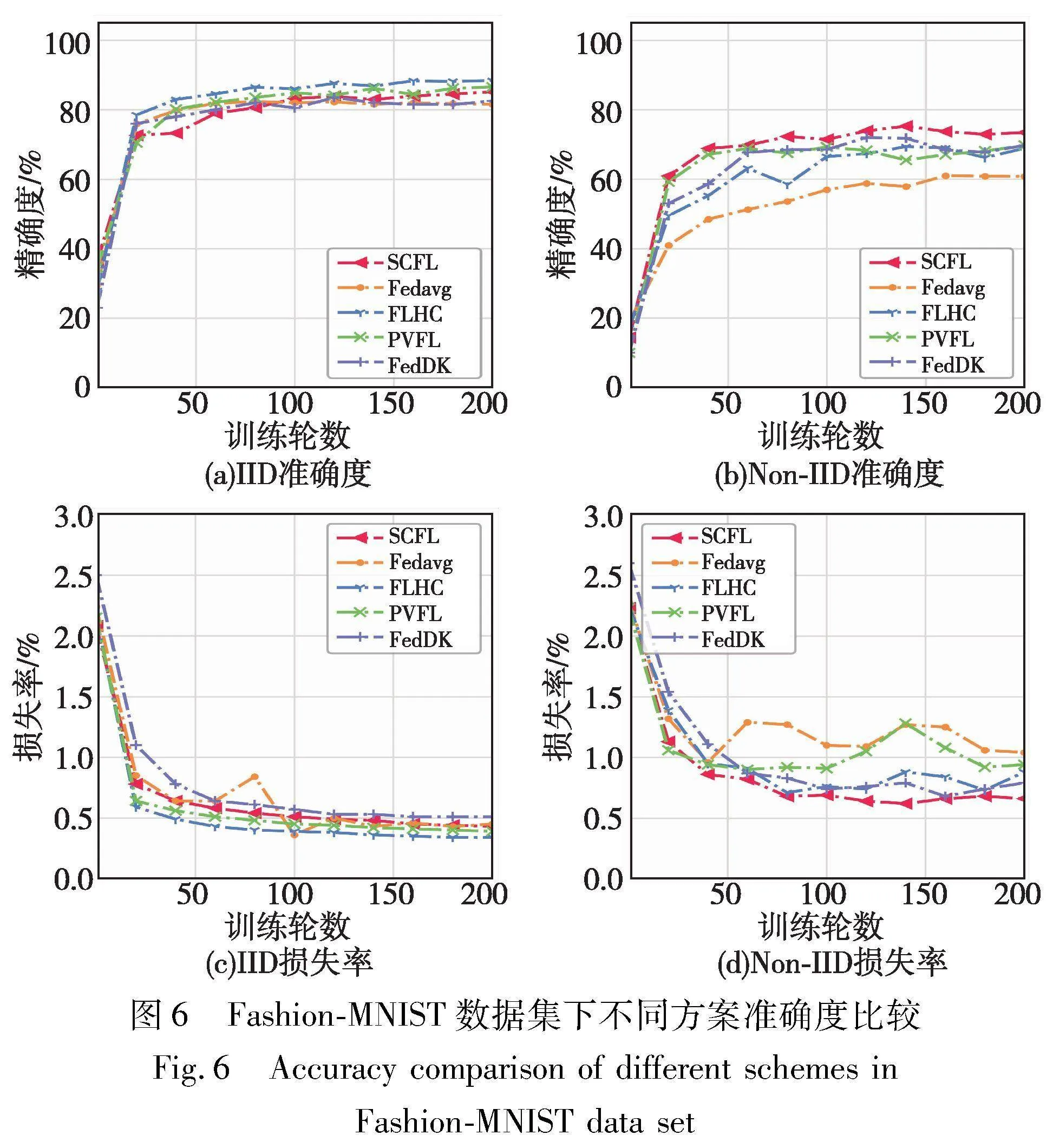
首先，为了评估SCFL方案的正确性与准确性，根据5.1节的实验设置，比较了SCFL离线协议与FLHC、FedDK 、FedAvg和PVFL方案在IID和Non-IID数据集上的性能。前三个方案并不适用于离线场景，设置该部分实验的离线率d为0。图5显示了五个方案在MNIST数据集下，各个方案能够达到的最高模型精度和模型损失率。从图5（a）可以观察到，在IID数据分布下，SCFL与采用聚类分层的FedDK和FLHC方案的准确度几乎接近，准确度都比FedAvg提升约5%；与隐私保护方案的PVFL相比，SCFL的准确度有所提高。图5（b）为Non-IID分布，FedAvg方案的准确度明显下降，且增长幅度也较为平缓。本文SCFL方案相较于FLHC、FedDK 、PVFL和FedAvg方案来说，准确度分别提升了3.13%、8.18%、4.16%和16.03%。据分析，FLHC、FedDK和PVFL方案在MNIST数据集的设置下准确度变化不大的原因如下：FedDK与FLHC方案采用聚类分层来缓解Non-IID数据的影响，簇内训练有利于梯度的累计，增强数据关联性，而PVFL方案采用了加权聚合的方法改善了异构数据的不利影响，相较于FedAvg方案均能较好地提高模型性能。不同方案最终的模型损失率如图5（c）～（d）所示，SCFL在不同设置下损失率均最小，进而证明了本文方案预测正确的概率更高。此外，本文在Fashion-MNIST数据集上也进行了评估。如图6（a）所示，在IID设置下四种方案的准确度都能达到80%以上，且如图6（c）所示的损失率均呈现较为稳定的趋势。然而，由于样本多样化及数据不平衡分布，如图6（b）所示，在Non-IID设置下所有算法性能均有明显下降，降低幅度约在10%～20%。在该数据分布下，SCFL方案的准确度与FLHC、FedDK 、PVFL和FedAvg方案相比，准确度分别提升了4.52%、3.71%、3.68%和12.64%。据本文分析，数据之间的差异将严重影响模型的聚合结果，使用了聚类的方案，均能够在一定程度上抵御异构的数据，而SCFL借助算力较强的云服务器计算两两用户之间的余弦相似度，以提升计算速度。此外，图6（d）显示SCFL的损失率低于其他方案，相对稳定的损失率反映了在该方案下模型与实际数据之间的差异。从以上两个数据集的实验结果可以看出， SCFL在处理Non-IID数据时比其他方案具有更好的性能。

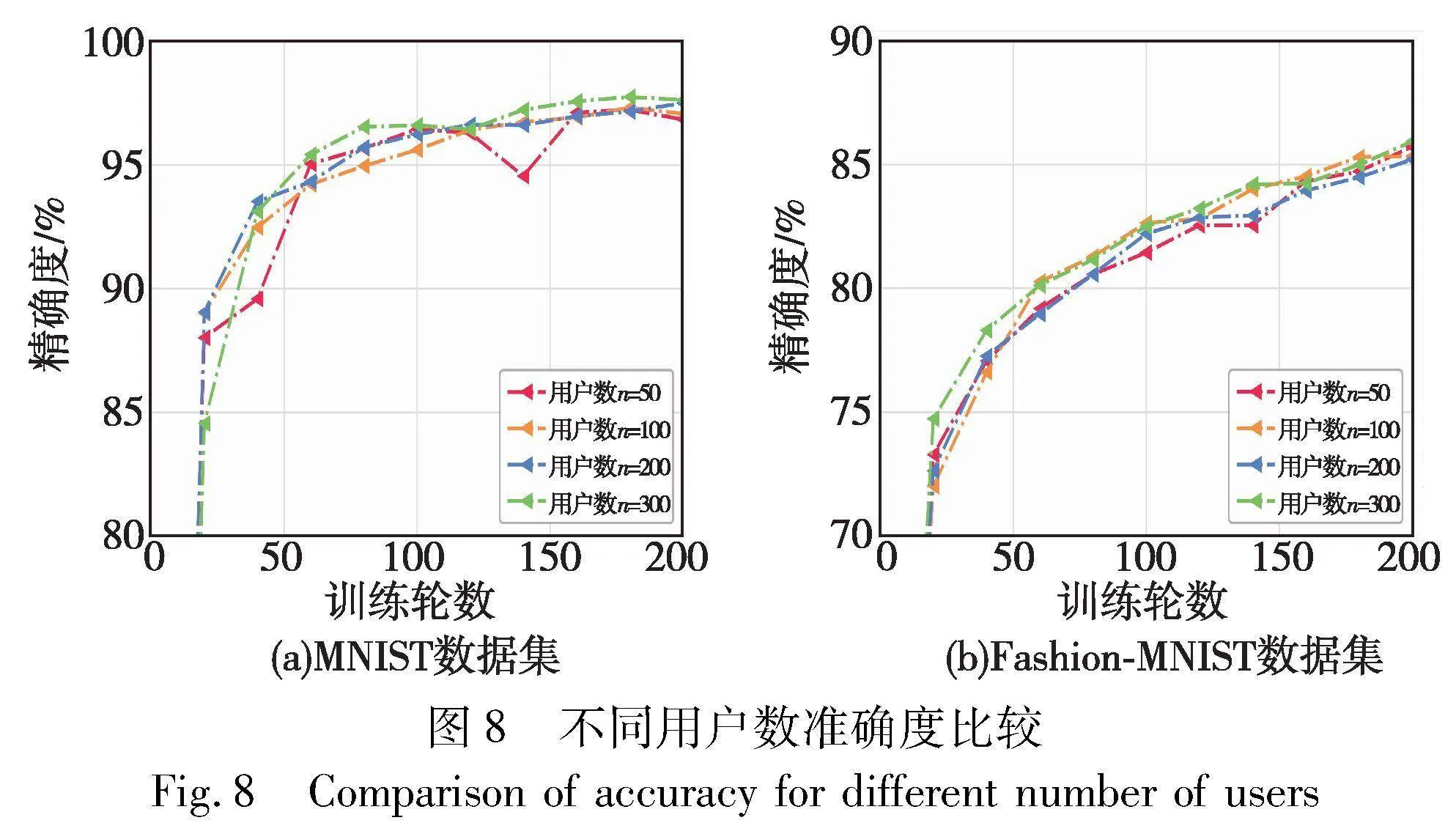
为了比较用户数量对模型准确度的影响，本文在IID情况下，分别测试了SCFL在MNIST和Fashion-MNIST数据集上的性能表现，如图8（a）（b）所示。通过将用户总数从50增加至300，观察SCFL能够达到的最优准确度。从图8（a）可以看出，MNIST数据集下，用户数量的增长对模型准确率起到了积极作用。50与300个用户时的准确度相差约2%。但是，如图8（b）所示，在Fashion-MNIST数据集下，用户数量与模型准确度之间的线性关系不太明显，最优准确度与最差准确度仅相差约0.6%。

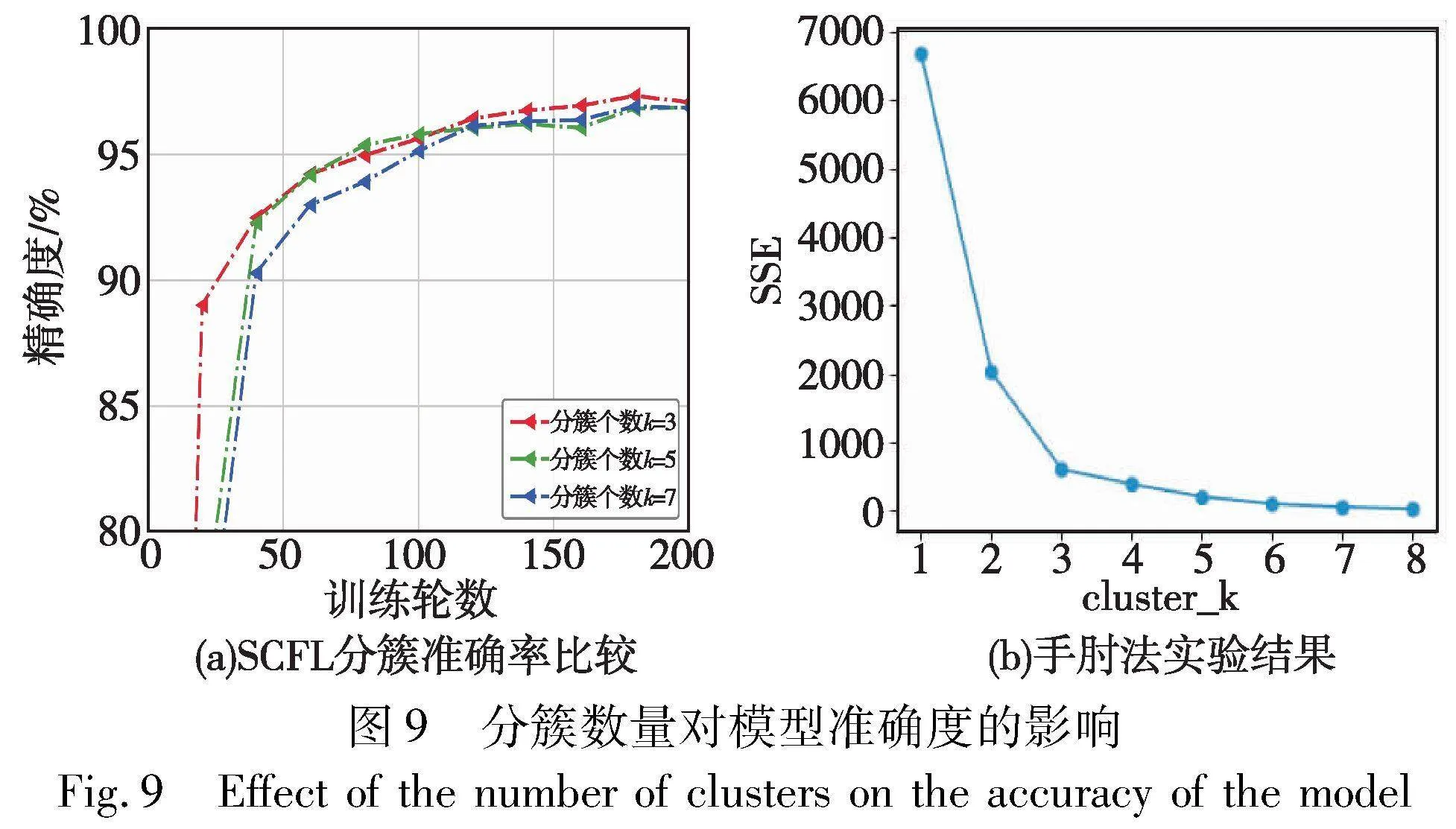
此外，本文还评估了边缘服务器个数对模型精度的影响。图9（a）显示了SCFL在MNIST数据集下，边缘服务器个数k分别为3、5、7时模型的精确度。k值越大则边缘服务器管理的簇内用户越少，通信及聚合压力也就越小。图9（b）通过手肘法计算最优的分簇个数应为k=3，与图9（b）相结合可以观察到，当k=3时SCFL准确度最高。对于这个实验结果本文认为，k值越大则簇内设备的个数越少，簇内数据集特征分布越相似，云服务器在聚合边缘局部梯度时并不能很好地权衡数据样本，使得模型特征融合略差。但从实验数据上看最低与最优精度相差约1%，实现了SCFL算法的稳定性。在精度范围变化不大的前提下，k值增大有利于减轻各个边缘服务器的通信压力。

最后，为了验证旋转与缩放并不会改变用户梯度间的余弦相似度。本文特地选择了10个用户，设置为Non-IID数据。首次模型训练后，比较原始梯度与旋转缩放后的余弦相似度结果，以热力图的形式展示在图10中。其中，图10（a）显示的是原始梯度间的余弦相似度，图10（b）显示的是旋转缩放后梯度间的余弦相似度，可以看出，梯度的旋转缩放操作并不会改变两两用户之间的相似度，表明旋转缩放策略对梯度隐私保护的正确性与可行性。与此同时，由热力图可知，数据的异构性直接决定了余弦相似度，余弦相似度越高说明数据越相似，余弦相似度越低则说明数据差异性越大。

5.3 抵御重构攻击

为了验证经过旋转与缩放的梯度和添加随机数的梯度是否能抵御重构攻击，本文复现了DLG算法来验证梯度信息是否能被安全的保护。当模型梯度泄露时，利用DLG算法不断最小化虚拟数据梯度与真实训练数据梯度之间的差距，以窃取更多隐私数据。图11（a）显示的是未经变化的初始梯度，经过DLG算法多次迭代后，在20轮左右逐渐恢复出原始数据大致轮廓，迭代至100轮后大量干扰噪声已被去除，真实数据被恢复。如图11（b）（c）所示，经过旋转缩放或添加零共享随机数的梯度，置于DLG算法中迭代100轮也无法根据梯度重构出原始数据信息。对于模型梯度获得者来说，其所得到的信息与随机数没有差别。在SCFL中，边缘服务器与云服务器最终得到的是用户模型梯度之和，为此，本文检测了梯度之和是否会间接泄露用户信息，如图11（d）所示。实验结果表明，聚合结果并不会泄露某个特定用户的隐私信息。

5.4 计算与通信开销

在比较计算与通信开销时，存在一个假设：PPML、PVFL和SCFL方案中共有n个用户，且SCFL在初始化阶段不分簇，即k=1，这样能够更加直观清晰地比较出三个方案之间的性能差异。实际上，基于Non-IID数据集的应用场景，分簇将使簇内用户数量均远小于n，并行执行能达到更高的性能。

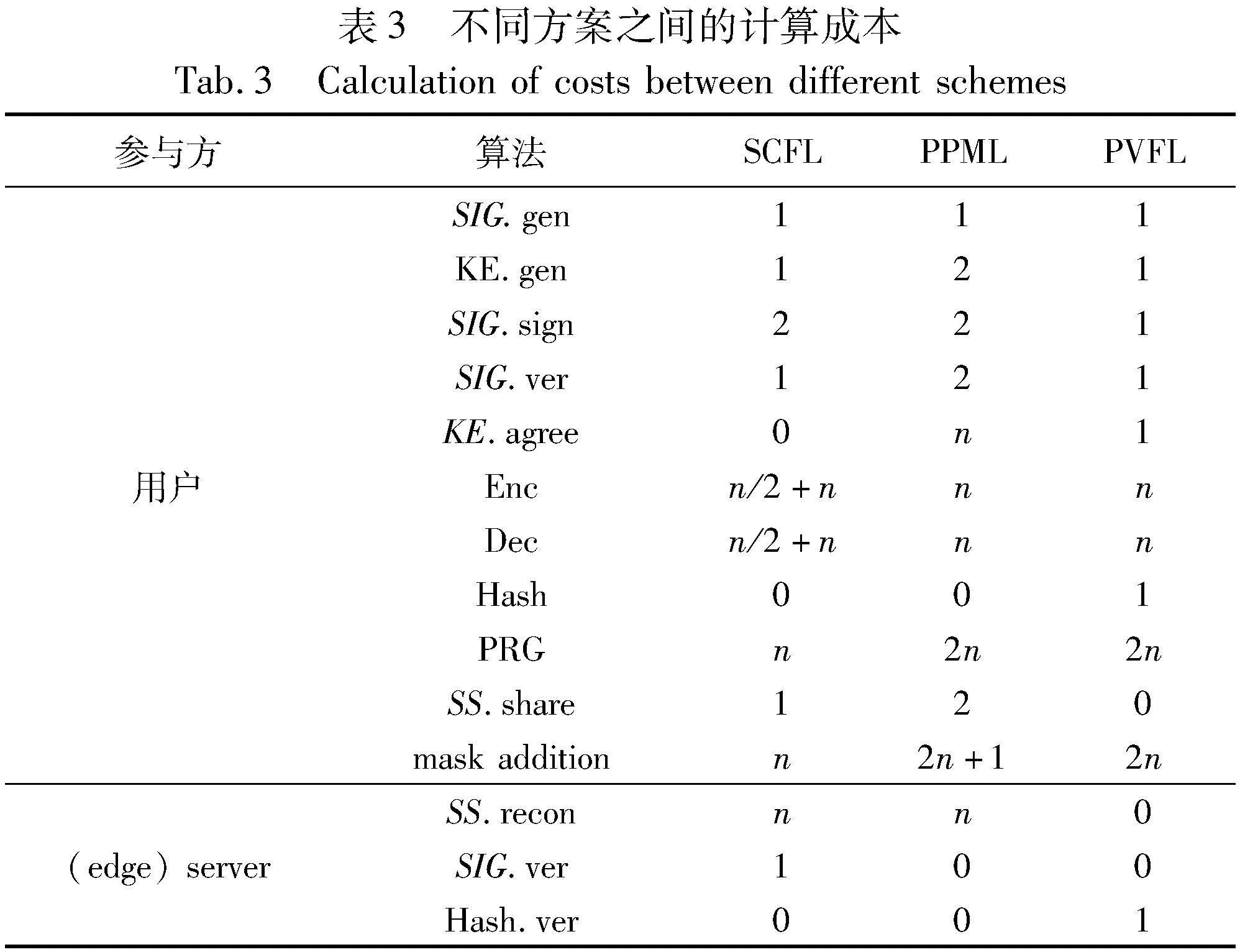
a）计算开销。表3列出了SCFL协议2、PPML与PVFL各模块在一轮中被调用的次数。SCFL中每个用户的计算成本主要取决于：（a）加解密n/2个随机种子和n个随机数子份额；（b）对随机数r进行（t，n）秘密共享。因此，用户的总计算复杂度为O（n）。边缘服务器的计算开销分为离线用户随机数秘密重构与模型梯度聚合，因此计算开销为O（n）。根据表3，本文可以观察到SCFL相较于PPML来说，SS.share和Mask Addition算法的效率都提升了一半。SCFL在随机数生成算法中比PVFL更高效，减少了一半的计算开销。较低的计算开销可以提高用户的响应速度，增加系统模型的准确率。

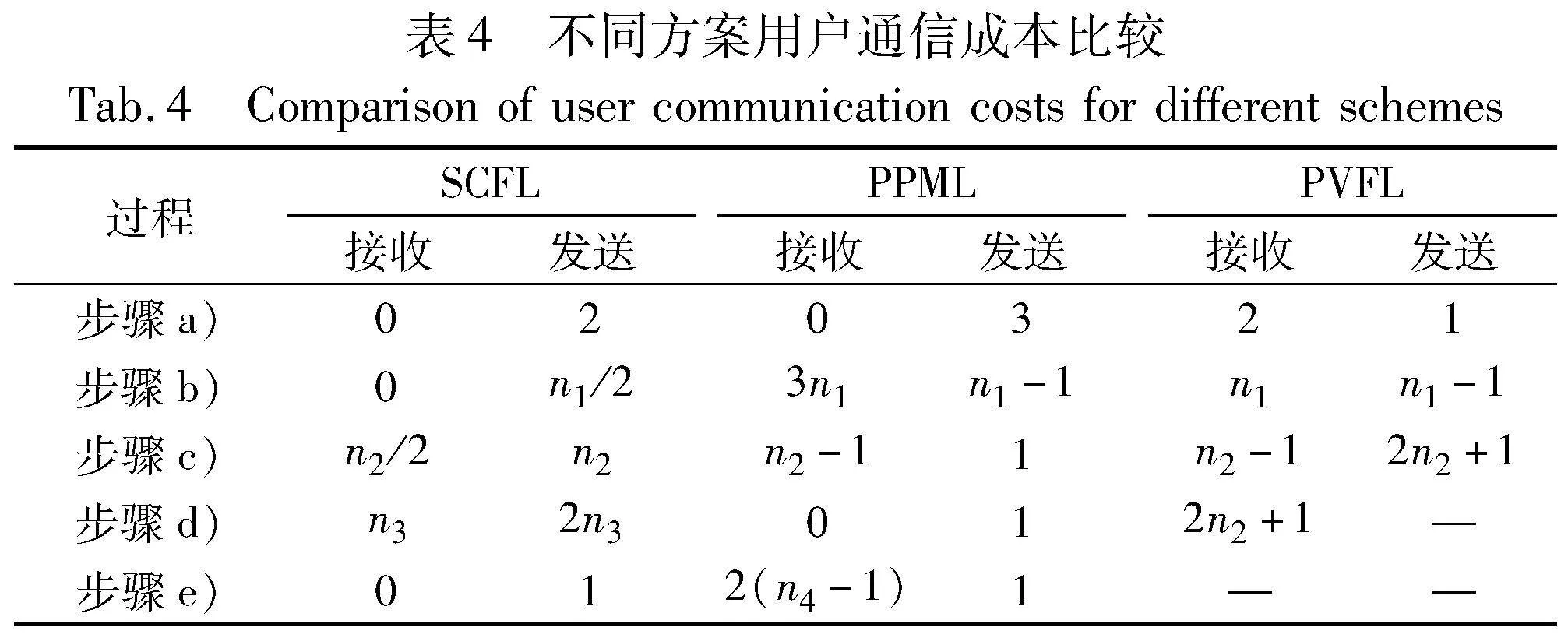
b）通信开销。在表4中，SCFL协议2的每一轮通信成本与PPML、PVFL方案进行了比较。边缘服务器在线用户集合转发并没有列在表4中，因为边缘服务器转发成本与用户接收成本是相同的。其中，值得说明的是ni=|Euclid Math OneUApi|（i=1，2，3）表示每一步在线用户集合大小。PVFL在步骤a）阶段收到来自可信第三方发送的加密密钥与签名密钥。从表4可明显看出，SCFL中接收的信息量远小于其他两个方案，特别是在步骤b）阶段。与其他两个方案相比，通信成本降低2～3倍。在SCFL中，步骤b）～d）分别生成随机数、共享子份额和掩码梯度，导致用户发送量有所增加。但综合对比每一轮次（步骤a）～e））的接收与发送成本能够发现，与PPML和PVFL相比，SCFL每一轮的通信开销降低了约30%。总的来说， 通信与计算占优的SCFL方案更加适用于大规模训练场景，且更高效、快速。

5.5 运行时间

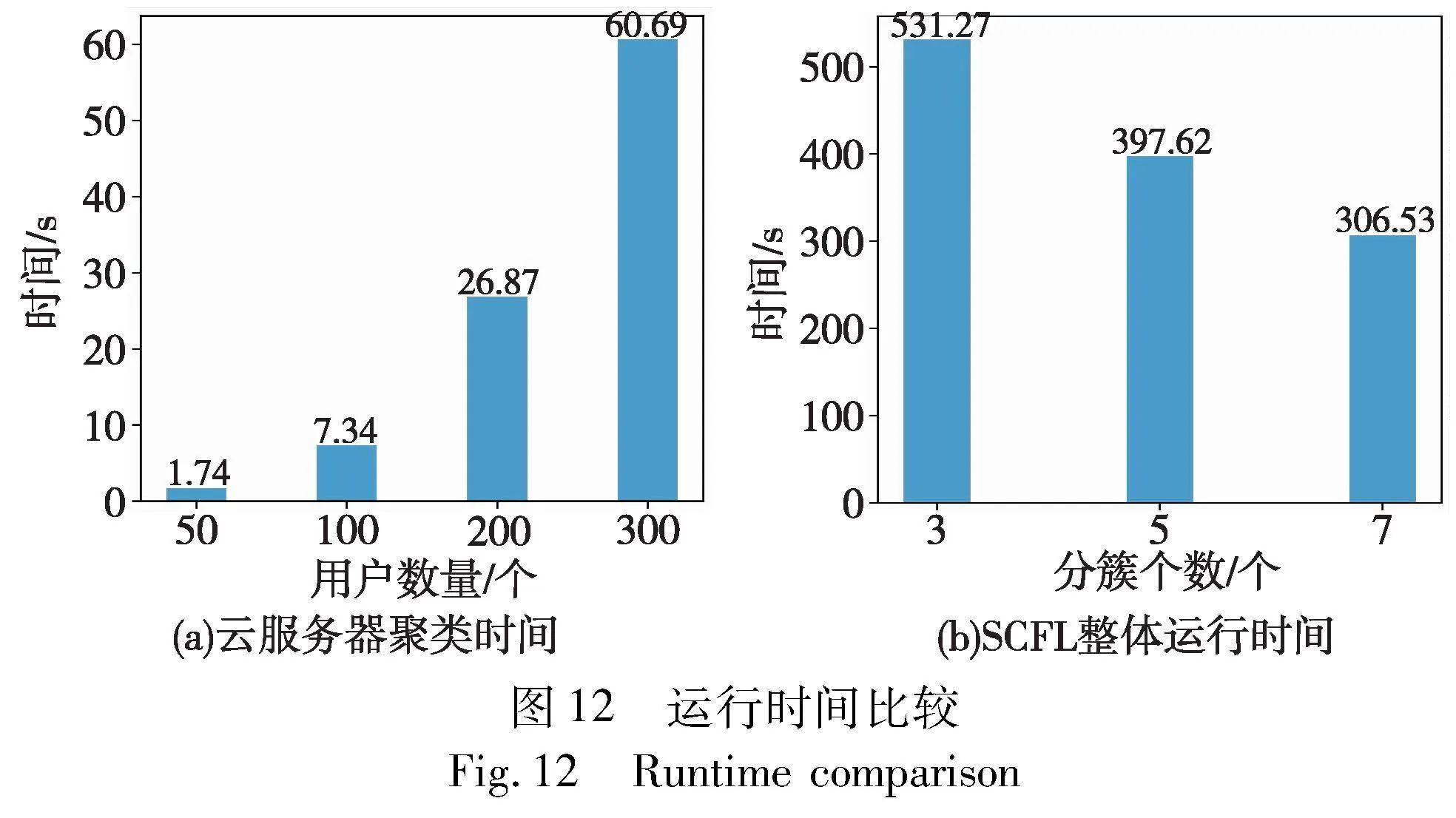
最后，本文比较了聚类与聚合分别需要的运行时间。首先图12（a）展示了分簇个数k=3时，用户数从50增长到300，云服务器完成聚类所需的运行时间。从图中可以看出，随着用户数量的增长，聚类时间直线上升。这是由于云服务器要计算两两用户之间的余弦相似度，时间复杂度为O（n2）。但是，聚类仅在初始化时执行一次，其分层结果将极大地降低聚合阶段的运行时间。SCFL整体运行时间与分簇个数k成反比，如图12（b）所示。其中，用户数n=300、迭代轮数T=300，分簇个数k分别取3，5，7。

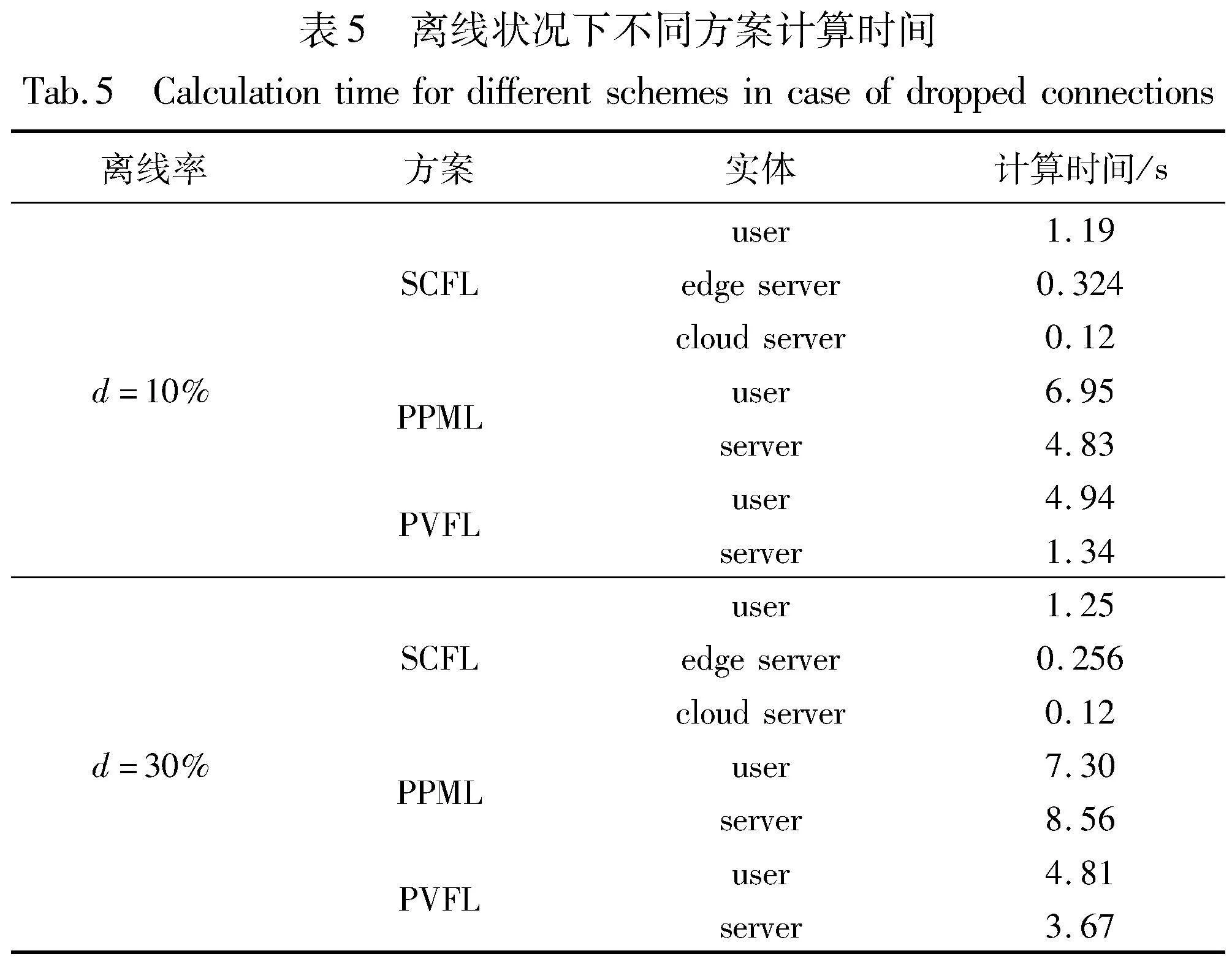
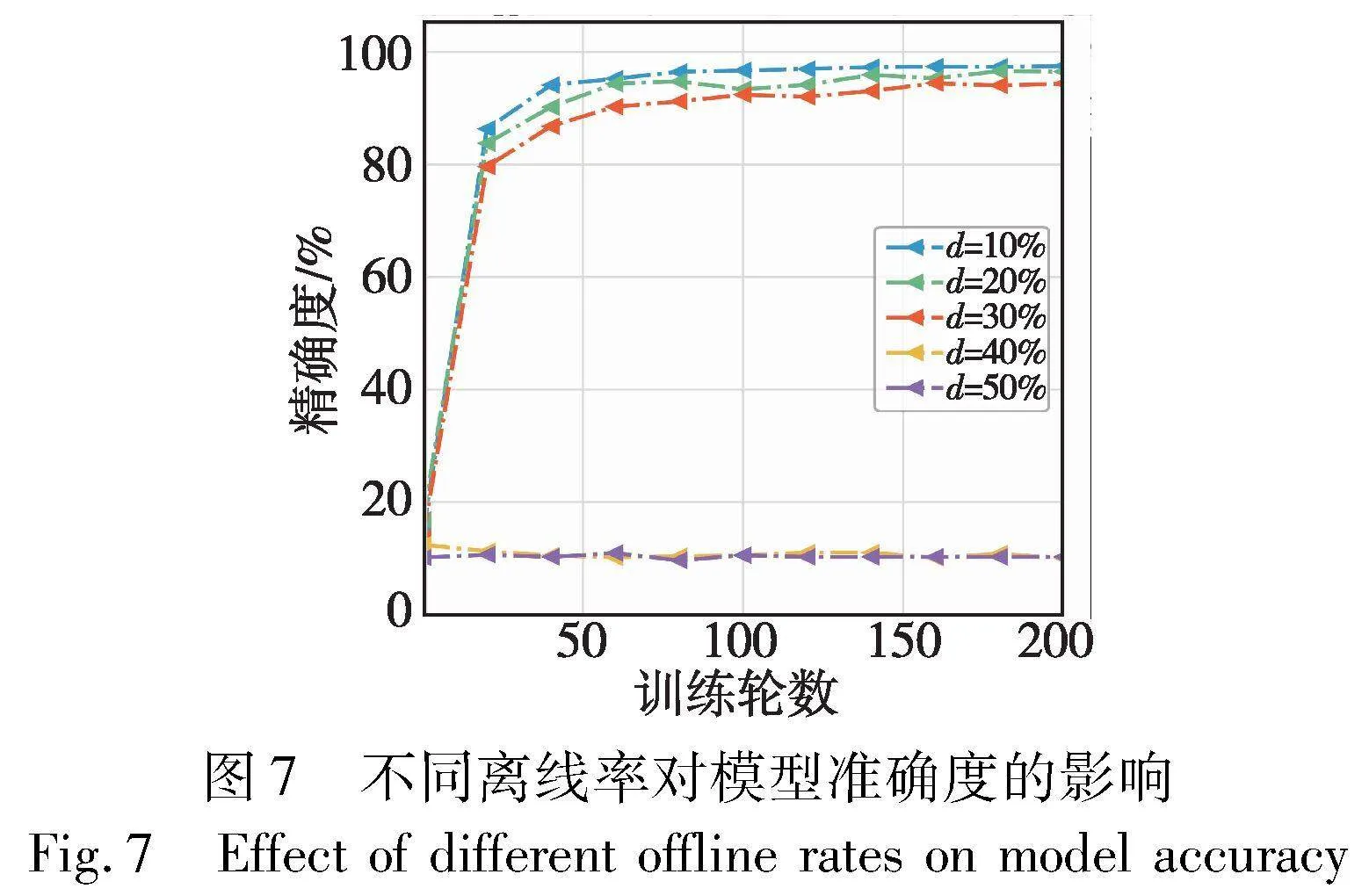
除此之外，本文还评估了n=200时，不同离线率下SCFL、PPML和PVFL方案聚合一次所需要的运行时间。所有方案的秘密共享门限率tratio=0.7，SCFL中的边缘服务器个数为3，则不同簇Euclid Math OneCApj的门限值t=tratio×nj，nj=|Euclid Math OneCApj|。本文测试了离线率d=10%和30%时三个算法的执行一轮的计算时间。在表5中，云服务器的计算时间仅为训练阶段的聚合时间，其聚合时间与模型大小和边缘服务器个数有关，当边缘服务器个数k=3时，聚合时间仅需要0.12 s。当离线率d=10%时，边缘服务器计算时间反而略高于离线率d=30%，这是因为离线率越低时在线用户数量就越多，边缘服务器所需要等待和处理的时间就将更长。值得注意的是，表5记录的SCFL边缘服务器计算时间为多个边缘服务器并行计算所需的最长时间。每个边缘服务器管理的用户数远小于200，进而在零共享、秘密共享、梯度重构与聚合过程中所需的时间均会减少。总体看来，SCFL所需的时间远远短与其他两个方案，在离线率为10%时，聚合时间分别缩短约7.23倍和3.85倍。除去边缘服务器并行执行、簇内用户数量少这些原因，与PPML相比，SCFL减少了密钥协商和秘密共享的时间；与PVFL相比，SCFL随机数选取次数缩短了一半。

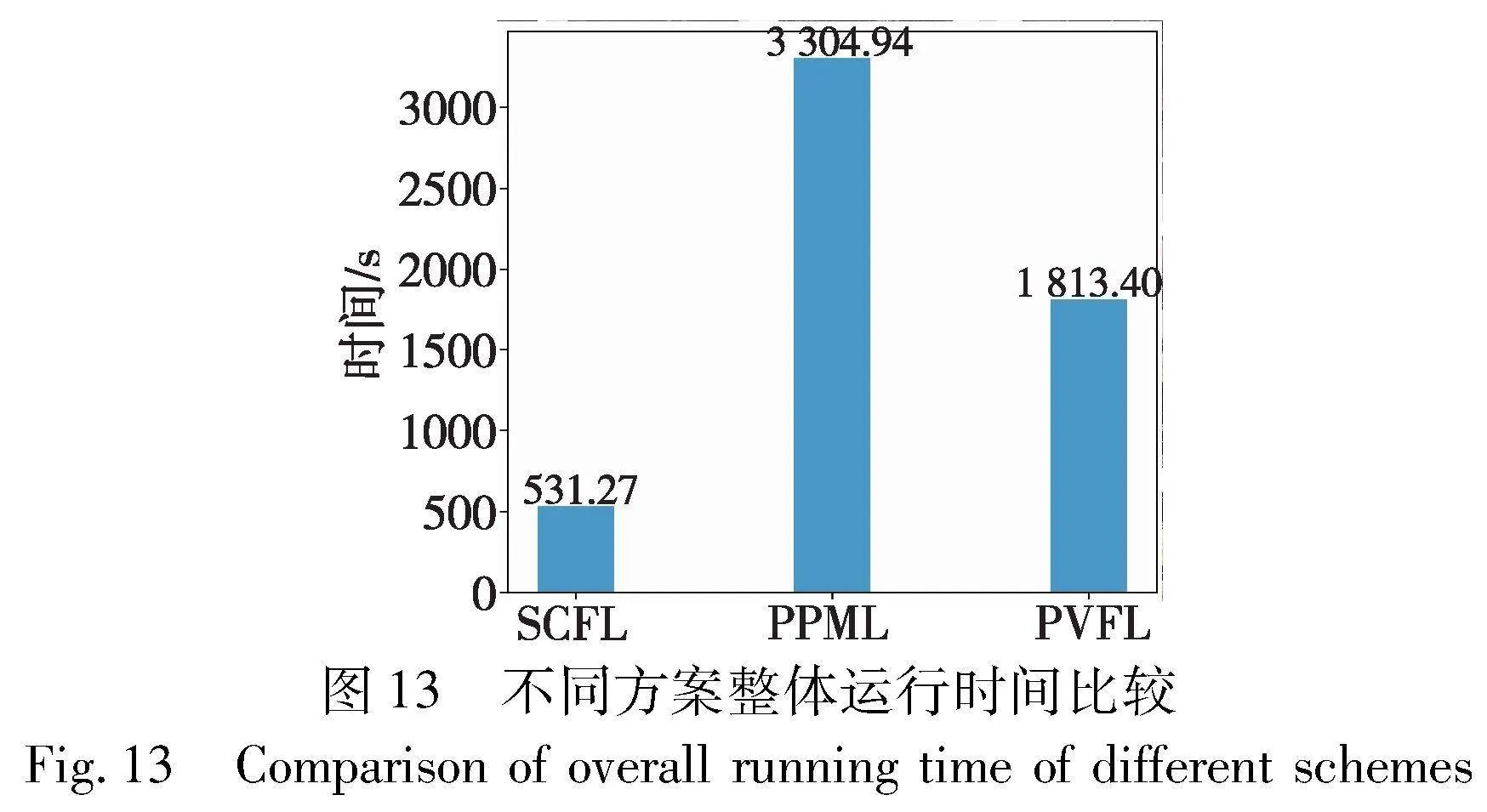
图13显示了在300名用户参与的情况下，进行200次迭代训练，SCFL、PPML和PVFL所需的整体运行时间。其中SCFL的分簇个数k=3，三个方案的离线率d=10%。从图中可以明显看出，SCFL的整体运行时间相较于其他方案约提升3～6倍。主要原因是分簇降低了簇内用户数量，边缘服务器分摊聚合压力；其次是因为簇内掩码生成速度较快。尽管SCFL在聚类阶段需要花费60.69 s进行用户聚类，但为后续的并行执行提供了基础，从而提高了整体运行效率。

6 结束语

本文同时关注了Non-IID数据和安全聚合的问题，提出了一种在聚类和聚合阶段均保护梯度隐私且对用户离线具有鲁棒性的FL方案。为了解决偏差问题和提高训练效率，综合四元数旋转、向量缩放、边缘计算架构实现对模型梯度的保护和训练架构重建。边缘计算“云边端”三层架构降低了通信和计算成本，加快了用户请求的处理速度。其次，本文设计了一种巧妙的零共享方案，采用单掩码策略提升运行效率，保护梯度安全性。针对用户动态离线情况，使用秘密共享技术，保证离线用户的随机数也能够被消除，进而实现正确聚合。一种反向簇间加权聚合策略被设计并应用于云服务器上，以解决簇间用户数量不平衡导致的模型偏离问题。因此，本文方案更适合动态、异构的大规模应用场景，在保证系统安全性的同时进行轻量、简单、有效的FL训练。

参考文献：

［1］McMahan B， Moore E， Ramage D， et al. Communication-efficient learning of deep networks from decentralized data［C］//Proc of the 20th International Conference on Artificial Intelligence and Statistics.［S.l.］： PMLR， 2017： 1273-1282.

［2］Han Mu， Xu Kai， Ma Shidian， et al. Federated learning-based tra-jectory prediction model with privacy preserving for intelligent vehicle［J］. International Journal of Intelligent Systems， 2022，37（12）： 10861-10879.

［3］Xu Jie， Glicksberg B S， Su Chang， et al. Federated learning for healthcare informatics［J］. Journal of Healthcare Informatics Research， 2021， 5： 1-19.

［4］Zheng Xiao， Shah S B H， Bashir A K， et al. Distributed hierarchical deep optimization for federated learning in mobile edge computing［J］. Computer Communications， 2022，194： 321-328.

［5］Vogels T， He L， Koloskova A， et al. Relaysum for decentralized deep learning on heterogeneous data［C］//Proc of Advances in Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2021： 28004-28015.

［6］Zhu Hangyu， Xu Jinjin， Liu Shiqing， et al. Federated learning on Non-IID data： a survey［J］. Neurocomputing， 2021， 465： 371-390.

［7］Zhu Ligeng， Liu Zhijian， Han Song. Deep leakage from gradients［C］//Proc of the 33rd International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2019： 14774-14784.

［8］Hitaj B， Ateniese G， Perez-Cruz F. Deep models under the GAN： information leakage from collaborative deep learning［C］//Proc of ACM SIGSAC Conference on Computer and Communications Security. New York： ACM Press， 2017： 603-618.

［9］Luo Xinjian， Wu Yuncheng， Xiao Xiaokui， et al. Feature inference attack on model predictions in vertical federated learning［C］//Proc of the 37th International Conference on Data Engineering. Pisca-taway， NJ： IEEE Press， 2021： 181-192.

［10］Malekzadeh M， Borovykh A， Gündüz D. Honest-but-curious nets： sensitive attributes of private inputs can be secretly coded into the classifiers’ outputs［C］//Proc of ACM S6e6QfPC5fO6F8T4nG3cgyQ==IGSAC Conference on Computer and Communications Security. New York： ACM Press， 2021： 825-844.

［11］Li Tian， Sahu A K， Zaheer M， et al. Federated optimization in heterogeneous networks［EB/OL］.（2020-04-21）. https：//arxiv.org/abs/1812.06127.

［12］Yu Feng， Lin Hui， Wang Xiaoding， et al. Communication-efficient personalized federated meta-learning in edge networks［J］. IEEE Trans on Network and Service Management， 2023，20（2）： 1558-1571.

［13］Cheng Yanyu， Lu Jianyuan， Niyato D， et al. Federated transfer lear-ning with client selection for intrusion detection in mobile edge computing［J］. IEEE Communications Letters， 2022，26（3）： 552-556.

［14］Smith V， Chiang C K， Sanjabi M， et al. Federated multi-task lear-ning［C］//Proc of the 31st International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2017： 4427-4437.

［15］Sattler F， Muller K R， Samek W. Clustered federated learning： mo-del agnostic distributed multitask optimization under privacy constraints［J］. IEEE Trans on Neural Networks and Learning Systems， 2020， 32（8）： 3710-3722.

［16］Briggs C， Fan Zhong， Andras P. Federated learning with hierarchical clustering of local updates to improve training on Non-IID data［C］//Proc of International Joint Conference on Neural Networks. Pisca-taway， NJ： IEEE Press， 2020： 1-9.

［17］Zhang Yanci， Yu Han. Towards verifiable federated learning［C］//Proc of the 31st International Joint Conference on Artificial Intelligence. 2022： 5686-5693.

［18］徐晨阳， 葛丽娜， 王哲， 等. 基于差分隐私保护知识迁移的联邦学习方法［J］. 计算机应用研究， 2023，40（8）： 2473-2480. （Xu Chenyang，Ge Lina，Wang Zhe，et al. A federated learning approach based on differential privacy-preserving knowledge transfer［J］. Application Research of Computer， 2023，40（8）： 2473-2480.）

［19］Hu Yuke， Liang Wei， Wu Ruofan， et al. Quantifying and defending against privacy threats on federated knowledge graph embedding［C］//Proc of ACM Web Conference 2023. New York： ACM Press， 2023： 2306-2317.

［20］Moriai S. Privacy-preserving deep learning via additively homomorphic encryption［C］//Proc of the 26th Symposium on Computer Arithmetic. Piscataway， NJ： IEEE Press， 2019： 198.

［21］Ma Jing， Naas S A， Sigg S， et al. Privacy-preserving federated lear-ning based on multi-key homomorphic encryption［J］. International Journal of Intelligent Systems， 2022，37（9）： 5880-5901.

［22］Wang Rui， Lai Jinshan， Zhang Zhiyang， et al. Privacy-preserving federated learning for internet of medical things under edge computing ［J］. IEEE Journal of Biomedical and Health Informatics， 2022，27（2）： 854-865.

［23］Xie Lunchen， Liu Jiaqi， Lu Songtao， et al. An efficient learning framework for federated XGBoost using secret sharing and distributed optimization［J］. ACM Trans on Intelligent Systems and Technology， 2022， 13（5）： 1-28.

［24］Zhang Yu， Duan Moming， Liu Duo， et al. CSAFL： a clustered semi-asynchronous federated learning framework［C］//Proc of International Joint Conference on Neural Networks. Piscataway， NJ： IEEE Press， 2021： 1-10.

［25］Morafah M， Vahidian S， Wang Weijia， et al. FLIS： clustered federated learning via inference similarity for Non-IID data distribution［J］. IEEE Open Journal of the Computer Society， 2023， 4： 109-120.

［26］Shu Jiangang， Yang Tingting， Liao Xinying， et al. Clustered federated multi-task learning on Non-IID data with enhanced privacy［J］. IEEE Internet of Things Journal， 2022，10（4）： 3453-3467.

［27］Chen Junbao， Xue Jingfeng， Wang Yong， et al. Privacy-preserving and traceable federated learning for data sharing in industrial IoT applications［J］. Expert Systems with Applications， 2023， 213： 119036.

［28］常黎明， 刘颜红， 徐恕贞. 基于数据分布的聚类联邦学习［J］. 计算机应用研究， 2023，40（6）： 1697-1701. （Chang Liming， Liu Yanhong， Xu Shuzhen. Clustered federated learning based on data distribution［J］. Application Research of Computer， 2023， 40（6）： 1697-1701.）

［29］刘艺璇， 陈红， 刘宇涵，等. 联邦学习中的隐私保护技术［J］. 软件学报， 2022，33（3）： 1057-1092. （Liu Yixuan， Chen Hong， Liu Yuhan， et al. Privacy-preserving techniques in federated learning［J］. Journal of Software， 2022， 33（3）： 1057-1092.）

［30］Bonawitz K， Ivanov V， Kreuter B， et al. Practical secure aggregation for privacy-preserving machine learning［C］//Proc of ACM SIGSAC Conference on Computer and Communications Security. New York： ACM Press， 2017： 1175-1191.

［31］李文亮. 四元数矩阵［M］. 长沙： 国防科技大学出版社， 2002： 1-12. （Li Wenliang. Quaternion matrices［M］. Changsha： National University of Defense Technology Press， 2002： 1-12.）

［32］陈宛桢， 张恩， 秦磊勇， 等. 边缘计算下基于区块链的隐私保护联邦学习算法［J］. 计算机应用， 2023， 43（7）： 2209-2216. （Chen Wanzhen， Zhang En， Qin Leiyong， et al. Privacy-preserving federated learning algorithm based on blockchain in edge computing［J］. Journal of Computer Applications， 2023， 43（7）： 2209-2216.）

［33］Shamir A. How to share a secret［J］. Communications of the ACM， 1979， 22（11）： 612-613.

［34］Song Jingcheng， Wang Weizheng， Gadekallu T R， et al. EPPDA： an efficient privacy-preserving data aggregation federated learning scheme［J］. IEEE Trans on Network Science and Engineering， 2023，10（5）： 3047-3057.

［35］Goldreich O， Goldwasser S， Micali S. How to construct random functions［J］. Journal of the ACM， 1986， 33（4）： 241-264.

［36］Zhou Hao， Yang Geng， Huang Yuxian， et al. Privacy-preserving and verifiable federated learning framework for edge computing［J］. IEEE Trans on Information Forensics and Security， 2023， 18： 565-580.