基于嵌套剖分的位姿图分层优化算法

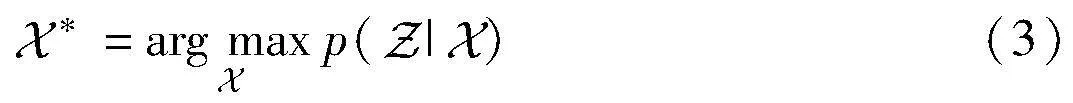
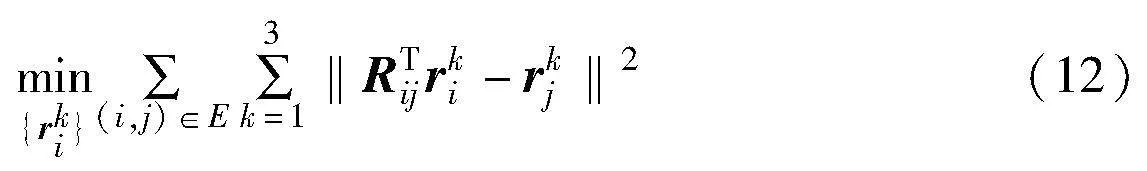
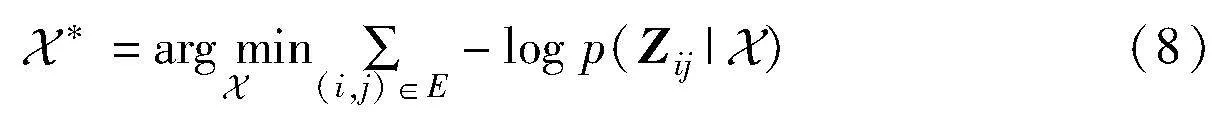
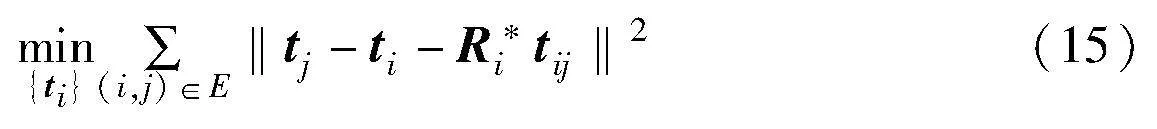
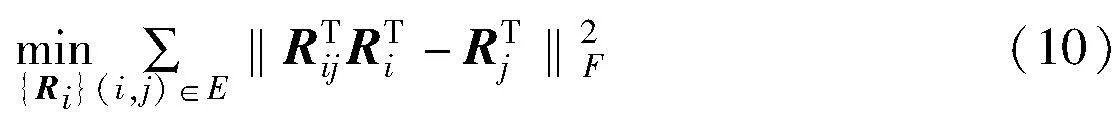
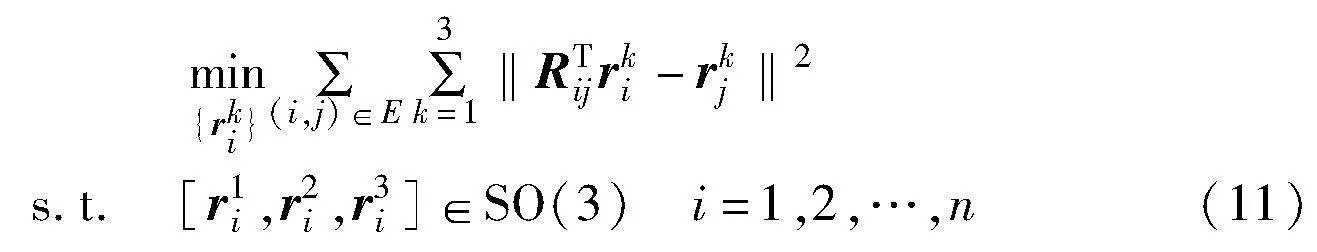
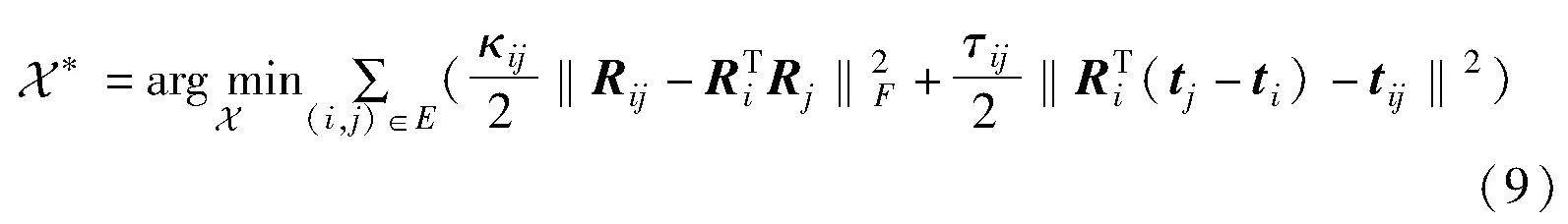
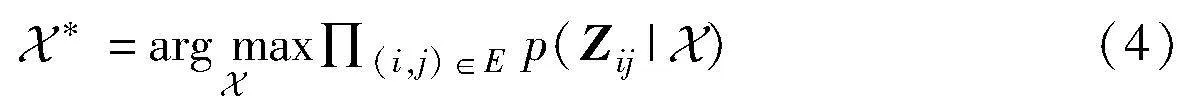
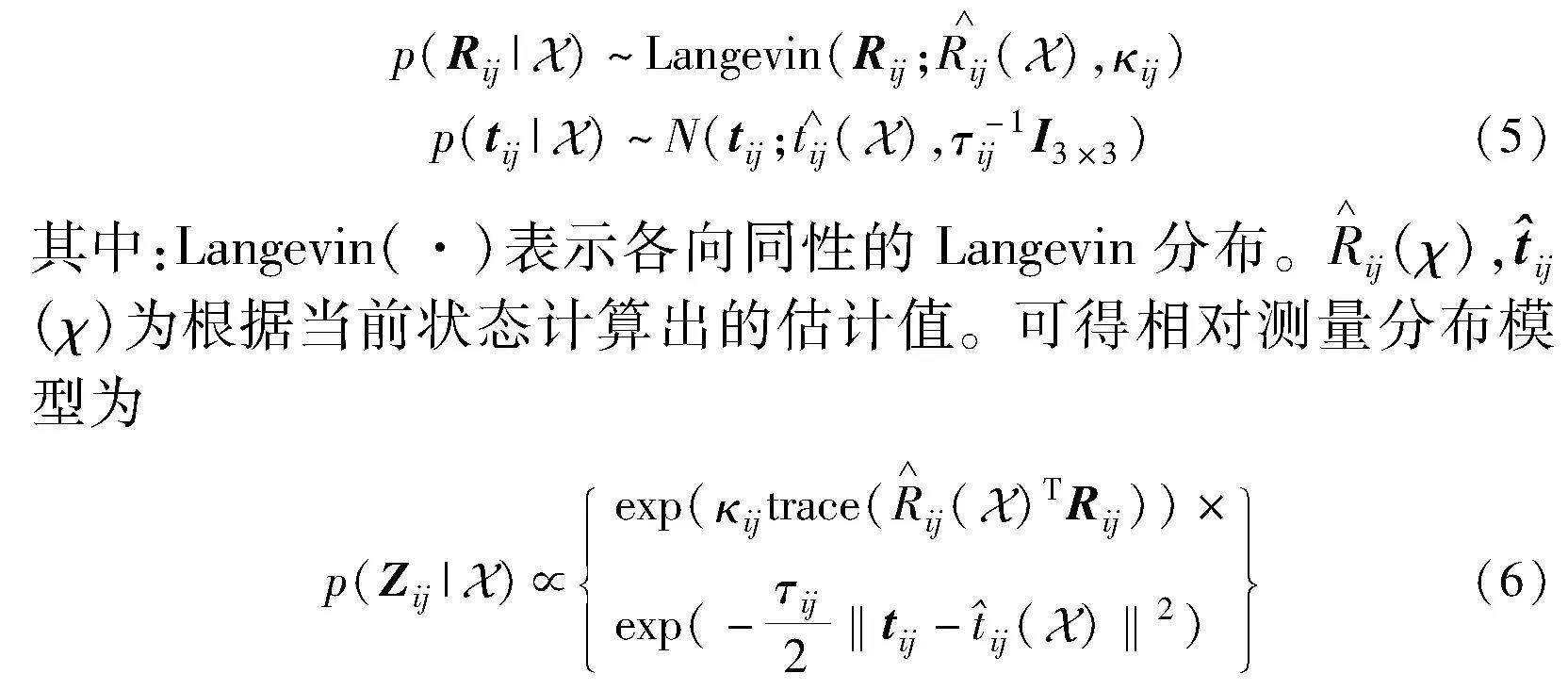
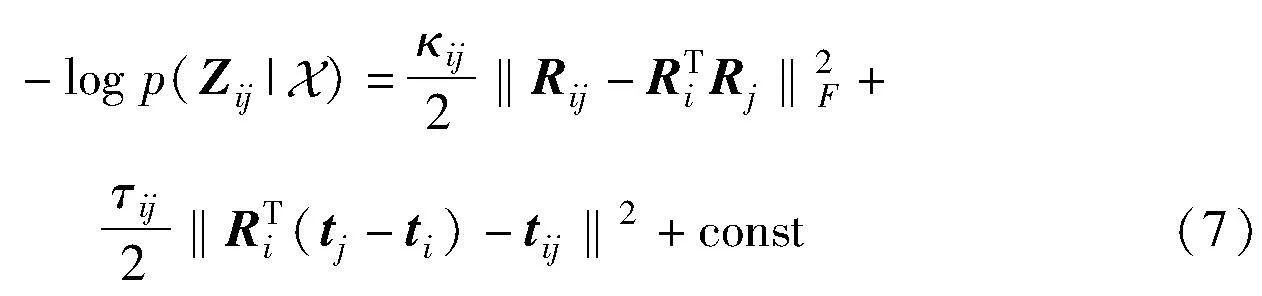
摘 要：位姿图优化 （pose graph optimization，PGO）是一种在同时定位与地图构建（simultaneous localization and mapping，SLAM）后端优化中常用的高维非凸优化算法，通常建模成极大似然估计。由于目前的PGO算法优化大规模大噪声数据集时很难在保证精度的同时提升速度，所以提出了一种基于嵌套剖分的位姿图分层优化算法。该算法首先建立不同距离度量的χ2检验模型，进而剔除异常值点。然后利用嵌套剖分算法将位姿图分割成一组子图，再从这些子图中提取出一个表示原SLAM问题的抽象拓扑的骨架图，从而优化该骨架图，完成初始化。最后在模拟和真实的位姿图数据集上进行实验评估，结果表明该算法在不影响精度的情况下，可以提高算法的计算速度，具有可伸缩性。

关键词：位姿图优化； 嵌套剖分； 噪声； χ2检验; 最大似然估计

中图分类号：TP391 文献标志码：A

文章编号：1001-3695（2024）06-046-1916-05

doi：10.19734/j.issn.1001-3695.2023.08.0386

Hierarchical pose graph optimization algorithm based on nested dissection

Abstract：PGO is a high-dimensional non-convex optimization algorithm commonly used in the back-end optimization of SLAM， which is usually modeled as maximum likelihood estimation. Since the current PGO algorithm faces difficulties in improving speed while ensuring accuracy when optimizing large-scale noise datasets， this paper proposed a hierarchical pose graph optimization algorithm based on nested dissection algorithm for large noise datasets. The algorithm firstly established a χ2 test model with different distance measures， and then removed outlier points. Secondly， it used nested dissection method to split the original pose graph into a set of subgraphs and extracted a skeleton graph from these subgraphs. The skeleton represented the abstract topology of the original SLAM problem. Then， the algorithm optimized the skeleton graph and completed the initialization. Finally， experimental evaluation on simulated and real pose graph datasets show that the proposed algorithm can improve the calculation speed and scalability of the algorithm without affecting the accuracy.

Key words：pose graph optimization; nested dissection; noise; χ2 test; maximum-likelihood estimation

0 引言

在缺乏环境先验信息的情况下，SLAM使机器人能依据自身搭载的传感器实现自主定位和导航［1］，其本质是从相对测量中估计机器人位姿。位姿图是该问题的图形表示，其中节点表示位姿，通常用特殊欧氏群SE（3）上的元素表示；边表示节点对之间的空间约束，即相对测量［2］，通常用概率的方式来表示由外部观测引起的不确定性。由于位姿图优化 （pose graph optimization，PGO） 具有非凸性，所以已有研究［3～5］将其建模成一个非凸极大似然估计问题。传统的求解方法是将该问题转为非线性最小二乘问题，通过高斯牛顿［6］、列文伯格-马夸尔特［7，8］等迭代优化算法来获得与概率约束最大一致的节点估计［9～11］。在实际应用中，随着问题规模的扩大和复杂性的提升，PGO算法的研究开始向分层策略迁移。Bosse等人［12］首次将分治法［13］应用于SLAM领域，并解决了城市尺度区域的空中三角测量和测绘问题。文献［14］提出一种用于大规模环境的精确局部建图方法，通过缓存分解的子图来提升运行的速度。之后，Ni等人［15］将嵌套剖分算法运用到原始的SLAM图上，将其递归地划分为多个层次的子图，极大地减少了两棵子树之间的依赖，并沿相应的聚类树采用自底向上的推理对原始的SLAM图优化。同时，Grisetti等人［16］提出了一种层级式的局部图，在得到一个新的观测值时，位于高层级的局部图会被立刻修改，而在低层级的局部图中只有受影响的区域才会被更改。Tang等人［17］提出了一种高效的分层位姿图优化算法，该方法利用一种修改后的标准切割算法自动将位姿图分割成在关键节点条件下相互独立的子图。然后通过位姿图稀疏算法将关键节点生成一个上层图，并在优化上层图后再独立解决每个子图的优化问题。Tian等人［18］提出一种基于段的分层优化方法，该方法提出了一种可靠的轨迹分割方法以提高优化的效率，并首次提出一种缓冲机制来提高分割的鲁棒性。 Korovko等人［19］将部分优化与分层位姿相结合，提出一种构建层次结构的方法，允许快速添加新节点进入层次结构，无须重建，极大地提升了运行速度。Guadagnino等人［20］提出 HiPE 算法，该算法通过结合来自输入局部区域的最大似然估计，将问题进行几何图形的抽象表示，再将其编码为粗粒度图。相较于Cauchy 算法［21］，该算法通过利用这种表示的稀疏性，能更加稳健地初始化姿态图。

在实际应用中，光照、天气、温度变化等环境因素会对传感器性能造成影响，使得传感器获取的测量数据具有较大的噪声，从而导致HiPE算法迭代次数显著增加，鲁棒性较低，极大地增加了陷入局部极小值无法收敛到全局最优解的可能。因此，本文针对大噪声数据集提出了一种基于嵌套解剖的位姿图分层优化方法ND-PGO。其贡献如下：a）提出了一种基于不同距离度量的χ2检验模型，对大噪声数据集进行处理，检测剔除大噪声数据集中的异常值点；b）利用嵌套剖分算法将数据处理后的位姿图分割成一组子图，再提取一个骨架图来抽象表示待解决的SLAM问题，然后通过对该图骨架非线性优化来初始化位姿变量，最后，将优化后的图骨架位姿变量放入原始位姿图中固定，对剩余变量进行优化；c）在PGO数据集Sphere5000、Parking-garage、torus3D和grid3D上进行对比实验。结果表明，相较于其他先进的位姿图算法，ND-PGO算法在不牺牲精度的情况下，显著提高了优化运行速度。

1 PGO算法介绍

1.1 PGO模型

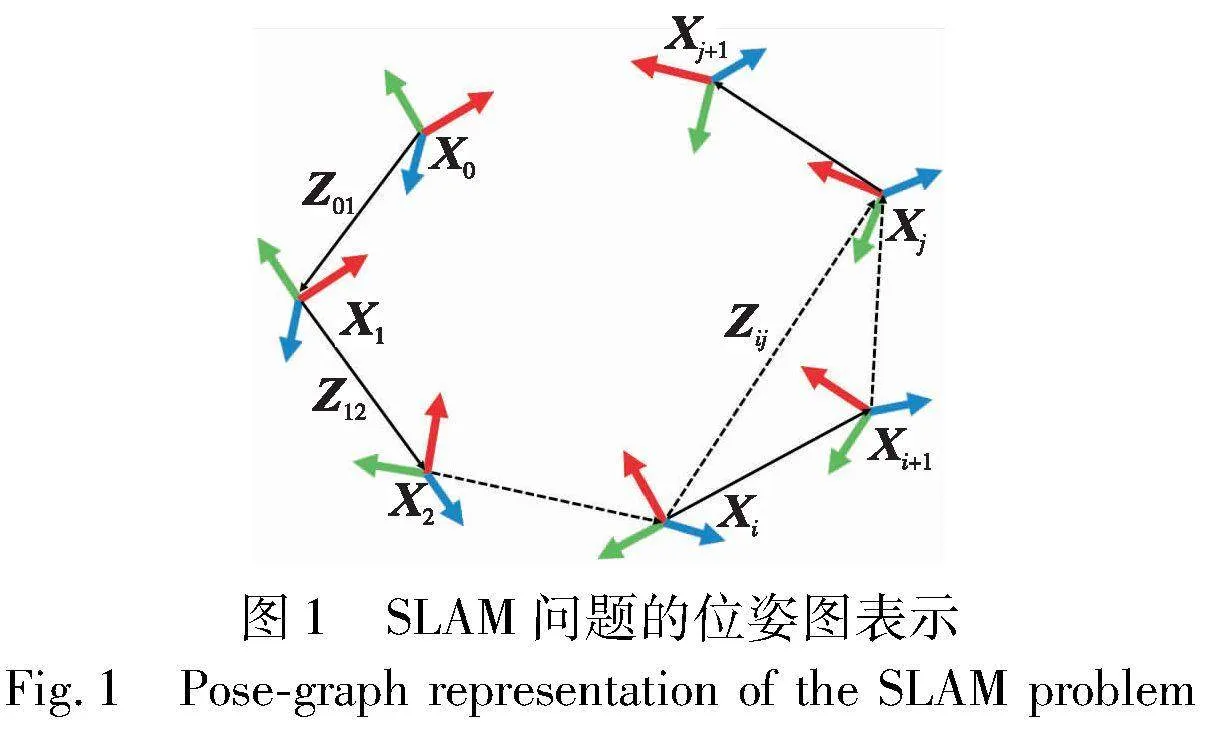
位姿图通常用一个有向图G={V，E}表示（图1）。其中V是非空集合，称为节点集；E是V中元素构成的无序二元组集合，称为边集。相邻节点之间的边为里程约束（图1实线），其余边为闭环约束［22］ （图1虚线）。位姿节点i，i∈V可用SE（3）中的元素表示：

PGO问题的目标是在位姿图所有相对测量的约束下找到绝对位姿最小二乘误差的节点构型。采用极大似然估计（maximum likelihood estimation，MLE）方法，即求解：

假设测量值是独立同分布的，则：

1.1.1 相对测量分布模型

在MLE中最常见的选择是假设测量值服从高斯分布。然而，通过高斯分布获得的测量值在求代价函数的过程中引入了对数映射，从而导致该优化问题具有很高的非凸性。为了克服这一问题，Rosen等人［23］提出了SE（3）上相对测量分布的解耦：

1.1.2 极大似然估计

式（6）在负对数下有较好的数学形式，将其取负对数得：

求解位姿的MLE等价于最小化负对数似然，则式（4）变为

其中：‖·‖F为Frobenius范数。将式（7）代入式（8）中，得到PGO问题的解为

1.2 PGO初始化

式（9）通常采用迭代的方法求解，但是迭代的方法非常依赖初值。一个良好的初始化结果不仅可以大大降低收敛到次优配置的风险，还可以加快迭代的收敛速度，减少优化的计算时间。因此求解式（9）非常关键的一步是寻找尽可能接近最优值的初始值。然而PGO初始值是通过前端里程计测量获得的，精度较低，迭代求解时容易陷入局部最小值，甚至难以收敛。因此研究者们提出了一些经典的PGO初始化方法，其中最广泛使用的算法就是弦初始化算法［24］。该方法首先通过弦松弛估计旋转矩阵，然后利用这个旋转估计来计算平移向量的估计量。最后将这个位姿的粗略估计用作迭代优化算法的初始值。弦初始化算法将式（9）的旋转部分替换为［25］

定义rki为RTi（k=1，2，3）的第k列，则式（10）为

放松SO（3）约束，则式（11）转换为一个无约束问题：

求解式（12）可得到n个矩阵Ai=［r1i，r2i，r3i］。这些矩阵不一定是旋转矩阵，但可以通过Ai找到满足旋转约束的矩阵Ri：

式（13）可通过SVD分解算法［26］得到一个封闭的解。对矩阵Ai进行奇异值分解Ai=USVT，则有

R*i=U diag（［1 1 det（UVT）］）VT（14）

已知旋转矩阵，可以通过线性最小二乘估计平移向量，即求解：

该算法在实践中表现良好。此外，由于初始化是由两个线性问题组成的，所以计算会更高效。

2 本文方法

2.1 基于不同距离度量的χ2检验模型

a）测地线距离（又称角距离）：表示相对旋转RTaRb对应的旋转角度，公式如下：

dang （Ra，Rb）=‖Log（RTaRb）‖=‖Log（RTbRa）‖（17）

其中：Log（R） 表示SO（3）在恒等式处的对数映射。

b）弦距离：Ra-Rb的Frobenius范数：

dchord（Ra，Rb）=‖Ra-Rb‖F=‖RTaRb-I3‖F（18）

c）四元数距离：

dquat（Ra，Rb）=min（‖qa－qb‖，‖qa+qb‖）（19）

其中：qa、qb是旋转矩阵Ra、Rb的四元数表示。因为qa与-qa表示同一旋转，所以式（19）中的最小运算符用于解决符号歧义。

分别将式（17）～（19）引入式（16）可得基于不同距离度量的χ2检验模型如下：

假设里程计中无异常值，则不含异常值的回环边须满足以下条件［27］：

rij<χ2α，dij（21）

其中：dij是i、j之间的约束自由度；α为χ2检验显著性水平。

2.2 基于嵌套剖分的骨架图提取算法

针对式（9），一般求解其泰勒展开的线性估计的最小值。在线性代数［28］和图论［29］文献中，已经证明了线性系统求解的效率在很大程度上取决于消去顺序。将同样的思想应用于SLAM问题［11］，良好的消去排序在图三角化过程中产生小团，并在矩阵分解过程中引入较少的非零填充。虽然找到一个最优排序是NP完全问题［30］，但是找到一个有效的排序有最小度［31，32］和嵌套剖分［33，34］两种方法，其中最小度方法又包括多重最小度［31］（multiple minimum degree，MMD）、近似最小度［32］ （approximate minimum degree， AMD）等变种。针对基于子映射的方法，嵌套剖分比最小度剖分的性质更好。虽然这两种方法生成的消除顺序质量相当，但嵌套剖分倾向于在大型图上执行得更好，并且它的消除树通常更低、更平衡，因此更适合本文的分层划分。

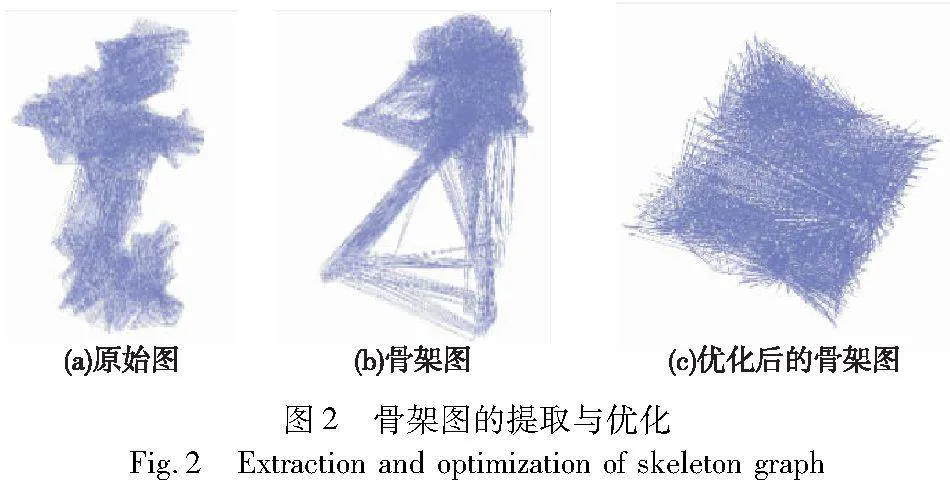
本文利用嵌套剖分算法递归地将输入划分为代表问题空间连通区域的分区。划分过程旨在最小化分区之间的连接，并使得每个分区具有相对均衡的负载。嵌套剖分算法首先初始化图结构和变量索引，再根据变量索引构造近似的Hessian矩阵模式。通常情况下，近似的Hessian矩阵模式是一个稀疏矩阵，用于表示变量之间的相关性。使用近似的Hessian矩阵模式，对问题的图进行嵌套分解。嵌套分解是一种递归分割图的过程，类似于树的分解。在每一次递归中，选择一个分割点，将图分成两个子图。继续对每个子图进行递归分解，直到子图足够小，不再进行分解。对于这些分区，使用局部图中可用的测量值提取一个由变量子集组成的骨架图，该骨架图必须在保持问题空间结构的同时保持其稀疏性。图2展示了骨架图的优化效果，其中（a）为原始图，（b）为利用嵌套剖分算法分区后提取出的骨架图，（c）为利用弦初始化算法优化后的骨架图。

2.3 ND-PGO算法流程

对于含有大噪声的数据，ND-PGO方法使用2.1节中提出的χ2检验模型筛选和剔除相对观测值中的异常值。然后利用嵌套剖分算法递归地划分分区，形成分区集后，使用局部估计来形成骨架图，然后对输入分两个阶段进行初始化。

算法1 ND-PGO算法

形成骨架图首先需要对每个分区进行优化，获得其变量的局部估计（算法1第8行）。由于形成原问题抽象表示的骨架图仅可使用相对度量，所以需要从每个分区的变量中选择一个锚点变量作为后续优化过程中固定变量的值。本文选择度数最高（连接的因子数量最多）的变量作为锚点变量（算法1第6行）。此外，本算法在锚点变量和每个边界变量之间添加虚拟测量，从而得到局部图的稀疏近似（算法1第10行）。整体骨架将由一组锚点变量和边界变量χS以及相应的虚拟测量值Euclid Math OneZApS组成。

分阶段进行初始化时，首先通过极大似然估计计算骨架图中变量的初始猜测值，合并块中的局部信息。由于边界变量在不同分区中的估计不一致，所以需要对骨架的一致估计对齐块（算法1第19行）。然后再固定得到的骨架变量的初始值，优化得到剩余变量χR=χ＼χS的初始猜测（算法1第21行）。其中χS和χR均是通过1.2节中的弦初始化方法来引导收敛的（算法第18、20行）。

3 实验

本文采用PGO公开数据集，首先在低噪声环境下的公共数据集上验证算法的性能，接着向这些数据集中添加噪声。本文选取g2o［10］和HiPE［20］算法作为实验对比方案。其中g2o算法是最广泛使用的SLAM框架后端优化算法，具有很高的鲁棒性；HiPE算法是最新的分层算法，在运行速度方面有很大提升。因此将提出的ND-PGO与g2o、HiPE算法在大噪声数据集上进行实验对比，评估ND-PGO算法在大噪声数据集下的性能。本文使用归一化χ2度量作为实验的评估标准。

其中：m为相对测量边数；n为位姿点数。一般将χ2度量数值作为评价标准，χ2度量数值越低，机器人轨迹优化结果越精确，算法越鲁棒。实验的硬件条件为Intel Xeon CPU E5-1620 v3 @ 3.50 GHz×8、NVIDIA Corporation GP104，软件环境为Ubuntu 20.04，编程语言为C++。

3.1 数据集

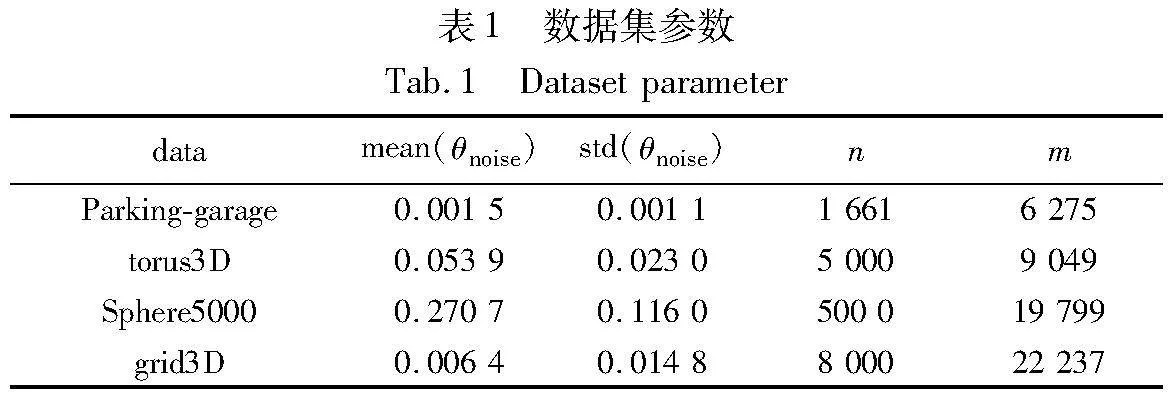
在3DSLAM中，PGO公共数据集主要有Sphere5000、Parking-garage、torus3D和grid3D。其中Sphere5000、torus3D和grid3D数据集均为模拟生成的数据集，分别模拟了机器人在球面、环面表面和三维网格世界上运动时的轨迹。Parking-garage是Vertigo收集的用于研究自动停车的斯坦福停车场的3D地图，为真实场景数据集［35］。本文将含有大量错误和异常的数据称之为大噪声数据集，包括相对观测值中含有较大的随机误差以及偏离正常数据较远的异常值点。

表1记录了每个数据集的具体参数，θnoise表示相对旋转测量的噪声（单位：弧度（rad））。mean、std分别为其均值与标准差，n为位姿节点数量，m为相对测量边的数量。

为评估算法的抗噪能力，在数据集的相对方向测量中分别加入均值μR=0，标准差σR为0.1 rad、0.2 rad、0.3 rad、0.4 rad、0.5 rad的噪声，以比较算法在大噪声数据集下的鲁棒性。

3.2 实验结果

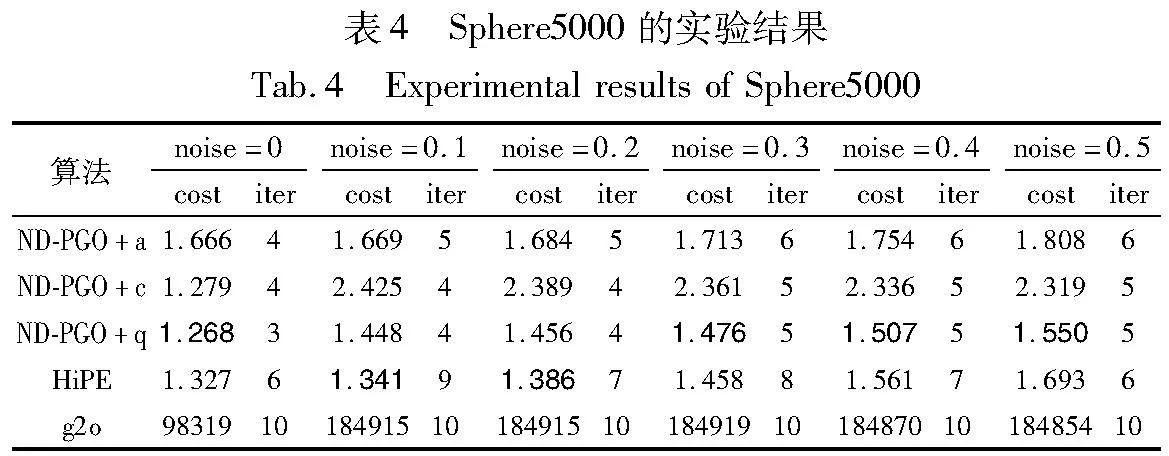
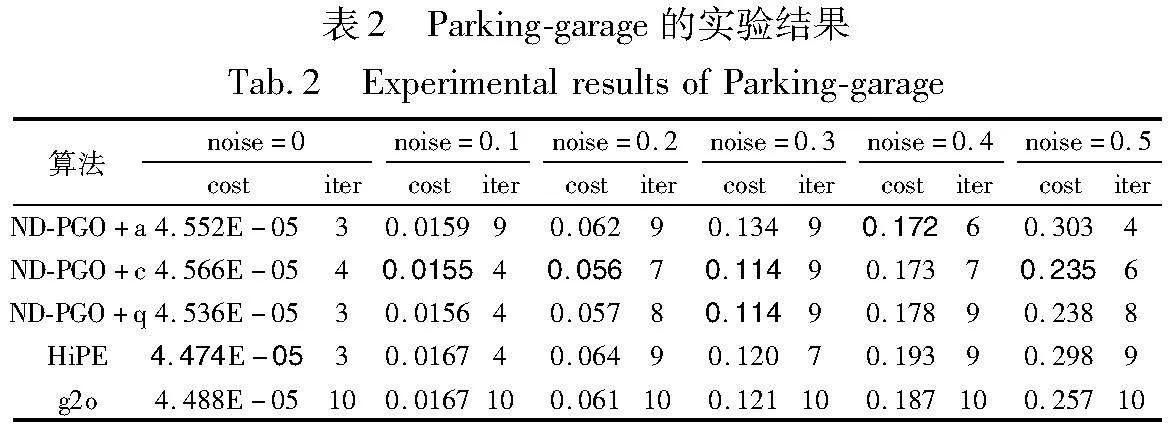
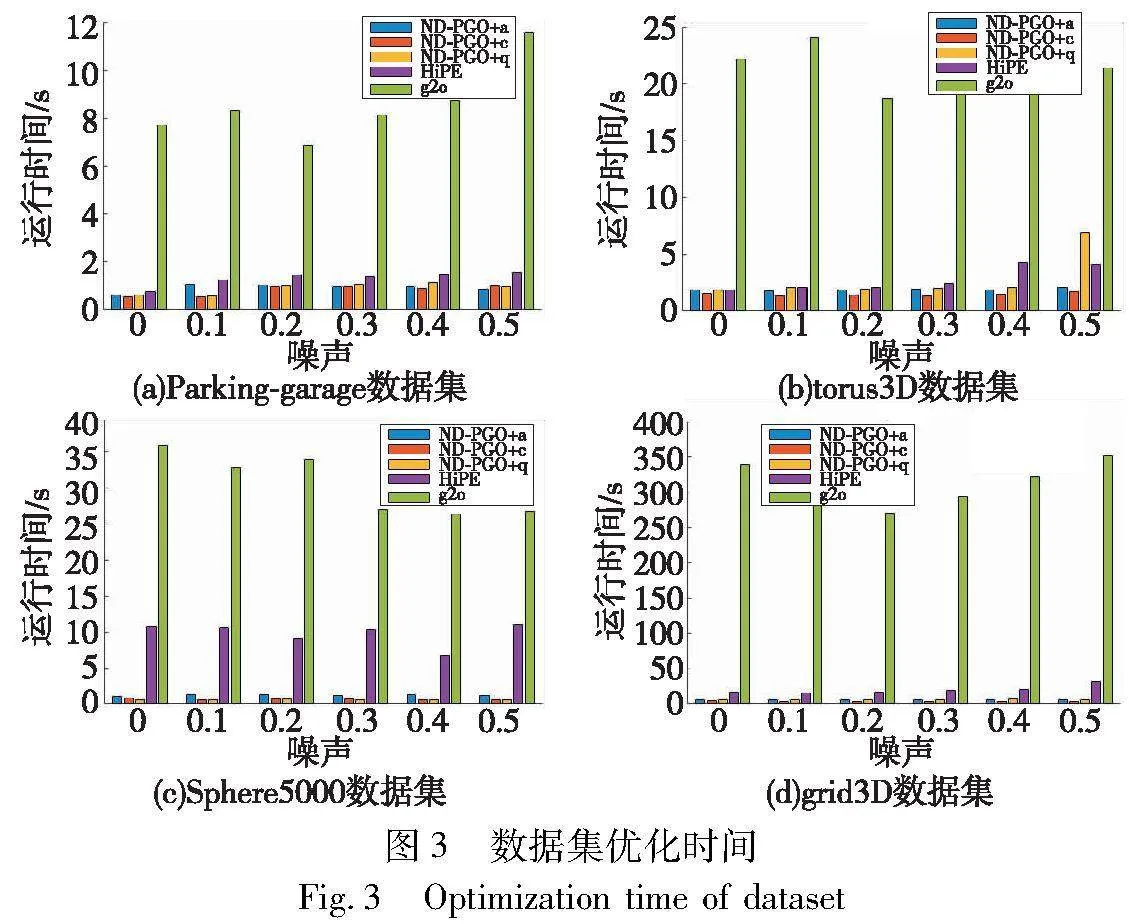
在PGO数据集中加入不同水平的噪声，重复实验50次取平均值。此次实验采用模型中的rij（χ）ang、rij（χ）chord、rij（χ）quat作为χ2检验函数的ND-PGO算法，分别记为ND-PGO+a、ND-PGO+c和ND-PGO+q。图3记录了Parking-garage、torus3D、Sphere5000和grid3D数据集在无噪声和有噪声的情况下，ND-PGO+a、ND-PGO+c、ND-PGO+q、HiPE和g2o算法对数据集优化所用的时间。从图3可得，ND-PGO算法明显快于g2o算法，相较于HiPE算法，运行速度也有显著优势。在基于ND-PGO的三种算法中，ND-PGO+c稍微快于其他两种算法。

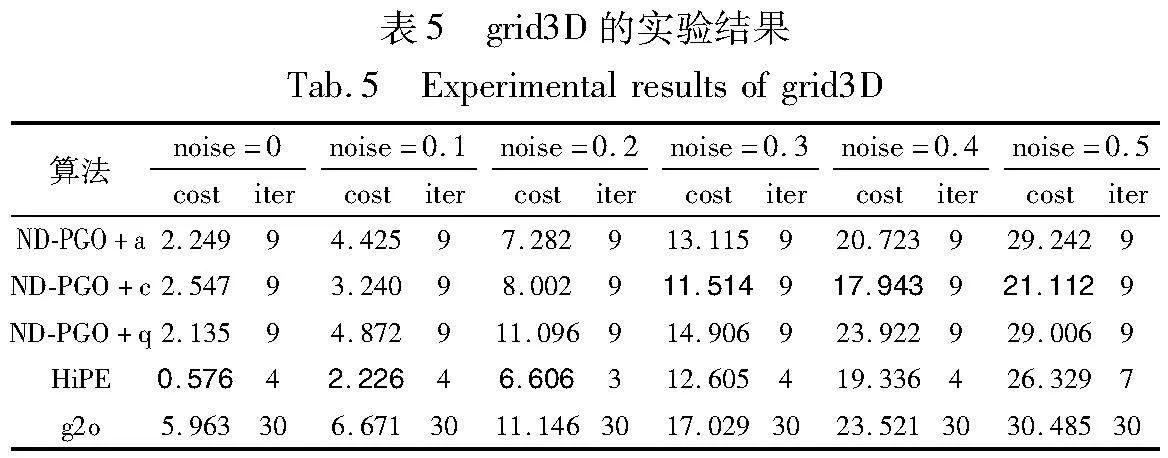
表2～5分别记录了各个算法对四个数据集优化得到的χ2度量值和迭代次数（表中加黑数据说明对应的算法最优）。从表2～5中的数据可知，分层优化算法会比传统算法的效率更高，其中在中小噪声集中，HiPE算法在运行精度上会比本文算法更有优势。但随着噪声增大，HiPE算法需花费时间考虑异常值的影响，计算速度受到影响，ND-PGO的运行时间明显少于HiPE算法。此外，基于ND-PGO的三种算法的χ2度量值基本低于HiPE算法和g2o算法。其中ND-PGO+c算法在Parking-garage、torus3D和grid3D上的表现稍优于其他两种基于ND-PGO的算法。ND-PGO+q在Sphere5000数据集上表现最佳。ND-PGO算法首先采用χ2检验来剔除异常值，这在一定程度上可以帮助算法在大噪声情况下避免局部极小值，保证算法精度的同时提升后续优化速度。此外，本文算法优先优化骨架图，再利用优化后的骨架图优化剩余变量以提升运行速度。

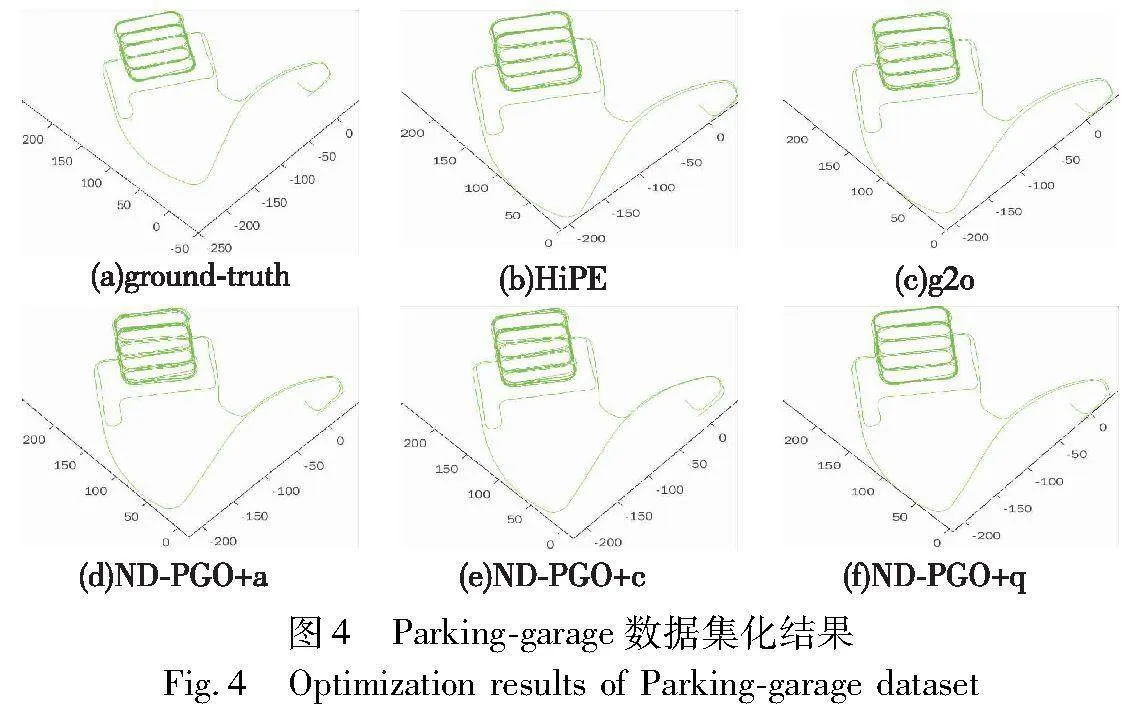
图4是各个算法对Parking-garage数据集优化的轨迹图。HiPE算法和g2o算法可以优化出较为精确的轨迹结果，从图4中可以看出ND-PGO算法优化的轨迹图并不亚于HiPE算法与g2o算法。这表明ND-PGO在保证算法精度的同时，提升了运行速度，总体性能优于HiPE法和g2o法。

4 结束语

本文提出了一种基于嵌套剖分的分层位姿图优化方法（ND-PGO）。首先利用χ2检验剔除外点后提取出一个骨架图，该骨架图对图形几何的高级表示进行编码，以快速地初始化变量。为验证本文算法的有效性，在多个不同的数据集上进行实验，并将其与最先进的方法进行比较。实验结果表明，与现有的优化方法相比，ND-PGO在不损失优化精度的情况下具有更高的优化效率。在以后的工作中可以将χ2检验改为自适应的，根据数据集自身的特点选择最优的距离度量。需要指出的是，χ2检验剔除一些异常值后会损失一部分信息，未来可进一步研究适合该算法的鲁棒核函数，通过降低异常值权重的方式来减少异常值对优化精度的影响。最后，希望能将本文算法整合到一个完整的SLAM系统中，以进一步验证和增强算法的实际性能。

参考文献：

［1］Durrant W H， Bailey T. Simultaneous localization and mapping： part I［J］. IEEE Robotics and Automation Magazine， 2006，13（2）： 99-108.

［2］王苗苗，魏国亮，蔡洁，等. 基于偏差矩阵的3D SLAM位姿图优化算法［J］. 信息与控制， 2023，52（3）： 334-342. （Wang Miaomiao， Wei Guoliang， Cai Jie， et al. Deviation matrix based for 3D SLAM pose graph optimization［J］. Information and Control， 2023， 52（3）： 334-342.）

［3］Carlone L， Rosen D M， Calafiore G， et al. Lagrangian duality in 3D SLAM： verification techniques and optimal solutions［C］//Proc of IEEE International Conference on Intelligent Robots and Systems. Piscataway，NJ： IEEE Press， 2015： 125-132.

［4］Tron R， Rosen D M， Carlone L. On the inclusion of determinant constraints in Lagrangian duality for 3D SLAM［C］//Robotics： Science and Systems Workshop. 2015.

［5］Briales J， Gonzalez J J. Convex global 3D registration with Lagrangian duality［C］//Proc of IEEE Conference on Computer Vision and Pattern Recognition. Piscataway，NJ：IEEE Press， 2017： 4960-4969.

［6］郝亚东， 张奇志， 周亚丽. 基于高斯牛顿的局部优化 SLAM 系统［J］. 传感器世界， 2018， 24（3）： 7-11. （Hao Yadong， Zhang Qizhi， Zhou Yali. Local optimization SLAM system based on Gauss-Newton method［J］. Sensor World， 2018， 24（3）： 7-11.）

［7］Dou Xinglei， Huo Yuzhou， Liu Yongchang， et al. An unmanned aerial vehicle pose estimation system based on SLAM［C］//Proc of IOP Conference Series： Materials Science and Engineering. London： IOP Press， 2019.

［8］曾俊飞， 杨海清， 吴浩. 面向三维重建的自适应列文伯格-马夸尔特点云配准方法［J］. 计算机学， 2020， 47（3）： 137-142. （Zeng Junfei， Yang Haiqing， Wu Hao. Adaptive Levenberg-Marquardt cloud registration method for 3D reconstruction［J］. Computer Science， 2020， 47（3）： 137-142.）

［9］Grisetti G， Guadagnino T， Aloise I， et al. Least squares optimization： from theory to practice［J］. Robotics， 2020， 9（3）： 51.

［10］Kyummerle R， Grisetti G， Strasdat H， et al. g2o： a general framework for graph optimization［C］//Proc of IEEE International Confe-rence on Robotics and Automation. Piscataway，NJ： IEEE Press， 2011： 3607-3613.

［11］Dellaert F， Kaess M. Square root SAM： simultaneous localization and mapping via square root information smoothing［J］. The Internatio-nal Journal of Robotics Research， 2006， 25（12）： 1181-1203.

［12］Bosse M， Newman P， Leonard J， et al. Simultaneous localization and map building in large-scale cyclic environments using the Atlas framework［J］. The International Journal of Robotics Research， 2004， 23（12）： 1113-1139.

［13］Paz L M， Tardos J D， Neira J. Divide and conquer： EKF SLAM in o （n）［J］. IEEE Trans on Robotics， 2008， 24（5）： 1107-1120.

［14］Ni K， Steedly D， and Dellaert F. Tectonic SAM： exact， out-of-core， submap-based SLAM［C］//Proc of IEEE International Conference on Robotics and Automation. Piscataway，NJ： IEEE Press， 2007： 1678-1685.

［15］Ni K， Dellaert F. Multi-level submap based SLAM using nested dissection［C］//Proc of IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway，NJ： IEEE Press， 2010： 2558-2565.

［16］Grisetti G， Kyummerle R， Stachniss C， et al. Hierarchical optimization on manifolds for online 2D and 3D mapping［C］//Proc of IEEE International Conference on Robotics and Automation. Piscataway，NJ： IEEE Press， 2010： 273-278.

［17］Tang Hengbo， Liu Yunhui， Li Luyang. Pose graph optimization with hierarchical conditionally independent graph partitioning［C］//Proc of IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway，NJ： IEEE Press， 2016： 3255-3260.

［18］Tian Yuxin， Wang Yujie， Ouyang Ming， et al. Hierarchical segment-based optimization for SLAM［C］//Proc of IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway，NJ： IEEE Press， 2021： 6573-6580.

［19］Korovko A， Robustov D. Partial hierarchical pose graph optimization for SLAM［EB/OL］. （2021）. https：//arxiv.org/abs/2110. 08639.

［20］Guadagnino T， Di Giammarino L， Grisetti G. HiPE： hierarchical initialization for pose graphs［J］. IEEE Robotics and Automation Letters， 2021， 7（1）： 287-294.

［21］Hu G， Khosoussi K， Huang Shoudong. Towards a reliable SLAM back-end［C］//Proc of IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway，NJ ： IEEE Press， 2013： 37-43.

［22］Juric＇ A， Kende F， Markovic＇ I， et al. A comparison of graph optimization approaches for pose estimation in SLAM［C］//Proc of the 44th International Convention on Information， Communication and Electronic Technology. Piscataway，NJ： IEEE Press， 2021： 1113-1118.

［23］Rosen D M， Carlone L， Bandeira A S， et al. SE-Sync： a certifiably correct algorithm for synchronization over the special Euclidean group［J］. The International Journal of Robotics Research， 2019， 38（2-3）： 95-125.

［24］Martinec D，Pajdla T. Robust rotation and translation estimation in multiview reconstruction［C］//Proc of IEEE Conference on Computer Vision and Pattern Recognition. Piscataway，NJ： IEEE Press， 2007： 1-8.

［25］Carlone L， Tron R， Daniilidis K， et al. Initialization techniques for 3D SLAM： a survey on rotation estimation and its use in pose graph optimization［C］//Proc of IEEE International Conference on Robotics and Automation. Piscataway，NJ： IEEE Press， 2015： 4597-4604.

［26］Hartley R， Trumpf J， Dai Yuchao， et al. Rotation averaging［J］. International Journal of Computer Vision， 2013， 103： 2LMRmduukxA045i57pkxWZQ==67-305.

［27］Latif Y， Cadena C， Neira J. Robust loop closing over time［M］//Robotics： Science Systems Ⅷ. Cambridge，MA： MIT Press， 2013： 233-240.

［28］George A， Liu J W. Computer solution of large sparse positive definite［M］.[S.l.]：Prentice Hall， 1981.

［29］Blair J swS0yeEuWKBl8kXUqGktXg==R S， Peyton B. An introduction to chordal graphs and clique trees［M］//Graph Theory and Sparse Matrix Computation. New York： Springer， 1993： 1-29.

［30］Yannakakis M. Computing the minimum fill-in is NP-complete［J］. SIAM Journal on Algebraic Discrete Methods， 1981， 2（1）： 77-79.

［31］Liu J W H. Modification of the minimum-degree algorithm by multiple elimination［J］. ACM Trans on Mathematical Software， 1985， 11（2）： 141-153.

［32］Amestoy P R， Davis T A， Duff I S. An approximate minimum degree ordering algorithm［J］. SIAM Journal on Matrix Analysis and Applications， 1996，17（4）： 886-905.

［33］George A. Nested dissection of a regular finite element mesh［J］. SIAM Journal on Numerical Analysis， 1973，10（2）： 345-363.

［34］Lipton R J， Rose D J， Tarjan R E. Generalized nested dissection［J］. SIAM Journal on Numerical Analysis， 1979， 16（2）： 346-358.

［35］李雨洁， 魏国亮， 蔡洁，等. 基于特征分解的快速位姿图优化算法［J］. 计算机应用研究， 2022， 39（10）： 3065-3070. （Li Yujie， Wei Guoliang， Cai Jie，et al. Fast pose optimization algorithm based on eigen decomposition［J］. Application Research of Computers， 2022， 39（10）： 3065-3070.）