非完美频谱感知下认知超密集网络的资源分配
2024-07-31李凡仇润鹤
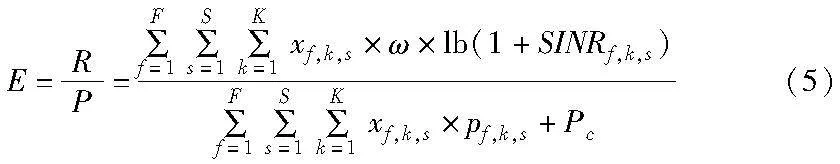
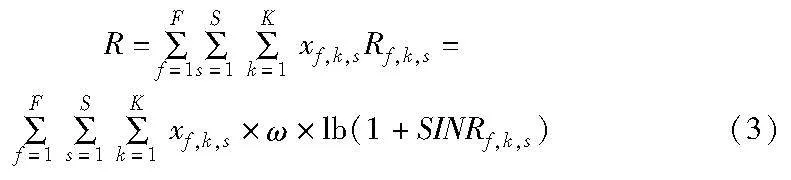

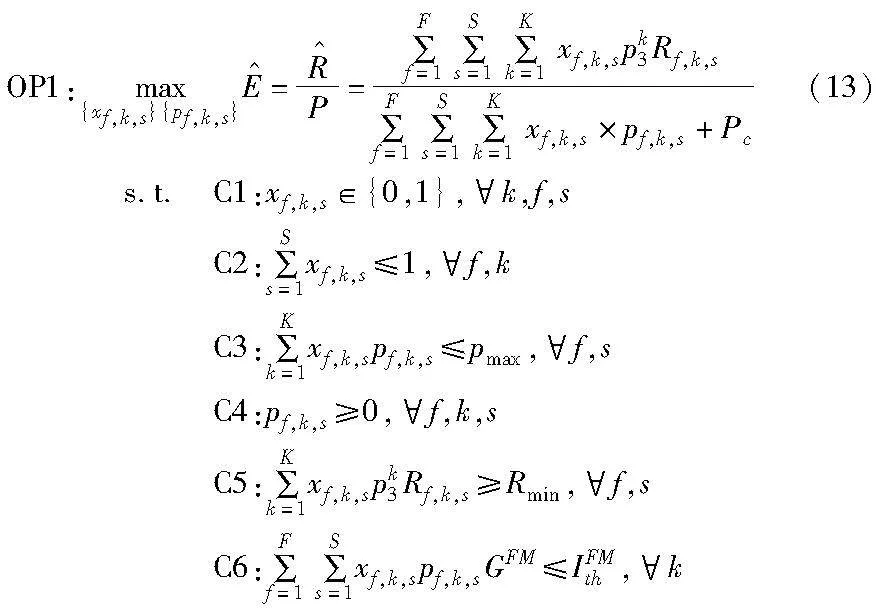





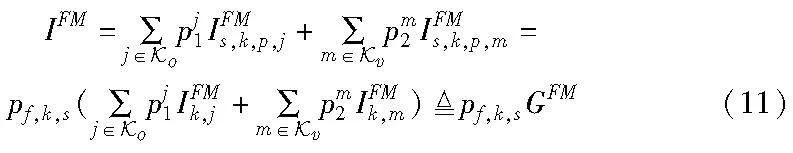

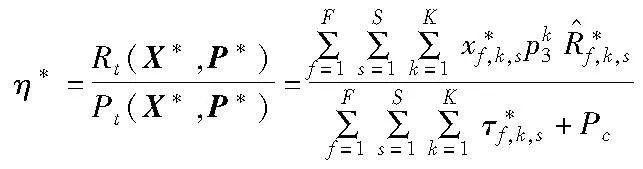
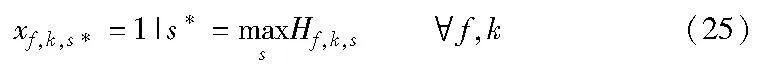

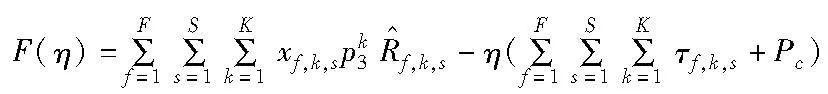
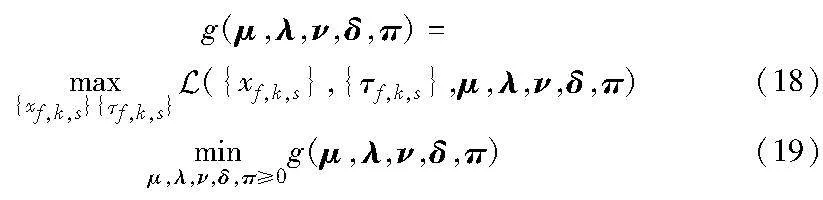



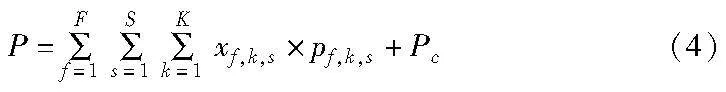
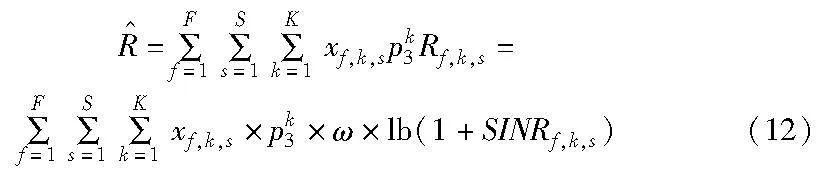


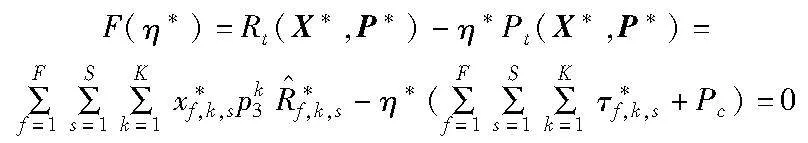



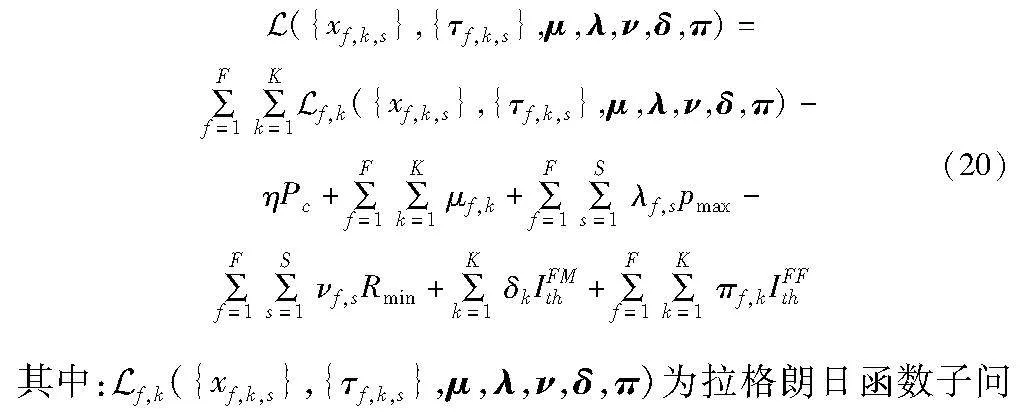
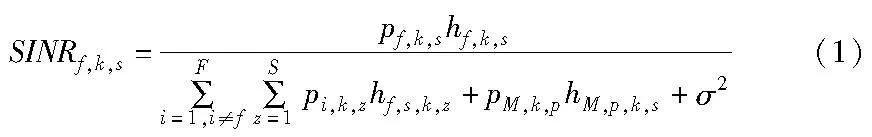
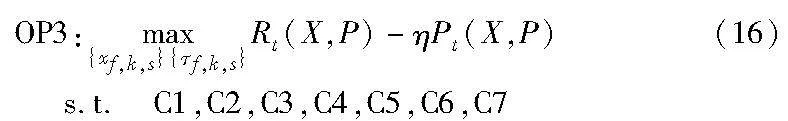

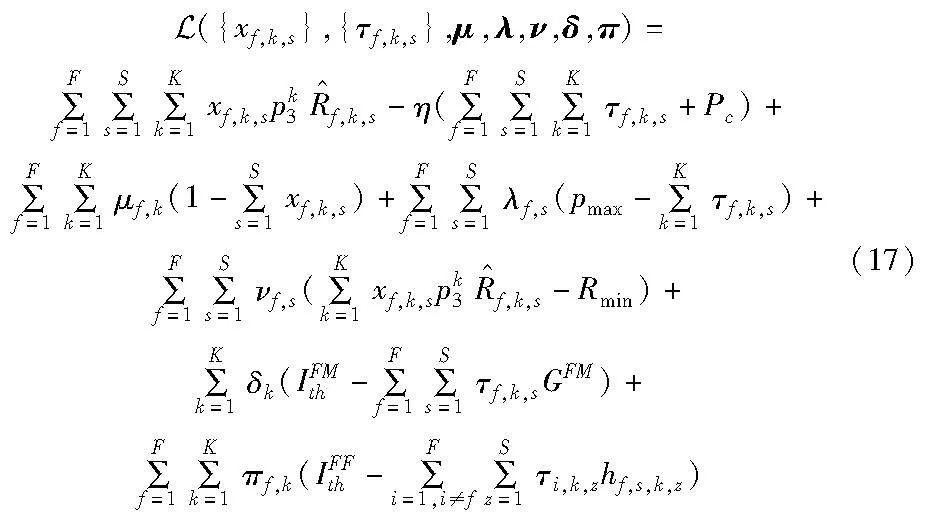


摘 要:针对实际认知超密集网络场景中认知无线电存在非完美频谱感知的情况,提出了一种基于非完美频谱感知的资源分配方案,目标是在考虑跨/同层干扰约束、保障用户服务质量下,最大化非完美频谱感知下认知超密集网络中次级网络的能效。为此,依据网络模型构建能效优化问题,其为混合整数非凸规划问题,先通过分时共享松弛法和丁克尔巴赫法将其转换成等价的凸优化问题,再使用拉格朗日对偶法求其最优解,以此获得最优能效时的子信道和功率分配策略。基于此,提出了一种迭代的子信道和功率分配算法;为权衡计算复杂度,还提出了一种实用的子信道和功率分配算法。仿真结果表明,所提算法都有效地提升了网络能效。
关键词:非完美频谱感知;认知超密集网络;跨/同层干扰约束;能效
中图分类号:TN929.5 文献标志码:A文章编号:1001-3695(2024)06-034-1833-07
doi: 10.19734/j.issn.1001-3695.2023.10.0536
Resource allocation of cognitive ultra-dense network with imperfect spectrum sensing
Abstract: Aiming at the situation of imperfect spectrum sensing of cognitive radio in actual cognitive ultra-dense network scenarios, this paper proposed a resource allocation scheme based on imperfect spectrum sensing. The target was to maximize the energy efficiency of secondary network in cognitive ultra-dense network with imperfect spectrum sensing while taking into account cross-tier/co-tier interference constraints and ensuring users’ quality of service. And this paper constructed the energy efficiency optimization problem based on the network model, which was a mixed integer non-convex programming problem, then transformed it into an equivalent convex optimization problem by the time-sharing relaxation method and Dinkelbach me-thod, and finally used the Lagrangian dual method to get its optimal solution, thereby obtained the sub-channel and power allocation strategy for optimal energy efficiency. Based on this, this paper proposed an iterative sub-channel and power allocation algorithm. In order to trade o5OsA+djx1J6sOJUtQDk/9w==ff the computational complexity, this paper also proposed a practical sub-channel and power allocation algorithm. Simulation results show that the proposed algorithms effectively improve energy efficiency.
Key words:imperfect spectrum sensing; cognitive ultra-dense network(UDN); cross-tier/co-tier interference constraint; energy efficiency
0 引言
超密集异构网络简称为超密集网络(UDN)[1,2],是5G时代解决容量紧张、降低网络能耗、实现绿色通信的新型组网方式。但这种超密集、多层次、异构化网络中的信道资源采用共享方式,容易导致用户对频谱资源的竞争进一步加剧,由此带来的跨层干扰(宏小区与小小区之间的干扰)及同层干扰(不同小小区间的干扰)严重影响了网络性能。具备频谱感知与分配功能的认知无线电(cognitive radio,CR)[3,4]技术可有效提高频谱利用率,缓解因频谱资源共享导致的干扰。因此,把CR集成到UDN而构成的CR-UDN能很好地缓解干扰、提高频谱利用率,且合理的资源分配方案也能减少资源浪费和提升网络性能。
文献[5,6]提出了CR-UDN的实现框架,并比较了遗传算法和图着色算法在提升网络吞吐量上的优劣。文献[7,8]对认知异构网络中因频谱共享导致的干扰进行协调,有效地抑制了干扰,提升了性能。文献[9]为提高CR-UDN中次级用户的吞吐量,提出了一种改进的基于用户分簇的资源分配算法,该算法以次级用户受到的平均弱干扰来进行分簇,仿真结果表明该算法在保障资源分配公平性的同时提升了吞吐量。文献[10]提出一种以认知毫微微小区用户吞吐量最大为目标的联合优化用户关联和资源分配的改进遗传算法,缩小了可行解的搜索空间,能在较低复杂度下有效提高CR-UDN的总吞吐量。文献[11]优化了基于正交频分多址(orthogonal frequency division multiple access,OFDMA)的异构网络能效。文献[12]提出一种动态搜索功率分配算法来提升多用户异构认知无线电网络中次级用户的吞吐量和整个网络的能效。
以上文献主要研究的是基于完美系统参数(如完美的频谱感知和确定的信道信息状态)来进行资源分配,但在实际的认知超密集网络中,实现完美的频谱感知是极其困难的。文献[13]基于OFDMA接入的认知毫微微小区场景,在同时考虑用户服务质量(quality of service,QoS)、跨层干扰约束和非完美频谱感知下,提出了一种联合子信道和功率分配的算法来最大化认知毫微微小区网络的吞吐量。文献[14]结合贝叶斯理论,提出子载波状态信任指数和统计平均干扰功率的概念,利用拉格朗日对偶分解理论求解资源分配问题,得到一种分布式多用户资源分配算法,有效提高了非完美频谱感知下认知无线电网络容量。文献[15]最大化了基于认知异构非正交多址网络的工业认知物联网在非完美频谱感知下的总吞吐量。文献[16]为方便求解,将资源分配方案分为子信道分配和功率分配两个步骤,把混合整数非线性规划的优化问题转变成线性规划问题,再基于分数规划和次梯度方法,给出了一种在非完美频谱感知情况下提高异构认知无线电网络中次级网络能效的分配算法。文献[17]为减少跨层干扰,利用窗函数来抑制OFDM信号旁瓣中的功率泄露,并提出一种次优资源分配算法来优化多用户认知无线电网络在非完美频谱感知下次级网络的能效。文献[18]同时考虑非完美频谱感知和信道状态信息不确定,提出了联合优化功率分配、子载波分配和传输时间的算法,在有效保障认知异构网络中次级用户QoS需求的同时提升次级网络的能效。
可以看到,现有大多文献主要优化吞吐量。文献[11,12,16~18]虽然优化了能效,但文献[11]只进行了信道分配,并没有功率分配,文献[12,16~18]没有考虑次级网络的层间干扰,这对实际情况来说过于理想化,文献[17]也没有考虑次级用户的QoS需求。针对以上问题,本文提出了一种基于非完美频谱感知下的认知超密集网络的资源分配方案,旨在考虑跨/同层干扰约束、保障用户服务质量下,最大化非完美频谱感知下认知超密集网络中次级网络的能效。为此,基于非完美频谱感知下的认知超密集网络模型,构建能效优化问题,其因布尔变量的引入和分数形式的表述,属于混合整数非凸规划问题。为了求得全局最优解,本文使用分时共享松弛法和丁克尔巴赫法将此问题转换为等价形式的凸优化问题,再通过拉格朗日对偶法求得其解;根据求解过程总结出一种迭代的子信道和功率分配算法。全局最优求解方案的计算复杂度随着网络规模的增大呈指数增长,为了给出合理计算复杂度下的求解方案,本文还提出一种次优的资源分配算法。最后仿真结果表明,与现存资源分配算法相比,所提两种算法均能有效地提升能效。
1 系统模型
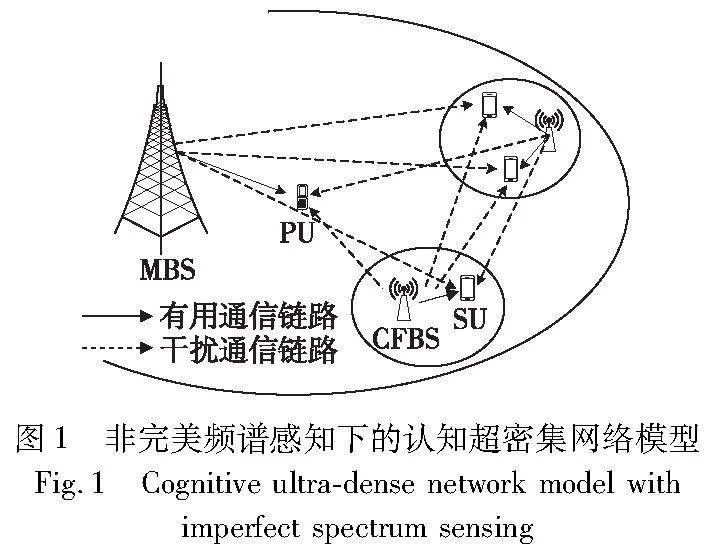
非完美频谱感知下的认知超密集网络模型如图1所示。该模型基于OFDMA,由一个宏基站(macro base station,MBS)和F个随机地部署在宏基站覆盖区域中的认知毫微微基站(congitive femto base station,CFBS)共同部署构成,且考虑下行链路传输。
扰;因非完美频谱感知,主网络会受到次级网络的跨层干扰。CFBS的工作方式为下垫模式,即SU可在不影响PU服务质量的前提下与PU同时使用授权信道。
由构建的网络模型可知,与CFBS-f关联的SU-s在SC-k上接收到的信干噪比(signal-to-interference-plus-noise ratio,SINR)为
其中:pf,k,s是CFBS-f在SC-k上对SU-s的发射功率;hf,k,s是在SC-k上从CFBS-f到SU-s的信道增益;pi,k,z是CFBS-i(i≠f)在SC-k上对SU-z(SU-z与CFBS-i关联)的发射功率;hf,s,k,z是在SC-k上从服务于SU-s的CFBS-f到SU-z的信道增益;pM,k,p是服务于PU-p的MBS在SC-k上的发射功率;hM,p,k,s是在SC-k上从服务于PU-p的MBS到SU-s的信道增益;σ2为加性高斯白噪声功率。基于香农公式可知,认知毫微微小区f中的SU-s在SC-k上可实现的传输速率为
Rf,k,s=ω×lb(1+SINRf,k,s)(2)
用布尔变量xf,k,s表示SC-k是否通过CFBS-f分配给SU-s,如果其为1表示分配,否则不分配。所以次级网络总容量为
每个CFBS的损耗功率包括发射功率和电路运行功率两个部分,所以在下行链路传输中,次级网络总功耗可定义为
其中:Pc为认知毫微微基站群的总电路运行功率。
能效是指单位能量消耗所获得的吞吐量,因此次级网络的能效为
次级网络对主网络的跨层干扰由带外发射和非完美频谱感知两个原因导致。
带外发射是因为OFDM信号旁瓣中的功率泄漏导致的[13]。SU-s在SC-k上以功率pf,k,s传输对被PU占用的SC-j造成的带外发射干扰量为
当CFBS无法检测到低于频谱感知阈值的微弱信号时,就会出现非完美频谱感知。完美频谱感知时,次级用户无论采用哪种频谱共享接入方式都不会对主用户造成跨层干扰,但非完美时就会引起干扰,影响主用户。CFBS可以确定子信道是否被PU占用,有四种不同的情形,即:情形1:信道被PU所占用,且CFBS感知的结果也为其被占用;情形2:信道被PU所占用,但CFBS感知的结果是其为空闲;情形3:信道没有被PU所占用,且CFBS感知的结果也是其为空闲;情形4:信道没有被PU所占用,但CFBS感知的结果是其被占用。情形1和3是正确感知,情形2是漏检感知,它会引起同信道干扰;情形4是虚警感知,它不会增加干扰水平,但会导致SU失去传输机会。
根据以上四种情形,显然有两种情况会对主网络造成有害干扰。首先,SU在SC-k上传输会对PU使用的SC-j造成带外发射干扰,即情形1;其次,任何SC-m被CFBS感知为空闲,但它实际上被PU占用,即情形2,这将导致同信道干扰。因此,SC-k上SU的接入对PU造成的下行链路总跨层干扰表示为
其中:GFM表示由带外发射和非完美频谱感知引起的跨层干扰。
基于以上分析,在两种情况下SU-s将使用SC-k。首先,空闲子信道被直接检测为空闲,即情形3;其次,繁忙子信道被错误地检测为空闲,即情形2,但此情形下SU-s的信号会与PU的传输发生冲突而丢失,吞吐量为零。因此,在非完美频谱感知下次级网络吞吐量变为
本文的目标是最大化CR-UDN中次级网络的能量效率,需考虑在一个认知毫微微小区中子信道不能同时分配给多于一个用户,且每个CFBS的发射功率不能超过其最大发射功率,每一个SU需要满足最低速率要求以实现可靠传输,另外跨层干扰也需要限制在门限值内以保护PU传输。因此优化问题可以描述为
其中:约束条件C1为子信道分配标志;C2表示在认知毫微微小区内一条子信道只分给一个SU;C3表示CFBS最大发射功率限制,pmax为每个CFBS的最大发射功率;C4保证功率的有效利用;C5表示SU最低数据速率的限制,保证SU的QoS要求;C6表示允许的最大跨层干扰,IFMth为宏小区中被PU占用子信道的最大跨层干扰门限。
2 基于非完美频谱感知的资源分配方案
2.1 优化问题的变形
问题式(13)是一个混合整数非凸规划问题,是一个离散的NP(non-deterministic polynomial)难问题,不可能直接获得其最优解。为了使问题易于求解,本文引入一个同层干扰约束C7。
其中:X和P是子信道和功率分配策略向量组,该问题有非线性的分数目标函数。基于丁克尔巴赫方法[20],OP2的目标函数可以转变为
其中:η>0。
当η收敛到+∞时,F(η)<0,当η收敛到-∞时,F(η)>0;因此F(η)是关于η的凸函数且是η的递减函数。如果最优解是xf,k,s和τf,k,s,则最优能效η可由
得到,因此最优能效为
基于上述分析,优化问题OP2可转变为
对于给定的η,式(16)中的目标函数是关于xf,k,s 和τf,k,s 的凹函数,因此目标函数是凹的,凹性在附录中被证明。由于式(16)中的不等式约束是凸的,则目标函数的可行集是凸集,OP3是凸优化问题,所以OP3的闭式解可以通过拉格朗日对偶理论推导出来。
2.2 拉格朗日对偶分解法
本节通过使用拉格朗日对偶分解法用求解最优子信道和功率分配策略,优化问题OP3的拉格朗日函数为
其中:μ,λ,ν,δ,π分别为约束C2、C3、C5、C6、C7的拉格朗日乘子向量组,边界约束C1和C4被包含在KKT条件[21]中,对偶函数和对偶问题分别为
该拉格朗日对偶问题可以使用分解法来解决,可分解为一个主对偶问题和F×K个子问题,两类问题都可以使用迭代法解决。首先,通过给定的拉格朗日乘子,利用KKT条件获得最优子信道和功率分配策略;其次,使用次梯度法更新拉格朗日乘子,直到收敛。因此式(17)重写为
题,表达式为
所以,认知毫微微小区f中的SU-s在SC-k上获得的最优功率为
接下来,同理可知
基于式(24),SC-k应该分配给认知毫微微小区f中具有最大Hf,k,s的SU-s,即
以上是F×K个子问题的解决过程,由于主对偶问题是可微的,可以通过迭代更新的次梯度方法解决。基于次梯度方法,主对偶问题求解如下:
2.3 算法及其复杂度分析
2.3.1 算法
尽管式(23)(25)~(29)已经给出了资源分配问题的解决方案,但仍需设计一种算法来指示以上公式的执行结构。因此,总结上文,提出了迭代的子信道和功率分配(iterative sub-channel and power allocation,ISPA)算法,具体形式如下:
算法1 ISPA算法
算法1同时进行子信道分配和功率分配,使优化问题得到一个最优的解,但该算法的复杂度会随着认知毫微微基站数、每个认知毫微微小区中次级用户数和子信道数的增长呈指数上升,对未来超密集网络部署环境来说并不适用,因此提出一个低复杂度但次优(low complexity but suboptimal,LCS)的算法(算法2)。
算法2是由保障每个次级用户QoS需求的次优子信道分配和跨层干扰约束下的最优功率分配组成。这种做法的好处就是大大降低了算法的计算复杂度,坏处是与算法1相比,系统的吞吐量和能效将降低,具体形式如下:
算法2 LCS算法
2.3.2 复杂度分析
算法1在计算式(23)功率分配和式(25)子信道分配时都需要进行O(FKS)次运算,设拉格朗日乘子最大收敛次数为Δ,根据式(26)~(29)更新拉格朗日乘子时需要进行O(K4S2F)次运算,故Δ是关于K4S2F的多项式函数,设Δη为算法1收敛时更新η的次数,所以算法1的计算复杂度为O(ΔηK2S2F2Δ)。在算法2中,为每个次级用户分配子信道阶段的复杂度为O((Klog2K+K)FS),保障其QoS需求阶段的复杂度为O((K-S)Slog2S),再考虑更新拉格朗日乘子时的计算复杂度,得到算法2的计算复杂度为O(FKS log2K+KS log2S+K4S2F)。可见,算法2的复杂度低于算法1的复杂度。
3 仿真实验与结果分析
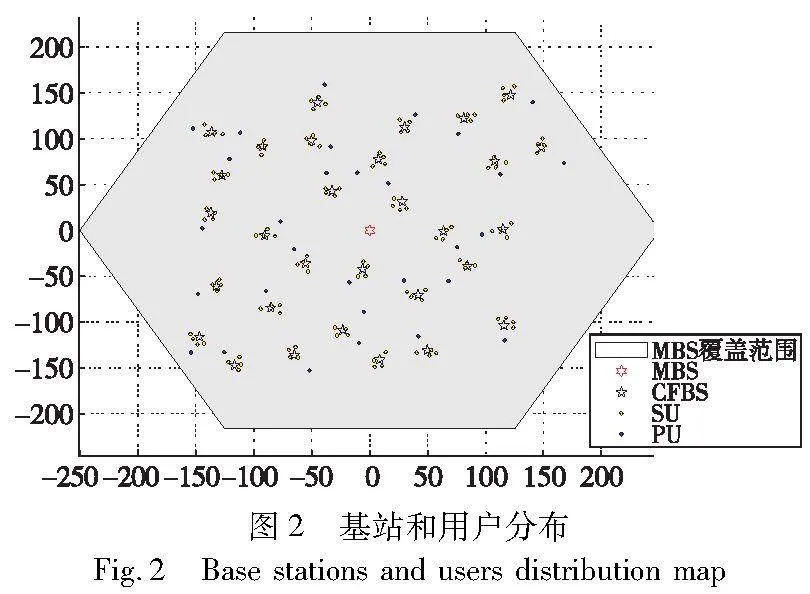
本文利用MATLAB软件进行实验仿真,使用计算机的配置如表1所示。仿真场景由MBS和密集部署的CFBS组成,PU和CFBS随机分布在MBS的覆盖范围内,SU随机分布在CFBS的覆盖范围内,每个CFBS服务的SU个数不超过6个;图2所示是1个MBS,30个CFBS,每个CFBS服务4个SU,30个PU的基站用户分布图。
将本文算法与其他两种资源分配算法进行性能比较,分别是文献[10]中的信道分配算法和注水功率分配算法构成的两阶段算法,记为算法3;文献[11]中的信道分配算法和等功率分配算法构成的两阶段算法,记为算法4。
对于信道模型,包括路径损耗和阴影衰落的大尺度衰落和瑞丽型小尺度衰落被考虑。且所有SU的QoS需求相同,其他参数如表2所示。
图3对比了四种算法在不同CFBS数量下次级网络的能效。设定的参数为:S=4,IFMth=IFFth=-110 dBm,Rmin=5 bit/s/Hz。仿真结果表明:能效随着CFBS数量的增加而降低,因为CFBS变多使网络中的干扰和能耗变大,导致网络性能下降。本文算法1、2的性能总是优于对比算法,算法1的优异性能是牺牲巨大计算复杂度换取的;算法2在权衡计算复杂度的同时性能表现也不错,其优于对比算法是因为其功率分配算法是最优的;不同的功率分配算法对能效的影响很大,算法3依据信道状态的好坏分配功率,对比于本文功率分配算法其性能较差,算法4将相等的功率分配给所有可用的子信道浪费了功率。
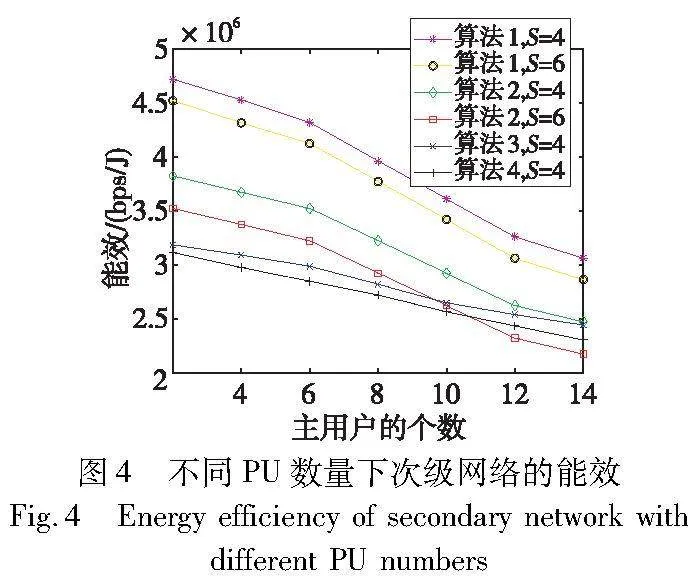
图4对比了四种算法在不同PU数下次级网络的能效。设定的参数为S=4或6,IFMth=IFFth=-90 dBm,Rmin=5 bit/s/Hz,F=15。
观察图4可得:随着PU的增多,四种不同算法所对应的次级网络能效都呈现下降趋势,这是因为PU增多会导致SU可使用的信道数减少,从而降低了次级网络的吞吐量,导致能效变差。且能效随着SU的增多而降低,因为在跨层干扰约束下,CFBS为了保证SU的QoS需求会向其分配足够大的功率,SU数量的增多会增加网络能耗,降低网络能效。
图5是本文算法1在CFBS不同发射功率阈值下实现的次级网络平均吞吐量。
从图中可以观察到,次级网络的平均吞吐量随着CFBS发射功率阈值的增加而增加;这是因为在一个认知毫微微小区中,具有较小吞吐量的SU被分配较小的功率,然而当SU有较高的吞吐量需求时,CFBS分配最优功率来满足其需求,但受制于最大发射功率阈值。且固定发射功率阈值,干扰门限越大,平均吞吐量越大;因为干扰门限越大,对宏小区而言,认知毫微微小区对其造成的可容忍干扰越大,SU接收到CFBS为其分配的功率上限越大,吞吐量越大。
图6给出了四种算法关于次级网络吞吐量的收敛性。设置的参数为:F=20,S=6,Rmin=5 bit/s/Hz,IFMth=IFFth=-90 dBm。观察可得,算法1相对于算法2更能提高次级网络的吞吐量,且它们都优于对比算法。算法1、2、4都能在很少的迭代次数中收敛到最优,算法2迭代至平稳达到最优所需次数最少,算法3虽收敛较慢但性能并不是最差的。
4 结束语
本文基于OFDMA的CR-UDN中下行传输场景,联合考虑次级用户QoS需求、次级网络同层干扰约束、主用户通信质量保障,提出了两种子信道资源和功率资源分配算法来最大化非完美频谱感知下CR-UDN中次级网络的能量效率。仿真结果表明与现有的一些算法相比,本文算法可以获得较高的能效。但本文所考虑的系统模型是基于完美的信道状态信息,在下一步研究中将考虑更加实际的场景,即研究非完美信道状态信息和非完美频谱感知模型下的资源分配问题。
附录
基于此可以求得
为了证明Euclid Math OneHAp的半负定性,引入引理1:Euclid Math OneAAp为N×N的对称矩阵,则Euclid Math OneAAp为半负定矩阵当且仅当Euclid Math OneAAp的k阶主子式在k为奇数时小于等于0,在k为偶数时大于等于0,其中1≤k≤N。可以很轻松地看出Euclid Math OneHAp的一阶主子式是负的,二阶主子式是零,因此Euclid Math OneHAp为半负定矩阵,f(xf,k,s,τf,k,s)为凹的。又因为凹函数的任何线性正加权之和仍是凹的,所以得证。
参考文献:
[1]Xu Yongjun,Gui Guan,Gacanin H,et al. A survey on resource allocation for 5G heterogeneous networks: current research,future trends,and challenges[J]. IEEE Communications Surveys & Tutorials,2021,23(2): 668-695.
[2]Sharma N,Kumar K. Resource allocation trends for ultra dense networks in 5G and beyond networks: a classification and comprehensive survey[J]. Physical Communication,2021,48: 101415.
[3]Nasser A,Hassan H A H,Chaaya J A,et al. Spectrum sensing for cognitive radio: recent advances and future challenge[J]. Sensors,2021,21(7): 2408.
[4]Koteeshwari R S,Malarkodi B. Spectrum sensing techniques for 5G wireless networks: mini review[J]. Sensors International,2022,3: 100188.
[5]Ivanov A,Tonchev K,Poulkov V,et al. Framework for implementation of cognitive radio based ultra-dense networks[C]// Proc of the 42nd International Conference on Telecommunications and Signal Proces-sing. Piscataway,NJ: IEEE Press,2019: 481-486.
[6]Tseng F H,Chou L D,Chao H C,et al. Ultra-dense small cell planning using cognitive radio network toward 5G[J]. IEEE Wireless Communications,2015,22(6): 76-83.
[7]王改花,谢健骊,李翠然. 基于博弈资源分配的认知异构网络干扰协调算法[J]. 计算机应用研究,2023,40(1): 244-248,256.(Wang Gaihua,Xie Jianli,Li Cuiran. Interference coordination algorithm for cognitive heterogeneous networks resource allocation based on game theory[J]. Application Research of Computers,2023,40(1): 244-248,256.)
[8]张达敏,王义,邹诚诚,等. 认知异构蜂窝网络中改进蜉蝣算法的资源分配策略[J]. 通信学报,2022,43(6): 156-167.(Zhang Damin,Wang Yi,Zou Chengcheng,et al. Resource allocation strategies for improved mayfly algorithm in cognitive heterogeneous cellular network[J]. Journal on Communications,2022,43(6): 156-167.)
[9]张俊杰,仇润鹤. 基于用户分簇的认知超密集网络资源分配[J]. 电讯技术,2022,62(9): 1321-1327.(Zhang Junjie,Qiu Runhe. Resource allocation for cognitive radio ultra-dense network based on user clustering[J]. Telecommunication Engineering,2022,62(9): 1321-1327.)
[10]张俊杰,仇润鹤. 认知超密集网络用户关联与资源分配联合优化遗传算法[J]. 计算机应用,2022,42(12): 3856-3862.(Zhang Junjie,Qiu Runhe. Joint optimization of user association and resource allocation in cognitive radio ultra-dense networks to improve genetic algorithm[J]. Journal of Computer Applications,2022,42(12): 3856-3862.)
[11]Yang Liwei,Jia Boyu,Wang Fang,et al. Energy efficiency optimization of heterogeneous network resources based on OFDMA[C]// Proc of the 20th International Conference on Optical Communications and Networks. Piscataway,NJ: IEEE Press,2022: 1-3.
[12]Prabhavathi S,Saminadan V. Energy efficient allocation of resources in NOMA based(MU-HCRN) with perfect spectrum sensing[C]// Proc of International Conference on Computing Science,Communication and Security. Cham: Springer,2022: 274-285.
[13]孙艳,彭代渊,梁宏斌. 基于不完美频谱感知的认知Femtocells资源分配算法研究[J]. 成都信息工程大学学报,2016,31(1): 35-41.(Sun Yan,Peng Daiyuan,Liang Hongbin. Resource allocation in cognitive femtocells with imperfect spectrum sensing[J]. Journal of Chengdu University of Information Technology,2016,31(1): 35-41.)
[14]唐丽萍,江逸伦. 基于不完美频谱检测的认知无线电网络资源分配[J]. 计算机工程,2019,45(8): 173-177,197.(Tang Liping,Jiang Yilun. Resource allocation in cognitive radio network based on imperfect spectrum detection[J]. Computer Engineering,2019,45(8): 173-177,197.)
[15]Xu Lei,Yin Weixin,Zhang Xiaoling,et al. Fairness-aware throughput maximization over cognitive heterogeneous NOMA networks for industrial cognitive IoT[J]. IEEE Trans on Communications,2020,68(8): 4723-4733.
[16]Thangaraj C A,Aruna T. Energy-efficient power allocation with gua-ranteed QoS under imperfect sensing for OFDM-based heterogeneous cognitive radio networks[J]. Wireless Personal Communications,2019,109: 1845-1862.
[17]Verma K,Bharti M R. Energy-efficient resource allocation in cognitive radio networks[C]// Proc of International Conference on Frontiers of Intelligent Computing: Theory and Applications. Singapore: Sprin-ger,2022: 137-150.
[18]Xu Yongjun,Yang Yang,Liu Qilie,et al. Joint energy-efficient resource allocation and transmission duration for cognitive HetNets under imperfect CSI[J]. Signal Processing,2020,167: 107309.
[19]Wong C Y,Cheng R S,Lataief K B,et al. Multiuser OFDM with adaptive subcarrier,bit,power allocation[J]. IEEE Journal on Selected Areas in Communications,1999,17(10): 1747-1758.
[20]Dinkelbach W. On nonlinear fractional programming[J]. Management Science,1967,13(7): 492-498.
[21]Boyd S,Vandenberghe L. Convex optimization[M]. Cambridge: Cambridge University Press,2004.
