多域网络中基于域间时延博弈的端到端动态协同切片方法
2024-07-31赵季红董莎胡晓燕崔文静
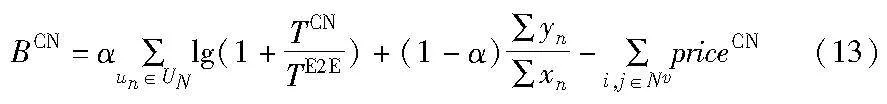

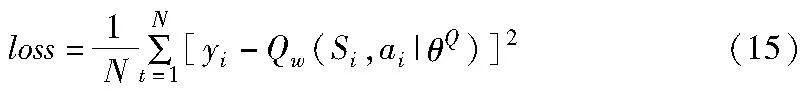
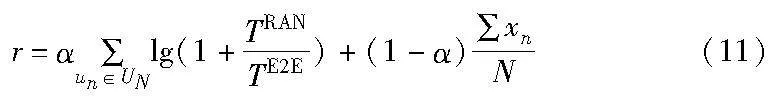

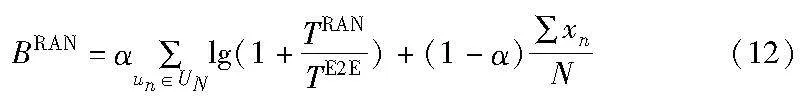
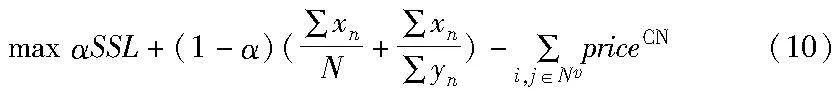


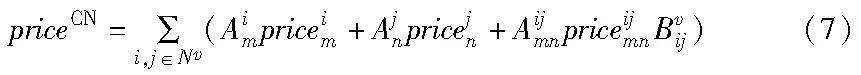
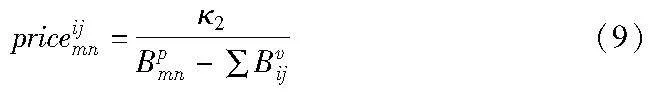


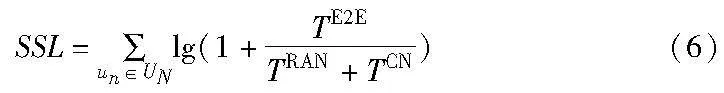
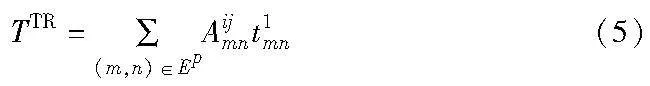






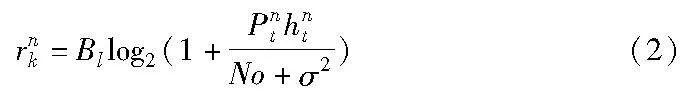
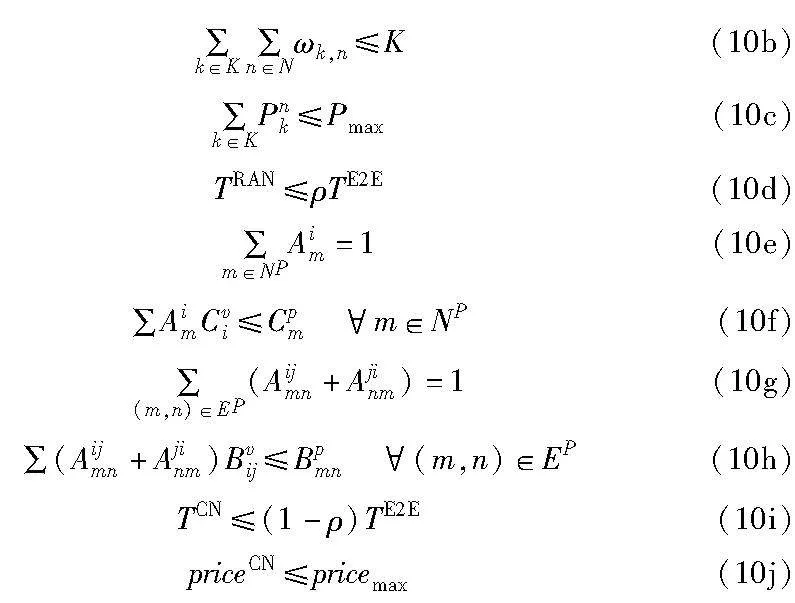
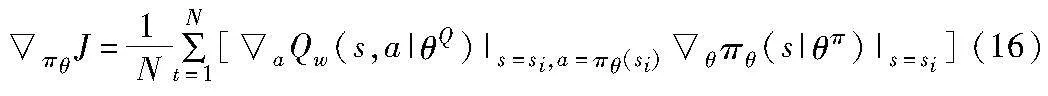
摘 要:针对多域网络中的切片存在域间时延不均的问题,提出了一种基于域间时延博弈的端到端动态协同切片方法(inter-domain dynamic game algorithm,IDGA)。采用博弈论方法将端到端时延约束分配到不同的网络域,通过在域内部署切片来获得相应的博弈收益,采用DDPG算法不断更新博弈策略,最终得到最佳的时延分配比例和切片部署方案。实验表明,该算法与传统的静态分配算法对比有明显优势,与经验迭代的DSDP方法以及DQN-SNAF算法相比,IDGA算法在100个切片请求下,切片部署成功率分别提高了8%和3%左右,同时节点资源利用率提高了5.75%和1.96%左右,在降低部署成本方面也有显著优势。
关键词:多域网络; 网络切片; 切片协同; 纳什博弈; 强化学习
中图分类号:TN929.5 文献标志码:A
文章编号:1001-3695(2024)06-032-1820-05
doi:10.19734/j.issn.1001-3695.2023.09.0434
End-to-end dynamic collaborative slicing method based on inter-domain
delay game in multi-domain network
Abstract:Aiming at the problem of uneven inter-domain delay in slicing in multi-domain networks, this paper proposed an end-to-end dynamic cooperative slicing method based on inter-domain delay game. This method used game theory methods to allocate end-to-end delay constraints to different network domains, and deployed slices within the domain to obtain correspon-ding game benefits. It used the DDPG algorithm to continuously update the game strategy, and finally obtained the optimal delay allocation ratio and slice deployment solution. Experiments show that compared with the traditional static allocation algorithm, the proposed algorithm has obvious advantages. Compared with the empirically iterative DSDP method and the DQN-SNAF algorithm, the IDGA algorithm increased the slice deployment success rate by about 8% and 3% respectively under 100 slice requests. At the same time, the node resource utilization rate increased by about 5.75% and 1.96%. There are also significant advantages in reducing deployment costs.
Key words:multi-domain network; network slicing; slice collaboration; Nash game; reinforcement learning
0 引言
多域网络切片是指将网络切片的概念扩展到跨多个网络域,每个网络域可以由不同的网络运营商或管理实体管理[1]。在5G端到端网络中,多域网络切片包括接入网域、传输网域以及核心网域。多域网络切片相比单域网络切片面临着跨域协调与管理、跨域资源共享[2]以及跨域管理复杂性[3]等问题。解决这些问题需要各个域之间的合作与协调,以确保多域网络切片的有效实施和资源的优化利用[4]。通过域间的协同合作,可以实现资源的跨域调配[5]和共享,提高资源利用效率,满足各个域的需求。
针对多域网络的域间协同,有学者也进行了相关研究。例如Chien等人[6]针对多域网络端到端时延分配采用了固定的分配比率,使端到端时延低于服务实际所需时延,但导致了资源浪费。Kovacevic等人[7]提出了一种自适应的三阶段多域切片算法,用于将网络切片映射到物理网络资源,以实现延迟有限的服务。但需要获取各域拓扑信息,损害了各域之间的隐私性[8]。Bai等人[9]提出了两种延迟均衡策略,根据不同切片划分不同比例和根据不同类型切片划分不同比例,提高了系统容量,但只是基于简单的比例分配调整,不能确定达到最优的分配比例。文献[10]提出了一种基于切片到节点接入因子(SNAF)的端到端切片资源供应方案,使用SNAF资源调整方案来调整切片权重以反映资源占用情况,再使用DRL算法进行资源分配,实时联合处理分片到节点的流量负载分配和端到端资源分配。虽然SNAF算法在一定程度上减少了资源浪费,提高了资源利用率,但在资源短缺的情况下不能很好地调节多域间的资源竞争和分配。
总之,现有的研究方法主要是针对多域网络切片的联合以及端到端网络切片的资源分配,主要考虑域间资源共享和域间合作进行资源的部署和调整,很少从多域博弈的角度考虑域间资源竞争问题。本文从时延可分割性[9]出发,在保证端到端整体性能的同时进行域间协同,提出了一种基于域间时延博弈的端到端动态协同切片方法(IDGA)。将端到端时延约束分割为接入网时延约束和核心网时延约束,使用纳什博弈[11]方法,接入网和核心网分别为博弈玩家,端到端时延约束分配比例作为博弈策略,使用深度确定型策略梯度(deep deterministic policy gradient,DDPG)算法更新博弈策略,得到最优的时延约束分配比例。针对博弈玩家内部,使用分配到的时延约束进行切片部署。其中,接入网使用深度Q学习(deep Q-network,DQN)进行切片部署,核心网切片部署同时考虑了部署成本问题。本文方法采用分布式架构,无须展示各域拓扑信息,保证了切片的隐私性;并且采用强化学习算法进行策略更新,能够动态适应网络变化,在满足端到端时延约束的同时最大化资源利用和切片部署成功率,以及最小化部署成本[12]。
1 系统模型与问题描述
1.1 系统模型
底层网络的基础设施由接入网络和核心网络组成。接入网为多个RRU组成的蜂窝网络,其资源可以抽象为物理资源块(PRB),将时域T分为M个时隙Δt,在每个时隙Δt时间内,BHz的总带宽可以被分为L个物理资源块(PRB)。所以PRB总量为K=M·L,一组时频资源的PRB可以表示为k={1,2,3,…,K}。核心网可用无向图Gp=(Np,Ep)表示,其中Np和Ep表示底层核心网的物理节点集合和物理链路集合。节点资源主要考虑计算资源,用Cpn表示节点n∈NP的计算资源容量。链路资源主要用带宽表述,用Bpmn表示链路(m,n)∈Ep的带宽容量。假设用户以泊松过程随机分布在基站的覆盖范围内,用户数量为N,用户集为UN={u1,u2,u3,…,uN}。用户请求到达时会识别出端到端时延要求TE2E,将TE2E分配给接入网ρTE2E和核心网(1-ρ)TE2E,以此为时延阈值进行切片部署。系统模型如图1所示。
1.2 问题描述
1.2.1 域间时延博弈系统描述
对于端到端的网络切片请求,用户的时延包括接入网时延和核心网时延,所以可以将端到端的时延预算TE2E分解为两部分,分别为RAN时延约束ρTE2E和CN时延约束(1-ρ)TE2E。两方都要争抢更多的时延预算来提高自身切片部署成功率,所以如何确定时延分配比例是研究的重点。使用纳什博弈的方法在接入网和核心网之间进行博弈,以确定最佳的时延分配比例。而在RAN和CN内部,以分配到的时延预算为约束进行切片部署和资源分配。
在RAN内部,假设业务流为M/M/1排队模型,数据包到达速率为μ,平均长度为λ bit。则用户的平均传输延迟可表示为
其中:Rn=∑ωk,nrnk为用户总吞吐量。
ωk,n为二进制变量,表示基站对用户的资源分配结果,当PRBk分配给用户un时ωk,n=1,否则ωk,n=0。
rnk为RRU在PRBk上给用户un提供的速率。
其中:Pnk表示基站在PRBk上给用户un分配的功率;hnt表示信道增益;Bl为在PRBk给用户分配的带宽;No为其他基站引起的噪声干扰;σ2为噪声功率。
在CN内部切片请求用有向图表示为Gv=(Nv,Ev),其中Nv表示VNF的集合,Ev表示虚拟链路的集合。假设i,j∈Nv两个前后相关的VNF,所需要的节点处理资源为Cvi和Cvj,它们之间直接连接的虚拟链路(i,j)∈Ev所需要的带宽资源为Bvij。用一个二进制变量Aim来表示VNF和物理节点的映射关系,用二进制变量Aijmn表示虚拟链路(i,j)是否映射到物理链路(m,n)。核心网的时延TCN由两部分组成,即节点处理时延TN和链路传输时延TTR。
节点处理时延与节点负载有关,节点负载可以定义为节点总VNF资源需求与物理节点处理能力的比率:
假设节点m的处理时延为tm=αCload m+β,节点处理总时延为
假设链路传输的每一跳时延是定值t1,则链路传输总时延为
核心网总时延TCN=TN+TTR。
1.2.2 优化目标
域间时延博弈的目的是在接入用户和请求尽可能多的前提下,最大化用户满意度和切片部署成功率以及最小化用户部署成本[12]。
用户的满意度为用户切片部署时延与时延要求的比较,部署时延越大,满意度越低,反之越高。
部署成本考虑核心网虚拟网络映射成本,定义为
其中:priceim为VNF映射到物理节点m的成本,与剩余资源量成反比,即
priceijmn为单位带宽的链路映射成本,与剩余带宽成反比,即
目标函数可以表示为
xn=1表示用户成功访问基站并满足相关约束;yn=1表示用户满足核心网约束成功部署切片。
约束条件为
约束条件式(10a)表示一个PRB只能分配给一位用户;式(10b)表示用户占用的PRB数量不能超过PRB总数;式(10c)表示给用户分配的功率不能超过最大功率;式(10d)表示接入网的时延不能超过给接入网分配的时延阈值;式(10e)表示每个VNF只能映射到一个物理节点上;式(10f)表示映射到物理节点上的资源需求不能超过物理节点的容量;式(10g)表示每个虚拟链路只能映射到一个物理链路上;式(10h)表示映射到物理链路上的资源需求不能超过物理链路的带宽容量;式(10i)表示核心网的时延不能超过给核心网分配的时延阈值;式(10j)表示核心网的部署成本不能超过运营商最大成本限制,使运营商有利可图。
由于上述优化问题难以直接求解,本文提出了一种基于域间时延博弈的端到端网络切片协同算法,使用强化学习方法在约束条件内经过多次博弈迭代,以优化目标为收益,寻找使长期收益最大的最优解。
2 基于域间时延博弈的端到端切片协同算法
为了在满足用户端到端QoS要求的基础上扩大网络系统容量,本文提出了一种基于域间时延博弈的端到端切片协同算法(IDGA)。算法主要由域间时延博弈和域内切片部署两部分组成。域间时延博弈采用博弈论方法将端到端时延分配给接入网(RAN)域和核心网(CN)域,并获得一定的博弈收益。将博弈收益作为奖励函数,使用强化学习方法不断进行博弈迭代,直到达到纳什均衡状态。域内切片部署则在RAN和CN域内,根据分配到的时延进行域内切片部署,并得到部署成功率及部署成本等数据作为域间时延博弈的博弈收益。经过强化学习算法的不断迭代,最终得到最佳的切片部署策略。
2.1 域间时延博弈
2.2 域内切片部署和博弈收益
2.2.1 RAN切片部署和博弈收益
强化学习算法[13]进行切片部署可以适应接入网环境的不确定性,优化策略并考虑长期回报,具备自适应性和自学习能力,因此考虑使用适用于高维状态空间的经验回放的DQN算法[14]进行接入网切片部署。在接入网中,优化目标是最大化用户满意度和接入成功率。对于RAN切片部署,假定一个用户代表一个切片,智能体为RAN域控制器。定义强化学习的{St,A,R,St+1}如下:
状态空间(state):sn∈SN表示切片资源分配状态,定义为用户的接收信干噪声比sn=SINRn。
动作空间(action):an∈AN表示用户的PRB和功率分配,ant=({PRBn}1×M,{pnt}1×M)1×N。
奖励(reward):以用户的满意度和接入成功率作为奖励函数。
使用具有优先经验回放的DQN算法进行切片部署,智能体将数据存储在一个数据库中,采用均匀随机采样的方式从数据库中抽取数据,然后利用抽取到的数据训练神经网络。利用训练好的神经网络进行切片部署。接入网切片部署成功后,得到用户接入实际时延TRANu,并且将奖励函数作为接入网博弈收益。
2.2.2 CN切片部署和博弈收益
在核心网中,虚拟网络映射[15]包括节点映射和链路映射。节点映射[16]指在物理网络中寻找合适的物理节点承载虚拟节点,需要考虑虚拟节点的资源需求和物理节点的资源能力,以保证映射后虚拟节点能够正常工作。同时,考虑节点部署成本问题,由于资源单价与物理节点剩余资源量成反比,所以本文采用基于排序的节点映射算法[17]。使用广度优先搜索算法[18]将虚拟节点和物理节点基于节点资源量等指标进行降序排序,按照切片部署算法将评分高的虚拟节点映射到评分高的物理节点上。这样不仅可以提高部署成功率,还能降低部署成本单价,从而降低部署成本。最后根据节点映射结果,使用最短路径算法[19]进行链路映射。
核心网切片部署成功后,得到用户核心网实际时延TCNu。CN的博弈收益定义为用户满意度和部署成功率以及部署成本的加权和。
2.3 基于DDPG的策略更新算法
DDPG是一种强化学习算法,通过训练一个深度神经网络[20]来估计策略函数,并通过连续动作空间中的策略梯度方法[21]来更新策略。DDPG算法具有较强的适应性和学习能力,可以在复杂的网络环境中自主学习并优化策略[22]。智能体从环境中得到的状态空间S表征为接入网和核心网的时延余量τ=TE2E-TRAN-TCN,智能体的动作空间A为博弈策略,即时延分配比例ρ、1-ρ,令博弈收益R=BRAN+BCN作为奖励函数,以最大化长期收益为目的进行训练和动作选择,当时延余量τ小于优化阈值D时,判定智能体达到终止条件。基于DDPG的策略更新算法框架如图3所示。
DDPG算法使用演员-评论家(Actor-Critic)算法[23]作为其基本框架,采用深度神经网络作为策略网络和动作值函数的近似,使用随机梯度法[24]训练策略网络和价值网络模型中的参数。Actor网络作出动作指令,再由Critic网络对其动作产生的回报值进行计算,并更新其参数权重。
Critic训练网络输出当前时刻状态-动作的Q值函数Qw(St,at),用于评价当前策略。Critic目标网络用于近似估计下一时刻的状态-动作的Q值函数Qw′(St+1,πθ′(St+1)),其中,下一动作值是通过Actor目标网络近似估计得到的πθ′(St+1)。当前状态下Q值函数的目标值为
yt=rt+γQw′(St+1,πθ′(St+1))(14)
通过最小化损失值(均方误差损失)来更新Critic网络的参数,Critic网络更新时的损失函数为
Actor目标网络用于提供下一个状态的策略,Actor训练网络则是提供当前状态的策略,结合Critic训练网络的Q值函数,可以得到Actor在参数更新时的策略梯度:
算法1 基于DDPG的策略更新算法
3 仿真验证与结果分析
本文在英特尔酷睿i5-7200U服务器上运行所有模拟。在Windows 64位操作系统下,通过Python 3.7中的Anacoda集成开发环境,使用PyTorch 1.4构建网络,并使用CUDA 10.1来加快操作速度。通过仿真实验来验证所提出的基于域间时延博弈的端到端动态协同切片方法的有效性,并与静态比例分割以延迟均衡策略[9]的DSDP(different slices different proportions)算法以及使用强化学习的DQN-SNAF算法[10]在切片部署成功率、资源利用率和部署成本方面进行对比分析。
3.1 仿真设置
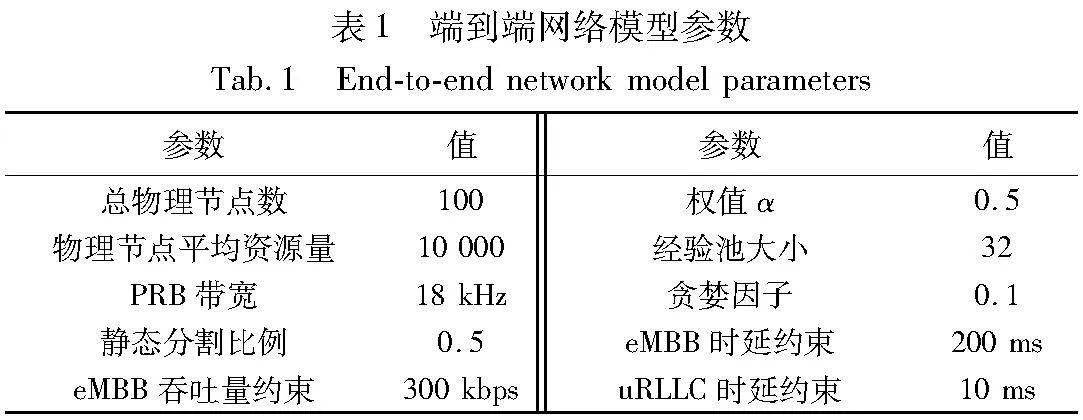
在仿真系统中,模拟了接入网环境和核心网环境,首先接入网设置了一个基站覆盖范围在半径100 m的圆内,在基站覆盖范围内用户随机分布,核心网拓扑结构使用典型的数据中心拓扑,由交换节点和服务节点组成,采用Fat-Tree网络结构[25],VNs的拓扑由预编程的拓扑生成器随机生成,VNs的生存时间在CloudSim中随机分布在[100,1000]个时间单位中。详细参数如表1所示。
3.2 仿真结果分析
从30个用户请求到100个用户请求反复测试,得到的请求部署成功数量如图4所示。可以看出,在用户数量较少时四种算法差异性不大,基本都可以成功部署。随着用户请求的增多,四种算法差异性逐渐明显,其中静态分割在某个域需求流量大时无法及时有效地分配资源,会造成时延增大从而无法达到用户SLA,导致不能成功部署切片。DSDP算法在经过迭代分配效果优于静态算法,但由于迭代的局限性,不能达到最佳分配。DQN-SNAF算法在请求数量少时有较优的性能,但在切片数量较多、资源不足的情况下不能协调各域资源,导致部署成功率较低。IDGA算法可以实现跨域资源的动态调整,并使用强化学习方法达到最优的分配比例。相比于其他三个算法有较优的性能,在100个请求下,其部署成功率比DSDP算法提高了8%左右,比DQN-SNAF算法提升了3%左右。
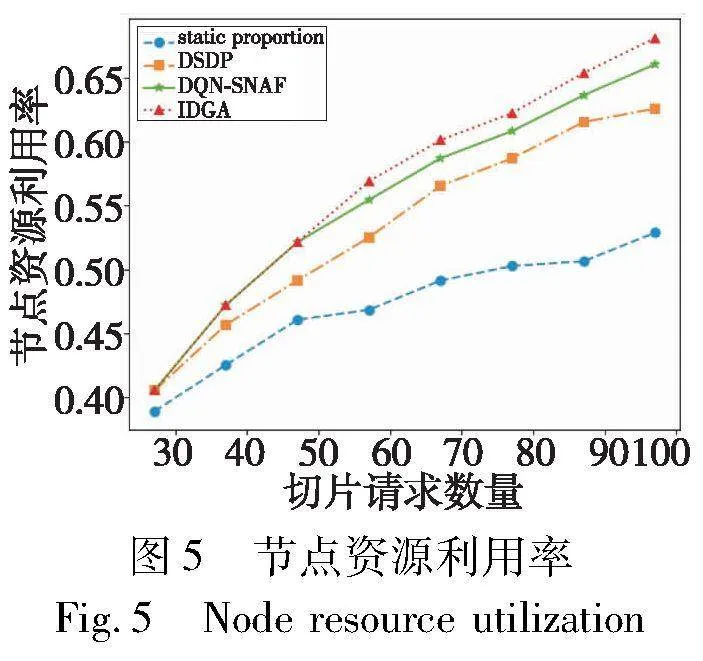
四种算法的节点资源利用率如图5所示。可以看到,随着切片数量增加节点资源利用率不断增大,静态分配的节点资源利用率远低于其他两种算法,因为静态分割法采用固定的分配比率,在某个域用户需求小时,仍占用较多资源导致资源浪费。DQN-SNAF算法通过调节节点资源分配提升了资源利用率,但随着切片数量的增加,IDGA算法域间资源协同优势更为突出,在100个请求下,平均节点资源利用率比DSDP算法提高了5.75%左右,比DQN-SNAF算法提升了1.96%左右。可以证明使用域间协同和强化学习算法,能进一步达到最优的时延分割比例,提升了资源的有效利用,扩大了系统容量。
四种算法的平均部署成本如图6所示。从图中可以看出,随着切片数量增多,资源紧缺导致部署成本不断增加。本文IDGA算法核心网切片部署时综合考虑了部署成本,以最小化部署成本为优化目标,通过节点排序的方式,优先映射资源单价较低的节点,从而降低了部署成本。但在切片请求数量较多的情况下,由于成功部署切片数量远多于静态分配算法,平均部署成本也略高于静态分配。
4 结束语
本文在多域网络环境下,针对域间时延分配不均的问题,提出了一种基于域间时延博弈的端到端动态协同切片方法。利用时延的可分割性,通过接入网域和核心网域之间的动态博弈将端到端时延进行最优分配。在寻优的过程中,使用强化学习算法进行博弈策略的更新,确保随着网络环境的变化能得到最优的时延分配。通过仿真实验证明,本文算法能够有效地增加成功部署切片的数量,提高节点资源利用率,扩大系统容量的同时降低部署成本。但本文研究中简化了端到端网络模型,忽略了传输网的影响,且只考虑了单一的业务类型,在后续的研究中会进一步完善端到端网络模型,同时考虑多业务的影响。
参考文献:
[1]Chahbar M, Diaz G, Dandoush A, et al. A comprehensive survey on the E2E 5G network slicing model[J]. IEEE Trans on Network and Service Management, 2020,18(1): 49-62.
[2]Wang Qi, Alcaraz-Calero J, Weiss M B, et al. SliceNet: end-to-end cognitive network slicing and slice management framework in virtua-lised multi-domain, multi-tenant 5G networks[C]//Proc of IEEE International Symposium on Broadband Multimedia Systems and Broa-dcasting. Piscataway, NJ: IEEE Press, 2018: 1-5.
[3]周新力. 基于马氏决策过程的多域网络切片资源管理[D]. 北京:北京邮电大学, 2020. (Zhou Xinli. Multi-domain network slice resource management based on Markov decision process[D]. Beijing:Beijing University of Posts and Telecommunications, 2020.)
[4]Afolabi I, Prados-Garzon J, Bagaa M, et al. Dynamic resource provisioning of a scalable E2E network slicing orchestration system[J]. IEEE Trans on Mobile Computing, 2019,19(11): 2594-2608.
[5]Baba H, Hirai S, Nakamura T, et al. End-to-end 5G network slice resource management and orchestration architecture[C]//Proc of the 8th International Conference on Network Softwarization. Piscataway, NJ: IEEE Press, 2022: 269-271.
[6]Chien H T, Lin Y D, Lai C L, et al. End-to-end slicing with optimized communication and computing resource allocation in multi-tenant 5G systems[J]. IEEE Trans on Vehicular Technology, 2019,69(2): 2079-2091.
[7]Kovacevic I, Shafigh A S, Glisic S, et al. Multi-domain network slicing with latency equalization[J]. IEEE Trans on Network and Service Management, 2020,17(4): 2182-2196.
[8]He Guobiao, Wei Su, Gao Shuai, et al. NetChain: a blockchain-enabled privacy-preserving multi-domain network slice orchestration architecture[J]. IEEE Trans on Network and Service Management, 2021,19(1): 188-202.
[9]Bai Haonan, Zhang Yong, Zhang Zhenyu, et al. Latency equalization policy of end-to-end network slicing based on reinforcement learning[J]. IEEE Trans on Network and Service Management, 2023,20(1): 88-103.
[10]Sebakara S R A, Boateng G O, Mareri B, et al. SNAF: DRL-based interdependent E2E resource slicing scheme for a virtualized network[J]. IEEE Trans on Vehicular Technology, 2023,72(7): 9069-9084.
[11]Greiner D, Periaux J, Emperador J M, et al. Game theory based evolutionary algorithms: a review with Nash applications in structural engineering optimization problems[J]. Archives of Computational Methods in Engineering, 2017,24: 703-750.
[12]Zhao Yujing, Shen Jing, Wang Qi, et al. Service function chain deployment for 5G delay-sensitive network slicing[C]//Proc of the 17th International Wireless Communications and Mobile Computing . Piscataway, NJ: IEEE Press, 2021: 68-73.
[13]Sánchez J A H, Casilimas K, Rendon O M C. Deep reinforcement learning for resource management on network slicing: a survey[J]. Sensors, 2022,22(8): 3031.
[14]Fhrmann D, Jorek N, Damer N, et al. Double deep Q-learning with prioritized experience replay for anomaly detection in smart environments[J]. IEEE Access, 2022,10: 60836-60848.
[15]Nguyen K, Huang C. Toward adaptive joint node and link mapping algorithms for embedding virtual networks: a conciliation strategy[J]. IEEE Trans on Network and Service Management, 2022,19(3): 3323-3340.
[16]Yaghoubpour F, Bakhshi B, Seifi F. End-to-end delay guaranteed SFC deployment: a multi-level mapping approach[EB/OL]. (2021-02-11). https://arxiv.org/abs/2102.06090.
[17]管婉青. 基于多层复杂网络理论的网络切片协作管理研究[D]. 北京:北京邮电大学, 2019. (Guan Wanqing. Research on collaborative management of network slicing based on multi-layer complex network theory[D]. Beijing :Beijing University of Posts and Telecommunications, 2020.)
[18]Akram V K, Asci M, Dagdeviren O. Design and analysis of a breadth first search based connectivity robustness estimation approach in wireless sensor networks[C]//Proc of the 6th International Conference on Control Engineering & Information Technology. Piscataway, NJ: IEEE Press, 2018: 1-6.
[19]Huang Guanghao, Lu Wei, Xie Jidong, et al. Improved route selection strategy based on K shortest path[C]//Proc of International Symposium on Networks, Computers and Communications. Piscataway, NJ: IEEE Press, 2019: 1-4.
[20]Cai Zhiqiang, Chen Jingshuang, Liu Min. Self-adaptive deep neural network: numerical approximation to functions and PDEs[J]. Journal of Computational Physics, 2022,455: 111021.
[21]Khalid J, Ramli M A M, Khan M S, et al. Efficient load frequency control of renewable integrated power system: a twin delayed DDPG-based deep reinforcement learning approach[J]. IEEE Access, 2022, 10: 51561-51574.
[22]张前, 何山, 黄嵩,等. 基于DDPG算法的风力发电机变桨距控制研究[J]. 科学技术与工程, 2023,23(18): 7764-7771. (Zhang Qian, He Shan, Huang Song, et al. Research on variable pitch control of wind turbine based on DDPG algorithm[J]. Science Technology and Engineering, 2023,23(18): 7764-7771.)
[23]Redder A, Ramaswamy A, Karl H. Asymptotic convergence of deep multi-agent actor-critic algorithms[EB/OL]. (2022-01-03). https://doi.org/10.48550/arXiv.2201.00570.
[24]Patel V, Zhang S, Tian B. Global convergence and stability of stochastic gradient descent[J]. Advances in Neural Information Processing Systems, 2022, 35: 36014-36025.
[25]Hacham S, Din N M, Balasubramanian N. Load balancing in software-defined data centre with fat tree architecture[C]//Proc of the 4th International Conference on Smart Sensors and Application. Pisca-taway, NJ: IEEE Press, 2022: 45-49.
[26]Qiu Chengrun, Hu Yang, Chen Yan, et al. Deep deterministic policy gradient (DDPG) -based energy harvesting wireless communications[J]. IEEE Internet of Things Journal, 2019,6(5): 8577-8588.
