考虑多源供能波动性的企业生产运作与能源计划耦合优化

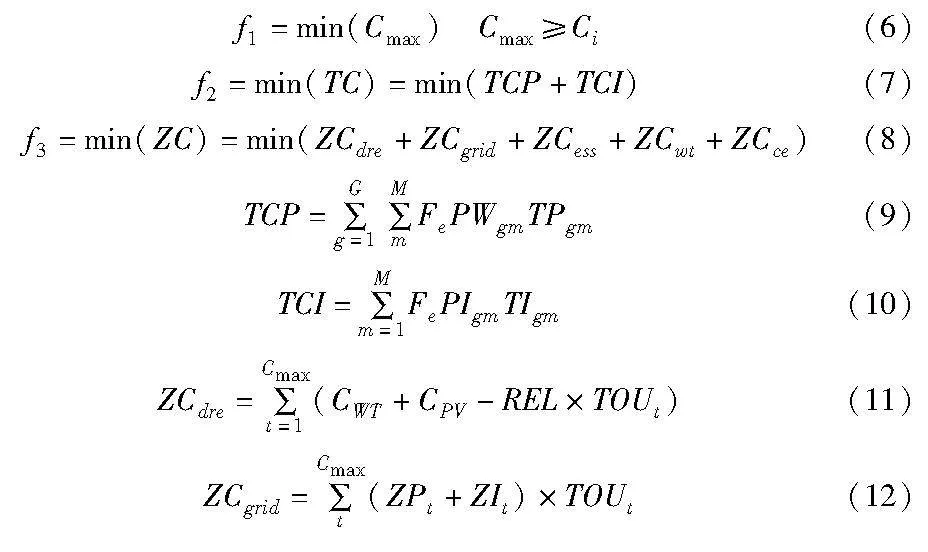
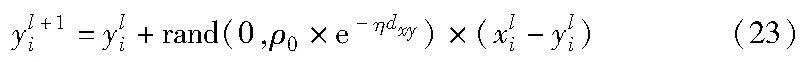
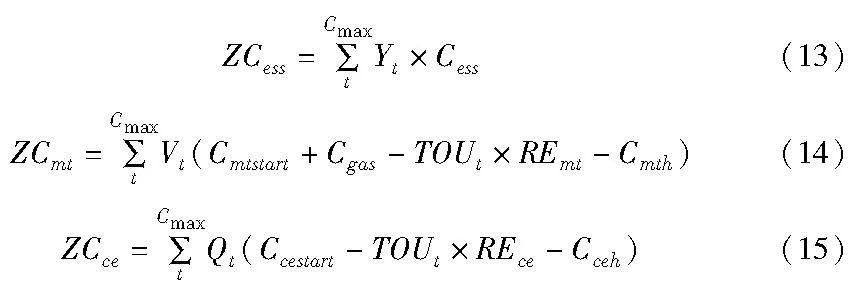
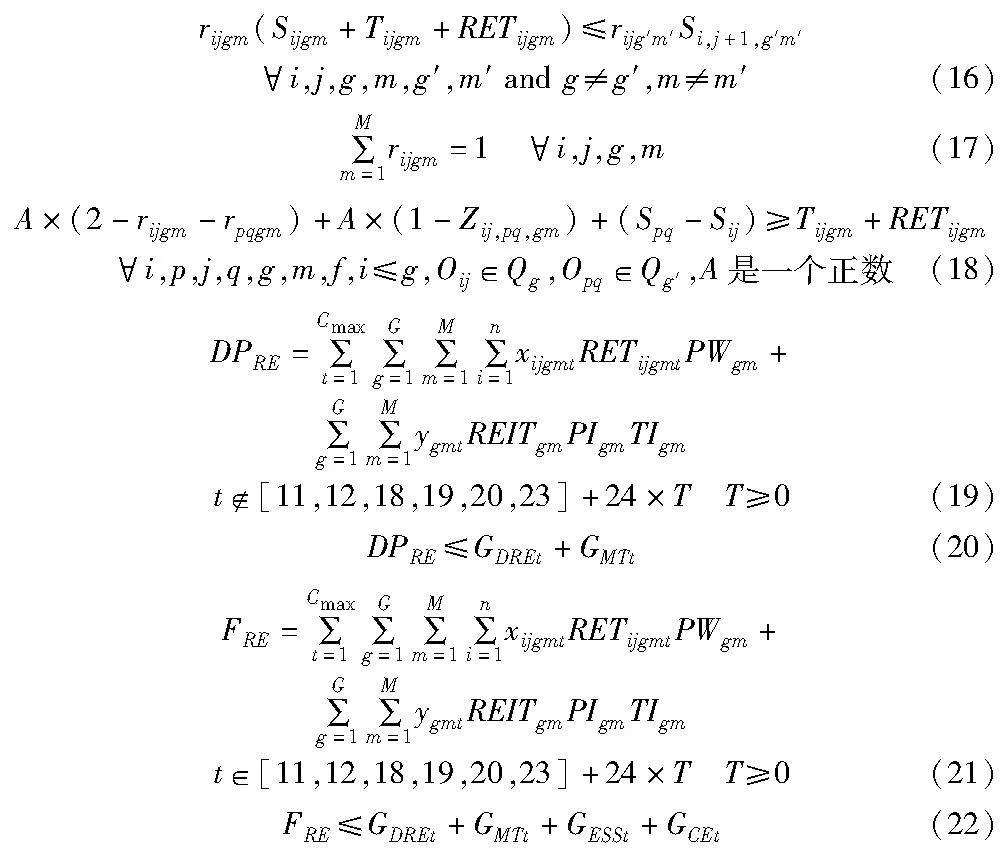
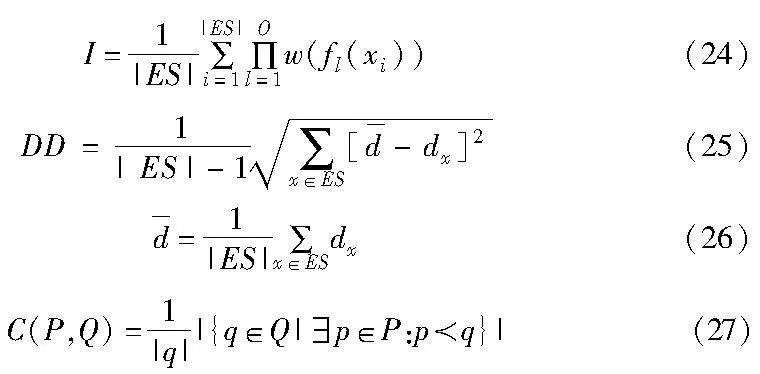
摘 要：多源供能是提高清洁能源占比，助力制造企业绿色低碳转型的有效方式。然而受季节、天气等因素影响，可再生能源出力存在波动性，影响能源系统供应的稳定性。针对该问题，构建了企业生产运作与能源计划耦合优化的不确定整数规划模型，利用区间数描述能源出力的不确定信息。同时通过设计多种群融合策略、外部档案更新策略，提出了多目标混合鲸鱼群算法，有效地利用各个算法的寻优特性，提升整体性能，获得更优的Pareto解集。最后通过算法性能和能源策略对比实验，证明了所构建模型及求解方法的可行性和有效性。同时验证了所设计算法对求解不确定优化模型的优势和竞争力，以及多源供能模式能够有效帮助企业实现节能减排、可持续生产目标。

关键词：鲸鱼群算法； 多源供能； 波动性； 耦合优化

中图分类号：TP301.6 文献标志码：A

文章编号：1001-3695（2024）06-030-1808-07

doi：10.19734/j.issn.1001-3695.2023.10.0442

Coupling optimization of enterprise production operation and energy planningconsidering multi-source energy supply fluctuation

Abstract：Multi-source energy supply is an effective way to increase the proportion of clean energy and assist manufacturing enterprises in green and low-carbon transformation. However， due to factors such as season and weather， renewable energy output fluctuates， affecting the stability of energy system supply. To address this problem， this paper constructed an uncertain integer programming model for the coupling optimization of enterprise production operation and energy planning， using interval numbers to describe the uncertain information of energy output. At the same time，it proposed a multi-objective hybrid whale swarm algorithm by designing multiple group fusion strategies and external file update strategies， which effectively utilized the optimization characteristics of each algorithm to improve overall performance and obtain a better Pareto solution set. Finally， it demonstrated the feasibility and effectiveness of the proposed model and solution method through comparative experiments on algorithm performance and energy strategies. At the same time， the advantages and competitiveness of the algorithm designed in this paper to solve uncertain optimization models and the multi-source energy supply mode can effectively help enterprises achieve energy conservation， emission reduction and sustainable production goals have been verified.

Key words：whale swarm algorithm; multi-source energy supply; fluctuation; coupling optimization

0 引言

据美国能源信息署（Energy Information Administration，EIA）统计，2018年全球仅制造业的总能源消耗为19.436万亿英热单位［1］。预计2040年，其仍将以每年1.2%的速度增长［2］。2021年上半年我国建材、石化、钢铁等产业增长量占全社会总增长量的42%［3］，这也导致制造企业用电成本持续攀高。在可持续的视角下重新思考企业生产运作，将会是未来企业行业领域中重要的竞争筹码。伴随着“双碳”重大战略的提出和实施，新型综合能源系统得到了快速发展，多源供能是新型综合能源系统的核心，鼓励制造企业使用价格更低廉的多种可再生清洁能源满足能耗需求，为制造企业实现节能减排绿色生产提供了新的思路和方法［4］。但是可再生能源出力容易受到天气、季节等原因的影响，其波动性是新型综合能源系统稳定性面临的严峻挑战，因此研究多源供能系统中能源组合出力的不确定性调度具有现实的价值和意义。

近年来的研究中，模糊数是最常用的不确定信息表示方法之一。杨枫等人［5］利用三参数和四参数灰数描述手术车间调度中的不确定问题，定义了新的可能性测度和必然性测度；张帅等人［6］引入双模糊数对再制造过程中的不确定时间和成本进行二维模糊处理，构建了考虑可重入工艺流程和机器特点的柔性调度不确定优化模型；Sun等人［7］利用具有非线性隶属函数的L-R模糊数来描述柔性装配车间调度问题的时间不确定性，建立了一个多目标不确定性优化模型，实现了工期、能耗和质量的同时优化；Yang等人［8］以工期和能耗为优化目标，研究了一个具有type-2类型模糊处理时间的绿色柔性车间调度问题。采用模糊数来表示不确定信息，需要事先知道其对应的隶属度函数，而在一个不确定的生产背景下，获得准确的隶属度函数是比较困难的。相比而言，预知不确定信息的上下界则较为容易。同时模糊数也能够通过截集水平转换为区间数，因此很多学者围绕区间数展开了不确定问题的求解。朱艳艳等人［9］构建了优化区间提前/拖期惩罚区间的可重入调度模型，并设计了改进的化学反应算法进行求解；李铁克等人［10］利用三角区间数来描述炼钢-连铸生产中工件的不确定加工时间，构建了区间多目标混合整数规划模型；Dong等人［11］设计了改进的区间数方法求解可重入混合流水车间的不确定性问题，同时表示多维对象的不确定性；Chen等人［12］针对不确定性数的广义灰数特征，研究加工时间不确定的柔性车间调度问题；Wang等人［13］以航空复合材料车间为背景，建立了带区间灰色处理时间的柔性流水车间调度模型，采用灰色理论和人工蜂群算法进行求解；Chen等人［14］考虑离散制造模糊柔性车间调度问题中的多个不确定性，与数字孪生技术结合，用区间数描述设备维修周期的不确定性；Xie等人［15］基于区间灰数及其相关定义、性质和定理，用区间数表示工件加工时间的不确定，构建单机调度不确定模型。

鲸鱼群算法（whale swarm algorithm，WSA）模拟鲸鱼群体的捕食行为，通过每个个体向其附近的“最近较优”个体移动，进一步改变自身位置，加速靠近食物源。该算法结构简单、参数较少、算法迭代流程较为精简，寻优效果较好。从目前相关研究中可以发现，鲸鱼群算法在电压控制［16］、物资应急调度［17］、车间调度［18］等方面已经成功应用，同时被验证具有较好的问题求解效果。但是至今尚未发现将其应用在考虑多源供能波动性的企业生产运作与能源计划耦合优化（coupling optimization of enterprise production operation and energy planning considering the multi-source energy supply fluctuation，COPOEP-MSEF）问题中。半导体企业是国家的战略新兴产业，是国民经济发展的关键中坚产业，同时又是高能源密集型产业。高额的水电消耗成本是双碳目标下半导体制造企业发展面临的严峻挑战，成为了半导体行业XT6ytn0oUXEAcMf7t8n2py5S8d/voW/Xh+/pm7NW20M=竞争力提升的重要制约因素。因此本文以半导体晶圆制造生产工艺流程为例，创新性地利用区间数方法构建COPOEP-MSEF模型，并利用鲸鱼群算法的自身优势，嵌入多种搜索机制，设计多目标混合鲸鱼群算法（multi-objective hybrid whale swarm algorithm，MHWSA）进行求解，获得最佳的优化方案，为重大耗能企业绿色转型发展提供重要的理论依据和方法指导，同时为相似工艺流程的制造企业低碳生产决策提供参考标杆。

1 COPOEP-MSEF问题描述

1.1 区间数知识介绍

定义3 区间Pareto支配（以最小化问题为例）：对于任意一个目标d，至少存在一个目标使得P（a≤b）>P（b≤a），同时其他优化目标均满足P（a≤b）≥P（b≤a），则称a支配b。因为篇幅有限，区间数的其他相关运算法则详见文献［20］。

1.2 问题描述

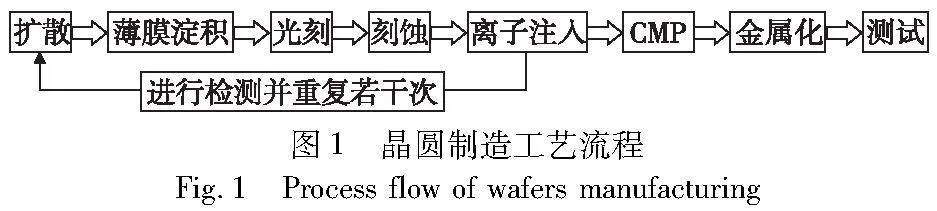
可重入制造是半导体晶圆生产工艺的典型特点，工件可能在加工的不同阶段重复访问某些设备，因此将其加工制造过程归结为可重入混合流水车间（reentrant hybrid flow shop，RHFS）调度问题，其已经被证明为NP-hard问题［18］。图1展示了晶圆制造的主要工艺流程。

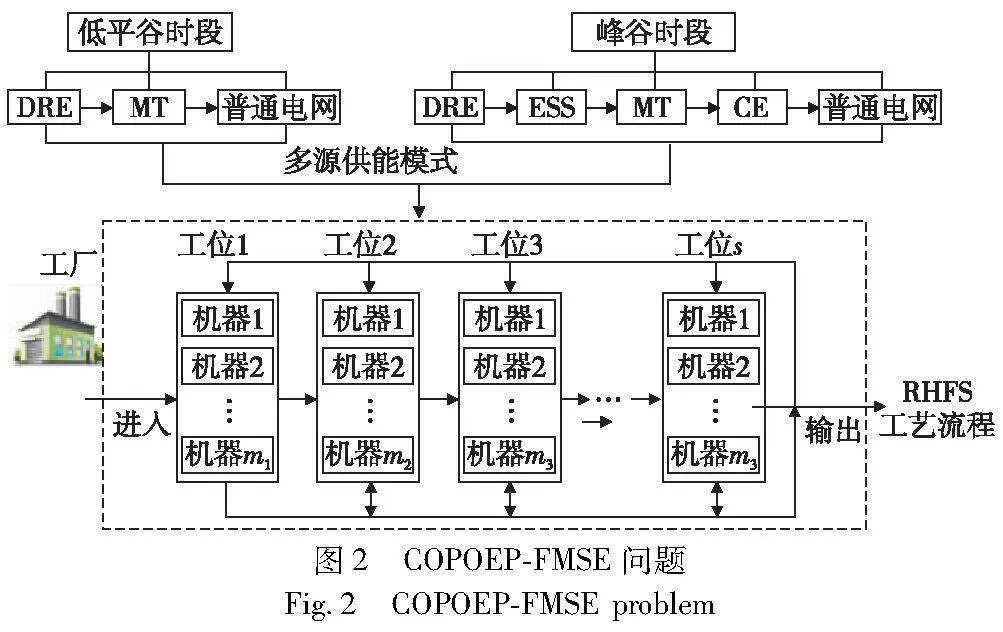
本文研究的COPOEP-MSEF问题描述如下：n个待加工工件在G个工位上进行加工，工位g上有mg（mg＞1）台不相关并行机可供选择。若干工件可能重复访问某几个加工工位。车间制造系统采用多源供能模式和能源组合策略，在分时电价低平谷时段供电顺序依次为分布式可再生能源（distributed renewable energy，DRE）、微型涡轮机（micro-turbine，MT）和普通电网，该时段内盈余电源首先满足向能源存储系统（energy storage system，ESS）充电，然后再向普通电网售卖。在峰谷时段供电顺序依次为DRE、ESS、MT、热电联产设备（cogeneration equipment，CE）以及普通电网。假设工位之间的缓冲区容量无限，工件加工优先权相同，不考虑机器维护等操作，ESS、MT、CE产生电能的成本依次增长。机器加工速度越快，则能耗越大。本文仅考虑可再生能源出力的不确定因素。COPOEP-FMSE问题示意图如图2所示。

本文主要考虑风电发电机和光伏的不确定出力。风电机组出力计算公式如式（2）（3）所示。

光伏出力计算公式如式（4）（5）所示。

强度。

1.3 模型构建

模型参数及意义如下所示。

j：工件i的工序索引，j=1，2，…，ni 。

Oij：工件Oij的第j道工序。

Tijgm：Oij工位g中机器m上消耗非RE的加工时间。

TPgm：工位g中机器m上消耗非RE的总加工时间。

RETijgmt：单位时刻t Oij在工位g中机器m上消耗RE的加工时间。

ITgm：Oij在工位g中机器m上消耗非RE的总空转时间。

REITijgm：工位g中机器m上消耗RE的空转时间。

Ci：工件i的完工时间。

Sijgm：Oij在工位g中机器m上开始加工时间。

Fe：电能的碳排放因子。

CWT/CPV：风电和光伏的单位时刻发电成本。

REL：每时刻DRE向ESS充电后的盈余电量。

TOUt：分时电价。

ZPt/ZIt：单位时刻t消耗普通电能的总加工能耗/总空转能耗。

Cess：ESS充放电的单位成本。

Cmtstart：MT的启动成本。

Cgas：MT消耗天然气的成本。

REmt：MT向ESS充电后的盈余电能。

Cmth：MT产生热能的售卖收入。

Ccestart：CE的启动成本。

Cceh：CE产生热能的售卖收入。

REce：CE向ESS充电后的盈余电能。

PWgm：工位g中的机器m的单位加工能耗。

TPgm：工位g中的机器m消耗非RE的加工时间。

PIgm：工位g中的机器m的单位空转能耗。

TIgm：工位g中的机器m消耗非RE的空转时间。

GDREt：单位时刻t DRE电能出力。

GMTt：单位时刻t MT电能出力。

GESSt：单位时刻t ESS可释放电量。

GCEt：单位时刻t CE产生的电能。

rijgm：若Oij在工位g中的机器m上加工则为1，否则为0。

Qt：单位时刻t热电联设备启动为1，否则为0。

Vt：单位时刻t MT启动为1，否则为0。

Yt：单位时刻t ESS充放电为1，否则为0。

xijgmt：1表示单位时刻t Oij在工位g中机器m上加工，否则为0。

ygmt：1表示单位时刻t工位g中机器m空转，否则为0。

Zij，pq，gm：Oij先于Opq在工位g中机器m上加工为1，否则为0。

本文研究中设置一个DRE发电周期为24 h，因此上述单位时刻t表示当前一个小时内。

目标函数：

其中：式（6）～（8）分别为三个优化目标，即最大完工时间Cmax、总碳排放TC、总成本ZC；TCP和TCI分别为制造和空闲状态下的设备总能耗，式（9）（10）分别为其详细计算公式；式（11）～（15）中的ZCdre、ZCgrid、ZCess、ZCwt和ZCce分别为DRE、普通电网、ESS、MT和CE的总成本，MT和CE产生的热能均进行出售，获得相应的热能收入。

约束条件：

其中：式（16）表示Oij+1的开始时间必须晚于Oij的完工时间；式（17）（18）分别约束任何一道工序都仅能在一台机器上加工及任何一台机器某个时间只能加工一道工序；式（19）（21）分别是对低平谷和峰谷时段机器消耗RE的定义，本文研究中设置一个发电周期（24 h）内的峰谷时刻为11、12、18、19、20和23时刻，其余时刻均为低平谷时刻；式（20）（22）分别是对前两者的电能负荷平衡约束。

2 问题求解

2.1 基础鲸鱼群算法介绍

受鲸鱼群捕食行为的启发，文献［21］及其团队提出了鲸鱼群算法。算法优化中每条鲸鱼代表问题的一个可行解，每条鲸鱼以自我为中心，其邻域中的其他个体均为关联的邻域解。每条鲸鱼向其“最近更优”个体学习和靠拢，以尽早寻觅到食物源。其移动方式如式（23）所示。

其中：xli 和yli 分别为鲸鱼x和y在第l次迭代时的位置；yl+1i为鲸鱼y在第l+1次迭代时的位置；η、ρ0和dxy分别为超声波的衰减因子、强度信息和两个鲸鱼个体之间的距离。

2.2 MHWSA

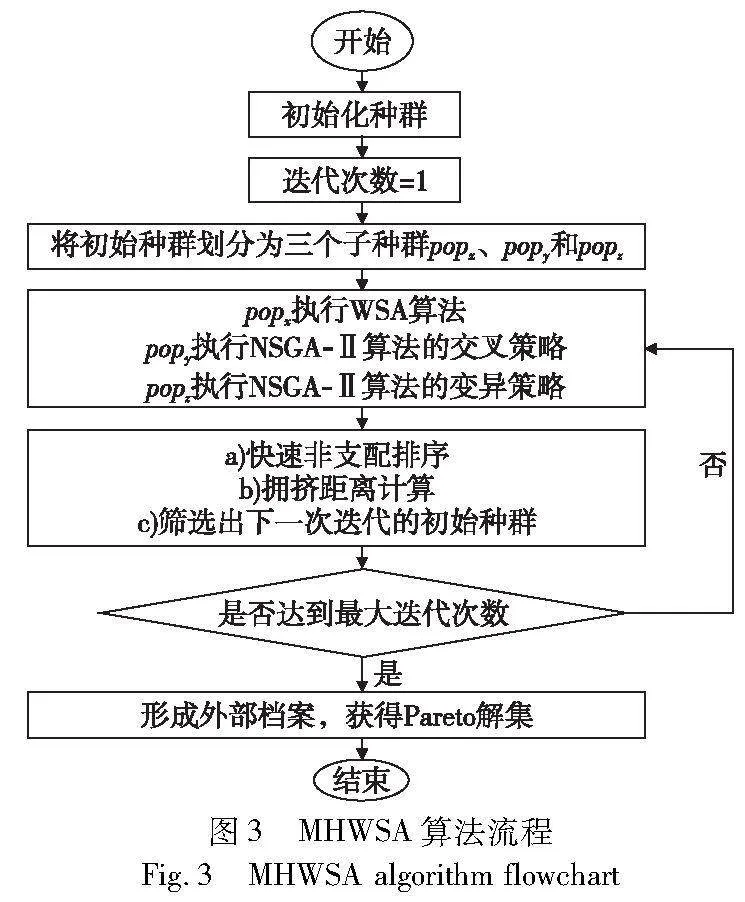
本文在WSA基础上通过设计多种群融合寻优策略、外部档案更新策略提出了MHWSA，进一步扩大种群多样性、提高算法寻优性能，寻找更高质量的Pareto解集。算法流程如图3所示，首先进行种群初始化，开始算法迭代寻优，相继执行多种群融合寻优策略、快速非支配排序、拥挤距离计算等操作，筛选出下次迭代的初始种群。循环往复，直至迭代结束，获得初始外部档案，执行外部档案更新策略，最终获得更优的Pareto解集。

2.2.1 多种群融合寻优策略

根据算法求解中“没有免费午餐原理”，没有任何一种算法适合求解所有优化问题。鲸鱼群算法涉及到的参数较少，容易控制，采用小生境算法结构，容易嵌入其他启发性算子；NSGA-Ⅱ算法在求解多目标问题时展现出了收敛速度快、寻优能力强的优点。因此本文设计多种群融合策略，结合不同算法的寻优优势，挖掘更多的最优解搜索空间，以期获得更好的Pareto解集。将初始化种群分为popx、popy和popz三个子种群。对于种群popx实施WSA，寻找“最近较优”个体xp，若xp存在则执行移动策略，若不存在则执行个体变异策略；对于个体popy和popz，分别执行NSGA-Ⅱ算法中的交叉策略和变异策略，产生新的种群个体，扩大搜索区域。每次迭代后将三个种群进行融合，再依次进行快速非支配排序和拥挤距离的计算，获得新的下次迭代的初始种群。本文将NSGA-Ⅱ的交叉和变异策略分别应用在两个子种群中，而不是像以往算法一样集中应用于同一个种群，这样更能挖掘出每种策略的搜索优势，扩大种群空间的多样性，降低不同算法相似搜索机制生成更多重复个体的几率，更有利于获得最优Pareto解集。

2.2.2 外部档案更新策略

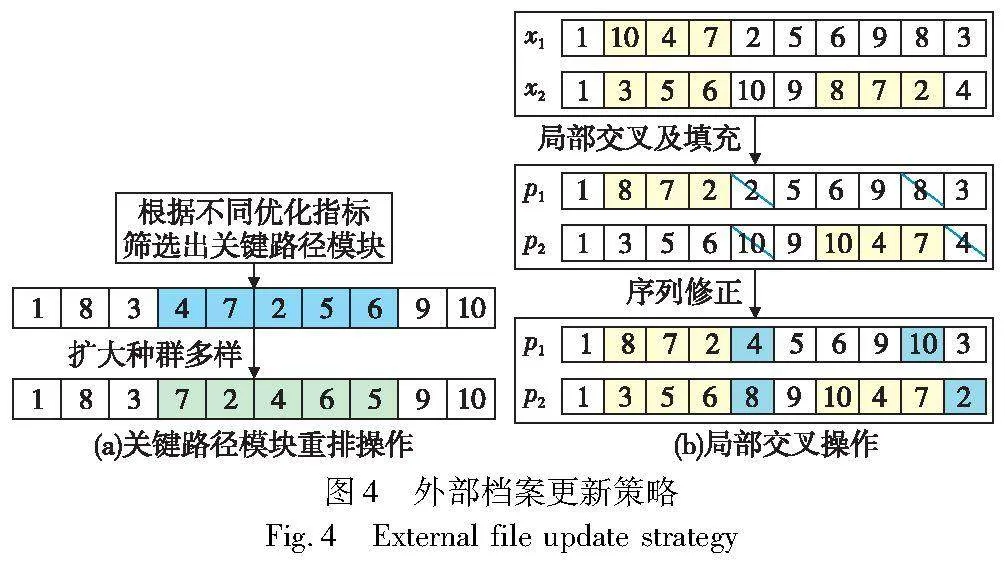
算法迭代结束后，从外部档案中获取Pareto解集。外部档案中的群体已是算法迭代后的较优个体，传统寻优算法一般到此结束搜索，但是这些个体附近的潜在空间往往被忽略。因此本文设计外部档案的更新策略，进一步扩大算法寻优时的可能性空间。采用基于概率的多邻域变异方式，为了更加清晰地说明外部档案更新策略，图4展示了一个小规模案例。获取一个随机数r（0<r<1），若r<1/4，选择Pareto解集中Cmax值最大的一半个体，依次找到关键路径模块，进行序列重排操作；若1/4≤r<1/2，选择Pareto解集中TC值最大的一半个体，依次找到关键路径模块，进行序列重排操作；若1/2≤r<3/4，选择Pareto解集中ZC值最大的一半个体，依次找到关键路径模块，进行序列重排操作，以上三种操作如图4（a）所示。若r≥3/4，则随机选择Pareto解集中一半个体（取对数值），进行序列局部交叉操作。首先进行父代个体局部交叉，再进行子代个体序列填充，最后完成子代个体序列修正，如图4（b）所示。该更新策略中，关键路径模块是策略成功的关键。本文研究的是Cmax、TC和ZC三个指标的平衡优化，因此分别以各个指标的关键路径模块为切入点，进行个体部分加工顺序的重置，能够在尽可能确保其他优化指标取值范围不发生较大变动的基础上，跳出局部最优解。

3 实验分析

本文是首次展开COPOEP-MSEF问题的研究和探讨，目前公开的文献中没有相关数据集，因此本文依据文献［22］的数据集设置方法，设置大、中、小三种规模的测试算例，其中工件数包括9个标准，工位数和加工层次均包含5个标准。例如50×5×3代表待加工工件数为50个，工位数为5，加工层次为3的测试算例。本文实验仿真环境为Windows 10操作系统，处理器为Intel CoreTM i7-4770 CPU@3.40 GHz，内存为8 GB，采用MATLAB R2019a进行算法编程。

3.1 算法性能对比

本文分别选取IMOMVO［23］、HHSGA［24］、PDHS［25］、NSGA-Ⅱ和NSGA-Ⅲ算法［26，27］进行对比分析，这些对比算法均已被证明具有较好的寻优性能和竞争力。本文选取文献［11］中的I、DD和C测度作为评价指标，计算公式分别如式（24）～（27）所示。

其中：ES为算法获得的Pareto解集;|·|为集合中的元素个数;dx为x的拥挤距离;C（P，Q）表示算法Q中存在被P中至少一个解支配的解所占的百分比。

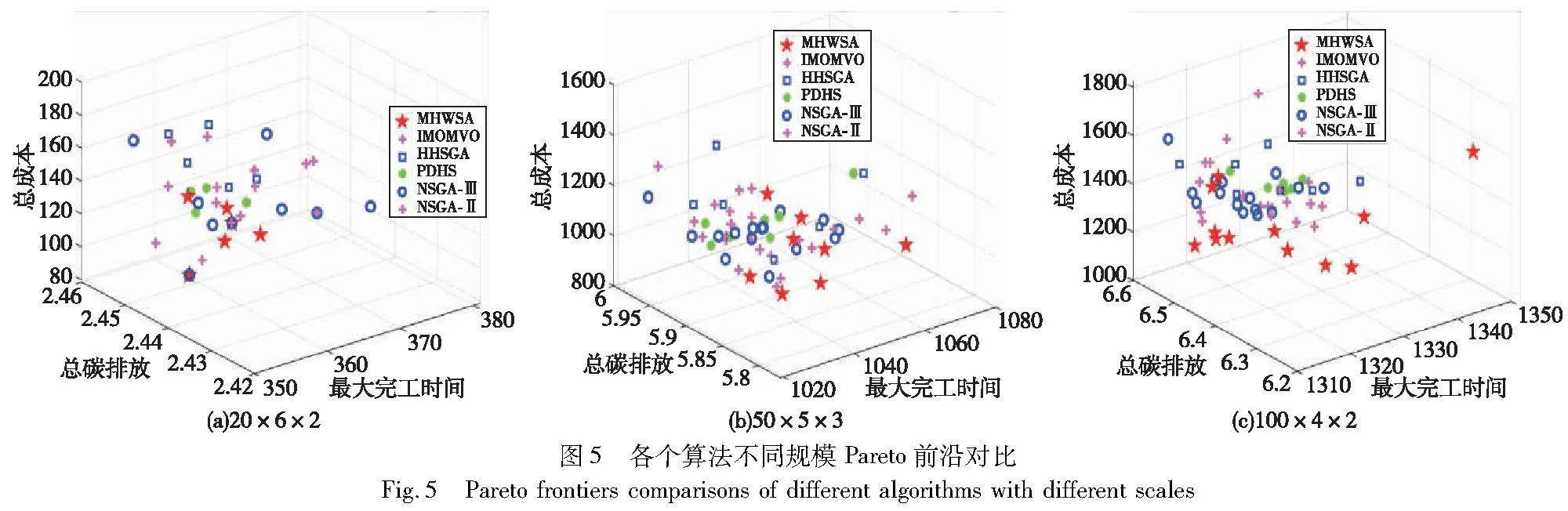
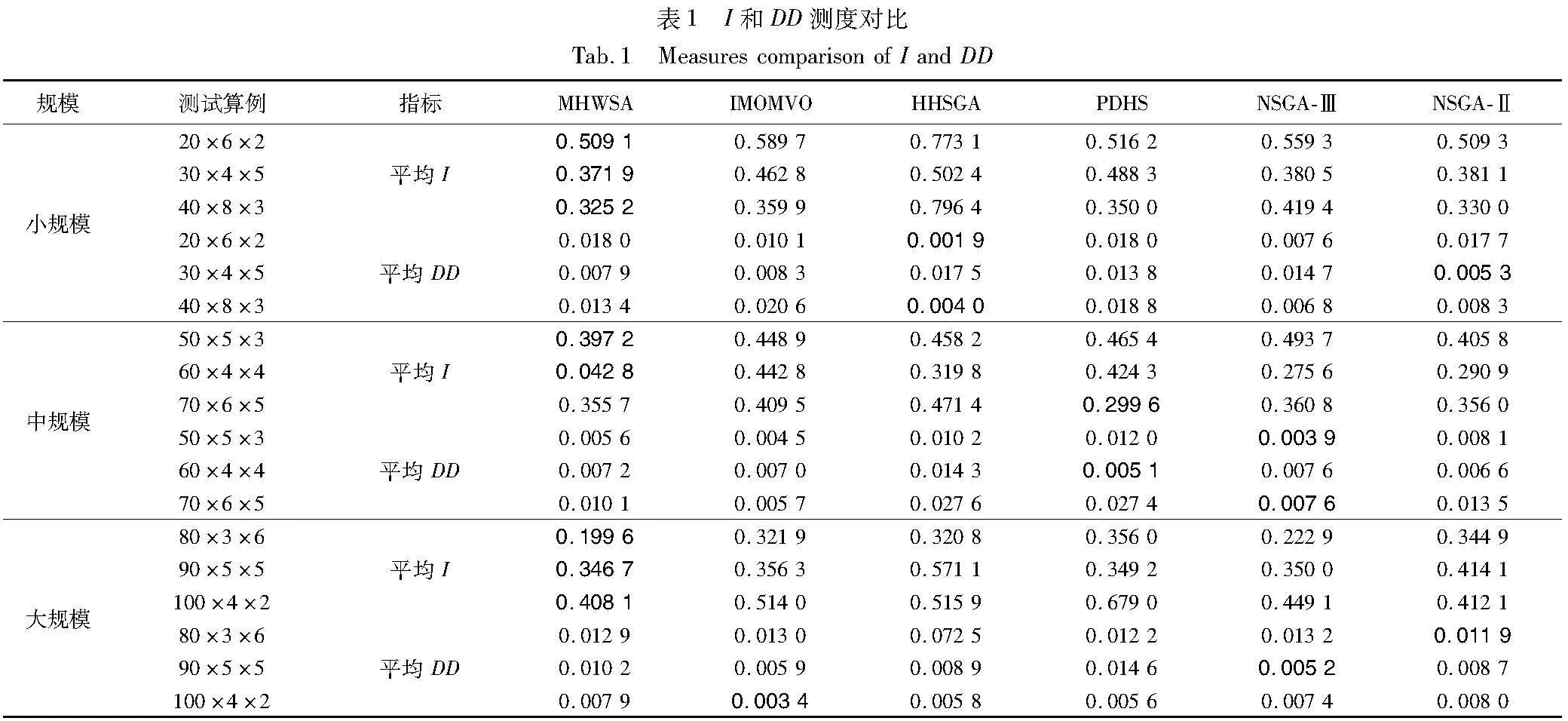
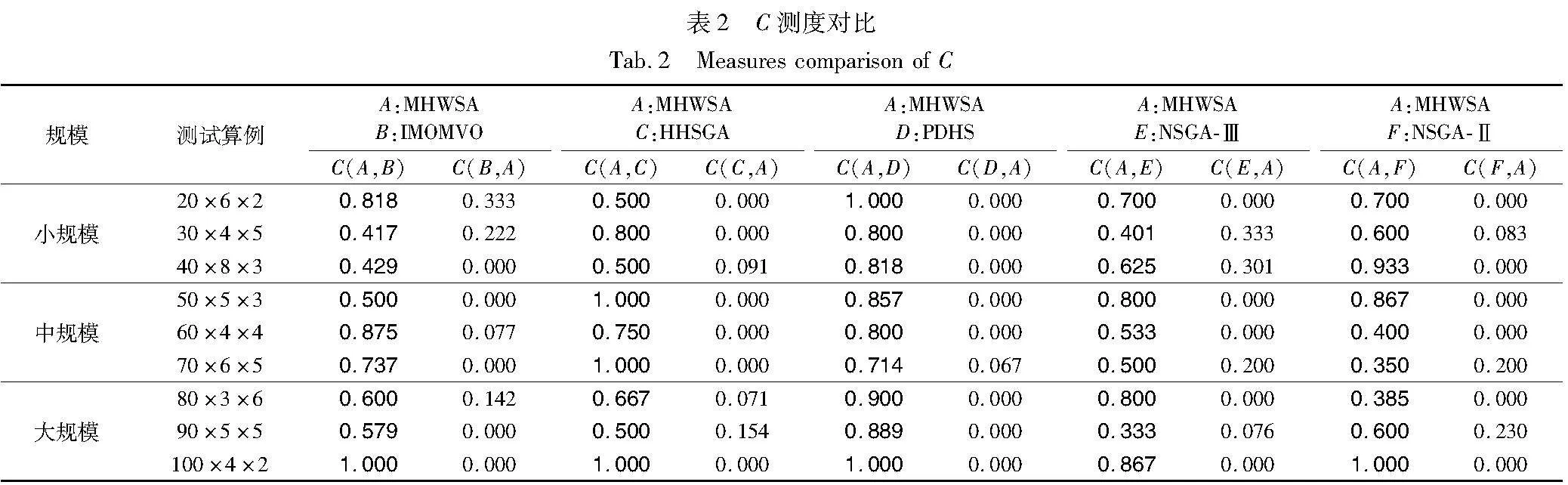
前两个指标分别代表解集的不确定性和均匀性，值越小越好；最后一个指标代表算法之间的支配关系，值越大表示算法寻优性能越好。实验过程中每个测试算例运行10次，取其平均值作为最终结果（区间数取区间中点作为最终值），并用粗体标志针对每个指标各个算法的最优解。由表1可以看出，针对I指标，MHWSA的占优率达到89%，PDHS算法为11%；针对DD指标，MHWSA表现性能较差，9个案例均没有占优，说明MHWSA获得Pareto解集的均匀性较差；但是从表2可以看出，对于C指标，MHWSA能够实现全部占优，具有压倒性的绝对优势。根据多目标优化问题解集性质，一个目标的改善必然引起另一个目标的恶化。因此NFWSA获得的Pareto解集具有一定竞争力，相比其他算法而言，质量有所提升，综合性能更优。为了更加清晰直观地展示各个算法的优劣，图5展示了不同规模的三个随机案例各个算法获得的Pareto前沿，可以明显看到MHWSA获得的Pareto前沿分布在右下方位置，解集更优。

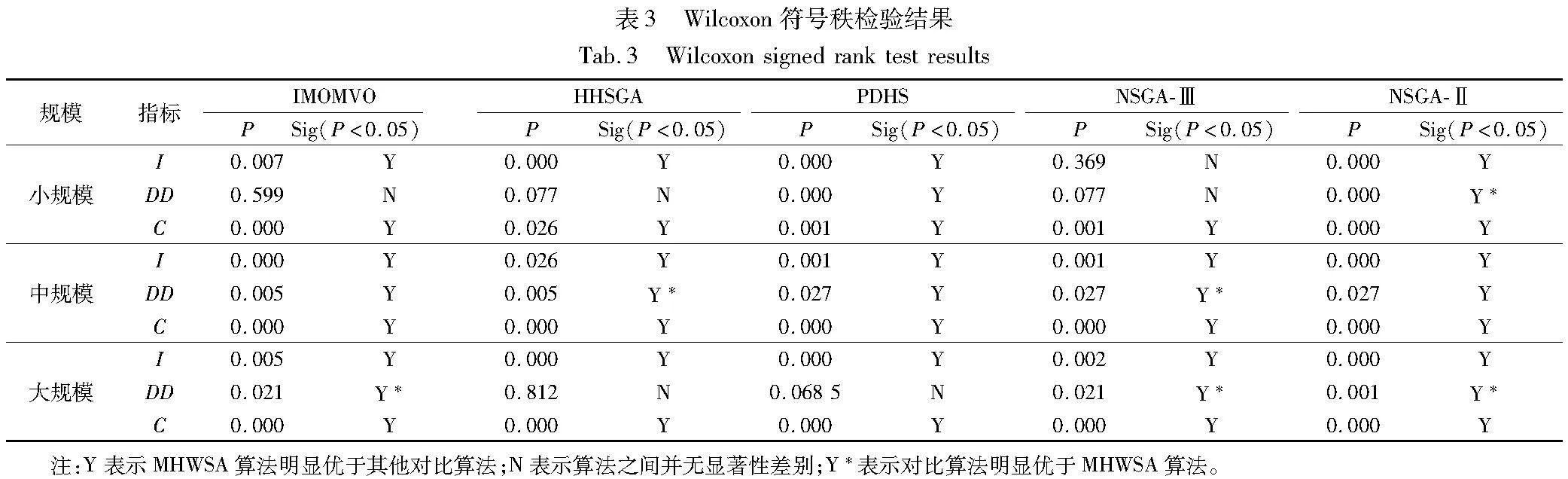
为了进一步验证对比算法之间是否存在显1lWF+LFFiFQ1BUSlug8CrdpUddSEVctDjPgoUdeiqVg=著性差异，表3列出了三个指标的Wilcoxon符号秩检验结果。可以明显看出，对于I指标，除在小规模案例和NSGA-Ⅲ算法之间不存在显著差异外，与其他算法比较均显著占优；但是对于DD指标，MHWSA表现并不是十分优秀，针对小规模测试算例，其显著劣于NSGA-Ⅱ算法。针对中、大规模算例，其分别显著劣于HHSGA、NSGA-Ⅲ，IMOMVO、NSGA-Ⅲ和NSGA-Ⅱ算法；但是对于C指标，MHWSA能够实现全部显著性占优，表现出较强的支配性。

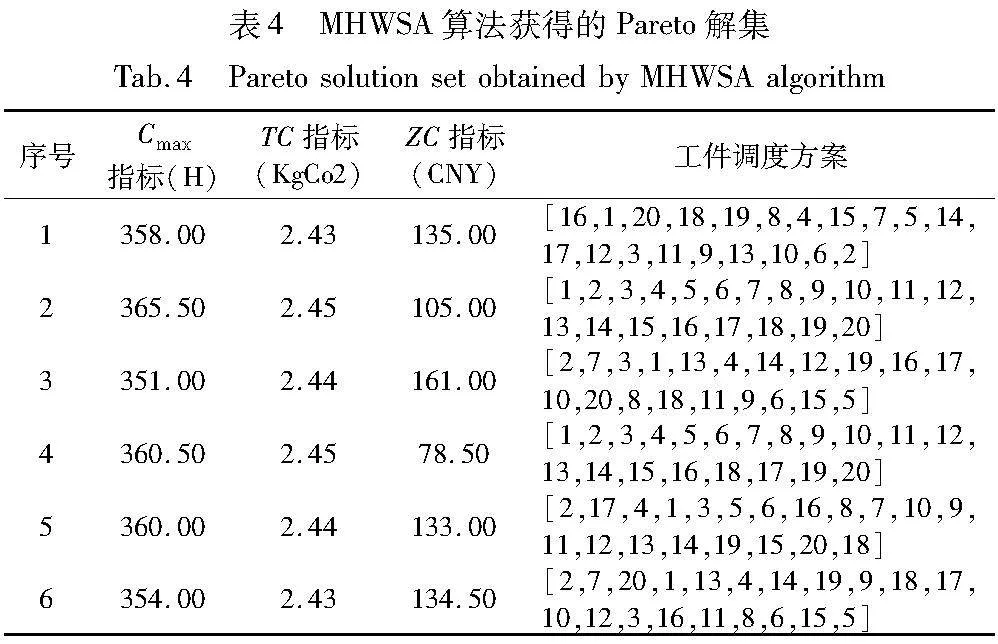
表4列举了图5（a）中MHWSA算法获得的Pareto解集及对应的调度方案。多目标优化问题中，一个指标的优化必然会引起其余至少一个指标的恶化，因此在获得的解集平衡方案中，企业决策可以依据实际生产运作情况，针对各自发展的利益倾向，选择不同的工件调度方案组织生产。

3.2 能源策略对比

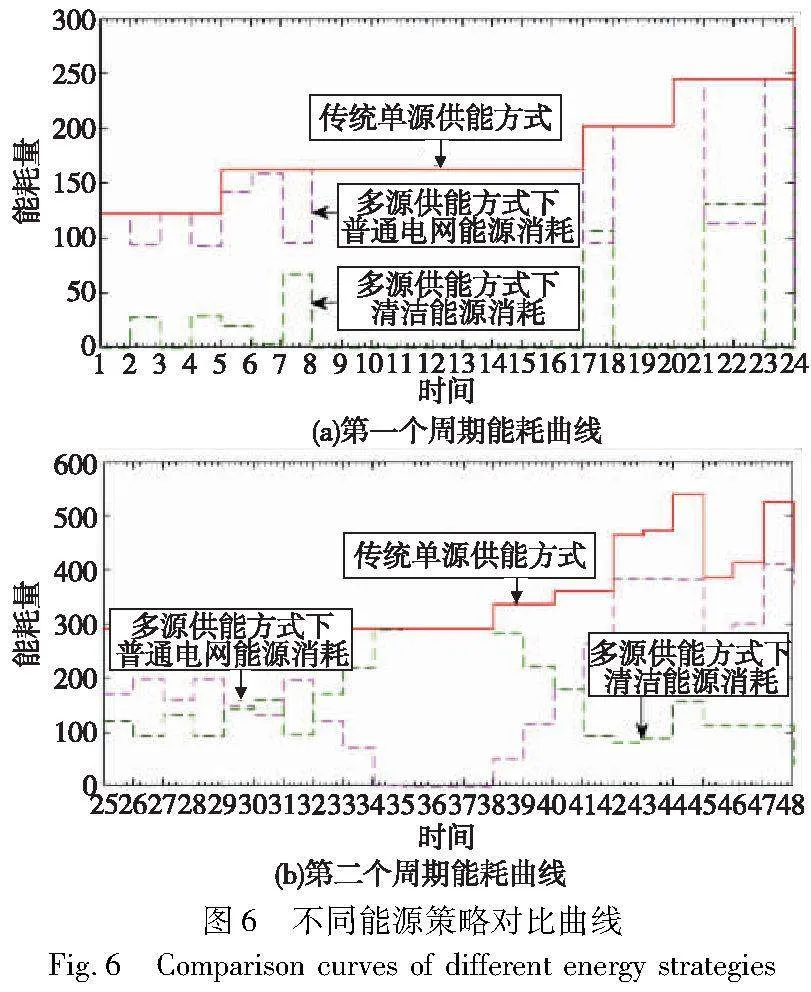
为验证多源供能策略能够有效减少普通电网能源的消耗，图6展示了包含20个工件的小规模案例两个发电周期（48 h内）不同能源策略下能耗对比曲线。其中工件加工顺序为［1，10，14，9，20，18，19，15，2，6，8，11，3，4，7，17，5，12，16，13］，工位数为8，加工层次为2，每个工位上的机器数分别为［3，3，6，6，4，3，5，3］，每个机器对应的单位加工能耗和空转能耗分别符合［30，50］及［10，20］的均匀分布，加工时间符合［15，30］的均匀分布。每24 h内的分时电价为［0.372，0.372，0.372，0.372，0.372，0.372，0.372，0.372，0.372，0.63，0.906，0.906，0.63，0.63，0.63，0.63，0.63，0.906，0.906，0.906，0.63，0.63，0.906，0.372］，每24 h内DRE中清洁能源出力上下限分别为［109.8，84.6，118.8，83.7，128.7，144.0，86.4，153.0，198.0，261.0，256.5，306.0，279.0，256.5，199.8，162.0，85.5，72.0，79.2，139.5，101.7，102.6，99.9，26.0］和［134.2，103.4，145.2，102.3，157.3，176.0，105.6，187.0，242.0，319.0，313.5，374.0，341.0，313.5，244.2，198.0，104.5，88.0，96.8，170.5，124.3，125.4，122.1，44.0］。

由图6（a）可以看到，在17、18、21和23时刻，清洁能源消耗量超过了普通能源的消耗量，清洁能源占比进一步提升；同时由图6（b）可以看出，在34～38时刻，制造系统可以完全实现清洁能源供能，无须消耗普通电能。综上所述，多源供能策略下每个时刻普通能源的消耗量均出现不同程度的减少，有利于实现节能减排的绿色目标。

4 结束语

本文研究了考虑多源供能波动性的企业生产运作与能源计划耦合优化问题，构建了不确定整数优化模型。设计了MHWSA进行求解，通过多种群融合寻优策略有效利用各个算法的寻优优势；通过设计外部档案更新策略扩大种群多样性，避免算法过早收敛。实验分析结果表明，多源供能策略可以有效提升清洁能源占比，减少对普通电网能源的依赖，助力企业低碳转型发展。同时通过多算法对比实验，证明MHWSA针对COPOEP-MSEF问题求解方面具有竞争性的优势。获得的Pareto解集可以帮助企业决策者制定多源供能下的企业低碳运作方案，帮助企业实现效益、成本和绿色指标的平衡。

未来将在本文的基础上，进一步探讨需求响应对多源供能及企业运作协同优化的影响，制定不同需求响应机制下的优化策略。同时将研究背景扩展至更多的车间工艺流程中，进一步进行成果的推广，助力制造企业可持续发展。

参考文献：

［1］U.S. Energy Information Administration. Manufacturing energy consumption survey［EB/OL］.（2021-03-31）.https：//www.eia.gov/consumption/manufacturing/pdf/MECS%202018%20Results%20Flip-book.pdf.

［2］International Energy Agency. World Energy Outlook 2016［EB/OL］. （2016-11）. https：//www.iea.org/reports/world-energy-outlook-2016.

［3］赵紫原. 高耗能行业用电戴上“紧箍咒”［N］. 中国能源报， 2021-10-18（19）. （Zhao Ziyuan. High energy consuming industries wear a “tight curse” on electricity consumption［N］. China Energy News， 2021-10-18（19）.）

［4］李远征， 倪质先， 段钧韬， 等. 面向高比例新能源电网的重大耗能企业需求响应调度［J］. 自动化学报， 2023，49（4）： 754-768. （Li Yuanzheng， Ni Zhixian， Duan Juntao， et al. Demand response scheduling of major energy consuming enterprises based on a high proportion of renewable energy power grid［J］. Acta Automatica Sinica， 2023， 49（4）： 754-768.）

［5］杨枫， 叶春明， 汪顶玉. 基于混合布谷鸟算法的不确定手术调度模型求解［J］. 计算机应用研究， 2020，37（3）： 768-773. （Yang Feng， Ye Chunming， Wang Dingyu. Solution of uncertain operation scheduling model based on hybrid cuckoo algorithm［J］. Application Research of Computers， 2020，37（3）： 768-773.）

［6］张帅， 王军， 张文宇. 不确定环境下再制造可重入柔性车间调度优化研究［J/OL］. 计算机集成制造系统. （2023-07-31）. https：//kns.cnki.net/kcms/detail/11.5946.tp.20230728.1710.008.html. （Zhang Shuai， Wang Jun， Zhang Wenyu. Uncertain remanufacturing re-entrant flexible job shop scheduling［J/OL］. Computer Integrated Manufacturing Systems. （2023-07-31）. https：//kns.cnki.net/kcms/detail/11.5946.tp.20230728.1710.008.html.）

［7］Sun Mengke， Cai Zongyan， Zhang Haonan. A teaching-learning-based optimization with feedback for L-R fuzzy flexible assembly job shop scheduling problem with batch splitting［J］. Expert Systems with Application， 2023， 224（8）： 120043.

［8］Yang Jinfeng， Xu Hua， Cheng Jinhai， et al. A decomposition-based memetic algorithm to solve the biobjective green flexible Job Shop scheduling problem with interval type-2 fuzzy processing time［J］. Computers & Industrial Engineering， 2023， 183：109513.

［9］朱艳艳， 徐震浩， 顾幸生. 工序加工时间不确定的可重入调度问题的求解［J］. 控制与决策， 2021，36（5）： 1127-1136. （Zhu Yanyan， Xu Zhenhao， Gu Xingsheng. Solution of reentrant scheduling problem with uncertain processing time［J］. Control and Decision， 2021，36（5）： 1127-1136.）

［10］李铁克， 苏艺璇， 张文新， 等. 加工时间不确定的炼钢-连铸区间多目标优化调度［J/OL］. 中国管理科学. （2022-09-13）. https：//kns.cnki.net/kcms/detail/11.2835.G3.20220909.1736.004.html. （Li Tieke， Su Yixuan， Zhang Wenxin， et al. Interval multi-objective optimal scheduling for steelmaking-continuous casting with processing time uncertainty［J/OL］. Chinese Journal of Management Science. （2022-09-13）. https：//kns.cnki.net/kcms/detail/11.2835.G3.20220909.1736.004.html.）

［11］Dong Jun， Ye Chunming. Joint optimization of uncertain distributed manufacturing and preventive maintenance for semiconductor wafers considering multi-energy complementary［J］. International Journal of Production Research， 2023， 61（9）： 3029-3050.

［12］Chen Nanlei， Xie Naiming， Wang Yuquan. An elite genetic algorithm for flexible job shop scheduling problem with extracted grey processing time［J］. Applied Soft Computing， 2022， 131： 109783.

［13］Wang Yuquan， Xie Naiming. Flexible flow shop scheduling with interval grey processing time［J］. Grey Systems Theory and Application， 2021，11（4）： 779-795.

［14］Chen Zhaoming， Zou Jinsong， Wang Wei. Digital twin-oriented collaborative optimization of fuzzy flexible job shop scheduling under multiple uncertainties［J］. Sādhanā， 2023，48（2）： 78-92.

［15］Xie Naiming， Wang Yuquan. Single machine scheduling with interval grey processing time［J］. Grey Systems： Theory and Application， 2023， 13（4）： 713-729.

［16］薛成， 曹戈， 王争冕， 等. 基于鲸鱼群算法的交直流混联系统无功电压控制方法研究［J］. 电网与清洁能源， 2023，39（9）： 67-73. （Xue Cheng， Cao Ge， Wang Zhengmian， et al. Research on the reactive power and voltage control method for AC-DC hybrid systems based on the whales warm algorithm［J］. Power System and Clean Energy， 2023， 39（9）： 67-73.）

［17］蒋华伟， 郭陶， 杨震， 等. 基于离散鲸鱼群算法的物资应急调度研究［J］. 电子与信息学报， 2022，44（4）： 1484-1494. （Jiang Huawei， Guo Tao， Yang Zhen， et al. Research on material emergency scheduling based on discrete whale swarm algorithm［J］. Journal of Electronics & Information Technology， 2022，44（4）：1484-1494.）

［18］王思涵， 黎阳， 李新宇. 基于鲸鱼群算法的柔性作业车间调度方法［J］. 重庆大学学报， 2020，43（1）： 1-11. （Wang Sihan， Li Yang， Li Xinyu. An improved whale swarm algorithm for flexible Job-Shop scheduling problem［J］. Journal of Chongqing University， 2020， 43（1）： 1-11.）

［19］董君， 叶春明. 区间数可重入混合流水车间调度与预维护协同优化［J］. 控制与决策， 2021， 36（11）： 2599-2608. （Dong Jun， Ye Chunming. Collaborative optimization of interval number reentrant hybrid flow shop scheduling and preventive maintenance［J］. Control and Decision， 2021， 36（11）： 2599-2608.）

［20］杨宏安， 王周锋， 吕阳阳， 等. 工序加工时间不确定条件下作业车间调度问题的区间数求解方法［J］. 计算机集成制造系统， 2014，20（9）： 2231-2240. （Yang Hongan， Wang Zhoufeng， Lyu Yangyang， et al. Interval number solving method for Job-Shop sche-duling problem with processing time variability［J］. Computer Integrated Manufacturing Systems， 2014， 20（9）： 2231-2240.）

［21］Zeng Bing， Gao Liang， Li Xinyu. Whale swarm algorithm for function optimization［C］//Proc of the 13th International Conference on Intelligent Computing. Cham： Springer， 2017： 624-639.

［22］董君， 叶春明. 基于新型多元宇宙优化算法的IPPS与多源供能协同优化［J］. 计算机应用研究， 2023，40（9）： 2639-2645. （Dong Jun， Ye Chunming. Collaborative optimization of IPPS and multi-source energy supply based on novel multi-verse optimizer algorithm［J］. Application Research of Computers， 2023， 40（9）： 2639-2645.）

［23］Geng Kaifeng， Ye Chunming， Cao Lei， et al. Multi-objective reentrant hybrid flowshop scheduling with machines turning on and off control strategy using improved multi-verse optimizer algorithm［J］. Mathematical Problems in Engineering， 2019， 2019： article ID 2573873.

［24］Lin Chuncheng， Liu Wanyu， Chen Y H. Considering stockers in reentrant hybrid flow shop scheduling with limited buffer capacity［J］. Computers & Industrial Engineering， 2020， 139： 106154.

［25］Shen Jingnan， Wang Ling， Deng Jin， et al. A Pareto-based discrete harmony search algorithm for bi-objective reentrant hybrid flow shop scheduling problem［C］//Proc of the 2nd International Conference on Harmony Search Algorithm. Berlin： Springer， 2016： 435-445.

［26］Deb K， Pratap A， Agarwal S， et al. A fast and elitist multi objective genetic algorithm NSGA-Ⅱ［J］. IEEE Trans on Evolutionary Computation， 2002，6（2）： 182-197.

［27］Deb K， Jain H. An evolutionary many-objective optimization algorithm using reference-point-based non dominated sorting approach， part I： solving problems with box constraints［J］. IEEE Trans on Evolutionary Computation， 2014， 18（4）： 577-601.