困难样本采样联合对比增强的深度图聚类

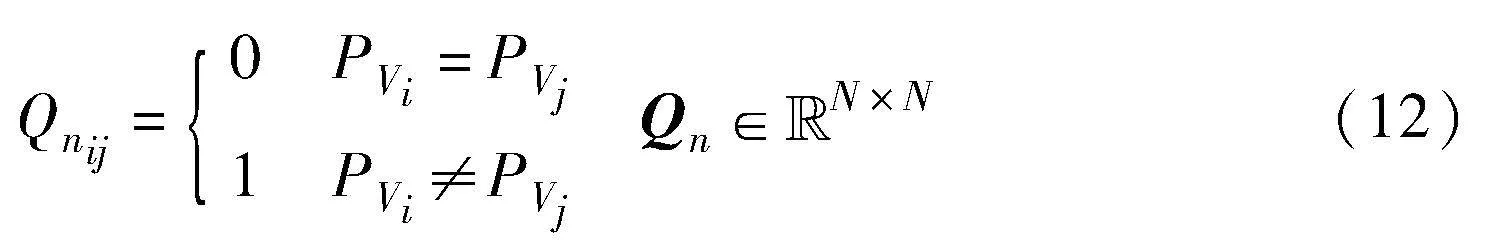
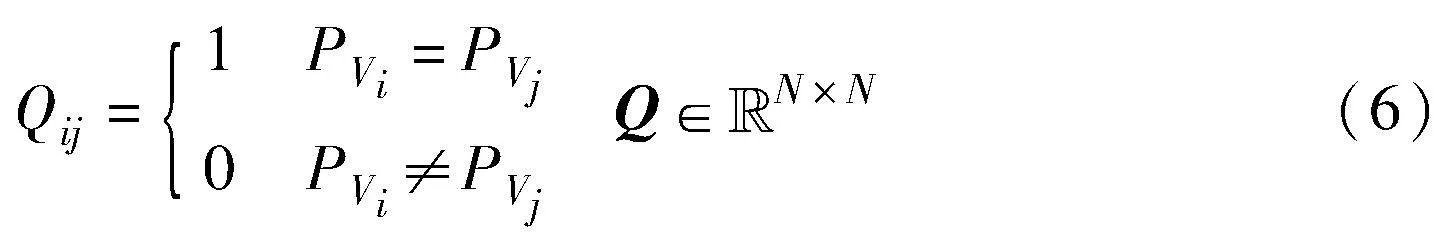
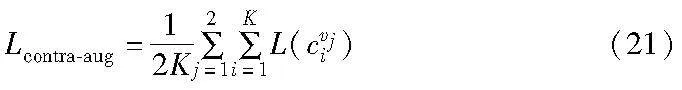
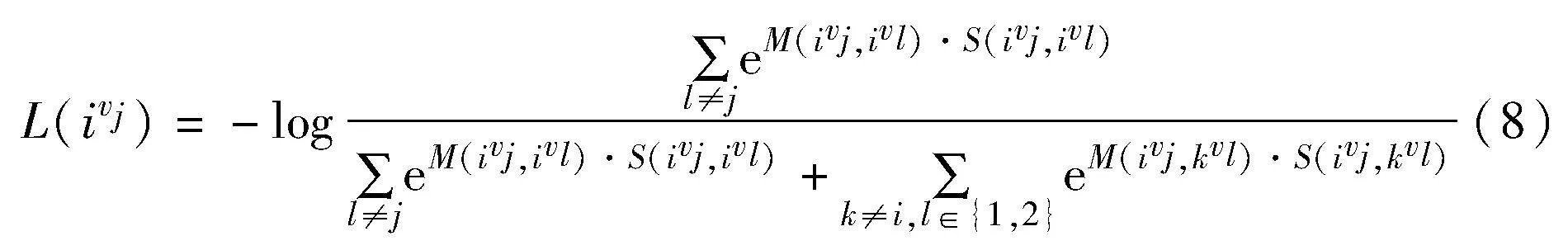
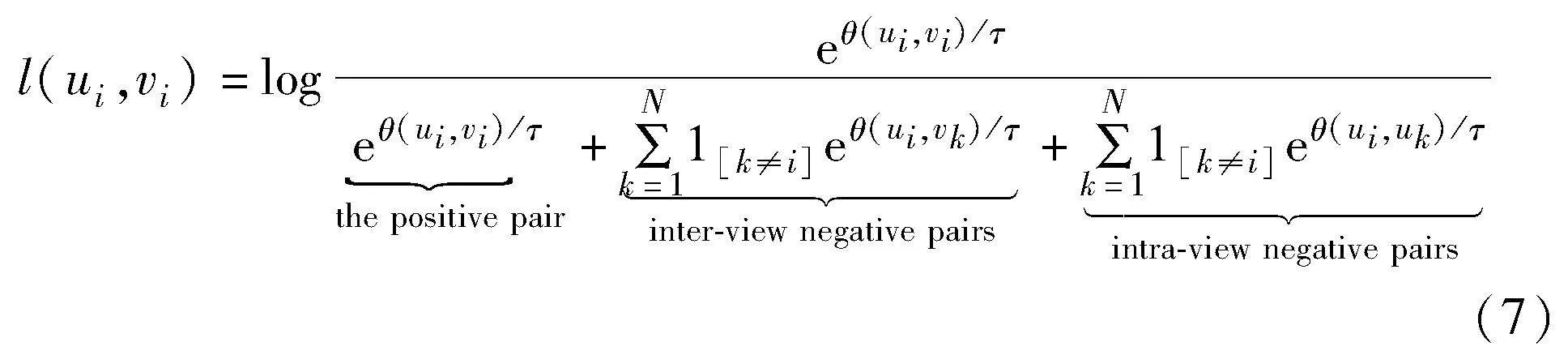
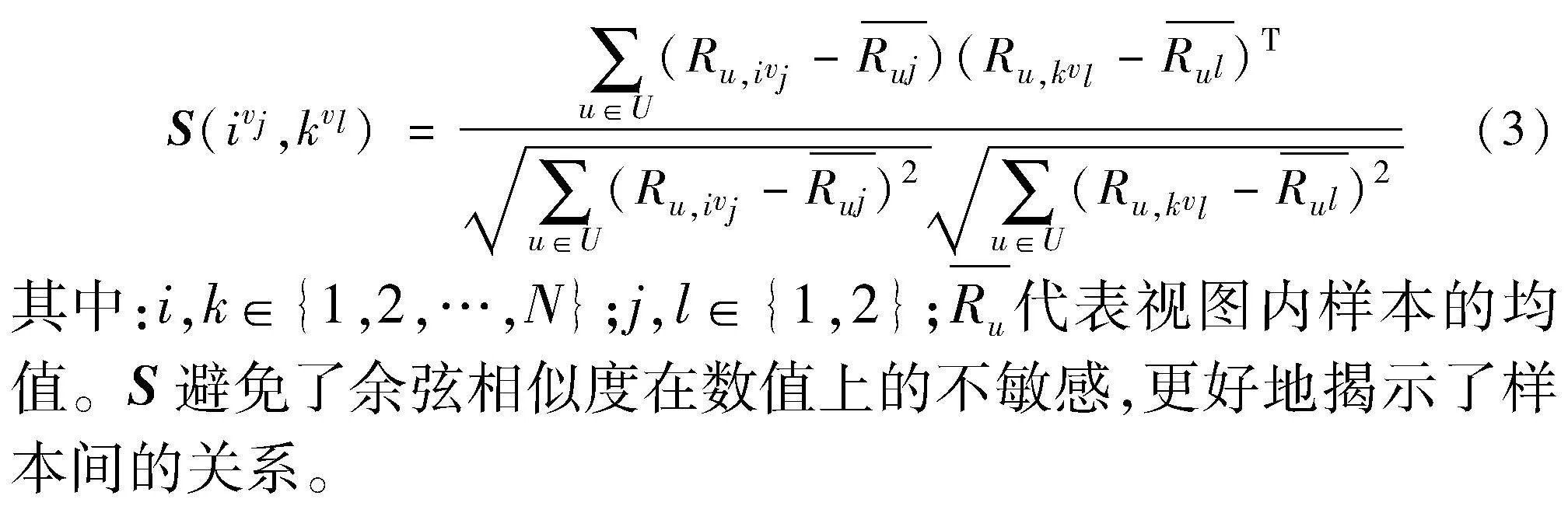
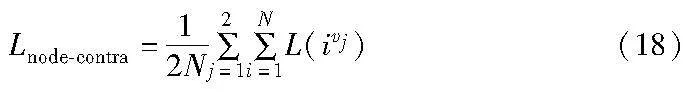
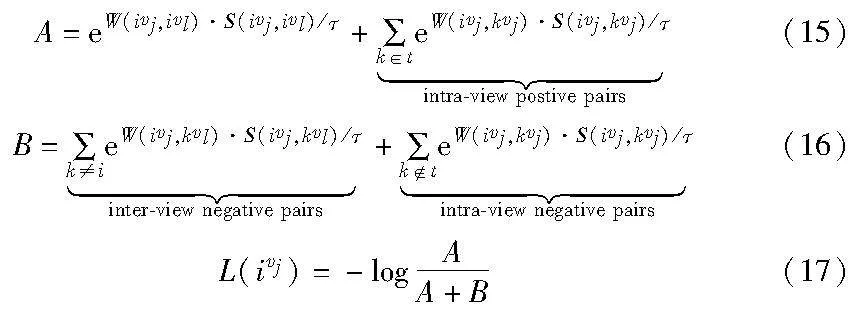
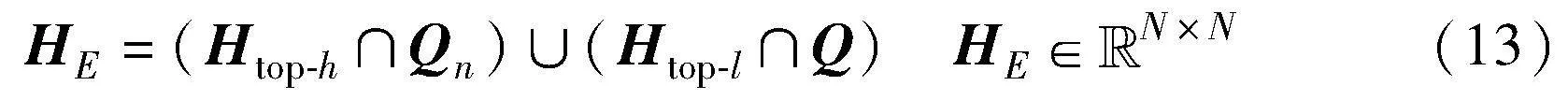
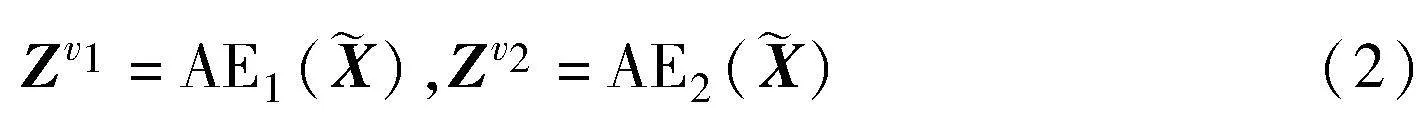
摘 要：针对困难样本挖掘的图聚类算法是最近的研究热点，目前算法存在的主要问题有：对比方法和样本对加权策略缺少良好的融合机制；采样正样本时忽略了视图内部的“假阴性”样本；忽视图级信息对聚类的帮助。针对上述问题，提出困难样本采样联合对比增强的图聚类算法。首先使用自编码器学习嵌入，根据计算的伪标签、相似度、置信度信息为表示学习设计一种自加权对比损失，统一不同视图下节点对比和困难样本对加权策略。通过调整不同置信区域样本对的权重，损失函数驱动模型关注不同类型的困难样本以学习有区分性的特征，提高簇内表示的一致性和簇间表示的差异性，增强对样本的判别能力。其次，图级表示经聚类网络投影，通过聚类对比损失最大化不同视图下聚类的表示一致性。最后联合两种对比损失，利用自监督训练机制进行迭代优化，完成聚类任务。该算法在5个真实数据集上与9个基准聚类算法对比，在4个权威指标上达到最优，聚类性能出色。消融实验表明两个对比模块的有效性和可迁移性。

关键词：图表示学习； 属性图聚类； 对比学习； 困难样本挖掘

中图分类号：TP311.13;TP181 文献标志码：A

文章编号：1001-3695（2024）06-024-1769-09

doi：10.19734/j.issn.1001-3695.2023.10.0521

Deep graph clustering with hard sample sampling joint contrastive augmentation

Abstract：The graph clustering algorithm for hard samples mining is a recent research hotspot. In the current algorithm， the main problems include the lack of a fusion mechanism for comparing methods and a sample pair weighting strategy; the algorithms ignore “false negative” samples within the view when sampling positive samples and disregarding the help of graph-level information for clustering. To address the issues above， this paper proposed a graph clustering algorithm based on hard sample sampling joint contrast augmentation. Initially，it utilized an autoencoder to learn embeddings，designed a self-weighted contrast loss for representation learning by utilizing the calculated pseudo-label， similarity， and confidence information， and unified the strategies of node comparison and hard sample pair weighting across different views. By adjusting the weights of sample pairs in different concJL75m6eWy/OomSwA/tN/g==fidence regions， the loss function derived the model to focus on different types of hard samples to learn discriminative features， improving the consistency of intra-cluster representation and the distinctiveness of inter-cluster representation and enhancing the ability to discriminate samples. Additionally， the clustering network projected the graph-level representation to maximize the representation consistency of clusters under different views through cluster contrast loss. Finally，combining the two comparison losses， the self-supervised training is used for iterative optimization to complete clustering. In the comparison with 9 benchmark algorithms on 5 real datasets， this algorithm achieves superior performance on 4 authoritative indicators， highlighting its excellent clustering capabilities. Ablation experiments demonstrate the effectiveness and transferability of the two contrasting modules.

Key words：graph representation learning; attributed graph clustering; contrastive learning; hard sample mining

0 引言

图数据作为描述现实世界的工具之一，在引文网络［1］、社交网络［2］、推荐系统［3］等领域发挥了重要作用。属性图提供一种结构化的方式表示属性实体间的关系。属性图聚类是数据挖掘领域的一项重要问题，目的是以无监督的方式将图中的节点划分成多个组，使得同一簇中的节点具有相似的属性。

传统的聚类算法（如K-means、Spectral）面向高维数据时聚类效果不够理想。近年来，基于深度学习的聚类方法达到了最佳性能。其中GCN［4］可学习属性图的结构信息和节点特征来嵌入低维表示。VGAE［5］采用GCN编码器和重构解码器，利用节点表示完成聚类。Pan等人［6］在GAE框架的基础上引入对抗性正则化器，开发对抗性正则化图自编码器网络（ARGA）完成聚类。Wang等人［7］受深度嵌入聚类DEC［8］的启发，通过聚类导向网络最小化聚类分布与聚类间的不匹配。虽然已有了长足的进步，但它们往往是通过聚类导向的损失函数使得生成的样本拟合预先生成的聚类分布，初始化的簇中心会影响模型的整体性能，且面临着数据依赖、过拟合、高计算复杂度等问题。

近年来，对比学习在计算机视觉［9］、图表示学习［10］等领域表现出强大的性能。受此启发，最近的一些研究［10～12］通过对比损失函数来取代聚类引导的损失函数，从而消除了初始簇中心所带来的人工误差。例如，GCA［10］在文献［11］的基础上提出了一种带有节点中心性度量的自适应图增强方法，增强图信息以实现节点表征同图级表征的对比；SCGC［12］设计了一种面向邻居的对比目标函数，促使跨视图相似性矩阵逼近自环邻接矩阵，使得模型可以保持跨视图的一致性，增强了网络的判别能力。

对比学习的成功取决于正样本对和负样本对的设计，例如SCGC中将节点的邻居作为正样本构造目标函数；AFGRL［13］挖掘图中共享局部结构信息和全局语义的节点对来构造对比学习的正、负样本实现对比。但这些方法往往忽略了困难样本的存在。在对比学习中寻找锚点附近的困难样本能够提供显著的梯度信息［14］，最近的研究［15～17］也表明，在对比过程中挖掘困难样本十分有效。例如，HCL［14］开发了一系列选择困难负样本的抽样方法；MoCHi［15］混合困难负样本来合成更多的困难样本；ProGCL［16］首先对假阴性样本进行过滤，借助样本相似性设计了一种更好的量化样本为负的概率和困难度的方案；HSAN［17］通过结构信息和属性信息计算相似度以辅助困难度的测量，同时关注困难的正、负样本并动态地调整样本对的权重。

虽然这些工作的有效性得到验证，但仍存在以下缺陷：a）困难样本的评估与对比机制缺少有效的融合机制［15～17］，现有困难样本挖掘方法在使用对比损失指导图表示学习时，只为样本对赋予权重，忽略了样本对在不同难度下与正负样本对比策略的结合；b）传统的图对比学习通过不同的增强方案将原始图扩展为两个视图［18］，将一个节点在两种不同增强下的表示视为正对，其余作负对，这种设计忽略了每个视图内存在的正样本，违背了“物以类聚”的聚类初衷；c）大多方法仅利用节点信息面向任务。然而对比表示学习中，跨视图对比图表示和节点表示在聚类上已经取得了良好成效，图级信息不应被忽略。

针对上述问题，本文提出一个困难样本采样联合对比增强的深度图聚类方法（deep graph clustering with hard sample sampling joint contrastive augmentation，HSCA）。首先，对原始数据滤波并经由简单的MLP编码器获得低维嵌入表示，在精心计算的相似度、置信度样本集合、伪标签信息下，提出了一种新的困难样本对调权策略，加权函数根据训练难度调整不同置信区域正、负样本对的权重；其次，根据低维嵌入构造图级表示，将其投影至聚类层，在两个视图间学习类别的一致性；最后，联合优化自加权对比损失和聚类对比损失以实现更优的聚类性能。

本文的主要贡献如下：

a）提出一个基于困难样本采样联合对比增强的聚类模型HSCA。通过巧妙的样本困难度计算方案，对高置信区域中的节点对，HSCA提高困难对的权重，降低容易对的权重；在低置信区域额外关注偏差节点对，引导网络自适应地采样多类型的样本对并调制权重。

b）为了消除传统对比学习中视图内“假阴性样本”的问题，通过伪标签和相似度的交叉信息，在视图内为锚点采样K个最相似的同簇节点作为正样本。跨视图融合正负样本采样和困难样本对的调权策略，提出一个自加权对比损失函数。

c）提出一个聚类表示对比方案。以往的节点聚类仅关注节点级特征而忽略了全局信息。HSCA构造图级表示并投影聚类层，在视图间学习聚类表示的一致性，利于模型优化。

d）在五个数据集上的大量实验证明了本文方法的优越性和有效性。

1 相关工作

1.1 深度图聚类

深度图聚类是近年来备受关注的研究方向，其目的是用神经网络对节点编码，并将其划分为不相交的多个类。现有方法可分为重构方法（TGC［19］，DAGC［20］）、对抗性方法（AGAE［21］，JANE［22］）和对比式的方法三类。本文着重于最后一类。对比图聚类首先经深度网络将样本嵌入低维空间，然后基于对比策略将正样本聚集在一起的同时推开负样本来提高对样本特征的辨别力。对比方法关心属性信息的同时通过样本之间有意义的关系（如相似度）构建自监督信号。AGE［23］设计一个自适应编码器实现节点级的对比学习。MVGRL［18］采用双参数非共享GCN编码器和共享MLP作为主干，然后在不同视图间学习节点表示和图表示的一致性，而本文的HSCA在图、节点表示两个层面上都设计了可靠的对比方案。文献［24］根据聚类层生成的伪标签解决了对比过程中负样本随机选择的问题，从负样本集合中根据伪标签删除与当前节点标签一致的节点。HSCA相比前者通过伪标签增强方案得到了更优质的伪标签，并将其巧妙地应用于困难度计算过程和对比学习中。文献［25］考虑不同深度的节点之间的影响，加入了结构信息，将R跳邻域内的节点作为当前节点的正样本，并将其与所有节点进行对比。AFGRL通过样本局部结构信息和全局语义信息捕捉到更可靠的正样本集合。本文综合考虑top-K近邻和伪标签信息，在跨视图的条件下选取到了更可靠的正样本。传统的对比聚类虽然设计了巧妙的对比策略并以对比损失引导模型优化，但大多方法将容易和困难的样本一视同仁，导致不易区分。本文考虑挖掘困难样本来提高对比学习在聚类任务上的应用性能，设计了一种高效的困难度度量方案。

1.2 困难样本挖掘

计算机视觉［26，27］中的工作表明，区分困难样本和容易样本虽然具有一定的挑战性，但对于对比学习十分有效。受此激励，研究人员开始关注对图中困难样本的挖掘。困难样本是表示学习过程中不好划分的样本，一种常用方法是负样本挖掘（negative sample mining）［15，16］。该方法在每一轮训练中选择最难区分的负样本以提高模型的泛化能力。Xia设计了一个概率估计器，为负样本的困难度和相似性建立起合适的一个度量，更关注属于同类但相似度较低的样本，但忽略了困难的正样本也值得关注。CuCo［28］将图级对比学习的负样本按相似性从易到难进行分类，并利用课程学习自动选择和训练负样本的方法。与此相反，本文研究了实例间消息传递的节点级对比学习。HSAN提出一个正负样本对的加权策略以引导网络，同时关注困难的正样本和负样本，从而实现更好的聚类效果。与之前的方法相比，HSAN同时关注了困难的正负样本，但是在正负样本的采样方式上仍延续了传统方式，将锚点在另外一个视图下的表示视作正样本，其余为负样本。本文则设计了一个高效的对比策略，跨视图为每个样本选取更合理的正负样本集合，并联合困难度评估，将两者融为一体；其次，将聚类表示应用对比学习来进一步提升聚类性能。

2 困难样本采样联合对比增强的深度图聚类模型

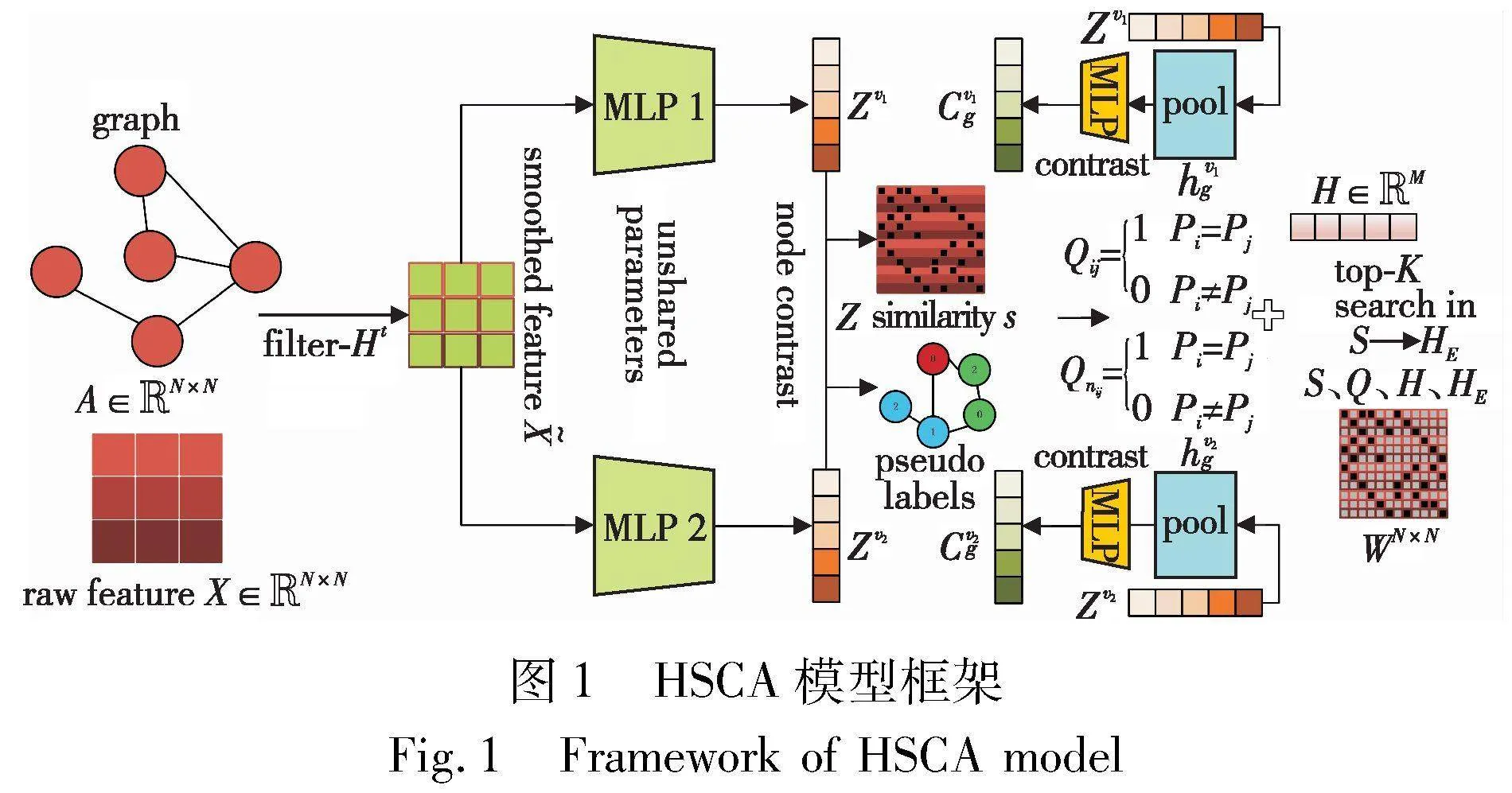
HSCA网络架构由特征增强及编码模块、自加权对比表示学习模块和对比增强模块组成。

本对调权策略，在高置信区域提高困难节点对的权重，降低容易节点对的权重，在低置信区域中关注不同类型的困难样本对，保持偏差节点对HE的权重最高。在对比表示的过程中调整不同难度的样本对权重是为了驱动网络学习区分性的特征，从而提高对比学习的性能。根据正负样本采样策略和加权策略形成的自加权对比损失进行迭代训练，促使同一个簇内的节点的表示趋近一致。

HSCA中的两种表示相互作用，并在端到端框架中共同发展；两种对比损失联合优化模型参数，从而进一步提高对样本的判别能力。

2.1 符号定义

2.2 特征增强及编码模块

经两个参数非共享的MLP编码器生成两个语义不同的属性嵌入，定义为

本文基于调整余弦相似度计算视图内和视图间的样本相似度矩阵S［29］，定义如下：

2.3 伪标签及置信增强模块

融合多个视图下的嵌入可以帮助模型更好地理解数据的多样性和复杂性，从而提高泛化能力。定义融合两个视图嵌入为

Z=（Z1+Z2）/2（4）

依据伪标签P计算样本对伪关系矩阵Q定义为

Qij=1表示节点i、j可能属于潜在的同类；Qij=0表示节点i、j可能分布在不同簇；Q揭示了节点间潜在的类别关系。

上述交集操作可以学习伪标签矩阵、置信集合间的一致性，增强了辅助信息的可靠度和鲁棒性。

2.4 自加权对比表示学习模块

本节介绍HSCA中的困难样本对调权策略、正负样本采样策略和自加权对比损失函数。图对比学习中的经典infoNCE［30］损失函数为

其中：1［k≠i］∈{0，1}是一个指示函数，当k≠i时为1；τ是温度系数。通过最小化损失函数，将不同视图中的正样本拉近，负样本推远。此损失函数中所有样本对的权重一致，它忽视了样本对间并非平等，限制了模型对节点的判别能力，故HSAN提出困难样本对和容易样本对自适应的加权，困难样本感知对比损失如下：

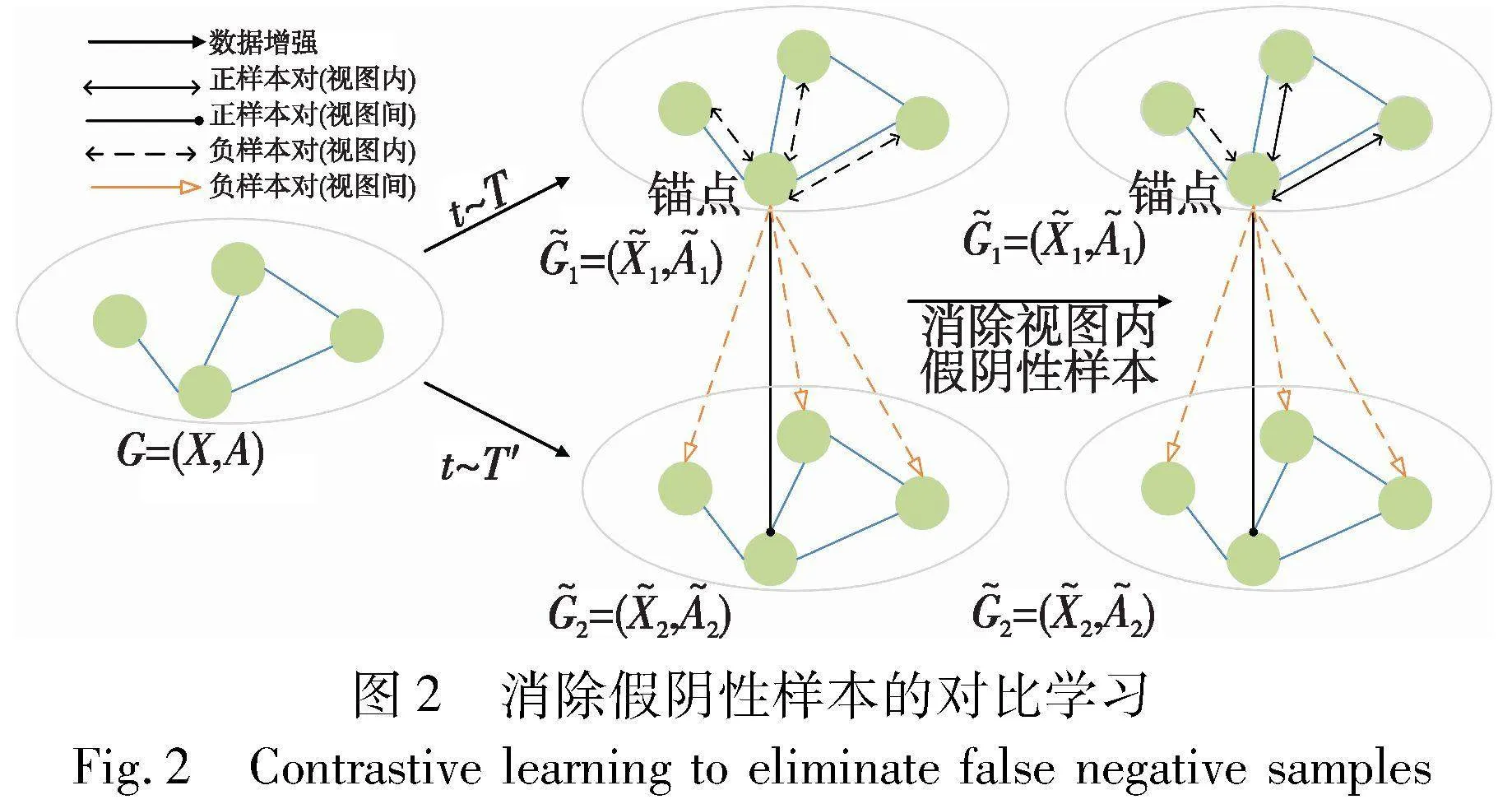
该对比损失函数动态地增加困难样本对的权重、降低容易样本对的权重，并拉近正样本，推移负样本。然而这两个对比损失函数都存在一个缺陷：传统对比学习在不同的增强方案上生成两个视图，随后将同一节点在不同视图下的表示视为正对，其余的2N-2个节点作负样本组成负对。这忽略了“假阴性样本”的存在，在聚类中，同一个簇中的节点相似性较高，而不同簇中的节点相似性较低。在视图内部，对当前锚点，存在与它相似度高的同簇样本，而传统的对比方式将视图内部的其余节点视为负样本，这违背了聚类的基本逻辑。

GDCL［24］使用聚类层得出的伪标签信息获得节点伪标签一致的节点，将其作为锚点的正样本而将其余样本作为负例。CAGC［31］通过KNN（K-nearest neighbor）来选择K个最近邻居节点作为当前节点的正样本。受其启发，本文提出top-K正样本选择策略——在视图间保持与传统对比方法一致，将节点在不同视图下的表示视为正对，在视图内当前节点的正样本由伪关系Q和相似度S确定，先由Q筛选出与当前节点同类的节点集，同时定义每个样本K个相似度最高的节点序列为

对Htop-h和Q求交集，在潜在的同簇样本中为节点选取最相似的K个节点作为正样本。故对任意节点i，其正样本定义为

（Htop-h∩Q）+1（10）

节点的负样本为两个视图中被过滤掉的其余样本。如图2所示，上述策略从伪标签和相似度两个信息求取共有特性，比以往方法更加可靠。

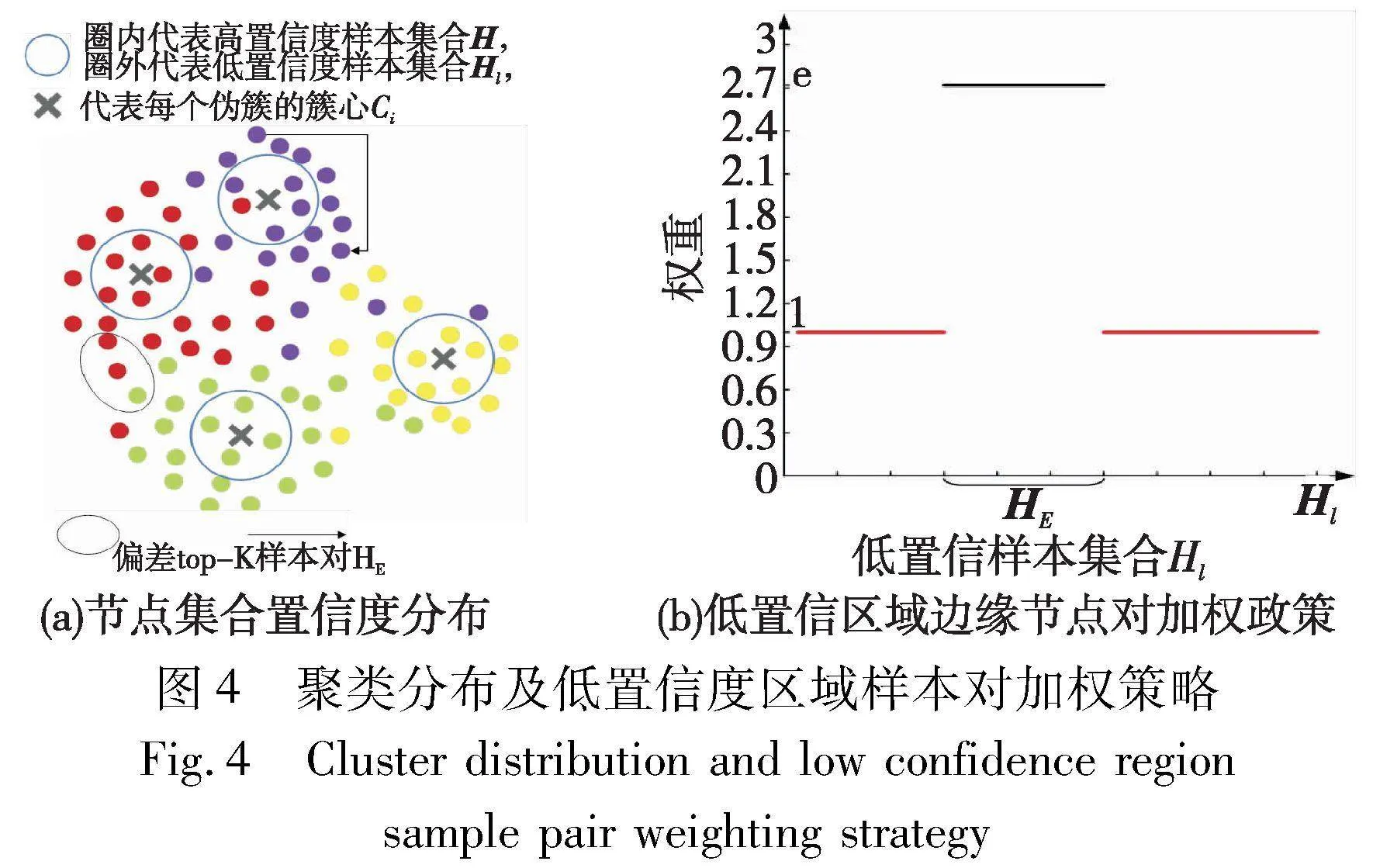
同式（9）。本文希望相似度和聚类结果能更一致：相似度高的样本伪标签最好一致，而相似度低的样本对类别应该不同。然而在低置信区域Hl中仍然存在偏差信息：节点i相似度最高的K个节点中有部分节点和i伪标签不一致；i相似度最低的K个样本中存在部分节点和i伪标签一致。

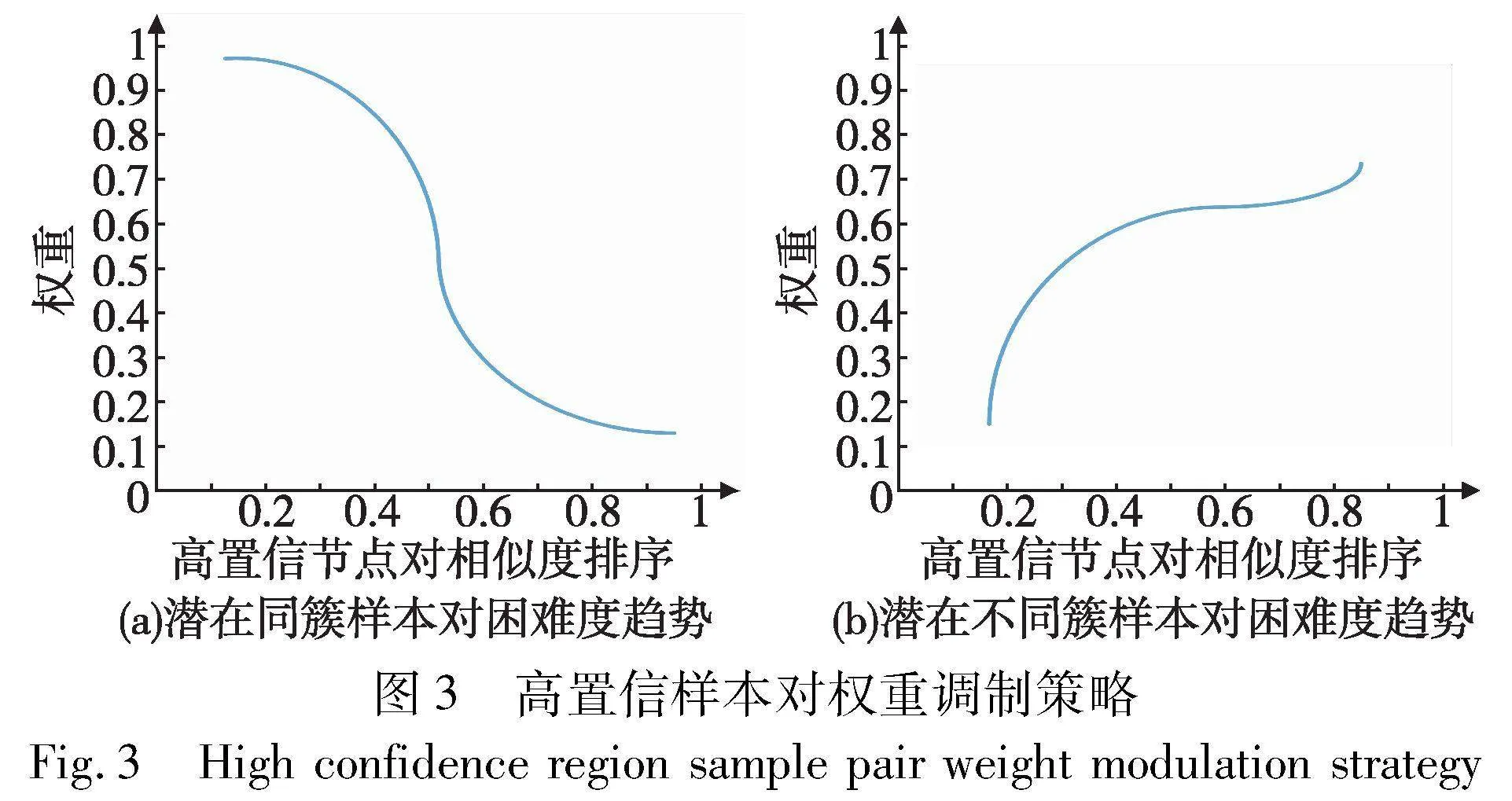
对这类低置信度区域中相似度和伪标签信息出现偏差的样本对定义为偏差top-K样本对HE。HE中第一种节点对的相似度很高但归属不同簇，即图4（a）中椭圆标注的聚类边缘重叠的区域，这类节点对极其相似但却是两类节点；第二种节点对相似度很低但伪标签一致，图4（a）中它们分布在聚类的两端。HE中的节点都位于低置信区域，为了纠正这种伪标签与相似度信息的偏差，对它们赋予更高权重以增强它们在对比过程中的影响力。

HE的计算分以下步骤，首先定义负伪关系矩阵Qn：

当节点i、j的伪标签一致时设置为0，相异时设为1。HE定义如下：

HE中的数值只有0或者1，HE（i，j）=1代表节点i、j处于低置信区域且属于偏差节点对。

基于上述信息，在视图内部，加权函数为

W基于两种不同方式来确定样本对困难度。第一种方式是在高置信度区域中根据相似度大小和伪关系来调整相对困难或相对容易的样本对的权重。第二种方式是将低置信区域中的样本全部视为潜在的困难节点，将其两两组合视作困难样本对并赋权为1，并且在低置信区域中继续筛选，从相似度和伪关系的偏差信息中筛选出偏差样本对继续放大权重。通过这两种方式能全面地评估样本对的困难度。

综上，根据上述的困难样本对调权策略W及正负样本选取策略，本文提出一种自加权对比损失函数定义为

其中：A和B分别表示当前锚点的正、负样本集合；intra-view表示视图内；inter-view表示视图间；k∈t表示k是当前节点i的视图内正样本集合，即式（10）中的Htop-h∩Q。上述函数将样本对困难度的计算和对比学习的过程联系起来，通过相似度和伪关系信息选取到更可靠的视图内正样本，函数W采用不同的加权策略关注不同置信度下样本对的分布情况而自适应加权。因此，本文方法的节点级整体对比损失如下：

2.5 对比增强模块

以往的图聚类仅关注节点级别的对比，忽略图级信息的辅助作用。受多视图对比学习最新进展的启发，通过最大化一个视图的节点表示和另外一个视图的图表示之间的互信息来学习节点表示［18］。本文提出一个基于图级表示的对比增强模块。

此时，i代表聚类中的第i类，正样本为另外一个视图中的同类，负样本为另外一个视图中的其他类。则图级表示的聚类对比损失函数如下，K为聚类数。

综上，联合损失函数如下：

Ltotal=λ1×Lnode-contra+λ2×Lcontra-aug（22）

其中：λ1和λ2是两个超参数，用于平衡自加权对比损失和聚类对比损失。

HSCA模型的算法流程如下：

算法1 困难样本采样联合对比增强的深度图聚类算法

对优化后嵌入Z执行K-means算法获得聚类结果Φ。

3 实验

3.1 基线数据集

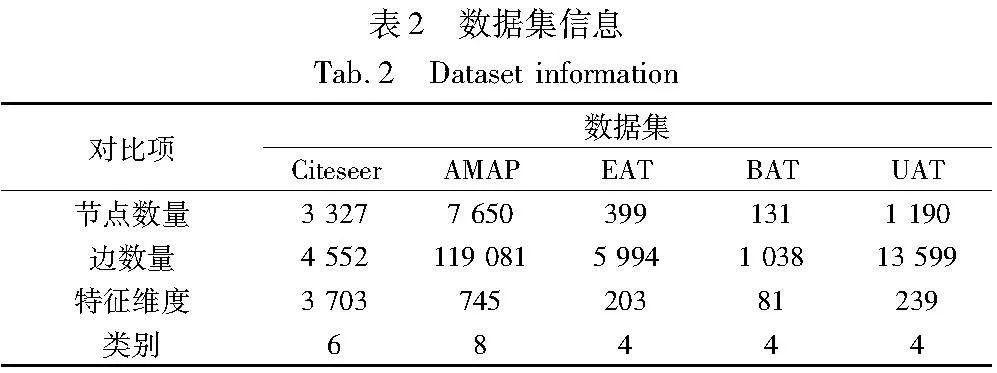
实验在五个基准图数据集上进行。这些数据集涵盖了多个领域，例如空中交通网络、引文网络、学术网络和购物网络。这些数据集皆为属性图，包含结构和特征信息，数据集的体量、维度、类别都不同，能更好地综合评估HSCA方法的性能。

Citeseer表示一个引文网络，一共收录3 312篇论文，论文间引用链接4 732条。所有论文都属于6个不同的学术研究领域，每篇论文都由一个3 703维的词向量表示。AMAP提取自亚马逊共购图，其中节点表示产品，边表示两种产品是否经常共购，特征表示用bag-of-words编码的产品评论，标签是预定义的产品类别。EAT数据来自欧盟统计局，包含399个节点，5 995条边。BAT数据来自巴西国家民航局，包含131个节点，1 038条边。UAT来自于美国空中交通，包含1 190个节点，13 599条边。这三个数据集都表示机场活动，每个节点代表一个机场，边描述了机场间的商业航班关系，由节点度的单热特征表示属性。包含多个级别作为类别，每一个都反映了机场的客流量，通过相应时期的着陆次数和起飞次数来衡量。数据集详细信息如表2所示。

3.2 基线方法

为了证明本文HSCA模型的优越性，在上述5个数据集上进行了广泛的实验，选择了9种最先进的方法作为对比，它们可以分为基于对比的深度图聚类方法（AGE、AUTOSSL［33］、MVGRL、AGC-DRR［34］、DCRN［35］、AFGRL）和基于困难样本挖掘的方法（GDCL、PROGCL、HSAN）两类。AUTOSSL选择合适的预训练任务来提高模型的性能。AGC-DRR将图的结构增强和样本聚类统一为一个通用的最小-最大优化框架，以减少输入和潜在特征空间中的信息冗余。DCRN通过表示相关性来解决样本视角和特征水平的表示坍塌。AFGRL通过KNN搜索发现的样本中过滤出假阳性样本来纠正样本选择偏差问题。其余基线已在第1章中介绍。

3.3 实验设置

实验运行在CPU Intel Core i9-12900K， GPU NVIDIA GeForce RTX 3090Ti，RAM 128 GB，PyTorch 1.11.0的环境中。基线方法的结果来自HSAN。HSCA的最大训练次数设置为400，计算一个平均指标来避免单此结果的随机性。使用Adam优化器最小化式（22）联合损失，然后对学习到的嵌入执行K-means。HSCA进行10轮实验，最后求取平均以避免单次结果的随机性。

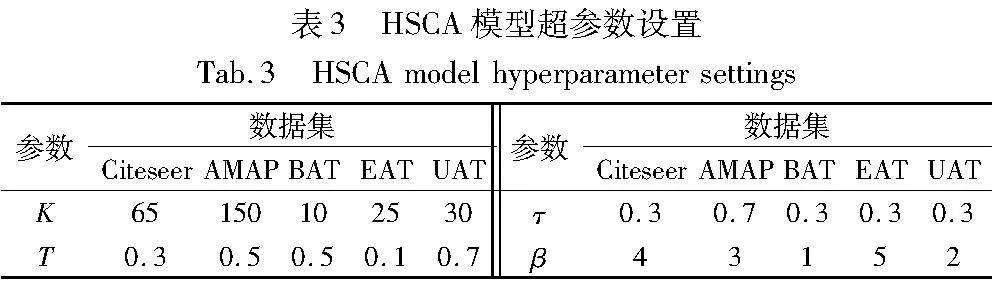
聚类性能由ACC（准确性）、NMI（标准化互信息）、ARI（平均兰德指数）和F1（宏观F1得分）四个广泛用于深度聚类领域的指标进行评估。本文HSCA的属性编码器由两个参数非共享的单层MLP组成，Adam优化器的学习率设为［1E-5，1E-3］。本文设计了多个超参数，K表示每个样本相似度最高或者最低的top-K样本序列，T是计算节点级对比损失时的温度系数，τ为置信参数，β是降权系数。超参数设置汇总在表3中。

3.4 实验结果

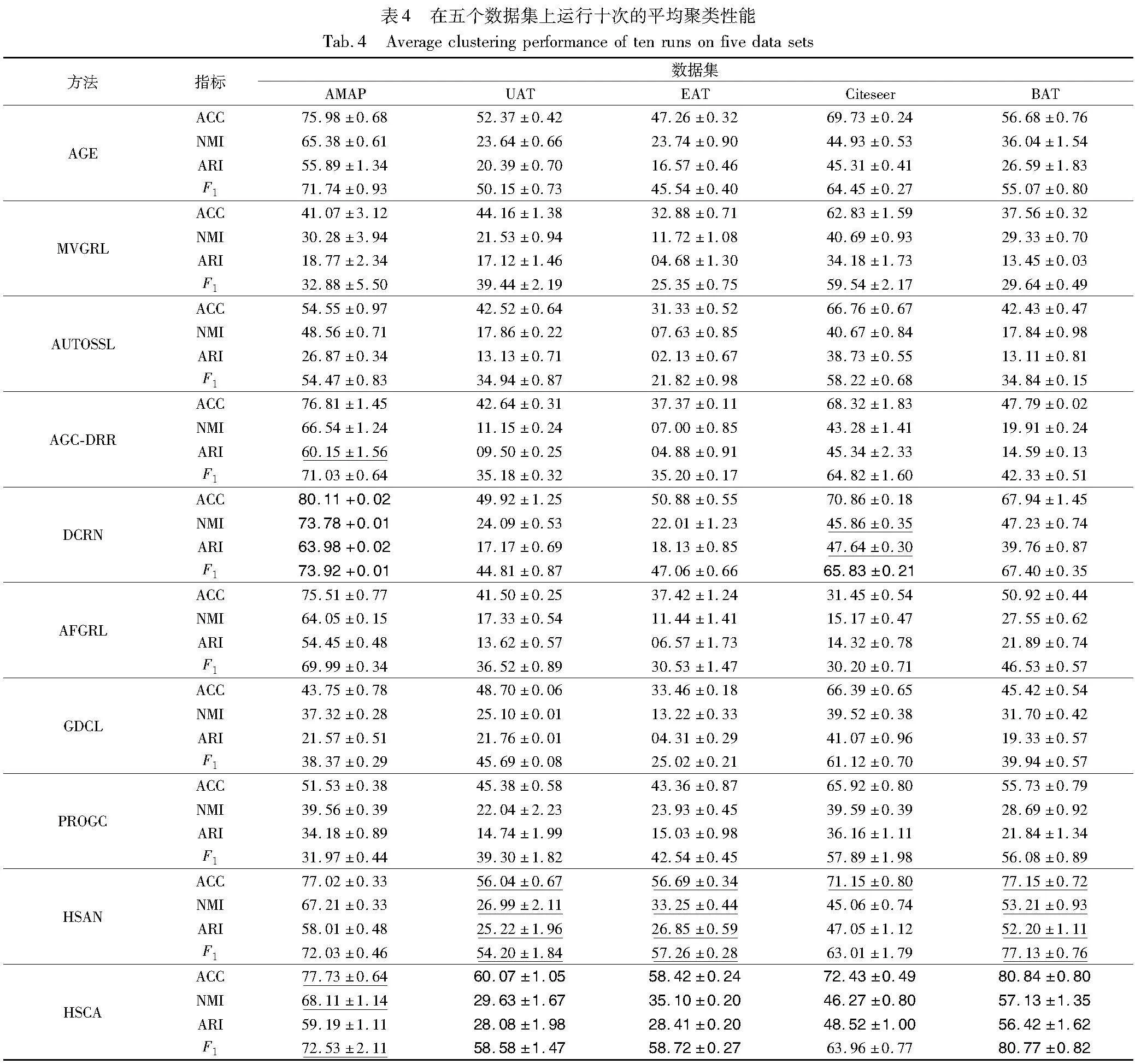
如表4所示，性能由四个具有平均值和标准差的指标来评估，其中加粗和下画线分别表示最优和次优的结果。根据实验结果可以得出以下结论：

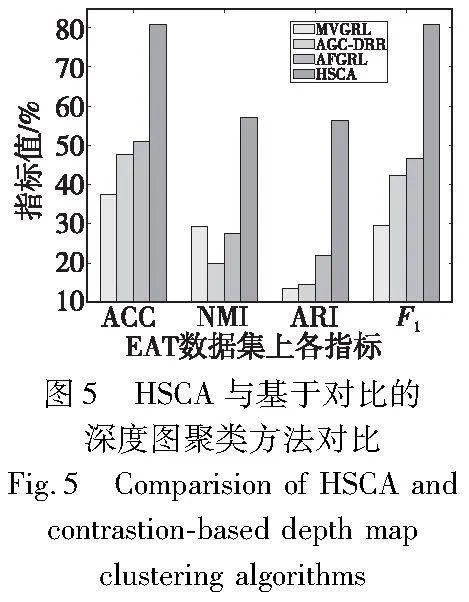
a）HSCA优于AFGRL、AGC-DRR、MVGRL、DCRN方法。HSCA与AFGRL有着相似的正负样本采样策略，但HSCA关注到节点学习难度的不平等，通过困难样本对调权函数W提高困难样本对的权重，降低容易样本对的权重，而传统的对比聚类方法在对比过程中样本对权重一致，并未将困难和容易的样本对区分开，图5表明，HSCA显著优于均权对比聚类方法，表明强调困难样本的有效性。

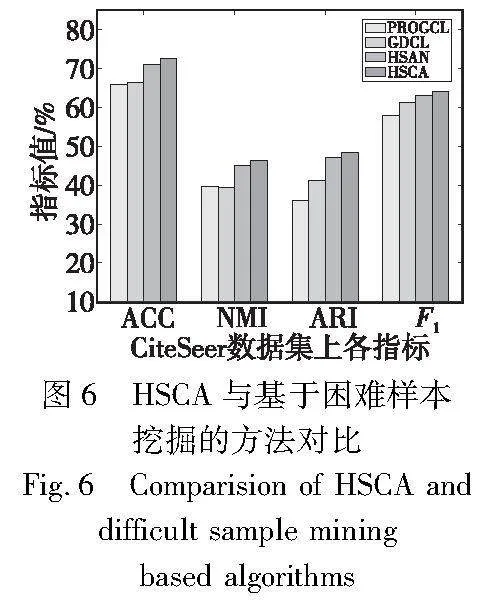
b）HSCA优于HSAN、PROGCL、GDCL。说明调权策略和正负样本采样策略的融合机制十分有效。从图6可以看出，HSCA显著优于GDCL、PROGCL方法，表明HSCA利用top-K搜索和相似度信息在跨视图条件下获得的正样本更加可靠，可以帮助提高学习的节点表示质量。同时，HSCA优于HSAN、PROGCL，在UAT数据集上HSCA相较于最接近的基线HSAN提升最为明显：ACC实现了7.1%的提高，NMI实现了9.7%的提高，ARI实现了11.3%的提高，F1实现了8%的提高，表明HSCA中的调权策略和对比策略融合形成的自加权对比损失函数更有效，它在对比过程中关注不同置信区域下的加权差异，在高置信区域中根据伪标签的区别调整不同相似度下样本对的权重，对低置信区域中困难的样本对额外关注偏差样本对的类别，提高了模型的判别能力。

c）由表4可知，相较于其他方法，HSCA联合了两种级别的对比损失，除节点级对比外，生成图级表示面向聚类完成对比的方式在五个数据集上的四个指标都取得了巨大的提高，在Bat数据集上，HSCA相较MVGRL方法，ACC提升115.2%，NMI提升94.7%，ARI提升319.5%、F1提升172.5%，表明HSCA在节点级和聚类级对比的联合对比损失捕捉到的信息在两个级别更好地引导模型面向聚类任务。

d）关注到HSCA在五个数据集上提升幅度存在差异，HSCA根据不同置信区域为样本对加权，由于UAT、BAT、EAT等数据集的样本数较少，维度也较低，而较低的样本数和维度更有利于保留数据间的结构信息和相似性，并且更少的样本数使得采样的正负样本和计算伪标签更贴近真实，所以提升的幅度较AMAP、Citeseer大。在AMAP数据集上，HSCA模型取得了次优的结果，由于AMAP节点和类别过多导致边界的节点不容易分辨，采样得到的困难样本不够精确，而DCRN过滤了冗余特征，在潜在空间中保留更明显的特征，误差信息更少。

3.5 消融研究

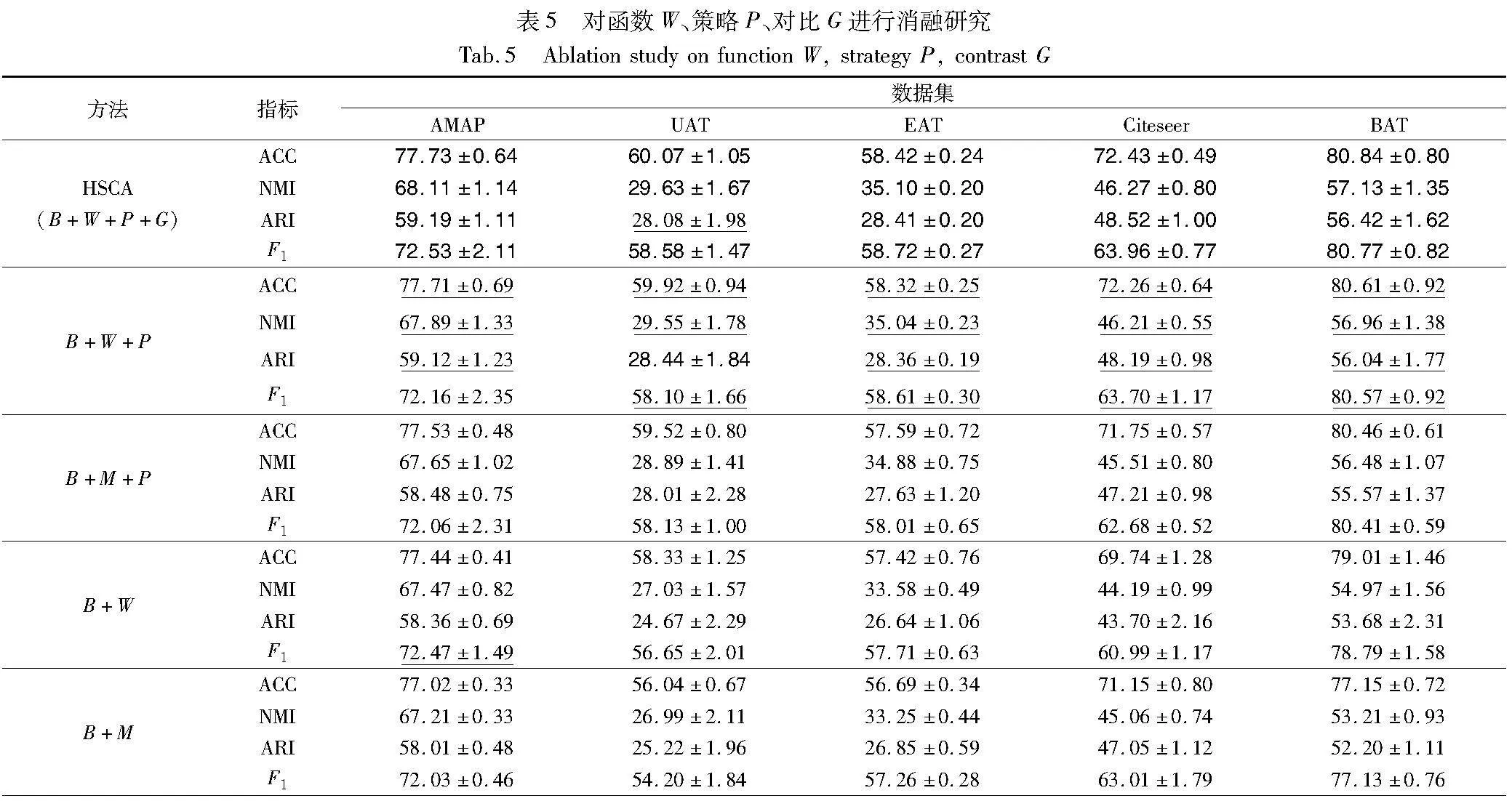
本节在AMAP、Citeseer、UAT、EAT、BAT五个数据集上实现三个消融场景，进一步验证HSCA中自加权对比表示学习模块和对比增强模块的有效性。消融实验的基线为设置B+M（即使用文献［17］中的调制函数M对样本对权重进行加权）。将采用HSCA中函数W为样本对加权的方案定义为W，使用top-K采样策略定义为P。对比增强模块定义为G。自加权对比表示学习模块等同B+W+P策略的叠加；HSCA方法等于B+W+P+G策略的叠加。

由消融结果可以得出以下结论：

a）在传统对比策略下，即每个节点将另外一个视图中的自己作为正样本时，由表5可知，B+W函数要优于B+M函数。视图内的相似度矩阵由同样语义的嵌入生成了更准确的信息。相较函数M，函数W在视图内、视图间采取不同加权策略。函数M自动为容易样本对降权、困难样本对升权，而函数W在此基础上，额外考虑到低置信区域中的偏差样本对的存在，赋予此类样本对更高的权重，表明了其有效性。B+W策略在BAT数据上的四个指标，较B+M分别提高了2.4%、3.3%、2.8%、2.1%，表明W提升了模型对低置信区域中困难样本的分辨能力。

b）对于两种加权策略同时采用提出的正负样本采样策略P，在UAT数据集上，B+M+P相较使用传统对比方案的B+M，在各个指标上分别提升了6.2%、7%、11%、7.2%，充分说明HSCA的正负样本采样策略的有效性，相比PROGCL、HSAN方法，策略P在视图内部解决了假阴性样本的问题，相比GDCL、CAGC，对于正样本的采样结合伪标签相似度信息，获得了更可靠的正样本。其次，表5中B+W+P策略的结果仍然要优于B+M+P，表明本文方法中自加权对比表示学习模块的有效性，它为正负样本对比策略和样本对加权方式提供了两个更可靠的范本，有利于提取有助于聚类的节点表示，同时说明HSCA困难样本对的加权策略同对比学习采样策略的融合机制非常有效。

c）对比增强模块G有助于聚类的表达。自加权对比表示模块叠加对比模块G后，在五个数据集上的四个指标上又表现出了新的提升并达到最佳。图级表示投影的聚类层代表了各个类别的概率分布，在聚类层进行对比更有利于在两个视图间学习类别分布的一致性，可以逼近更真实的聚类分布，而缺少G模块的HSCA无法更好地探索聚类结构，验证了G模块的有效性。

3.6 超参数分析

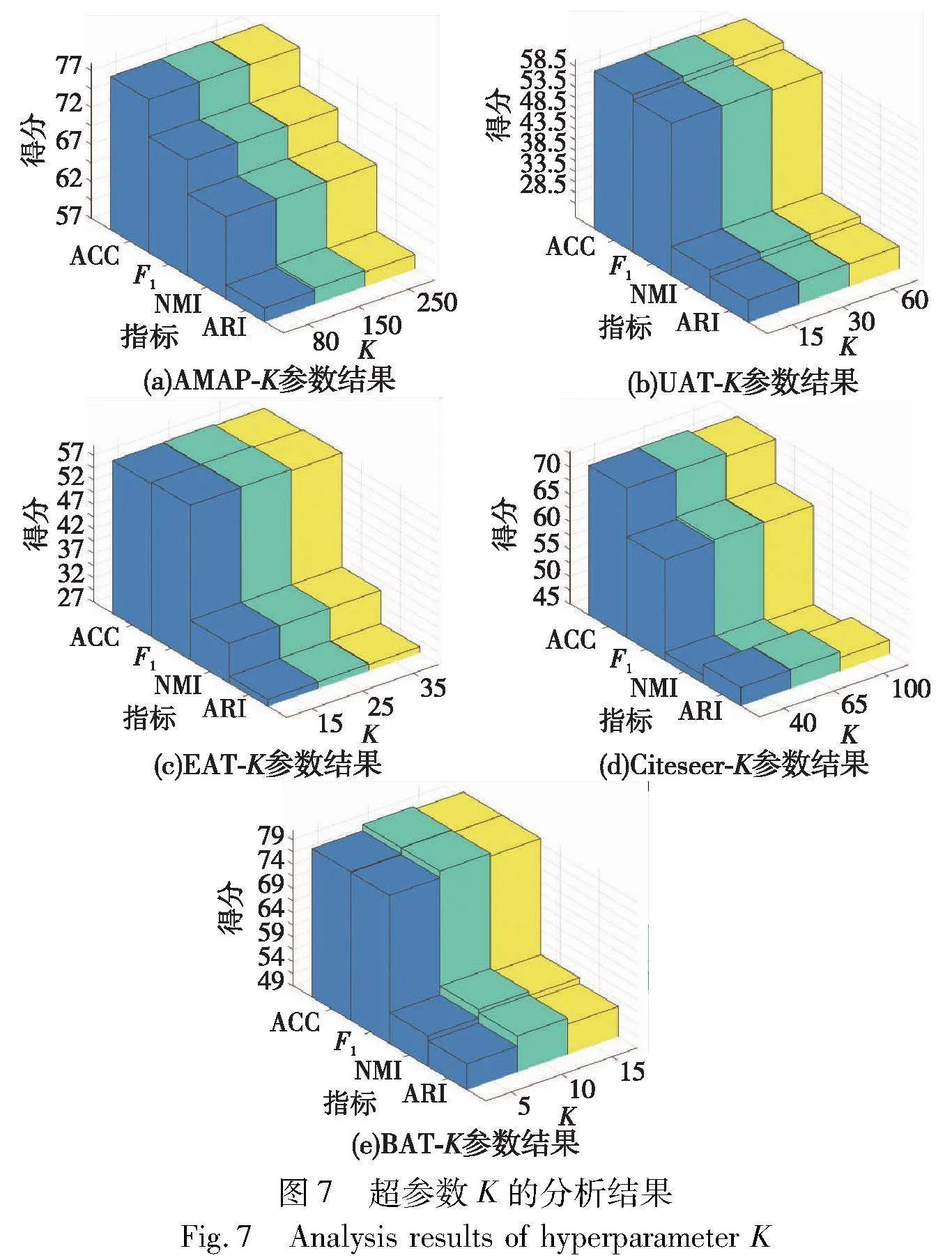
本节将分析算法中四个超参数置信度τ、降权系数β、top-K参数K、温度系数T的影响。对于top-K参数K的取值，K影响视图内正样本的数量和偏差节点对HE的范围，K过小时选取到的正样本数量会不够充分，K过大时偏差top-K样本数过多。实验中根据数据集样本数量，选取3%～15%的样本数作为K的最大值，并向下递减。如AMAP、Citeseer拥有数千个样本，故选择样本总数3%的数目作为最大K的取值，并向下选取两个比例更小的K。而BAT、EAT的样本数仅有几百个，故提高最小K的取值，并向上选取。如图7所示，参数K对算法的影响整体呈现一个先升后降的趋势，符合设计预期。

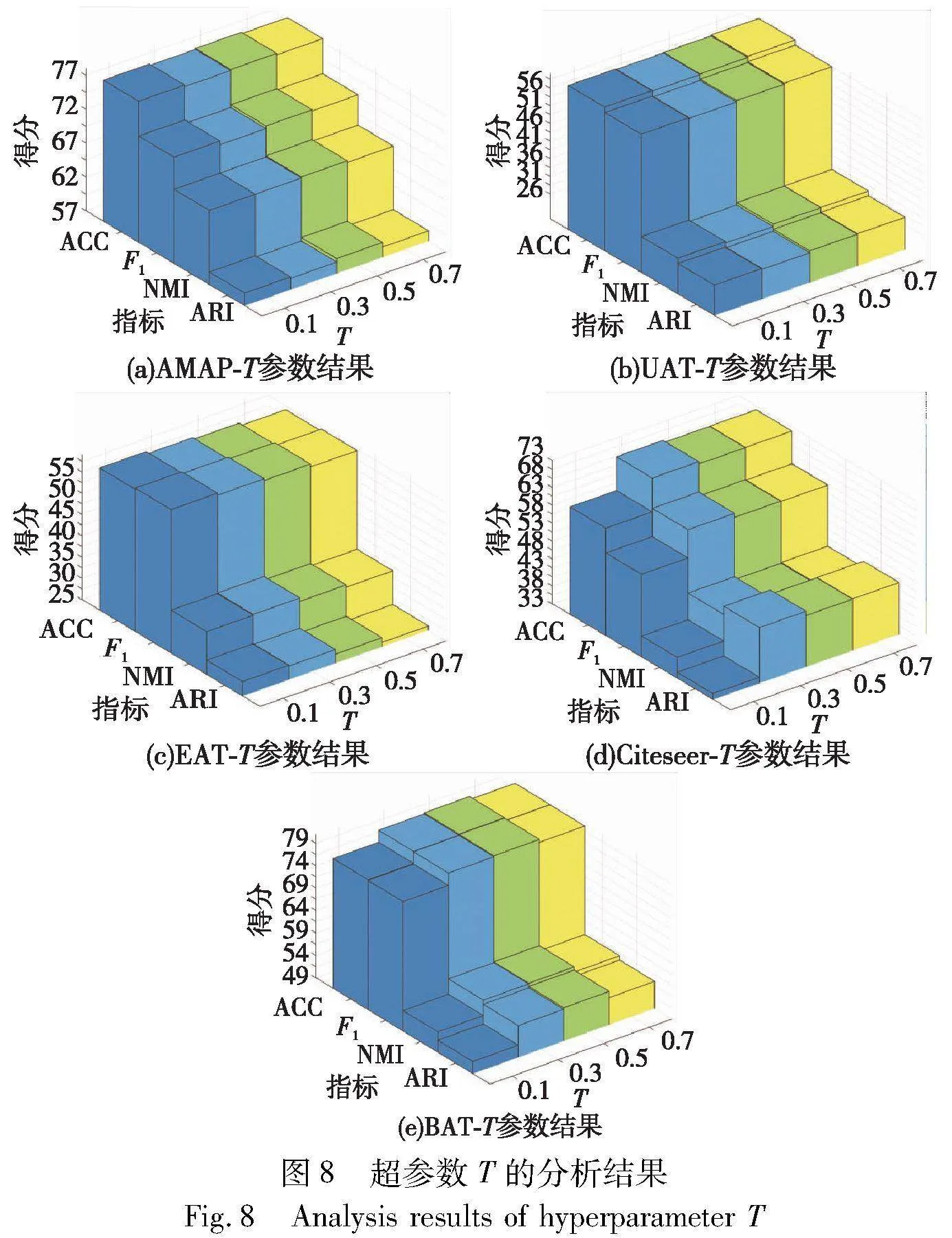
过去对比聚类的目标损失函数中，大多将T固定为1，而研究表明，越小的温度系数T越倾向于把最困难的负样本分开［36］。如图8所示，实验将其设置在［0.1，0.7］，HSCA已通过加权赋予了不同难度的样本一定的关注度，损失函数中的T旨在辅助模型找到一个平衡的系数来关注困难样本，并避免过度关注或忽视其他样本。当T为0.1时，在Citeseer、BAT上远逊于其他取值，除EAT数据集以外，其他数据集的T为［0.3，0.5］效果更好，这些都表明HSCA的设计一定程度上辨明了最困难的样本从而分担了温度系数的效用。

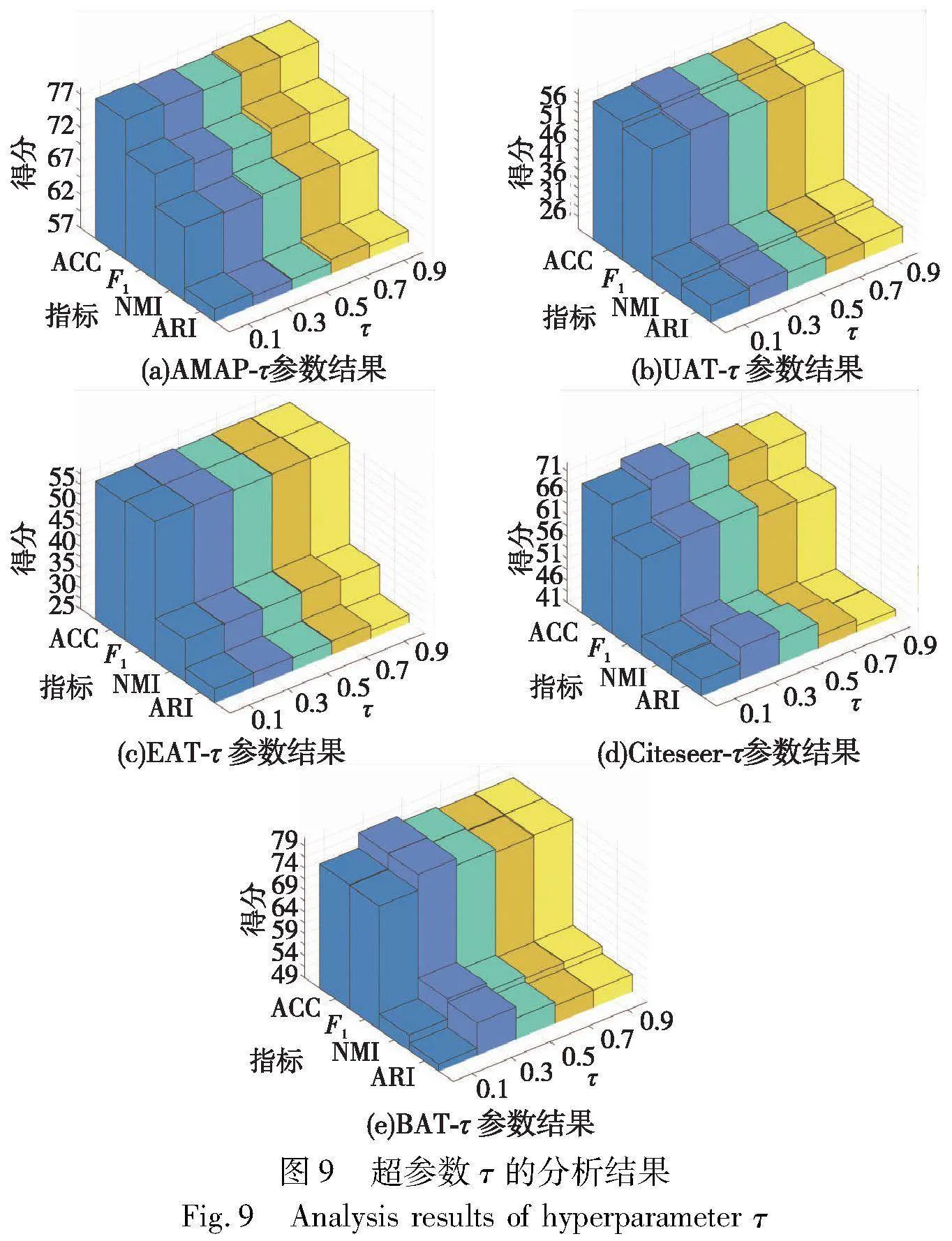
置信参数τ，表示将多少数据收纳进高置信区域，实验中设置为［0.1，0.9］，τ不能为0或者为1，这意味着所有的样本都是可信或者完全不可信的，事实上边界的样本不容易判定，而更靠近聚类的样本较容易判定。如图9所示，对AMAP数据集而言，τ=［0.7，0.9］比较合适，因为它的样本数量最多，对于其余数据集，τ=0.5时取得了不错的成效。

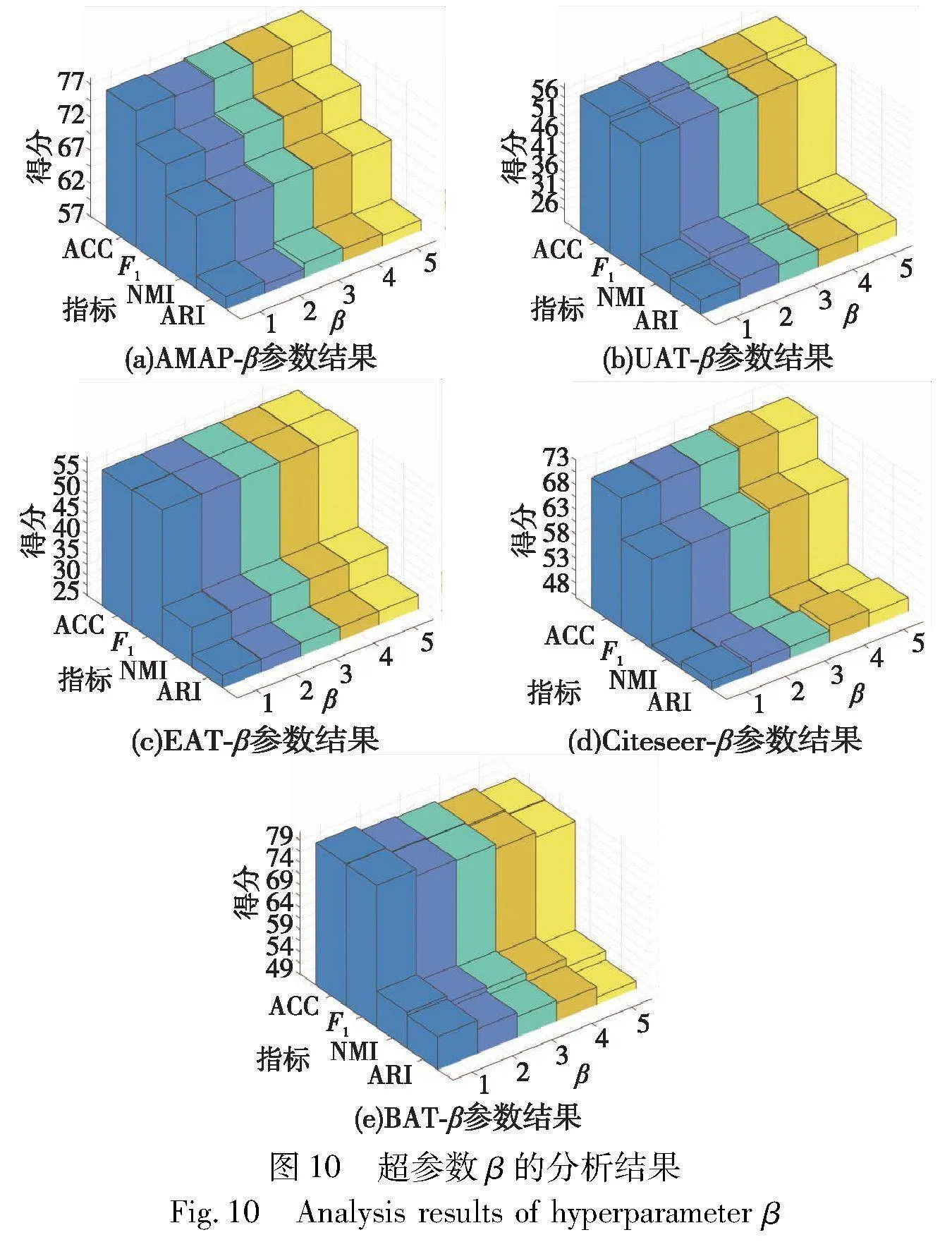
降权系数β降低容易样本对的权重，过高的降权系数会使容易样本对完全被忽略，实验中将其设定为［1，5］。如图10所示，注意到β为2或3时，在各个数据集上表现出良好的性能，符合预期。其中，EAT数据集中50%以上的节点都是需要额外关注的困难样本，容易样本对很少，故对参数β不敏感。

3.7 可视化

为了进一步直观地证明HSCA的优越性，在嵌入Z进行了2D t-SNE可视化，如图11所示。可以观察到与其他基线方法相比，HSCA更好地关注到了边缘节点的类别划分，并且簇内更加紧凑。

4 结束语

本文提出了困难样本采样联合对比增强的深度图聚类模型（HSCA）。该方法提供了一个根据不同视图针对性采样样本并实现对比的融合方案，自适应地为困难样本对增权，为容易样本对降权，驱动网络在对比的过程中更加关注不同类型的困难样本对，有效地提高了节点表示的质量。并且提出了一个基于图级表示的对比模块学习聚类表示的一致性，这些方法拥有很好的迁移性。通过实验验证了HSCA的有效性和优越性。但HSCA仍是通过K-means算法在生成的高质量嵌入上完成聚类，这一点还有待改进。

参考文献：

［1］Ding Shifei， Wu Benyu， Xu Xiao， et al. Graph clustering network with structure embedding enhanced［J］. Pattern Recognition， 2023，144： 109833.

［2］Xu Lei， Bao Ting， Zhu Liehuang， et al. Trust-based privacy-preserving photo sharing in online social networks［J］. IEEE Trans on Multimedia， 2018，21（3）： 591-602.

［3］Yi Jing， Chen Zhenzhong. Multi-modal variational graph auto-encoder for recommendation systems［J］. IEEE Trans on Multimedia， 2021，24： 1067-1079.

［4］Kipf N T， Welling M. Semi-supervised classification with graph con-volutional networks［C］//Proc of the 5th International Conference on Learning Representations. 2017： 1-14.

［5］Kipf T N， Welling M. Variational graph auto-encoders［EB/OL］. （2016-11-21）. https：//arxiv.org/abs/1611.07308.

［6］Pan Shirui， Hu Ruiqi， Fung S F， et al. Learning graph embedding with adversarial training methods［J］. IEEE Trans on Cybernetics， 2019， 50（6）： 2475-2487.

［7］Wang Chun， Pan Shirui， Hu Ruiqi， et al. Attributed graph clustering： a deep attentional embedding approach［EB/OL］. （2019-06-15）. https：//arxiv.org/abs/1906.06532.

［8］Xie Junyuan， Girshick R， Farhadi A. Unsupervised deep embedding for clustering analysis［C］//Proc of the 33rd International Conference on International Conference on Machine Learning.［S.l.］： JMLR.org， 2016： 478-487.

［9］Chen Ting， Kornblith S， Norouzi M， et al. A simple framework for contrastive learning of visual representations［C］//Proc of the 37th International Conference on Machine Learning.［S.l.］： JMLR.org， 2020： 1597-1607.

［10］Zhu Yanqiao， Xu Yuichen， Yu Feng， et al. Graph contrastive lear-ning with adaptive augmentation［C］//Proc of the 2021 Web Confe-rence. New York： ACM Press， 2021： 2069-2080.

［11］Peng Zhen， Huang Wenbing， Luo Minnan， et al. Graph representation learning via graphical mutual information maximization［C］//Proc of the 2020 Web Conference. New York： ACM Press， 2020： 259-270.

［12］Liu Yue， Yang Xihong， Zhou Sihang， et al. Simple contrastive graph clustering［J/OL］. IEEE Trans on Neural Networks and Lear-ning Systems. （2023-06-27）. https：//doi.org/10.1109/TNNLS.2023.3271871.

［13］Lee N， Lee J， Park C. Augmentation-free self-supervised learning on graphs［C］//Proc of AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2022： 7372-7380.

［14］Robinson J， Chuang C Y， Sra S， et al. Contrastive learning with hard negative samples［EB/OL］. （2021-01-24）. https：//arxiv.org/abs/2010.04592.

［15］Kalantidis Y， Sariyildiz M B， Pion N， et al. Hard negative mixing for contrastive learning［C］//Proc of the 34th International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2020： 21798-21809.

［16］Xia Jun， Wu Lirong， Wang Ge， et al. ProGCL： rethinking hard ne-gative mining in graph contrastive learning［EB/OL］. （2022-06-14）. https：//arxiv.org/abs/2110.02027.

［17］Liu Yue， Yang Xihong， Zhou Sihang， et al. Hard sample aware network for contrastive deep graph clustering［C］//Proc of AAAI Confe-rence on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2023： 8914-8922.

［18］Hassani K， Khasahmadi A H. Contrastive multi-view representation learning on graphs［C］//Proc of the 37th International Conference on Machine Learning.［S.l.］： JMLR.org， 2020： 4116-4126.

［19］Liu Meng， Liu Yue， Liang Ke， et al. Deep temporal graph clustering［EB/OL］. （2024-03-02）. https：//arxiv.org/abs/2305.10738.

［20］Peng Zhihao， Liu Hui， Jia Yuheng， et al. Deep attention-guided graph clustering with dual self-supervision［J］. IEEE Trans on Circuits and Systems for Video Technology， 2022， 33（7）： 3296-3307.

［21］Tao Zhiqiang， Liu Hongfu， Li Jun， et al. Adversarial graph embedding for ensemble clustering［C］//Proc of the 28th International Joint Conferences on Artificial Intelligence Organization. 2019： 3562-3568.

［22］Yang Liang， Wang Yuexue， Gu Junhua， et al. JANE： jointly adversarial network embedding［C］//

Proc of the 29th International Joint Conference on Artificial Intelligence. 2020： 1381-1387.

［23］Cui Ganqu， Zhou Jie， Yang Cheng， et al. Adaptive graph encoder for attributed graph embedding［C］//Proc of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York： ACM Press， 2020： 976-985.

［24］Zhao Han， Yang Xu， Wang Zhenru， et al. Graph debiased contrastive learning with joint representation clustering［C］//Proc of the 30th International Joint Conference on Artificial Intelligence. 2021： 3434-3440.

［25］Kulatilleke G K， Portmann M， Chandra S S. SCGC ： self-supervised contrastive graph clustering［EB/OL］. （2022-04-27）. https：//arxiv.org/abs/2204.12656.

［26］Zhang Jingfeng， Zhu J， Niu Gang， et al. Geometry-aware instance-reweighted adversarial training［EB/OL］. （2021-05-31）. https：//arxiv.org/abs/2010.01736.

［27］Fernando K R M， Tsokos C P. Dynamically weighted balanced loss： class imbalanced learning and confidence calibration of deep neural networks［J］. IEEE Trans on Neural Networks and Learning Systems， 2021， 33（7）： 2940-2951.

［28］Chu Guanyi， Wang Xiao， Shi Chuan， et al. CuCo： graph representation with curriculum contrastive learning［C］//Proc of the 30th International Joint Conference on Artificial Intelligence. 2021： 2300-2306.

［29］Sarwar B， KarypisG， Konstan J， et al. Item-based collaborative filtering recommendation algorithms［C］//Proc of the 10th International Conference on World Wide Web. New York： ACM Press， 2001： 285-295.

［30］Oord A V D， Li Yazhe， Vinyals O. Representation learning with contrastive predictive coding［EB/OL］. （2019-01-22）. https：//arxiv.org/abs/1807.03748.

［31］Wang Tong， Wu Junhua， Qi Yaolei， et al. Neighborhood contrastive representation learning for attributed graph clustering［J］. Neurocomputing， 2023，562： 126880.

［32］Kong Shu， Fowlkes C. Low-rank bilinear pooling for fine-grained classification［EB/OL］. （2016-11-30）. https：//arxiv.org/abs/1611.05109.

［33］Jin Wei， Liu Xiaorui， Zhao Xiangyu， et al. Automated self-supervised learning for graphs［EB/OL］. （2022-03-22）. https：//arxiv.org/abs/2106.05470.

［34］Gong Lei， Zhou Sihang， Tu Wenxuan， et al. Attributed graph clustering with dual redundancy reduction［C］//Proc of the 31st International Joint Conference on Artificial Intelligence. 2022： 3015-3021.

［35］Liu Yue， Tu Wenxuan， Zhou Sihang，et al. Deep graph clustering via dual correlation reduction［C］//Proc of AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2022： 7603-7611.

［36］Wang Feng， Liu Huaping. Understanding the behaviour of contrastive loss［C］//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2021： 2495-2504.