基于鲁棒和可靠对称交叉熵的测试时适应算法
2024-07-31熊浩宇向宇张亚萍














摘 要:测试时间适应(test-time adaptation,TTA)的目标是利用未标记的测试数据使已训练完成的神经网络模型在测试时适应测试数据分布。现有的TTA方法主要考虑在单个或多个静态环境中进行适应。然而,在非平稳环境中,测试数据分布会随着时间的推移而连续变化,这导致以往的TTA方法不稳定。因此,提出了一种基于鲁棒和可靠对称交叉熵的测试时适应(robust and reliable symmetric cross entropy test-time adaptation,RRSTA)算法。首先,为提高对噪声分布变化的鲁棒性和缓解灾难性遗忘,提出了基于均值教师模型的对称交叉熵,既鼓励模型正确预测又惩罚错误的预测。其次,为了提高对不同噪声样本的鲁棒性,提出了一种双流扰动技术,通过教师模型强视图,指导学生模型的由弱到强的扰动视图。最后,提出了可靠熵最小化策略,防止参数的剧烈变化,以稳定适应。广泛的实验和消融研究在CIFAR10C和CIFAR100C上证实了所提方法的有效性,相比于未经适应的模型,错误率降低了26.13%和14.69%,并且显著优于次优的方法。
关键词:测试时适应; 领域自适应; 连续适应; 分布变化
中图分类号:TP301 文献标志码:A
文章编号:1001-3695(2024)06-022-1756-06
doi:10.19734/j.issn.1001-3695.2023.10.0500
Robust and reliable symmetric cross-entropy-based test-time adaptation
Abstract:TTA aims to make the trained neural network model adapt to the test data distribution at test time using unlabeled test data. Existing TTA methods mainly consider adaptation in a single or multiple static environments. However, in non-stationary environments, the test data distribution changes continuously over time, which leads to the instability of previous TTA methods. Therefore, this paper proposed a test-time adaptation algorithm(RRSTA) based on robust and reliable symmetric cross entropy. Firstly, in order to improve the robustness to noise distribution changes and alleviate catastrophic forgetting, it proposed a symmetric cross entropy based on the mean teacher model, which encouraged the model to predict correctly and punished the wrong prediction. Secondly, in order to improve the robustness to different noise samples, it proposed a dual-stream perturbation technique, which guided the weak-to-strong perturbation view of the student model through the strong view of the teacher model. Finally, it proposed a reliable entropy minimization strategy to prevent the drastic change of parameters and stabilize adaptation. Extensive experiments and ablation studies on CIFAR10C and CIFAR100C confirm the effectiveness of the proposed method. Compared with the unadapted models, the error rate is significantly reduced by 26.13% and 14.69%, and it is significantly better than the second-best method.
Key words:test-time adaptation; domain adaptation; continuous adaptation; distribution change
0 引言
当前的深度神经网络(DNN)已经在广泛的领域取得了令人印象深刻的性能,包括计算机视觉[1]和自然语言处理[2]。不幸的是,当训练数据和测试数据取自不同的分布时,深度模型经常违反这一假设,出现了显著的性能下降的情况,因为许多环境通常是非平稳且不断变化的。为了解决这种退化问题,之前的研究通常寻求在训练过程中增强模型的鲁棒性,包括利用数据增强[3]、领域适应[4]、领域泛化[5]和对抗训练[6]。尽管这些方法试图从各个角度减少训练数据和目标数据之间的分布差异来解决退化问题,但在实际应用中,由于成本、时间和资源可用性的限制,仍然存在某些无法观察到的分布偏移[7],这可能对方法的有效性提出重大挑战。此外,这些技术需要在训练过程中进行干预,文献[8]指出这进一步增加了灾难性失败的风险。
尽管领域适应、领域泛化都广泛研究了分布变化的问题并取得了积极的结果. 然而在很多实际场景中, 由于隐私问题或法律约束源域数据并不总是可访问的,例如,用户身份信息、病人健康数据等。此外,现有方法需要额外附加的计算成本,并难以在训练期间推广到潜在未知的数据分布范围。测试时间适应[9~11]方法正成为一种替代解决方案,TTA仅利用当前未标记的测试数据在线更新模型参数以克服数据分布偏移。毫无疑问,TTA考虑了更具挑战性但更现实的问题,并引起了广泛的关注和应用,例如多模态[12]、医学图像分析[13]等。
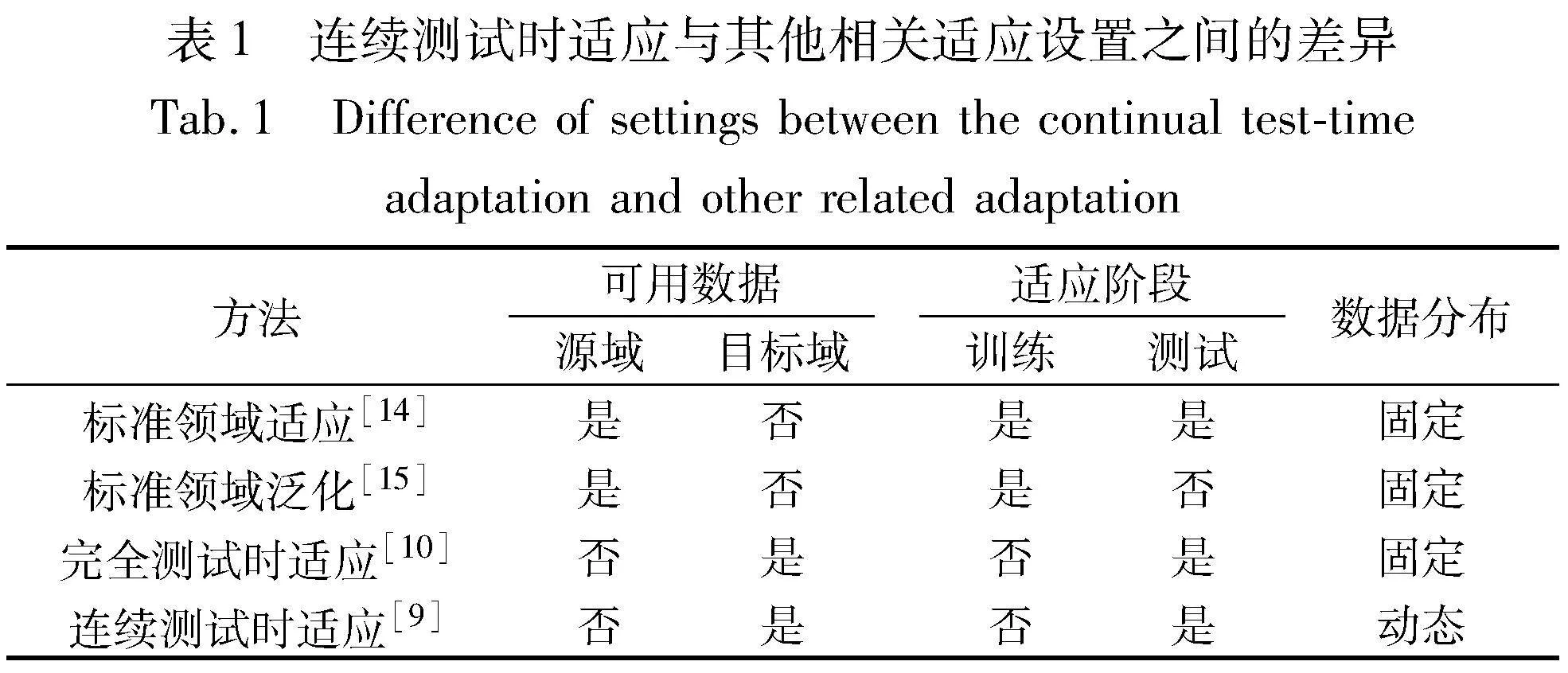
先前的TTA已被证明能通过熵最小化[10, 14, 15]、批量归一化统计[16]显著提高模型对分布偏移的鲁棒性。然而,其良好的性能通常是在较为温和的测试时设置下实现的,其中测试样本是从具有相同数据分布偏移类型的固定目标域中独立采样的。然而,在更为现实的环境中,这些方法的有效性可能会降低,这是因为数据环境会随着天气、地理位置、时间或其他因素而不断发生改变。例如,在自动驾驶系统中,汽车周围环境会随着时间的推移而不断变化、汽车进出隧道光线发生改变、街道上意外出现的儿童或是传感器镜头的自然老化或污损。以上都是现实中常见的场景,这通常会使得已经训练完成的模型出现性能退化。因此,本文进一步考虑更加现实的测试时设置,即文献[9]首次提出的连续测试时适应,其中测试数据分布会随着时间不断变化。相关方法的比较如表1所示。
为了提升模型在非平稳环境中的表现,本文首先深入研究了基于熵最小化的TTA方法失败的案例,发现以往的TTA方法表现良好,通常是在较为温和的环境下并且严重依赖于超参数的选择, 而当超参数发生细小的改变则有可能导致灾难性的失败;然后进一步分析了不同熵值样本对模型性能的贡献;最后提出了基于均值教师模型的鲁棒和可靠对称交叉熵的测试时适应(robust and reliable symmetric cross entropy test-time adaptation,RRSTA)算法来稳定测试时适应。 相比以往的方法而言,本文专注于更现实和更具挑战性的设置,其中数据分布不断变化。在广泛使用的CIFAR10C和CIFAR100C基准数据集上,所提出的测试时适应方法能够降低26.13%和14.69%的错误率,并显著高于次优方法。
1 问题定义
测试时适应算法的目标是仅利用当前未标记的测试数据,使已经预训练好的模型在测试时有效适应到新的目标域,解决目标域和源域的数据分布差异问题。为了详细说明,接下来将用公式化和具体符号来进行描述。
2 测试时适应的风险
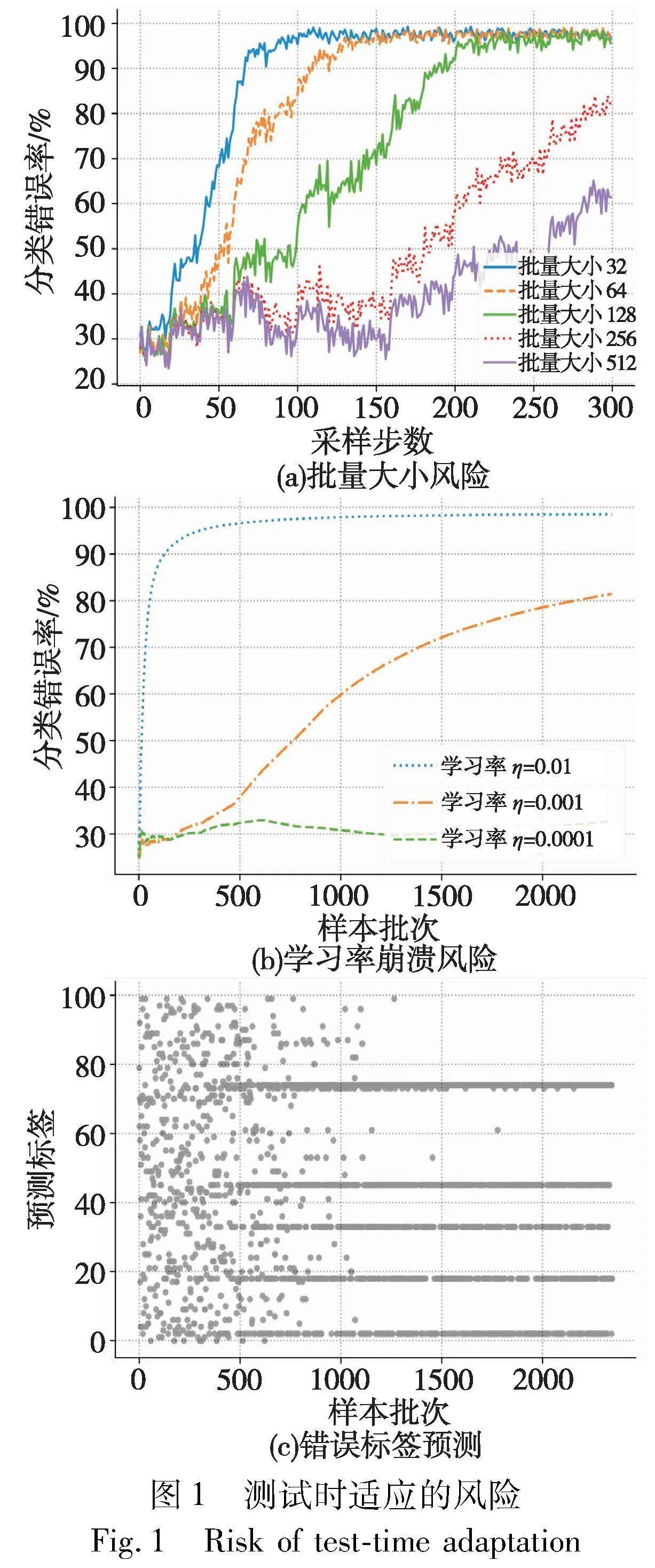
事实上,数据分布不断变化的设置很大程度上是由部署模型的实际需求驱动的。正如在引言中所提到的,自动驾驶汽车周围环境的总是会随着时间的推移而变化,并且会受到天气和地理位置等因素的影响。以往的一些测试时适应算法在较为温和的条件取得了成功。然而,由于目标域的数据分布不断变化,一些方法通常会无声地退化模型的性能,且在短时间内难以观察到这种性能退化的现象。本文进一步绘制了具有代表性的熵最小化方法[10]的失效模式, 总的结果如图1所示。
2.1 超参数敏感
首先本节选取具有代表性的纯熵最小化的测试时适应方法(tent[10]),并在不同批量大小和学习率上进行实验。结果如图1(a)(b)所示,五种不同批量大小中有三种发生了崩溃(即错误率>;90%),而所考虑的三种不同的学习率(η)中有两种同样也发生了崩溃。这表明以往的纯熵最小化的方法在动态分布变化的场景中进行连续的适应是不稳定的。虽然通过超参数能够避免这一现象的产生,但是为不同场景都单独准备超参数是不现实的。 此外,即便超参数调优或许能延缓崩溃现象的发生,但这种崩溃的发生最终是不可避免的。例如,当批量大小选取512或学习率为0.001时都表现出了崩溃的趋势。
2.2 低质量的伪标签
在测试时适应领域中,熵最小化是具有代表性的方法之一。在数据集分布相同且不包含噪声的情况下,传统的熵最小化通常是有效的,它鼓励模型对正确伪标签作出正确的预测结果。传统的纯熵最小化的公式表示为
Euclid Math OneLAp=-∑fθ(xt)log fθ(xt)(3)
其中:fθ(xt)表示模型对于输入xt的预测结果,并将模型自身预测结果作为伪标签。
然而,当数据存在分布变化或噪声时,这将使得伪标签变得嘈杂,从而容易出现低质量的伪标签。而且这些噪声会使得错误不断积累。结果如图1(c)中所示,模型最终发生崩溃,模型倾向于将所有输入样本预测为某几类,即使这些样本具有不同的真实类别。这是因为传统的熵最小化只鼓励正确预测结果,而不对错误预测结果进行惩罚。因此,迫切地需求已经部署的模型在以上场景中表现良好。
3 方法
在非平稳的现实环境中,面对分布不同的目标域数据,预训练模型fθ0的预测结果会变得不可靠。 为了防止性能进一步下降,本文提出了鲁棒和可靠对称交叉熵测试时适应算法,主要分为三个部分:基于对称交叉熵的均值教师模型、双流扰动技术以及可靠熵最小化。RRSTA算法框架如图2所示。
3.1 基于对称交叉熵的均值教师模型
给定测试数据xt和模型fθt,在测试时适应中,以往的TTA方法的目标通常是最小化预测的交叉熵来更新模型权重,这已被证实是有效的。然而在不断变化的测试流数据中,这些方法可能会因为数据分布的改变导致低质量的伪标签从而发生性能退化。
一种理想的方式是利用平均教师模型[17],这是因为教师模型通过移动指数平均(exponential moving average)[18]进行更新,其预测结果qt会包含过去迭代模型的信息,从而能提供更高质量的伪标签,缓解连续适应过程中的灾难性遗忘问题[19]。
其中:γ=0.99是初始平滑系数。
然而,基于常规交叉熵的平均教师模型主要关注增强正确标签的预测概率,而不惩罚预测错误的预测概率。如图1 (c)所示,这可能导致在面对噪声样本时过度自信或降低泛化能
其中:第一项是常规交叉熵损失,第二项是反向交叉熵[20]损失。相比常规交叉熵而言,对称交叉熵不仅关注正确标签的不确定性,同时能够惩罚模型对于错误标签的过度确定性。
3.2 双流扰动技术
本节提出了基于对称交叉熵的均值教师模型。但是由于数据分布不断变化,可能还会存在一些自然或合成的噪声样本。为了进一步提高模型对噪声分布变化的鲁棒性,本节在对称交叉熵的基础上进一步提出了一种双流扰动技术,通过在原始样本的弱视图的指导下,使由弱到强的扰动视图保持一致。 对于自然噪声,本节考虑通过原始级的扰动来进行应对,而对于合成噪声,采用一组人工合成的数据增强策略来进行补充。
本节强调将不同属性的扰动分离成独立流的必要性。这与最近将不同扰动混合到单个流中的工作不同,为了验证双流扰动之间能否可以很好地互补,本节进行了一个简单的实验进行验证,首先从xt独立地产生双流扰动与混合双流扰动进行对比。如图3所示,独立双流扰动带来了一致的改进,而混合扰动则相反。
3.3 可靠熵最小化策略
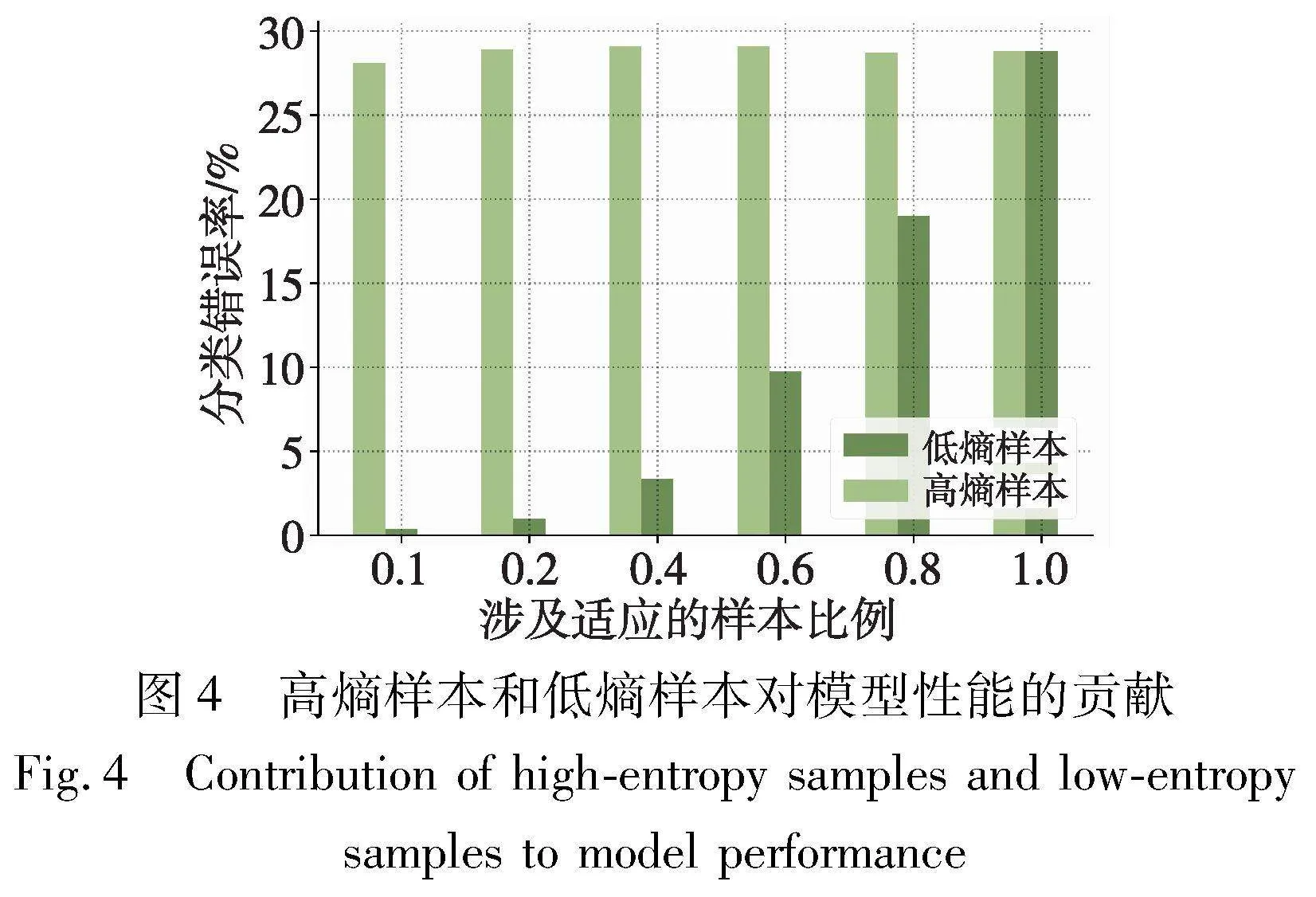
直觉上不同的样本在测试时适应过程中会对模型性能产生不同的贡献。为了验证这一点,本节首先根据熵值大小对样本的贡献程度进行了划分。图4为高熵样本和低熵样本对模型性能的贡献,其中通过tent方法在CIFAR100C(损坏类型motion blur,损坏严重等级为5)上调整模型。从图4中,毫无疑问的是低熵样本总是比高熵样本对模型性能的贡献更大,而高熵样本通常会损坏模型性能。这是因为高熵样本通常有偏差且不可靠。基于上述分析,受文献[23]启发,一种最直接的方案是通过熵值进行过滤。形式上,令E(xt;Θ)表示样本xt的熵。那么,熵最小化的目标可以表示为
4 实验
4.1 数据集
本文主要在广泛使用的基准上评估所有方法,即CIFAR10C、CIFAR100C[24]。它们分别是基于CIFAR10、CIFAR100测试集然后通过各种算法合成不同噪声来构建的。如图5所示,主要包括噪声(Gaussian noise、shot noise、impulse noise)、模糊(defocus blur、frosted glass blur、motion blur、zoom blur)、天气(snow、frost、fog)和数码(brightness、contrast、elastic、pixelate、JPEG),共计15种不同的损坏类型组成。其中每种损坏类型具有5个不同的严重性级别,并且严重性级别越大意味着分布变化越严重。
4.2 实施细节
在CIFAR10→CIFAR10C中使用预训练的WideResNet-28[25]模型,在CIFAR100→CIFAR100C中使用ResNeXt-29[26]模型进行实验。需要注意的是本文不对训练过程做任何调优,在所有任务中预训练模型的权重均由鲁棒评测基准RobustBench[27]提供,并保持所有的预定义模型设置。
在测试时,本文方法采用SGD优化器,动量设置为0.9,学习率大小设置为η=1×10-3。关于超参数设置,熵过滤阈值ε=0.4×ln C,C是类别总数,式(8)中的扰动数量n设置为4,式(5)中指数移动平均系数γ=0.99,与CoTTA[9]方法保持一致,关于其他超参数均保持默认。为了公平比较, 本文在所有实验中将批量大小设置为64。
4.3 对比方法
为了验证本文算法的有效性, 考虑以下典型的强有力的基线方法进行比较,其中包括:a)tent[10]将模型的预测概率值作为伪标签并最小化熵来更新模型参数;b)CoTTA[9]通过权重平均和增强样本平均来提升伪标签的质量,并通过持续将一小部分神经元随机恢复到源预训练的权重;c)SHOT[11]通过利用信息最大化和自监督伪标签来学习目标特定特征提取模块,以隐式地将目标域的表示与源假设对齐;d)BN[16]仅使用批量归一化统计量, 而无须任何参数更新。需要注意的是,source方法直接在目标域上进行评估,无须进行任何调整和适应。关于所对比的其他方法,本文都遵循其官方代码的实现方式并保持与其论文一致的超参数设置。
4.4 实验结果
表2中显示了连续测试时适应设置下连续适应不同损坏类型的结果,并且所有TTA方法都共享相同的损坏类型顺序。其中,损坏等级最高为5级,下画线表示性能低于source的结果,粗体表示最佳结果,“±”代表标准差。从总体来看,直接使用预训练模型(source)的性能不佳,在CIFAR10C和CIFAR100C上的平均错误率分别低至43.52%和46.44%,这表明在测试时对模型进行适应是有必要的。当仅使用批量归一化统计量(BN)进行适应时,在CIFAR10C和CIFAR100C上的错误率分别降低了22.59%和10.22%。虽然大多数方法在CIFAR10C上表现良好,但当在较难的CIFAR100C数据集时,甚至部分方法在适应后的性能反而出现了下滑。如果把注意力转向适应过程,可以观察到基于纯熵最小化的方法tent的性能退化十分显著,并由于错误的不断积累,导致模型最终发生崩溃(即错误率大于90%)。虽然CoTTA方法在CIFAR10C上取得了次优的结果,但这是以额外扩增32次增强样本并前向传播的代价取得的。
相反,本文RSSTA方法在所有数据集上都取得了优异的结果。从总体来看,相比于未经适应的模型,在CIFAR10C和CIFAR100C上分别将平均错误率降低了26.13%和14.69%。此外,所提出的RSSTA在所有腐败类型上都取得了最好的结果。广泛的实验结果强有力地验证了RSSTA能有效适应不同的损坏类型,并拥有更低的错误率。
5 消融研究
5.1 不同损坏严重等级的影响
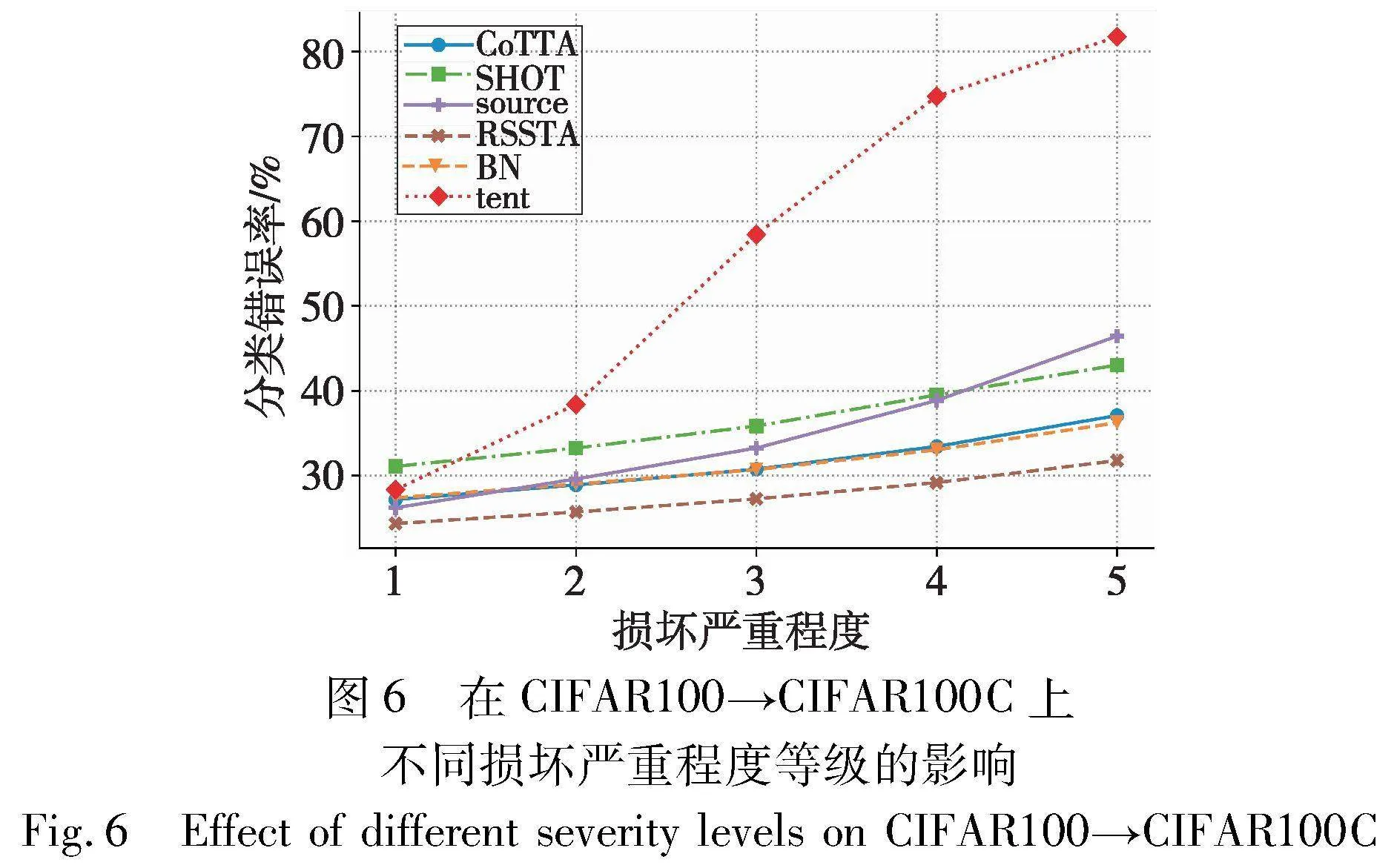
在真实的场景中,考虑到损坏严重等级并不总是最严重的。因此,为了验证本文方法RSSTA在不同损坏严重等级的有效性, 本节进一步改变不同的损坏严重等级并与其他方法进行比较。如图6所示,随着损坏等级的增加,tent方法的错误率提升尤为显著。相反,RSSTA与次优方法相比仍保持较大优势。最重要的是,RSSTA在所有损坏等级下都保持一致的最佳性能。
5.2 不同扰动数量的影响
为了验证式(8)中不同扰动数量n的影响,本节改变n的数值大小。如图7所示,最大与最小的数值都不利于模型性能提升。而在数值为4时取得了最佳优势,因此在所有实验中,本文方法RSSTA中的参数n默认数值设置为4。此外,不建议n的数量超过5,是因为会出现较大dropout概率值,导致切断层之间的连接太多,从而限制模型的学习能力[28]。
5.3 损失表面可视化
本节通过Loss landscape[29]分别绘制了具有代表性的熵最小化的方法tent与所提出的RSSTA方法的损失表面。如图8所示,RSSTA的损失表面更为平坦和光滑,且在更小的步数就已达到更平坦的表面,这表明RSSTA具有更好的泛化性,对噪声样本具有更好的鲁棒性。
5.4 计算开销
表3总结了本文中所涉及方法的详细特征。综合实验结果和时间开销来看,所提出的RSSTA取得了一个理想的平衡。而CoTTA方法通过额外的32次数据增强,导致了最高的计算时间开销。众所周知,反向传播通常占据大部分计算开销,虽然RSSTA对增强样本和原始样本通过了两次前向传播,但受益于RSSTA只最小化可靠熵,因此反向传播的数量能大大减少。
6 结束语
本文分析了以往测试时适应方法的失败的案例,发现以往的TTA方法表现良好,通常是在较为温和的环境下并且依赖于超参数的选择,如果超参数发现细微的改变往往会导致灾难性的失败。针对深度学习模型在不同的目标域性能退化的问题,本文考虑了更加现实的测试场景,即目标域的数据分布是不断变化的,提出了鲁棒和可靠的对称交叉熵的测试时适应算法,以提高模型在新领域上的性能。首先,引入了基于均值教师模型的对称交叉熵来缓解灾难性遗忘。此外,本文还对样本熵值对模型的贡献进行分析,发现高熵值样本往往会损害模型适应,基于此本文提出只最小化可靠熵值的样本。大量的实验和消融研究证明了本文方法的稳健性和有效性,相比于未经适应的模型,错误率降低了26.13%和14.69%。本文方法的代码可在https://anonymous.4open.science/r/test-time-adaptation-20231018获得。
参考文献:
[1]Alzubaidi L, Zhang Jinglan, Humaidi A J, et al. Review of deep learning: concepts, CNN architectures, challenges, applications, future directions[J]. Journal of Big Data, 2021,8: 1-74.
[2]Liu Yinhan, Ott M, Goyal N, et al. Roberta: a robustly optimized BERT pretraining approach[EB/OL]. (2019-07-26). https://arxiv.org/abs/1907.11692.
[3]Zhong Zhun, Zheng Liang, Kang Guoliang, et al. Random erasing data augmentation[C]//Proc of AAAI Conference on Artificial Intelligence. Palo Alto,CA:AAAI Press, 2020: 13001-13008.
[4]Wang Mei, Deng Weihong. Deep visual domain adaptation: a survey[J]. Neurocomputing, 2018, 312: 135-153.
[5]Zhou Kaiyang, Liu Ziwei, Qiao Yu, et al. Domain generalization: a survey[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2022,45(4): 4396-4415.
[6]Tramer F, Boneh D. Adversarial training and robustness for multiple perturbations[C]//Proc of the 33rd International Conference on Neural Information Processing Systems. Red Hook, NY:Curran Associates Inc., 2019:5866-5876.
[7]Koh P W, Sagawa S, Marklund H, et al. Wilds: a benchmark of in-the-wild distribution shifts[C]//Proc of International Conference on Machine Learning. 2021: 5637-5664.
[8]Bommasani R, Hudson D A, Adeli E, et al. On the opportunities and risks of foundation models[EB/OL]. (2021-08-16). https://arxiv.org/abs/2108. 07258.
[9]Wang Qin, Fink O, Van Gool L, et al. Continual test-time domain adaptation[C]//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway,NJ:IEEE Press, 2022: 7201-7211.
[10]Wang Dequan, Shelhamer E, Liu Shaoteng, et al. Tent: fully test-time adaptation by entropy minimization[EB/OL]. (2020-06-18). https://arxiv.org/abs/2006.10726.
[11]Liang Jian, Hu Dapeng, Feng Jiashi. Do we really need to access the source data?Source hypothesis transfer for unsupervised domain adaptation[C]//Proc of International Conference on Machine Lear-ning. 2020: 6028-6039.
[12]Shu Manli, Nie Weili, Huang De’an, et al. Test-time prompt tuning for zero-shot generalization in vision-language models[C]//Proc of NeurIPS.2022.
[13]Liu Quande, Chen Cheng, Dou Qi, et al. Single-domain generalization in medical image segmentation via test-time adaptation from shape dictionary[C]//Proc of AAAI Conference on Artificial Intelligence. Palo Alto,CA:AAAI Press, 2022: 1756-1764.
[14]Ben-David S, Blitzer J, Crammer K, et al. Analysis of representations for domain adaptation[C]//Advances in Neural Information Processing Systems. 2006.
[15]Wang Jindong, Lan Cuiling, Liu Chang, et al. Generalizing to unseen domains: a survey on domain generalization[J]. IEEE Trans on Knowledge and Data Engineering, 2022,35(8):8052-8072.
[16]Nado Z, Padhy S, Sculley D, et al. Evaluating prediction-time batch normalization for robustness under covariate shift[EB/OL]. (2020-06-19). https://arxiv.org/abs/2006.10963.
[17]Tarvainen A, Valpola H. Mean teachers are better role models: weight-averaged consistency targets improve semi-supervised deep learning results[C]//Advances in Neural Information Processing Systems.2017.
[18]Cai Zhaowei, Ravichandran A, Maji S, et al. Exponential moving average normalization for self-supervised and semi-supervised learning[C]//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway,NJ:IEEE Press, 2021: 194-203.
[19]Kirkpatrick J, Pascanu R, Rabinowitz N, et al. Overcoming catastrophic forgetting in neural networks[J].Proc of National Academy of Sciences, 2017,114(13): 3521-3526.
[20]Wang Yisen, Ma Xingjun, Chen Zaiyi, et al. Symmetric cross entropy for robust learning with noisy labels[C]//Proc of IEEE International Conference on Computer Vision. Piscataway,NJ:IEEE Press, 2019: 322-330.
[21]Yang Lihe, Qi Lei, Feng Litong, et al. Revisiting weak-to-strong consistency in semi-supervised semantic segmentation[C]//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2023: 7236-7246.
[22]Wagner T, Guha S, Kasiviswanathan S, et al. Semi-supervised lear-ning on data streams via temporal label propagation[C]//Proc of International Conference on Machine Learning. 2018: 5095-5104.
[23]Niu Shuaicheng, Wu Jiaxiang, Zhang Yifan, et al. Efficient test-time model adaptation without forgetting[C]//Proc of the 39th Internatio-nal Conference on Machine Learning. 2022: 16888-16905.
[24]Hendrycks D, Dietterich T. Benchmarking neural network robustness to common corruptions and perturbations[C]//Proc of International Conference on Learning Representations. 2019.
[25]Zagoruyko S, Komodakis N. Wide residual networks[EB/OL]. (2016-05-23). https://arxiv.org/abs/1605.07146.
[26]Xie Saining, Girshick R, Dollár P, et al. Aggregated residual transformations for deep neural networks[C]//PronA9LgqUp/xvZ+AvFZwFy52dguG6M2IhEVFefmvuOdfg=c of IEEE Conference on Computer Vision and Pattern Recognition. Piscataway,NJ:IEEE Press, 2017: 1492-1500.
[27]Croce F, Andriushchenko M, Sehwag V, et al. RobustBench: a standardized adversarial robustness benchmark[EB/OL]. (2020-10-19). https://arxiv.org/abs/2010.09670.
[28]Baldi P, Sadowski P J. Understanding dropout[C]//Advances in Neural Information Processing Systems. 2013.
[29]Li Hao, Xu Zheng, Taylor G, et al. Visualizing the Loss Landscape of neural nets[C]//Proc of Neural Information Processing Systems. 2018.
