基于自适应重加权和正则化的集成元学习算法

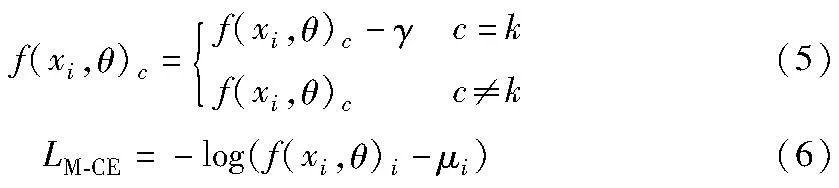
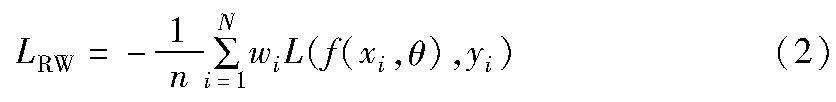
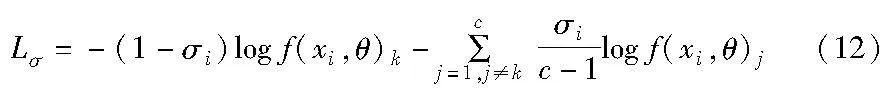
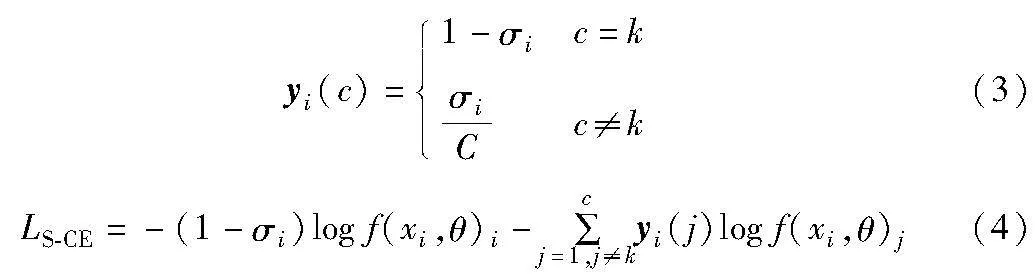
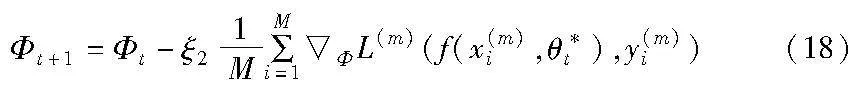
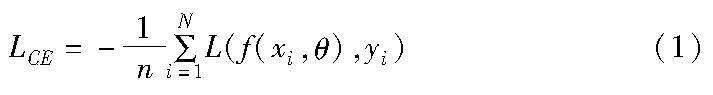
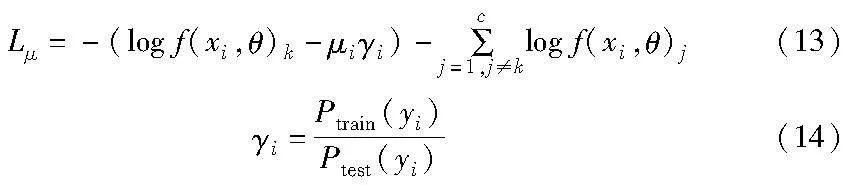
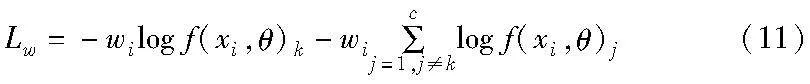
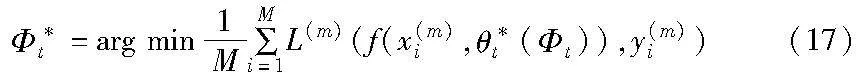
摘 要：在训练集存在噪声标签或类别不平衡分布的情况下，深度神经网络具有过度拟合这种有偏差的训练数据的不良趋势。通过设计适当的样本权重，使用重加权策略是解决此问题的常用方法，但不适当的重加权方案会给网络学习引入额外的开销和偏差，仅使用重加权方法很难解决有偏差分布下网络的过拟合问题。为此，建议将标签平滑正则化和类裕度正则化与重加权结合使用，并提出了一种基于自适应重加权和正则化的元学习方法（ensemble meta net，EMN），模型框架包括用于分类的基本网络和用于超参数估计的集成元网。该方法首先通过基本网络获得样本损失；然后使用三个元学习器基于损失值以集成的方式估计自适应重加权和正则化的超参数；最终利用三个超参数计算最终的集成元损失更新基本网络，进而提高基本网络在有偏分布数据集上的性能。实验结果表明，EMN在CIFAR和OCTMNIST数据集上的准确率高于其他方法，并通过策略关联性分析证明了不同策略的有效性。

关键词：噪声标签； 不平衡； 元学习； 重加权； 正则化

中图分类号：TP391 文献标志码：A

文章编号：1001-3695（2024）06-021-1749-07

doi：10.19734/j.issn.1001-3695.2023.09.0501

Ensemble meta net based on adaptive reweight and regularization

Abstract：Deep neural networks tend to overfit to biased training data when there are noisy labels or imbalanced class distributions in the training set. Using reweighting strategies with appropriate sample weighting is a common method to address this issue. However， improper reweighting schemes will introduce additional overhead and bias to the network’s learning process， it is difficult to solve overfitting problems in biased distribution networks using only reweighting methods. To address this problem， this paper proposed a method that combined label smoothing regularization， class margin regularization， and reweighting， and presented an EMN method based on adaptive reweighting and regularization， which consisted of a base network for classification and an ensemble meta-net for hyperparameter estimation. The method first obtained the sample loss through the base network， then used three meta-learners to estimate the hyperparameters of adaptive reweighting and regularization in an integrated manner based on the loss， and finally used the three hyperparameters to calculate the final ensemble meta-loss and update the base network， thereby improving its performance on biased distribution datasets. Experimental results demonstrate that EMN achieves higher accuracy on CIFAR and OCTMNIST datasets compared to other methods， and the effectiveness of diffe-rent strategies are demonstrated through policy correlation analysis.

Key words：noise label; imbalance; meta learning; reweight; regularization

0 引言

深度神经网络由于其强大的表示能力，在各种现实世界的应用中大多数情况下都取得了显著的性能［1］。现在的绝大多数研究已经表明，这种成功主要依靠来自真实世界所收集的具有高质量和专业性标注的大规模数据集［2］。然而，当数据集存在较大偏差分布时，深度神经网络在训练过程中很容易出现过度拟合，进而导致网络在测试阶段使用测试集进行评估时性能较差，因此在具有偏差分布的训练集上训练一个鲁棒性和泛化性较强的模型是非常困难的。

对于训练集来说，偏差分布现象主要包括噪声标签和类别不平衡两种常见类型。具有噪声标签分布的数据通常来说是不可靠的，因为这些数据的标签会被误标注为错误的标签，给模型训练带来了很大的负面影响。据相关报道，来自真实世界的数据集大多都存在一定程度的噪声标签，例如，JFT200M数据集中约有20%左右的噪声标签［3］。苏逸等人［4］指出偏离期望值的数据会对数据分析带来较大的干扰。另一个经常遇到的偏差分布为不平衡分布，主要表现为多数类的样本数量大于少数类的样本数量。这会导致模型参数在学习的过程中具有向多数类数据分布过拟合的趋势，最终导致所学习到的深度神经网络模型在少数类数据上表现不佳。例如，Chest X-Ray数据集中的不平衡比例达到了38.3%［5］，在这种数据集上进行常规训练会影响模型的泛化能力［6］。因此，针对偏差分布的数据集设计合理的算法进而得到一个鲁棒性较强的深度学习网络模型具有至关重要的意义。

最近的研究者提出了许多方法尝试改善这一问题，最直观的想法是通过数据重采样方法对少数类进行过采样或对头类进行欠采样并选择标价良好的训练数据来尝试纠正网络参数的学习过程［7］。李昂等人［8］从特征选择角度对数据重采样方法进行了总结和和分析，不适当的过采样和欠采样的数据重采样方法将会损害模型的表征学习能力，影响最终模型在测试集上的性能。对于过采样方法来说，对少数类的过采样会导致模型在多数类上的性能下降，对多数类的欠采样会影响模型在少数类上的性能下降。一种更加通用的方法是重加权方法，通过降低噪声标签的权重或者为少数类分配较大的权重是重加权方法的主要思想［9］。基本的重加权思想，例如基于类频率的重加权方法，通过先验统计信息在计算损失函数的过程中为不同类数据分配不同的权重，基于样本置信度的重加权方法（focal loss）在计算损失函数的过程中基于损失值的动态变化来调整当前样本的权重［10］。顾永根等人［11］提出了一种联邦学习机制，通过估计一个预估函数来缓解不平衡数据造成的联邦模型精度下降的问题。Zheng等人［12］利用主动学习（active learning）专注挑选数据集中损失值较低的样本以尝试解决噪声标签问题。樊东醒等人［13］利用挑选重点缺失特征添补少数类样本提高了不平衡分类的效果。自步学习（self-placed lear-ning）基于样本的输出置信度按照一定的顺序引导网络学习［14］。

基于上述分析，对于类别不平衡问题来说，具有较高损失值的样本更有可能是少数类数据，对于噪声标签问题来说，具有较小损失值的样本更有可能是标签正确的样本，为这些样本分配较大的权重可以为深度神经网络的训练提供更好的梯度信息。然而事实上，在没有无偏差分布的数据分布的前提下，针对偏差分布的数据集的处理在本质上存在模糊性和不确定性。为了缓解这一现象，基于元权重网络学习的方法（meta weight net，MWN）提出了一种自适应重加权的方法，通过引入一个小的元数据集数据作为无偏差分布的数据代理，并设计了一种可学习的元权重网络来模拟重加权函数，该网络在训练过程中可以根据元数据在基本网络上的损失大小动态更新该重加权网络参数，从而模拟一个匹配训练数据的加权函数［15］。

虽然MWN可以缓解上述问题，但常受限制于元数据的规模，当元数据的规模较小时，MWN经常训练失败。本文将两种正则化方法标签平滑和类裕度引入基于元权重的重加权网络中，并进一步扩展了这两种方法的可学习性，提出了自适应标签平滑和自适应类裕度方法，并将其与自适应重加权结合形成一个可以进行集成学习的框架。该方法通过以集成的方式同时估计重加权和正则化的超参数，通过在更大的超参数范围空间中搜索可靠的超参数，可以获取鲁棒性和泛化性较强的用于估计重加权和正则化的显式函数。

综上所述，本文的主要贡献如下：a）提出了一种新的集成学习方法，将正则化纳入重加权策略，形成一种新的结合元学习的集成学习框架，通过元学习的方法在较大的超参数空间中搜索合适的超参数；b）实验表明，将自适应正则化和自适应重加权进行结合的策略在有偏差分布的训练数据上表现良好，这表明本文集成元学习具有较好的泛化能力，这为有偏差分布的数据训练提供了启发式的解决方案；c）通过实验找到了不同策略组成的集成元网与性能之间的关系，自适应类裕度方法对解决不平衡问题效果较好，标签平滑对解决噪声标签问题效果较好。

1 相关工作

1.1 重加权方法

重加权的基本思想是为每一类或者每个样本计算损失的过程中分配合适的权重，这可以促进分类器向着更好的分类边界的方向进行建模［16］。重新加权策略旨在根据一些先验知识为训练期间的每个训练样本分配一个公平的权重以调整网络参数的学习过程。目前的重加权函数的表现形式主要可以分为基于损失值的单调递增的加权函数和基于损失值单调递减的加权函数两大类。第一种形式主要关注在类别不平衡分布问题中损失值较大的样本。例如，Wang等人［17］使用类频率的倒数作为加权函数的参考，Lin等人［10］使用基于样本损失值作为加权函数的参考。第二种形式更多关注噪声标签任务的损失值较小样本。例如，Zheng等人［12］基于主动学习的思想在模型训练的过程中挑选损失值较小的样本；姚佳奇等人［18］提出了一种加权的成对损失函数WPLoss调整正负样本的权重大小。虽然重加权方法可以在一定程度上缓解偏差分布带来的网络学习偏差，但加权函数复杂的判断规则和针对不同数据集的繁琐的超参数的调整过程让这一方法缺乏灵活性。

1.2 正则化方法

标签平滑正则化方法的目的是提高分类问题的泛化能力，使用原本的硬标签训练可能会让模型在学习的过程中过度自信。近年来，研究人员提出了许多不同的标签平滑方法来解决这一问题，Zhang等人［19］提出了一种在线标签平滑的方法，为真实标签和非真实标签提供了更好的建模方式。另一种常见的正则化方法是类裕度，通过调整不同类分类边界的裕度来增加类间方差，使得分类器在类边界上更加倾向于将少数类分类正确。 文献［20］的学习目标是具有更加紧密的类内间距和更大以及更加灵活的类间可分性的特征空间。受此启发，本文将两种正则化方法与重加权进行结合使用。

1.3 元学习方法

元学习的基本思想是通过一个元学习器利用有限的元数据基于主任务的学习经验通过有限的迭代次数为具体的机器学习算法计算最合适的超参数，以快速适应新的任务。元学习机制可用于估计样本的权重因子，例如使用贝叶斯函数近似器的MentorNet［21］、使用多层近似器的元权重网和使用影响函数作为近似器的L2RW［9］。FSR提出了一种基于元学习的快速样本重加权方法，该方法可以从历史中学习来构建代理奖励数据和通过特征共享来降低优化成本［22］。尽管这些现有方法可以较为灵活地为有偏差的训练数据分配样本权重，但当元数据的数据规模较小时，从元数据中传输的元信息规模受到限制，元学习训练过程经常失败，通过元学习训练的模型泛化能力仍然很弱。

2 理论分析

2.1 问题假设

对于图像多分类问题来说，本文假设存在一个具有c类的多类分类任务，假设训练数据是从未知分布Ptrain中采样的，测试数据是从未知分布Ptest中采样的。训练集可以使用D={（xi，yi）}Ni=1来表示，其中i∈［1，N］，xi表示第i个样本实例，yi表示该样本的真实标签。多分类任务的学习目标是学习一个由θ进行参数化的网络模型f（·，θ），该模型可以最小化分类误差，即最小化yi≠arg max f（xi，θ）。为了最小化这一项，使用交叉熵损失来计算每个样本的损失，该损失表示为

其中：L（·）为似然函数，代表单个样本的损失函数；n为小批量数据大小，在深度学习训练过程中通常使用小批量梯度下降法代替整体梯度下降法来优化迭代过程。一般来说，测试集数据是分布均衡且不存在噪声标签分布的，当训练集存在类不平衡分布和噪声标签分布时，由于训练集和测试集之间的分布不匹配，在训练集上训练的模型通常在测试集上表现不佳。当训练集存在类不平衡和噪声标签时，交叉熵会使模型产生错误的分类决策，使得模型在学习的过程中过拟合到错误的类别上，从而导致模型在测试集上的准确性显著下降。为了解决这一问题，有必要重新制定无偏训练的训练策略。

2.2 重加权方法

重加权的思想是基于样本重新加权，源于重要性抽样，其目的是为训练样本分配不同的权重，以纠正有偏差的分布带来的过拟合的问题。在类不平衡问题中，期望通过分配更大的权重来优先考虑少数样本。在噪声的标签问题中，期望分配较小的权重来抑制有噪声的样本。样本重加权可以表述为

其中：wi表示训练集中第i个样本的重加权因子。虽然重加权可以在一定程度上缓解由于训练集和测试集分布不匹配带来的偏差问题。然而，由于加权函数通常与每类样本数量相关，如CB Loss需要提前知道数据集中每一类数据的具体数量才能确定其具体公式的超参数，在不参考无偏分布的情况下推导显式的重加权函数较为困难。因此，当数据集存在噪声标签或类别不平衡分布的情况时，单纯使用重加权方法很难解决对应的问题。为此，可以利用其他正则化方法的特性来辅助解决。

2.3 正则化方法

2.3.1 标签平滑正则化

标签平滑正则化的主要作用是提高模型的泛化能力，为了防止模型对原始数据的标签过于依赖，在训练过程中将原始的硬标签转换为软标签，从而让网络在学习过程中提高网络特征提取层的表达能力。

其中：yi是一个c维向量，每个维度的元素值（0或1）表示当前样本是否属于该类数据;k表示yi的真实类别;σi是样本xi的标签平滑超参数，经验上σi的取值为［0，1］;LS-CE表示经过标签平滑后的CE损失。从式（4）可以看出经过标签平滑后，来自于真实标签的损失值的贡献会减少，从而可以避免因过度相信当前样本而导致出现网络过拟合的现象。因此，这可以改善因噪声标签导致网络学习到错误的特征提取过程，从一定程度上提高网络的泛化能力。

2.3.2 类裕度正则化

类裕度正则化是一种对模型输出进行二次处理的正则化手段，可以从一定程度上鼓励模型的分类器产生较大的类间距离和较小的类内距离。这会促进模型学习到更加清晰的边界，从而缓解因训练集数据分布不均衡导致的模型参数过拟合到多数类的现象。通过修正模型输出可以改善网络的过拟合现象。

经过类裕度正则化后，模型输出的logit会降低，从而在后续分类器阶段计算softmax的过程中减少其属于类别k的概率，这会促使模型分类器的学习从而输出更加合适的f（xi，θ）i，以便在测试阶段提高对少数类别分类的准确性。

为解决噪声标签和类别不平衡问题，重加权方法在训练过程中通过设计合适的样本权重改善模型的学习，但由于其较难的调参规则以及较弱的任务适应性，重加权方法往往很难应用于实际过程。受到元学习和集成学习的启发［23］，本文将正则化引入重加权方法中，设计了一种自适应重加权和正则化的集成元学习算法，以解决噪声标签和类别不平衡问题。

3 基于自适应重加权和正则化的集成元学习算法

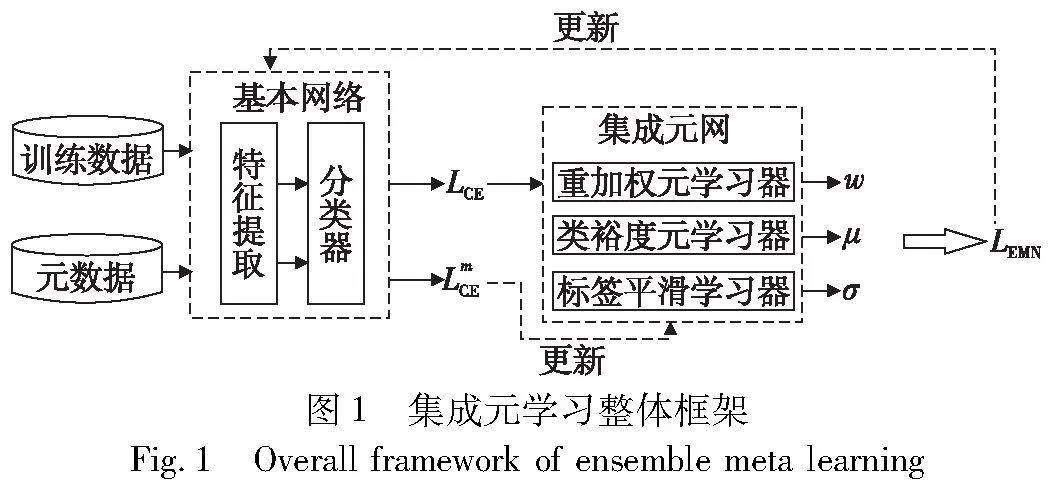
本文提出的EMN集成元学习算法的总体框架如图1所示，由用于分类任务的基本网络和用于超参数估计的集成元网两部分组成。其中基本网络包括特征提取器和分类器，特征提取器用于抽取视觉图像特征，分类器输入所抽取的视觉图像特征用于后续分类器完成多分类任务以及为后续集成元网估计超参数提供损失值。集成元网由重加权网络、标签平滑网络和类裕度网络三部分组成，用于计算自适应重加权损失因子、自适应标签平滑损失因子和自适应类裕度因子，然后使用集成元损失用于后续模型训练。

3.1 元学习器模块

传统元学习的任务目标是让模型能够利用已有模型的知识和经验快速适应新的数据集，相比于使用新数据集直接微调原模型的训练效率要提高很多。文献［9］提出可以利用元学习器配合基本网络学习来快速地搜寻合适的超参数以加快网络学习的进度，但其消耗较大。本文使用了一种基于损失的元学习器模块，只需要花费两个线性层的存储成本就可以让网络获得快速学习新任务的能力。

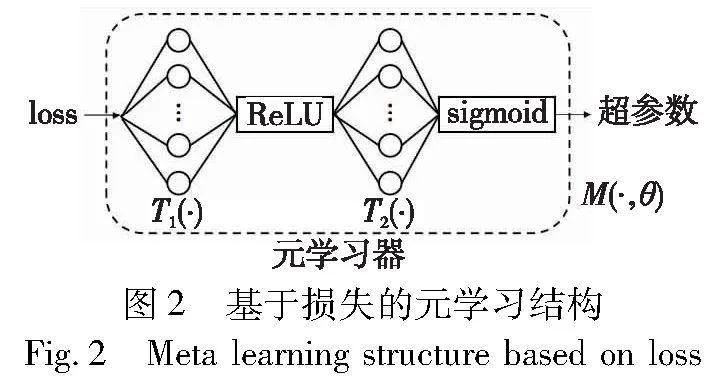
基于损失的元学习器如图2所示，其目的是为了拟合一个输入损失输出超参数的非线性函数，理论上两个线性层构建的网络即可模拟任意一个非线性函数。为了让拟合的非线性函数能够拟合得更好并限制其输出范围，在两个线性层中间插入ReLU激活函数以及在输出前使用sigmoid激活函数，通过使用元学习器即可在网络中实现学习子任务的目的。样本xi首先输入到基本网络中得到基本损失，然后经过第一个线性层得到初步的特征表示H1。

H1=T1（L（f（xi），yi））（7）

进一步使用ReLU激活函数对输入进行截断，得到阶段后的初步特征S1。

S1=ReLU（H1）（8）

然后经过第二个线性层得到进一步的特征表示H2。

H2=T2（S1）（9）

最后将输出经过sigmoid激活函数得到输出ε，将输出限制在［0，1］，以适应超参数的正常取值范围。

ε=sigmoid（H2）（10）

为方便表示整个过程，记元学习器为一个可学习的函数M（·，θ），该函数表示为当基本网络参数θ固定时，样本xi的当前输出超参数为ε=M（xi，θ），集成元网可以通过构造多个元学习器同时完成多个子任务超参数的学习目标。

3.2 集成元网模块

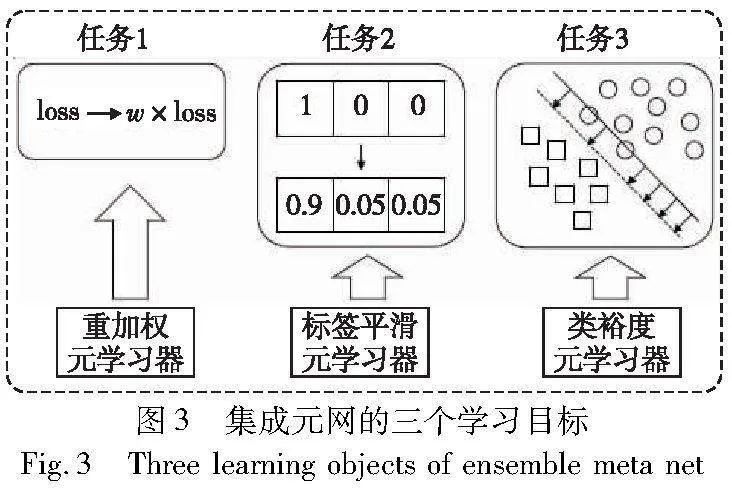
为解决重加权超参数调节较为复杂造成的训练成本较高的问题，本文使用标签平滑和类裕度两种正则化方法与重加权进行结合形成一种可学习的集成元网以缓解这一现象。如图3所示，本文使用了三个元学习器分别学习不同任务的超参数以省去针对不同数据集大量的调参过程，并为基本网络更新阶段提供更加合适的梯度信息来更新基本网络。

3.2.1 自适应重加权损失

重加权的主要作用是对小批量训练数据中的每一个样本施加一个合适的权重以重新调整每个样本损失对网络参数更新的贡献。重加权元学习器基于基本分类网络的损失计算当前样本xi的自适应重加权因子来自适应调整每个样本的当前重加权因子wi，进而得到自适应重加权后的损失值Lw，形式如下：

3.2.2 自适应标签平滑损失

标签平滑通过减少当前样本标签的置信度，在训练过程中将原始的硬标签转换成软标签，使得网络可以在学习真实类别的特征时也学习到其他类的特征。自适应标签平滑基于基本网络的一次损失值大小来自适应更新每个样本当前标签平滑因子σi，进而得到自适应标签平滑后的损失值Lσ，形式如下：

3.2.3 自适应类裕度损失

类裕度基于先验知识通过调整不同类的分类边界的偏好以促进更完善的判别特征学习，促进较大的类间距离和较小的类内距离。 自适应类裕度基于基本网络的一次损失值大小来自适应更新每个样本当前类裕度因子μi，进而得到自适应类裕度后的损失值Lμ，形式如下：

为促使类裕度学习因子μi能够沿着更好的方向进行学习，使用γi计算同一类的训练集和测试集之间的标签分布差异，将其作用于类裕度因子。

3.2.4 集成元损失

集成元损失将重加权和正则化结合形成一个可以联合更新的集成损失，省去了单独优化单个超参数的过程，大大节省了估计超参数所耗费的时间。集成元损失主要包括重加权损失、标签平滑损失和类裕度损失三个损失函数，根据式（11）～（13），经过聚合后的单样本集成元损失LEMN表示为三个损失函数的加权求和形式。

LEMN=t1Lw+t2Lμ+t3Lσ（15）

其中：t1～t3是三个损失权重调节因子，用于控制三个损失对最终损失的贡献程度。本文对于类别不平衡实验设置权重调节因子t1、t2和t3分别为0.25、0.5和0.25；对于噪声标签实验设置为0.25、0.25和0.5。由于本文算法包含对基本网络和集成元网的迭代更新，更新过程较为困难，所以提出了一种三阶段训练法来加速基本网络和集成元网的参数更新速度。

3.3 三阶段集成元学习训练方法

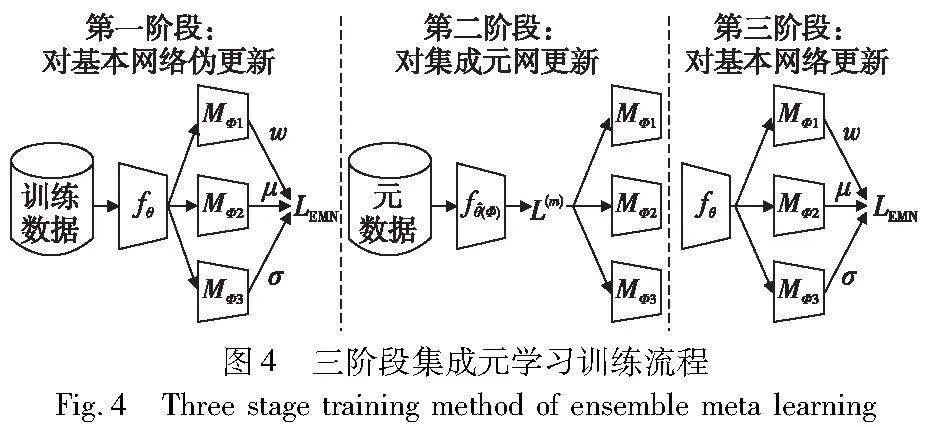
传统的元学习算法的流程一般分为两个嵌套循环来训练基本网络和元学习器。本文提出了一种三阶段训练法来加速集成元网的训练，具体流程如图4所示。总体框架主要包括两个模块的训练：由θ参数化用于多分类任务的基本网络训练和包含三个元学习器由Φ参数化的集成元网的训练，具体表现为以下三个阶段的训练。

a）第一阶段：对基本网络的伪更新。在第一阶段的训练过程中，基于小批量采样的数据训练法来搜索更好的网络参数，在每一次迭代过程中，从训练集中采样一小批量数据用来评估所学习到的基本网络参数的好坏。当集成元网参数固定时，通过在基本网络上执行梯度下降算法可以学习到此时在三个超参数固定的情况下基本网络的最优参数，为了加速训练过程，使用一次梯度下降来代替整体最优解：

θt（Φ）=θ1-ξ1θLEMN（16）

其中：ξ1是基本网络的学习率；θLEMN表示损失LEMN沿着基本网络计算的梯度信息，通过执行单步的梯度下降模拟基本网络在t时刻的最优解θt。

b）第二阶段：对集成元网的更新。在第二阶段的训练过程中，将在第一阶段训练得到的最佳基本网络参数θt用于集成元网训练。集成元网可以通过元数据对基本网络上计算的损失LEMN进行更新。

其中：x（m）i和y（m）i表示从元数据集中采样的第i个样本的实例和对应的标签值。元数据集样本是由人工划分的不存在噪声标签和不平衡分布的一个小规模数据集，每一类数据的数量相等。类似于第一阶段训练，采用一次梯度下降的过程来模拟当基本网络参数固定时集成元网所学习到的最优参数。

c）第三阶段：对基本网络的实际更新。集成元网从元数据中获取对应的元知识更新自身三个用于模拟超参数的集成元网的网络参数后，固定当前集成元网的参数可以指导基本网络的无偏训练：

θt+1=θt-ξ1θL′EMN（19）

其中：L′EMN表示当集成元网更新后使用第一阶段输入的训练样本数据重新进行计算得到的集成元损失，该损失用于第三阶段对基本网络的实际更新过程。

4 实验与分析

4.1 数据集说明

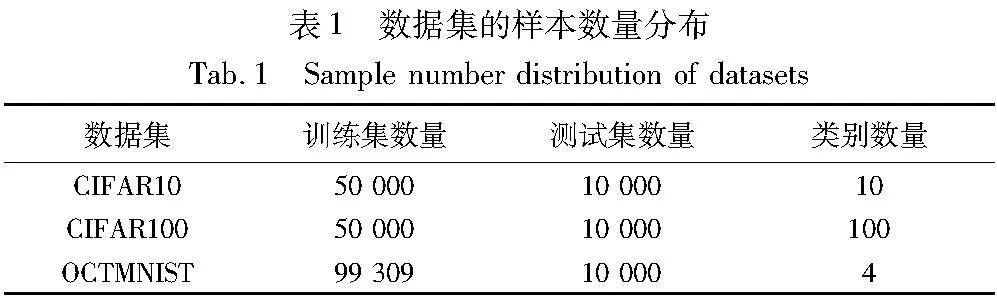
为了验证本文集成学习在针对不平衡分类任务和噪声标签任务的有效性，本文使用了高质量人工标注的CIFAR数据集以及OCTMNIST数据集进行算法评估，如表1所示。

a）CIFAR数据集包括CIFAR10和CIFAR100，是图像分类领域经常使用的最具有广泛意义的代表性数据集，来自于真实世界的图像经过压缩，每个样本为具有32×32×3像素分布的RGB图像，所有样本的标签均标注准确无误，训练集和测试集数据分布均衡［24］。

b）OCTMNIST数据集是近年由上海交通大学最新收集的数据集，通过将以往收集的视网膜OCT图像分类数据集进行分辨率压缩建立的医学图像数据集，训练集分布不均衡，测试集分布均衡［25］。

4.2 数据集预处理

本文主要针对类别不平衡和噪声标签情况下的偏差分布进行实验，并针对不同的任务进行了对应的数据预处理。对于不平衡实验，本文使用所有类中样本数量最大的类所包含的样本数量与样本数量最小的类所包含的样本数量的比值作为平衡程度的定义IF=Nmax/Nmin。为确保不平衡实验符合绝大多数可能出现的场景，本文选取了范围为IF=［10，50，100，200］进行实验，在该范围下可以很好地评估不平衡实验方法的有效性。对于噪声标签实验，本文参考大多数实验设置选择了两种可能出现的噪声标签的基本类型：a）均匀噪声，该噪声标签表现为将每个训练样本的真实标签均匀地转换到其他所有类上，其他类的标签数值总和为p，该样本的标签数值为1-p；b）翻转噪声，该噪声表现为将训练样本独立地转换到另一个相似的类别，该类别的标签数值为p，真实标签的数值为1-p。

4.3 实验设置

本文所有实验均在具有单张RTX-3090显卡的服务器上进行。对于类别不平衡实验，本文使用ResNet-20和ResNet-32进行实验。对于噪声标签实验，本文使用WideResNet-28进行实验。使用具有动量优化因子0.9的SGD优化器来训练基本网络和EMN。所有实验的重量衰减值都设置为0.000 5，基本网络的初始学习率设置为0.1。类别不平衡实验训练了120轮，噪声标签实验中均匀噪声实验训练40轮，翻转噪声实验训练了50轮。为让模型有较好的收敛性，本文使用线性退火策略来对学习率进行动态调整，在距离训练完全的前20和10轮降低10倍学习率。基本网络和集成元网的初始训练学习率设置为0.1和0.001。训练过程中从训练集单次采样的小批量数据的大小设置为128。在进行元学习训练过程中，训练开始前从验证集中针对每类数据选取10张图片组成元数据集。

4.4 对比方法

对于类别不平衡实验，本文对比了近年来最具有代表性的方法RS［26］、RW［27］、CB Loss［28］、Focal Loss［10］、LDAM［29］和对网络的微调方法Finetuning，以及基于元学习的方法L2RW［9］、Meta Weight Net［15］和FSR［22］。对于噪声标签实验，本文对比了常用于解决噪声标签的方法Focal Loss［10］、D2L［30］，基于元学习的方法L2RW［9］、GLC［31］和Meta Weight Net［15］。本文所有实验均使用相同的实验设置并自行训练，与对比方法进行了大量的对比实验并就实验结果进行了合理的分析和说明。

4.5 实验结果

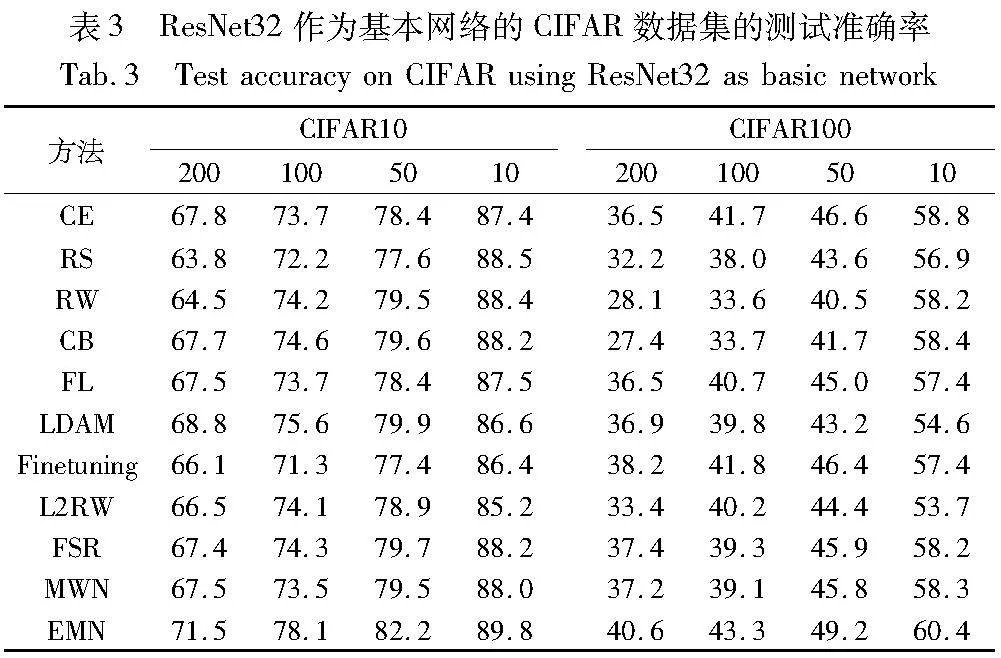
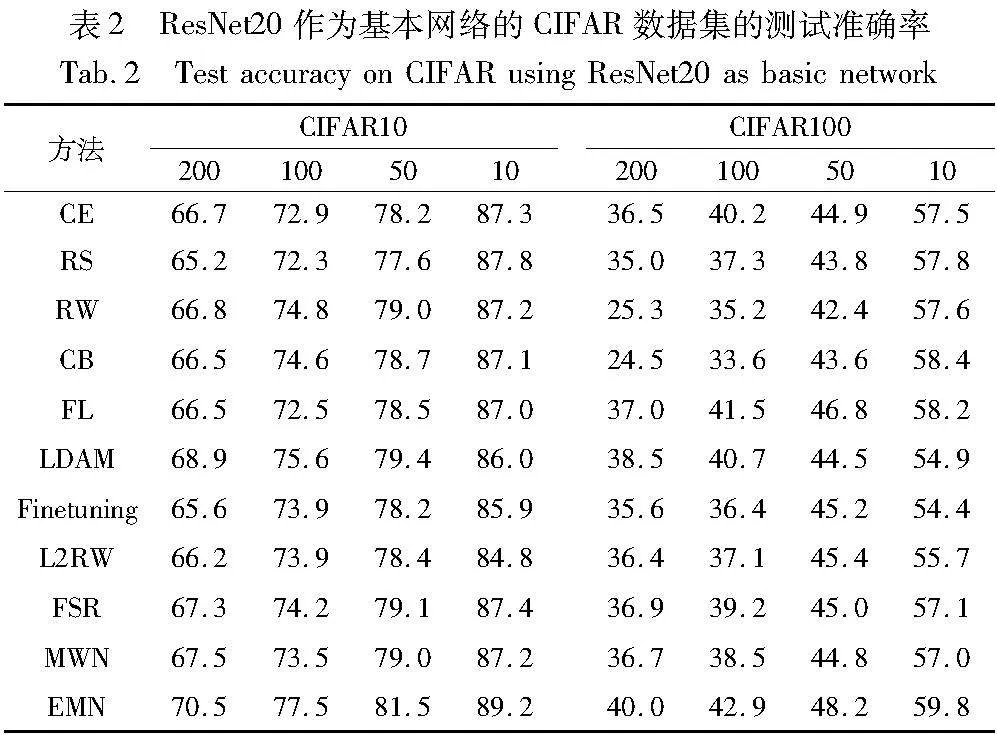
表2、3展示了本文在CIFAR数据集上进行的类别不平衡实验得到的结果，与大多数现有的经典算法的实验结果相比，EMN都取得了稳定的提高并表现出较为优异的性能。并且，不管使用ResNet-20还是ResNet-32作为基准网络，EMN在不同的骨干网络和不同的IF上都可带来稳定的性能提高，这说明将重加权和正则化结合形成的集成元学习框架可以显著提高网络的泛化能力，进而提高模型在测试集上的表现。

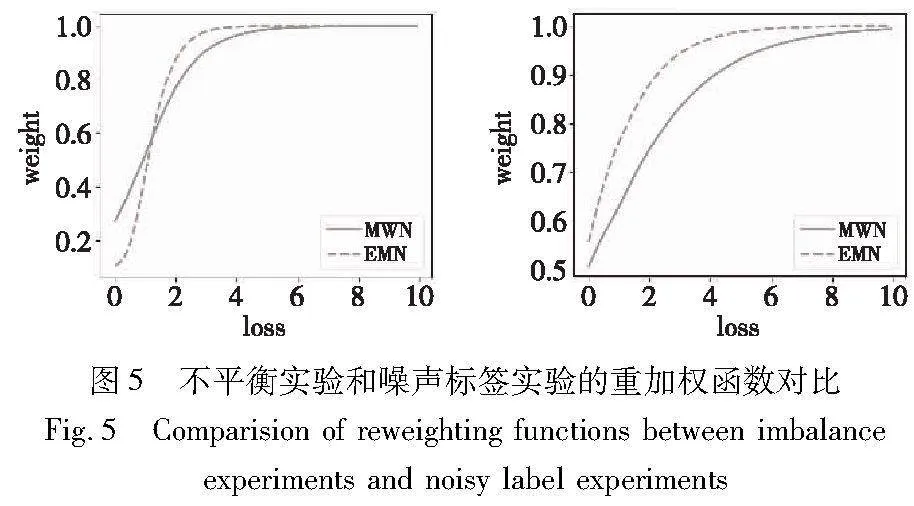
一些经验上被认为可以缓解不平衡分布问题的方法并不奏效。例如，在IF较大的情况下，RW的性能不如CE，这从一定程度上证实了笔者之前的猜想，即重加权因子是模糊而且较难被定义的。当类别数量较少时，RW可以有效缓解分布不平衡的负面影响，促进决策边界向少数类别边界移动［32］。因此，即使当IF达到200时，RW依然保持一定的效果，如图5所示。然而，当类别的总数目较大时，为大量的少数类分配高权重将损害网络特征提取层中的表示学习。这会严重影响网络的泛化性能，最终导致整体模型性能急剧下降。

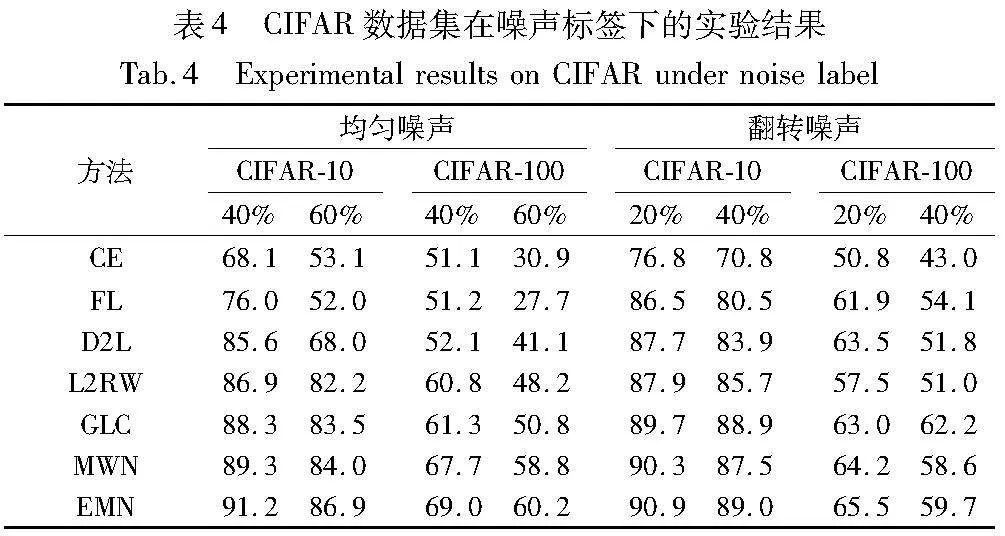
表4展示了本文方法在两种噪声标签任务下的实验结果，与其他方法相比，不管是在均匀噪声情况下还是在翻转噪声情况下，本文方法都取得了较好的效果，这表明集成元网对偏差分布学习具有重要作用。EMN的集成元学习中包括自适应标签平滑学习，这可以让网络在学习的过程中不仅可以关注自身类特征的学习还可以借鉴其他类的特征。

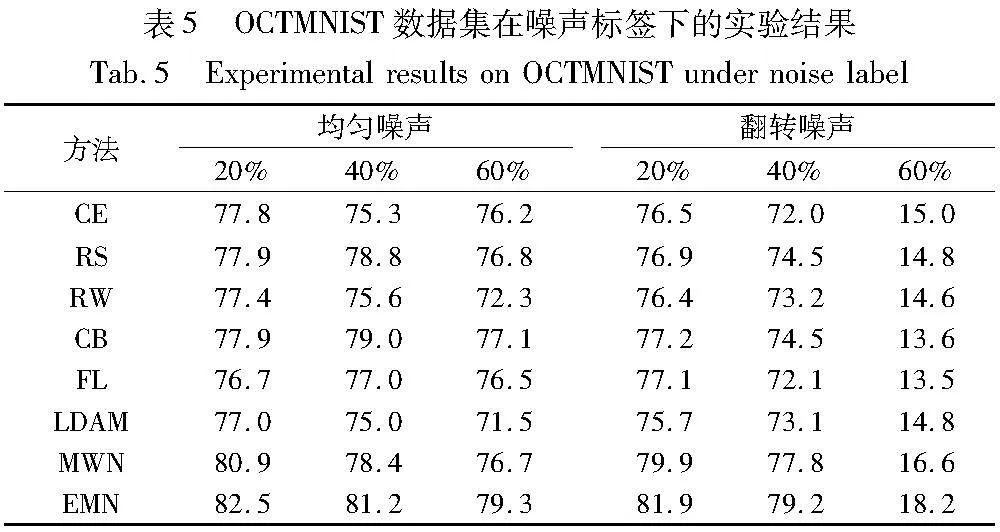
在OCTMNST数据集的实验中，本文向原本带有不平衡分布的数据集加入不同比例的噪声标签可以评估不同算法的鲁棒性，如表5所示。随着噪声率的增加，几乎所有方法的精度都有不同程度的下降，这表明噪声标签会显著降低网络的泛化能力。尽管如此，EMN仍然表现出良好的性能，这说明EMN对未知偏差分布的数据训练具有很强的自适应性。

EMN和MWN针对不平衡和噪声标签实验所学习到的自适应重加权函数的权重大小随着损失值增大的变化曲线，如图5所示。从图中可以看出当损失值较小时，重加权函数呈现出单调递增的趋势，这与传统用于解决不平衡任务的加权函数趋势是一致的，也就是损失值大小和权重大小的变化趋势应该是正相关的。相比于MWN方法，EMN可以更精细地为样本提供合适的权重，从而提高分类性能。

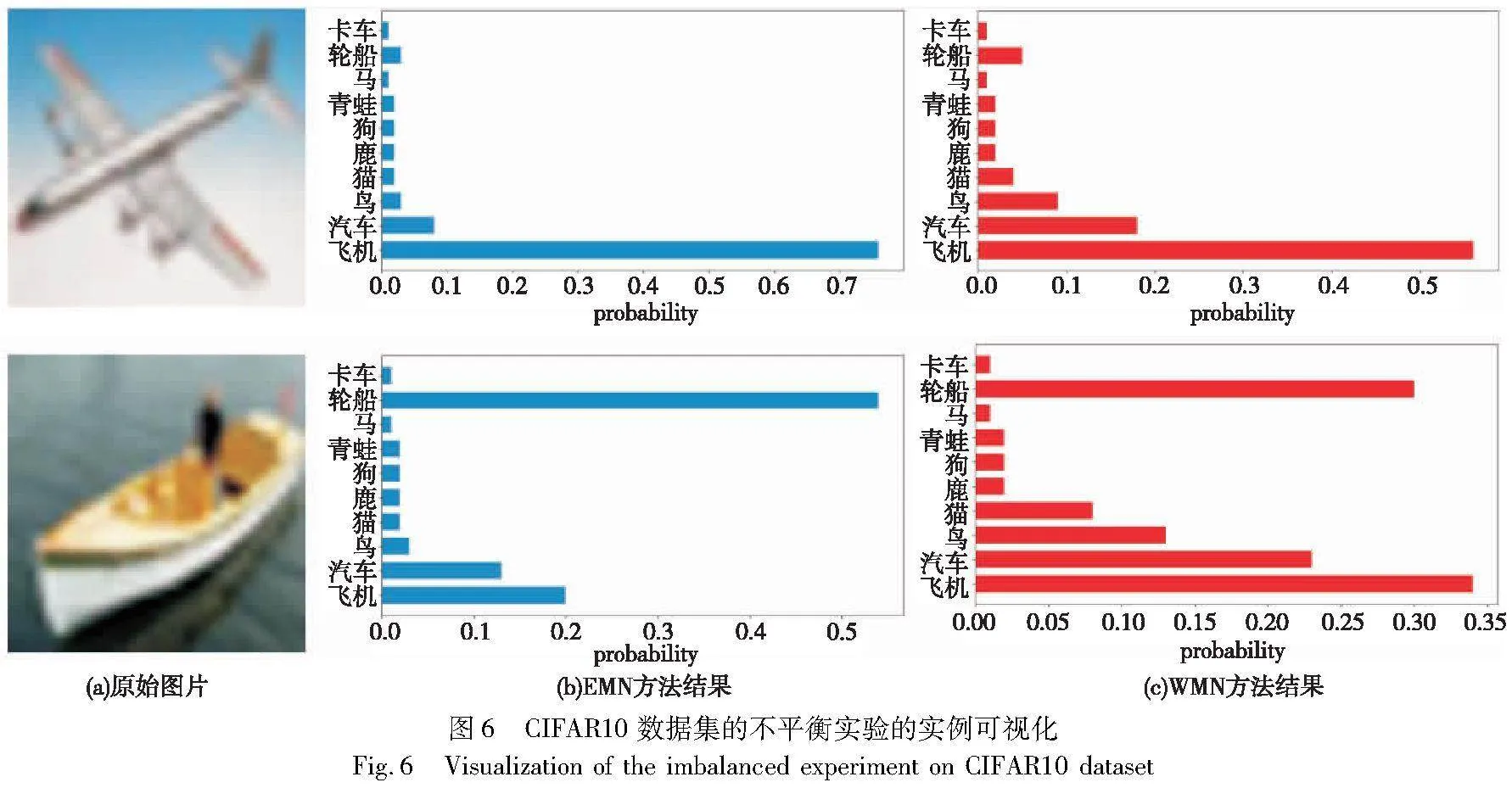
4.6 实例可视化分析

从CIFAR10数据集中飞机（多数类）和轮船（少数类）中选取两张图片，经过网络分类预测后的概率分布结果如图6所示。从图中可以看出，少数类数据在训练过程中会受到多数类影响，轮船被识别成飞机和汽车的可能性比较大。相比于MWN，EMN能够将预测概率从其他不相关的鸟和猫等多数类集中到轮船上，这表明EMN能够有效地抑制多数类对少数类造成的影响。

4.7 集成元网的策略关联性分析

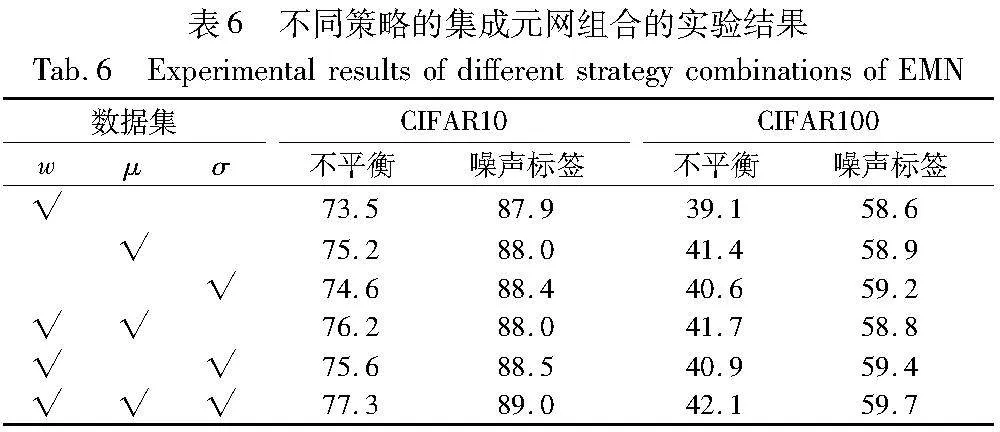
为进一步探索使用不同策略组合形成的EMN和最终网络性能之间的关联性，本文在IF=100的CIFAR10和翻转噪声比例为40%的CIFAR100数据集上进行了关联性分析实验，结果如表6所示。

研究发现，对于不平衡任务，类裕度的积极影响要大于重加权和标签平滑的作用。对于噪声标签任务，标签平滑的积极影响要大于重加权和类裕度的作用。这表明重加权和标签平滑结合的策略对于解决噪声标签问题的关联性很强，重加权和类裕度结合的策略对于解决类别不平衡问题的关联性很强。因此，针对不同的任务设计不同的集成元网至关重要，对特定任务设计合适的集成策略可以加速网络的学习过程和增强其对特定任务的适应能力。

5 结束语

为解决噪声标签和类别不平衡问题，本文提出了一种新的元学习方法EMN。该方法的核心思想是将正则化纳入重加权策略中以形成一种可以进行集成学习的框架。本文方法旨在解决当从真实世界收集的数据存在数据分布偏差时，如何高效合理地利用小部分无偏数据集快速让网络学习修正偏差。EMN通过在一个小的无偏元数据集的指导下可以获取较好的超参数，这使得基本网络可以基于有偏数据在更好的特征空间和更广泛的参数空间中搜索合适的网络参数以适应噪声标签和类别不平衡分布。与当前基于重加权的方法相比，本文方法可以从元数据中学习更有效的知识而无须繁琐和复杂的手动调节超参数的过程。本文实验结果表明，EMN在训练集存在类别不平衡分布和噪声标签的偏差分布的情况下依然表现良好，关联性分析的实验结果表明所提集成元网中正则化技术对不同任务具有不同的关联性。这为不同正则化技术在现实世界中的合理运用提供了见解，表明将正则化与重加权结合进行联合学习的思想可以应用于其他领域任务中。

下一步本文会将提出的自适应重加权与正则化算法和多个子分类模型进行融合，形成一个更加全面的集成学习框架，进一步增强网络的泛化能力，从而提高网络在有偏分布下的精度。

参考文献：

［1］Karimi D， Dou H， Warfield S K， et al. Deep learning with noisy labels： exploring techniques and remedies in medical image analysis［J］. Medical Image Analysis， 2020，65： 101759.

［2］Liu Lei， Lei Wentao， Wan Xiang， et al. Semi-supervised active lear-ning for COVID-19 lung ultrasound multi-symptom classification［C］//Proc of the 32nd International Conference on Tools with Artificial Intelligence. Piscataway， NJ： IEEE Press， 2020： 1268-1273.

［3］Xu Xin， Liu Lei， Zhang Xiaolong， et al. Rethinking data collection for person re-identification： active redundancy reduction［J］. Pattern Recognition， 2021，113： 107827.

［4］苏逸， 李晓军， 姚俊萍， 等. 不平衡数据分类数据层面方法：现状及研究进展［J］. 计算机应用研究， 2023，40（1）： 11-19. （Su Yi， Li Xiaojun， Yao Junping， et al. Data-level methods of imba-lanced data classification：status and research development［J］. Application Research of Computers， 2023，40（1）： 11-19.）

［5］Wang Xiaosong， Peng Yifan， Lu Le， et al. Chestx-Ray8： hospital-scale chest X-ray database and benchmarks on weakly-supervised classification and localization of common thorax diseases［C］//Proc of IEEE Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2017： 3462-3471.

［6］Vapnik V. Principles of risk minimization for learning theory［C］//Proc of the 4th International Conference on Neural Information Processing Systems. San Francisco， CA： Morgan Kaufmann Publishers Inc.， 1991： 831-838.

［7］Li Yi， Vasconcelos N. REPAIR： removing representation bias by dataset resampling［C］//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2019： 9564-9573.

［8］李昂， 韩萌， 穆栋梁， 等. 多类不平衡数据分类方法综述［J］. 计算机应用研究， 2022，39（12）： 3534-3545. （Li Ang， Han Meng， Mu Dongliang， et al. Survey of multi-class imbalanced data classification methods［J］. Application Research of Computers， 2022，39（12）： 3534-3545.）

［9］Ren Mengye， Zeng Wenyuan， Yang Bin， et al. Learning to reweight examples for robust deep learning［C］//Proc of the 35th International Conference on Machine Learning.［S.l.］： PMLR， 2018： 4334-4343.

［10］Lin T Y， Goyal P， Girshick R， et al. Focal loss for dense object detection［C］//Proc of IEEE International Conference on Computer Vision. Piscataway， NJ： IEEE Press， 2017： 2980-2988.

［11］顾永跟， 钟浩天， 吴小红， 等. 不平衡数据下预算限制的联邦学习激励机制［J］. 计算机应用研究， 2022，39（11）： 3385-3389. （Gu Yonggen， Zhong Haotian， Wu Xiaohong， et al. Incentive mechanism for federated learning with budget constraints under unba-lanced data［J］. Application Research of Computers， 2022，39（11）： 3385-3389.）

［12］Zheng Yaling， Scott S， Deng K. Active learning from multiple noisy labelers with varied costs［C］//Proc of IEEE International Conference on Data Mining. Piscataway， NJ： IEEE Press， 2010： 639-648.

［13］樊东醒， 叶春明. 一种面向高维缺失不平衡数据的信用评估方法 ［J］. 计算机应用研究， 2021，38（9）： 2667-2672. （Fan Dong-xing， Ye Chunming. Credit evaluation method for high dimensional missing unbalanced data[J]. Application Research of Compu-ters， 2021，38（9）：2667-2673.）

［14］Chawla N V， Bowyer K W， Hall L O， et al. SMOTE： synthetic minority over-sampling technique［J］. Journal of Artificial Intelligence Research， 2002，16（1）： 321-357.

［15］Shu Jun， Xie Qi， Yi Lixuan， et al. Meta-weight-net： learning an explicit mapping for sample weighting［C］//Proc of the 33rd International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2019： 1919-1930.

［16］Csáji B C. Approximation with artificial neural networks［D］. Budapest： Etvs Loránd University， 2001.

［17］Wang Yuxiong， Ramanan D， Hebert M. Learning to model the tail［C］//Proc of the 31st International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2017： 7032-7042.

［18］姚佳奇， 徐正国， 燕继坤， 等. WPLoss：面向类别不平衡数据的加权成对损失［J］. 计算机应用研究， 2021，38（3）：702-704，709. （Yao Jiaqi， Xu Zhengguo， Yan Jikun， et al. WPLoss：weighted pairwise loss for class-imbalanced datasets［J］. Application Research of Computers， 2021，38（3）：702-704，709.）

［19］Zhang Changbin， Jiang Pengtao， Hou Qibin， et al. Delving deep into label smoothing［J］. IEEE Trans on Image Processing， 2021，30： 5984-5996.

［20］Wang Feng， Cheng Jian， Liu Weiyang， et al. Additive margin softmax for face verification［J］. IEEE Signal Processing Letters， 2018，25（7）： 926-930.

［21］Jiang Lu， Zhou Zhengyuan， Leung T， et al. MentorNet： learning data-driven curriculum for very deep neural networks on corrupted labels［C］//Proc of the 35th International Conference on Machine Learning.［S.l.］： PMLR， 2018： 2304-2313.

［22］Zhang Zizhao， Pfister T. Learning fast sample re-weighting without reward data［C］//Proc of IEEE/CVF International Conference on Computer Vision. Piscataway， NJ： IEEE Press， 2021： 705-714.

［23］Wang Xudong， Lian Long， Miao Zhongqi， et al. Long-tailed recognition by routing diverse distribution-aware experts［EB/OL］. （2020-10-05）. https：//arxiv.org/abs/2010.01809.

［24］Krizhevsky A. Learning multiple layers of features from tiny images［D］. Toronto ： University of Tront， 2009.

［25］Yang Jiancheng， Shi Rui， Ni Bingbing. MedMNIST classification decathlon： a lightweight autoML benchmark for medical image analysis［C］//Proc of the 18th International Symposium on Biomedical Imaging. Piscataway， NJ： IEEE Press， 2021： 191-195.

［26］Buda M， Maki A， Mazurowski M A. A systematic study of the class imbalance problem in convolutional neural networks［J］. Neural Networks， 2018，106： 249-259.

/iAG7e5gtfxEucQkWm+8Eg==

［27］Huang Chen， Li Yining， Loy C C， et al. Learning deep representation for imbalanced classification ［C］//Proc of IEEE Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2016： 5375-5384.

［28］Cui Yin， Jia Menglin， Lin T Y， et al. Class-balanced loss based on effective number of samples［C］//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2019： 9260-9269.

［29］Hong Y， Han S， Choi K， et al. Disentangling label distribution for long-tailed visual recognition［C］//Proc of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE Press， 2021： 6622-6632.

［30］Ma Xingjun， Wang Yisen， Houle M E， et al. Dimensionality-driven learning with noisy labels［C］//Proc of the 35th International Confe-rence on Machine Learning.［S.l.］： PMLR， 2018： 3355-3364.

［31］Hendrycks D， Mazeika M， Wilson D， et al. Using trusted data to train deep networks on labels corrupted by severe noise［C］//Proc of the 32nd International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2018： 10477-10486.

［32］El Hanchi A， Stephens D， Maddison C. Stochastic reweighted gradient descent［C］//Proc of the 39th International Conference on Machine Learning.［S.l.］： PMLR， 2022： 8359-8374.

［33］Cai Jiarui， Wang Yizhou， Hwang J N. ACE： ally complementary experts for solving long-tailed recognition in one-shot［C］//Proc of IEEE/CVF International Conference on Computer Vision. Pisca-taway， NJ： IEEE Press， 2021： 112-121.