面向简化规则的集成学习模型及规则约简策略

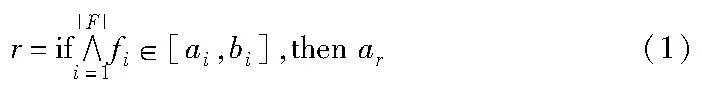
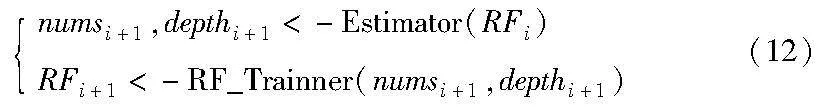
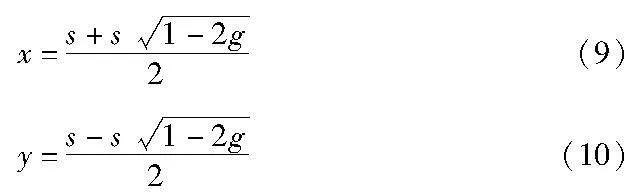
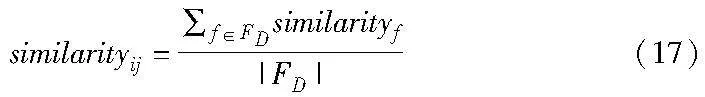
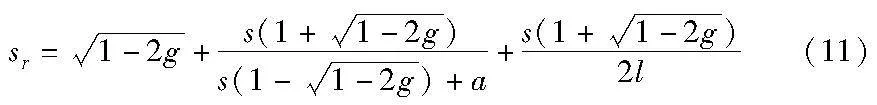
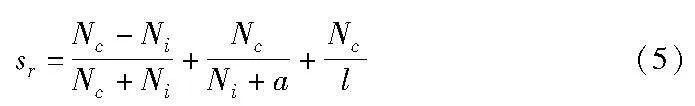
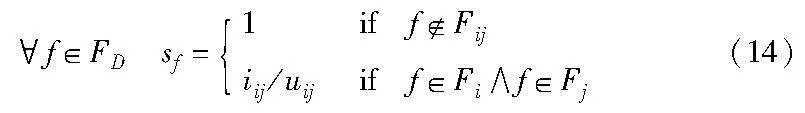
摘 要：随着机器学习模型的广泛应用，研究者们逐渐认识到这类方法的局限之处。这些模型大多数为黑盒模型，导致其可解释性较差。为了解决这一问题，以集成学习模型为基础，提出了一种基于规则的可解释模型以及规则约简方法，包括生成优化的随机森林模型、冗余规则的发现和约简等步骤。首先，提出了一种随机森林模型的评价方法，并基于强化学习的思想对随机森林模型的关键参数进行了优化，得到了更具可解释性的随机森林模型。其次，对随机森林模型中提取的规则集进行了冗余消除，得到了更加精简的规则集。在公开数据集上的实验结果表明，生成的规则集在预测准确率和可解释性方面均表现优秀。

关键词：可解释模型； 规则学习； 集成学习； 规则约简

中图分类号：TP391 文献标志码：A

文章编号：1001-3695（2024）06-020-1743-06

doi：10.19734/j.issn.1001-3695.2023.10.0523

Research on ensemble learning model for simplified rules and rule reduction strategy

Abstract：With the widespread application of machine learning models， researchers have gradually recognized the limitations of such methods. Most of these models are black-box models， resulting in poor interpretability. To address this issue， this paper proposed a rule-based interpretable model and rule reduction method based on ensemble learning models， which included generating optimized random forest models， discovering and reducing redundant rules， and other steps. Firstly， this paper proposed an evaluation method for random forest models， and optimized the key parameters of random forest models based on the idea of reinforcement learning， resulting in a more interpretable random forest model. Secondly， the rule sets extracted from the random forest model were subjected to redundancy elimination， resulting in a more concise rule set. Experimental results on public datasets show that the generated rule sets perform well in terms of prediction accuracy and interpretability.

Key words：interpretable model; rule learning; ensemble learning; rule reduction

0 引言

随着机器学习方法、人工智能技术的广泛应用，这类方法的良好性能得到了更多的关注。然而，绝大多数机器学习方法与人工智能技术构建的模型都是人类难以理解的黑盒模型，在一些对稳定性、安全性要求较高的领域中，专家们往往更看重模型决策的逻辑，从而避免模型给出的解决方案带来的负面影响。因此，研究可解释的模型是一种可行的尝试。值得注意的是，可解释性模型的建立不仅仅是学术与工程上的要求，在未来很可能演变为法律中应承担的责任［1］。

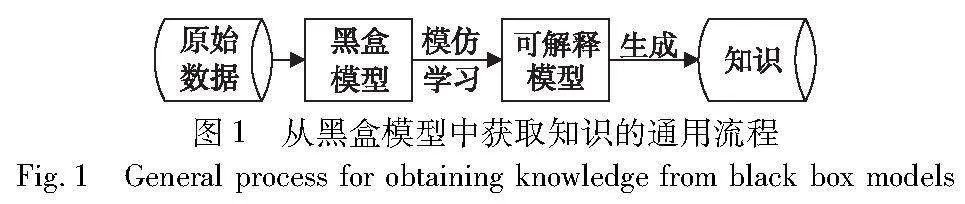
黑盒模型虽然解释性弱，但其预测性能往往较好，因此以黑盒模型为对象，以模仿的形式从中学习知识是一种不错的选择。图1展示了从黑盒模型中获取知识的通用流程，以模仿学习的方法从黑盒模型中构建一种可解释的模型，再从中生成知识。其中，模仿学习使用的主要是黑盒模型与原始数据交互生成的数据。

在可解释的模型中，基于规则的模型代替人类较难理解的模型和方法［2，3］，可以做到决策准确性和可解释性的平衡。所谓规则，即有限定条件、有结论的一种易于理解的知识。在分类问题的场景下，集成学习模型综合了多个单一模型的预测结果，具有良好的预测性能。因此，以集成学习模型作为模仿学习的生成对象，从中进一步提取规则是一种可行的思路。

if-then规则的形式化表示如下：

其中：r为规则；F为规则中包含的特征的集合;fi∈F;ai、bi分别表示规则中第i个特征的上下界;ar表示此规则采取的动作。

为了与规则紧密联系起来，本文主要以随机森林模型这一集成学习模型的经典范例为示例，引入规则生成及约简的方法。注意到基于树结构的模型天然具有一定的可解释性，可以根据根节点至叶节点的路径导出if-then形式的规则。而随机森林模型可以看作多个树模型的集成，从中可以提取大量规则，便于后续对规则的进一步处理。

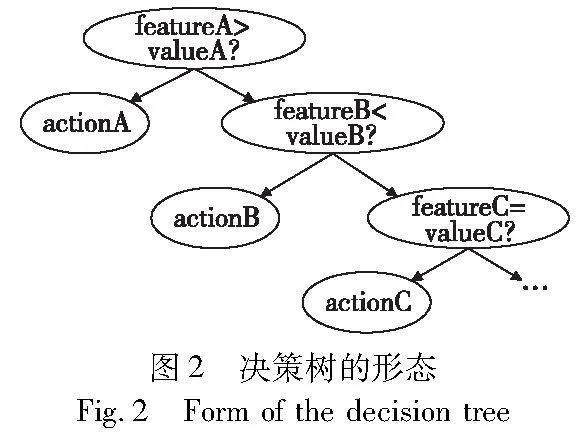
图2展示了一个决策树模型的形态，从根节点出发，依次扩展到各个叶节点，可以生成如下几条规则：

a）if featureA>valueA， then actionA.

b）if featureA≤valueA and featureB<valueB， then actionB.

文献［4］提出了一种模仿学习的方法，以决策树模型拟合黑盒模型的决策过程，再从决策树模型中提取规则。从决策树模型到规则的转换，可以将决策过程直观地展示出来，这是一种可解释性较强的方法。文献［5］在文献［4］的基础上，以随机森林模型替换了决策树模型，可以生成更多的规则，准确率较高。

文献［4，5］的方法虽然获得了一定的知识，但这类方法生成的规则集仍有进一步优化的空间。首先，当数据集规模很大时，得到的规则数量巨大，后续对规则的处理较为棘手。如果能在维持较好预测准确率的情况下，建立一种决策树数量更少、决策树深度更低的随机森林模型，则从中提取的规则数量也将大大减少。

其次，规则集的处理是本文研究的另一个核心问题。从随机森林模型中导出的规则集会包含较多规则，其中必然有冗余的规则，而每条规则也可能有冗余的约束，消除这些冗余对于规则集的可解释性较为重要。近年来在规则学习的研究中，已有一些文献开始对规则的简化进行探索，但对于规则之间的关联有所忽略，利用规则之间的相似性对规则集进行约简是较为新颖的一种思路。

综上，本文在随机森林模型拟合黑盒模型效果较好的基础上，对随机森林模型的生成进行优化，使之更具可解释性。同时，本文对规则的约简进行了研究，提出了更彻底的规则约简算法，实现了基于规则的可解释模型在预测性能与可解释性两方面的均衡。本文方法的整体流程如图3所示。

1 基于随机森林模型的规则学习

随机森林模型可以看作决策树模型的集成，其保真性有了较大的提高。但基于随机森林模型拟合黑盒模型后，导出的规则数量较多，需要采取一些方法对规则进行处理，本章介绍的几种方法都是基于随机森林模型的规则约简方法，均取得了较好的结果。

Adnan等人［6］提出了一种简洁的规则约简方法，从规则与训练数据的交互入手，给出了规则的准确度、覆盖度和长度等几个重要定义。

定义1 规则的长度：设F为每条规则中包含的特征的集合，F中包含特征的数量称为规则的长度。

定义2 规则的覆盖度：表示规则可以匹配的数据实例在数据集中的比例。设数据实例的总数为N，一条规则可以匹配的数据实例个数为Nrule，则覆盖度Cov可以用式（2）表示。

Cov=Nrule/N（2）

定义3 规则的预测准确率：指规则在预测测试数据集时产生的正确预测的比例。设一条规则可以匹配的数据实例个数为Nrule，其中预测正确的数据实例个数为Ncorrect，则预测准确率Acc可以用式（3）表示。

Accuracy=Ncorrect/Nrule（3）

文献［6］指出，在规则集中，若规则的准确度、覆盖度小于所有规则的平均值，或长度大于所有规则的平均值，则规则显然是低质量的，这部分规则可以约简。

Mashayekhi等人［7］首先引用了一种被证明较为合理的规则得分公式，其针对的是if-then形式的规则。其次，在原始的规则集中，使用了基于爬山法的搜索策略，对规则进行约简，而确定规则在规则集中的位置是该规则得分公式给出的排名。这种方法实质上是将规则集看作一个整体进行化简，当新加入规则可以提高规则集的预测效率时，会将该规则保留，否则仍然维持原状。

Dong等人［8］也以随机森林模型生成的规则为基础，提出了一种两阶段的规则提取算法。两阶段分为对规则的局部处理和全局处理，局部处理主要指对单条规则的化简，而全局处理则是把所有规则作为一个整体进行约简。

在局部化简中，文献［8］使用了一种启发式的方法，不断尝试将规则中的特征约束消除，通过判断消除约束后的规则是否优于原规则来决定是否保留化简后的规则。这里评估规则质量时使用的是文献［7］涉及的规则得分公式。对于全局约简问题，类似于文献［7］的思路，将其抽象为搜索问题，使用了基于遗传算法的搜索策略，进一步提取规则，简化结果规则集。

Qiu等人［9］基于基于深度神经网络的Q学习（deep neural network-based Q-learning，DQN）模型提出了一种规则提取的方法。在该方法中，提取规则的过程较为简单，其中输入向量的每一维数据依次转换为式（1）中对应特征feature的取值，而输出即为式（1）中的动作action。该文献将初始提取得到的规则作为实例规则，经过规则泛化、合并及修正等步骤，获得最终的结果规则集。

上述几种方法涉及规则的评价、规则的全局与局部化简，虽然都对规则进行了一定程度的约简，但没有考虑生成规则的随机森林模型的可解释性，导致初始规则集的规模较大，且将规则的全局简化简单地抽象为搜索问题，对大量规则进行处理时效率较低。本文以这几种方法为基础，提出了一种基于规则约简的随机森林模型的生成策略，并对规则的约简方法进行了优化，生成兼具预测准确率与可解释性的规则集模型。

2 面向规则约简的随机森林模型

本章方法的目标是获取一种面向规则约简的随机森林模型，模型的输入是黑盒模型与环境进行交互得到的原始数据，由（状态，动作）构成的数据集。显然，这类数据集适用于训练分类模型，其中状态可以表示为特征向量，动作可以表示为分类的标签。

基于这样的训练数据，现有的方法大多直接训练一个经典的随机森林模型。经典的随机森林模型为了保证较高的预测准确率，会导致随机森林中决策树的数量较多，决策树的深度也较大，从中导出的规则数量很多，后续对规则的处理是较为繁琐的。因此，本阶段方法的目标是训练一个在预测性能与可解释性两方面较为均衡的随机森林模型——面向规则约简的随机森林（random forest for Fules reduction，RR-RF）模型。综合上述分析，对RR-RF模型的生成问题作如下定义：设目标为生成一个面向规则约简的随机森林模型，要求此模型满足式（4）。

其中：s表示随机森林模型的预测准确率;n表示随机森林模型中决策树的数量;d表示所有决策树的平均深度;max（）表示最大值函数;min（）表示最小值函数。

2.1 RR-RF模型的评价方法

对于经典的随机森林模型，一般根据其对测试集的准确率等机器学习模型的指标进行评价。但本文研究RR-RF模型的最终目的是获得规则，准确率不是最重要的目标。因此本节从对规则的评价入手，设计了以下方法对随机森林模型进行评价。

当前一些研究提出的对于规则的评价公式是有效的，但从随机森林模型中提取规则，再对规则进行测试的效率较低。为了解决这一问题，本阶段方法提出这样一种思路：将对规则的评价转换为对随机森林模型的评价，以便在训练RR-RF模型时可以实时地进行评价。

文献［7］中提出的规则得分公式可以对规则进行合理的评价，本阶段方法选择对此公式进行改造，将其转换为对随机森林模型的评价公式。式（5）给出了文献［7］中提出的规则得分公式。

其中：sr表示规则r的得分;Nc表示训练集中该规则预测正确的样本数;Ni表示训练集中该规则预测错误的样本数;l表示规则的长度；a是一个大于0的常数，避免出现Ni为0的情况。这一公式的前两项主要是对规则的预测能力进行评价，使那些准确率较高的规则具有优势。而第三项引入规则长度为分母，对过长的规则进行了限制，使得简短的规则具有更高的得分。

考虑将式（5）转换为与随机森林模型相关的表达式，在得到一个随机森林模型后可对其进行评价，间接地对即将生成的规则进行评价。观察到式（5）中的Nc、Ni与随机森林训练过程中叶节点的基尼系数gini（用于判断一个节点中数据分类后的纯度）、叶节点包含的样本数量samples是相关的，因此将式（5）改造为与gini、samples相关的得分。首先，令

samples=s，gini=g，Nc=x，Ni=y

对于式（5），其第一项分母可以写为x+y，而x、y的和即叶节点包含的样本个数，此关系可以用式（6）表示。

x+y=s（6）

对于基尼系数g，当数据集中特征均为数值型时，可以简化为二分类的情况。在二分类的场景下，容易得到基尼系数的计算公式，即式（7）。

g=1-［a/（a+b）］2-［b/（a+b）］2（7）

其中：a+b=s。当决策树准确率较高时，根据样本纯度划分得到的a、b和根据规则判断得到的x、y是近似相等的，故可以用x、y替换式（5）中的a、b，将基尼系数的计算式重新整理为式（8）。

g=1-（x/s）2-（y/s）2（8）

联立式（4）（6）得到x、y关于s、g的值，如式（9）（10）所示。

将式（9）（10）代入式（5），就将规则得分转换为了关于samples、gini的表达式，如式（11）所示。

式（11）实质上是将对规则的评价转换为了对决策树模型中任一叶节点的评价，将所有叶节点的评价整合在一起，就可以完整地评价RR-RF模型。在得到一个随机森林模型后、没有直接使用规则进行测试前，就可以间接地根据式（11）判断后续生成的规则的质量，从而确定是否要调整随机森林模型的关键参数。

2.2 RR-RF模型的生成策略

经过2.1节的计算，本文已经具备了对随机森林模型进行评价的条件，接下来的工作是根据这个条件训练RR-RF模型。

训练一个形态适宜的随机森林模型，需要设置的参数主要是决策树的个数n_estimators和决策树的最大深度max_depth。这里需要补充的是，在式（11）中，规则长度l可以使用决策树的最大深度max_depth近似。如何确定随机森林模型的参数已经达到最佳值，即式（11）给出的评价何时达到最大值？观察式（11），当g=0、s为训练集中样本总数时是最好的情况，实际上这是只有一个节点的情况，不符合实际情况。而随着决策树向下分裂，g、s呈现不断减小的趋势，但l会不断增大，导致式（11）中第2、3项的变化趋势难以确定。

结合上述分析，较难通过数学计算给出这几个参数的最佳值。为了解决该问题，本阶段方法考虑设计一种迭代的方法来训练随机森林模型，每一轮得到一个新的随机森林模型后，可根据式（11）来评价模型，这一过程用式（12）表示。

其中：RFi表示上一轮训练得到的随机森林模型;RFi+1表示本轮将要得到的随机森林模型；numsi+1、depthi+1分别表示根据式（11）评估后调整得到的随机森林模型的最佳决策树个数、决策树的最大深度；Estimator（）表示根据式（11）得出的随机森林模型评估方法;RF_Trainner（）表示随机森林模型的训练方法。

在每一轮训练时调整随机森林模型的关键参数。本阶段方法考虑一种类似强化学习的奖惩机制，首先对参数max_depth和n_estimators进行随机调整，调整后，如果随机森林模型生成的评价降低则给负奖励，否则给正奖励；然后根据奖励确定参数的调整方向（增大或减小），直到随机森林模型评价基本不再变化。

本阶段方法的具体细节见算法1。

算法1 RR-RF模型的生成策略

应用算法1后，即可得到RR-RF模型，再根据引言中提出的规则提取方法即可生成原始的规则集。

2.3 实验与分析

2.3.1 实验数据及对比方法

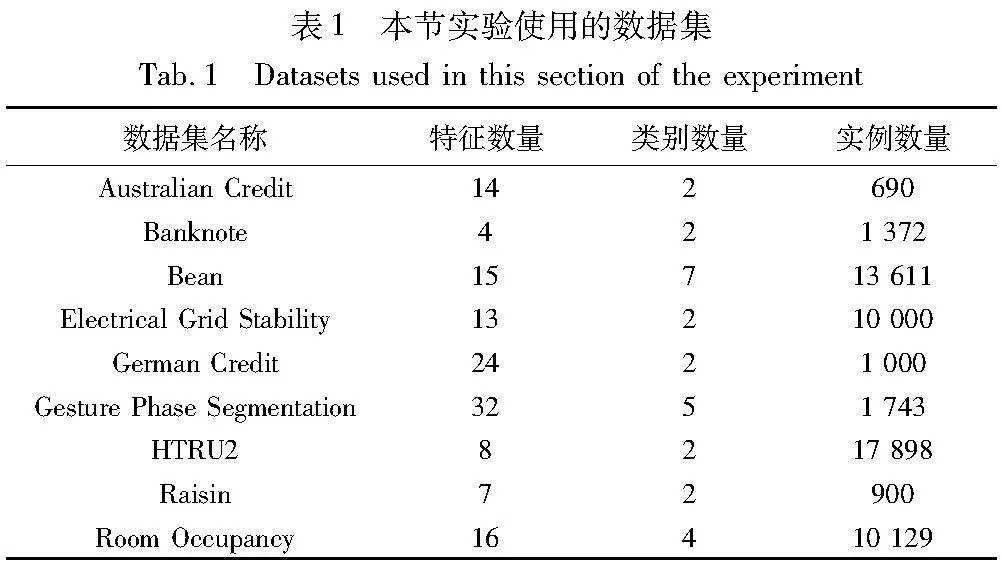
为了更好地验证本文方法的效果，本阶段方法主要在计算机领域的分类问题上进行了实验。本节使用的数据集主要来自UCI［10］公开数据集，均为分类问题的数据集，且特征均为数值型。表1展示了本节实验使用的9个数据集，给出了数据集的名称、特征数量、类别数量和实例数量。

为了更充分地展示RR-RF模型在准确率和可解释性两方面的均衡，本节实验采用经典随机森林模型［10］与经典决策树模型［11］作为对比方法，这两个模型仅考虑预测的准确率。在经典随机森林模型中，max_depth设置为20，n_estimators设置为30；在经典决策树模型中，均采用默认参数。

2.3.2 实验结果与分析

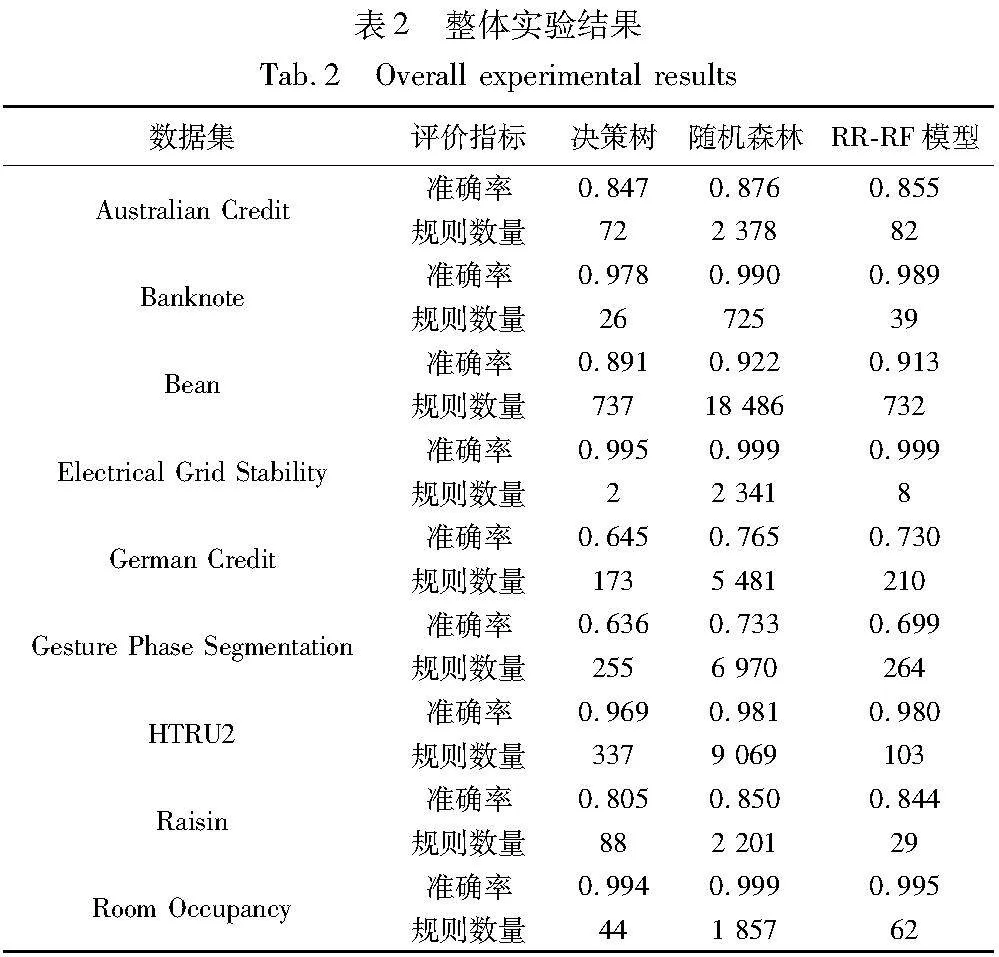
整体的实验结果如表2所示，其中主要设置了两个指标来衡量规则的质量，分别是三种模型生成的规则数量和三种模型对于测试集的预测准确率。

首先，RR-RF模型的预测准确率在9个数据集上均明显好于经典决策树模型，这是因为RR-RF模型包含多个决策树，在预测性能上势必优于单一的决策树。而在规则数量上，RR-RF模型的结果也仅比经典决策树模型多一些，除在Electrical Grid Stability数据集上两者得到的规则数量都很少外，在其余数据集上的差距基本不超过20%，在HTRU2和Raisin两个数据集上甚至得到了更少的规则数量。

其次，观察RR-RF模型与经典随机森林模型的对比结果。在生成的规则数量上，RR-RF模型具有很大的优势，这就证明RR-RF模型对于可解释性的贡献优于经典的随机森林模型。而在预测准确率上，优化模型虽然略低于经典随机森林模型，但在9个数据集上基本不超过3%，因此是可以接受的。

综合上述分析，RR-RF模型在保持了较高预测准确率的同时，生成了更少的规则，使得规则集更具可解释性。此外，本文提出对随机森林模型优化的思想也是比较新颖的。目前的主流方法通常忽略了这一点，仅使用经典的树集成模型，导致后续会生成较大量的规则，对规则集进行处理势必要耗费很多时间，而本阶段方法基本上解决了这一问题。

3 冗余规则的约简策略

RR-RF模型中提取的if-then规则的数量相比经典随机森林模型减少了很多，但所得的规则集规模仍然比较庞大。这样的“知识”不易被人类理解，也难以在实际应用中由领域专家进行选择。因此，本文以RR-RF模型中提取的原始规则集作为输入，对其进一步约简，输出一个兼具预测性能和可解释性的规则集。

从if-then规则的形式上看，主要可以从两个维度进行约简。首先，对于单条规则，其中包含多个特征约束的判断，部分特征约束可能是冗余的，可以进行简化，这种思路称为规则的局部简化。其次，将规则集作为一个整体来看待，其中很多规则的作用是相似的，导致存在大量冗余的规则，可以从规则集中删除，这种思路称为规则的全局约简。

第2章方法训练得到的RR-RF模型通过降低决策树模型的深度，实质上完成了对规则的局部约简，因此本章方法专注于完成对规则的全局约简。设每条规则的特征约束数量为C，规则集中规则的数量为N，则本文的具体目标表示为

其中：min（）表示最小值函数;第一个式子表示期望得到所有规则的特征约束数量平均值的最小值;第二个式子表示期望得到规则数量最少的规则集。

3.1 冗余规则发现与约简

针对式（13）提出的目标，当下有较多方法进行处理。一些方法把约简的过程抽象为搜索问题，从规则集中搜索部分质量较高的规则。这类方法没有考虑规则间的联系，当规则数量较多时，搜索性能可能遇到瓶颈。还有一些方法，如Mollas等人［12］提出使用关联规则挖掘思想对规则集进行化简。

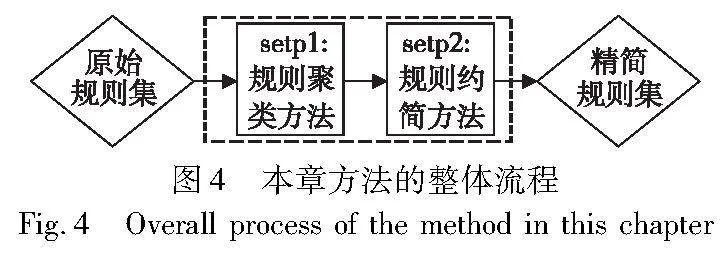
本阶段方法考虑通过相似规则的聚类方法实现对规则的全局约简，整体流程如图4所示。该方法的输入是从RR-RF模型中导出的原始规则集。第一步是规则的聚类方法，通过计算规则之间的相似性，将可能冗余的相似规则聚类至每个子规则集中。第二步则是从规则集全局的维度出发，在每个子规则集中选取部分有代表性的规则，得到精简的规则集。

3.1.1 规则相似性计算与规则方法

本节方法的目标是削减整个规则集的维度，但直接对规则集进行约简效率较低，且没有考虑到相似规则造成的冗余。因此，本阶段方法首先对规则进行聚类，进而在各个相似的子规则集中发现一些具有代表性的规则，从而约简冗余的规则。

进行规则聚类的计算，首先要解决的问题是如何计算规则之间的相似性。本方法参考文献［12］，提出了一种规则相似性的计算方式。对于任意两条规则ri、rj，设Fij为两条规则中涉及的所有特征的并集，即设FD为数据集中包含的所有特征。对于FD中的任意特征f，ri、rj在f上的相似度sf可以按式（14）计算。

其中：iij和uij分别由式（15）（16）表示。

iij=min（ui，uj）-max（li，lj）（15）

uij=max（ui，uj）-min（li，lj）（16）

在ri中，f∈［li，ui］；在rj中，f∈［lj， uj］。最终得到ri、rj之间的相似度similarityij，由式（17）表示。

在具体对if-then规则进行聚类时，需要考虑规则的特点。首先，规则之间没有明显的层次结构，因此基于层次的聚类算法不宜使用。基于划分的聚类算法简洁可行，处理大规模数据的可用性更高，因此本阶段选取基于划分的聚类算法。此外，规则的每个特征值是一个范围，不宜计算其均值，而选取一条规则代表每个聚簇是比较合适的，因此决定采用经典的K-medoids聚类算法对规则集中的规则进行聚类。

完成规则的聚类后就将每一类相似的规则置于同一个子规则集中，下一步需要对每个子规则集中的冗余规则进行约简。

3.1.2 冗余规则的全局约简方法

本节的目标是在每个子规则集中发现具有代表性的规则，这一步的处理可以称为规则的全局约简。

在每个子规则集中寻找代表性规则，其实质可以抽象为搜索问题，搜索集是聚类后的每个子规则集，搜索结果是其中的代表性规则。这一过程可以用式（18）表示。

Rs=SearchS（R）（18）

其中：R表示原始规则集；Rs表示搜索后得到的结果规则集;Search（）表示搜索函数;S表示搜索依据的最佳策略。本阶段方法尝试提出一种搜索的策略，配合对规则的评价，对每个子规则集进行搜索，获得质量较好的部分规则。

对于任意一个子规则集，首先计算其中每条规则的得分和规则对于训练数据集的覆盖度，其中规则得分使用式（5）进行计算。其次，将规则按照规则得分进行降序排序。确定一个候选集C，每次取规则集中前n个规则依次加入候选集，n为可调整的超参数，选取的规则覆盖度必须超过此规则集中所有规则覆盖度的平均值。从C中依次取出规则加入结果规则集R_new，再利用测试集对R_new的预测准确性进行测试，若其准确性优于该规则加入R_new之前的准确性，则保留该规则，并在原规则集中删去该规则。具体细节见算法2。

算法2 规则全局约简方法

这一算法充分利用了规则长度、覆盖度和准确性几个指标，使得约简后的规则集的质量较高。此外，本算法使用的搜索策略参考了文献［13］的beam search思想，搜索效率较高。经过算法2的处理，获取了每个子规则集中具有代表性的规则，将这些规则合并，可以得到一个完整的结果规则集，这也是本章方法消除了原始规则集中的冗余部分后得到的精简规则集。

3.2 实验与分析

本节实验中使用的数据集同2.3节介绍的9种数据集，使用的对比方法即第1章介绍的四种基于随机森林模型的规则学习方法，主要对比几种方法处理后的规则集的质量。其中，本文方法处理的规则集为RR-RF模型中生成的初始规则集，而其他几种方法处理的规则集为经典随机森林模型中生成的规则集。

3.2.1 规则整体质量对比

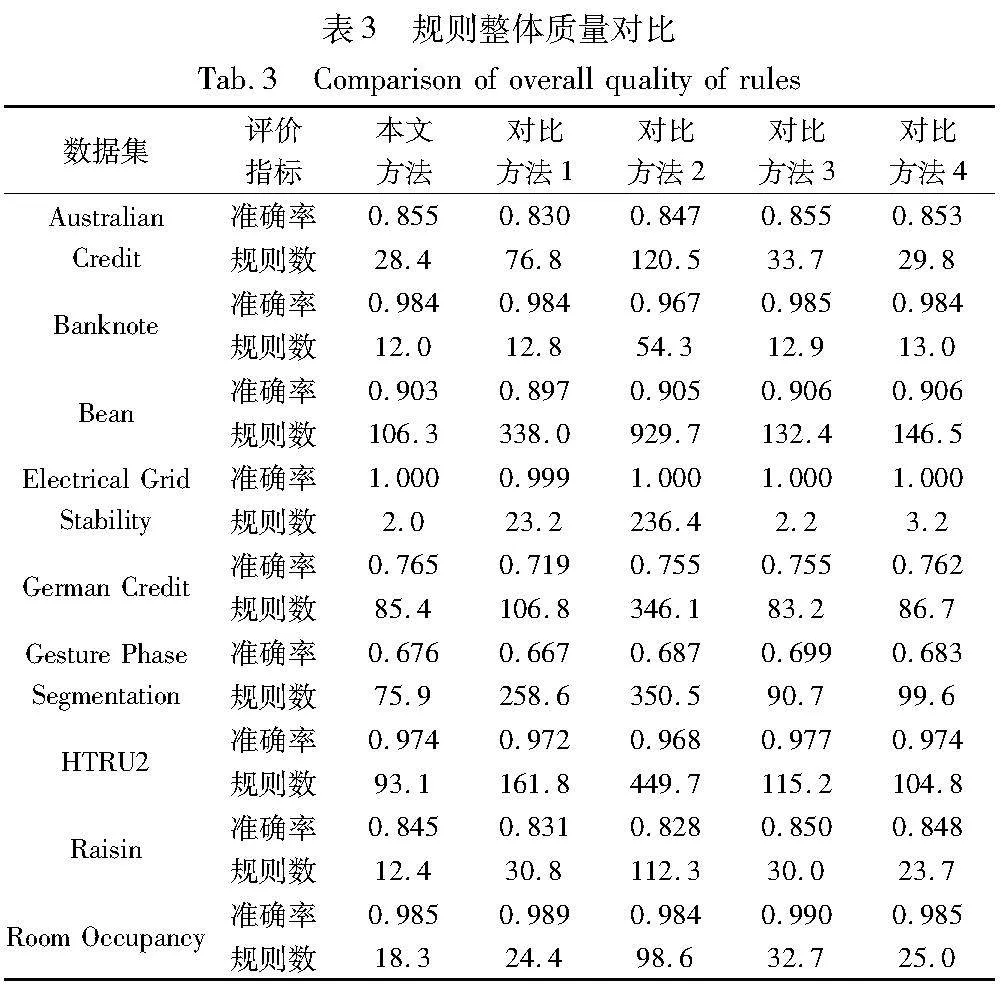
表3展示了本文方法与对比方法生成的规则集的实验效果，给出了规则集的预测准确率和规则的数量，其中前者指示规则集的预测性能，而后者指示规则集的可解释性，期望规则集在这两方面做到均衡。

分析表3的结果可知，本文方法在两个指标上基本都优于对比方法1、2。本文方法与对比方法1、2都是以规则得分筛选规则并对规则集进行整体搜索的，但本文方法通过聚类消除冗余规则的思路使获得的结果规则集更具优势。

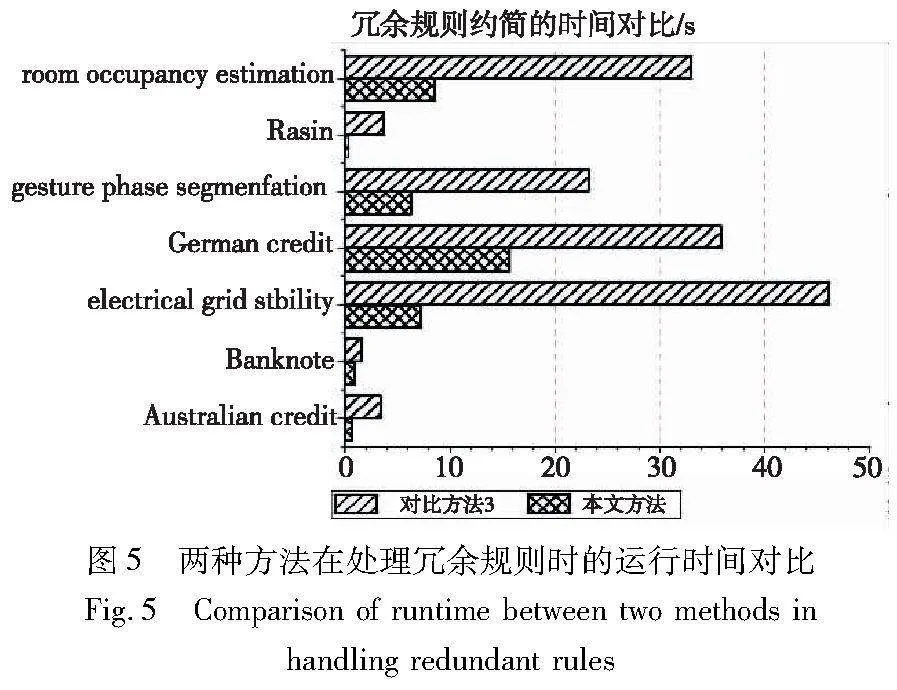
观察本文方法与对比方法3、4，三种方法生成的规则集的效果很接近。其中，在规则数量方面，本文方法得到的结果规则集在数量上更少，明显优于另外两种方法；在预测准确率方面，本文方法的效果在4个数据集上低于另外两种方法，但这种差距不超过0.5%，而在其他数据集上均能持平或者效果更佳。此外，本文方法的可用性更好，图5给出了本文方法与对比方法3在7个数据集上处理规则集时所用的时间，对比方法4的处理时间过长，没有参与对比。

由图5可知，本文方法处理规则的速度更快，在规模较大的数据集时表现得更明显。综合而言，相较于四种对比方法，本文方法处理得到的规则集兼具准确性与可解释性，同时能更高效地处理冗余规则。

3.2.2 相似规则发现对结果的影响

这一节主要讨论本节方法中，规则聚类方法对整体实验效果的影响。需要补充说明的是，在不同数据集上最终得到的最佳聚类数K是不同的，需要根据实验结果具体分析。

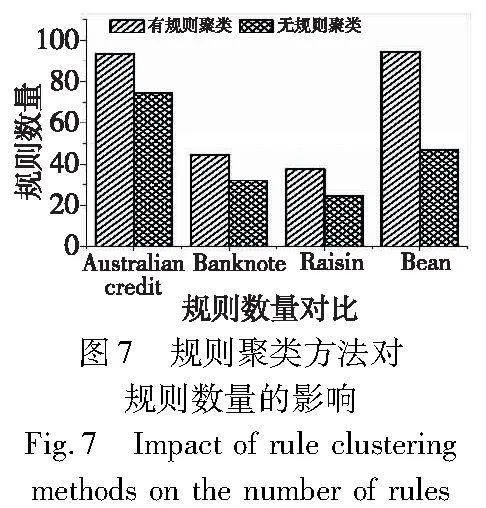
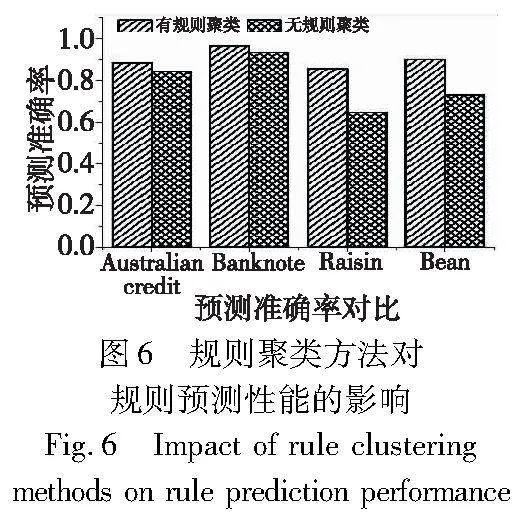
采取相似规则发现的初衷是将每类相似的规则聚为一个子规则集，在每个子规则集中进行规则的全局搜索，期望提高搜索的效率。本节主要在Australian credit等四数据集上对比应用规则聚类算法前后规则集的质量。图6和7展示了规则的特征数量、规则集的预测性能和规则数量的对比。

观察图6和7的对比结果可知，应用了规则聚类算法后，规则集数量有所增加，但有效保障了规则集的预测准确率。此外，应用了规则聚类算法后，对每一个子规则集搜索更快捷，提高了方法的整体效率。

4 结束语

本文主要研究了面向规则约简的随机森林模型的生成策略，提出了冗余规则约简的方法。经过实验验证，这种基于规则的可解释方法可以代替经典的机器学习，针对决策问题给出准确而可理解的答案。

具体而言，本文的创造性工作主要如下：

a）以黑盒模型与原始数据集交互形成的数据集为训练数据，提出了面向规则约简的随机森林模型的生成策略。在训练的过程中以迭代的方式生成随机森林模型，并根据模型的评价，利用强化学习的思想对模型的关键参数进行相应的调整。为了适当地评价随机森林模型，提出了一种随机森林模型的评价公式，简化了评价的过程。

b）对于随机森林模型中提取的初始规则集，本文提出了一种基于规则聚类的冗余规则约简方法。该方法分为两步，首先应用K-medoids规则聚类算法，将规模较大的规则集分散到了小的子规则集中。其次，在每个子规则集中应用了一种快速搜索的算法，提取了其中最具代表性的规则，去除了大量的冗余规则。最终可以获取一个精简的、预测性能较好的规则集，公开数据集上的实验表明，本文方法处理得到的规则集具有可靠的性能与较好的可解释性。

上述两个阶段前后呼应，相辅相成，具有明确的逻辑顺序，覆盖了规则学习中模仿黑盒模型、规则生成与规则约简这一流程。当然，本文的研究还有几个方面可以继续深入：首先，本文方法的第二阶段采取了规则聚类的方法，其中聚类后的规则聚簇可以根据问题场景发现其具体的含义。其次，可以进一步对if-then形式的规则进行抽象，提取更高层次的知识。

参考文献：

［1］Wachter S， Mittelstadt B， Floridi L. Transparent， explainable， and accountable AI for robotics［J/OL］. Science Robotics， 2017，2（6）. https：//www.science.org/doi/10.1126/scirobotics.aan6080.

［2］Angelov P P， Soares E A， Jiang R，et al. Explainable artificial intel-ligence： an analytical review［J/OL］. Wiley Interdisciplinary Reviews： Data Mining and Knowledge Discovery， 2021，11（5）. https：//doi.org/10.1002/widm.1424.

［3］Adadi A， Berrada M. Peeking inside the black-box： a survey on explainable artificial intelligence（XAI）［J］. IEEE Access， 2018，6： 52138-52160.

［4］张昊. 面向大电网潮流断面功率调整的知识挖掘方法研究［D］. 哈尔滨： 哈尔滨工业大学， 2021. （Zhang Hao. Research on know-ledge mining method for power flow section power adjustment of large power grid［D］. Harbin： Harbin Institute of Technology， 2021.）

［5］吕司涛. 基于规则的黑盒模型可解释方法研究［D］. 哈尔滨： 哈尔滨工业大学， 2022. （Lyu Sitao. Research on interpretation me-thods of rule-based black-box models［D］. Harbin： Harbin Institute of Technology， 2022.）

［6］Adnan M N， Islam M Z. ForEx++： a new framework for knowledge discovery from decision forests［J/OL］. Australasian Journal of Information Systems， 2017， 21. https：//doi.org/10.3127/ajis.v21i0.1539.

［7］Mashayekhi M， Gras R. Rule extraction from random forest： the RF+HC methods［C］//Proc of the 28th Canadian Conference on Artificial Intelligence. Berlin： Springer， 2019： 223-237.

［8］Dong Luan， Ye Xin， Yang Guangfei. Two-stage rule extraction me-thod based on tree ensemble model for interpretable loan evaluation［J］. Information Sciences， 2021，573（9）： 46-64.

［9］Qiu Mingming， Najm E， Sharrock R， et al. PBRE： a rule extraction method from trained neural networks designed for smart home services［C］//Proc of International Conference on Database and Expert Systems Applications. Cham： Springer， 2022： 158-173.

［10］Frank A. UCI machine learning repository［EB/OL］. （2023-10-16）. http：//archive.ics.uci.edu/ml.

［11］Pedregosa F， Varoquaux G， Gramfort A， et al. Scikit-learn： machine learning in Python［J］. Journal of Machine Learning Research， 2011，12： 2825-2830.

［12］Mollas I， Bassiliades N， Vlahavas I， et al. LionForests： local interpretation of random forests［EB/OL］. （2020-07-23）. https：//arxiv.org/abs/1911.08780.

［13］Kumar A， Vembu S， Menon A K， et al. Beam search algorithms for multilabel learning［J］. Machine Learning， 2013，92（1）： 65-89.