基于GPU的zk-SNARK中多标量乘法的并行计算方法
2024-07-31王锋柴志雷花鹏程丁冬王宁

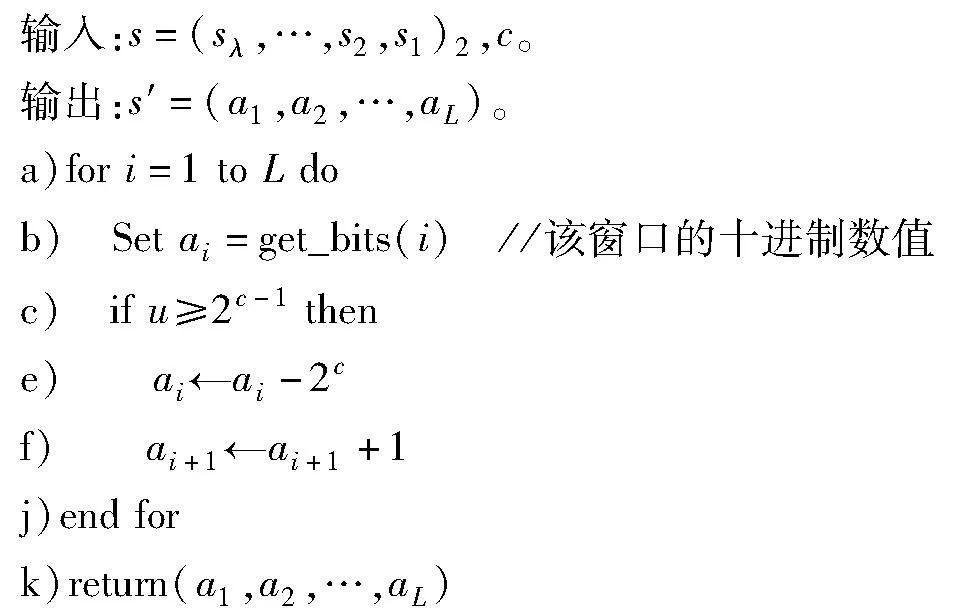
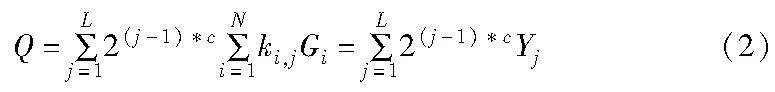



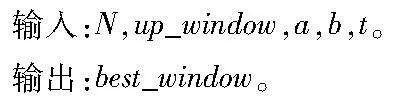



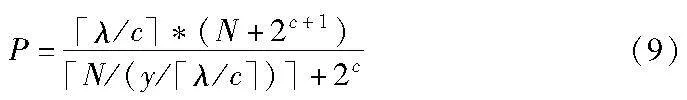




摘 要:针对zk-SNARK(zero-knowledge succinct non-interactive argument of knowledge)中计算最为耗时的多标量乘法(multi-scalar multiplication,MSM),提出了一种基于GPU的MSM并行计算方案。首先,对MSM进行细粒度任务分解,提升算法本身的计算并行性,以充分利用GPU的大规模并行计算能力。采用共享内存对同一窗口下的子MSM并行规约减少了数据传输开销。其次,提出了一种基于底层计算模块线程级任务负载搜索最佳标量窗口的窗口划分方法,以最小化MSM子任务的计算开销。最后,对标量形式转换所用数据存储结构进行优化,并通过数据重叠传输和通信时间隐藏,解决了大规模标量形式转换过程的时延问题。该MSM并行计算方法基于CUDA在NVIDIA GPU上进行了实现,并构建了完整的零知识证明异构计算系统。实验结果表明:所提出的方法相比目前业界最优的cuZK的MSM计算模块获得了1.38倍的加速比。基于所改进MSM的整体系统比业界流行的Bellman提升了186倍,同时比业界最优的异构版本Bellperson提升了1.96倍,验证了方法的有效性。
关键词:简洁非交互式零知识证明; 多标量乘法; CUDA; 异构计算系统; 并行计算
中图分类号:TP311;TP309.7 文献标志码:A
文章编号:1001-3695(2024)06-019-1735-08
doi:10.19734/j.issn.1001-3695.2023.11.0498
Parallel computation method for multi-scalar multiplication inzk-SNARK based on GPU
Abstract:In the context of zk-SNARK, MSM emerges as the predominant computational bottleneck. To address this problem, this paper proposed a GPU-based parallel MSM computation approach. Firstly, the method performed fine-grained task decomposition of MSM to enhance algorithmic computational parallelism, fully leveraging the extensive parallel computing capabilities of GPU. Additionally, it reduced data transfer overhead by employing shared memory for the parallel reduction of sub-MSM tasks within the same window. Secondly, the method introduced a window partitioning strategy based on thread-level task load analysis of the underlying computational modules to search for the optimal scalar window, thereby minimizing the computational cost of MSM subtasks. Lastly, the method optimized the data storage structure used for scalar form transformation and mitigated latency issues in the large-scale scalar form conversion process by employing data overlap transfer and hidden communication time. This paper implemented the MSM parallel computation method based on CUDA on NVIDIA GPU and established a comprehensive zero-knowledge proof heterogeneous computing system. Experimental results show that the proposed method achieves an acceleration ratio of 1.38 times compared to the current state-of-the-art MSM calculation module of cuZK. The overall system based on the improved MSM is 186 times better than the industry-popular Bellman, and 1.96 times better than cutting edge heterogeneous version Bellperson, validating the effectiveness of the approach.
Key words:zk-SNARK; multi-scalar multiplication; CUDA; heterogeneous computing system; parallel computing
0 引言
零知识证明(zero knowledge proof,ZKP)作为一种密码学协议,可以在不泄露任何隐私信息的情况下证明数据的正确性[1],具有广阔的应用前景。但如果要在实际系统中应用ZKP,还需要大幅度提升其“证明生成”和“证明验证”的效率。在证明验证效率的提升方面,简洁非交互式零知识证明(zero-knowledge succinct non-interactive arguments of knowledge, zk-SNARK)在保持高度安全性和可靠性的同时做到了证明验证的简洁性,可以在通信成本高或验证者计算能力较弱的情况下实现高效证明[2,3],因此已被广泛应用于数字货币[4]、区块链[5,6]、金融[7]、隐私保护[8]等多个领域。然而,尽管zk-SNARK提升了证明验证的效率,但其证明生成仍十分复杂和耗时。在实际应用场景中,证明生成也会被频繁调用,过长的证明生成时间严重阻碍了zk-SNARK的广泛应用。
zk-SNARK的证明生成过程主要用到数论变换(number theoretic transformation,NTT)和多标量乘法(multi-scalar multiplication,MSM)。其中MSM是zk-SNARK证明生成过程中最主要的计算瓶颈[9,10],例如:在著名的zk-SNARK开源库Bellman中MSM的执行时间占据了整个证明生成总时间的90%以上。
基于上述原因,如何有效缩短以MSM为主的zk-SNARK证明生成过程成为研究热点。除了算法方面的改进,利用硬件进行加速是其中的重要方法之一。PipeZK[11]提出了一种以ASIC为目标硬件用于加速zk-SNARK的高效流水线结构,将其中最为耗时的两个子系统NTT和MSM设计为专用硬件加速器,同时与CPU进行异构设计来实现端到端系统。该方案虽然可以显著提高零知识证明的计算效率,但其通用性相对较差而且不利于更新。Wu等人[12]提出了一种用于加速椭圆曲线上点乘运算的高性能硬件架构,能够同时适用于Xilinx和Intel FPGA平台,并基于点乘模块设计了一个高效的MSM硬件加速器,但相较于Bellperson中基于GPU的异构加速方法,在计算效率上仍有数倍的差距。Yang等人[13]通过在GPU上加速zk-SNARK中耗时的计算内核实现零知识证明,利用GPU全局内存和共享内存中的数据布局和洗牌方法来维护数据空间的一致性,从而加速NTT/INTT计算模块,其计算效率相较于Bellperson有了明显的提高,但其并没有针对计算时延更高的MSM模块给出更有效的加速方案。在上述的各种硬件加速方法中,最重要的工作是如何充分挖掘算法本身的并行性,这样才能更好地发挥并行硬件的潜力。此外,在并行计算时,多个计算节点需要进行通信与同步,如何减少节点间通信对整体计算性能的影响也是需要重点解决的问题。而在上述硬件加速相关工作中,针对上述两点,如何与相应的硬件结构相适配方面的研究尚不够深入。
MSM作为一种计算密集型任务具有高度的并行性,需充分考虑硬件的并行计算能力以最大程度发挥MSM的计算特性[14]。FPGA受限于板上资源无法完全发挥其潜在的并行计算能力,ASIC的定制化特点难以应对MSM数据位宽的灵活变换。而CUDA作为一种单指令多线程的编程模型,其高并行性和灵活性的特点为满足MSM的计算特性提供了理想选择[15]。
本文针对zk-SNARK中计算最为耗时的多标量乘法,提出一套高效的基于GPU的MSM并行加速方案。主要工作如下:
a)对MSM进行细粒度任务分解,提升算法本身的计算并行性,以充分利用GPU的大规模并行计算能力。采用共享内存对同一窗口下的子MSM并行归约,减少了数据传输开销。
b)提出了一种基于底层计算模块线程级任务负载搜索最佳标量窗口的窗口划分方法,以最小化MSM子任务的计算开销。
c)对标量形式转换所用数据存储结构进行优化,并通过数据重叠传输和通信时间隐藏,解决了大规模标量形式转换过程的时延问题。
此外,基于CUDA在NVIDIA GPU上实现了该MSM并行计算方法,并构建了完整的零知识证明异构计算系统。相比目前业界最优的cuZK的MSM计算模块,获得了1.38倍的加速比,基于所改进MSM的整体系统比业界流行的Bellman提升了186倍,同时比业界最优的异构版本Bellperson提升了1.96倍。
1 预备知识
1.1 zk-SNARK协议
零知识证明作为现代密码学中的基本原语之一,它允许证明者向验证者证明某个语句的真实性,而无须透露任何关于证明的信息[16]。传统的交互式零知识证明(interactive zero-knowledge proofs,IZKP)需要证明者和验证者之间进行多轮交互,证明者需要多次响应验证者的挑战才能最终完成证明过程,性能较低,难以应用于大规模网络中[17]。为了解决该问题,zk-SNARK协议应运而生,zk-SNARK作为一种简洁非交互式的零知识证明协议,在其证明过程中证明者只需要进行一次计算就可以生成证明,验证者根据生成的证明自行验证,避免了双方的多次通信[18,19]。Groth16作为应用最为广泛的zk-SNARK协议,在椭圆曲线密码学的基础上构建而成,证明过程主要包括设置参数(setup)、生成证明(prove)、验证(verify)三个阶段[20]。
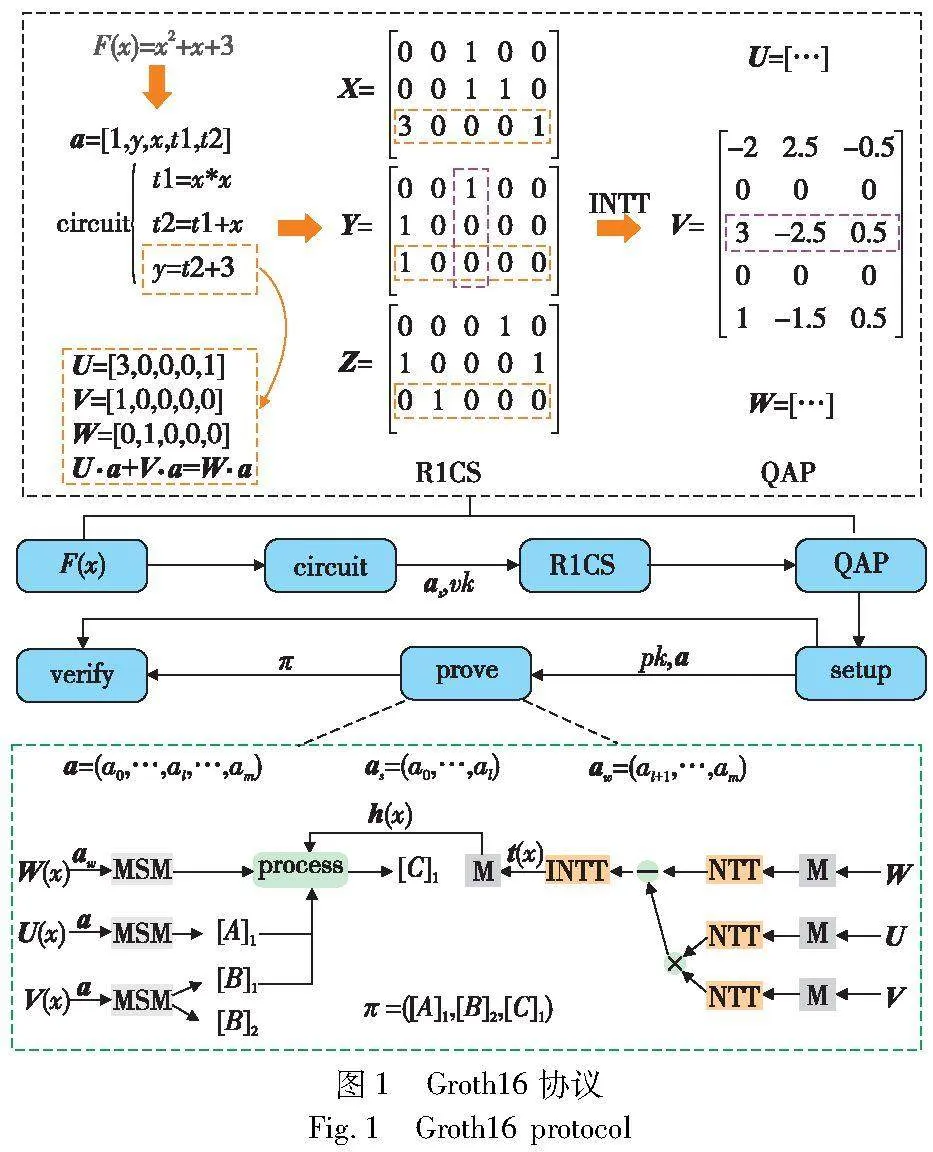
在Groth16协议中对于一个问题多项式F(x),证明者要向验证者证明其知道一组完整的解向量a,同时不对验证者泄露任何关于解向量的信息。该协议是基于QAP(quadratic arithmetic program)进行证明的生成和验证,所以在生成证明之前需要先将原始的问题多项式转换为QAP形式,转换过程如图1上半部分所示,先根据解向量将多项式转换为一组二元算数电路(circuit),然后根据电路生成R1CS(rank-1 constraint system),最后通过逆傅里叶变换得到QAP的相关多项式系数矩阵,如图中的U、V、W所示。参数设置阶段由可信的第三方随机生成一些公开参数,同时选取一个私有的随机变量(挑战点),将其带入到QAP多项式中来生成证明密钥(pk)和验证密钥(vk)并公开。任何人都可以使用证明密钥和验证密钥来生成和验证证明,但只有使用解向量的非公开部分(aw)生成的证明才能通过验证。生成证明阶段是计算最为复杂的阶段,其计算步骤主要包括利用QAP和已知多项式t(x)进行三次NTT和一次INTT求得h(x)以及根据证明密钥和解向量通过MSM生成证明两个过程,如图1的下半部分所示。验证阶段则是根据生成的证明(π)和解向量的公开部分(as)以及验证密钥(vk),通过双线性配对来进行验证。
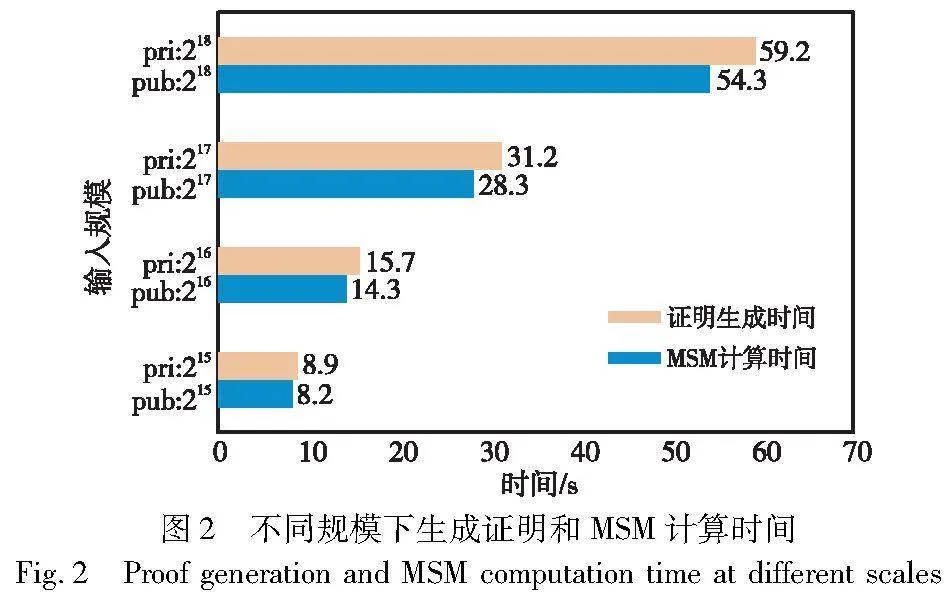
为了提高安全性,QAP的规模通常会达到数百万,这也导致了在prove阶段要花费大量的时间来生成证明。图2展示了在AMD Ryzen 9 5900X处理器上,不同规模下证明生成过程总的运算时间和MSM计算时间的对比情况。从图中可以看出MSM的计算占据了证明生成过程总时间的绝大部分,zk-SNARK证明系统的整体性能在很大程度上取决于MSM的计算效率。因此,通过提高MSM的计算效率可以明显缩减生成证明的时间,使零知识证明系统在应用中更加高效。
1.2 多标量乘法(MSM)
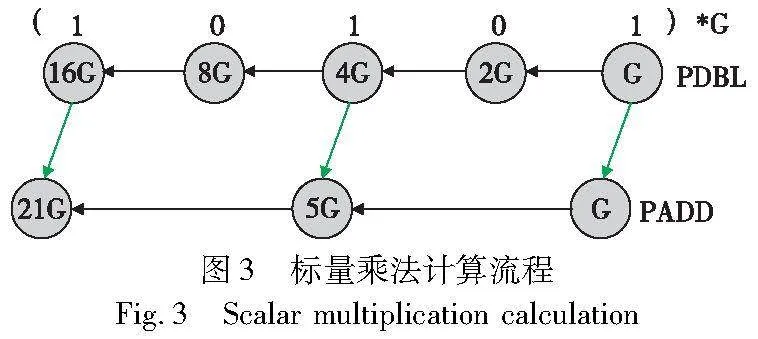
多标量乘法是指对于给定的椭圆曲线上的点集合和标量集合,计算这些点与对应标量相乘再相加的运算过程。其数学定义如式(1)所示。
从算法中可以看出,标量的位宽越大,PDBL和PADD总的计算次数越多,PMULT的计算量也越大。以Filecoin为例,MSM的规模为数百万,标量位宽为256 bit。如果计算出每一个PMULT的结果,然后再通过PADD相加来得到MSM的结果,将会产生巨大的计算时延。
1.3 用于MSM的Pippenger算法
Pippenger算法也叫桶方法,是一种用于计算大规模MSM的高效算法。其核心思想是通过对标量的划分,将一个高位宽的MSM分解成多个低位宽的MSM,以减少总体的PMUL计算,从而提高计算效率[21]。Pippenger算法的计算细节主要由三个步骤组成:
a)将一个原始的MSM分解成多个较小的子任务。选定一个窗口c(c<λ),将每一个λ bit的标量ki划分成L=「λ/c个部分,那么一个λ bit的MSM就被分解成了L个c bit的MSM(如果是非等量划分,最高位的部分进行补零),Yj表示第j个c bit的MSM,ki,j表示第i个标量的第j部分,其中i∈[1,N],j∈[1,L]。式(1)也就等价于
b)计算出每一个子MSM的结果。初始化2c-1个空桶,然后将Gi累加到与其系数ki,j相对应的桶中。那么Yj的计算公式也就变为
其中:[Bj]u表示第j个c bit的MSM的第u个桶中所有点累加的结果,通过霍纳法则可以快速计算出Yj。
2 本文方法ParMSM
Pippenger算法对于子任务的划分是将一个规模为N的λ bit的MSM划分为L=「λ/c个规模同样为N的c bit的MSM,如图4的第一级子任务划分所示。以需要计算的椭圆曲线点加(PADD)和点加倍(PDBL)的数量作为计算成本来进行量化分析。每一个子任务的计算成本为
W=(N+2c+1)×PADD(4)
对于一个完整的MSM串行执行的总的计算成本为
Tot_ser=W×L+((L-1)*2c)×PDBL+L×PADD(5)
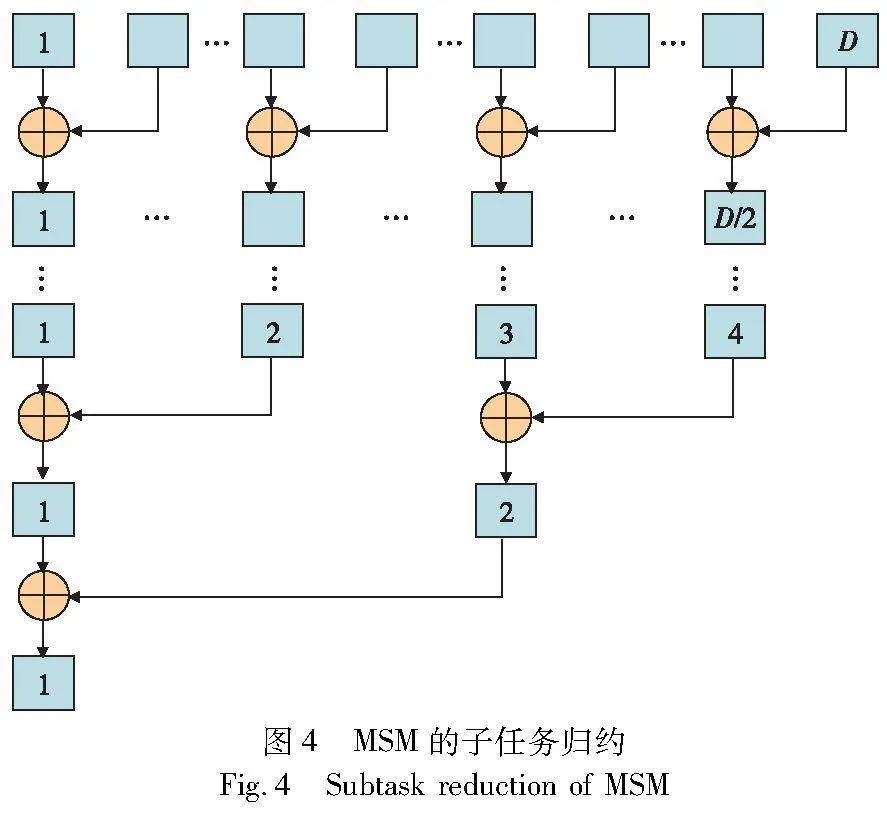
该方法最多可以将MSM分解成L个子任务,难以满足更高水平的并行计算要求。因此,有必要对MSM进行更细粒度的任务分解。这里在原子任务划分方式的基础上将每一个规模为N的c bit的MSM继续拆分成D=「N/M个的规模为M(M<N)的c bit的MSM,相比于原来的L个子任务变成了L*D个子任务,如图4的第二级子任务划分所示,这些子MSM之间没有任何数据依赖,可以并行执行。在应用中可以根据实际的并行处理能力以及MSM的规模来选择最佳的窗口大小,使子MSM的计算成本最低。
在第二级的子任务划分中对每一个规模为N的c bit的MSM进行细粒度分解得到的D个规模为M的c bit的MSM,它们位于同一窗口下可以直接进行合并。对此,本文设计了一种用于同一窗口下子MSM结果规约的并行算法。具体的实现方法如图5所示。首先,将位于同一窗口下的D个子MSM分成「D/2组,其中每一组两个元素,然后将每一组内的两个元素相加,由于每组之间的元素没有任何数据依赖,所以这「D/2组之间的计算可以并行执行。经过第一轮的合并之后由原来的D个元素缩减为「D/2个元素,对这「D/2个元素按照同样的方法进行并行合并,经过逐级合并后最终只有一个元素,而该元素就是位于同一窗口下的子MSM相加后的结果。该方法将原来的D-1次点加运算缩减为log2(D)次,对于每一个窗口下的子MSM都采用该方法进行并行归约,可以在很大的程度上节省计算开销。
假设y为子任务的数量,即y=L*D,那么本文所提出的并行方法中每一个子任务的计算成本为
W=(「N/L+2c)×PADD(6)
同一窗口下子任务归约的计算成本为
W_red=log2(D)×PADD(7)
一个完整的MSM并行执行的计算成本为
Tot=W+W_red+((L-1)*2c)×PDBL(8)
相比串行计算的理论加速比约为
从式(9)可以看出,当N为百万数量级时该并行算法相比于串行计算加速效果非常显著,并且随着并行处理能力的增强该并行算法的效率也随之提高。
3 基于GPU的ParMSM实现
3.1 ParMSM的计算架构
在第二级的子任务划分中位于同一窗口下的D个规模为M的c bit的MSM由一个或多个线程块处理,线程块内的每一个线程对应一个子MSM。保证了同一线程块内的线程所对应的子MSM都位于同一窗口下,而线程块内具有共享内存可以用于同一个线程块内的线程之间共享数据。相较于全局内存,共享内存的访问速度更快,通信延迟更低,在并行计算任务中发挥着重要作用,特别是对于需要线程之间进行数据共享和协作的算法。因此,本文设计了一种利用线程块内共享内存来实现子MSM的并行归约的方法。具体的实现细节如图6所示。
假设一个线程块内有8个线程,其中每一个线程所计算的子MSM都位于同一窗口。首先,定义一个大小为8的共享内存数组,每一个线程都将其计算的子MSM结果存放在与其块内线程号对应的共享内存数组中,如图6中的A0~A7分别表示0~7号线程所计算的结果。随后,同时启动0~3号线程进行第一次合并,每一个线程都将其块内线程号对应的数组下标中的值和距离步长为4的另一个值相加,并将结果更新到0~3号线程对应的共享内存数组中,如图6中的step1所示,其中B0~B3为更新后的结果。step1结束后将步长减半,启动0~2号线程进行第二次合并,其中C0和C1为更新后的结果。直到第三次合并步长变为1,启动0号线程计算出的结果D0就是整个线程块内归约后的结果。相比于串行归约在计算效率上得到了极大的提升,其次在设备端进行块内归约后使得需要回传到主机端的数据量减少,进一步降低通信开销。在实际应用中可以根据GPU的算力大小以及MSM的规模来选择最佳的窗口大小,进而完成子任务的合理划分,具体的窗口查找策略见3.2节。
3.2 最佳窗口查找策略
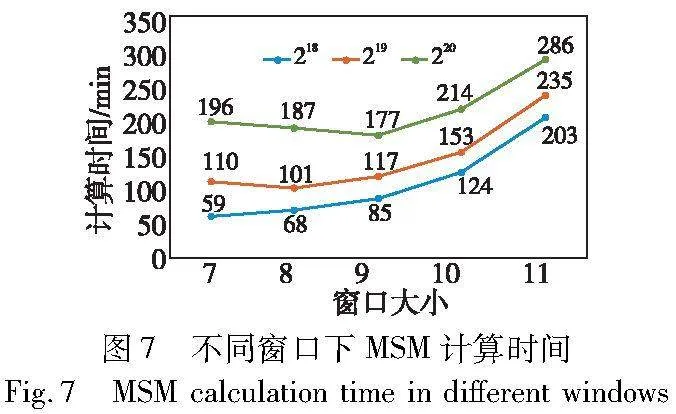
不同的标量窗口会导致子任务的工作负载不同,从图7可以看出,当MSM的规模为220、窗口大小为9时计算时间为177 ms,然而当窗口调整为11其计算时间增大到了286 ms,相比于最佳的窗口在计算时间上有了0.62倍的差距。因此,在同一规模下不同的窗口对于计算时间的影响是十分显著的,那么如何在总的线程数量和MSM计算规模一定的情况下找到最佳的窗口就成为了一个关键的问题。
椭圆曲线密码学中,常用的坐标系有仿射坐标系和投射坐标系。仿射坐标系下每个点只需要存储两个数据,内存占用更小,一般用于主机端和设备端之间的数据传输,投射坐标在进行点加运算时会避免乘法逆元操作,相比于仿射坐标具有更高的计算效率。在MSM的计算过程中主要涉及了相同坐标系的点加(add)和混合坐标系的点加(add_mix),在以往的窗口划分中都是以点加的数量来衡量工作负载,进而确定最佳的窗口。点加中最主要的计算是大整数的蒙哥马利模乘,在具体的计算中add的计算量明显高于add_mix,以目前最常用的也是计算复杂度相对最低的点加公式add-2007-bl为例,add使用了16蒙哥马利模乘,add_mix使用了11次蒙哥马利模乘,所以通过点加的数量来衡量工作负载的大小并不合理。
本文根据更为底层的蒙哥马利模乘计算模块进行线程任务负载分析来寻找最佳的标量窗口。假设a、b分别表示add_mix和add中使用蒙哥马利模乘的次数,t为线程数量,up_window表示窗口大小的上限值,cost表示窗口大小为window_size时每一个线程执行的计算任务需要使用的蒙哥马利模乘的次数,那么最佳窗口查找算法如算法1所示。该算法的核心思想是:逐一遍历各个窗口,计算出在该窗口划分下的每一个线程所需要计算的蒙哥马利模乘的次数,并与现有的最小值对比,从而确定最优的窗口大小。
算法1 最佳窗口查找算法
3.3 标量形式转换的并行计算
在Pippenger算法的计算过程中提前将标量重新编码为有符号的二进制形式,可以将桶的数量减半,降低桶间归约的时间开销。对此,本文设计了一种标量的形式转换算法,可以直接将标量的每一个c bit的窗口值固定在[-2c-1,2c-1-1],从而使Pippenger算法第二步的计算量减半,算法细节如算法2所示,从最低位的窗口开始遍历,如果当前窗口的十进制数值大于2c-1就将其减去2c,然后将下一个窗口的值加1,否则不变。
算法2 标量形式转换
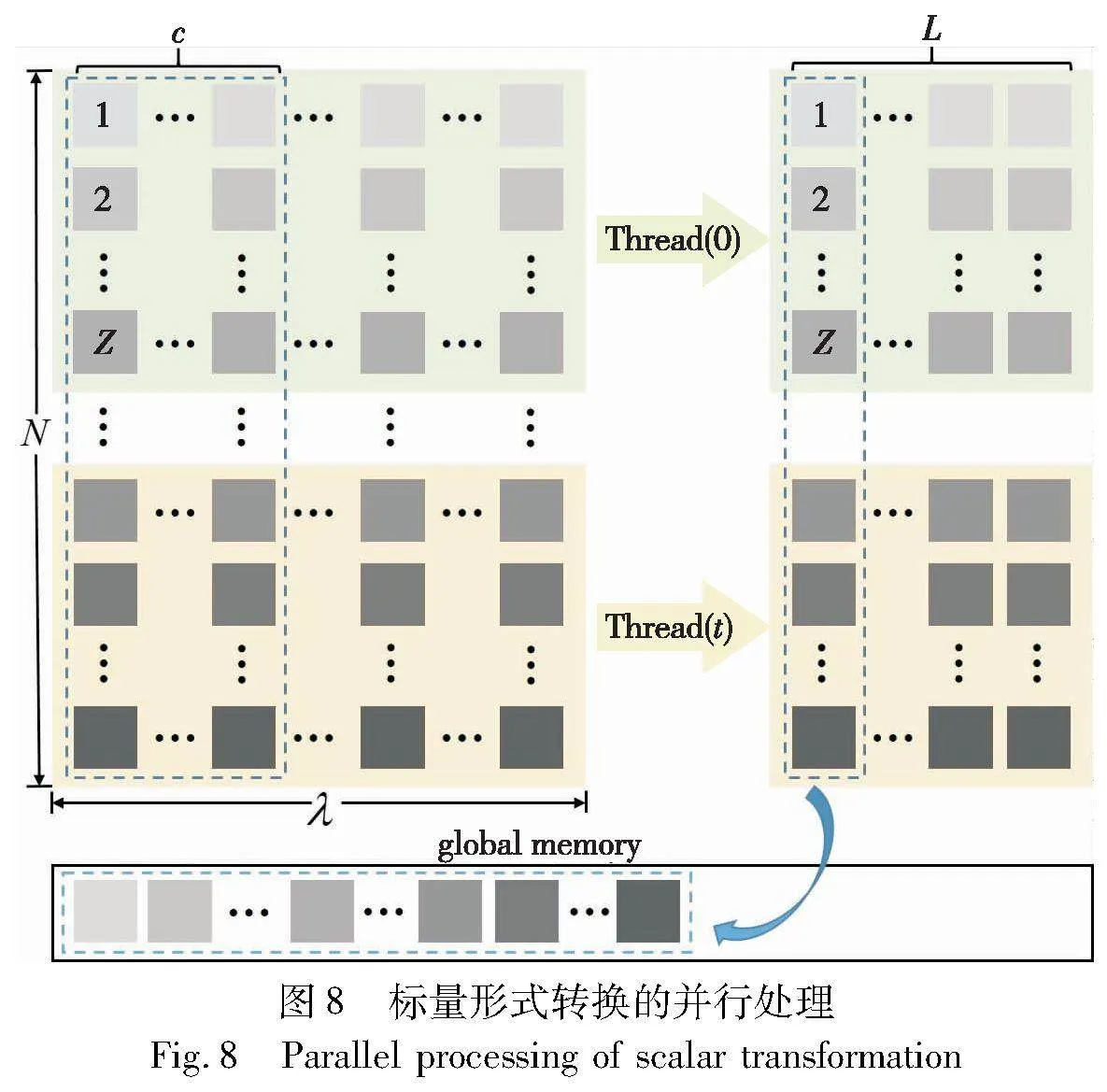
对于数百万规模的MSM,如果在主机端进行数据的处理然后再传输到设备端将会产生巨大的计算时延。GPU作为一种支持多线程并发执行的计算平台,相比于CPU具有支持大规模并行的特征[23]。利用GPU的这种特性来对大规模的标量进行并行计算可以极大地节省计算时间。具体的处理方法如图8所示。
首先,将N个标量平均分配给所有的线程,假设一共有t个线程,那么每一个线程处理规模为Z=N/t标量形式转换的计算,经过转换后原本λ bit的标量变成了L=「λ/c个int类型的数据表示。其次,由于每一个线程对于数据的访问都是按列进行的,如果按行去存储会降低缓存的命中率,从而增加数据访问的延迟。因此,在数据存储方面,为了能够实现连续性访问,选择将每个标量同一窗口下的数据依次存放在一起,然后放在设备端全局内存中作为MSM计算核心的输入,无须拷贝到主机端,避免了数据传输的时间开销。虽然,存储上相比于按行存储会增加一部分的时间开销,但可以使在椭圆曲线上的点集从主机端传输到设备端的同时,无缝地进行标量形式转换的并行计算,有效解决了存储过程中寻址所占用的时间开销问题。
3.4 基于CPU-GPU异构的MSM整体设计
3.4.1 CPU-GPU异构架构
CPU-GPU异构架构是一种使用CPU和GPU协同工作的计算架构,CPU和GPU具有各自的存储空间,通过PCI-e总线进行数据传输。该架构允许CPU和GPU在处理不同类型的任务时发挥各自的优势,从而提高整体的性能[24,25]。CUDA作为一种在异构计算环境中实现并行计算的编程框架,它基于NVIDIA的GPU架构提供了专门针对GPU进行并行计算的编程接口和工具集[26]。其异构架构如图9所示。
3.4.2 整体优化设计
在整体的异构设计中,GPU上的计算模块主要有标量的形式转换内核和MSM计算内核,其中标量形式转换数据依赖于标量集,MSM计算数据依赖于点集和经过形式转换后的标量。CUDA流作为一种并行计算模型,它是在CUDA编程模型中实现主机端和设备端异步操作的机制。利用CUDA流的异步机制,可以在GPU执行标量形式转换内核的同时,将点集从主机端传到设备端。图10展示了ParMSM与Bellperson的MSM计算方案对比。相比于Bellperson的单个CUDA 流模式,本文将标量集的传输和标量形式转换内核的启动依次添加到stream1,点集的传输和MSM计算内核的启动以及结果的回传依次添加到stream2,通过重叠主机端到设备端的数据传输和GPU计算提高了系统工作效率。
对于从设备端回传到主机端的结果,需要进一步计算才能得到最终的结果,由于这部分的数据规模和计算量比较小,同时计算过程中数据的依赖性比较强,所以将该部分的计算放到CPU上。计算细节如算法3所示,从最高位的窗口开始,先将其对应的线程块结果累加到初始零点,随后将结果乘以2c继续累加下一个窗口下的线程块返回值,直到最低位。其中T是回传到主机端的所有线程块进行归约后的结果,num_window表示一个λ bit的标量被c bit的窗口切分的数量。
算法3 主机端归约算法
4 系统实现与结果评估
4.1 实验平台和环境
本文的实验是在一台带有3.7 GHz的AMD Ryzen 9 5900X处理器(每个处理器有12个核心),12 GB显存的RTX3060显卡与128 GB DRAM的服务器上进行的,运行Ubuntu 20.04.5和 CUDA 11.8。
4.2 系统实现
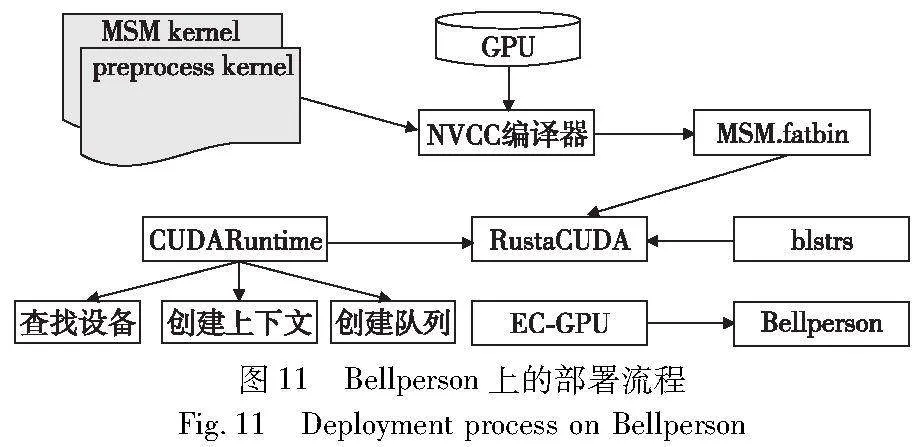
Bellperson 是一个使用Rust编程语言实现的高效的零知识证明库,可用于构建和验证零知识证明,已经应用在一个著名的去中心化加密货币网络Filecoin中。本文基于CUDA C平台实现了更加高效的MSM计算模块ParMSM,并将其集成在Bellperson中,从而构建一个完整的零知识证明系统,代码开源在https://github.com/20171759/msm-stream.git。具体的实现过程如图11所示。
在目前最新版本的Bellperson中,其最主要的计算被封装在了EC-GPU库中。在EC-GPU中使用的是Rust封装的CUDA API——Rust-GPU-tool,由于其对CUDA的支持比较有限,并不支持CUDA流的操作,这里引入了另一个对CUDA支持更友好的库RustaCUDA。在数据传输过程中,由于Rust封装的CUDA API只支持最基本的数据类型,并不支持Affine、Projective,Scalar等类型的数据,在EC-GPU中是将所有的数据全部切分成u8的类型,用数组的形式进行存储,然后再通过PCI-e进行数据传输。实际应用中数据位宽高达384 bit,同时数据规模比较大且数据结构比较复杂,导致传输效率并不理想。因此,为了提高数据的传输效率,在RustaCUDA库中引入blstrs库,在底层添加了所需要的数据结构,避免了因数据切分而造成的时间浪费。
对于设备端源码的调用,本文选择在主机端使用NVCC编译器将CUDA源代码编译成.fatbin文件,通过调用RustaCUDA库进行设备查找,创建上下文,加载二进制文件。然后,创建所需要的CUDA流,将需要启动的任务放到与之对应的流中,最后为了保证CUDA流中操作的正确执行顺序和结果,使用RustaCUDA库中的synchronize()函数来同步流。
4.3 实验评估
为了验证本文方案的有效性,选择了目前最为主流的Groth16协议的CPU实现版本Bellman和当前应用最为广泛、性能最优的CPU-GPU异构实现版本Bellperson作为主要的对照实验。在同类工作对比中选择了目前最新的cuZK[27]作为对照来评估ParMSM的性能。同时为了验证ParMSM的通用性,选择与不同ZKP系统中的MSM进行实验对比分析。
在实验数据规模的选择上,以Filecion应用为例,其在实际应用中数据规模大多数集中在220~221,同时随着安全性能的提升,数据规模也将变得更高。因此,本文的实验数据规模选择到223以上。这样可以确保本文的方案能够与业界最为先进的解决方案进行比较,并且充分验证其有效性。
4.3.1 同类工作对比
文献[27]提出了一种新的MSM并行计算方法,基于CSR稀疏矩阵来存储每一个子MSM,利用并行稀疏矩阵转置算法对其进行并行转置来保证数据的连续,之后将其系数相同的点都累加到对应的桶中,利用霍纳法则将所有桶中的点进行加权求和。最后,基于C语言实现了一个完整的零知识证明库cuZK。
与cuZK将MSM的计算全部迁移到GPU上不同,本文重点在于研究如何充分利用CPU和GPU的协同计算,根据任务的不同计算特性,灵活地将任务分配给最适配的处理器,以获得最佳性能。此外,一方面鉴于Rust语言具有出色的内存安全性和并发安全性,能够防范多种安全漏洞和内存错误,从而提高系统的稳定性,本文基于Rust语言实现该CPU-GPU异构加速模块。另一方面,本文是将异构加速模块集成到了当前应用最为广泛的零知识证明库Bellperson中,以适应更高的应用前景。
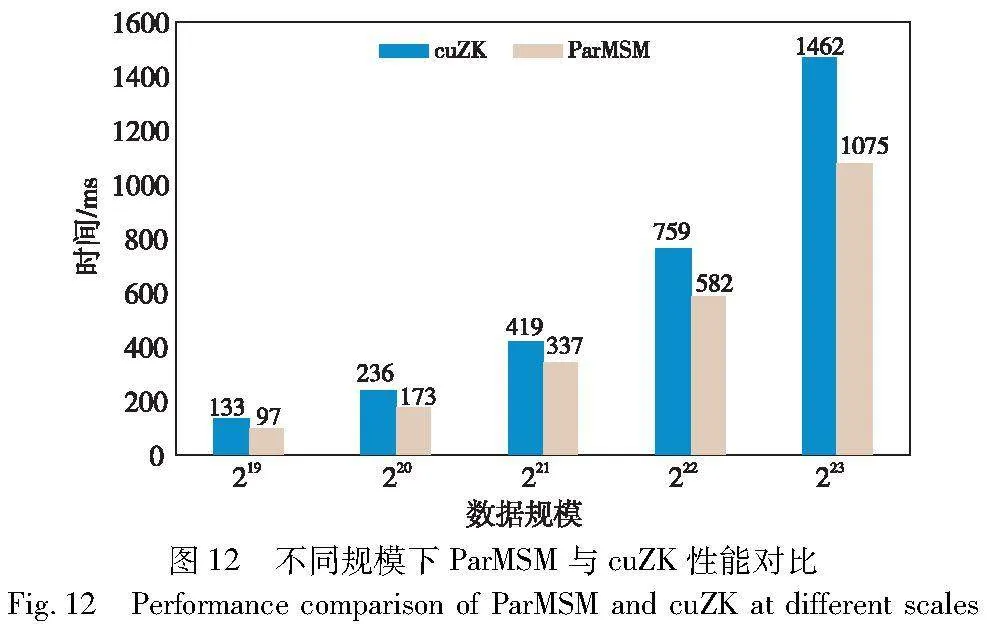
cuZK对线程进行组织时使用了太多的线程块,而每一个线程块内的线程数量过少,导致了线程块在流式多处理器之间的频繁切换;另一方面,为了避免数据传输而使用GPU来做串行计算,影响了计算效率。图12展示了在GPU为RTX 3060,CPU为AMD Ryzen 9 5900X设备上,本文提出的ParMSM与cuZK在219~223规模下完整的MSM计算时间对比。结果表明,ParMSM相比cuZK实现了1.38倍的加速。
4.3.2 ParMSM通用性分析
为了评估本文所提出的ParMSM加速方案的通用性,选择两种应用比较广泛的ZKP系统,针对不同位宽的MSM进行对比分析。halo2和Bulletproofs分别为基于CPU实现的halo协议和Bulletproofs协议的零知识证明开源库,数据位宽分别位256 bit和320 bit,表1展示了本文提出的ParMSM对比halo2和Bulletproofs的加速效果。结果表明,相比于halo2本文的ParMSM在数据规模为220~224时最高可以获得289倍的加速比,相比于Bulletproofs最高可以获得225倍的加速比。因此,ParMSM针对于不同位宽的MSM仍然有稳定的加速效果。
4.3.3 基于ParMSM的Bellperson系统的性能评估
Bellperson是在Bellman系统的基础上对其中的主要计算模块基于GPU进行了并行加速,其对MSM任务的划分相当于图4的逆过程。首先将MSM的规模均等划分,然后利用选定的窗口分别对每一个小规模的MSM进行进一步子任务分解。经过分解后每一个小规模的MSM都被划分成多个同等规模的低位宽的MSM,每一个低位宽的MSM由一个CUDA线程利用桶方法进行计算。等到所有线程都计算完成后将结果传输到主机端内存中,在主机端进行加权求和,最终计算出一个完整的MSM。
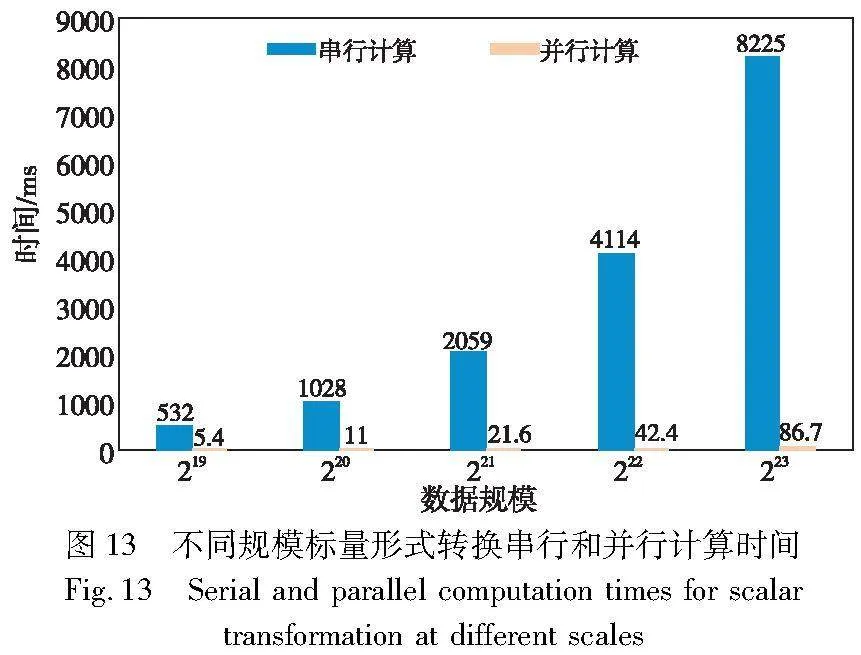
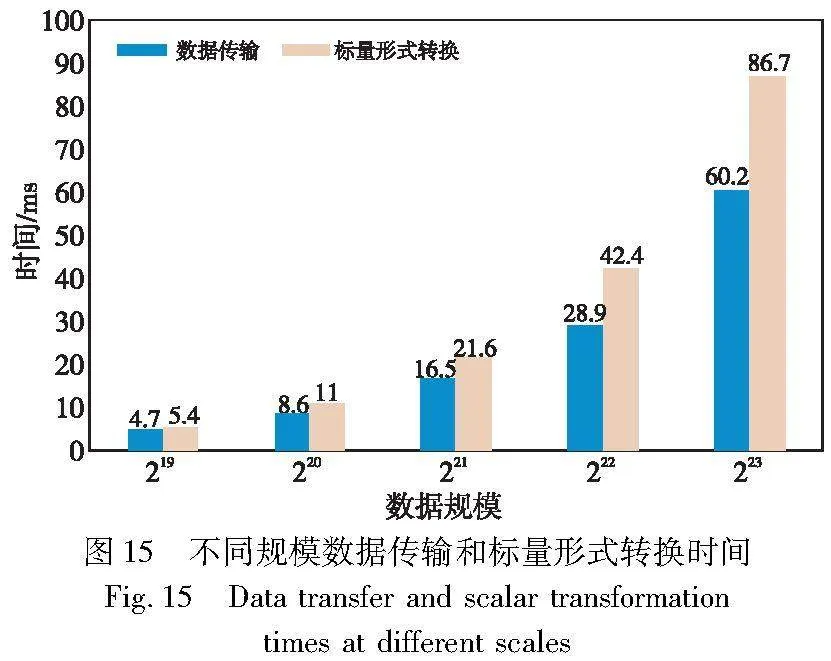
图13展示了不同规模下标量形式转换串行和并行计算时间,可以看出本文提出的对大规模标量形式转换的并行计算方法比串行计算获得了97.9倍的加速比。图14展示了本文提出的集成了ParMSM的Bellperson系统与原Bellperson在不同规模下点集从主机端到设备端数据传输时间对比。由于本文在RustaCUDA库的底层添加了Affine类型的数据结构,减少了数据切分所占用的时间,其传输效率相比于Bellperson有了明显的提升。图15则展示了本文设计方案中点集的传输和标量形式转换计算时间对比,可以看出GPU进行标量处理所用的时间高于去掉数据切片操作后点集的传输时间,低于Bellperson方案中的点集传输时间。综上所述,通过CUDA流技术可以完美地掩盖通信所占用的时间。
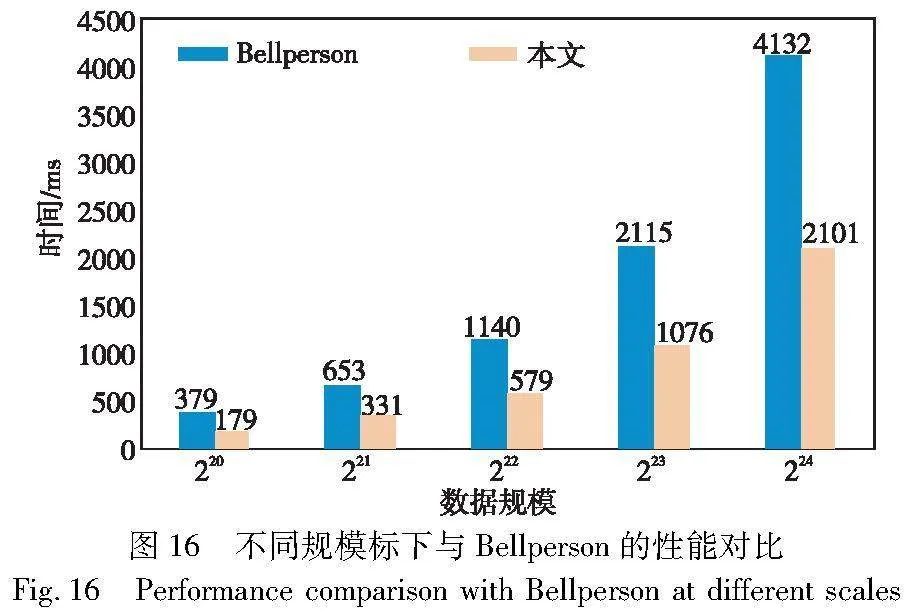
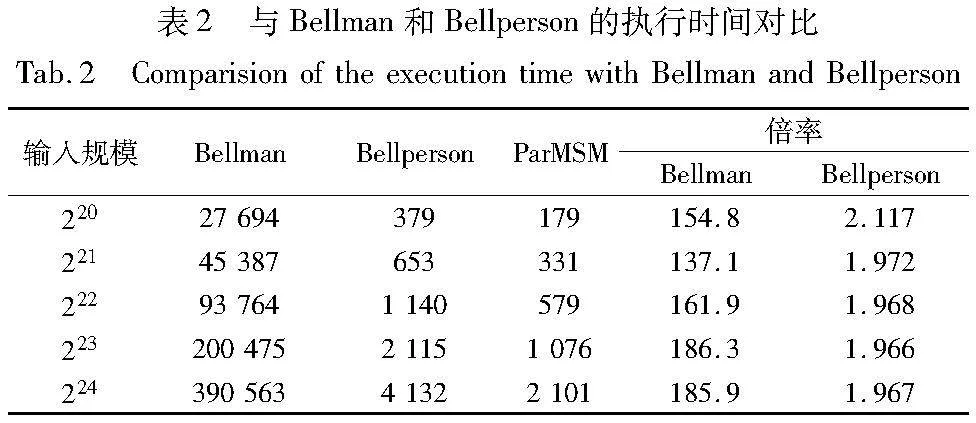
异构设计中,CPU主要负责将回传的结果进一步处理以得到最终的MSM结果,这部分计算的数据量比较小,经过测试在5900X上的执行时间为4~5 ms。表2展示了本文构建的零知识证明系统与Bellman和Bellperson在不同规模下完整的MSM的计算时间对比,图16则更直观地展示了在不同规模下本文与Bellperson的性能对比。实验结果表明,本文方案相比于Bellman获得了高达186倍的加速,相比于Bellperosn在220规模时有2.12倍的加速比,在221~224时有1.96倍以上的加速比。在220规模时由于Bellperson中选择的窗口并不是最佳,所以在220时获得了更高的加速比,而在221~224规模时其窗口大小为最佳,因此在221~224时获得稳定的加速比。
5 结束语
本文提出了一种基于GPU的MSM并行加速方案。首先,对MSM进行更细粒度的任务分解,以适应GPU高并行性能。利用共享内存对同一窗口下的子MSM并行归约,提高计算效率的同时减少数据传输。其次,基于底层计算模块的线程级任务负载分析寻找最佳标量窗口,解决了MSM子任务划分不合理的问题。最后,对标量形式转换的数据存储结构进行优化,并基于GPU对其进行并行计算,通过重叠数据传输和计算掩盖了通信时间。实验结果表明,与目前应用最为广泛、性能最优的Bellperson实现以及目前最优的GPU实现cuZK相比,在1b5242c37e72cb68b6091a761f0d9ed0计算效率上有显著的提高。
在对零知识证明中主要的计算模块进行加速后其主性能瓶颈已由原来的多标量乘法和多项式运算转变为R1CS的生成过程。在未来的工作中,计划为zk-SNARK协议中R1CS的生成过程设计有效的加速方案。
参考文献:
[1]Goldwasser S, Micali S, Rackoff C. The knowledge complexity of interactive proof-systems[M]. New York: ACM Press, 2019.
[2]Ben-Sasson E, Chiesa A, Tromer E, et al. Succinct{non-interactive}zero knowledge for a von Neumann architecture[C]//Proc of the 23rd USENIX Security Symposium. Berkeley, CA: USENIX Association, 2014: 329-349.
[3]Banerjee A, Clear M, Tewari H. Demystifying the role of zk-SNARKs in Zcash[C]//Proc of IEEE Conference on Application, Information and Network Security. Piscataway, NJ: IEEE Press, 2020: 12-19.
[4]Miers I, Garman C, Green M, et al. Zerocoin: anonymous distributed e-cash from bitcoin[C]//Proc of IEEE Symposium on Security and Privacy. Piscataway, NJ: IEEE Press, 2013: 394-411.
[5]Kosba A, Miller A, Shi A, et al. Hawk: the blockchain model of cryptography and privacy-preserving smart contracts[C]//Proc of IEEE Symposium on Security and Privacy. Piscataway, NJ: IEEE Press, 2016: 839-858.
[6]Liu Jingwei, Jiang Weiyang, Sun Rong, et al. Conditional anonymous remote healthcare data sharing over blockchain[J]. IEEE Journal of Biomedical and Health Informatics, 2023,27(5): 2231-2242.
[7]Patel R, Migliavacca M, Oriani M E. Blockchain in banking and finance: a bibliometric review[J]. Research in International Business and Finance, 2022,62: 101718.
[8]Sasson E B, Chiesa A, Garman C, et al. Zerocash: decentralized anonymous payments from bitcoin[C]//Proc of IEEE Symposium on Security and Privacy. Piscataway, NJ: IEEE Press, 2014: 459-474.
[9]赵海旭, 柴志雷, 花鹏程, 等. zk-SNARK中数论变换的硬件加速方法研究[J]. 计算机科学与探索, 2024,18(2):538-552. (Zhao Haixu, Chai Zhilei, Hua Pengcheng, et al. Hardware accele-ration of number theoretic transform for zk-SNARK[J]. Journal of Frontiers of Computer Science and Technology, 2024,18(2):538-552.)
[10]Cilliers S, Mishra A K. Exploration of algorithms for the hardware acceleration of multi-scalar multiplication on FPGA[C]//Proc of International Conference on Emerging Trends in Networks and Computer Communications. Piscataway, NJ: IEEE Press, 2023: 264-274.
[11]Zhang Ye, Wang Shuo, Zhang Xian, et al. PipeZK: accelerating zero-knowledge proof with a pipelined architecture[C]//Proc of the 48th Annual International Sympo-sium on Computer Architecture. Piscataway, NJ: IEEE Press, 2021: 416-428.
[12]Wu Guiming, He Qianwen, Jiang Jiali, et al. A high-performance hardware architecture for ECC point multiplication over Curve25519[C]//Proc of the 30th Annual International Symposium on Field-Programmable Custom Computing Machines. Piscataway, NJ: IEEE Press, 2022: 1-9.
[13]Yang Kang, Wang Xiao. Non-interactive zero-knowledge proofs to multiple verifiers[C]//Proc of International Conference on Theory and Application of Cryptology and Information Security. Cham: Springer, 2022: 517-546.
[14]Botrel G, El Housni Y. Faster Montgomery multiplication and multi-scalar-multiplication for SNARKs[J]. IACR Trans on Cryptographic Hardware and Embedded Systems, 2023(3):504-521.
[15]Hijma P, Heldens S, Sclocco A, et al. Optimization techniques for GPU programming[J]. ACM Computing Surveys, 2023,55(11): 1-81.
[16]Qi Huayi, Cheng Ye, Xu MingHui, et al. Split: a hash-based me-mory optimization method for zero-knowledge succinct non-interactive argument of knowledge(zk-SNARK)[J]. IEEE Trans on Compu-ters, 2023,72(7): 1857-1870.
[17]Ishai Y, Kushilevitz E, Ostrovsky R, et al. Zero-knowledge proofs from secure multiparty computation[J]. SIAM Journal on Computing, 2009,39(3): 1121-1152.
[18]Guan Zhangshuang, Wan Zhiguo, Yang Yang, et al. BlockMaze: an efficient privacy-preserving account-model blockchain based on zk-SNARKs[J]. IEEE Trans on Dependable and Secure Computing, 2022, 19(3): 1446-1463.
[19]Reddy S B. A zk-SNARK based proof of assets protocol for bitcoin exchanges[C]//Proc of the 15th International Conference on Communication Systems & Networks. Piscataway, NJ: IEEE Press, 2023: 135-140.
[20]Groth J. On the size of pairing-based non-interactive arguments[C]//Proc of the Annual International Conference on Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2016: 305-326.
[21]Pippenger N. On the evaluation of powers and related problems[C]//Proc of the 17th Annual Symposium on Foundations of Computer Science. Piscataway, NJ: IEEE Press, 1976: 258-263.
[22]Phalakarn K, Suppakitpaisarn V. Optimal representation for right-to-left parallel scalar and multi-scalar point multiplication[J]. International Journal of Networking and Computing, 2018,8(2): 166-185.
[23]Liu Chenran, Feng Jian, Fang Ming. Heterogeneous CPU-GPU acce-lerated parallel subgridding FDTD algorithm[C]//Proc of Internatio-nal Applied Computational Electromagnetics Society Symposium. Piscataway, NJ: IEEE Press, 2023: 1-3.
[24]张峰, 翟季冬, 陈政, 等. 面向异构融合处理器的性能分析, 优化及应用综述[J]. 软件学报, 2020, 31(8): 2603-2624. (Zhang Feng, Zhai Jidong, Chen Zheng, et al. Survey on performance analysis, optimization, and applications of heterogeneous fusion processors[J]. Journal of Software, 2020,31(8): 2603-2624.)
[25]Fang Juan, Zhou Kuan, Tan Chen, et al. Dynamic block size adjustment and workload balancing strategy based on CPU-GPU heterogeneous platform[C]//Proc of IEEE International Conference on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking. Piscataway, NJ: IEEE Press, 2019: 16-18.
[26]Zhou Tao, Cai Qiangming, Cao Xin, et al. GPU-accelerated HO-SIE-DDM using NVIDIA CUDA for analysis of multiscale problems[C]//Proc of Asia-Pacific International Symposium on Electromagnetic Compatibility. Piscataway, NJ: IEEE Press, 2022: 1-4.
[27]Lyu Tao, Wei Chenkun, Yu Ruijing, et al. cuZK: accelerating zero-knowledge proof with a faster parallel multi-scalar multiplication algorithm on GPUs[J]. IACR Trans on Cryptographic Hardware and Embedded Systems, 2023(3): 194-220.
