基于测距与GNSS信息融合的车联网协同定位技术

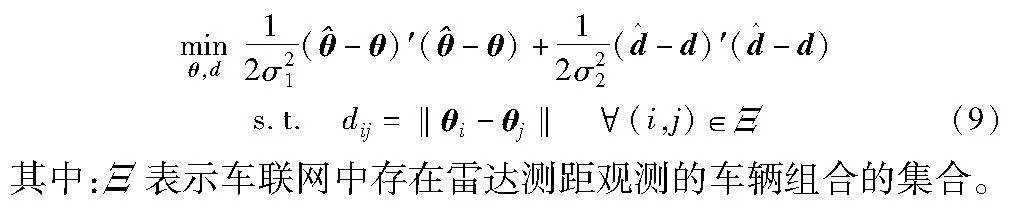
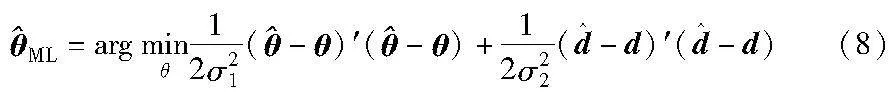
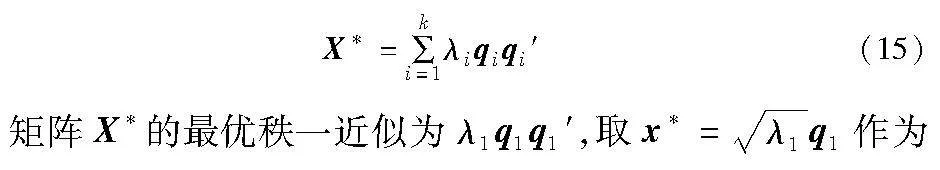
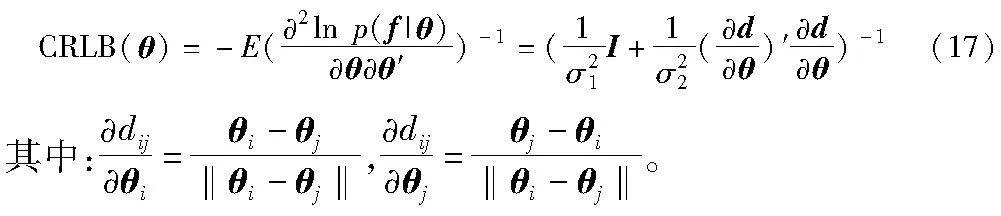
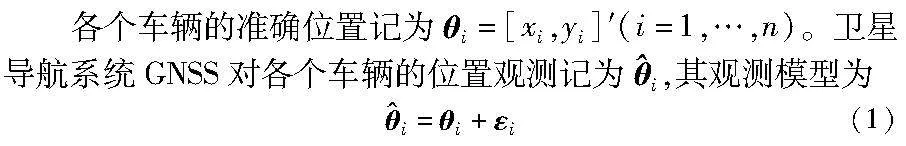
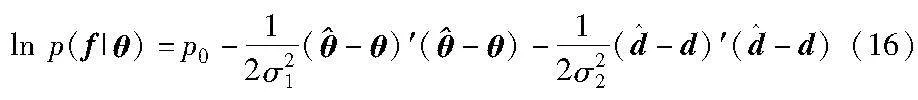
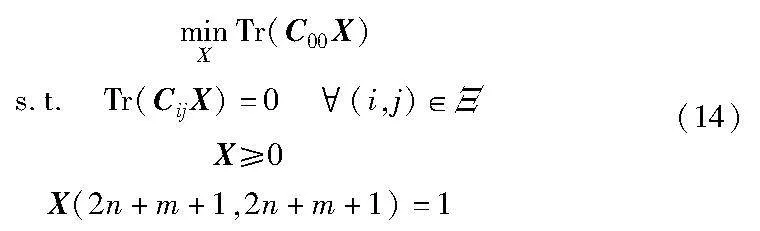
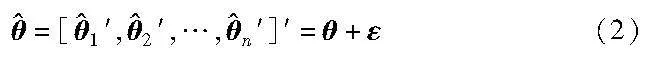
摘 要：为了提高车联网中车辆定位的精度，提出了基于车载雷达测距信息与全球卫星导航系统（global navigation satellite system，GNSS）信息融合的车联网协同定位方法。该方法使用极大似然估计策略建立数学模型，其本质是一个非线性优化问题。将其化简为具有多个二次等式约束的二次规划问题，并给出一种半正定松弛方法，可以高效地近似求解原问题，最后通过特征值分解法进一步改进该近似解。仿真结果表明，该信息融合方法得到的协同定位比线性化加权最小二乘方法的定位精度有显著提高；且能达到基于较大数据集的BP（back propagation）神经网络定位方法的定位精度，但无须事先训练模型，可实现高精度实时定位。

关键词：车联网； 协同定位； 车载雷达测距； 半正定松弛

中图分类号：TP391 文献标志码：A

文章编号：1001-3695（2024）06-017-1722-06

doi：10.19734/j.issn.1001-3695.2023.10.0525

Cooperative positioning in vehicular networks based onfusion of ranging and GNSS information

Abstract：In order to enhance the accuracy of vehicle positioning in the Internet of Vehicles， this paper proposed a collaborative positioning method for the Internet of Vehicles based on fusing vehicle-mounted radar ranging information with GNSS information. This method established a mathematical model using the maximum likelihood estimation strategy， which essentially solved a nonlinear optimization problem. It simplified the problem as a quadratic programming problem with multiple quadratic constraints， presented a semi-definite relaxation method to efficiently approximate the original problem， and used the eigenva-lue decomposition method to further improve the approximate solution. Simulation results demonstrate that the accuracy of the collaborative positioning achieved by this information fusion method significantly improves compared to the linearized weighted least squares method. It can also achieve the positioning accuracy of BP（back propagation） neural network localization method based on a large dataset， without the need for pre-training the model， enabling high-precision real-time positioning.

Key words：Internet of Vehicles; cooperative positioning; vehicle radar ranging; semi-definite relaxation

0 引言

随着我国汽车保有量的持续增长，交通安全、出行效率、环境保护等问题日益突出。车联网（Internet of Vehicles）通过车载自组织网络（vehicular Ad hoc network，VANET）使得道路上的车辆成为移动无线接入点，为其附近的其他车辆节点及路侧单元（roadside unit，RSU）提供无线连接［1～3］。不仅能使车辆节点之间进行通信，车辆与路侧单元之间也能进行通信，共同实现车联网大数据环境下的新型智能交通信息体系［4，5］。

车辆精确定位作为车联网的核心技术之一，为车联网在车辆调度、防碰撞、辅助驾驶甚至无人驾驶等应用中提供最基本的位置信息，是智能网联交通系统背景下解决交通安全问题的重要基础［6］。传统的车载定位采用全球导航卫星系统 （global navigation satellite system，GNSS）技术。GNSS能全天候地向全球范围的导航接收设备提供连续的定位服务。然而，GNSS易受钟差、卫星轨道偏差、多径效应等多种误差源的影响，其中电离层的误差范围为几米到二十米，对流层的误差范围为两米到数十米，多径误差从几厘米到上百米不等。 目前，民用卫星导航的标准位置服务可提供5～10 m的定位精度［7，8］。

通常，智能交通系统对车辆位置精度的要求可分为三个级别，即哪条道路、哪条车道和车道内的具体位置［6］。为了知道特定车道上的准确位置以实现自动驾驶，可接受的精度必须低于1 m。因此，仅靠GNSS观测信息的车辆定位无法满足未来智能交通应用的精度需求。在实际行驶过程中，车辆实时获得的GNSS数据质量也在不断地改变，在信号极差路段甚至出现GNSS数据漂移现象。

基于GNSS与惯性导航系统（inertial navigation system，INS）信息融合的组合导航技术，在一定程度上提高了车辆定位的精度［9］。然而，组合导航定位方法仅利用了单个车辆节点自身的观测信息。在高架遮挡、地下隧道等应用场景中，无论对单车组合导航算法进行何种优化，都很难得到理想的定位效果［10］。车联网可以实现车辆节点之间、车辆与路侧单元之间的互联互通，进而实现车辆之间的协同定位，以进一步提高定位精度［11］。近年来，已有国内外学者对车联网协同定位开展了大量研究［12，13］，但是大多是在动态场景下的协同定位，需要每个目标车辆与其邻居车辆进行实时信息交互。由于车联网通信带宽和速率的限制，在车辆数量较大的情况下容易造成数据延迟、丢包等现象，影响协同定位的时效性和精度。文献［14］研究了无线传感器网络中基于到达时间差信息融合的静态协作目标定位问题。罗平等人［15］利用到达时间差观测，提出一种基于自然选择的线性递减权重粒子群优化与Taylor算法协同定位的方法。 文献［16］提出了多无人机协作的静态多目标定位算法，也是基于各目标到观测平台的到达时间差信息融合。

目前车载激光雷达测距的精度能达到厘米级，可以为协同定位提供准确的测距信息。已有大量研究基于车载激光雷达与GNSS数据融合，实现智能车的高精度协同定位［17～23］，其中大部分是关于车联网的动态协同定位算法，如扩展卡尔曼滤波法［18］、容积卡尔曼滤波法［19］、无迹卡尔曼滤波法［12］、协方差交滤波法［20］等。也有部分文献针对车载雷达与GNSS观测信息融合的静态协同定位问题进行研究［21～23］，主要基于加权最小二乘方法。文献［23］提出的线性化加权最小二乘（linearized weighted least-squares， LWLS）法，采用一阶泰勒近似来处理雷达观测的非线性问题。最近，已有一些研究将深度学习方法引入到协同定位中［24，25］，通过建立相关的观测数据库训练出用于定位任务的多层前馈神经网络。基于深度学习的方法虽然能获得较好的定位精度，但训练模型需要收集大量的数据集。

本文提出一种车联网环境下的静态协同定位方法，旨在通过RSU实时融合VANET中的车载雷达测距观测信息与车辆GNSS观测信息，来改进车辆位置估计的精度。解决该问题的关键在于如何利用测距观测和GNSS观测这两方面的信息，对车辆的位置进行准确估计，其本质是一个参数估计问题。常用的参数估计方法有最小二乘法、加权最小二乘法、矩估计法、极大似然估计法等，其中极大似然（maximum likelihood，ML）估计方法是概率统计中估算模型参数的一种经典和重要的方法，同时具有一致性、渐进正态性、有效性和不变性等统计特性。因此，本文使用极大似然估计策略建立车联网静态协同定位的数学模型，该模型本质上是一个非凸的非线性优化问题。

通过一些代数化简，将原始问题等价变换为具有多个二次等式约束的二次规划问题。这是国际上公认的NP（non-deterministic polynomial）难问题，尚无具有多项式复杂度的算法进行有效求解。因此，本文提出了一种半正定松弛（semi-definite relaxation，SDR）方法，即通过忽略等价问题的秩一约束来近似求解原问题。理论分析表明，该近似解的秩应该小于等于一个很小的上界，所以大多数情况下秩一约束是满足的，即SDR方法能得到协同定位的最优解。针对近似解的秩大于一的情况，通过设计特征值分解法进一步改进该近似解，从而得到更加精确的车辆定位。

本文的SDR协同定位方法与其他方法相比具有明显的优势：首先，传统的线性化加权最小二乘方法需要车辆位置的初始估计，且具有较大的线性化近似误差，本文方法无须初始估计，且在大多数情况下能得到协同定位的最优解；其次，基于深度学习的协同定位方法需要大量的数据集进行训练，在数据量不充分的情况下其定位精度也不理想，本文方法无须先验数据集，可实现只根据当前观测信息的实时定位。

从蒙特卡罗数值模拟结果可以看出，SDR方法得到的协同定位比已有的LWLS方法的车辆定位精度有显著提高。SDR定位方法的均方根误差（RMSE）明显小于基于较小数据集的卷积神经网络定位方法，与基于较大数据集的卷积神经网络的RMSE接近。此外，SDR协同定位方法的均方误差与相应的CRLB（cramer-rao lower bound）下界接近，说明该方法达到了理论上可行的最优水平。

1 车联网协同定位模型

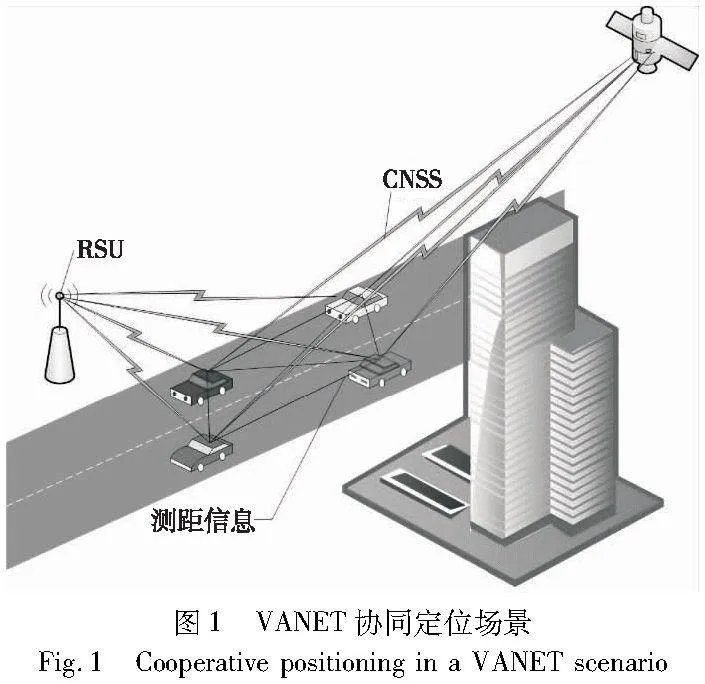
本文考虑一个单向的城市交通VANET场景，包括n（n≥2）部车辆，这些车辆部署在给定的路段，固定宽度等于W m，长度小于车联网的无线通信传输范围。属于该VANET的车辆与路边部署的一个RSU完全连接。每个车辆都配备了GNSS接收机，加载了车载前置激光雷达，因此可以较精确地测量自己与邻居车辆的距离，并融合GNSS定位的观测信息，一起发送到RSU。然后RSU根据收集的VANET中所有车辆的相对距离测量和GNSS定位测量，对各个车辆的位置进行协同定位计算，这种协同定位场景如图1所示。

其中：εi为观测噪声，假设其服从具有协方差σ21I的零均值高斯分布。车载自组织网络中所有车辆的GNSS观测集合为GNSS观测向量。

其中：θ=［θ1′，θ2′，…，θn′］′为各个车辆精确位置组成的向量，也是本文需要估计的未知参数；ε=［ε1′，ε2′，…，εn′］′为高斯观测噪声向量，其协方差矩阵为σ21 I2n×2n。

另一方面，车载激光雷达发射特定频率和波形的探测信号，然后处理反射回波，利用物体反射波束的时间差得到与邻居车辆的距离观测。记第i辆车与第j辆车之间的实际距离为dij=‖θi-θj‖，车载激光雷达的测距观测模型为

其中：d为车辆间精确距离的向量；δ为高斯观测噪声向量，其协方差矩阵为σ22Im×m。

使用极大似然估计策略，建立基于测距观测和GNSS观测信息融合的车联网协同定位数学模型。

因此，车辆位置向量θ的极大似然估计可以通过最大化对数似然函数来获得，即

由于距离dij与车辆位置向量θ存在非线性关系dij=‖θi-θj‖，所以问题式（7）本质上是一个非凸的非线性优化问题，没有解析最优解。为了处理这种非线性关系，本文将dij引入到优化变量，将其扩维为η=［θ′，d′］′，优化问题式（8）可以等价转换为

2 车联网协同定位方法

极大似然估计策略下的车联网协同定位的数学模型式（9）实际上是一个二次规划问题，其约束条件为多个二次等式约束。一般情况下，二次等式约束是非凸的。具有多个二次等式约束的二次规划是国际上公认的NP难问题，尚无具有多项式复杂度的算法可以有效求解。另外，由于式（8）的非凸性，意味着其目标函数存在多个局部最小值，全局最小值很难得到。实际上，使用任何本地搜索算法都有受困于局部最小值的风险，因此可能导致非常不准确的局部最优解。

本文通过分析，设计一种半正定松弛方法来融合车载雷达测距信息和 GNSS观测信息，以实现更高精度的协同定位。为此，首先通过数学推导，证明车联网协同定位数学优化模型式（9）可以等价于一个带齐次二次等式约束的齐次二次规划问题，然后应用SDR松弛技术来求解该问题。

定理1 极大似然估计策略下，车联网协同定位的非线性优化问题式（9）等价于一个带齐次二次等式约束的齐次二次规划问题，即可通过求解该问题来得到问题式（9）的最优解。

通过代数化简问题式（9）中约束dij=‖θi-θj‖的欧氏距

证毕。

由定理1可知，非线性优化问题式（9）可以等价化简为具有多个二次等式约束的二次规划问题式（10）。不难看出，问题式（10）的目标函数是关于η的凸函数，然而二次等式约束是非凸的。下面通过一系列推导，将非凸优化问题式（10）近似为一个标准半正定规划的凸优化问题。

分析问题式（13）的约束条件发现，其根本困难点在于非凸的秩约束rank（X）=1。因此，半正定松弛方法关键的一步就是先忽略这个非凸约束，从而得到问题式（13）的一个松弛问题：

松弛非凸秩约束后得到的问题式（14）是一个标准的半正定规划（semidefinite programming，SDP）问题，也是一个凸优化问题，这是SDR方法的最大优点。随着凸优化技术和优化软件的发展，凸优化内点算法能够高效地以任意精度求解SDP问题。然而，将NP难问题式（13）松弛为可高效求解的凸优化问题式（14）的代价是：问题式（13）的最优解X*未必满足rank（X*）=1的约束条件。因此，一个关键的问题是如何从松弛问题式（14）的最优解构造出满足原问题式（13）约束的可行解。为此，设计如下的特征值分解法。

假设问题式（14）最优解X*的秩为k。如果k=1，那么X*直接满足原问题式（13）的约束条件，即X*也是原问题式（13）的最优解。 如果k>1，则对X*进行特征值分解，记λ1≥λ2≥…≥λk>0为X*的k个特征值，按照从大到小排序，qi为λi对应的特征向量。那么，X*可以分解为

问题式（13）的SDR最优解，从而求解出最优的η*=［（θ*）′，（d*）′］′，作为基于车载雷达测距和GNSS观测信息融合的车联网协同定位估计。

算法1 本文车联网协同定位算法

注意到本文提出的车联网协同定位算法并未要求所有车辆之间的测距信息。在实际应用中，由于车联网的通信带宽、时效等限制，RSU可能只收集到部分车辆之间的测距信息，但仍可以采用本文提出的协同定位方法，融合可得的测距与GNSS信息，从而提高车辆定位的精度。

3 CRLB计算及性能分析

3.1 CRLB计算

CRLB（Cramer-Rao下界）为任何无偏估计器建立了一个误差协方差矩阵的下界，因此可以用来检验一个估计器的精度是否达到了理论上可行的最高水平。现在推导使用GNSS和距离信息融合的车辆定位问题的CRLB。

根据式（7）中的似然函数，可以得到概率密度函数的对数形式：

其中：p0是一个不依赖于未知变量θ的常数。因此，CRLB可以推导为

3.2 现有方法的对比

现有的线性化加权最小二乘方法［23］，通过一阶泰勒近似来线性化雷达观测，其需要车辆位置的初始估计，且必然引入线性化近似误差，导致其定位的均方误差无法达到相应的CRLB下界。

最近，文献［24，25］提出了基于多层前馈神经网络的车联网协同定位方法。此类基于深度学习的方法虽然能获得较好的定位精度，但训练模型需要事先收集大量的数据集。在数据量不充分的情况下，其定位精度也不理想，SDR方法无须先验数据集，可实现仅根据当前观测信息的实时定位。

的CRLB下界。

3.3 计算复杂度分析

定位方法的计算复杂度反映了其在实际应用中的效率，特别是在车联网应用中尤为重要。SDR协同定位算法1的主要计算量集中在步骤c）d）f）。其中，步骤c）的计算量主要是求解SDP式（14）。文献［27］给出了求解标准SDP问题的计算复杂度为O（max{a，b}4b1/2），其中a为线性约束的个数，b为SDP问题中优化向量的维数。在问题式（14）中，a=m+2，b=2n+m+1，因此求解问题式（14）的计算复杂度为O（（2n+m）4.5）。步骤d）f）的计算量主要在于对X*进行Cholesky分解和特征值分解，其计算复杂度均为O（（2n+m）3）。综合上述分析，SDR协同定位方法算法1的计算复杂度仅为O（（2n+m）4.5），在现有的边缘计算设备上能高效求解。

4 数值实验

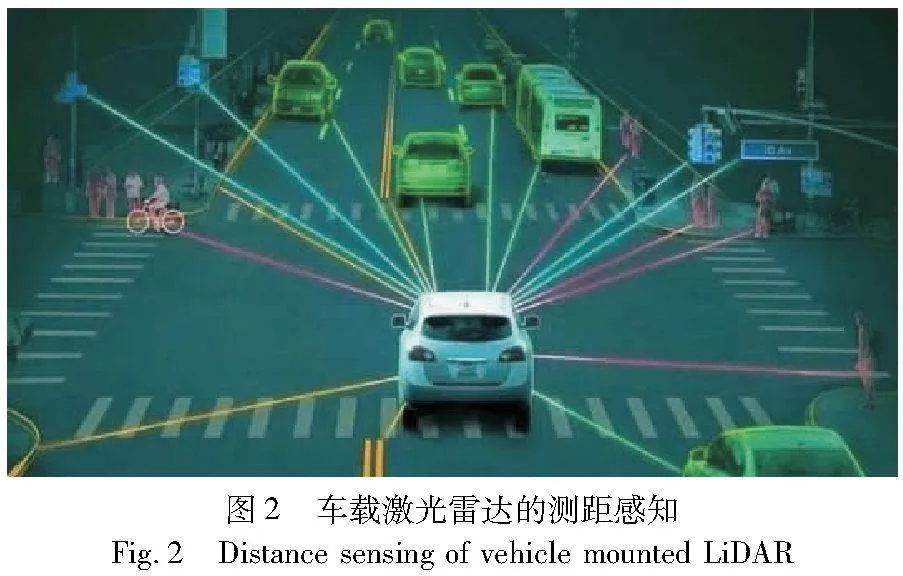
将本文的SDR协同定位方法应用于一个VANET协同定位场景，其中车辆沿给定道路部署在长100 m、宽50 m的路段。本实验中的每辆汽车均搭载了3D激光雷达，激光雷达正在成为L4级及以上自动驾驶的核心配置。在实际应用中，国产的蔚来汽车选择图达通的激光雷达作为ET7的标配，小鹏P5也搭载了大疆旗下览沃的激光雷达。图2展示了由车载激光雷达获取的与其他邻居车辆的距离信息。

各个车辆都通过激光雷达获取自己与邻居车辆的距离信息，将这些信息与车载GNSS模块获取的自身GNSS观测信息一起发送到路测单元（RSU）。路测单元设置在路侧，与附近过往车辆进行双向通信和数据交互，是实现车路协同的关键设备。图3展示了部署在车路协同试点的多个路段的路测单元实例。

路测单元将收集到的各个车辆基于车载雷达的测距观测和基于卫星导航系统的GNSS观测进行信息融合，应用本文提出的SDR协同定位方法进行车联网定位。为展示SDR协同定位方法的性能，将其与已有的线性化加权最小二乘（LWLS）方法和BP（back propagation）神经网络方法进行比较。在BP神经网络方法中，设置了3层，每层10个神经元的全连接神经网络结构，并分别用100个样本数据（small data）和1 000个样本数据（large data）来进行训练。此外，CRLB下界是数理统计中参数无偏估计量方差的下限，因此本文的仿真实验也通过比较RMSE与CRLB根来评判是否达到理论上可达的最优估计。定位精度根据车辆位置估计值同真值的均方根误差（RMSE）来衡量。

4.1 模拟实验1

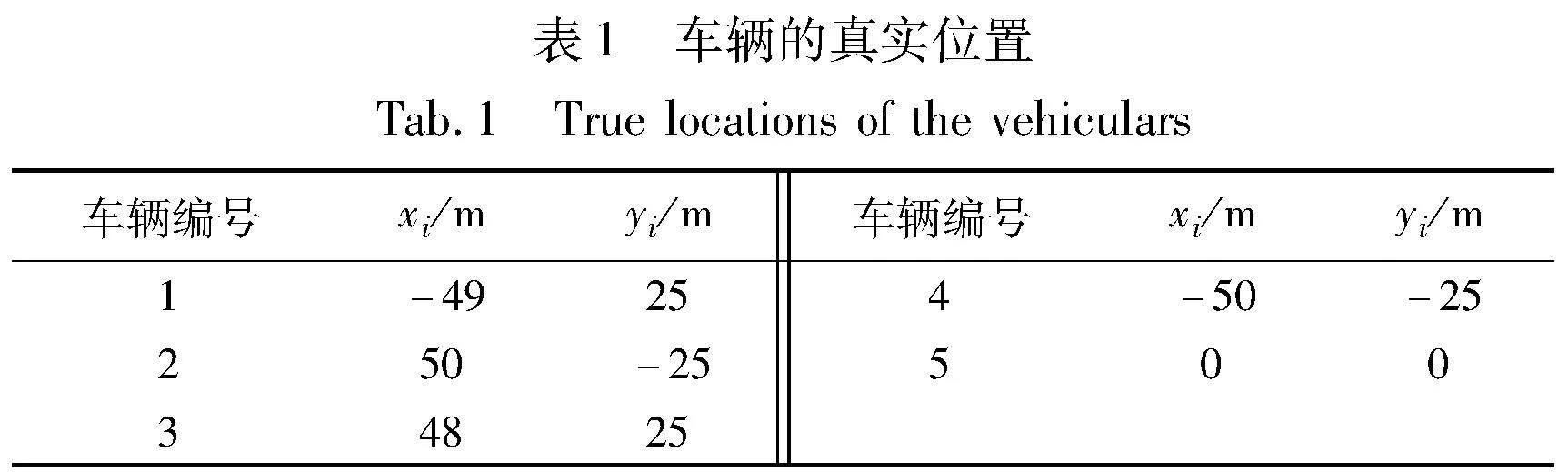
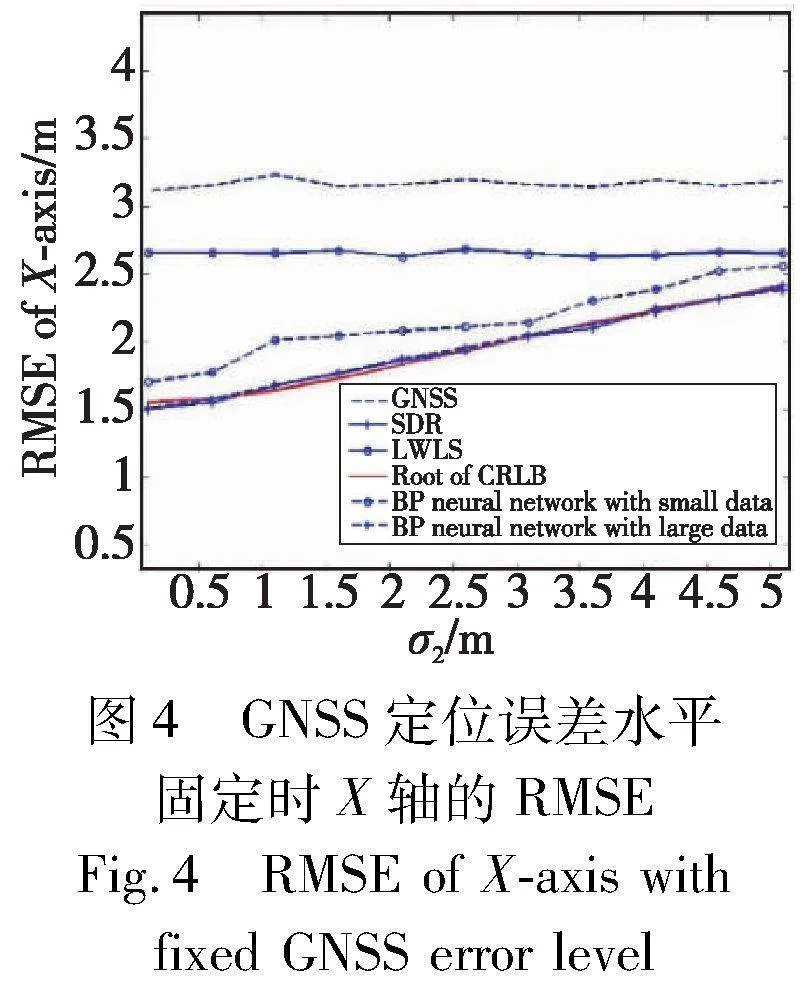
属于VANET的车辆数量 n=5，其真实位置在表1中给出。本次数值模拟中，设定GNSS定位误差的标准差σ1=10 m，通过变化雷达测距误差的标准差σ2来考察测距信息对车辆定位精度的改进。图4、5分别展示了σ2从0.1 m逐渐增加到5.1 m的过程中，SDR协同定位方法和LWLS方法在X轴和Y轴的均方根误差，其中蒙特卡罗数值模拟次数L=1000。

从图4、5的结果可以看出，虽然LWLS方法的定位精度比只用GNSS信息定位的方法有所改进，然而其RMSE仍然远远大于CRLB根。SDR协同定位方法通过融合车载雷达测距信息，其定位精度比LWLS方法和只用GNSS信息定位的精度有明显提高。特别是σ2较小的情况下，例如σ2=0.1时，LWLS方法和GNSS定位的X轴RMSE分别约2.65 m和3.17 m，SDR方法的X轴RMSE仅约1.51 m。

BP神经网络方法在训练样本较少的情况下也无法达到CRLB根。SDR方法和BP神经网络方法在大样本情况下，X轴和Y轴的RMSE都与相应的CRLB根接近，说明这两种方法能达到理论上可行的最优水平。但是BP神经网络方法依赖大量的数据来训练模型，在数据量不充分的情况下其定位精度也不理想，SDR方法无须先验数据集，可实现只根据当前观测信息的实时定位。

4.2 模拟实验2

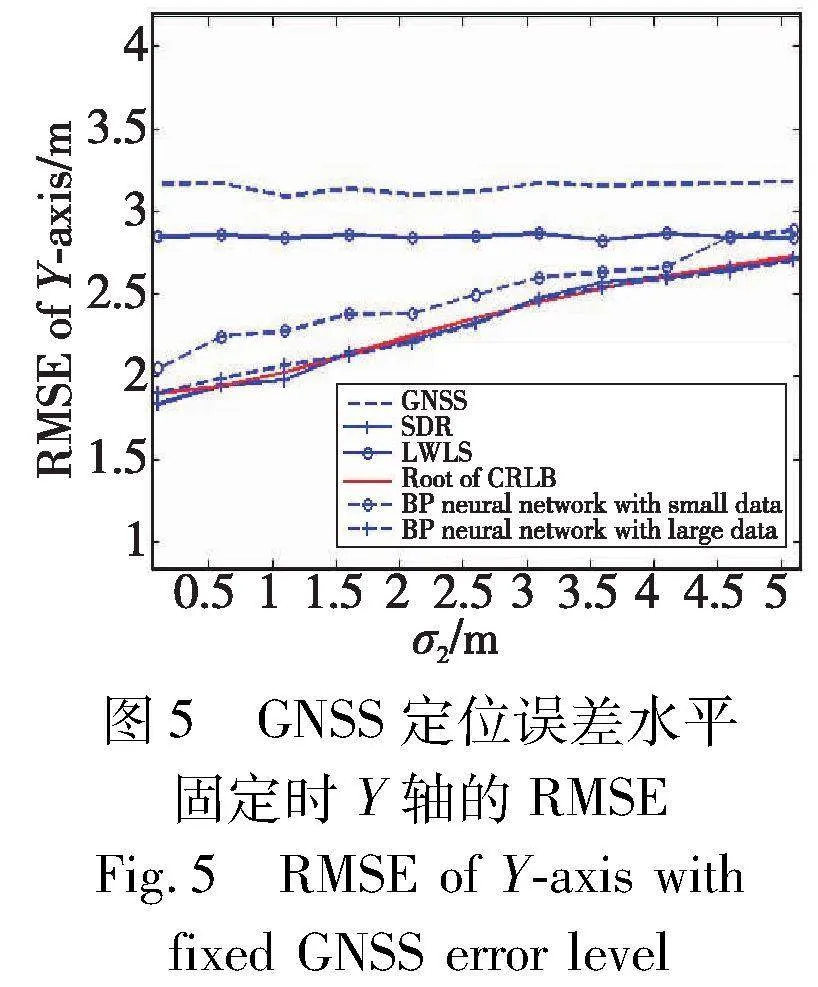
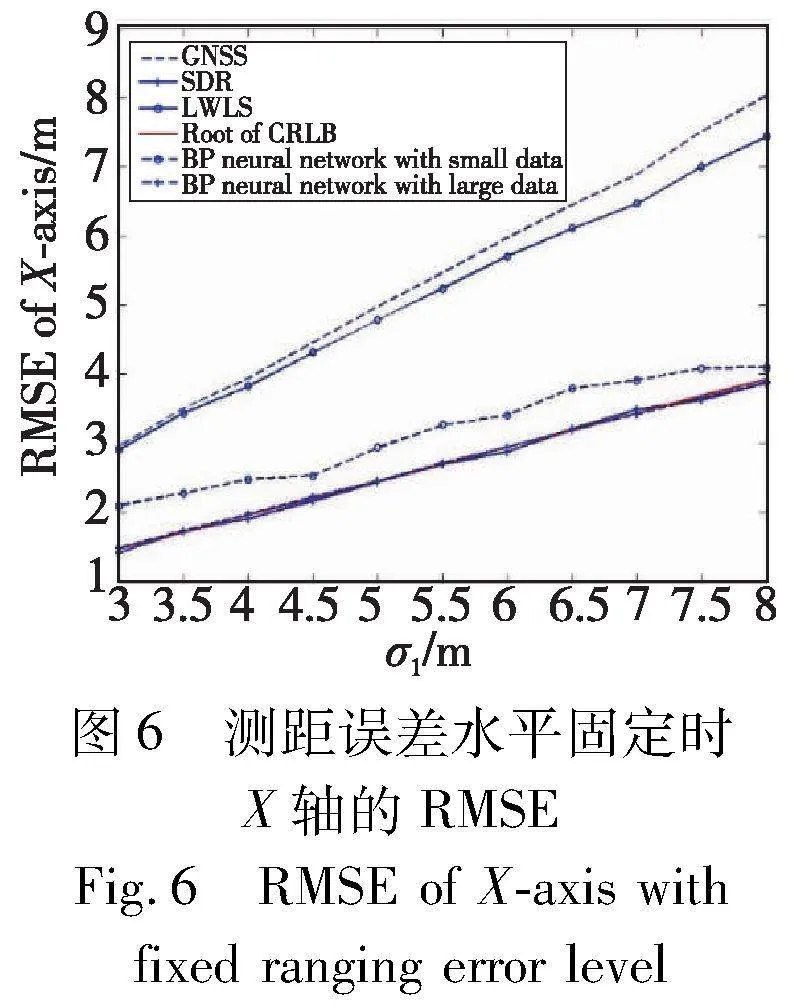
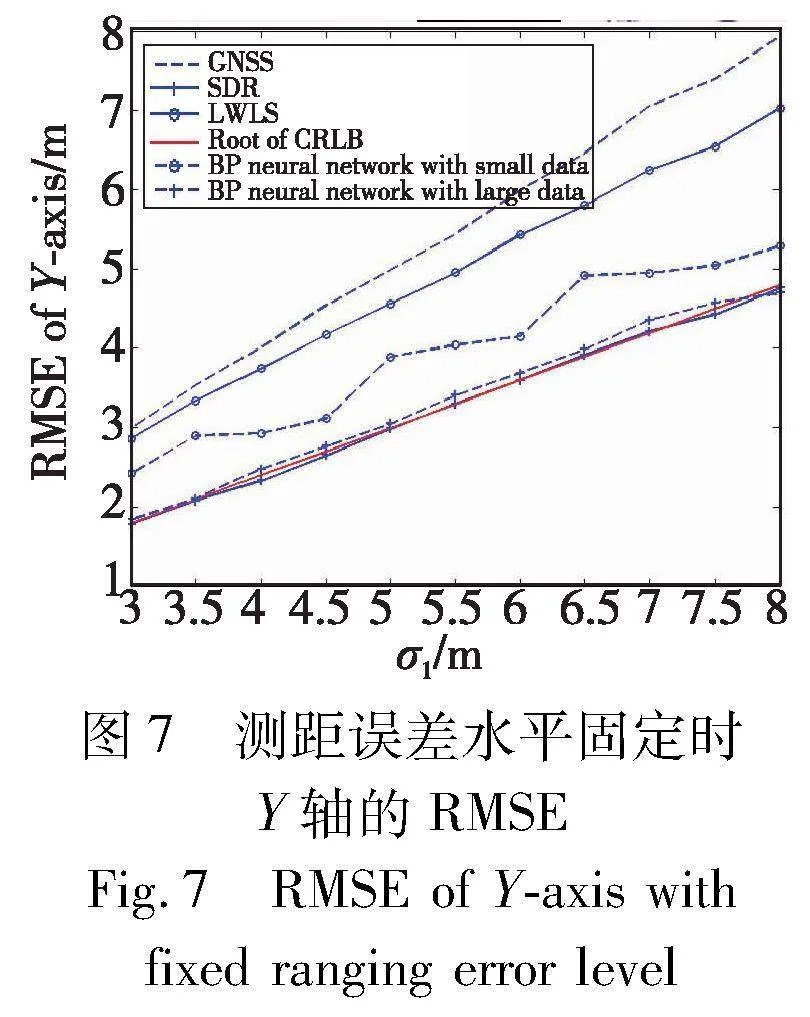
本数值实验中车辆数目和位置不变，设定车载雷达测距信息的标准差σ2=0.1 m，通过变化GNSS定位的标准差σ1，来考察不同GNSS定位精度对SDR协同定位方法的性能影响。图6、7分别展示了σ1从3 m逐渐增加到8 m的过程中，各方法在X轴和Y轴的RMSE，其中蒙特卡罗数值模拟次数L=1000。

从图6、7的结果可以看出，LWLS方法的定位误差RMSE仅略微低于只用GNSS信息定位的方法，而SDR协同定位方法的定位误差RMSE显著低于只用GNSS信息定位的方法。随着σ1的增加，意味着GNSS定位误差越来越大，SDR协同定位方法通过融合车载雷达测距信息，仍能提供较高的定位精度。此外，BP神经网络方法在训练样本较少的情况下仍然无法达到CRLB根的定位精度。SDR方法和大样本情况下的BP神经网络方法在X轴和Y轴的RMSE都与相应的CRLB根接近，再一次验证了这两种方法均达到理论上可行的最优水平。然而，SDR方法仅利用了实时的GNSS信息和车载雷达测距信息，无须事先利用大量样本数据进行模型训练。

4.3 模拟实验3

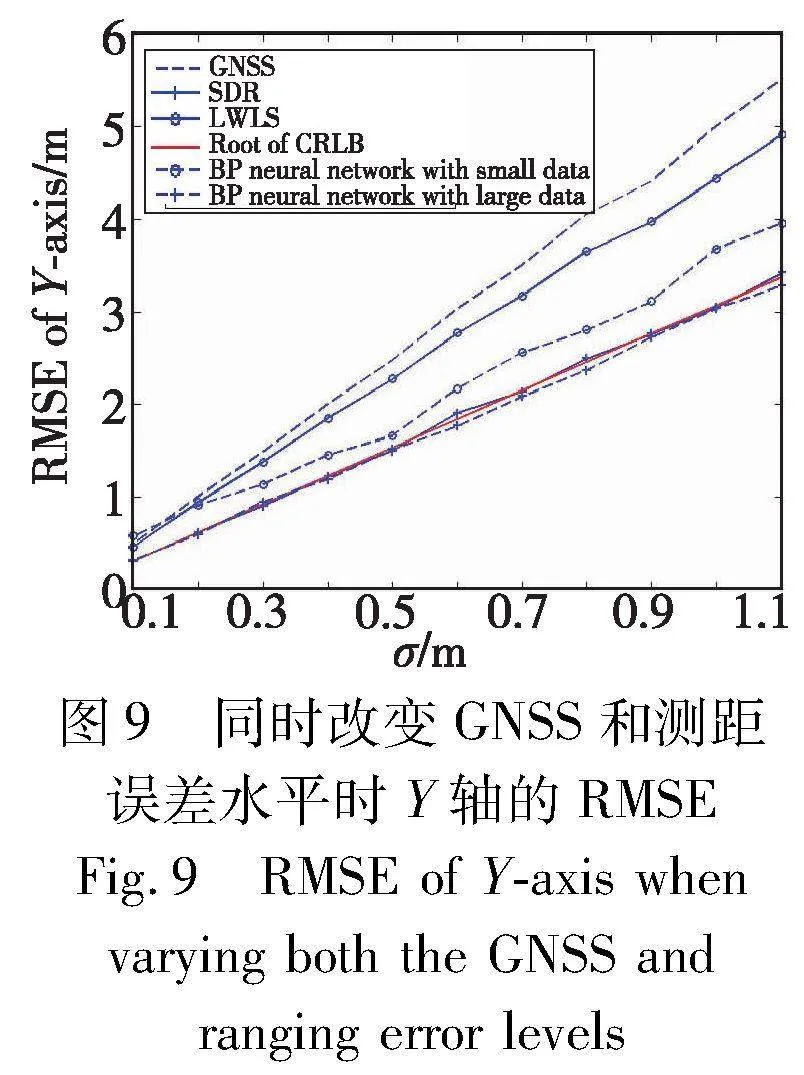
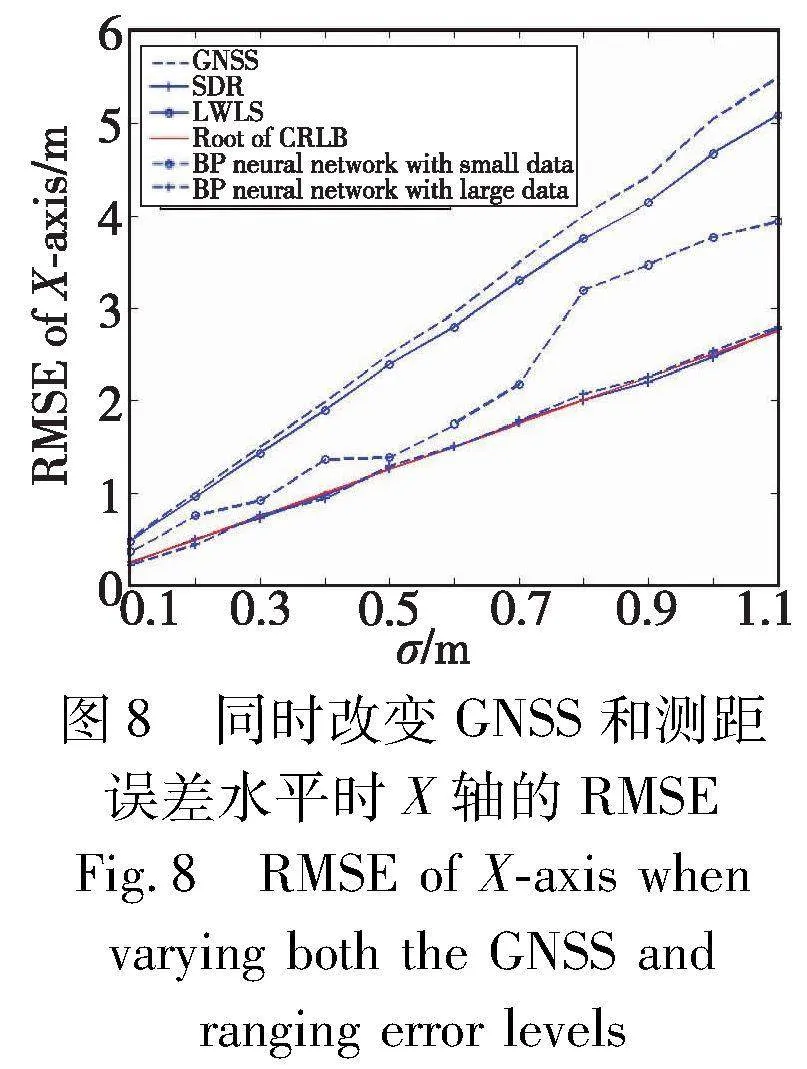
本数值实验中车辆数量n=8，各车辆的真实位置随机生成，服从［-50，50］m×［-25，25］m区域内的均匀分布。通过同时变化GNSS定位的标准差σ1=5σ和车载雷达测距的标准差σ2=σ来考察SDR协同定位方法的性能。图8、9分别展示了 从0.1 m逐渐增加到1.1 m的过程中，各种方法在X轴和Y轴的RMSE，其中蒙特卡罗数值模拟次数L=1000。

从图8、9的结果可以看出，SDR协同定位方法和大样本情况下的BP神经网络方法在X轴和Y轴的RMSE都与相应的CRLB根接近，而LWLS方法虽然比只用GNSS信息定位的方法有所改进，但其RMSE远大于CRLB根。当σ≤0.3时，SDR协同定位方法在X轴和Y轴都能得到亚米级的定位精度。实验结果说明，SDR协同定位方法通过实时融合GNSS信息和车载雷达测距信息，能提供高精度的实时定位，并且无须事先采集数据，是一种高效精准的方法。

5 结束语

本文提出的半正定松弛协同定位方法能有效融合车联网中的车载雷达测距信息和GNSS 定位信息，实现车载自组织网络的高精度协同定位。与BP神经网络定位方法相比，该方法无须事先采集数据进行模型训练，可根据当前的观测信息进行实时定位。蒙特卡罗数值模拟实验结果表明，SDR协同定位方法得到的定位精度比已有的LWLS方法有显著提高，且能达到基于较大数据集的BP神经网络定位方法的定位精度。后续工作中，将在本文SDR静态协同定位的基础上，考虑车辆的动态运动模型，研究车载自组织网络的车辆动态协同定位问题，进一步提高该方法的实用性与普适性。

参考文献：

［1］王润民， 邓晓峰， 徐志刚，等. 车联网仿真测试评价技术研究综述［J］. 计算机应用研究， 2019，36（7）：1921-1926，1939. （Wang Runmin， Deng Xiaofeng， Xu Zhigang， et al. Survey on simulation testing and evaluation of Internet of vehicles［J］. Application Research of Computers， 2019，36（7）： 1921-1926，1939.）

［2］程翔， 张浩天， 杨宗辉，等. 车联网通信感知一体化研究： 现状与发展趋势［J］. 通信学报， 2022，43（8）：188-202. （Cheng Xiang， Zhang Haotian， Yang Zonghui， et al. Research on integrated communication and perception of Internet of Vehicles： current status and development trends［J］. Journal of Communications， 2022，43（8）：188-202.）

［3］陆忠梅， 陈巍， 魏杰，等. 车联网极低时延与高可靠通信： 现状与展望［J］. 信号处理， 2019，35（11）： 1773-1783. （Lu Zhongmei， Chen Wei， Wei Jie， et al. Ultra-low latency and high-reliability communication in Internet of Vehicles： current status and prospects［J］. Signal Processing， 2019，35（11）： 1773-1783.）

［4］Khelifi H， Luo Senlin， Nour B， et al. Named data networking in vehicular Ad hoc networks： state-of-the-art and challenges［J］. IEEE Communications Surveys & Tutorials， 2019，22（1）： 320-351.

［5］周雯雯， 陆阳， 石雷. 面向5G车联网场景的移动任务动态卸载策略研究［J］. 计算机应用研究， 2022，39（11）： 3427-3431. （Zhou Wenwen， Lu Yang， Shi Lei. Research on dynamic offloading strategy of mobile task for 5G vehicle networks［J］. Application Research of Computers， 2022，39（11）： 3427-3431.）

［6］丁飞， 张楠， 李升波，等. 智能网联车路云协同系统架构与关键技术研究综述［J］. 自动化学报， 2022，48（12）： 2863-2885. （Ding Fei， Zhang Nan， Li Shengbo， et al. A review of research on the architecture and key technologies of intelligent networked vehicle-road-cloud collaboration systems［J］. Journal of Automation， 2022，48（12）： 2863-2885.）

［7］张楷时， 焦文海， 李建文. Android智能终端GNSS定位精度分析［J］. 武汉大学学报 ：信息科学版， 2019，44（10）： 1472-1477. （Zhang Kaishi， Jiao Wenhai， Li Jianwen. Analysis of GNSS positioning accuracy of Android smart terminals［J］. Journal of Wuhan University：Information Science Edition， 2019，44（10）： 1472-1477.）

［8］陈建华， 陈树新， 吴昊，等. 多路GNSS欺骗干扰互相关噪声模型［J］. 计算机应用研究， 2019，36（8）： 2488-2491. （Chen Jianhua， Chen Shuxin， Wu Hao， et al. Cross correlation noise model of multiple GNSS spoofing signals［J］. Application Research of Compu-ters， 2019，36（8）： 2488-2491.）

［9］Chiang K W， Tsai G J， Chu H J， et al. Performance enhancement of INS/GNSS/Refreshed-SLAM integration for acceptable lane-level na-vigation accuracy［J］. IEEE Trans on Vehicular Technology， 2020，69（3）： 2463-2476.

［10］肖广兵， 王蓝仪， 孙宁，等. 基于车路协同的地下停车场车辆定位算法发散性研究［J］. 计算机应用研究， 2021，38（2）： 530-533. （Xiao Guangbing， Wang Lanyi， Sun Ning， et al. Divergence of coo-perative vehicle localization in underground parking lots［J］.Application Research of Computers， 2021，38（2）： 530-533.）

［11］杨阳， 林菲， 俞定国，等. 一种基于车联网的车辆定位方法［J］. 计算机应用研究， 2020， 37（11）： 3461-3466. （Yang Yang， Lin Fei， Yu Dingguo， et al. A vehicle positioning method based on Internet of Vehicles［J］. Application Research of Computers， 2020，37（11）： 3461-3466.）

［12］谯小康， 屈小媚. 基于车辆与车辆的车联网分布式协同感知定位［J］. 控制理论与应用， 2021， 38（7）： 988-996. （Qiao Xiaokang， Qu Xiaomei. Vehicle to vehicle-based distributed cooperative sensing positioning for Internet of Vehicles［J］. Control Theory & Applications， 2021，38（7）： 988-996.）

［13］Yu Quanzhou， Wang Yongqing， Shen Yuyao， et al. Cooperative multi-rigid-body localization in wireless sensor networks using range and doppler measurements［J］. IEEE Internet of Things Journal， 2023，10（24）： 22748-22763.

［14］Qu Xiaomei， Xie Lihua. An efficient convex constrained weighted least squares source localization algorithm based on TDOA measurements［J］. Signal Processing， 2016，119： 142-152.

［15］罗平， 向凤红， 毛剑琳，等. 基于自然选择的线性递减权重PSO与Taylor算法的TDOA协同定位算法研究［J］. 计算机应用研究， 2014， 31（4）： 1144-1146，1150. （Luo Ping， Xiang Fenghong， Mao Jianlin， et al. TDOA co-location method based on natural selection linear decreasing weight PSO and Taylor algorithm［J］. Application Research of Computers， 2014，31（4）： 1144-1146，1150.）

［16］屈小媚， 刘韬， 谈文蓉. 基于多无人机协作的多目标无源定位算法［J］. 中国科学： 信息科学， 2019，49（5）： 570-584. （Qu Xiaomei， Liu Tao， Tan Wenrong. Multi-target passive positioning algorithm based on multi-UAV collaboration［J］. Chinese Science： Information Science， 2019，49（5）： 570-584.）

［17］吴壮， 唐伦， 蒲昊，等. 车联网中基于轨迹预测的无人机动态协同优化覆盖算法［J］. 计算机应用研究， 2022， 39（8）： 2322-2328. （Wu Zhuang， Tang Lun， Pu Hao， et al. UAV dynamic collaborative optimization coverage algorithm based on trajectory prediction in Internet of Vehicles［J］. Application Research of Compu-ters， 2022，39（8）： 2322-2328.）

［18］Rohani M，Gingras D，Vigneron V，et al.A new decentralized Bayesian approach for cooperative vehicle localization based on fusion of GPS and VANET based inter-vehicle distance measurement［J］. IEEE Intelligent Transportation Systems Magazine， 2015，7（2）： 85-95.

［19］Liu Jiang， Cai Baigen， Wang Jian. Cooperative localization of connected vehicles： integrating GNSS with DSRC using a robust cubature Kalman filter［J］. IEEE Trans on Intelligent Transportation Systems， 2016，18（8）： 2111-2125.

［20］Fang Susu， Li Hao， Yang Ming. LiDAR SLAM based multi-vehicle cooperative localization using iterated split CIF［J］. IEEE Trans on Intelligent Transportation Systems， 2022，23（11）： 21137-21147.

［21］Liu Kai， Lim H B， Frazzoli E， et al. Improving positioning accuracy using GPS pseudo range measurements for cooperative vehicular localization［J］. IEEE Trans on Vehicular Technology， 2013，63（6）： 2544-2556.

［22］Fascista A， Ciccarese G， Coluccia A， et al. A localization algorithm based on V2I communications and AOA estimation［J］. IEEE Signal Processing Letters， 2016，24（1）： 126-130.

［23］钟日进， 陈琪锋. 利用集群内测距和对目标测向的协同定位方法［J］. 航空学报， 2020， 41（S1）： 140-148. （Zhong Rijin， Chen Qifeng. Cooperative positioning method using intra-cluster ranging and target direction finding［J］. Acta Aeronautica Sinica， 2020， 41（S1）： 140-148.）

［24］Yapar C， Levie R， Kutyniok G， et al. Real-time outdoor localization using radio maps： a deep learning approach［J］. IEEE Trans on Wireless Communications， 2023，22（12）： 9703-9717.

［25］Praveen C S， Humaira N， Deepa B， et al. A machine learning based accurate localization technique for 5G networks［C］//Proc of the 3rd International Conference on Artificial Intelligence and Smart Energy . Piscataway， NJ： IEEE Press， 2023： 622-626.

［26］Wang Gang， Li Youming， Ansari N. A semidefinite relaxation method for source localization using TDOA and FDOA measurements［J］. IEEE Trans on Vehicular Technology， 2013，62（2）： 853-862.

［27］Helmberg C， Rendl F， Vanderbei R J， et al. An interior-point me-thod for semidefinite programming［J］. SIAM Journal on Optimization， 1996，6（2）： 342-361.