基于自变量简约的大规模稀疏多目标优化

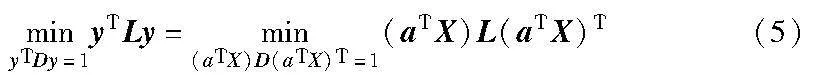
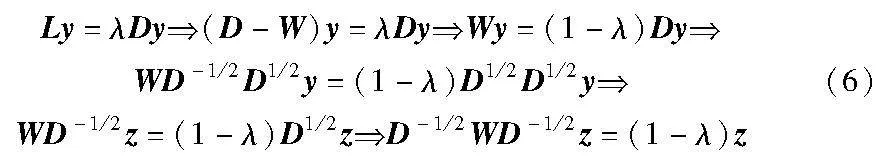
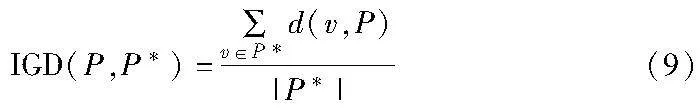
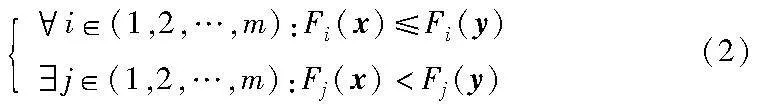
摘 要：现有的大多数进化算法在求解大规模优化问题时性能会随决策变量维数的增长而下降。通常，多目标优化的Pareto有效解集是自变量空间的一个低维流形，该流形的维度远小于自变量空间的维度。鉴于此，提出一种基于自变量简约的多目标进化算法求解大规模稀疏多目标优化问题。该算法通过引入局部保持投影降维，保留原始自变量空间中的局部近邻关系，并设计一个归档集，将寻找到的非劣解存入其中进行训练，以提高投影的准确性。将该算法与四种流行的多目标进化算法在一系列测试问题和实际应用问题上进行了比较。实验结果表明，所提算法在解决稀疏多目标问题上具有较好的效果。因此，通过自变量简约能降低问题的求解难度，提高算法的搜索效率，在解决大规模稀疏多目标问题方面具有显著的优势。

关键词：局部保持投影；进化算法；大规模稀疏多目标优化问题

中图分类号：TP18 文献标志码：A文章编号：1001-3695（2024）06-009-1663-06

doi： 10.19734/j.issn.1001-3695.2023.10.0522

Evolutionary algorithm using dimensionality reduction for sparse multi-objective optimization

Abstract： The performance of most existing evolutionary algorithms tends to decrease as the dimension of the decision variables increases for solving large-scale optimization problems. The Pareto solution set of a multi-objective optimization is a low dimensional manifold in the decision space， whose dimension is much smaller than that of the decision variables space. Accordingly， this paper proposed a multi-objective evolutionary algorithm based on dimensionality reduction of decision variables to solve large-scale sparse multi-objective optimization problems. It preserved local neighborhood information in the original decision variables space by using locality preserving projections， and designed an archive set to train the non-dominated solutions as much as possible to raise the accuracy of projection. The proposed algorithm was compared with four popular evolutionary multi-objective optimization algorithms on a series of test problems and practical application problems. Experimental results show that the proposed algorithm is effective in solving sparse multi-objective problems. Therefore， the reduction of indepen-dent variables can reduce the difficulty of solving the problem， improve the search efficiency of the algorithm， and have significant advantages in solving large-scale sparse multi-objective problems.

Key words：locality preserving projection; multi-objective evolutionary algorithm; large-scale sparse multi-objective optimization problems

0 引言

多目标优化一直是进化计算研究中一个有挑战性的领域。多目标优化问题（multi-objective optimization problem，MOP） 不同于单目标优化问题，它没有唯一的最优解，MOP的最优解通常是一组非劣解［1］。多目标优化进化算法（multi-objective optimization evolutionary algorithm，MOEA） 在求解MOP时可以通过种群的不断进化迭代，找到一组类似于Pareto前沿界面的最优解［2］。与传统的优化方法相比，MOEA在求解多目标优化问题时具有更好的效果，已成为求解MOP最有效的工具之一［3，4］。目前，MOEA已被证明能够很好地解决一些测试问题，并在实际问题中得到了很好的应用［5］。近年来，人们提出了许多经典的多目标进化算法。根据选择策略的不同，MOEA大致可分为基于支配关系的MOEA、基于指标评价的MOEA和基于分解的MOEA三类。基于支配关系的MOEA利用Pareto支配关系促进种群向Pareto前沿的进化，典型代表有NSGA-Ⅱ［6］、SPEA2［7］和PESA［8］。基于指标评价的MOEA通常采用HV等性能指标来评价解的收敛性和多样性［9，10］。基于分解的MOEA算法利用数学规划将复杂的MOP转换为一系列简单的单目标优化子问题进行求解［11］。

随着问题维度的增加，当输入决策变量超过100维时，这类优化问题被定义为大规模优化问题［12］。随着大规模多目标优化问题的出现，近年来也提出了多种求解大规模优化问题的方法。目前，大规模优化问题的求解方法主要有协同进化策略和非协同进化策略两种。其中协同进化策略采取的是分治思想，它把原始的大规模问题分解为多个低维度的子问题，每个子问题单独进化，将复杂的问题简单化，只有在迭代过程中交换信息，合作产生适应度值［13］。例如，Peng等人［14］提出的基于ε约束的协同进化粒子群算法求解大规模优化问题、Aguilar-Justo等人［15］设计的一种大规模优化问题的局部合作搜索策略等。另一种非协同进化策略则是运用一些特殊的策略或联合其他有效的算法，如群体智能优化算法来改进，将大规模优化问题当作整体进行求解［16］。陈暄等人［17］提出了一种改进的狼群算法，利用深度神经网络求解大规模优化问题。Wang等人［18］通过改进粒子群算法，在进化的不同阶段采用不同的学习策略，以提高算法的搜索能力。Tian等人［19］提出了一种求解具有稀疏Pareto最优解的大规模多模态多目标优化问题的进化算法。

所谓降维，就是将高维数据映射到低维空间，然后对得到的低维数据进行处理，在机器学习、数据挖掘中得到了广泛的应用。因此，自变量降维也叫自变量简约，有望成为求解大规模优化问题的有利工具，从而有效避免维数灾难问题。通过简约，将高维自变量压缩映射到低维空间中，并尽可能保留数据的有效信息［20］。通常，根据映射关系是否为线性，简约技术可以细分为线性方法和非线性方法［21］。主成分分析（principal component analysis，PCA）是一种流行的线性降维方法，它通过线性投影，将高维数据嵌入低维线性空间，并通过最大化低维空间数据的方差来尽可能多地保留原始数据信息［22］。线性判别分析利用最大化类间距离与最小化类内距离的思想来提取判别信息，寻找最优的投影矩阵（linear discriminant analysis，LDA）［23］。线性降维方法不能有效地处理高维复杂非线性数据，为了处理非线性数据，出现了一些非线性方法。其中等距离映射（isometric feature mapping，Isomap）和局部线性嵌入（locally linear embedding，LLE）是目前为止最具有代表性的两种非线性降维方法。局部线性嵌入假设高维数据点可以被其邻居线性逼近，并在此假设的基础上保留数据的非线性流形结构［24］。等距映射引入了测地距离的概念，通过最小化高维空间中的成对测地距离矩阵和低维空间中的成对欧氏距离矩阵之间的距离来得到低维嵌入结果［25］。一般线性降维方法只保留了学习投影子空间中的全局线性结构，导致分类性能较差。局域保持投影（locality preserving projections，LPP）作为一种线性降维技术，不仅拥有线性降维方法的速度，还利用线性投影映射来保持数据的局部邻域结构，并且LPP具有许多非线性技术的数据表示特征［26］。此外，LPP算法的局域保持特性使其对异常值和噪声相对不敏感。

随着决策变量的增加，现有算法依旧不能很好地解决大规模多目标优化问题，且随着问题维数的增加，问题愈加复杂，同时解在决策空间中的分布也变得稀疏，使得算法的搜索效率显著下降［27，28］。事实上，维度灾难是大规模优化问题求解困难的根本原因，优化问题的求解难度与自变量的维度息息相关。因此，如何提高算法的可扩展性，以应对复杂大规模优化问题，以及如何有效解决稀疏的大规模多目标优化问题，是当前进化算法急需面对的重要问题。

为了保证在大规模多目标优化问题下算法的搜索效率和准确率，以及针对稀疏解在决策空间中的分布问题，本文提出一种基于自变量简约的稀疏多目标进化算法（sparse multi-objective decision variable dimensionality reduction，SMDVDR）。该算法将MOEA和局部保持投影的降维技术相结合，使其不仅拥有进化算法的自我学习能力，保证了算法的搜索效率，还拥有LPP降维技术的优势，即在降维的时候不受到异常值和数据噪声的影响，能使得数据最大化地精减且明显提升数据准确率。该算法在迭代的过程中加入了一种采用非支配排序调整内部个体的归档集，其目的是在目标子代中寻找非劣解存入归档集进行训练，在考虑当前最优解的同时考虑其他非劣解，并使用归档集训练转换向量。该归档集能够进行动态调整，在面对大样本时考虑非劣解以提升结果的准确性；在面对小样本时，也能通过这种方法扩充样本进行训练，使得算法在小样本的情况下也能求得问题更真实的Pareto前沿。与此同时，用局部保持投影进行降维得到低维空间，并在低维空间上进行交叉变异操作获得子代，以提高算法的效率和可延展性，将来自每一代子代的非劣解存入归档集，并设置归档集的个数上限，在归档集达到上限的时候使用非支配排序调整归档集，最终得到代表原问题的近似Pareto前沿。实验选取稀疏多目标问题进行测试，并选取实际应用问题对比，验证了该方法的有效性。

1 研究现状

1.1 大规模多目标优化问题

现实中的许多优化问题都包含几个相互冲突的目标，本文称这类问题为多目标优化问题，其定义如下：

两个解x和y之间的支配关系可以定义为

如果满足上述条件，则x支配y，表示为xy。不受其他决策向量支配的向量x称为帕累托最优解。决策空间中的Pareto最优解集称为Pareto集合（Pareto set，PS），对应的目标向量集称为Pareto前沿（Pareto front，PF）［28］。

一般来说，多目标优化算法不能得到决策空间中所有的Pareto最优解和Pareto前沿的所有目标向量。因此，多目标优化的目标在于两个方面：a）得到的目标向量要尽可能接近真实的目标向量；b）得到的目标向量应尽可能分散地分布在目标向量上。

1.2 局部保持投影

LPP构造邻接图的方式有两种：a）使用ε邻接，任意取两个节点i和j，这两个节点之间的欧氏距离小于等于ε，就认定满足条件，但是这种方式ε的取值难以把握；b）直接计算节点i和j之外的所有点的欧氏距离并进行排序，找到距离最近的k个点。

选择权重的方式也有两种，分别是使用热核函数和简单的无参数近邻选择方法，其中热核函数的选择权重方法也受到参数的影响。

在计算投影矩阵的方式上，LPP采用的是广义特征值分解的方法计算广义特征向量问题的特征向量和特征值。

2 SMDVDR算法

2.1 基于局部保持投影的降维算法设计

结合稀疏多目标问题的特征，本文在原有的局域保持投影算法上进行改进，使用特征值分解的方法代替原本的广义特征值分解方法，得到最小特征值和特征向量。本文算法的降维具体步骤如下：

a）设G表示为具有m节点的邻接图。使用K近邻来确定两个数据点是否相邻。如果点xi和xj是相邻点，则节点i和j通过边连接，构成一个邻接图。

b）如果节点i和j之间存在边连接，则使用式（3）对节点i和j进行权值分配。

假设a是一个转换向量，得到yT=aTX，其中，X的第i个列向量是xi，得到关于y的最小化问题可以化简为

其中：D是对角矩阵，对角线上的元素值是对于W的行（或列）的和，即Dii=∑jWji。L=D－W是拉普拉斯矩阵，L是对称的正半定矩阵，它可以看作是定义在邻接图G顶点上的函数算子。为防止消除任意的缩放因子，故施加了限制yTDy=1。

接下来用拉格朗日公式来表示这个最小化问题，引入拉格朗日乘子λ，并设z=D1/2y，使目标函数最小的向量y由特征值分解的方法给出。

在经过拉普拉斯特征映射后，特征向量y将是原始数据点的低维表示。

d）假设b是一个逆转换向量，则需要最小化目标函数min‖byT－X‖，进而求得进化过后低维空间投影到高维空间的数据X′。

X′=byT（7）

2.2 基于非支配排序调节的归档集设计

种群规模在进化过程中起到不可忽视的作用，种群规模越小收敛越快，但是对于大规模问题而言容易进入局部最优解。而种群规模越大，个别的最优解虽不容易主导全体解的进化方向，避免陷入局部最优解，但将导致计算复杂度提高，收敛速度变慢。如何在固定种群下规模尽可能有效和精准地求出转换向量a也是一个关键问题。

因此，结合以上问题，本文建立一个可进行自我动态调整的归档集，在种群规模为N的情况下，初始化种群的同时也对归档集进行初始化，即先让种群进化几代，从这个过程中提取出2N个非劣解加入到归档集，并对归档集设置一个上限3N，避免规模无限增大，并将后续种群进化过程中产生的非劣解加入该归档集。当归档集里非劣解的个数超过3N的时候，通过非支配排序更新归档集，提取出非支配解，使归档集里解的数量降低到2N。

在非支配排序中，为了衡量在同一个等级中各个解质量的优劣，引入了一个拥挤度的计算，其目的是让求得的Pareto最优解在空间中尽量分散，也就有更大可能让解在Pareto最优前沿上均匀分布，第i个解的拥挤度ci的计算如下：

其中： fi+1j、fi－1j分别为第j个目标函数数值排序后与第i个解相邻的函数值； fmaxj和fminj分别为第j个目标函数数值排序后的最大和最小值。

算法1 基于非支配排序调节的归档集

从公式以及算法1可以看出，在设计归档集时，对归档集设置上限和加入非劣解扩充规模，保证了训练转换向量a的归档集规模。

2.3 算法步骤

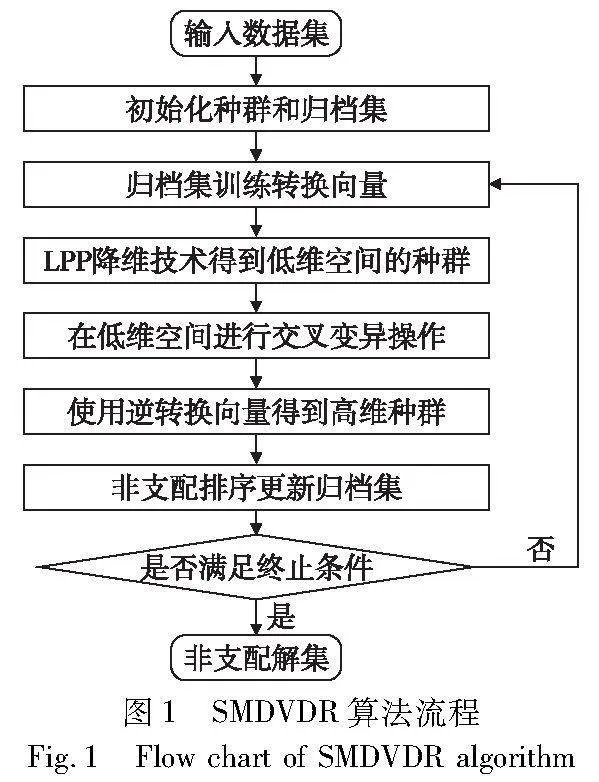
算法的具体流程如算法2和图1所示。首先，本文初始化种群大小为N，种群为X，迭代数的最大值为T。然后，初始化归档集Arc，先将归档集设为空集，从种群中取交叉突变后新生成的非劣解加入到归档集中，生成具有流行结构的归档集，以便于训练转换向量a。

当迭代数t小于迭代最大值T时，继续对种群进行进化计算。对于种群Xt，低维空间的种群yt可由公式训练过后的转换向量a得到。对于每个解yi∈yt，从yi中随机选择一个解yj∈yt，通过在yi和yj上用遗传算子生成子代。然后通过逆转换向量b转换得到一个新的种群X′t，并从X′t中提取新生成的非劣解，添加到归档集Arc中进行更新。归档集Arc的更新如算法1所示。SMDVDR算法流程如图1所示。

算法2 SMDVDR算法

3 实验与结果分析

3.1 对比算法

将基于自变量简约的稀疏多目标进化算法与五个MOEA进行比较，以研究所提算法的性能。这五个MOEA分别为NSGA-Ⅱ［6］、CMOPSO［29］、MOEA/D-DRA［30］和LMOCSO［31］，其中NSGA-Ⅱ为遗传算法，CMOPSO为粒子群优化算法，MOEA/D-DRA为差分进化算法，LMOCSO是一种针对大规模优化问题粒子群优化的仿生搜索算法。

3.2 测试问题

本文使用SMOP1～SMOP8八个基准问题测试算法性能［12］。在这八个基准问题中，每个函数都定义了一组稀疏Pareto最优解。其中对于SMOP1～SMOP3，以及SMOP7和SMOP8，只有当指定的决策变量设置为0时，它们的函数才能最小化。对于SMOP4～SMOP6，解的稀疏性直接涉及到函数，类似于特征选择问题可以测试算法寻找稀疏Pareto最优解的性能，总之，SMOP1～SMOP8具有多种函数且函数定义一组稀疏Pareto最优解，其侧重于测试算法寻找稀疏Pareto最优解的性能。

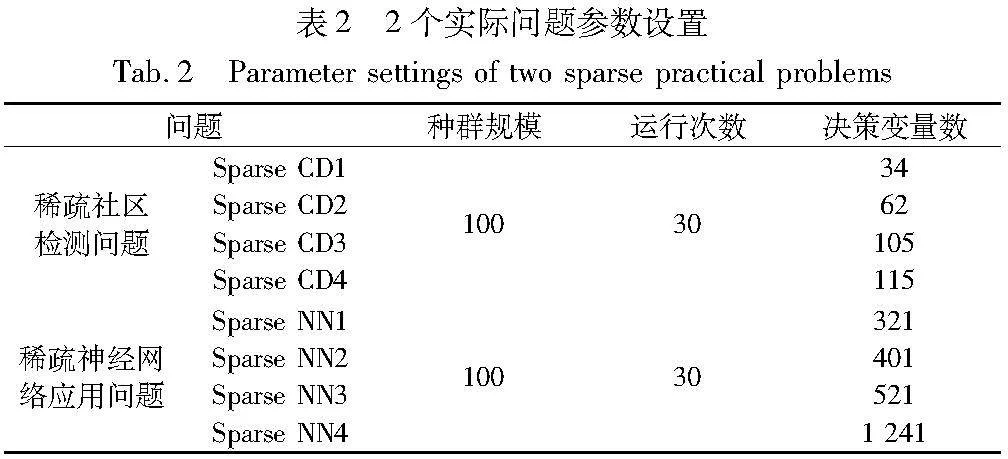
除此以外，为了研究该算法在具体案例上的应用。本文还使用了两个实际问题，即稀疏社区检测（community detection problem，Sparse CD）和稀疏神经网络应用问题（neural network training，Sparse NN）。

对于SMOP1～SMOP8，本文在实验中将目标个数M设为2，决策变量个数D设为100、500、1 000，Pareto最优解的稀疏度θ设为0.1。在Sparse CD和Sparse NN中，目标个数M设为2，Sparse CD的决策变量个数D设为34、62、105和115，Sparse NN的决策变量个数D设为321、401、521和1 241。

3.3 性能指标

1）倒代距离IGD

倒代距离（inverted generational distance， IGD）可以用来评估不同算法的Pareto最优集。IGD的空间意义可以理解为每个点到最近候选解的平均欧氏距离，解集的综合性能越好，候选解集和点集更接近，因此IGD的值越低，代表结果越好。IGD的计算公式为

其中：P*为均匀分布在Pareto前沿的点的集合；P为算法得到的解的集合；d（v，P）是从v到P的欧氏距离。

2）超体积HV

超体积（hypervolume，HV）可以同时评价MOEA的收敛性和多样性，是一个综合性指标。一个MOEA所获得的解集的HV越大，说明该解集的收敛性和多样性更好。HV的计算公式为

其中：Vol代表勒贝格测度，用来测量体积；S代表非支配解集；vi代表参考点和非支配个体构成的超体积。

3.4 实验参数设置

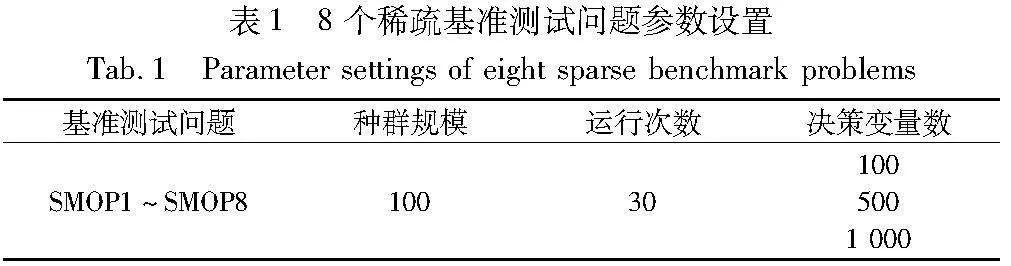
表1、2列出了SMOP1～SMOP8测试基准问题和两个实际问题的参数设置，包括种群规模、运行次数、决策变量数D。实验采用模拟二元交叉和多项式突变产生子代，当所有测试问题达到最大进化生成数且最大生成数100×D时，算法终止。

3.5 实验结果及分析

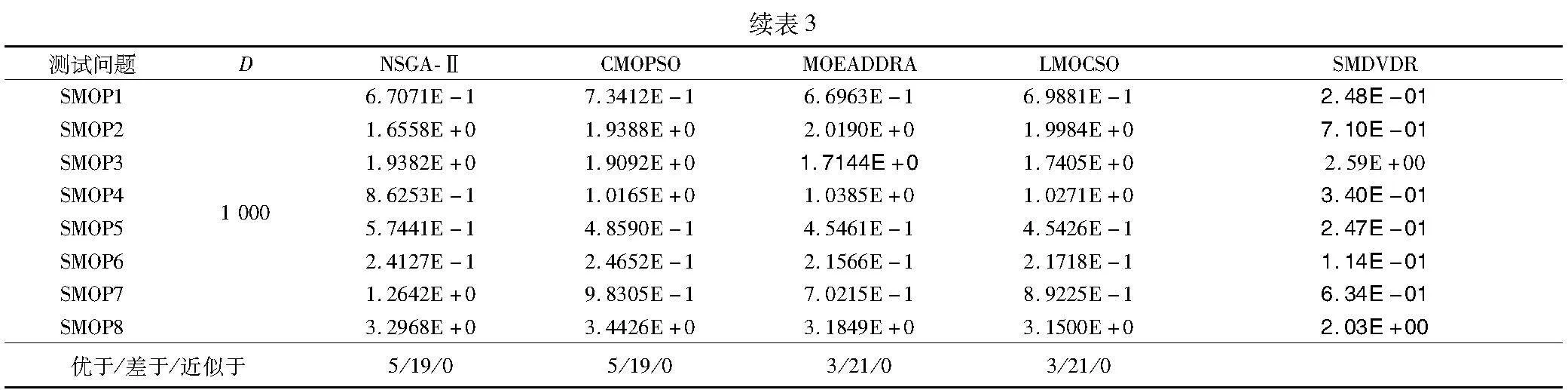
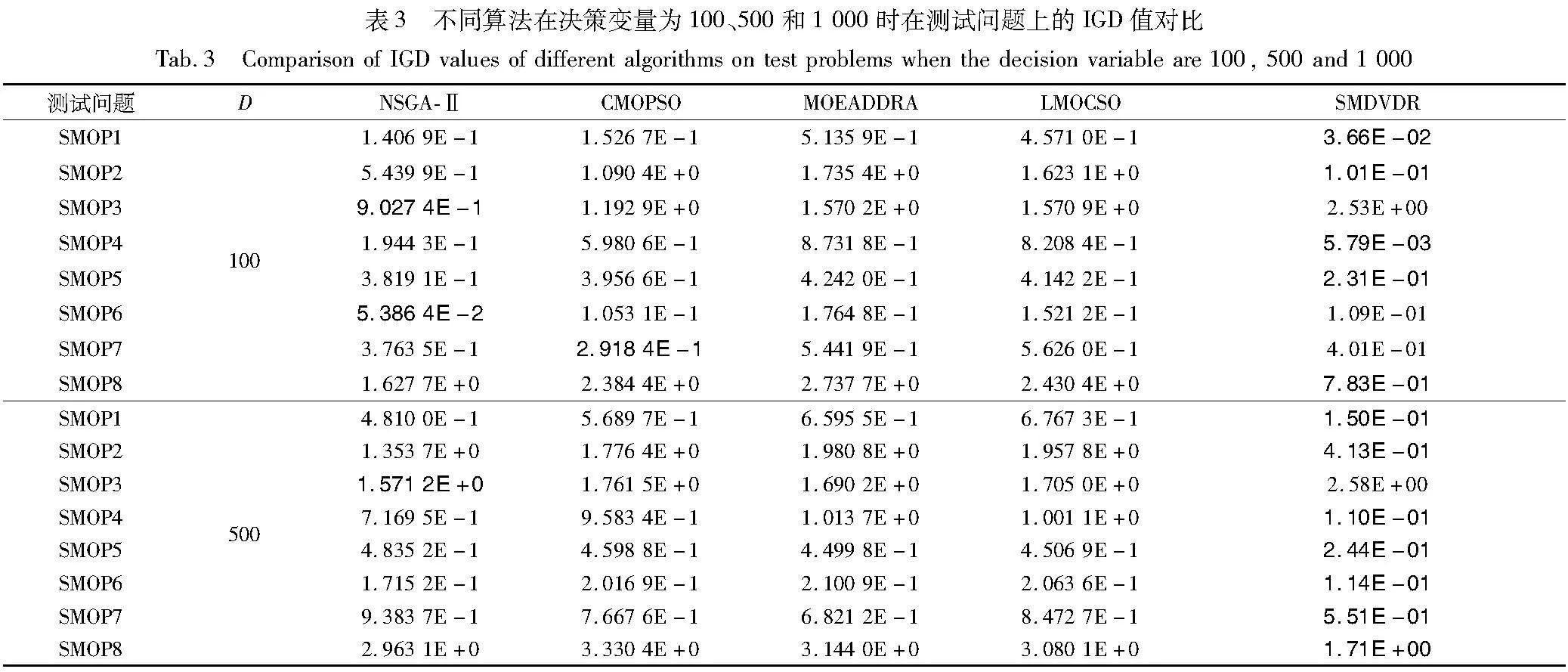
首先在SMOP基准测试问题的不同决策变量上进行实验，用表3列出在决策变量为100、500和1 000时，五种算法在测试问题上的IGD对比，并对本文算法与NSGA-Ⅱ、CMOPSO、MOEA/D-DRA、LMOCSO和MOEA/DVA五种进化算法在SMOP测试问题上运行30次得到的IGD值进行比较。在表中，“优于”“近似于”“差于”表示本文SMDVDR在5%显著性水平下的Wilcoxon秩和检验与其他算法的对比结果。其中最好的结果已用粗体表示。

从表3可以看出，SMDVDR算法相比其他算法有明显的优势。具体来说，在24个基准测试例子中，SMDVDR获得了19个最优的结果，其中NSGA-Ⅱ获得了3个最优的结果，CMOPSO和MOEADDRA各自获得了1个最优的结果。SMDVDR在除SMOP3以外的测试问题上均有较良好的结果。

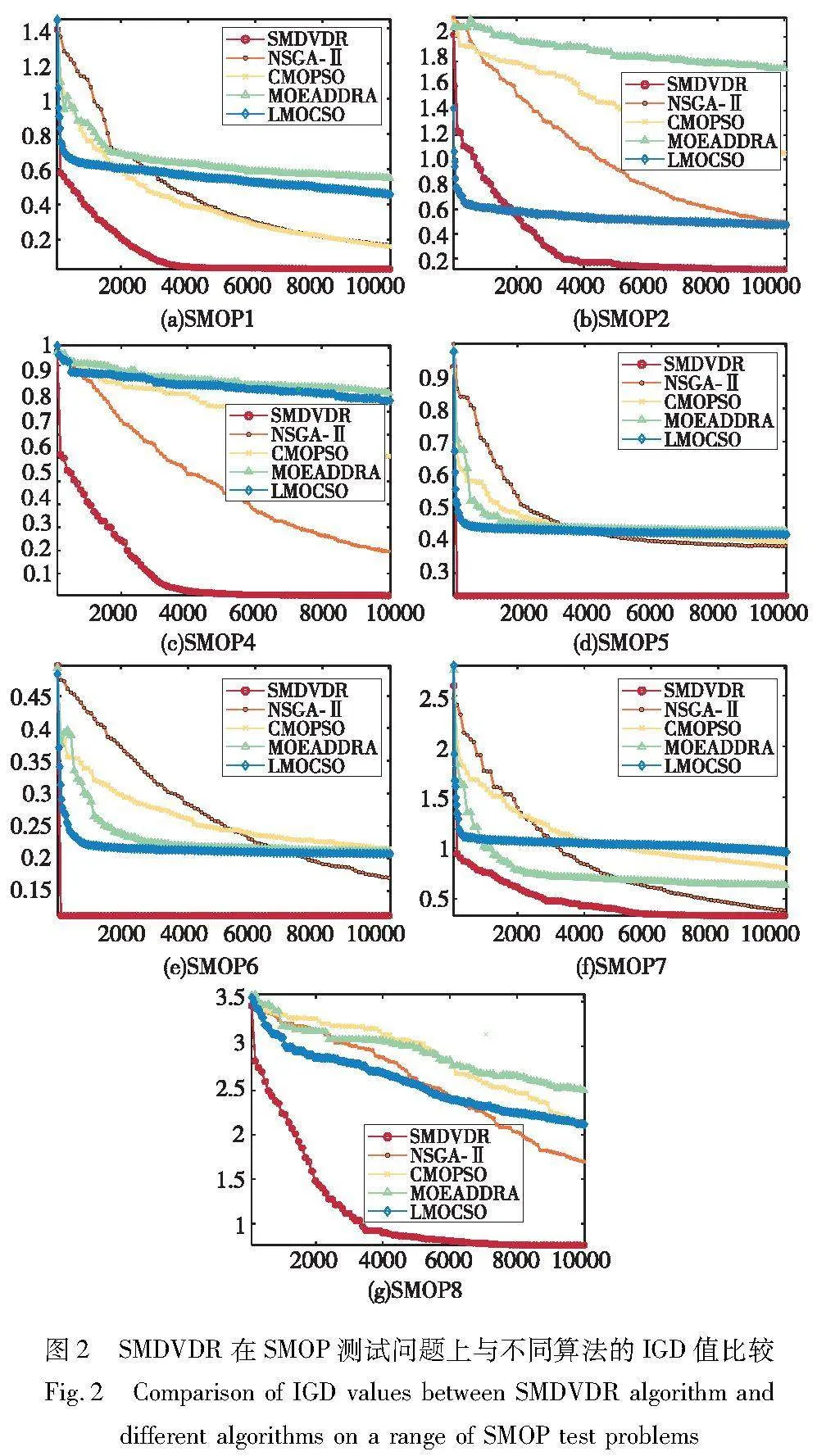
为了进一步观察基于自变量简约的稀疏多目标进化算法的优劣，在决策变量为500时，通过图2将基于自变量简约的稀疏多目标进化算法与NSGA-Ⅱ、CMOPSO、MOEA/D-DRA和LMOCSO四种进化算法的IGD值进行对比。

观察图2可知，SMOP1、SMOP2、SMOP4～SMOP8这几个稀疏测试问题中，NSGA-Ⅱ、CMOPSO、MOEA/D-DRA和LMOCSO都无法较好收敛到Pareto前沿，而SMDVDR算法在这几个测试问题上获得了较好的收敛种群。

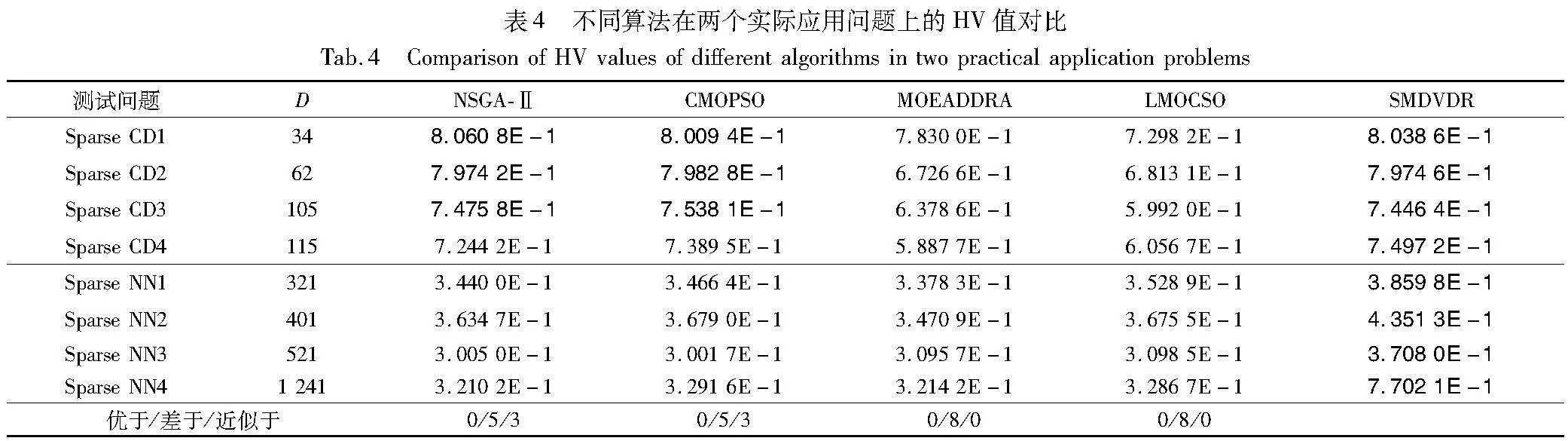
接着在实际应用问题上进行实验测试，由于实际问题中的真实Pareto最优解不可知，IGD指标往往不可以直接用来评价实际问题中的算法性能，所以本文使用HV评价实际问题的算法性能。表4列出本文算法在Sparse CD和Sparse NN两个实际问题上，与NSGA-Ⅱ、CMOPSO、MOEA/D-DRA、LMOCSO和MOEA/DVA五种进化算法的HV值对比，其中最好的结果加粗显示。

从表4可以看出，相比其他算法，SMDVDR在解决这些实际问题中具有显著优势。具体而言，SMDVDR在八个测试例子中一共取得了八个最优的结果，NSGA-Ⅱ和CMOPSO同时在稀疏社区检测问题上获得了三个最优结果。总的来说，SMDVDR在决策变量的个数大于100的时候，表现得比其他算法更好，能说明SMDVDR在大规模多目标优化问题上有显著的优势。

因此，SMDVDR算法在基准测试问题上取得了较优的结果，且在实际问题的应用上也有显著优势。

4 结束语

本文设计了一种基于自变量简约的大规模稀疏多目标进化算法。首先，提出了一种基于LPP降维的自变量简约方法，既保持数据的局部邻居结构不变，又降低原始数据的维数，从而达到提取数据特征的目的。在进化过程中，算法利用新生成的非劣解补充优秀个体加入归档集，并利用归档集训练降维矩阵。然后利用降维矩阵将种群投影到低维空间上，并在低维空间进行交叉变异操作。最后利用当前已知的原始矩阵和低维矩阵，通过最小范数求低维空间到高维空间的逆矩阵，进而求得进化后的矩阵。通过8个SMOP测试问题和2个实际应用问题，对基于自变量简约的稀疏多目标进化算法的性能进行了研究。实验结果表明，基于自变量简约的稀疏多目标进化算法在解决SMOP问题时有较好的效果，在解决实际应用问题上也有明显的优势。

参考文献：

［1］Cui Yunfei，Geng Zhiqiang，Zhu Qunxiong，et al. Review： multi-objective optimization methods and application in energy saving［J］. Energy，2017，125： 681-704.

［2］Suzuki S，Takeno S，Tamura T，et al. Multi-objective Bayesian optimization using Pareto-frontier entropy［C］// Proc of the 37th International Conference on Machine Learning. ［S.l.］： PMLR，2020： 9279-9288.

［3］Cai Xingjuan，Hu Zhaoming，Zhao Peng，et al. A hybrid recommendation system with many-objective evolutionary algorithm［J］. Expert Systems with Applications，2020，159： 113648.

［4］Pan Linqiang，Li Lianghao，He Cheng，et al. A subregion division-based evolutionary algorithm with effective mating selection for many-objective optimization［J］. IEEE Trans on Cybernetics，2019，50（8）： 3477-3490.

［5］Coelho D，Madureira A，Pereira I，et al. A review on MOEA and metaheuristics for feature-selection［C］// Proc of International Conference on Innovations in Bio-Inspired Computing and Applications. Cham： Springer，2021： 216-225.

［6］Verma S，Pant M，Snasel V. A comprehensive review on NSGA-Ⅱ for multi-objective combinatorial optimization problems［J］. IEEE Access，2021，9： 57757-57791.

［7］Singh J. A review and comparison of two archive based algorithms： SPEA2 and PAES［J］. AIP Conference Proceedings，2023，2819（1）： 090003.

［8］Ouelmokhtar H，Benmoussa Y，Diguet J P，et al. Near-optimal cove-ring solution for USV coastal monitoring using PAES［J］. Journal of Intelligent & Robotic Systems，2022，106（1）： 24.

［9］Guerreiro A P，Fonseca C M，Paquete L. The hypervolume indicator： computational problems and algorithms［J］. ACM Computing Surveys，2021，54（6）： 1-42.

［10］Bader J，Zitzler E. HypE： an algorithm for fast hypervolume-based many-objective optimization［J］. Evolutionary Computation，2011，19（1）： 45-76.

［11］Bao Chunteng，Gao Diju，Gu Wei，et al. A new adaptive decomposition-based evolutionary algorithm for multi-and many-objective optimization［J］. Expert Systems with Applications，2023，213：119080.

［12］Tian Ye，Zhang Xingyi，Wang Chao，et al. An evolutionary algorithm for large-scale sparse multiobjective optimization problems［J］. IEEE Trans on Evolutionary Computation，2019，24（2）： 380-393.

［13］Zhou Xiangbing，Cai Xing，Zhang Hua，et al. Multi-strategy competitive-cooperative co-evolutionary algorithm and its application［J］. Information Sciences，2023，635： 328-344.

［14］Peng Chen，Hui Qing. Epsilon-constrained CCPSO with different improvement detection techniques for large-scale constrained optimization［C］// Proc of the 49th Hawaii International Conference on System Sciences. Piscataway，NJ： IEEE Press，2016： 1711-1718.

［15］Aguilar-Justo A E，Mezura-Montes E. A local cooperative approach to solve large-scale constrained optimization problems［J］. Swarm and Evolutionary Computation，2019，51： 100577.

［16］Cheng Ran，Jin Yaochu. A social learning particle swarm optimization algorithm for scalable optimization［J］. Information Sciences，2015，291： 43-60.

［17］陈暄，孟凡光，吴吉义. 求解大规模优化问题的改进狼群算法［J］. 系统工程理论与实践，2021，41（3）： 790-808. （Chen Xuan，Meng Fanguang，Wu Jiyi. Improved wolf pack algorithm for large-scale optimization problems［J］. Systems Engineering-Theory and Practice，2021，41（3）： 790-808.）

［18］Wang Hao，Liang Mengnan，Sun Chaoli，et al. Multiple-strategy lear-ning particle swarm optimization for large-scale optimization problems［J］. Complex & Intelligent Systems，2021，7： 1-16.

［19］Tian Ye，Liu Ruchen，Zhang Xingyi，et al. A multipopulation evolutionary algorithm for solving large-scale multimodal multiobjective optimization problems［J］. IEEE Trans on Evolutionary Computation，2020，25（3）： 405-418.

［20］Suganya A，Singh R A，Velliangiri S，et al. Feature extraction using a residual deep convolutional neural network（ResNet-152） and optimized feature dimension reduction for MRI brain tumor classification［J］. Diagnostics，2023，13（4）： 668.

［21］Cunha B Z，Droz C，Zine A M，et al. A review of machine learning methods applied to structural dynamics and vibroacoustic［J］. Mechanical Systems and Signal Processing，2023，200： 110535.

［22］Hasan B M S，Abdulazeez A M. A review of principal component analysis algorithm for dimensionality reduction［J］. Journal of Soft Computing and Data Mining，2021，2（1）： 20-30.

［23］Anowar F，Sadaoui S，Selim B. Conceptual and empirical comparison of dimensionality reduction algorithms （PCA，KPCA，LDA，MDS，SVD，LLE，ISOMAP，LE，ICA，t-SNE）［J］. Computer Science Review，2021，40： 100378.

［24］Levada A L M. A curvature based isometric feature mapping ［C］// Proc of the 26th International Conference on Pattern Recognition. Piscataway，NJ： IEEE Press，2022： 557-563.

［25］Roth M，Franke G，Rinderknecht S. A comprehensive approach for an approximative integration of nonlinear-bivariate functions in mixed-integer linear programming models［J］. Mathematics，2022，10（13）： 2226.

［26］Zhang Kai，Shen Chaonan，Yen G G，et al. Two-stage double niched evolution strategy for multimodal multiobjective optimization［J］. IEEE Trans on Evolutionary Computation，2021，25（4）： 754-768.

［27］Wang Xiangyu，Zhang Kai，Wang Jian，et al. An enhanced competitive swarm optimizer with strongly convex sparse operator for large-scale multiobjective optimization［J］. IEEE Trans on Evolutionary Computation，2021，26（5）： 859-871.

［28］Hua Yicun，Liu Qiqi，Hao Kuangrong，et al. A survey of evolutionary algorithms for multi-objective optimization problems with irregular Pareto fronts［J］. IEEE/CAA Journal of Automatica Sinica，2021，8（2）： 303-318.

［29］Zhang Xingyi，Zheng Xiutao，Cheng Ran，et al. A competitive mechanism based multi-objective particle swarm optimizer with fast convergence［J］. Information Sciences，2018，427： 63-76.

［30］Xu Meng，Zhang Maoqing，Cai Xingjuan，et al. Adaptive neighbourhood size adjustment in MOEA/D-DRA［J］. International Journal of Bio-Inspired Computation，2021，17（1）： 14-23.

［31］Tian Ye，Zheng Xiutao，Zhang Xingyi，et al. Efficient large-scale multiobjective optimization based on a competitive swarm optimizer［J］. IEEE Trans on Cybernetics，2019，50（8）： 3696-3708.