基于自适应交叉与协方差学习的改进平衡优化器算法
2024-07-31侯新宇鲁海燕卢梦蝶胡清元
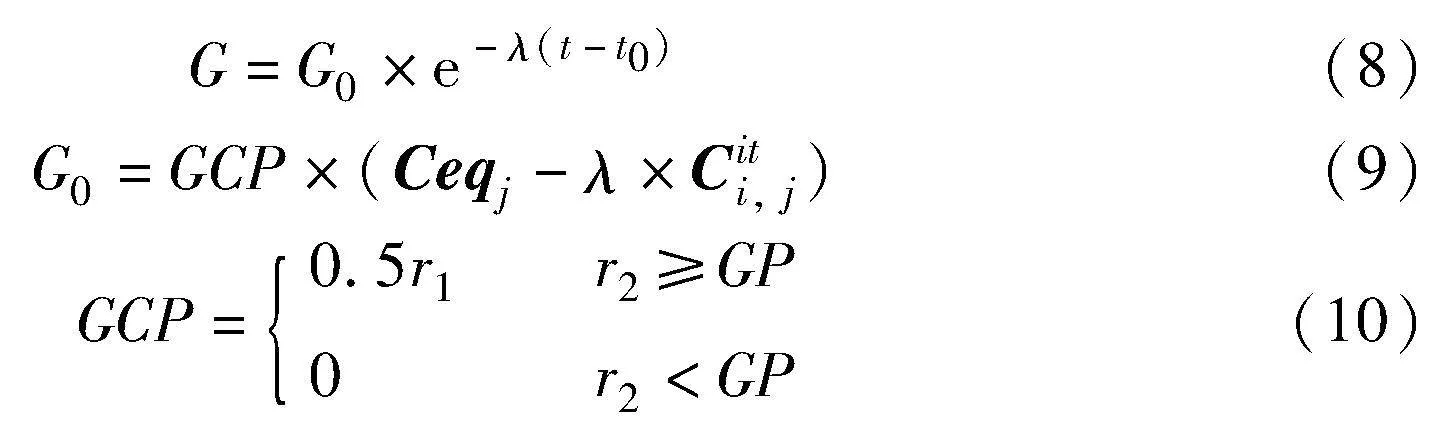


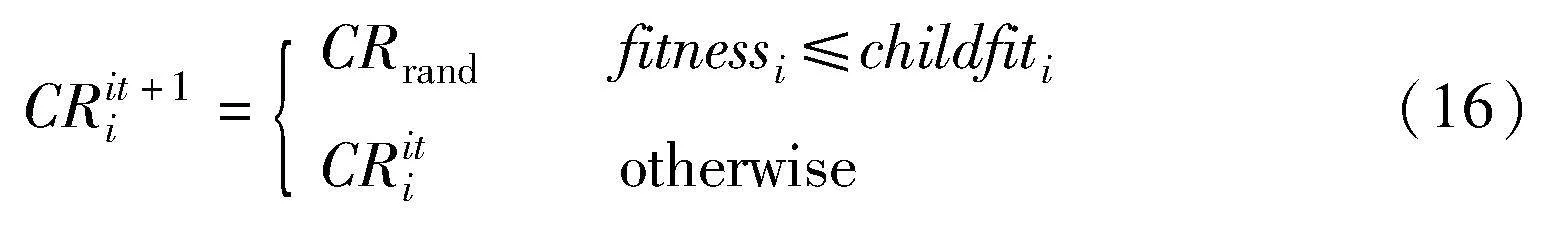
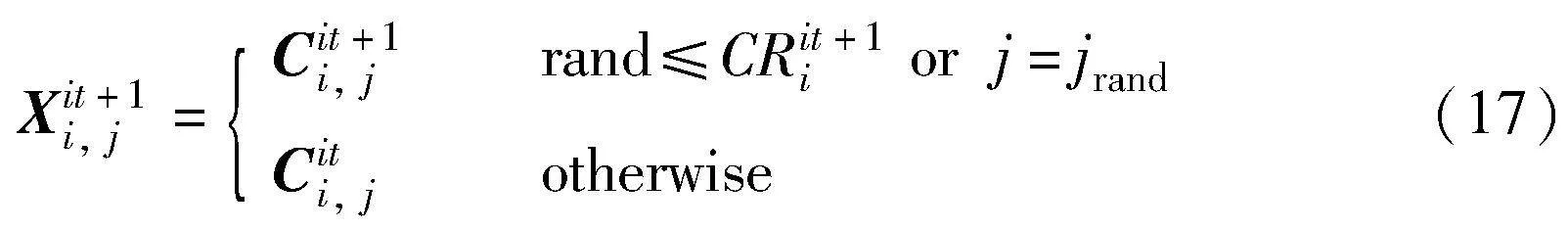



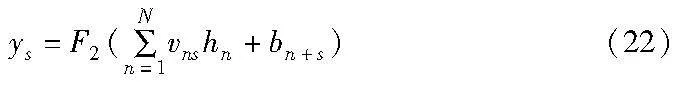

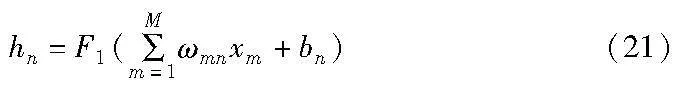
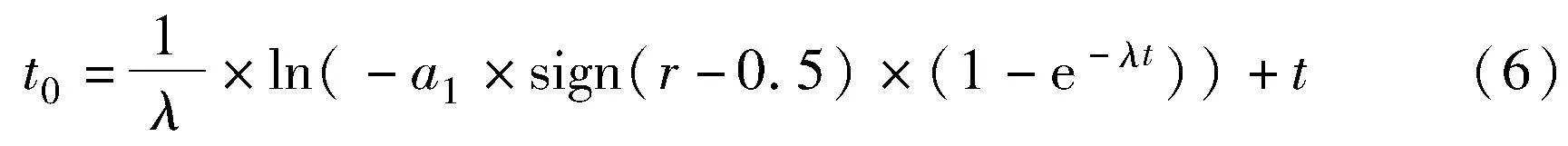




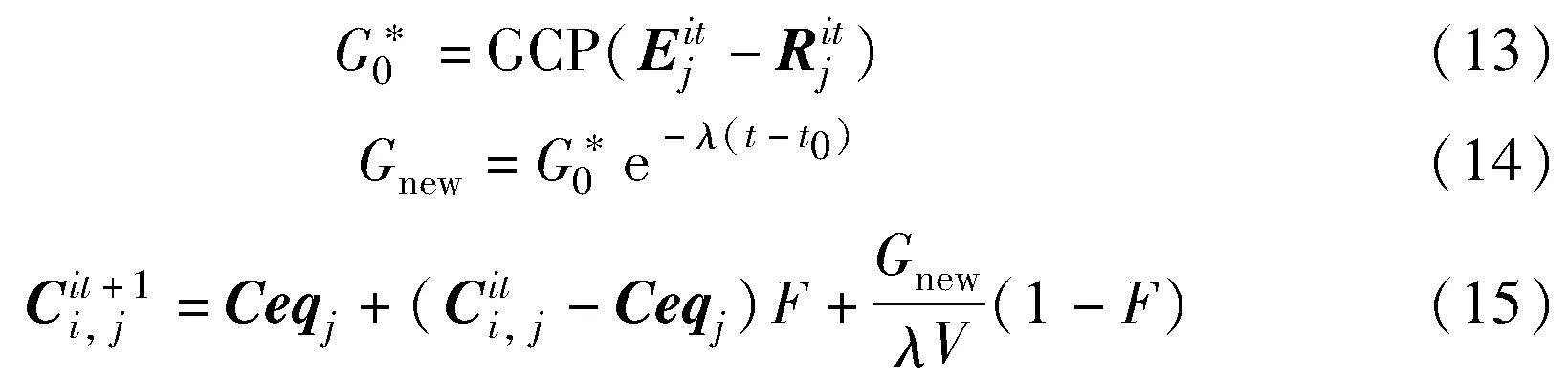
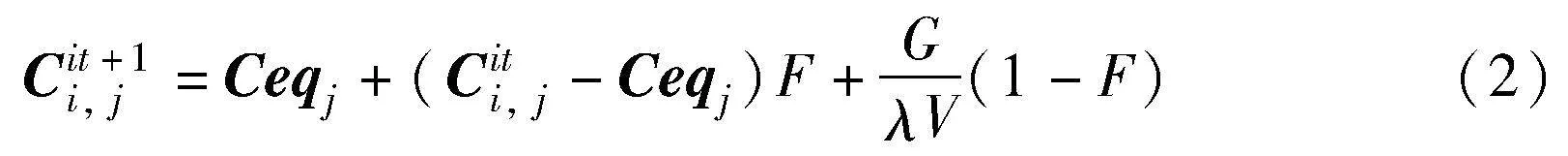
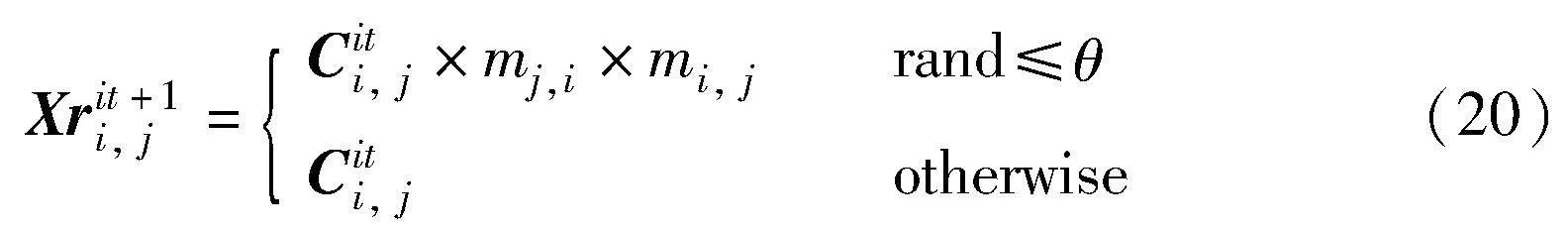

摘 要:针对平衡优化器算法存在的收敛精度低和易陷入局部停滞的问题,提出一种基于自适应交叉与协方差学习的改进平衡优化器算法。首先,构建外部存档来保留历史优势个体,增加种群多样性,以提高算法的全局寻优能力。其次,引入自适应交叉概率来平衡算法的全局探索能力和局部开发能力,以提高算法的寻优精度和鲁棒性。最后,采用协方差学习策略,充分利用浓度向量之间的关系来增强种群间信息交流,以避免算法陷入局部停滞。通过对CEC2019测试函数进行仿真实验,并将改进算法与反向传播(back propagation,BP)神经网络相结合用于预测新疆玛纳斯河的径流情况,实验结果表明,改进算法在收敛精度和鲁棒性方面有显著提升,且大幅提高了BP神经网络的径流预测效果。
关键词:平衡优化器算法;智能算法;外部存档;自适应交叉概率;协方差;径流预测
中图分类号:TP301.6 文献标志码:A文章编号:1001-3695(2024)06-008-1656-07
doi: 10.19734/j.issn.1001-3695.2023.10.0518
Improved equilibrium optimizer based on adaptive crossover and covariance learning
Abstract: Aiming at the problems of low convergence accuracy and ease of trapping into local stagnation in the equilibrium optimizer, this paper proposed an improved equilibrium optimizer based on adaptive crossover and covariance learning. Firstly, this algorithm constructed an external archive to retain the historically dominant individuals and increase the population diversity for improving the global optimization ability. Secondly, it introduced an adaptive crossover probability to balance the global exploration ability and local exploitation ability of the algorithm, so as to improve the optimization accuracy and robustness of the algorithm. Finally, it applied a covariance learning strategy to make full use of the relationship between the concentration vectors to enhance the information exchange among the populations and thereby to avoid local stagnation. Through simulation experiments on the CEC2019 test functions and combining the improved algorithm with back propagation (BP) neural network to predict the runoff situation of the Manas River in Xinjiang, the experimental results show that the improved algorithm remarkably improves convergence accuracy and robustness, and significantly enhances the runoff prediction performance of the BP neural network.
Key words:equilibrium optimizer; intelligence algorithm; external archive; adaptive crossover rate; covariance; runoff prediction
0 引言
目前,优化问题变得更加复杂,因为随机算法可以在不计算目标函数导数的情况下找到最优解,所以在解决优化问题时比传统的数值方法更有优势。元启发式算法是目前应用最广泛的随机算法,大多数元启发式算法属于群体智能和物理启发算法,前者包括蝴蝶优化算法(butterfly optimization algorithm,BOA)[1]、蜜獾算法(honey badger algorithm,HBA)[2]和人工蜂鸟算法(artificial hummingbird algorithm,AHA)[3]等,后者包括算数优化算法(arithmetic optimization algorithm,AOA)[4]、流向算法(flow direction algorithm,FDA)[5]和能量谷优化算法(energy valley optimizer, EVO)[6]等。
玛纳斯河是新疆最具代表性的河流之一,高精度的径流预测对农业、经济以及社会稳定至关重要,是当下迫切需要解决的关键科学问题[7]。传统径流预测模型通过历史经验来推算未来信息,其预测精度难以满足水资源精细化管理的需求[8]。机器学习模型是数据驱动的径流预测模型,在水文预报领域得到了广泛应用。人工神经网络(artificial neural network,ANN)是机器学习的分支之一,反向传播(back propagation,BP)神经网络是目前水文建模中应用最为广泛的ANN[9]。许多学者用智能算法代替BP的梯度下降算法来优化网络参数,从而提高径流预测模型精度。陈芳等人[10]用BOA优化BP神经网络的初始权值和阈值,提高了北京市密云水库潮河流域的预测精度。李代华[11]借助斑点鬣狗算法来优化BP网络参数,更精确地预测了云南省盘龙河径流。然而这些研究只是把算法应用于径流预测模型,没有比较分析算法在不同测试函数上的性能,实验缺少算法泛化能力的讨论。
平衡优化器(equilibrium optimizer,EO)算法是由Faramarzi等人[12]提出的一种物理启发式算法,因其结构简单且求解能力强,已有研究者将其应用于识别燃料电池参数、微电网动态经济调度问题等领域[13~16]。但面对不同问题时,EO表现出收敛精度低、容易陷入局部停滞等缺陷。近年来,已有研究者探索了不同的途径来解决这些缺点。例如,Abdel-Basset等人[17]将线性减少多样性技术与局部最小值消除方法相结合来改进EO;张梦溪等人[18]引入自适应因子来平衡EO的全局搜索和局部开发能力;Hemalatha等人[19]利用高斯变异和基于种群划分的搜索机制来避免EO陷入局部停滞。虽然上述改进算法在不同程度上对EO进行了优化,但是这些算法仍然存在种群多样性不足、探索开发能力不平衡和种群间信息交流不够等问题。为此,本文首先构建外部存档改进的生成率来提高种群多样性,其次引入自适应交叉概率来平衡探索开发能力,最后采用协方差学习策略来增加种群间信息交流,结合上述策略提出基于自适应交叉与协方差学习的改进平衡优化器(improved equilibrium optimizer based on adaptive crossover and covariance learning,ACCLIEO)算法。为检验ACCLIEO的泛化能力,本文首先在CEC2019测试函数上检验其收敛精度和跳出局部停滞的能力,然后将ACCLIEO与BP结合来建立玛纳斯河径流预测模型,并进行模型预测精度的实验分析。
1 平衡优化器算法
平衡优化器算法的灵感来自于控制体积上简单的动态质量平衡,其物理原理为控制体积质量随时间的变化与进出系统质量的差值相等。本文假设有N个D维的浓度向量,第i个浓度向量在第it次迭代的位置记为Citi(i∈1,2,…,N)。EO运用随机初始化方式种群,初始化公式如下:
Cit+1i, j=LBj+randj×(UBj-LBj)(1)
其中:Cit+1i, j是Cit+1i第j维分量, j∈1,2,…,D;rand是位于(0,1)的随机数;UBj和LBj分别表示第j维的上界和下界。在算法迭代中,用式(5)更新浓度向量:
其中:λ是由[0,1]组成的随机数;V是单位体积;Ceq是从平衡池中随机选择的浓度向量;Ceqj是Ceq的第j维分量。平衡池Cpool的构造如下:
Cpool={Ceq(1),Ceq(2),Ceq(3),Ceq(4),Ceqave}(3)
其中:Ceq(1)、Ceq(2)、Ceq(3)、Ceq(4)、Ceqave分别是当前迭代中4个最好的浓度向量和它们的平均向量。F是指数项参数,其表达式为
其中:时间t的公式为
其中:a2是控制常量;T是最大迭代次数。t0具体如下:
其中:a1是控制常量;r是位于(0,1)的随机数。将式(6)中给出的表达式代入式(4)后,得到的指数项参数F为
F=a1×sign(r-0.5)×(e-λt-1)(7)
式(2)的生成率G是EO中的主要影响因素之一,该参数的值定义如下:
其中:GP为生成率概率;GCP为生成率G的控制参数;G0控制是否使用GCP来更新浓度向量;r1和r2是(0,1)中均匀分布的随机数。
2 基于自适应交叉与协方差学习的改进平衡优化器算法
2.1 引入外部存档优化生成率
生成率G是EO中的主要影响因素之一,但是在EO中,G仅由本次迭代中平衡池和随机的浓度向量得到,不考虑前几代产生的浓度向量,不利于算法的全局寻优。外部存档[20]能够保护种群的历史信息,以提高算法全局寻优能力。因此,本文引入外部存档来优化EO的生成率G。
首先,构造一个用来保存部分历史个体的外部存档Cea,公式如下:
Cea={Cea(1),Cea(2),…,Cea(κ)}(11)
κ=round(ω×N)(12)
其中:Cea(1),Cea(2),…,Cea(κ)是所有迭代中适应度值排名前κ的浓度向量;round是四舍五入的取整函数;ω是比例系数;N为种群大小。
其次,用第it代随机挑选的浓度向量Eit和外部向量Rit来改进生成率Gnew,并最终更新浓度向量。具体公式如下:
其中:Eitj和Ritj分别是Eit和Rit的第j维分量;Gnew为改进的生成率。
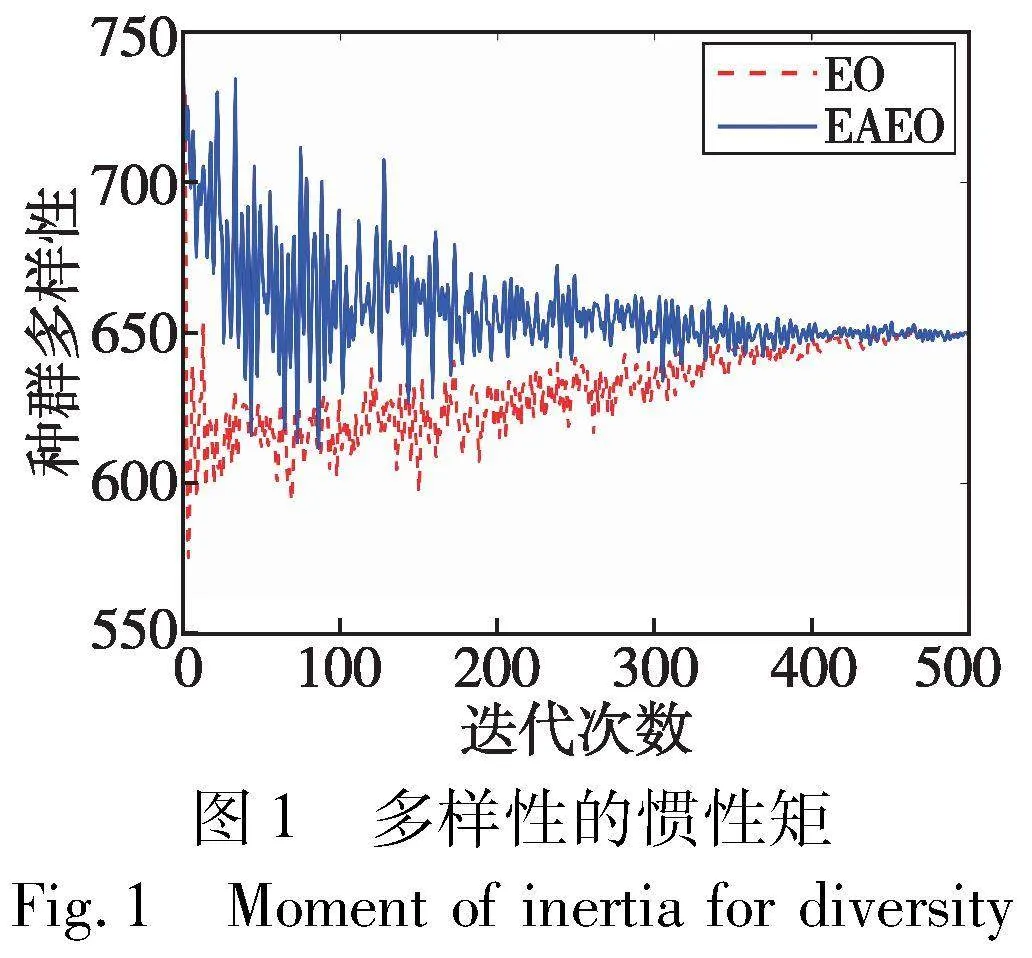
为了研究上述策略对算法种群多样性的影响,本节采用Morrison[21]提出的惯性矩来测量算法的种群多样性,图1为EO和引入外部存档优化生成率的EO(EAEO)在CEC2019[22]多峰函数F7上测量的惯性矩。
由图1可知,EAEO的种群多样性波动更大,并且多样性优于EO,表明改进策略提高了算法的全局寻优能力。
2.2 自适应交叉概率
交叉变异策略有利于算法跳出局部最优,可以平衡算法的探索和开发能力,但是仅仅引入交叉概率会导致寻优的盲目性,因此许多研究者[23~25]将自适应交叉概率作为控制交叉变异策略的重要因素。为了提高EO的寻优精度和鲁棒性,本文引入自适应交叉概率来控制浓度向量的选择。
首先,本文根据父代和子代浓度的适应度值,挑选适应度值更小的优势位置来调整交叉概率,具体公式如下:
其中:CRiti为第it代的i个位置的交叉概率,初始值设置为0.5;fitnessi和childfiti分别为第i个父代和子代适应度值;CRrand为服从均值为0.5、方差为0.1的正态分布的随机数。
最后,本文用自适应交叉概率来更新浓度位置,具体公式如下:
其中:Xit+1i, j为第it+1代经自适应交叉概率选择的第(i, j)个浓度位置;Cit+1i, j是浓度向量Cit+1i的第j个位置,Cit+1i由式(15)得到;rand为(0,1)的随机数; jrand为1~D中随机挑选的整数,确保Xit+1i, j中至少有一部分来自Cit+1i。
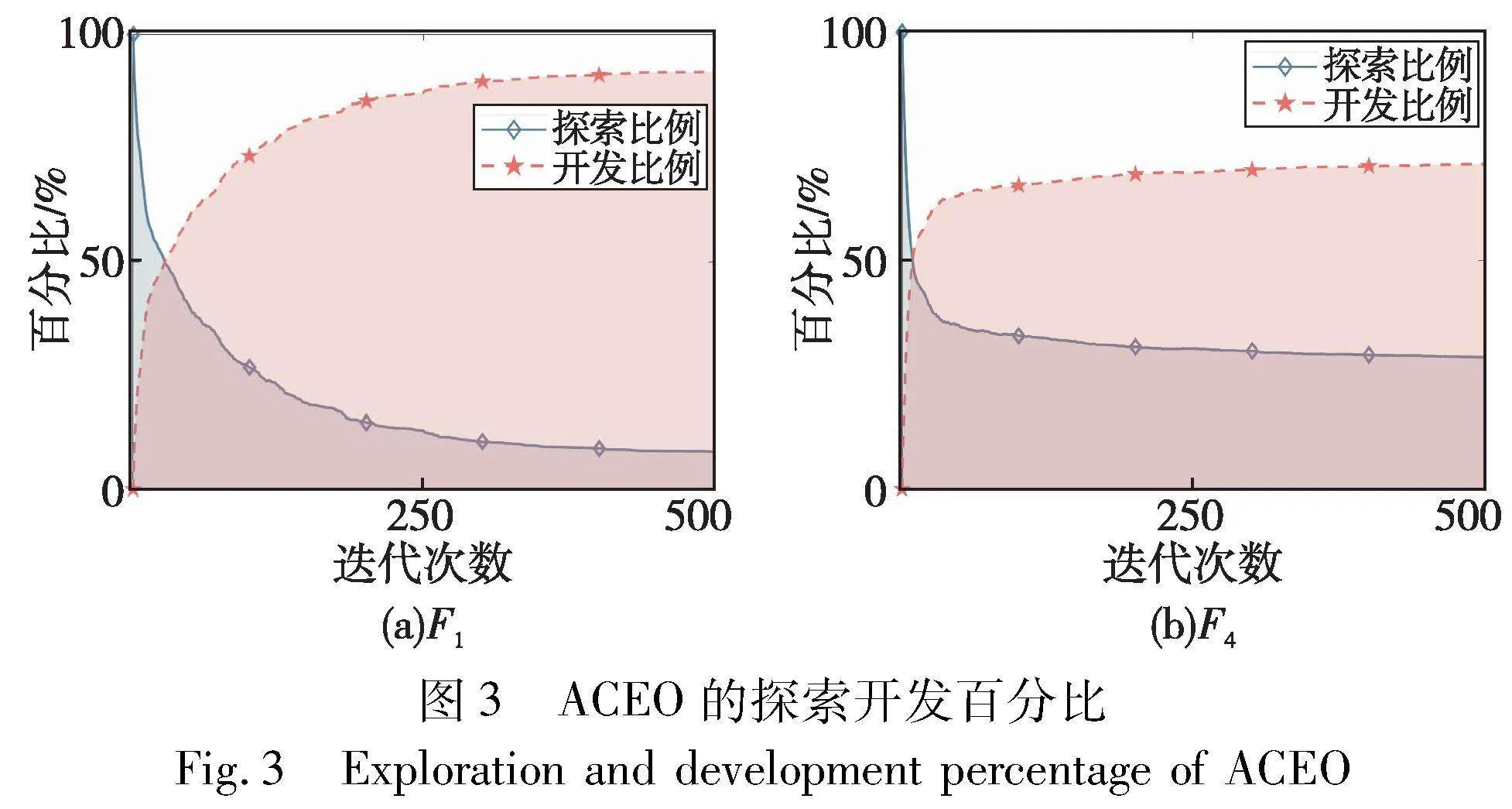
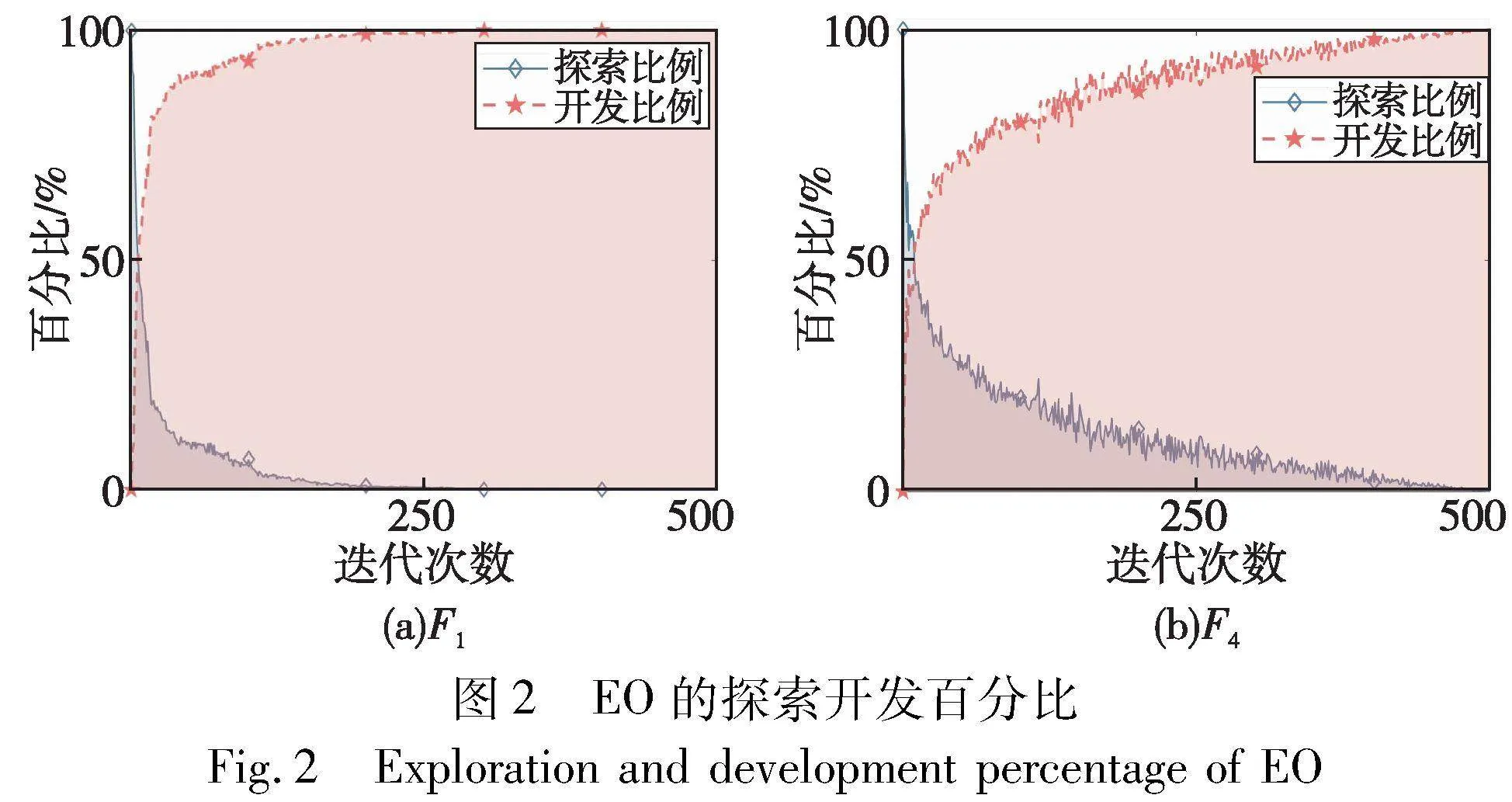
算法的全局探索和局部开发过程分别是增加和降低个体之间距离的过程,因此两者的平衡可以保证算法保留多样性的同时提高收敛精度。本节采用Hussain等人[26]提出的探索开发百分比进行对比实验,图2为EO分别在CEC2019单峰函数F1和多峰函数F4上得到的探索开发百分比,图3为融合自适应交叉概率的EO(ACEO)在相同测试函数下得到的探索开发百分比。
由图2可知,EO的开发能力更强,探索能力更弱,两种能力不平衡,因此容易陷入局部最优,由图3可知,ACEO开发能力随迭代平缓增加,并且时刻保持一定的探索能力,因此自适应交叉概率平衡了算法的探索和开发能力。本文在后续实验中验证了该策略对算法收敛精度的影响。
2.3 协方差学习策略
为了提高浓度向量之间的联系,避免算法陷入局部停滞,本文采用协方差矩阵[27~29]搭建一个有相关性的特征坐标系,令更新后的浓度向量在这个坐标系中进行更新。具体操作如下:
在种群第it代中,第i、 j维的协方差矩阵为
A={ai, j|ai, j=cov(i, j)}(19)
随后进行协方差学习策略,具体操作如下:首先利用特征分解来得到协方差矩阵A的特征向量矩阵M=(mj,i)∈CD×N;其次根据M组成一个种群特征坐标系;最后根据变异参数选择个体,并将其映射在特征坐标系中。具体公式如下:
其中:Xrit+1i, j为经过协方差学习策略更新后的第(i, j)个浓度位置;θ为控制协方差学习的参数,设置为0.4。
2.4 ACCLIEO算法伪代码
在EO的基础上,首先,AMSLEO引入外部存档来优化生成率;其次,结合自适应交叉概率来平衡EO的全局探索和局部开发;最后,采用协方差学习策略来增强种群间信息交流。
算法1 ACCLIEO算法
3 仿真实验与分析
3.1 测试函数与实验算法
本文使用全套CEC2019测试函数来评估ACCLIEO的有效性,以上测试函数的信息如表1所示。实验中,计算机的操作系统为Windows 11,CPU为AMD Ryzen 7 5800H,主频3.20 GHz,内存16 GB,编程软件为MATLAB 2022a。本文使用蝴蝶优化算法、蜜獾算法、算数优化算法、流向算法、人工蜂鸟算法、能量谷优化算法、平衡优化器算法与ACCLIEO进行实验对比,以上算法的参数设置与原文献保持一致。
3.2 算法寻优性能实验与分析
为了实验的公平性,本文设置最大迭代次数为1 500,并记录8种算法在CEC2019测试函数上分别独立运行30次所得最优解的平均值(mean)和标准差(Std)。实验结果如表2所示,最优结果加粗处理。
由表2可知,虽然在F1上ACCLIEO的结果达不到最优值,但是显著提高了EO的收敛精度和稳定性,且接近理论最优值;在F2上所有算法都达不到理论最优值,但是ACCLIEO相比于EO的收敛效果得到较大提升;在F3~F10上,ACCLIEO的收敛精度和鲁棒性均优于其他8种算法。综合来看,在CEC2019测试函数上,ACCLIEO有更好的收敛精度和鲁棒性。
3.3 收敛曲线分析
为了直观比较算法的收敛性,本节绘制了算法在CEC2019测试函数上的收敛曲线,如图4所示。
在F1和F2上,虽然ACCLIEO收敛速度弱于BOA、HBA和AHA,但是其收敛曲线在缓慢下降,不断接近理论最优值,收敛精度和跳出局部最优的能力比其他算法更有优势。
在F3上,虽然ACCLIEO前期收敛速度略逊于AHA、HBA和EO,但是最终迭代18475ed5a1d97b95882c908fdfaef2cd76c76f4d5224325671db1df6c6ea6958结果优于其他7种算法。在F4和F6上,ACCLIEO收敛速度最快且精度最高。在F5和F9上,除BOA和AOA之外的算法几乎同时收敛,并且表2中ACCLIEO的收敛精度最高,说明其收敛精度的提高并未牺牲收敛速度。在F7、F8和F10上,ACCLIEO收敛速度和收敛精度远远优于其他算法。
综合来看,ACCLIEO整体实验结果比其他7种算法更接近理论最优值、持续寻优能力更强、收敛精度更高。
3.4 改进策略有效性分析
为了验证ACCLIEO中3种改进策略的有效性,将ACCLIEO与EO、EAEO、ACEO、引入协方差学习策略的EO(CLEO)进行比较。本节实验统一设置种群规模为30、迭代次数为1 500且独立运行30次,以保证实验的公平性。表3记录实验结果,最优结果加粗标出。由表3可知,EAEO在一半CEC2019测试函数上寻优性能比原始EO强,说明引入外部存档来优化EO生成率的策略增加了种群多样性,提高了EO的全局寻优能力;ACEO的整体性能比EO更优,且稍逊于ACCLIEO,验证了自适应交叉概率平衡EO的全局探索和局部开发能力,提高了EO的寻优精度和鲁棒性;CLEO在F1和F2上的收敛效果是最好的,且整体性能比EO有优势,说明协方差学习策略充分利用了浓度向量之间的关系来增强种群间的信息交流,避免算法局部收敛。
整体来看,虽然EAEO、ACEO和CLEO都对EO有一定的提升,甚至在某些测试函数上比ACCLIEO精度和鲁棒性更优,但是只有ACCLIEO在每个测试函数上都比原始EO有更优的收敛性能。由此可知,ACCLIEO牺牲了某些单独改进策略的优势,换取了算法整体效果的提升。因此,3种策略相结合比单一策略效果好,能够更好地提高EO的寻优精度和鲁棒性。
4 玛纳斯河径流预测
4.1 BP神经网络原理
BP神经网络是目前水文建模中应用最为广泛的ANN,图5为一个典型的三层BP结构示意图。
输入值x=(x1,x2,…,xM)和预测值y=(y1,y2,…,yS)通过隐藏层h=(h1,h2,…,hN)连接,其中M、N、S分别是输入层、隐藏层和输出层的神经元总数。输入层到隐藏层:
其中:hn是第n个隐藏层神经元;xm是第m个输入数据;ωmn是两层间的连接权重;bn是hn的偏置项。隐藏层到输出层:
其中:ys是第s个输出值;vns是连接两层的权重;bn+s是ys的偏置项;F1(·)和F2(·)是激活函数。BP神经网络每层之间激活函数必须可微[30],因此双曲正切sigmoid函数和线性函数分别作为激活函数F1(·)和F2(·),连接输入层到隐藏层,隐藏层到输出层。误差反向传播过程:
vns(t+1)=lEs+vns(t)(23)
其中:vns(t+1)和vns(t)分别为t+1和t时刻的权值;l为学习率;Es为第s个输出层的误差。输出层到隐藏层的权值ωmn(t+1)同理更新,达到误差设定时结束。此外,BP神经网络借助MATLAB工具箱中的Newff、Train和Sim函数实现。
4.2 基于ACCLIEO的BP预测模型
传统BP网络基于梯度下降训练方式,网络的学习容易陷入局部最优,求解径流预测结果的能力较差。因此,本节采用ACCLIEO代替BP的梯度下降算法实现模型率定,以寻找神经网络的最优参数。利用ACCLIEO优化BP神经网络参数的具体步骤如下:
a)将1954—2016年玛纳斯河的月径流作为原始数据,并按照0.55∶0.2∶0.25[31]将其划分为训练集、验证集、测试集。
b)输入ACCLIEO算法的参数,随机生成初始解,每个解代表个体的位置,如图6所示。
c)根据ACCLIEO的迭代寻优机制,更新个体位置,得到新种群。在每一次迭代过程中,利用种群个体在训练集上建立模型,并借助验证集检验模型的训练结果,将训练结果与实际结果之间的误差作为适应度值。
d) 判断是否满足ACCLIEO的迭代终止条件,若满足输出最优解,此时将原来的训练集和验证集合并成新的训练集,利用最优解重新训练模型,最后利用训练后的模型实现测试集的预测;否则,重复步骤c)d),直到满足终止条件。
4.3 径流预测评价指标
为了全面比较智能算法与BP网络结合后的效果,本节采用标准化后的均方根误差(NRMSE)、平均绝对相对误差(MAPE)和纳什效率系数(NSE)三种水文领域经典指标[32]进行测试,具体公式如下:
的优劣,其值越小,预测精度越优;NSE描述样本信息的拟合程度,其范围为(-∞,1),越接近1说明预测结果越稳定。
4.4 实验分析
实验数据为1954—2016年玛纳斯河的月径流,来源于肯斯瓦特水库。改进BP预测建模过程参照4.2节,8种改进BP神经网络预测模型分别记为BOABP、HBABP、AOABP、FDABP、AHABP、EVOBP、EOBP和ACCLIEOBP。
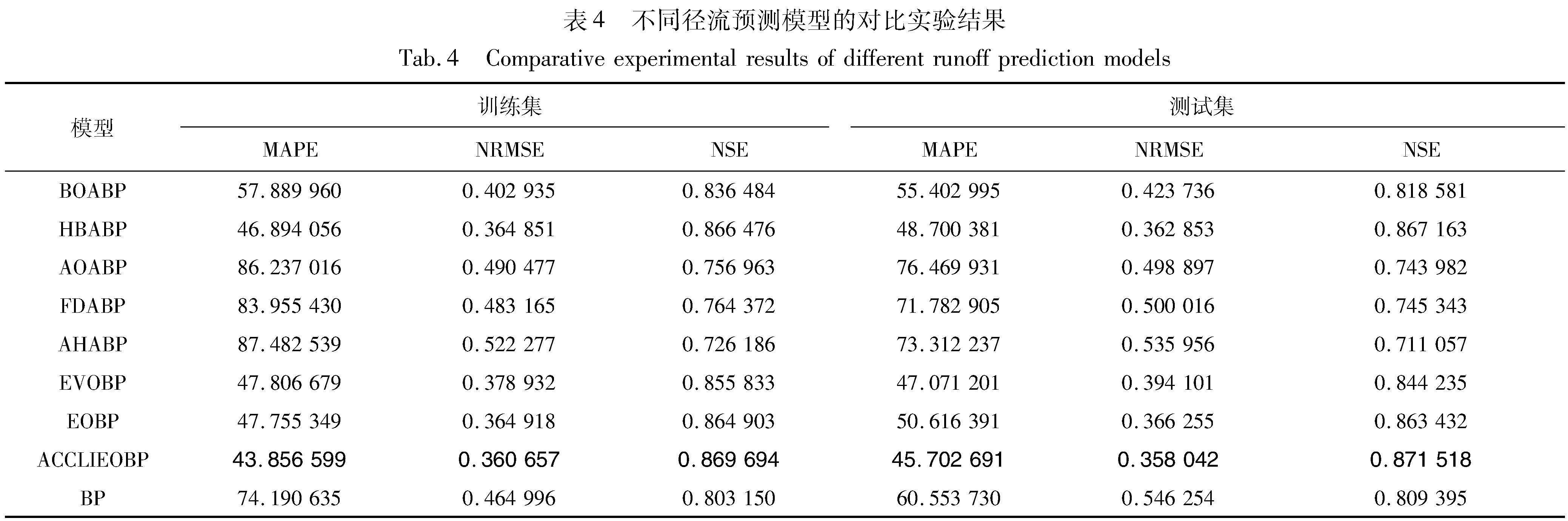
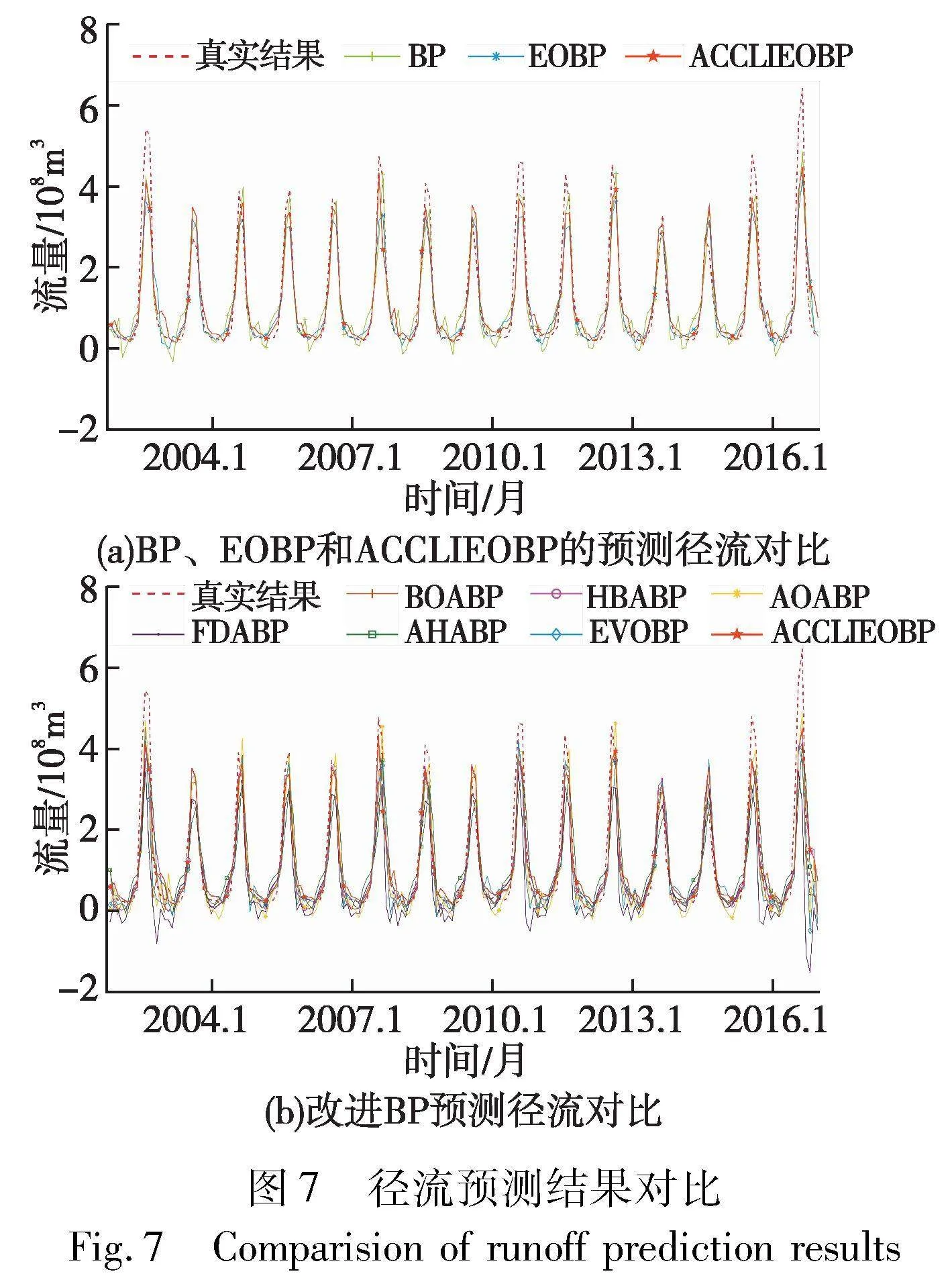
为了保证NRMSE、MAPE和NSE的公平性,上述3个指标为8种改进BP模型和BP模型独立运行20次的平均值,记录在表4中,最优结果加粗处理。为了直观比较径流预测模型的效果,图7给出了预测模型的结果对比。图7(a)为BP、EOBP和ACCLIEOBP的预测结果与真实值的对比;图7(b)为优化模型BOABP、HBABP、AOABP、FDABP、AHABP、EVOBP、ACCLIEOBP的预测结果与真实值的对比。
由表4可知,ACCLIEOBP与改进模型和原始BP预测模型相比,在训练集和测试集上评价指标最优。因此ACCLIEOBP是收敛精度和稳定性最好的改进BP径流预测模型。
由图7(a)可知,径流模型在最高点都存在预测偏差,但是由ACCLIEOBP预测的径流和真实值最吻合。BP预测在最高点的预测上有优势,但是在最低点预测出现负值,偏离真实结果的问题较严重。由图7(b)可知,在预测过程中,FDABP预测结果较差,AOABP预测经常超过最大径流,波动过大,ACCLIEOBP相较于其他模型更加接近真实值。
综上所述,ACCLIEOBP模型用于径流预测是可行和可靠的,可以有效提高BP模型的预测精度和泛化能力,因此ACCLIEO算法在径流预测领域有一定的优势。
5 结束语
针对平衡优化器算法收敛精度低和易陷入局部停滞的问题,本文提出一种基于自适应交叉与协方差学习的改进平衡优化器算法。改进算法引入外部存档来保留历史优势个体,增强了浓度向量多样性,从而提高了算法的全局寻优能力;该算法引入自适应的交叉概率,更好地平衡了算法的全局勘探和局部开发能力;协方差学习策略的引入加强了浓度向量之间的信息交流,避免了算法陷入局部停滞。上述三种策略共同作用下的ACCLIEO在全套CEC2019测试函数上的收敛精度和鲁棒性都得到显著提高,在改进径流预测模型的性能方面也有一定的优势,验证了ACCLIEO的收敛精度、收敛速度和实用可靠性。在未来研究中,可将改进算法应用到最新的测试函数和其他机器学习预测模型中。
参考文献:
[1]Arora S,Singh S. Butterfly optimization algorithm: a novel approach for global optimization [J]. Soft Computing,2019,23: 715-734.
[2]Hashim F A,Houssein E H,Hussain K,et al. Honey badger algorithm: new metaheuristic algorithm for solving optimization problems [J]. Mathematics and Computers in Simulation,2022,192: 84-110.
[3]Zhao Weiguo,Wang Liying,Mirjalili S. Artificial hummingbird algorithm: a new bio-inspired optimizer with its engineering applications [J]. Computer Methods in Applied Mechanics and Enginee-ring,2022,388: 114194.
[4]Abualigah L,Diabat A,Mirjalili S,et al. The arithmetic optimization algorithm [J]. Computer Methods in Applied Mechanics and Engineering,2021,376: 113609.
[5]Karami H,Anaraki M V,Farzin S,et al. Flow direction algorithm (FDA): a novel optimization approach for solving optimization problems [J]. Computers & Industrial Engineering,2021,156: 107224.
[6]Azizi M,Aickelin U,Khorshidi H A,et al. Energy valley optimizer: a novel metaheuristic algorithm for global and engineering optimization [J]. Scientific Reports,2023,13(1): 226.
[7]Wang Qingjie,Yue Chunfang,Li Xiaoqing,et al. Enhancing robustness of monthly streamflow forecasting model using embedded-feature selection algorithm based on improved gray wolf optimizer [J]. Journal of Hydrology,2023,617: 128995.
[8]陈守煜,薛志春,李敏,等. 基于可变集的年径流预测方法 [J]. 水利学报,2014,45(8): 912-920. (Chen Shouyu,Xue Zhichun,Li Min,et al. Annual runoff prediction method based on the variable sets [J]. Journal of Hydraulic Engineering,2014,45(8): 912-920.)
[9]Tan Qiaofeng,Lei Xiaohui,Wang Xu,et al. An adaptive middle and long-term runoff forecast model using EEMD-ANN hybrid approach [J]. Journal of Hydrology,2018,567: 767-780.
[10]陈芳,张志强,李扉,等. 基于EEMD分解与BOA算法优化神经网络的密云水库大阁水文站径流预测 [J]. 西北林学院学报,2021,36(6): 188-194. (Chen Fang,Zhang Zhiqiang,Li Fei,et al. Run-off prediction of Dage Hydrological Station of Miyun Reservoir based on EEMD decomposition and neutral network optimized by BOA algorithm [J]. Journal of Northwest Forestry University,2021,36(6): 188-194.)
[11]李代华. 基于PCA-SHO-SVM和PCA-SHO-BP模型的径流预测 [J]. 水资源与水工程学报,2021,32(1): 97-102. (Li Daihua. Run off prediction based on PCA-SHO-SVM and PCA-SHO-BP models [J]. Journal of Water Resources &Water Engineering,2021,32(1): 97-102.)
[12]Faramarzi A,Heidarinejad M,Stephens B,et al. Equilibrium optimizer: a novel optimization algorithm [J]. Knowledge-Based Systems,2020,191: 105190.
[13]Menesy A S,Sultan H M,Kamel S. Extracting model parameters of proton exchange membrane fuel cell using equilibrium optimizer algorithm [C]// Proc of International Youth Conference on Radio Electronics,Electrical and Power Engineering. Piscataway,NJ: IEEE Press,2020: 1-7.
[14]Bastawy M,Ebeed M,Rashad A,et al. Micro-grid dynamic economic dispatch with renewable energy resources using equilibrium optimizer [C]// Proc of IEEE Electric Power and Energy Conference. Pisca-taway,NJ: IEEE Press,2020: 1-5.
[15]Gupta S,Deep K,Mirjalili S. An efficient equilibrium optimizer with mutation strategy for numerical optimization [J]. Applied Soft Computing,2020,96: 106542.
[16]李守玉,何庆,陈俊. 改进平衡优化器算法的WSN覆盖优化 [J]. 计算机应用研究,2022,39(4): 1168-1172. (Li Shouyu,He Qing,Chen Jun. Improved equilibrium optimizer algorithm for WSN coverage optimization [J]. Application Research of Computers,2022,39(4): 1168-1172.)
[17]Abdel-Basset M,Mohamed R,Mirjalili S,et al. Solar photovoltaic parameter estimation using an improved equilibrium optimizer [J]. Solar Energy,2020,209: 694-708.
[18]张梦溪,马良,刘勇. 融合浓度平衡和菲克定律的新平衡优化器算法 [J]. 计算机工程与应用,2023,59(3): 66-76. (Zhang Mengxi,Ma Liang,Liu Yong. New equilibrium optimizer algorithm combining concentration equilibrium and Fick’s law [J]. Computer Engineering and Applications,2023,59(3): 66-76.)
[19]Hemalatha R,Umamaheswari R,Jothi S. Optimal route maintenance based on adaptive equilibrium optimization and GTA based route discovery model in MANET [J]. Peer-to-Peer Networking and Applications,2021,14(6): 3416-3430.
[20]Zhang Jingqiao,Sanderson A C. JADE: adaptive differential evolution with optional external archive [J]. IEEE Trans on Evolutionary Computation,2009,13(5): 945-958.
[21]Morrison R W. Designing evolutionary algorithms for dynamic environments [M]. Berlin: Springer,2004.
[22]Price K V,Awad N H,Ali M Z,et al. Problem definitions and evaluation criteria for the 100-digit challenge special session and competition on single objective numerical optimization [D]. Singapore: Nanyang Technological University,2018.
[23]Gong Wenyin,Cai Zhihua,Wang Yang. Repairing the crossover rate in adaptive differential evolution [J]. Applied Soft Computing,2014,15: 149-168.
[24]Zhou Yinzhi,Yi Wenchao,Gao Liang,et al. Adaptive differential evolution with sorting crossover rate for continuous optimization problems [J]. IEEE Trans on Cybernetics,2017,47(9): 2742-2753.
[25]Haenel Q,Laurentino T G,Roesti M,et al. Meta-analysis of chromosome-scale crossover rate variation in eukaryotes and its significance to evolutionary genomics [J]. Molecular Ecology,2018,27(11): 2477-2497.
[26]Hussain K,Salleh M N M,Cheng S,et al. On the exploration and exploitation in popular swarm-based metaheuristic algorithms [J]. Neural Computing and Applications,2019,31: 7665-7683.
[27]Mohamed A W,Hadi A A,Fattouh A M,et al. LSHADE with semi-parameter adaptation hybrid with CMA-ES for solving CEC 2017 benchmark problems [C]// Proc of IEEE Congress on Evolutionary Computation. Piscataway,NJ: IEEE Press,2017: 145-152.
[28]毛睿达,李骥阳,罗明. 一种基于协方差矩阵重构和EMP的宽带波束形成算法 [J]. 计算机应用研究,2019,36(4): 1197-1199. (Mao Ruida,Li Jiyang,Luo Ming. Broadband beamforming algorithm based on covariance matrix reconstruction and EMP [J]. Application Research of Computers,2019,36(4): 1197-1199.)
[29]张莉,李彬,田联房,等. 基于Log-Euclidean协方差矩阵描述符的医学图像配准 [J]. 计算机学报,2019,42(9): 2087-2099. (Zhang Li,Li Bin,Tian Lianfang,et al. Medical image registration based on Log-Euclidean covariance matrices descriptor [J]. Chinese Journal of Computers,2019,42(9): 2087-2099.)
[30]Yang Tiantian,Asanjan A A,Welles E,et al. Developing reservoir monthly inflow forecasts using artificial intelligence and climate phenomenon information [J]. Water Resources Research,2017,53(4): 2786-2812.
[31]王庆杰. 基于特征选择和时频分析的径流预测机器学习模型研究 [D]. 乌鲁木齐: 新疆农业大学,2023. (Wang Qingjie. A machine learning model for runoff prediction based on feature selection and joint time-frequency analysis [D]. rümqi: Xinjiang Agricultu-ral University,2023.)
[32]Meng Erhao,Huang Shengzhi,Huang Qiang,et al. A hybrid VMD-SVM model for practical streamflow prediction using an innovative input selection framework [J]. Water Resources Management,2021,35(4): 1321-1337.
