基于相对距离和历史成功率机制的增强麻雀搜索算法

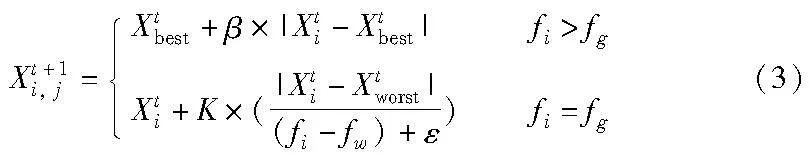
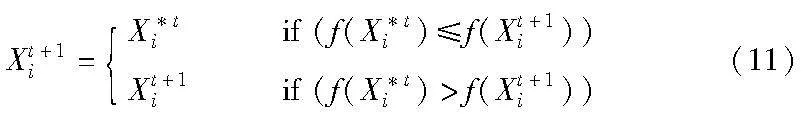
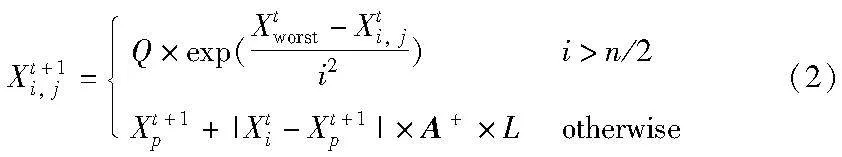
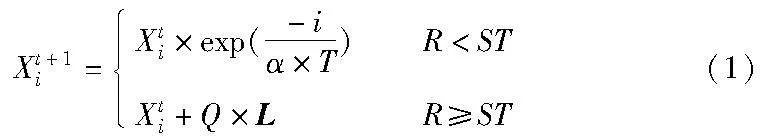
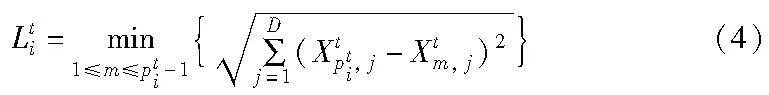
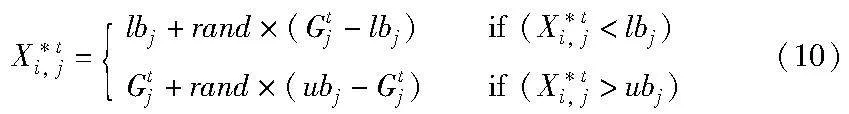
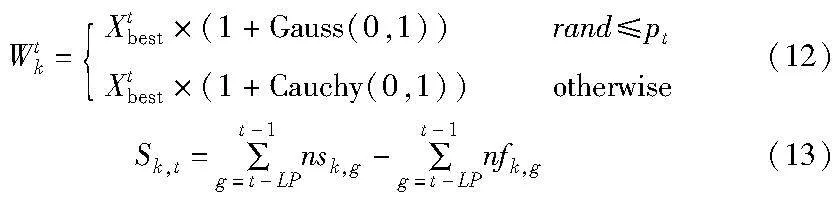
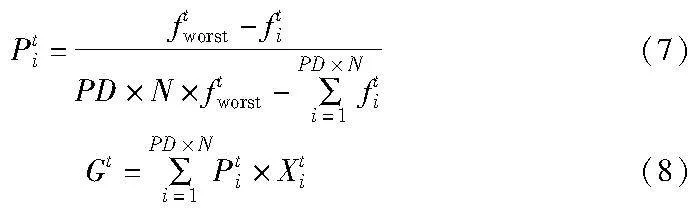
摘 要：针对麻雀搜索算法收敛精度低、易陷入局部最优等问题，提出了一种融合相对距离和历史成功率的增强麻雀搜索算法（RHSSA）。首先，RHSSA引入一种融合适应度值与相对距离的发现者选择方式，使选出的发现者既保持较高质量，又保持在搜索空间的分布广泛；其次，RHSSA在麻雀发现者搜索过程中，采用融合加权重心的反向学习策略，充分挖掘搜索空间的优质位置信息并减弱发现者向原点聚集的趋势；最后，RHSSA引入基于历史成功率的自适应选择算子动态地选择柯西变异与高斯变异对最优解做扰动，提高算法跳出局部最优的能力。选用CEC2017测试函数集中的12个函数作为性能基准函数，将RHSSA与其他五种改进的麻雀搜索算法（AMSSA、SCSSA、SHSSA、ISSA、CSSOA）进行性能评测。基于实验数据的Friedman检验表明，RHSSA能获取最优的结果。为验证提出的改进策略的有效性，还对改进策略进行了消融实验。实验结果表明在综合改进策略的共同作用下，RHSSA的综合优化性能排名为第一名。

关键词：麻雀搜索算法；适应度值与相对距离；加权重心；反向学习；自适应选择算子

中图分类号：TP306.1 文献标志码：A文章编号：1001-3695（2024）06-006-1640-09

doi： 10.19734/j.issn.1001-3695.2023.09.0502

Enhanced sparrow search algorithm by adopting mechanism based on relative distance and historical success rate

Abstract：Aiming to overcome faults of lower convergence accuracy and susceptibility to local optima in sparrow search algorithm （SSA）， this paper proposed an enhanced sparrow search algorithm by adopting the mechanism based on relative distance and historical success rate， namely RHSSA. Firstly， RHSSA introduced a discoverer selection method that integrated fitness values and relative distance to make selected discoverers maintaining high quality and wider distribution in search space. Secondly， RHSSA adopted a reverse learning strategy that integrated weighted center of gravity during each search iteration of discovers in order to fully mining the high-quality location information in the search space and weakening discoverers’ trend to gather towards the origin. Finally， RHSSA also used an adaptive selection operator based on historical success rate to dynamically select between Cauchy and Gaussian mutations to disturb the optimal solution to improve the algorithm’s ability to jump out of local optimal. 12 functions were selected from the CEC2017 test function suit as the benchmark to evaluate RHSSA with five other improved sparrow search algorithms（AMSSA， SCSSA， SHSSA， ISSA， and CSSOA）. The result of Friedman test based on experimental data shows that RHSSA can achieve the supreme performance among all evaluated algorithms. To futher verify effectiveness of the proposed improvement strategies， ablation experiments were conducted. The result illustrates that under the combination of all proposed improvement strategies， RHSSA ranks first in comprehensive optimization performance.

Key words：sparrow search algorithm; fitness value and relative distance; weighted center of gravity; opposition-based lear-ning; adaptive selection operator

0 引言

现实生活中的工程优化问题可以转换为最优化问题，一般具有多峰值、非线性、多约束等特点［1］，例如车辆侧面碰撞设计［2］、发电机优化调度［3］等。其中单目标寻优问题为在搜索空间中寻找给定的单个目标函数的最小值及最小值在搜索空间中的位置。随着工程问题的规模不断扩大并且维度越来越高，所对应的最优化问题的目标函数也越来越复杂。传统的优化算法，如梯度下降法、牛顿迭代法等已经难以解决上述的优化问题。受自然界启发，学者们提出了多种智能优化算法，如粒子群算法［4］、灰狼优化算法［5］、鲸鱼优化算法［6］等，用于解决复杂且高维度的工程问题，并且在无人机路径规划［7］、车间调度［8］等实际工程问题中都取得了较好的效果。

麻雀搜索算法（sparrow search algorithm，SSA）［9］是一种新型的高效单目标智能优化算法。SSA通过模拟麻雀觅食行为进行目标寻优，然而伴随麻雀种群的不断进化，SSA仍存在收敛精度低、种群多样性减少、易陷入局部最优［10］等问题。目前，许多学者已经提出了若干种改进的SSA。

唐延强等人［11］提出自适应变异的麻雀搜索算法（AMSSA）。AMSSA通过Cat映射混沌序列对种群初始化，并且采用柯西变异或Tent混沌扰动对个体进行调整，最后引入自适应发现者，跟随者数量来平衡全局搜索和局部勘探能力。

李爱莲等人［12］提出融合正余弦和柯西变异的麻雀搜索算法（SCSSA）。SCSSA采用折射反向学习对麻雀种群进行初始化，并且在发现者更新过程中引入含有动态权重的正余弦策略，SCSSA还在跟随者位置更新公式中对最优解进行差分变异，以增大算法跳出局部最优的概率。

陈功等人［13］提出了螺旋探索与自适应混合变异的麻雀搜索算法（SHSSA）。SHSSA引入ICMIC混沌初始化种群，使初始分布更加均匀，且融入螺旋探索策略以增强发现者探索未知区域的能力。SHSSA还在当前最优解引入融合精英差分与随机反向的自适应混合变异，提高算法的收敛速度和跳出局部最优的能力。

欧阳城添等人［14］提出了一种折射麻雀搜索算法（RSSA）。RSSA在发现者位置更新阶段引入折射反向学习来扩大发现者搜索范围，并且在跟随者阶段引入疯狂算子使跟随者寻优手段多样化。RSSA还使用模拟退火机制对当前最优解进行精炼，以改善解的质量。

毛清华等人［15］提出融合柯西变异与反向学习的麻雀搜索算法（ISSA）。ISSA引入Sine混沌映射初始化麻雀种群来丰富解的多样性，同时在发现者更新位置中引入上一代全局最优解，以提升全局搜索的充分性。ISSA还添加自适应惯性权重来动态地选择对最优解进行柯西变异或者反向学习，以有效地平衡算法的全局探索与局部开发能力。

段玉先等人［16］提出结合Sobol序列和纵横交叉策略的麻雀搜索算法（SSASC）。SSASC在初始化阶段引入Sobol序列使初始麻雀的位置分布更加均匀并使用非线性惯性权重优化发现者位置更新方式。SSASC还引入纵横交叉策略保持算法在局部搜索能力和全局开发能力上的平衡。

吕鑫等人［17］提出了一种结合Tent映射和高斯变异的改进麻雀搜索算法（CSSOA）。CSSOA将Tent映射用于优化种群初始分布并且在迭代过程中会依据种群个体的分布情况来选择对麻雀个体进行高斯变异或者Tent映射扰动。

Ma等人［18］提出了一种增强型多策略麻雀搜索算法（EMSSA）。EMSSA使用了三种策略对SSA进行改进：a）使用自适应Tent混沌映射，使初始种群中具有更丰富的多样性和更大的随机性；b）在警戒者位置更新处引入加权的正余弦算法，以避免算法陷入局部最优；c）利用三角形相似性原理对当前最优麻雀位置进行扰动，提高了算法的搜索能力。

Liu等人［19］提出一种基于构建相似度的混合麻雀搜索算法 （HSSA）。首先，HSSA在种群初始化位置引入改进的Circle 混沌方法来增强初始种群的质量；其次，HSSA根据各麻雀适应度的大小计算相似度，并根据相似度分别使用 Circle混沌和 T 分布对当前最优进行扰动，以增强跳出局部最优的能力。

上述学者提出的SSA改进算法一般是通过增加初始种群分布的均匀性、改进全局与局部的惯性参数、增加种群跳出局部最优的概率三个方面对SSA进行增强和改进。因为SSA总体上结构简单，具有较高的搜索性能，且仍具备进一步改进的空间和潜力，所以持续对SSA进行改进仍具有一定的研究价值。本文提出一种融合多策略增强的麻雀搜索算法（enhanced sparrow search algorithm by adopting the mechanism based on relative distance and historical success rate，RHSSA）。RHSSA采用了以下三项改进策略进一步提升SSA的性能：

a）SSA仅以适应度值选择发现者，容易造成发现者种群内部多样性较少的现象。本文引入融合适应度值与相对距离的发现者选择方式，使发现者种群具有较好的适应度值且彼此分散。

b）发现者在进化过程中，存在向原点聚集的现象。本文提出融合加权重心的反向学习策略来减弱发现者向原点聚集的趋势，并充分挖掘搜索空间的优质信息。

c）SSA易陷入局部最优且大部分文献的改进方法未考虑其适应度值景观，本文提出一种基于历史成功率的自适应选择算子，动态地选择柯西变异或高斯变异对最优解做扰动，根据适应度值景观动态调节算法的全局勘探与局部搜索，提高算法跳出局部最优的能力。

本文选用CEC2017测试函数集中的12个测试函数作为性能基准函数，将RHSSA与五个改进的麻雀搜索算法AMSSA［11］、SCSSA［12］、SHSSA［13］、ISSA［15］和CSSOA［17］进行性能测试评估，并对于RHSSA采用的改进策略进行了消融实验。实验结果表明在综合改进策略的共同作用下，RHSSA能获得最优的综合优化性能，且具备较为稳定的全局收敛性能。

1 麻雀搜索算法

SSA是一种模拟麻雀觅食机制的群智能优化算法，该算法的优化模型中存在发现者、跟随者和警戒者三种角色。发现者负责寻找整个搜索区域中食物较充足的位置，并为所有的跟随者提供觅食区域或方向。在每轮迭代中，搜寻到更优食物所在位置的麻雀个体都可能成为发现者，但发现者在整个种群中的占比PD是固定的，受捕食者的影响，发现者存在两种状态：当周围不存在捕食者，发现者会进入广域搜索；否则所有的发现者会向安全区移动。发现者的位置根据式（1）更新。

其中：t表示当前迭代次数；T表示最大迭代次数；ST∈［0.5，1］为预先设置的正常数，表示种群的安全值；R∈［0，1］为均匀分布的随机数，表示种群的预警值；α是介于（0，1］均匀分布的随机数；Q是服从标准正态分布的随机数；L表示一个元素全为1的1×d的矩阵。

跟随者时刻观察发现者的行为并伴随着发现者的行为调整自己的位置，跟随者的位置更新如式（2）所示。

其中：Xt+1p表示发现者发现的当前最优位置；Xworst表示当前全局最差位置；A+=AT（AAT）-1，A表示一个1×d的矩阵，其中的元素随机赋值为1或者-1。

警戒者在种群中会意识到危险，从而调整在麻雀种群的整体位置。警戒者个体在整个麻雀种群中随机产生，占整个种群的10%～20%，其位置更新方式如式（3）所示。

其中：Xbest是当前全局最优的位置；β是服从标准正态分布的步长控制参数；K∈［－1，1］是一个均匀分布的随机数，表示麻雀移动的方向； fi是当前麻雀个体的适应度； fg和fw分别是当前全局最优个体和全局最差个体的适应度；ε是一个避免分母为零的正常数。

2 改进的麻雀搜索算法

2.1 融合适应度值与相对距离的发现者选择方式

SSA中，发现者种群占据种群中的优质资源并负责发现搜索空间中有希望的区域，引导跟随者到有希望的区域进行精细搜索，所以发现者种群应具有分布范围大且适应度值小的特点［20］。SSA仅以麻雀个体适应度值从小到大排序的结果选择前PD×N个麻雀个体作为发现者，发现者的若干个体可能是已陷入局部最优或者聚集在局部最优附近的麻雀个体，这可能导致严重的种群聚集现象，当跟随者在发现者附近进行搜索时，种群多样性迅速减弱。

本文提出一种融合个体适应度值和相对距离的新发现者选择方式。新方式在选择发现者时不仅考虑个体的适应度值，也同时考虑麻雀发现者之间的相对距离。设已经将经过第t轮迭代的所有个体按个体适应度值完成从小到大的排序，并以排序序号pti作为个体的编号。即pti=i且对于第pti个个体Xtpti，其适应度值fti不小于标号介于1和pti－1之间的个体的适应值，先计算第pti个个体与前pti－1个个体之间的欧氏距离的最小值Lti，并将Lti作为第pti个个体与前pti－1个个体形成的种群之间的相对距离，如式（4）所示。

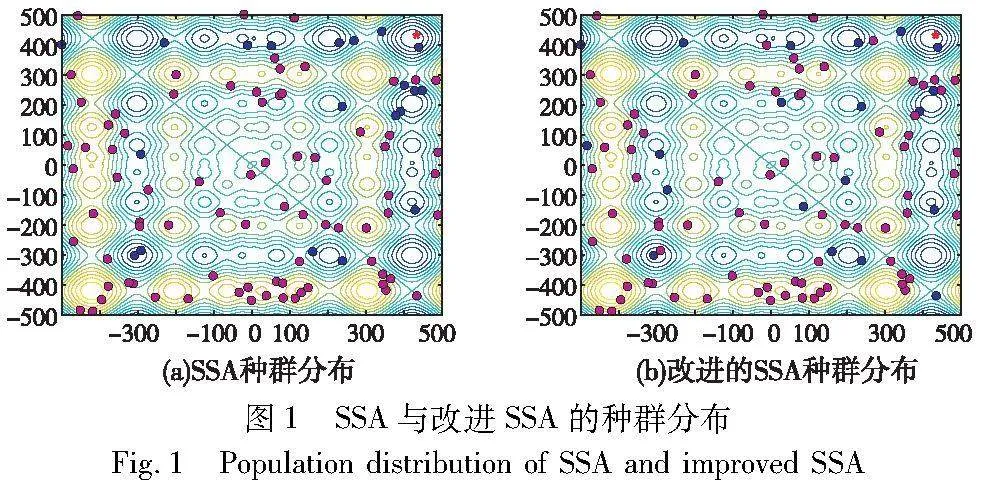
为了使最优个体引导算法搜索，Lt1等于其余非最优个体相对距离Lti的最大值。即在每轮迭代中，Xt1都会以适应度最小且相对距离最大的个体为发现者。受文献［21］启发，相对距离Lti的公式设计是基于以下原因：欧氏距离的最小值能准确衡量出该个体与前pti－1个个体构成的种群之间的偏离程度。此外，结合图1（a）可看出，适应度值比其小且欧氏距离最小的个体很有可能比该个体更加靠近附近波谷的位置，两者之间的距离能有效表示该个体在附近波谷的聚集程度。

依个体的适应度值fti计算个体的pti与依个体的相对距离Lti的从大到小的排序序号qti后，以pti与qti之和divti作为个体进行由小到大排序的统一标准，并选择排序后的前PD×N 个麻雀个体作为发现者。divti的定义如式（5）所示。

divti=pti+qti（5）

按上述方式对麻雀个体进行排序的原因是：适应度小的个体的pti值也小，相对距离大的个体的qti值偏小，所以当个体满足适应度值小且相对距离大时，其对应的排序之和选择divti也会偏小。

取相同的种群分布并分别使用原SSA与融合上述策略的改进SSA分别从麻雀个体中选出发现者的结果如图1所示，其中蓝色圆点代表发现者（参见电子版）。从图1（a）中可以看出，原麻雀算法仅依麻雀个体适应度值从小到大排序的结果选择排序靠前的PD×N个麻雀个体作为发现者，可能会导致被选出的发现者聚集在一个或若干个波谷附近的现象。从图1（b）可以看出，使用融合适应度值与相对距离的发现者选择方式可以使被选出的发现者，即具有适应值较低的特征又具有位置相对比较分散的特性，可以使距离波谷较远且适应度值较小的麻雀个体也转变为发现者，从而有助于提高算法的全局勘探性能。

2.2 融合加权重心的反向学习策略

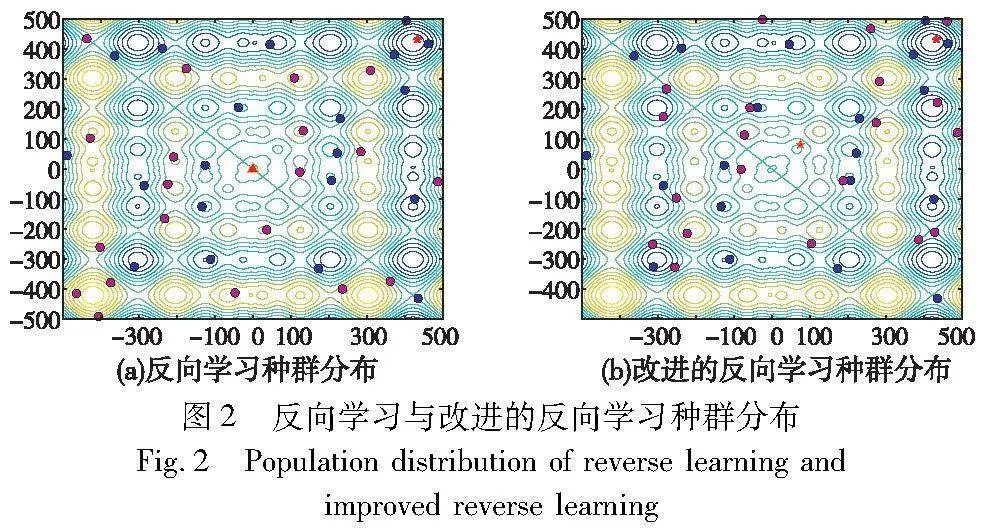
根据发现者位置更新式（1），标准SSA在R<ST时，对当前位置乘以小于1的指数值，导致发现者位置每一维都在减小，使发现者个体向原点聚集，加大了种群的聚集程度。反向学习策略［22］被证明是一种有效扩大算法搜索空间并避免陷入局部最优的有效改进方法。反向学习策略的基本形式如式（6）所示。

X*ti， j=ubj+lbj－Xti， j（6）

其中：X*ti， j为Xti， j的反向点；ubj、lbj分别为搜索空间的第j维的上下界。从式（6）可以看出，反向学习策略实际上是以（ubj+lbj）/2为对称中心来求出Xti， j的反向解，然后再保留原解与反向解中具有更小适应度值的个体进入下一代算法迭代。在大多数寻优问题中，种群搜索空间的每一维通常是关于原点对称的，即该维的上下界互为相反数，当原解向原点聚集时，反向解同样向原点聚集，难以解决麻雀搜索算法发现者向原点聚集的缺陷。此外，反向学习策略的对称中心与种群的信息无关，无法根据种群信息自适应地调整对称中心，使算法的效率变低。

本文提出融合加权重心的反向学习策略，能根据发现者种群信息动态地调整对称中心，使发现者远离原点搜索。

标准重心的构成方式中，每一个个体以等比例的方式构成标准重心，难以差异化地利用个体信息，容易造成搜索过程的不平衡。加权重心Gt的构成与发现者个体的适应度值有关，如式（7）（8）所示。其中，Pti是调节Xti构成Gt的比重，ftworst为整个麻雀种群的适应度最大值，所有发现者的Pti的和为1。对每一个发现者而言，适应度值越小的麻雀个体，所得到的Pti越大，对构成Gt的比重越大。对发现者种群而言，每一个发现者构成Gt的比重Pti都受到其他所有发现者个体的分散，即Pti能使算法在多样性和收敛性之间取得平衡。此外，发现者个体是融合适应度值与相对距离策略选出的未进化的发现者，能避免早熟收敛，因此，加权重心Gt能更准确地表示发现者种群的中心。

设Xt+1i是Xti经发现者位置更新后的麻雀个体，Xt+1i执行以Gt为加权重心的反向学习策略［23］，产生反向解X*ti：

X*ti=2×Gt－Xt+1i（9）

当所得的反向解超出搜索区域时，按式（10）重新计算反向解：

取两者之间适应度值更小的个体进入下一代，如式（11）所示。

取相同发现者信息，分别用反向学习与加权重心的反向学习进行位置更新，结果如图2所示，其中蓝色圆点表示发现者，红色三角形表示反向学习的对称中心，红色五角星表示改进后的反向学习的对称重心，粉红色圆点表示经反向学习或改进反向学习的发现者个体。从图2（a）可看出，一般反向学习无法降低发现者向原点聚集的趋势；从图2（b）可看出，使用融合加权重心反向学习策略，使个体能有效利用种群的信息，远离原点搜索。

2.3 结合历史成功率的自适应选择算子的高斯与柯西变异

文献［24］提出对最优解进行扰动能有效地增强麻雀搜索算法的性能，因此，本文选择对最优解施加扰动。但大多数文献［25～27］对最优解扰动的幅度与当前迭代次数与种群的聚集程度有关。当前迭代次数小，扰动幅度大，反之，扰动幅度小。种群聚集程度大，扰动幅度大，反之，扰动幅度小。此种方式的缺陷是没有考虑到目标函数的适应度景观，存在扰动幅度与适应度景观不匹配的问题，造成寻优效率下降［28］。

本文提出一种结合历史成功率的自适应选择算子的高斯与柯西变异策略，选择算子是在文献［29］基础上改进而来，高斯变异提供小范围内的扰动，柯西变异提供大范围内的扰动，以满足算法多样化的寻优需求。结合历史成功率的自适应选择算子能够考虑到历史迭代次数的适应度景观，在当前迭代次数中以较大概率选择对寻优效果促进最有效的变异方式。

定义学习周期LP，LP的目的是提供需要累积的历史经验的范围。pt值指高斯变异发生的概率，其能动态调节算法发生高斯变异与柯西变异的可能性。Wtk是高斯变异或柯西变异生成的解，k代表变异方式的编号，其中，k=1代表高斯变异，k=2代表柯西变异。扰动成功是指选中的变异所生成的Wtk的适应度值f（Wtk）小于当前最优解的适应度值f（Xtbest），反之，则代表扰动失败。本文用nsk，g、nfk，g分别标志在第g轮迭代中用第k种变异扰动成功与扰动失败的状态。扰动成功时，nsk，g=1，nfk，g=0；扰动失败时，nsk，g=0，nfk，g=1；Sk，t指从t－LP到t－1代中，扰动成功的次数与扰动失败的次数之差，如式（12）（13）所示。

算法开始寻优时，由于没有历史经验的累积，为了使每种变异的性能都有充分利用的机会，形成LP代的先验信息，所以在最初的LP代中，pt值设置为1/2。

LP+1代及之后的寻优过程中，当前代选择概率pt的取值与Sk，t的大小有关，如式（14）所示。

度景观促进效果小但可能对变化后的适应度景观促进效果大的变异匹配当前的适应度景观，如果此时的寻优效果更好，也可能促进pt值趋势的逆转，使pt值动态响应适应度景观变化。

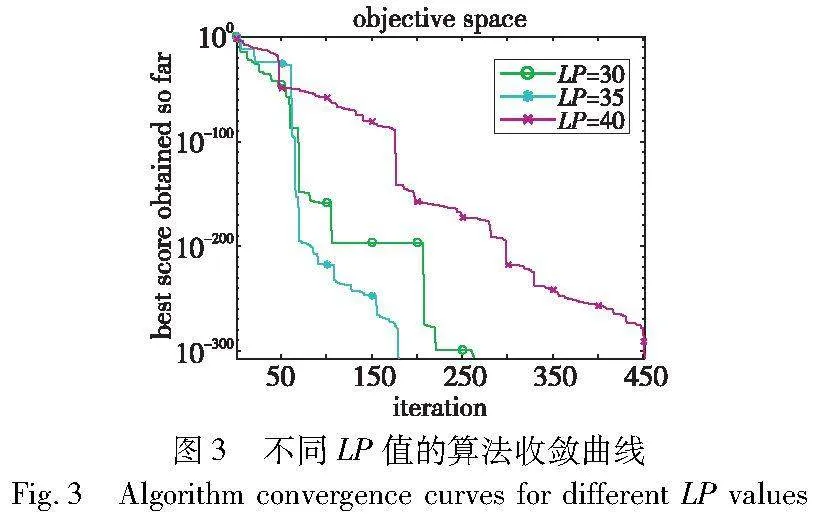
LP大小的设置影响着算法的寻优效率。过大的LP导致当算法已经远离积累经验的区域搜索时，选择概率pt仍然受该区域的适应度景观的影响，容易出现适应度景观与搜索方式的不匹配性；过小的LP可能导致没有足够经验的积累，无法有效地指导算法动态搜索，难以找到精度更高的解。因此，应选择合适的LP以保证算法寻优过程的准确性。为了精确控制LP的大小，选用Rastrigin函数作为对比不同LP的测试函数，实验中种群数量设置为100，最大迭代次数设置为500，结果如图3所示，分别为LP取值为30、35、40的算法收敛情况。可以看出取值为35时效果最好，过大和过小都会影响算法的寻优效率。

保留Wtk与Xtbest中更小的适应度值个体进入下一代。计算学习周期LP内控制发生高斯变异或柯西变异的选择概率pt，使算法根据适应度景观动态地勘探与开发，选择对寻优效果促进最有效的变异方式，增大算法找到更加优质解的可能性。

3 算法伪代码和时间复杂度

3.1 算法伪代码

3.2 时间复杂度分析

种群规模为N，待解决的问题维度为D，最大迭代次数为T， 麻雀发现者在种群中的比例为PD，SSA的算法时间复杂度为O（N×D×T），对整个麻雀种群初始化并评估其适应度值，其时间复杂度为O（N×D+N）。采用融合适应度值与相对距离的发现者选择方式时间复杂度为O（N×D×（N－1）/2×T），发现者采用融合加权重心的反向学习策略的时间复杂度为O（T）+O（PD×N×D×T），在当前最优解施加结合历史成功率的自适应选择算子的柯西与高斯变异的复杂度为O（1×D×T）。

4 算法性能测试与分析

4.1 基准函数的选取

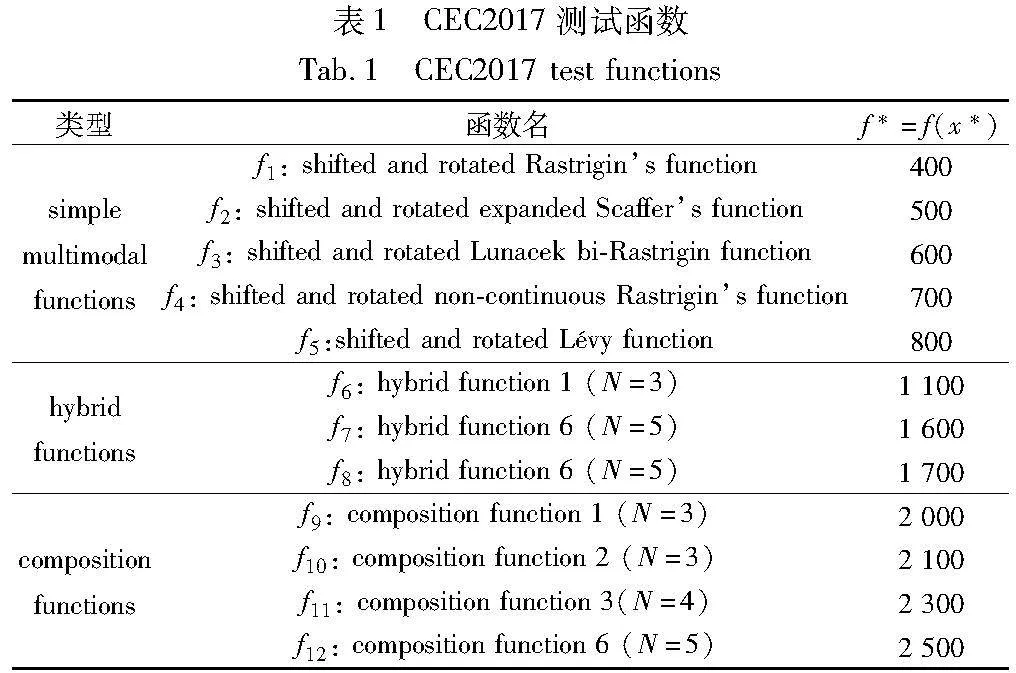
为了验证改进算法的寻优能力，本文选取12个CEC2017函数来评估算法在收敛速度和搜索精度方面的性能。这些基准函数分为三类，包括5个多峰函数（f1～f5）、3个混合函数（f6～f8）和4个复合函数（f9～f12）。本文选取的函数都具有大量的局部最优点。测试函数的名称与相关参数如表1所示。

4.2 算法与其他改进算法的对比分析

为测试RHSSA的性能，将其与AMSSA［10］、SCSSA［12］、SHSSA［13］、ISSA［15］、CSSOA［17］在上述的12个测试函数上进行实验评估。本文中的仿真实验均处于同一实验环境，使用MATLAB R2021b作为算法仿真软件，操作系统为Windows 10，硬件配置为AMD Ryzen 5 5500U with Radeon Graphics 2.10 GHz，16.0 GB内存。为了保证算法比较的公平，所有改进麻雀搜索算法的参数统一设置为种群数量为 100、运行次数为 30、总迭代次数为 500，搜索空间为［－100，100］D，发现者比例PD为0.2，警戒者比例 ST为0.1，预警值ST为0.6。

性能测试使用平均值mean（均值越小表示算法具有更好的寻优能力）、标准差Std（标准差越小表示算法更具鲁棒性）作为评判算法寻优能力优劣的性能指标。同时规定mean值为主要标准，Std次之。先对比mean值，若mean值相等，则对比Std，对比结果采取排名（rank）表示。表中count表示各算法rank排第一的总次数，Ave rank为平均排名情况，total rank为以Ave rank为基准的算法总排名。

4.3 实验结果

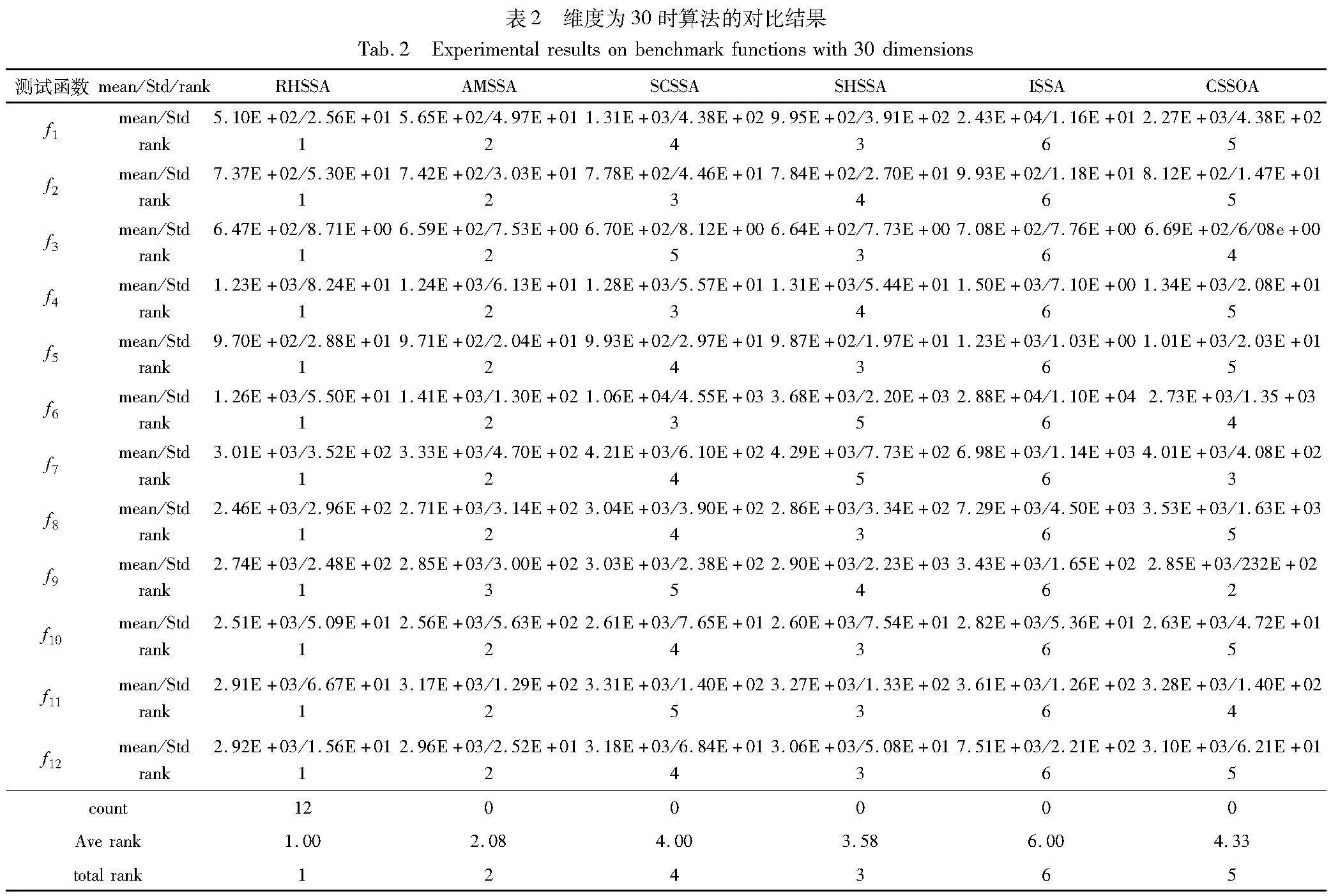
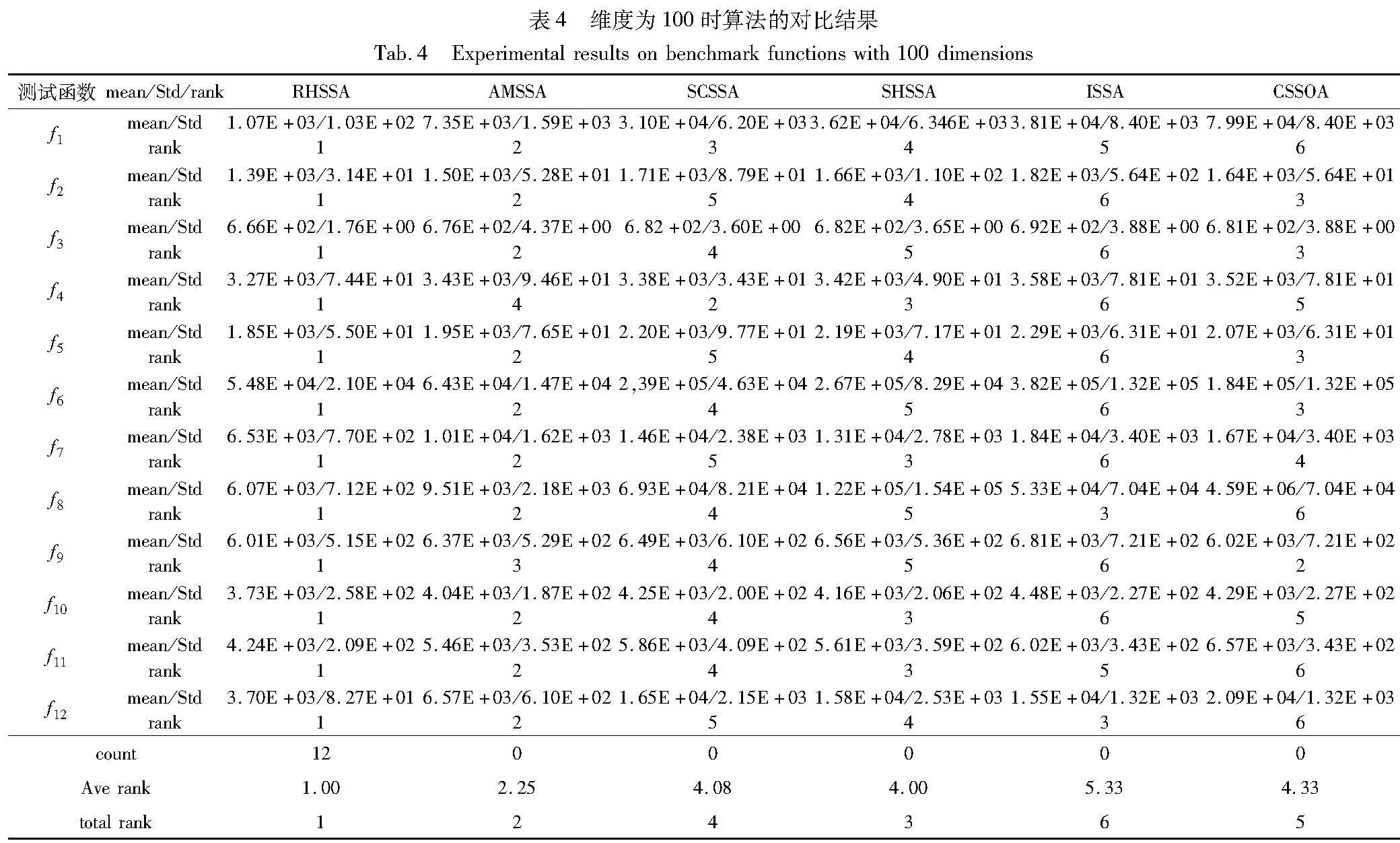
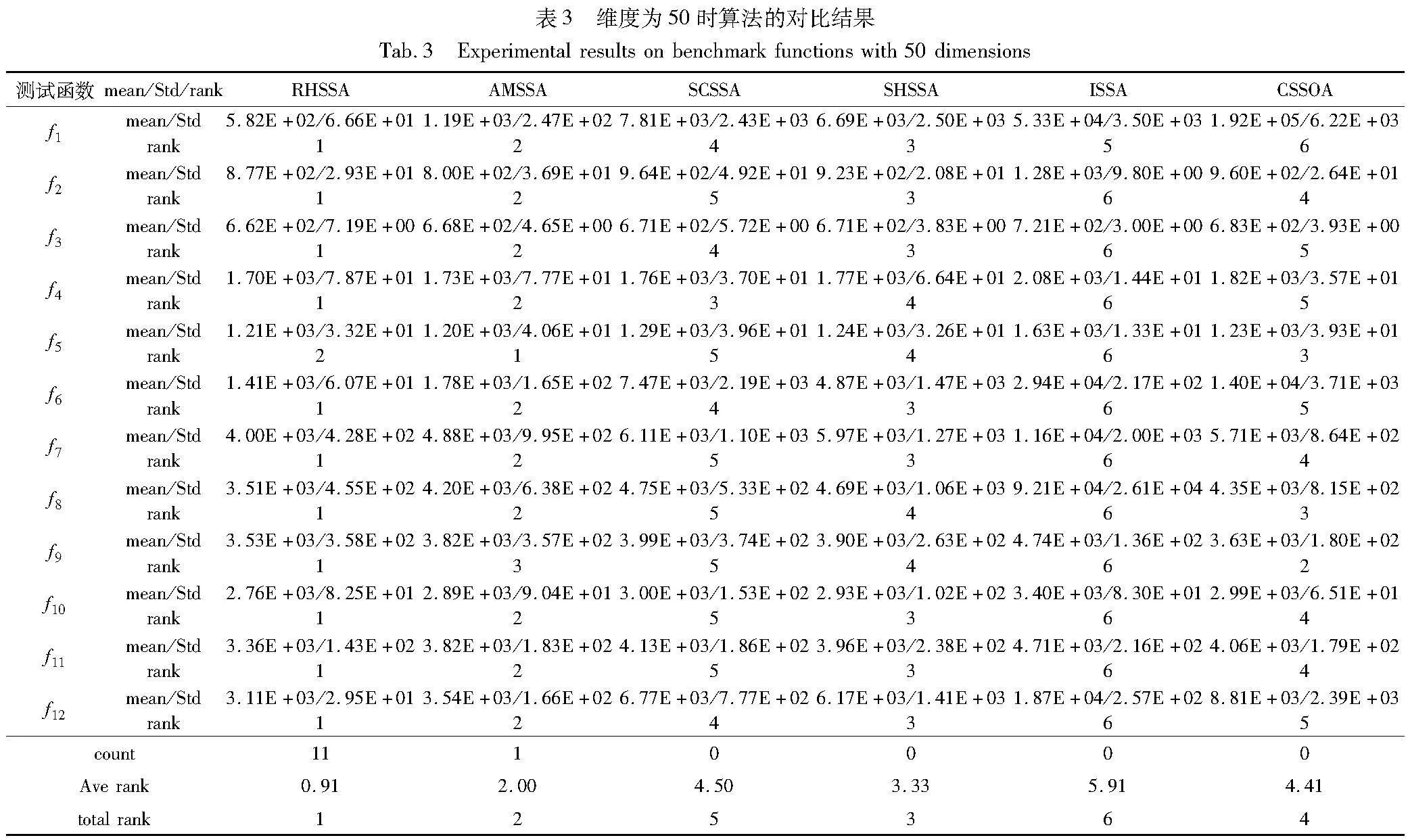
表2～4分别列出了各算法在12个测试函数为30、50、100维情况下的实验数据。从表2～4可以看出，在不同维度的问题中，RHSSA在50维度的f5的收敛精度略低于AMSSA，其余情况均获得了第一，同时在total rank总排名中也取得第一名的好成绩。算法在Std方差上取得的成绩代表了算法在处理复杂问题上的鲁棒性，在测试函数为30维时，RHSSA仅在 f2～f5上劣于对比算法，在测试函数为50维时，RHSSA仅在f1、 f3、 f4、 f9上劣于对比算法，在测试函数为100维时，RHSSA仅在f10、 f12上劣于对比算法。其余情况下，RHSSA均比改进的SSA更具优势，表示在引入策略后，RHSSA在处理复杂问题上具有更好的鲁棒性。

4.4 算法收敛曲线对比分析

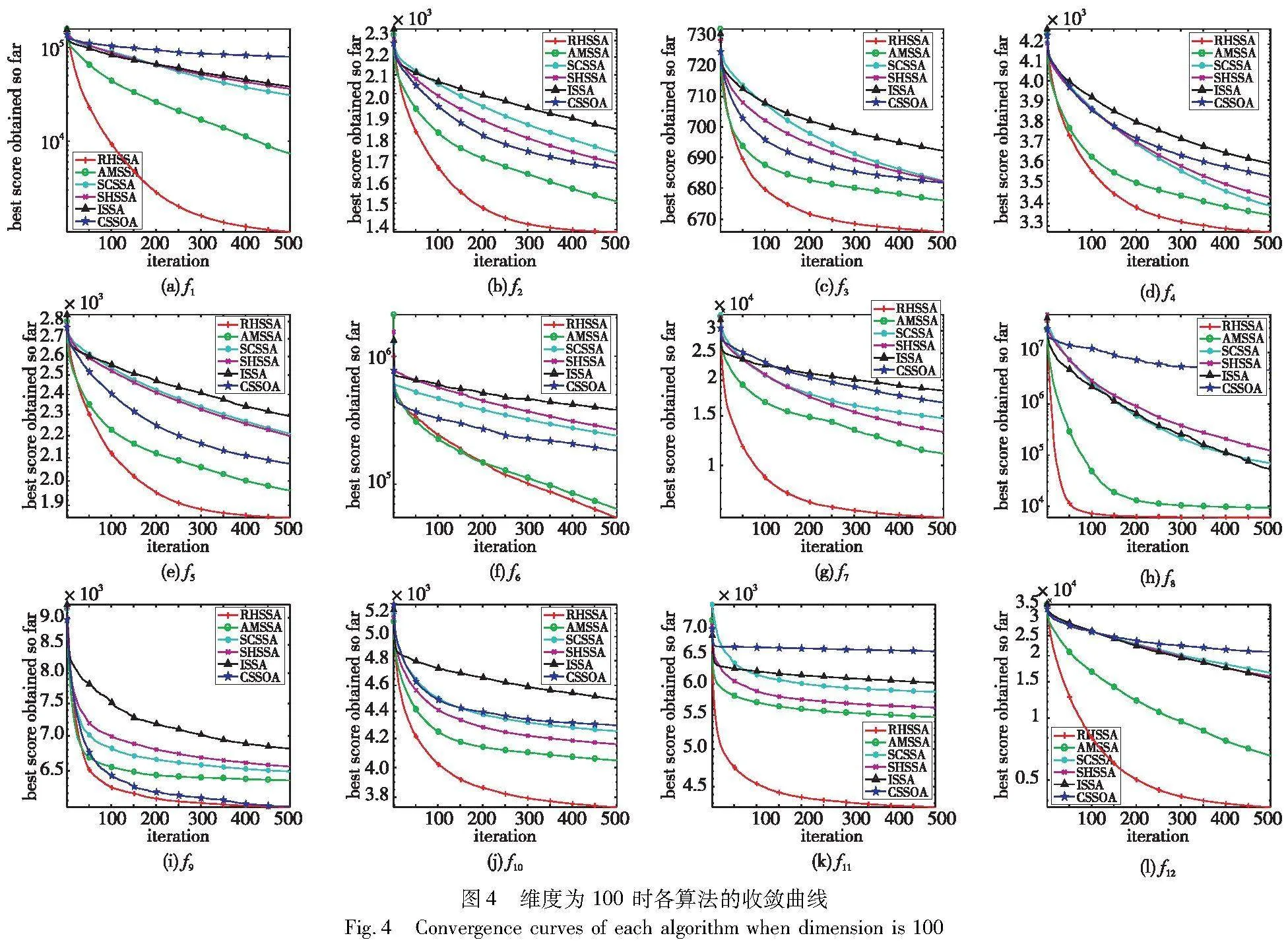
收敛曲线可以直观地展现算法的收敛速度和是否陷入局部最优。图4列出了六种算法对上述12个测试函数在维度为100时的收敛曲线。从图4可以看出，在12个函数中，RHSSA在全部的测试函数中都有更好的收敛精度，其中在f7中甚至高了一个量级左右。在其他参评算法因为陷入局部最优从而导致种群多样性下降时，RHSSA仍能保持较高的种群多样性，拥有较强的跳出局部最优的能力。从函数类别上看，对于简单多峰函数f1～f5，RHSSA在前期的收敛速度都快于其他参评算法，这很有可能是融合适应度值与相对距离的发现者选择方式与融合加权重心的反向策略使发现者的分布及搜索范围都变大的原因造成的。在迭代后期，RHSSA获取的收敛精度也优于其他参评算法，这有可能是因为融合历史成功率的自适应高斯与柯西变异利用历史学习周期的信息加强跳出局部最优的能力造成的。对于混合函数f6～f8， RHSSA在迭代前期的收敛速度略快于其他参评算法，在迭代后期，RHSSA跳出局部最优的能力显著增强，最终获取了比其他参评算法更好的收敛精度。对于组合函数f9～f12，当其他参评算法陷入局部最优，从而导致收敛速度减慢，收敛精度减小时，RHSSA仍然继续向前探索，从而获取了更优的收敛精度。

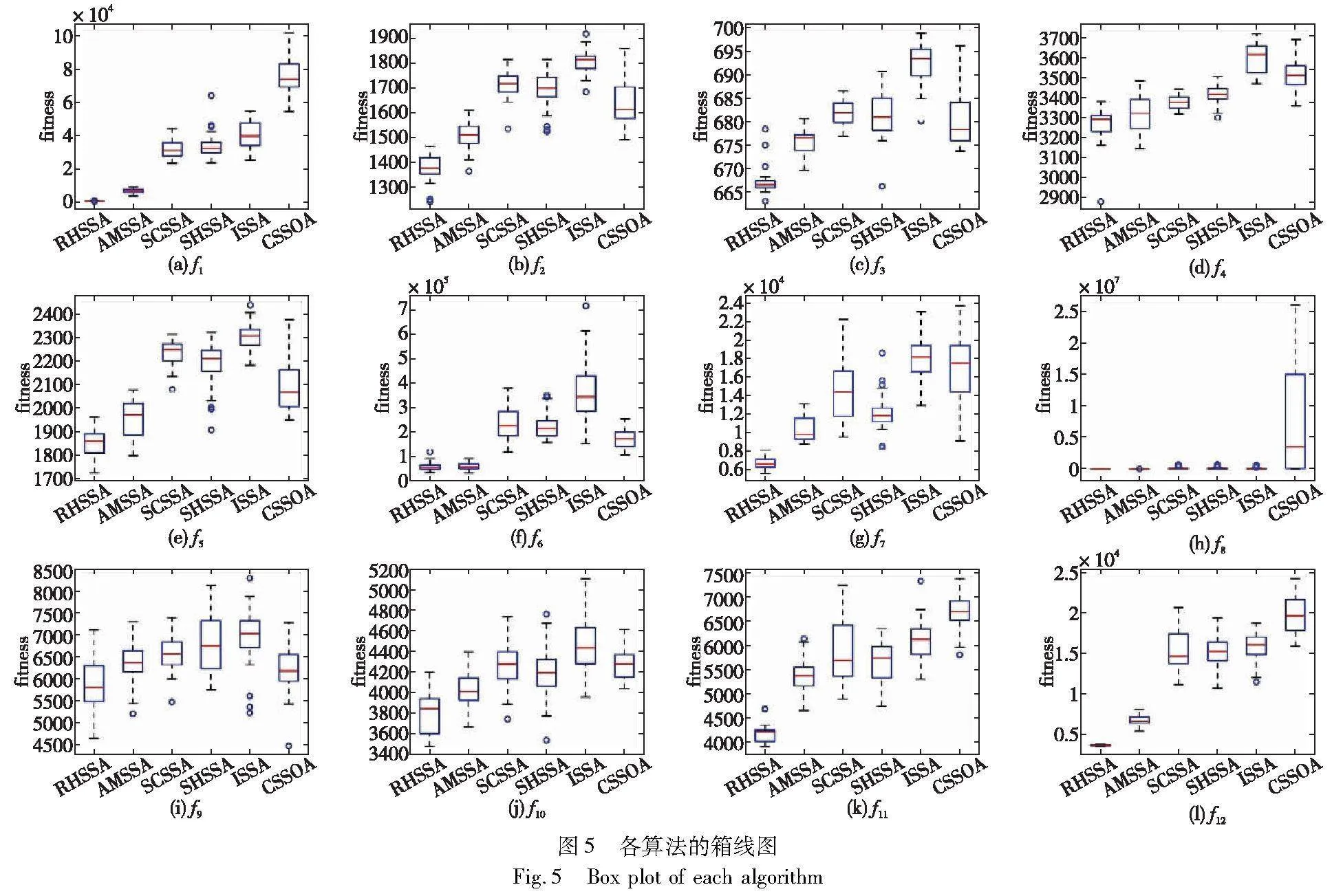
同时，图5包括了RHSSA与各参评算法独立执行30次条件下获取最优解的12个CEC2017函数箱线图。箱体的高度代表了算法最优值的波动情况，箱体底部表示算法的最优值。 f1、f6、f8、f12等函数中RHSSA的箱体较窄，代表它的所有最优值波动情况小，也就是算法收敛速度较快，导致每一代的最优解之间跨度较小。而包括CSSOA、ISSA等在内的参评算法的箱体较宽，代表算法从开始搜索到迭代结束获取的所有解变化大，鲁棒性比RHSSA低。与此同时，也可以明显看出，RHSSA在f1～f5、f7～f12等函数中箱体的下限比其他算法更低，也就代表它的搜索精度更高。以上表明，由于三种策略的协助有利于RHSSA跳出局部最优解，并能够指导算法后续的搜索。

综上所述，RHSSA是一种高效的单目标算法，并且RHSSA的改进措施是有效的。

4.5 完整性消融实验

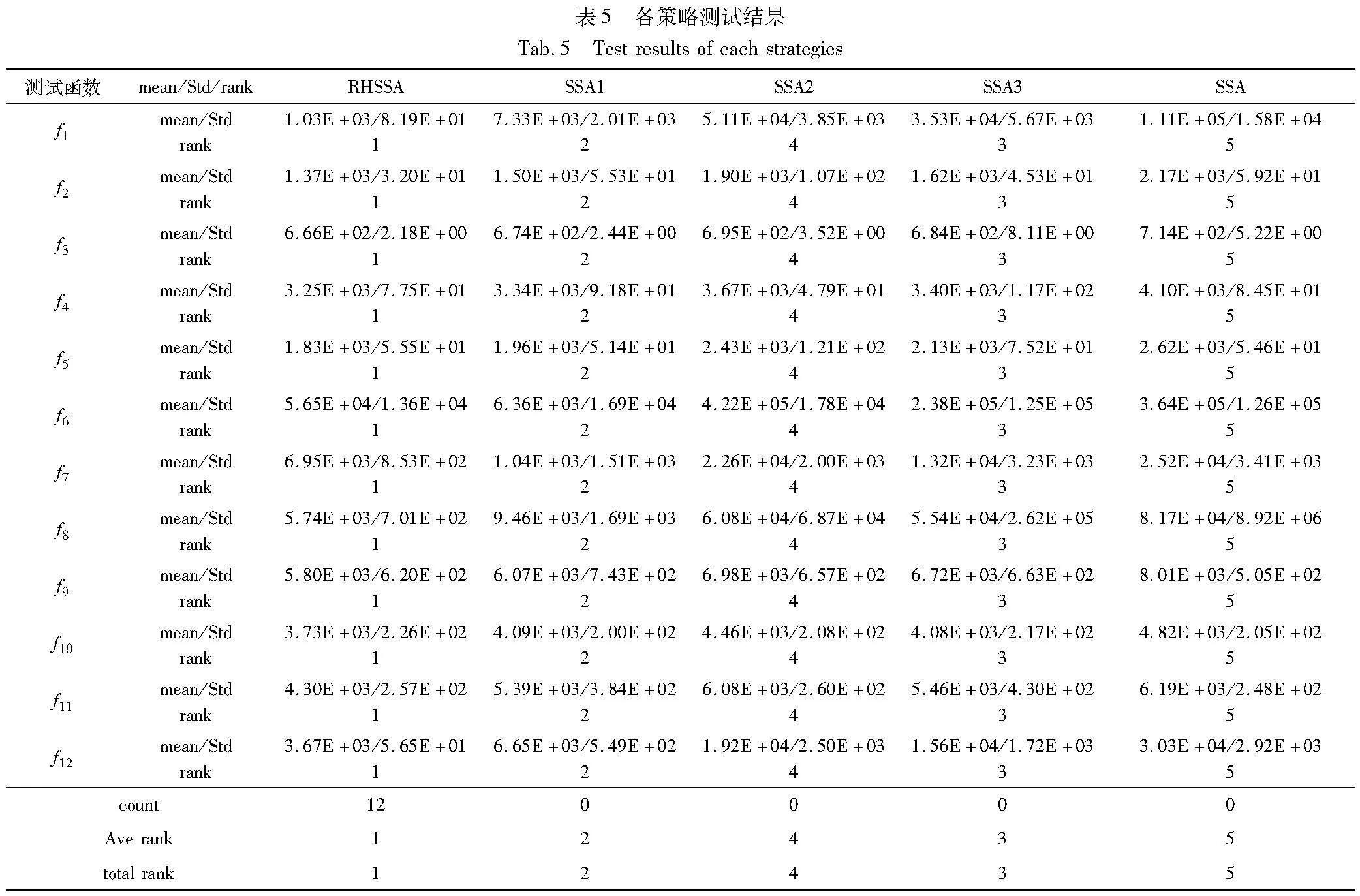
为体现本文各自策略的有效性，对RHSSA中策略进行完整性消融实验。设SSA中，只融入融合适应度值与相对距离的策略的算法为SSA1，只融入融合加权重心的反向学习策略的算法为SSA2，只融入结合历史成功率的自适应选择算子的高斯与柯西变异策略的算法为SSA3。本文将标准的SSA与SSA1、SSA2、SSA3和RHSSA一起进行函数测评，函数的信息如表1所示。各算法的参数与4.2节相同，维度为100维且独立运行10次。表5展现了不同改进策略的收敛精度情况。从表5可以看出，SSA1、SSA2、SSA3在12个函数上都优于SSA，这证明了每个策略在SSA上都是有效的。而对于RHSSA，其收敛精度高于参与测评的能力算法，这表明所有的改进策略都是相辅相成并且稳定有效的，可以共同提高RHSSA求解复杂问题的能力。

4.6 Friedman检验

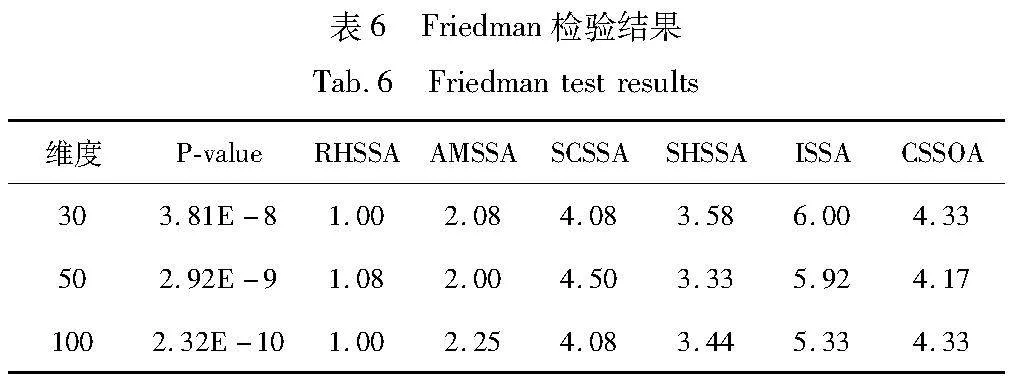
本文还对记录的六种算法各运行30次后得到的平均值数据进行Friedman检验［30］，结果如表6所示。表中的P-value表示渐进显著性，它是判断算法之间是否存在显著性差异的重要指标，若该值小于0.01，则表示各项数据之间存在显著性差异。其他的值为各个算法在不同维度中的秩的平均值。从表6可以看出，30、50、100维中P-value都远远小于0.01，且随着维度的变大而变小。在三种不同维度中，RHSSA的秩的平均值都是最小的，这表明RHSSA和其他对比算法之间存在显著的性能差异，再次证明RHSSA的性能相比于其他参评算法的优越性。

5 结束语

本文针对SSA易早熟和易陷入局部最优的缺陷，提出一种融合相对距离与历史成功率的麻雀搜索算法RHSSA。RHSSA首先使用融合适应度与相对距离的新指标选择发现者，使发现者在搜索空间中占据优质位置且彼此分散。其次，RHSSA在发现者寻优过程中引入融合加权重心的反向学习策略，充分挖掘搜索空间的优质位置信息并减弱发现者向原点聚集的趋势。最后，RHSSA通过融合历史成功率的自适应选择算子的高斯与柯西变异，增强了算法跳出局部最优的能力。基于12个CEC2017测试函数的实验证明，RHSSA在不同维度的多个测试函数中都可以获得更好的寻优精度和收敛精度。实验的测试结果表明，RHSSA是一种高效的单目标优化算法，为求解复杂单目标优化问题提供了新的解决办法。RHSSA的不足之处在于，其求解种群个体的相对距离时的时间复杂度较高。下一步将对RHSSA进行进一步的改进，以降低其时间复杂度并提升算法的搜索效率，并将RHSSA运用到多目标优化问题上。

参考文献：

［1］刘小龙，李荣钧，杨萍. 基于高斯分布估计的细菌觅食优化算法［J］. 控制与决策，2011，26（8）： 1233-1238. （Liu Xiaolong，Li Rongjun，Yang Ping. Optimization algorithm for bacterial foraging based on Gaussian distribution estimation［J］. Control and Decision，2011，26（8）： 1233-1238.）

［2］Sultan B Y，Nantiwat P，Sujin B，et al. Robust design of a robot gripper mechanism using new hybrid grasshopper optimization algorithm［J］. Expert Systems，2021，38（3）： e12666.

［3］Paul K，Dalapati P，Kumar N. Optimal rescheduling of generators to alleviate congestion in transmission system： a novel modified whale optimization approach［J］. Arabian Journal for Science and Engineering，2021，47（3）： 3255-3279.

［4］Kennedy J，Eberhart R. Particle swarm optimization［C］// Proc of International Conference on Neural Networks. Piscataway，NJ： IEEE Press，1995： 1942-1948.

［5］Mirjalili S，Mirjalili S M，Lewis A. Grey wolf optimizer［J］. Advances in Engineering Software，2014，69： 46-61.

［6］Mirjalili S，Lewis A. The whale optimization algorithm［J］. Advances in Engineering Software，2016，95： 51-67.

［7］Liu Yang，Zhang Xuejun，Guan Xiangmin，et al. Adaptive sensitivity decision based path planning algorithm for unmanned aerial vehicle with improved particle swarm optimization［J］. Aerospace Science and Technology，2016，58： 92-102.

［8］张宇嘉，宋威. 双档案粒子群算法求解柔性作业车间调度问题［J］. 计算机工程与应用，2023，59（11）： 294-301. （Zhang Yujia，Song Wei. Dual file particle swarm optimization algorithm for flexible Job Shop scheduling problem［J］. Computer Engineering and Application，2023，59（11）： 294-301.）

［9］Xue Jiankai，Shen Bo. A novel swarm intelligence optimization approach： sparrow search algorithm［J］. Systems Science & Control Engineering，2020，8（1）： 22-34.

［10］苏莹莹，王升旭. 自适应混合策略麻雀搜索算法［J］. 计算机工程与应用，2023，59（9）： 75-85. （Su Yingying，Wang Shengxu. Adaptive hybrid strategy sparrow search algorithm［J］. Computer Engineering and Application，2023，59（9）： 75-85.）

［11］唐延强，李成海，宋亚飞，等. 自适应变异麻雀搜索优化算法［J］. 北京航空航天大学学报，2023，49（3）： 681-692. （Tang Yanqiang，Li Chenghai，Song Yafei，et al. Adaptive mutation sparrow search optimization algorithm［J］. Journal of Beihang University，2023，49（3）： 681-692.）

［12］李爱莲，全凌翔，崔桂梅，等. 融合正余弦和柯西变异的麻雀搜索算法［J］. 计算机工程与应用，2022，58（3）： 91-99. （Li Ailian，Quan Lingxiang，Cui Guimei，et al. Sparrow search algorithm combining sine cosine and Cauchy mutation［J］. Computer Engineering and Application，2022，58（3）： 91-99.）

［13］陈功，曾国辉，黄勃，等. 螺旋探索与自适应混合变异的麻雀搜索算法［J］. 小型微型计算机系统，2023，44（4）： 779-786. （Chen Gong，Zeng Guohui，Huang Bo，et al. Sparrow search algorithm with spiral exploration and adaptive hybrid mutation［J］. Journal of Chinese Computer System，2023，44（4）： 779-786.）

［14］欧阳城添，朱东林，王丰奇，等. 基于折射麻雀搜索算法的无人机路径规划［J］. 电光与控制，2022，29（6）： 25-31. （Ouyang Chengtian，Zhu Donglin，Wang Fengqi，et al. Path planning for unmanned aerial vehicles based on refractive sparrow search algorithm［J］. Electrooptic and Control，2022，29（6）： 25-31.）

［15］毛清华，张强. 融合柯西变异和反向学习的改进麻雀算法［J］. 计算机科学与探索，2021，15（6）： 1155-1164. （Mao Qinghua，Zhang Qiang. Improved sparrow algorithm combining Cauchy mutation and reverse learning［J］. Computer Science and Exploration，2021，15（6）： 1155-1164.）

［16］段玉先，刘昌云. 基于Sobol序列和纵横交叉策略的麻雀搜索算法［J］. 计算机应用，2022，42（1）： 36-43. （Duan Yuxian，Liu Changyun. Sparrow search algorithm based on Sobol sequence and cross strategy［J］. Journal of Computer Applications，2022，42（1）： 36-43.）

［17］吕鑫，慕晓冬，张钧，等. 混沌麻雀搜索优化算法［J］. 北京航空航天大学学报，2021，47（8）： 1712-1720. （Lyu Xin，Mu Xiaodong，Zhang Jun，et al. Chaotic sparrow search optimization algorithm［J］. Journal of Beihang University，2021，47（8）： 1712-1720.）

［18］Ma Jie，Hao Zhiyuan，Sun W. Enhancing sparrow search algorithm via multi-strategies for continuous optimization problems［J］. Information Processing & Management，2022，59（2）： 102854.

［19］Liu Jianhua，Wang Zhiheng. A hybrid sparrow search algorithm based on constructing similarity［J］. IEEE Access，2021，9： 117581-117595.

［20］徐鹏飞. 基于麻雀搜索算法的改进研究与应用［D］. 重庆： 西南大学，2022. （Xu Pengfei. Improved research and application based on sparrow search algorithm［D］. Chongqing： Southwest University，2022.）

［21］陶新民，郭文杰，李向可，等. 基于密度峰值的依维度重置多种群粒子粒子群算法［J］. 软件学报，2023，34（4）： 1850-1869. （Tao Xinmin，Guo Wenjie，Li Xiangke，et al. Multidimensional reset multi particle swarm optimization algorithm based on density peaks［J］. Journal of Software，2023，34（4）： 1850-1869.）

［22］Tizhoosh H R. Opposition-based learning： a new scheme for machine intelligence［C］// Proc of International Conference on Computational Intelligence for Modelling，Control and Automation and International Conference on Intelligent Agents，Web Technologies and Internet Commerce. Piscataway，NJ： IEEE Press，2005： 695-701.

［23］Rahnamayan S，Jesuthasan J，Bourennani F，et al. Computing opposition by involving entire population［C］// Proc of IEEE Congress on Evolutionary Computation. Piscataway，NJ： IEEE Press，2014： 1800-1807.

［24］Gao Bingwei，Shen Wei，Guan Hao，et al. Research on multistrategy improved evolutionary sparrow search algorithm and its application［J］. IEEE Access，2022，10： 62520-62534.

［25］Fan Xin，Wang Junyan，Wang Haifeng，et al. LQR trajectory tracking control of unmanned wheeled tractor based on improved quantum genetic algorithm［J］. Machines，2023，11（1）： 62.

［26］Zhou Mu，Long Yuexin，Zhang Weiping，et al. Adaptive genetic algorithm-aided neural network with channel state information tensor decomposition for indoor localization［J］. IEEE Trans on Evolutionary Computation，2021，25（5）： 913-927.

［27］李大海，李鑫，王振东. 融合多策略的增强麻雀搜索算法及其应用［J］. 计算机应用研究，2023，40（10）： 3032-3039. （Li Dahai，Li Xin，Wang Zhendong. Enhanced sparrow search algorithm with multi strategy fusion and its application［J］. Application Research of Computers，2023，40（10）： 3032-3039.）

［28］邓志诚，孙辉，赵嘉，等. 方波触发勘探与开发的粒子群优化算法［J］. 自动化学报，2022，48（12）： 3042-3061. （Deng Zhicheng，Sun Hui，Zhao Jia，et al. Particle swarm optimization algorithm for square wave triggered exploration and development［J］. Acta Automatica Sinica，2022，48（12）： 3042-3061.）

［29］Qin K A，Huang V L，Suganthan P N. Differential evolution algorithm with strategy adaptation for global numerical optimization［J］. IEEE Trans on Evolutionary Computation，2009，13（2）： 398-417.

［30］李大海，刘庆腾，艾志刚. YYPO-SA： 一种新的基于YYPO和SA的混合单目标随机优化算法［J］. 计算机应用研究，2021，38（7）： 2018-2024. （Li Dahai，Liu Qingteng，Ai Zhigang. YYPO-SA： a new hybrid single objective random optimization algorithm based on YYPO and SA［J］. Application Research of Computers，2021，38（7）： 2018-2024.）