基于递推最小二乘算法的感应电机参数辨识

收稿日期：2024-03-04

*基金项目：国家自然科学基金（51377058）。

作者简介

喻皓（1983—），男，硕士，高级工程师，主要从事新能源汽车电驱动系统开发与研究工作；张金良（1985—），男，博士。

【摘 要】实现感应电机良好的矢量控制性能的前提是需要获取精准的电机参数。传统使用堵转、空转来测取感应电机参数的方法不但受试验环境的影响，同时也大幅增加了人力成本。为解决这一问题，文章提出一种适用于静止状态下感应电机递推最小二乘算法参数辨识的策略，在MATLAB/Simulink中构建适用递推最小二乘算法的感应电机数学模型及辨识系统，仿真结果表明所提的辨识策略能够有效地对电机电气参数进行精准的辨识。

【关键词】感应电机；递推最小二乘法；参数辨识；静止状态

中图分类号：U463.6 文献标识码：A 文章编号：1003-8639（ 2024 ）07-0040-03

Parameter Estimation of Induction Motor Based on Recursive Least Squares Method*

YU Hao1，ZHANG Jinliang2，JIANG Wei1

（1.GAC Aion New Energy Automotive Co.，Ltd.，Guangzhou 511434；

2. Guangdong Polytechnic Normal University，Guangzhou 510630，China ）

【Abstract】A good knowledge of electric parameters is precondition for high performance field oriented controlled（FOC）induction motor（IM）. Conventional methods to obtain the IM parameters known as locked-rotor and no-load tests have problems of limited experimental conditions and increases the labor costs. To solve this problem，this paper presents a recursive least squares（RLS）algorithm for the parameters estimation of the IM at standstill. The RLS estimation model of IM and identification system were established in Matlab/Simulink. Simulation results show the effectiveness of the proposed identification strategy for parameter estimation of IMs.

【Key words】induction motor；recursive least squares；parameter estimation；standstill

1 引言

感应电机以其高可靠性、低成本、易维护等优点已被广泛应用于各工业领域。基于转子磁场定向矢量控制技术的感应电机获得与直流电机相媲美的调速性能而成为主流控制算法[1]。感应电机参数尤其转子时间常数的精准与否直接影响转子磁场定向的精准度，进而影响转子磁场定向矢量控制的性能。因此感应电机参数辨识技术已成为了一个热门的研究课题，许多学者对感应电机参数辨识方法进行了不同层面的研究，力求能获取较精准的电机参数[2-3]。

传统测量感应电机参数的通用方法是离线状态下通过空载、堵转来测取，但该方法存在操作复杂、易受试验条件影响的缺点，因此近些年不断有新的电机参数辨识策略被提出，这些方法避免了额外的硬件成本，让参数辨识的流程更加智能化。Habibur Rehman[4]选用感应电机的电流模型作可调模型，利用转子磁链在同步旋转坐标系q轴上的分量为0的特点，通过设计q轴转子磁链观测器来设计转子电阻估计的自适应机制，该方法取得较为精准的辨识效果，算法运算量也较少，但这种方法对感应电机转子电感不能同时辨识，从而无法获取准确的转子时间常数。Huang Bin等[5]提出了一种基于感应电机无功功率的模型参考自适应方法来辨识电机的转子电阻，该方法的优点在于不需要依赖定子电阻精度，也可以认为辨识性能不受环境温度的影响，但该方法同样无法识别出电机所有的电气参数。递推最小二乘算法以其计算量少、计算简单等优点可以较好地应用在感应电机参数辨识中。Y He等[6]以感应电机静止状态下的模型为基础，通过矢量重构输入信号后，电机的各个电气参数可通过递推最小二乘的方法进行准确估算，但该方法过于复杂，不易数字信号的实现。

本文合理地构建适用递推最小二乘算法的感应电机数学模型，提出一种电机静止状态下较易实现的参数辨识策略，仿真结果表明该方法能够有效地辨识出感应电机各电气参数。

2 静止状态下感应电机模型

2.1 静止状态动态电机模型

若忽略空间谐波、磁路饱和、铁心损耗以及频率变化和温度变化对绕组电阻的影响，感应电机在两相静止坐标系下的数学状态方程可表示为[7]：

式中：usα、usβ——定子电压；isα、isβ——定子电流；Ψrα、Ψrβ——转子磁链；Rs——定子电阻；Rr——转子电阻；p——电机极对数；Ls——定子电感；Lr——转子电感；Lm——定转子互感；ωr——电机转子的机械角速度；Tr=Lr / Rr——感应电机转子时间常数表达式，

。

由式（1）可知，若两相静止坐标系下的任一相施加激励电压信号为0，则该相绕组不能产生相应的转子磁链及定子电流，由两相静止坐标系下转矩表达式可知，此时电机转矩为0，电机处于静止状态。因此式（1）可变为：

将式（2）、（3）进行拉斯变换后相互代入，可得到拉斯域的传递函数：

式中： ，

。

定义二阶转换滤波器[7]，很容易得到适用递推最小二乘算法参数辨识的感应电机数学模型，如下：

（5）

式中：θ——待辨识的参数；φ——能观数据组。

2.2 电机模型离散化

递推最小二乘算法最终需要在数字信号处理芯片中实现，因此有必要对所建模型进行离散化处理，使式（5）满足以下形式：

（6）

将式（5）进行双线性Z变化，也就是将拉斯域的s由

替换，那么

记θ为系数θ的估计值，假设感应电机定子电感与转子电感相等，那么感应电机各电气参数估计值表达式可表示为：

静止状态下感应电机电气参数辨识策略图如图1所示，β轴上的激励电压给定为0，α轴上施加的激励电压Usα*通过电流环的PI调节器得出，以保证感应电机处于静止状态。

3 激励信号选择

在递推最小二乘算法辨识电机参数时，激励信号的选取合适与否是影响辨识精度的一个关键因素[8]。

在递推最小二乘辨识过程中，存在激励信号最优选择问题，选择不同类型的激励信号，就有不同的辨识精度。文献[8]表明若选择的输入信号矢量φ（t）持续有界，那么待辨识的参数θ就能收敛于θ，由于所构建递推最小二乘数学模型中的φ（t）是定子电压usa，定子电流isa通过2个不同截止频率的低通滤波器所得，usa由电流环控制器输出所得，因此，只要保证isa持续有界，就能保证参数辨识的收敛。

由于所构建的感应电机递推最小二乘数学模型所要辨识的参数个数有n=4个，因此所选的激励信号isa至少需要由n/2个不同频率的正弦信号叠加构成。

4 递推最小二乘算法辨识

由前文构建的合理的感应电机数学模型，通过以下递推最小二乘算法[9]，辨识精准的电机参数：

式中：θ（k）——上一个采样周期的参数估计值；y（k+1）——本次采样周期内系统实际输出值；G（k+1）——增益相；θ（k+1）——本次采样周期内对预测的参数辨识值进行修正后的结果。

通过式（9）不断地迭代计算，便能准确估计出待辨识参数。

5 系统仿真研究

在MATLAB/Simulink中建立感应电机最小二乘模型，并对所提参数辨识策略进行仿真，仿真中系统给定的电机模型参数分别为：Ls=0.107H，Lr=0.108H，Lm=0.105H，Rs=0.64Ω，Rr=0.51Ω，极对数为2。给定的两相静止坐标系α轴上的参考电压U*sα是由激励电流信号I*sα通过PI控制器调节输出所得，设计PI参数为kp=50，ki=5，给定I*sα=20+10sin（30t）+2sin（10t），它是由频率4.7Hz和1.6Hz的正弦信号叠加而成。β轴上的参考电压U*sβ给定为0V，以确保电机处于静止状态。

另外，由于输入信号矢量φ（t）的获取与低通滤波器参数h0、h1有关，它们的选取准则要求1/hi大于采样周期Ts，因此仿真中选择h0=40，h1=90。整个仿真结果如图2～图4所示。

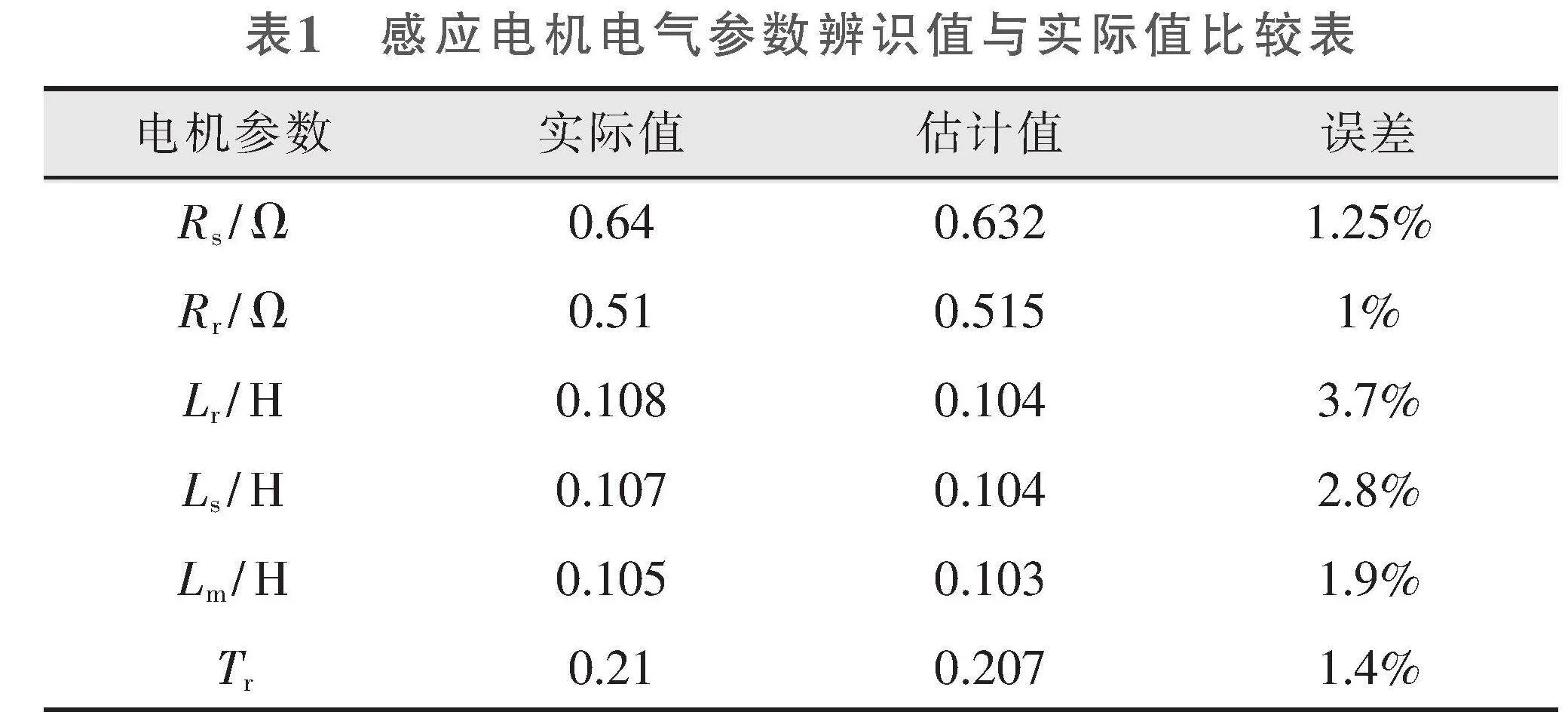
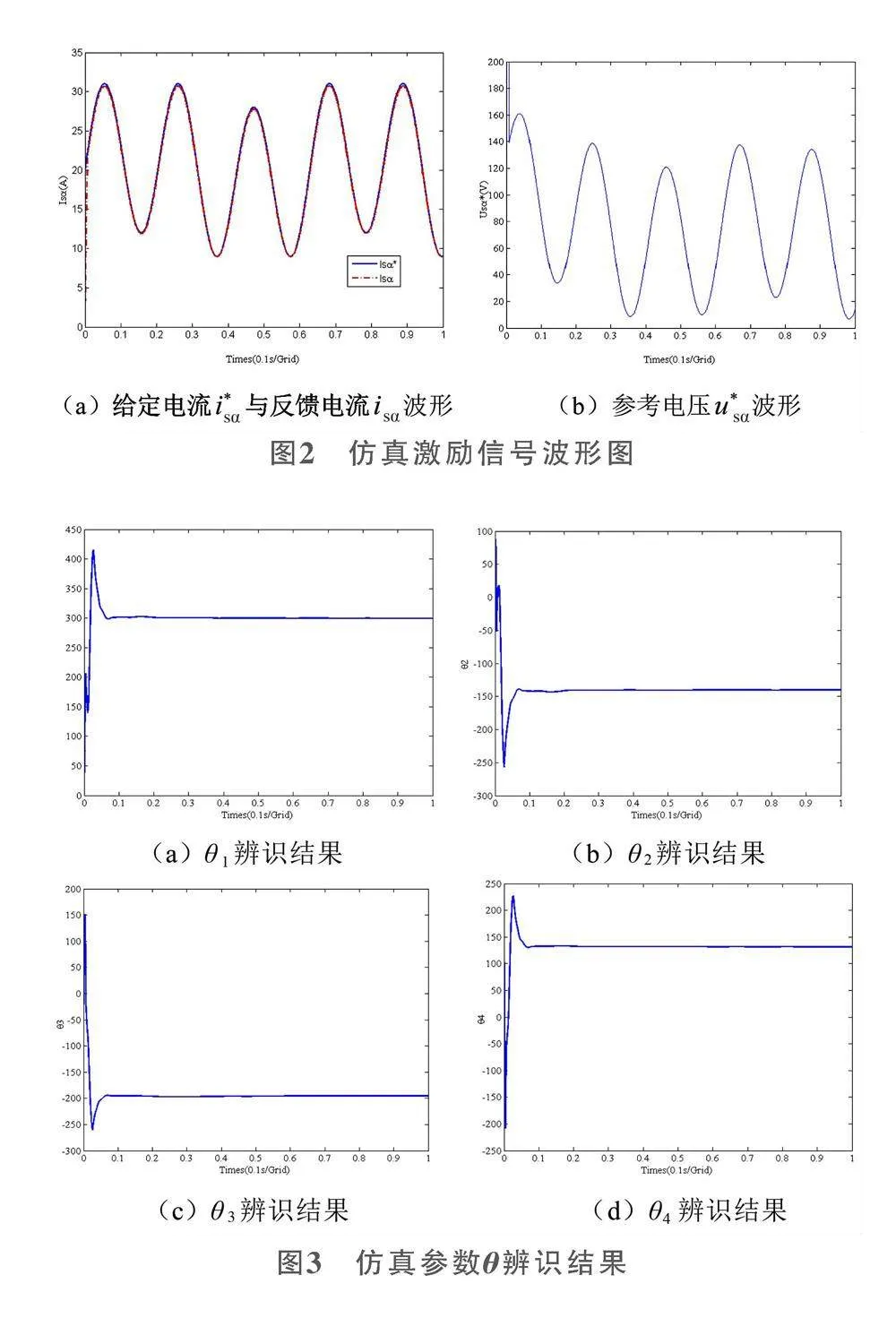
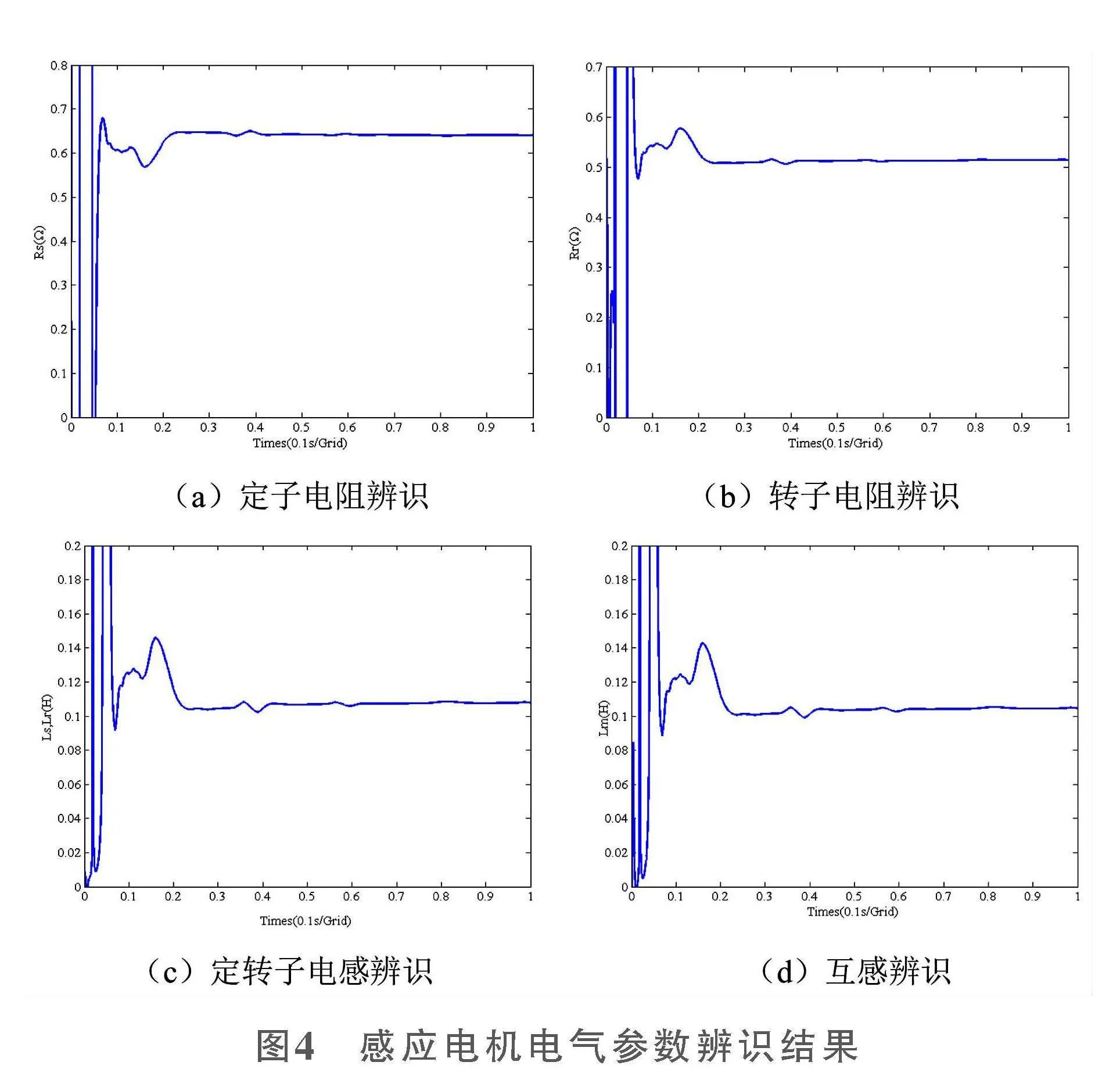
图2为仿真激励信号波形，图2a为给定的电流i*sα与反馈电流isα的波形，从图中可以看出由于PI控制器的作用，反馈的电流值能够实时地跟踪给定值。图2b是α轴电流环PI控制器的输出值u*sα，从图中可以看出u*sα在频率上能够满足辨识的需求。图3为仿真参数θ辨识结果，图4为感应电机电气参数辨识结果。从图中可以看出，参数的辨识结果能迅速地收敛于实际值，体现了算法的有效性。具体感应电机电气参数辨识值与实际值比较见表1。从表1中也可以清晰地看出所提辨识策略能非常精准地辨识出电机参数，最大的辨识误差出现在转子电感上为3.7%，但影响电机控制性能的转子时间常数辨识误差仅1.4%，这对电机控制性能上的影响是非常小的。

6 结语

本文首先推导了感应电机静止状态下的数学模型，并在此基础上构建适用递推最小二乘算法的电机数学模型，提出可进行电机参数递推最小二乘算法辨识策略，通过合理的激励信号选择用于电机相关电气参数的辨识，在MATLAB/Simulink环境中仿真，验证了电机参数辨识策略的有效性及精准性。

参考文献：

[1] 阮毅，陈伯时. 电力拖动自动控制系统-运动控制系统（第4版）[M]. 北京：机械工业出版社，2014.

[2] 徐奇伟，宋立伟，崔淑梅. 感应电机矢量控制中转子参数自适应辨识[J]. 电工技术学报，2011，26（6）：81-87.

[3] F.R.Salmasi，T.A.Najafabadi.An adaptive observer with online rotor and stator resistance estimation for induction motors with one phase current sensor[J]. IEEE Transactions on Energy Conversion，2011，26（3）：959-966.

[4] Habibur Rehman，Adnan Derdiyok，Mustafa K. Giiven，et al. An MRAS Scheme for On-Line Rotor Resistance Adaptation of an Induction Machine[C]//IEEE Annual Power Electronics Specialists，2001（2）：817-822.

[5] Huang Bin，Qu Wenlong，Lu Haifeng.A Novel On-Line Rotor Resistance Estimation Method for Vector Controlled Induction Motor Drive[C]//IEEE IPEMC，2004（2）：655-660.

[6] Y He，W Yue，Y Feng，et al. Parameter identification of an induction machine at standstill using the vector constructing method[J]. IEEE Transactions on Power Electronics，2012，27（2）：905-915.

[7] CH Fang，SK Lin，SJ Wang. On-line parameter estimator of an induction motor at standstill[C]//in Proceedings of the European Control Conference（ECC）.UK Cambridge，2003（1）：3200-3203.

[8] M.Cirrincione，M. Pucci，G. Vitale，et al.A least-squares based methodology for estimating the electrical parameters of induction machine at standstill[C]//in Proceedings of the IEEE International Symposium on Industrial Electronics，2002，56（8）：541-547.

[9] 萧德云. 系统辨识理论及应用[M]. 北京：清华大学出版社，2010.

（编辑 杨凯麟）