电线世界与模拟神经元的游戏

摘要：图灵机是一种抽象的计算模型，可以模拟其他任何规则的计算机器，但计算机的初学者可能较难把握图灵机的工作原理和特点，以至于难以领悟“通过计算模型的相互模拟来解决问题”这一重要的思想方法。针对这种情况本文提出，模拟神经元的游戏可以为学习者提供一种领悟这种思想方法的简单路径，如可以用电线世界这种元胞自动机作为探索搭建模拟人工神经元的平台，这个平台也可能成为一个基于有限规则的实现多样性的创新设计的环境。

关键词：人工神经元；计算模型；电线世界；元胞自动机；游戏

中图分类号：G434 文献标识码：A 论文编号：1674-2117（2024）13-0016-05

设想一个由大量形状、质量不一的多米诺骨牌组成的巨大的错综复杂的阵列，阵列中架设有高架桥甚至是隧道，使得排列好的骨牌连通不同区域，还通过分支线路将骨牌推倒的连锁反应并行传播到多个区域，其中，有些骨牌的排列通过多次弯曲来延长路线用以控制信号传递的时间，某些骨牌的质量和摆放位置被精心选择和安排，其是否能被推倒取决于倒在它身上的骨牌的数量或重量是否超过一定限度，从而实现了一种判断，类似于神经元根据输入信号的阈值来决定是否发出信号。笔者认为，一个理论上的多米诺骨牌阵列可以模拟出神经网络的行为，当看到侯世达很早之前说过的“这幅（多米诺骨牌阵列的）图景与脑内神经网络相去无几”[1]的时候，笔者就知道应该有不少人曾经有过类似的想法。

考虑一下“用一组多米诺骨牌模拟了神经网络模型”和“用一组多米诺骨牌搭建了神经网络模型”这两句话之间有什么样的区别。与之相比较的是，虽然人们会说“用积木搭了一个宫殿的模型”，但不说“用积木模拟了一个宫殿模型”。其中的原因大概有这样一些：虽然说（理论上）搭建成功的这个神经网络模型的基底正是现实中物理材料的多米诺骨牌，但这些物理材料并不是自然而然地用于搭建神经网络的，而是巧妙地利用了这些材料的某些物理特性，对神经元的行为进行了同构，从而使得这个多米诺骨牌阵列具有神经网络的功能。这里值得注意的有趣之处是，如果某个计算模型能够被模拟出来，那么模型本身就实现了计算模型的功能，模型和被模拟物从计算功能的角度看是等价的。

实现模型的基底并非必须是真实的物理材质，某些虚拟的对象只要其行为具有同构的潜力就能被利用来构造计算模型，如游戏《我的世界》中的红石，或《泰拉瑞亚》里的神秘电路和可疑镀层。不过，红石和神秘电路具有太强的用于计算的指向性，实际上存在大量游戏，人们可以利用这些游戏中其本意绝不是用于构造计算模型的元件来构造计算模型，如扫雷或超级玛丽奥。用多米诺骨牌搭建出来的模型本身的运作过程实质上就是一种骨牌被陆续推倒的过程，此游戏首先表现为一种“从搭建到推倒”的有趣过程，其原始意图也不是为了进行特定计算，利用这种推倒过程来实现神经网络，而是基于原有游戏规则的更上一层的游戏。研究游戏哲学的伯纳德·舒兹称其为“玩笑者”的游戏，“玩笑者”们不注重原先的游戏目标，而是对游戏规则的兴趣更大，他们会重新利用规则，并实现对游戏控制本身的控制。[2]“玩笑者”自己设定的游戏目标可以是多种多样的，如以最少消耗的弹药来通关、搜集游戏中的全部彩蛋、扮演NPC等。

考虑到在课堂上搭建多米诺骨牌阵列并不容易，本文将围绕利用一种具有类似多米诺骨牌阵列的连锁反应特性的电线世界（WireWorld）来模拟神经元行为的游戏过程，并思考规则和创新的关系。本文还将略微扩展讨论一下关于游戏是否能被定义的老问题，伯纳德·舒兹认为可以，而维特根斯坦认为游戏不能被定义，不同的游戏之间仅存在一种家族相似性。[3]

电线世界的基本规则

电线世界是一种二维的元胞自动机，因为其规则设置、布局和运行的过程相当有趣，使得大多数学生可以认同这是一个游戏：首先是玩电线世界，然后才有可能产生出兴趣来研究电线世界。电线世界的运行规则基于若干种不同类型的元胞，在一个简单而被广泛运用的设计案例中，有这样四种元胞：电子头、电子尾、导线和空间。这些元胞在一个以矩阵排列的二维网格上相互作用，模拟出类似于电路的行为。元胞每经历一个时刻，集体同步地按以下基本规则（在基本规则没有被自定义或扩展的情况下）运行：

空间总是变为空间，也就是保持不变，没有任何活动的空间常被视作电线世界的背景。可以将空间标号为数字“0”；

电子头总是变为电子尾，电子头标号为“1”，电子尾标号为“2”；

电子尾总是变为导体，电子尾标号为“2”，导体标号为“3”；

当仅有1个或2个电子头作为邻居时（观察当前导体周围8个元胞状态），导体变为电子头，否则，导体保持不变。导体标号为“3”，电子头标号为“1”。

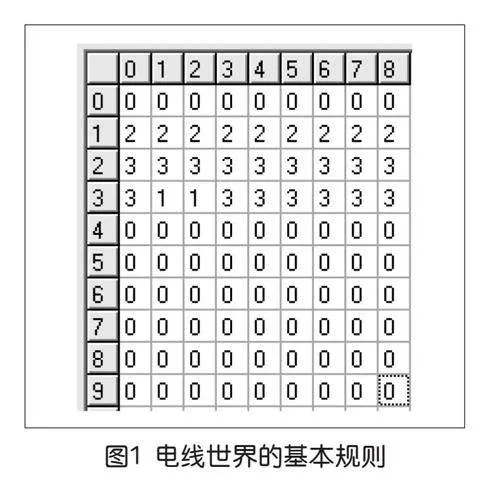
可以用一个二维表来表达元胞的状态变化规则，如标号为3的导体的行为可见表中标为“3”的行，每一列的数字对应当前元胞周围存在电子数量所对应的变化目标。例如，标为“3”的行与标为“1”的列的交叉处空格所填写的数字为“1”，与标为“2”的列的交叉处空格所填数字也是“1”，这就表示当标号为“3”的导体周围有1个或2个电子头时，导体在下一时刻变为标号“1”的电子头。再如，标为“2”的行的所有列空格都填写了“3”，表示标号为“2”的电子尾无论怎样都会变成标号为“3”的导体。规则表如图1所示。

电线世界的运行规则非常简洁，直观地观察电线世界的演变，可以很轻松地领悟演化规则。然而，由于元胞之间的相互作用和动态变化，基于简单的规则可以产生出非常复杂和多样的行为。假设绘制一段导体，在导体的某处绘制一对紧挨着的电子头和电子尾，那么在持续的时间变化中，就会产生出一种电子头和电子尾在导体中移动的效果。虽然说，实际上每个元胞都没有移动，但元胞的状态变化产生出一种移动的效果，这与多米诺骨牌游戏被推倒过程中所产生的效果类似。在不同形状的导体中，电子的移动和碰撞会产生出不同的效果，可以用来同构不同的逻辑运算。电线世界是研究复杂性科学、自组织现象的一个有力的工具，当然也可以将其视作一种游戏：在背景上画出图案，观察其复杂且难以预料的行为，仅仅是这样就已经相当有趣。用人脑很难跟踪电线世界的元胞变化过程，可以使用元胞自动机模拟器MCell或Golly来设置电线世界的元胞布局并观察运行变化过程。

创造性地利用规则

有相当多的文献研究了如何利用电线世界构造逻辑电路，然后再利用逻辑电路来构造各种功能的计算装置。然而，游戏目标可以是多样化的，如造一个导体迷宫，让电子从迷宫的左下角入口自行寻找到路径移动到右上角出口（如图2）。

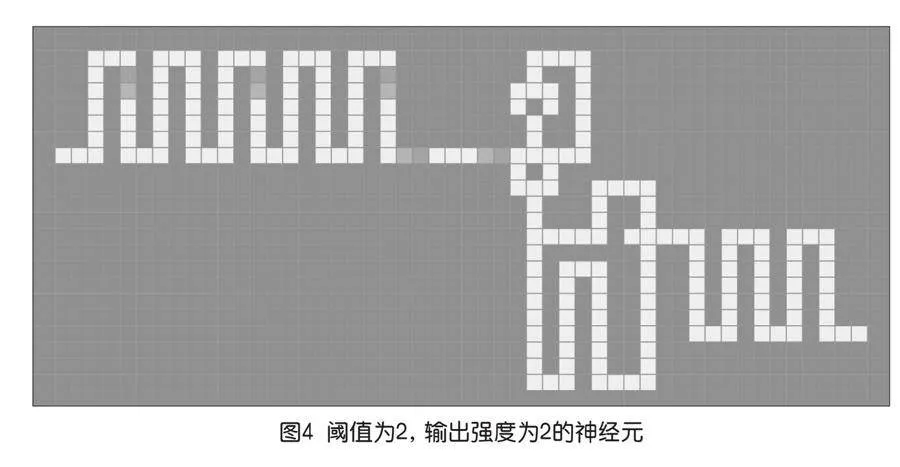
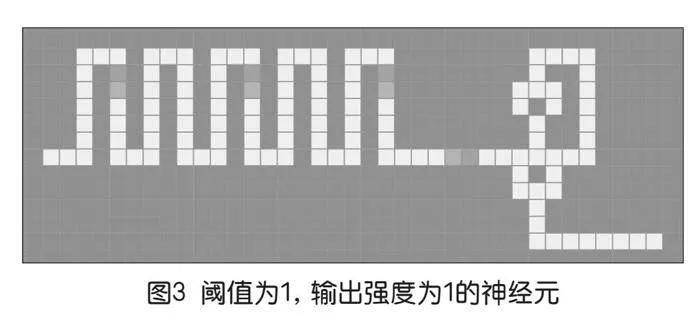
既然利用电线世界中的某些行为属性能设计逻辑电路，那么也可以利用另外一些属性来设计出其他一些有趣的东西。笔者试着用电线世界来模拟的神经元，图3所示的这个神经元的行为法则是这样的：当输入信号强度大于1时，激发动作电位，对外产生出强度为1的信号。当然，可以轻松地调整神经元的行为，图4所示的神经元的行为法则是，当输入信号强度大于2时，激发动作电位，对外产生出强度为2的信号。

规则的自定义和扩展

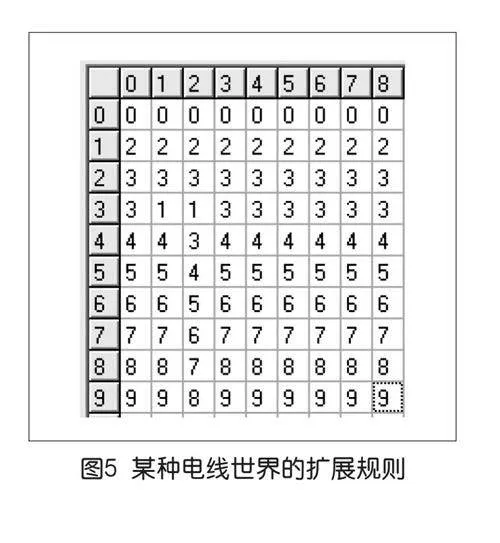
当然，也可以打破电线世界的基本规则，对规则进行自定义和扩展，如设定图5所示的相对复杂的变化规则，并按此规则实现一种图样相对简单的神经元（如下页图6）。

但从某个角度说，也可以认为本质上并没有真正自定义或扩展规则，原因是，电线世界是图灵完备的，它本来就可以模拟出各种计算规则，所有自定义或扩展的规则，都可以认为是基于基础规则的一种功能的封装和模块化。

计算模型在模拟和解析复杂系统方面发挥着重要的作用，用一种计算模型模拟另一种计算模型，常常为跨领域的问题的解决提供新的思路。作为计算机科学的先驱，图灵提出了图灵机的概念，这是一种用机器模拟人通过改写纸带上的符号以及移动纸带来实现计算的模型，这种模型能模拟任何其他的计算过程，图灵的研究展示了计算模型之间具有模拟能力，这样也就证明了图灵机以及能模拟图灵机的计算模型具有通用性。不过，由于对图灵机的基本原理以及其解决问题的思维方法的熟悉过程需要较多精力，这样就较难在有限的时间里，向学习计算机的初学者展现出不同的计算模型相互模拟的过程。相对而言，人工神经元是一个简单的计算模型，人工神经元的输入有多个通道，当输入信号强度总和超过某个阈值时，发送信号给其他神经元。

在人工智能教学中，涉及人工神经元的教学可能有不同路径，如利用人工神经元的属性搭建特定的神经网络；在知晓一个理论的人工神经元的工作过程后，构造一个人工神经元使其能够用于搭建神经网络。这两者涉及的能力有所不同，后者没有预设框架，虽然存在若干底层规则，但并不规定人们应该用规则去做什么或不该做什么，在规则的运用过程中，思维是敞开的。例如，可以出乎意料地利用int函数来模拟神经元，实现神经网络，图7所示的是用“int”函数架构神经网络进行异或运算的代码，简单到仅有数行。

略谈游戏和创新

伯纳德·舒兹这样给出游戏的定义：玩一场游戏，是指企图去达成一个特定的事件状态，在这个过程中只用规则所允许的方法，这些规则禁止玩家使用较有效率的方法而鼓励低效率的方法，而规则会被接受只是因为规则让这项活动得以进行。[4]在这个定义中，“禁止玩家使用较有效率的方法而鼓励低效率的方法”有一定的启发意义，但对游戏的玩家来说，与其说是“鼓励采用低效率的方法活动”，不如说是“被强制采用低效率的方法活动”更为合理，这一条件会使得玩家多样性地去思考如何克服这种低效率，于是激发出创新。

需要进一步考虑的是，在电线世界中，新的规则能在底层的规则上被模拟出来，反过来，底层规则其实也并不是真的底层，可以用其他规则来模拟出所谓的底层规则。在电线世界中，企图去达成的那个特定的事件状态，也是不确定的，玩家可以随意在矩阵中绘图，观察其在一段时刻后究竟发展出怎样的效果，并思考怎样组合利用不同的效果来创设出一种新的游戏规则。那么，创造游戏规则是否属于一种游戏？创造规则使得原本不可能之事成为可能，即便存在基础规则，创造规则的方式仍然是多样的、未被预先设定的，并且以创造规则作为规则的游戏，从技术实现上说完全可能，正如电线世界。这样看来，伯纳德·舒兹或许只是给某类游戏做出了定义，甚至可以说这种定义尽可能涵盖了大部分的游戏，但没有给出普遍意义上游戏的定义。考虑定义游戏是为了对游戏的属性进行一种描述，那么“挑战已有的描述”这件事本身也可以是一种游戏，这种具有自指和递归特性的描述就使得为游戏设定普适的定义成为不可能。

蓝江说某些游戏具有这样的潜力：“（让玩家）看到那些没有关系的关系，看到无法被观念和框架呈现出来的不可见物，从而在新的地基上实现无关系的关系”。[5]笔者认为，具有这种特性的游戏可以作为培养创新的平台，因为人们在这样的平台中，不仅可以对现实世界进行部分程度的同构，还可以构造现实世界中不存在的事物，也就是架构出本没有关系的某种关系，相信这是人所专有的而非机器能企及的一种能力。人的这种构造能力，也是当今世界如此丰富多彩的重要原因。

电线世界是一种游戏吗？大多数学生认为是。然而，要求在没有图纸的情况下，用电线世界自行设计一个人工神经元，这还是一种游戏吗？只有极少数学生仍然说是。这是因为对于当前的立足点来说，“新的地基”过于遥远，不妨先尝试一些小的任务，如试着实现一个按特定频率发送信号的装置、实现一个只允许信号单向通过的装置、实现一个信号汇聚的装置……在探索中会发现，有些功能装置已经有人设计出来了，有时随机绘制的图案就已经显现出某种恰好能被利用的功能，某些现象可以组合起来用以达成某种功能……对着虚拟物进行“观察—归纳—假设—验证—构造”，学习者可能需要有意识地将现实自然中的研究过程迁移至虚拟世界中，甚至可以说，在虚拟世界中更容易真实完整地达成“观察—归纳—假设—验证—构造”的过程，这应当是信息意识的一部分。

参考文献：

[1]（美）侯世达，（美）丹尼尔·丹尼特.我是谁，或什么——一部心与自我的辩证奇想集[M].舒文，马健，译.上海：上海三联书店，2020：52.

[2][4]（美）伯纳德·舒兹.蚱蜢：游戏、生命与乌托邦[M].胡天玫，周育萍，译.重庆：重庆出版集团，2022：200，44.

[3]维特根斯坦.哲学研究[M].北京：商务印书馆，1996：48.

[5]蓝江.双重凝视与潜能世界：电子游戏中的凝视理论[J].上海大学学报：社会科学版，2022，39（03）：78-89.