浮点数的教与学

摘要：浮点型数据在计算机系统中广泛应用，但其表示精度存在一定的限制，客观存在不能精确表示的现象。在教学工作中，关于IEEE754规格化浮点数有效位数的内容难以理解，导致学生对浮点数精度的学习存在困难。基于IEEE754标准，通过大量图表、实例，将浮点数的基本格式、数据范围、精度等问题具象阐释。对精度问题提出了两种理解方式：一是从数值分析的角度根据有效数字的严格定义来进行确定；二是从近似值能准确表示的十进制数的位数来确定。开发了一个可视化的教学辅助工具，能够直观展示浮点数的精度判断结果，对于教学工作具有实际应用价值。

关键词：浮点数；IEEE754；有效位数；取值范围；计算机系统

中图分类号：TP301 文献标识码：A

文章编号：1009-3044（2024）17-0168-04 开放科学（资源服务）标识码（OSID） ：

0 引言

自教育部在2017年提出开展新工科建设后，随着新工科专业建设的不断深入，复杂应用型人才的培养成为高校人才培养的方向。高校计算机科学与技术专业教指委对计算机专业学生的培养提出了专业能力培养目标，特别强调计算机系统能力培养的重要性[1-2]。2021年12月31日，教育部启动了一个旨在改进计算机专业课程教学的“101计划”[3]。计算机专业人才的能力培养最终体现在专业教学中的课程内容和课堂教学过程。计算机系统基础是计算机专业的基础课程，是“ 101计划”12门核心课程之一。

作为“101计划”教材试点项目单位，浙大城市学院计算机系统基础课程注重课堂教学细节的打磨，力求将培养学生的系统思维能力落实到具体的知识点。计算机系统基础教学过程中，高级语言中的浮点数在机器底层的表示是教学重点和难点。浮点型数据在编程使用中存在不能精确表示实数的现象，并且关于IEEE754标准中规格化浮点数有效位数内容的教学深度难以把握，导致学生对浮点数精度的理解有一定困难。本文通过对IEEE754标准的基本介绍，对规格化浮点数范围和精度的深度分析，并开发一个可视化的应用程序显示输入数据的有效位数，具体具象地帮助学生更好地理解IEEE754标准中的规格化浮点数，从而引导学生在编程中有意识地避免因精度问题导致科学计算的错误。

1 IEEE754标准简介

IEEE754标准具有两种基本浮点格式：32位单精度float格式和64位双精度double格式。

如图1所示，这两种类型数据在存储中都由两个定点数和一个符号位来存储表示[4]。

1） 符号位 S：float 类型和 double 类型都占 1 位，将正负号进行符号数字化，0 代表正，1 代表负。

2） 指数位 E： float 类型占 8 位，double 类型占 11 位，指数采用移码表示，即将原来的实际指数值加上一个偏移量固定值，该固定值为 B= 2e - 1 - 1（B表示偏移量，e表示指数部分比特长度，对于 float 类型，e=8，偏移量 B= 127；对于 double 类型，e=11，B=1023） 。

3） 尾数位M：float类型占23位，double 类型占52 位。尾数采用定点小数原码表示，对于规格化后的尾数，首位默认位1，并缺省隐藏，使得对于float类型，只保存23位尾数便可用来表示 24 个有效信息，对于double 类型，52位尾数部分可以表示53 个有效信息。

2 浮点数的范围

2.1 规格化浮点数的范围

首先讨论规格化浮点数在一个数轴上的分布情况。float类型的阶码部分存储的是一个无符号整数，取值范围为00000000～11111111，即[0，255]，则实际指数取值范围为[-127，128]。而规格化浮点数，阶码范围去掉了全0 和全1 的情况，即00000001～11111110，实际指数取值范围为[-126，127]。

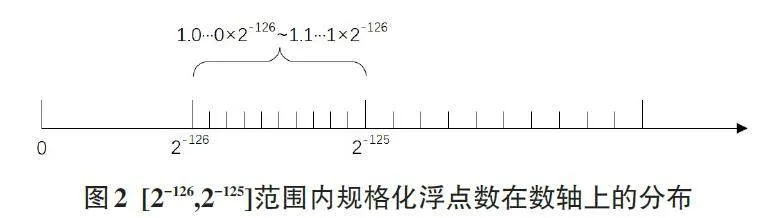
对于其中任意一个阶，其23位尾数，从1.0...0 ～ 12.-112.6.。.1因将此一，个 以阶[2均-12匀6，2分-125成]范了围2内23段的，规每格一化段浮间点距数为为2例-23×，其在数轴上的分布如图2所示：

对于下一段，每一小段的间距为2-23×2-125，是前面一段的2倍。因此，规格化浮点数在数轴上的分布如图3所示，每一个阶的区间内等距分布223个数，下一区间是上一区间相邻数间隔的2倍，分布越来越稀疏。

由此可以得出规格化浮点数的范围[5]：float类型能表示的绝对值最小数为1×2-126，对应十进制数约为 1.1754943508222875×10-38，最大数为1.M×2127，M为全1，对应十进制数约为3.40282×1038 ;而double类型则同理，能表示的规格化绝对值最小数为 1×2-1022，对应十进制数约为 2.2250738585072012×10-308，规格化绝对值最大数为1.M×21023，M 为全1，对应十进制数约 为1.7976931348623157×10308。

2.2 非规格化浮点数的范围

非规格化浮点数在数轴上的分布如图4所示，通过在-2-126～0和0 ～2-126这两段区间内，都均匀地插入223个数，用来表示比最小规格化数还要小的数。

当遇到不能用规格化数表示的极小的浮点数时，采用“逐级下溢”的操作，尾数的首位隐藏位不再是1而是0，将阶统一为2-126，再根据舍入方式来近似表示。

由此可以得出非规格化浮点数的范围[5]：float类型能表示的非零绝对值最小数为0.M×2-126，尾数部分1M.40最129后846一432位481为71 ×11，0-对45，非应零十绝对进值制最大数数约为为0. M×2-126，M为全1，对应十进制数约为1.175494×10-38；而double类型则同理，能表示的非规格化非零绝对值最小数为0.M×2-1022，尾数部分M最后一位为1，对应十进制数约为4.9406564584124654×10-324，非零绝对值最大数为0.M×2-308，M 为全1，对应十进制数约为2.2250738585072009×10-308。

3 浮点数的精度

3.1 IEEE754表示浮点数的方式

根据上文对IEEE754标准中浮点数分布的分析，可以看到IEEE754标准就是将实数分割成一个一个的“离散”的值在内存中存储，使得计算机能够尽可能地在无限的实数中表示出更多的浮点数。

通常，当我们给出某一高精度浮点数时，很可能不是IEEE754 标准下能够恰好表示出来的那个数。因此，在规定的舍入规则下，该数会被舍入到邻近某一精确的可表示数来存储。

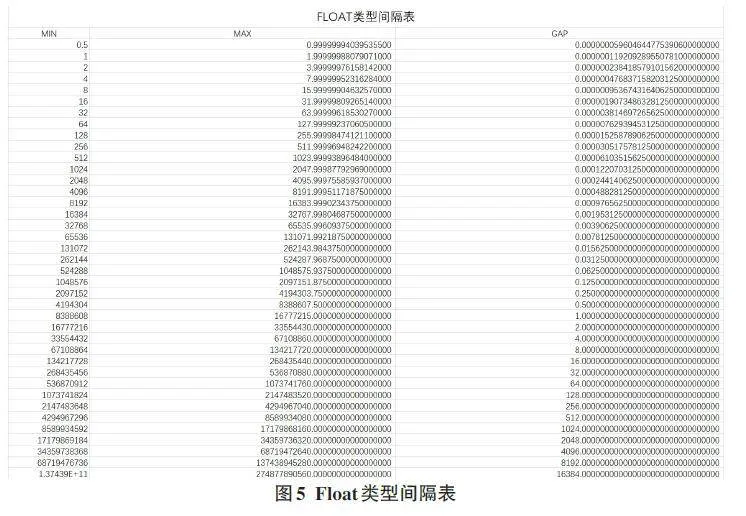
如图5所示，为了更直观地计算，在此给出整理后的部分32位浮点数的间隔表。表中Min、Max、Gap三列，反映的即为区间[Min，Max]上的GAP值，也就是在数轴上每个区间内等间隔相邻数的间距。

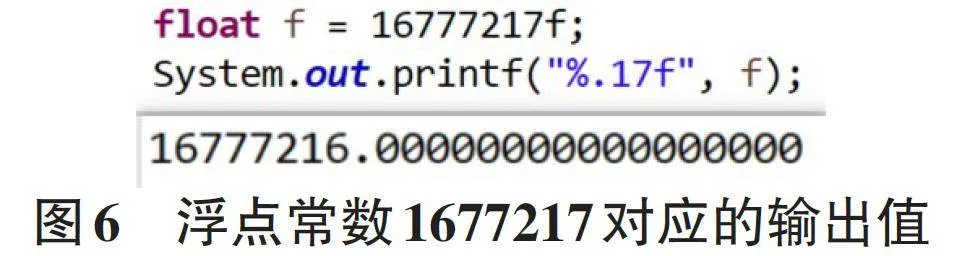
例如，当需要表示16777217 时，结果将被舍成16777216，如图 6所示。因为在区间[16777216，33554430]上的GAP值为2，IEEE754只能表示16777216和16777218，16777217就是图4表示的数轴上没有刻度的一个位置。

验证更多数据，发现均是如此，如图7所示。

了解了IEEE754最底层的存储方式后，那么此时便存在着“真值”“近似值”的概念。那些输入的不能被恰好精确表示的即为“真值”，内存中存储的则是“ 近似值”。进而便存在近似值的精度问题，即IEEE754舍入后表示的数相比于给定的浮点数接近程度的讨论。

3.2 浮点数精度分析

3.2.1 相关概念及术语

真值A：一个真实准确的数值。

近似值A*：接近真值的一个值。

精度：观测值与真值的接近程度。

有效数字：反映近似值准确程度的概念。当近似值的绝对误差限是其某一位上的半个单位时，就称其“准确”到这一位，且从该位起直到前面第一位非零数字为止的所有数字都称为有效数字。

有效位数：有效数字的个数。假设A是真值，A*是近似值。A = ±0.a1a2...an...×10m，其中m是整数，a1到a1n0都-k，即是A0到的9误中差的不某超个过数10字-k，的a1半 ！=个 0单.如位果，|则A-称A*近| ≤似0.5数×A*准确到10-k 位，并说A*有m+k位有效位数。

绝对误差η：η=|A - A*|。

绝对误差限：η绝对值的一个上限，即如果存在一个正数e，使得|η|≤e，那么称e为A*的绝对误差限。

相对误差：绝对误差与被测量真值之比。

相对误差限：相对误差的上限。

3.2.2 两种理解方式

一种理解的描述是32位浮点数的精度是6～8位十进制有效数字，64位浮点数的精度是15～17位十进制有效数字。

另一种理解的描述是32位浮点数的精度是6～8 位十进制数，64 位浮点数的精度是15～17 位十进制数。

两个结论看似一样，但对于float、double精度的讨论，从不同的角度看，两种理解方式皆有其合理性。

1） float 的精度是6～8 位十进制有效数字。给定真值π 和其近似值3.1416。若求近似值的有效位数，则根据有效数字的定义，|π-3.1416|≤0.5×10-4，即近似值的绝对误差限是小数点后第四位上的半个单位，近似值准确到该位，并且从该位起直到前面第一位非零数字为止的所有数字都称为有效数字，故3.1416的有效位数为5位。这种方法即严格意义上的有效位数计算方式，也就是第一种结论的分析方式。

2） float 的精度是6～8 位十进制数。对于同样的例子，如果对近似值精度的理解是近似值从左到右正确表示了多少位的十进制数，那么只需从左到右对3.1416 和3.1415926 依次逐位比较，发现精确到了0.001，即可得出近似值正确表示了4位十进制数。

此时，相较于第一种判断精度的方式，这种方式似乎给人一种不准确的感觉，因为其并没有引入“有效位数”的概念。但笔者认为只要厘清定义，两种方式都可以用来分析精度。

3） 比较与总结。第一种理解的判准，引入了“有效位数”的概念，是从严格的数值分析[6]角度来确定近似值具有多少个有效数字的；第二种理解的判准没有引入“有效位数”的概念，而是用近似值从左到右准确表示了多少个真值中的十进制数来表示精度。我们要确定精度，就是要确定近似值和真值的接近程度，那么这种方式在一定程度上的确是能够描绘出这一概念的。

值得注意的一点是，根据第一种判断方式，有n 位有效数字的近似值A*是真值A的准确到第n 位的近似值，那么只有以下两种情形：A*的这n 位数字与A中的n 位数字完全相同；A*的前n-1位数字与A中的n-1位数字完全相同，只有第n 位数字不同，并且不同时，两者相差1。由此可以发现，实际上用近似值从左到右正确表示了多少位的十进制数的方式来表示精度，就是第一种判断方式的子集。因为采用十进制数判准方法获得的有效位数，用数值分析的方式一定也能判断出来。

并且，结合实际调查询问，许多学生在一开始查看float或double的精度时，就是通过输入一系列值，简单地比对有多少十进制位相同，来依次确认6～8位“有效位数”的结论。也就是说，这种判准在某种意义上是更为常用的判断方式，更简单便捷，易于学生理解。但要分清楚基本概念，在这种方式的使用场景下，并不能用“有效位数”来描述衡量。

3.3 具体数据实例说明

下面通过实际数据样例，具象直观地查看float类型精度为何是6～8位有效数字。

按照有效数字的严格定义，2048.0001～2048.0008的有效位数如图8所示：

4532.50～4532.85的有效位数如图9所示：

由此可以大致看出，输入一定高精度的浮点数，float的精度是6～8位十进制有效数字。而上述只是部分数据的简单反映，要想严格证明有效位数，还需要数学层面的严格证明。同样，按第二种处理方式，2048.0001～2048.0008的精度如图10所示：

注意，图10的第7、9、15行即与第一种处理方式结论“不同”（有效位数为x位，而精确到y位十进制数）的情形。

综上，在第二种理解方式下，通过简单的数据罗列能看出，输入一定高精度的浮点数，float的精度能精确到6～8位十进制数。

4 教学辅助工具

通过如上分析可以发现，想要在教学过程中直观清晰地阐明浮点数的精度问题属实不易，学生在学习过程中也极易因精度理解的不同产生疑惑[7]。故开发一个可视化程序，实现浮点数的精度判断，辅助学生进行学习。

学生可以输入任意数值，选择float 类型或者double类型，程序将给出机器数以及两种角度下判断的精度。

源数字：即输入的值，真值。

机器内转换后的数字：即真实存储在机器中的值。

精确到了几位十进制数： 从左边第一个数开始比较，直到第一个与真值不同的数字结束，中间所有数字即有效数字。如图12运行结果二，从第一个数字0 到数字6，存在11位相同的十进制数。

严格意义下的有效数字：即按照前文所述的有效位数的严格定义，即7位有效数字。

5 总结

在计算机系统工作原理的教学中，高级语言中的浮点数在机器底层的表示是重要的教学内容。浮点数的表示范围和精度，是其理解的难点和重点。本文对IEEE754标准中的浮点数表示范围和精度进行了详细的分析，为了能够在教学过程中让学生对这个问题理解得更透彻，并没有进行非常严格的数学角度的推理，而是从图形和程序展示的角度，让学生能够有直观感受，从而能够更好地理解浮点数在机器底层表示的原理和局限性，为日后工程开发中合理正确地使用浮点数奠定基础，避免在最终计算结果中产生重大错误。

【通联编辑：王力】

基金项目：2023年度计算机领域本科教育教学改革试点工作计划“（ 101计划”） 教材试点应用项目；国家级大学生创新创业训练计划项RoadSense-基于路面坑洼检测的智慧交通决策支持系统（202313021005） ；2021 年度教育部第二批产学合作协同育人项目“面向系统能力培养的计算机系统原理在线教学资源建设”（202102533017） ；2023 年校级在线开放课程建设项目“计算机系统原理实验”；2023 年校级七期重点教材建设项目“计算机系统原理实验”；2022 年校级本科实践教学改革研究项目“逆向工程综合实验”（SJ2201）