基于Cook-Torrance 光照模型改进BRDF 计算方式的研究实现

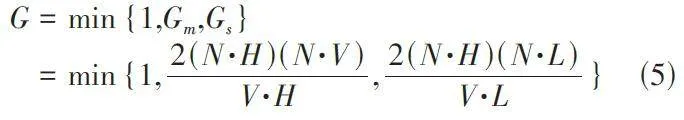
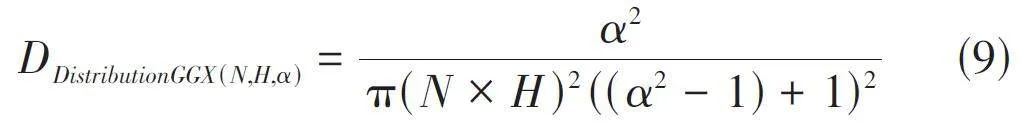
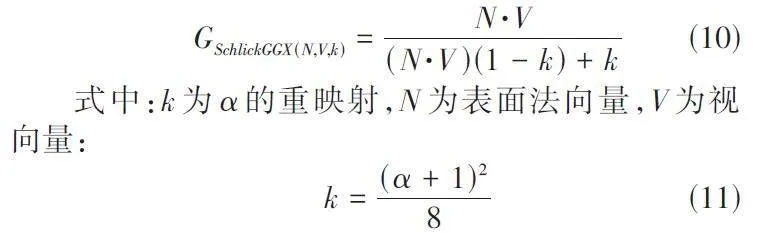
摘要：光照模型在计算机图形学领域中具有至关重要的作用，直接影响着图像的逼真度和视觉真实感。本研究旨在改进传统的光照模型，以更准确地模拟真实世界中光照的物理特性。综合考虑了光的反射、折射、散射以及不同材质表面对光的吸收、反射特性和能量守恒原则。结合菲涅尔效应、微表面法线分布函数以及能量守恒等物理原理，建立了一个更精细、更真实的基于物理的光照模型。通过对比实验和改进后模型的渲染效果，验证了改进后的模型能够更准确地渲染不同材质和光照条件下的反射和阴影效果，从而提高了渲染图形的逼真度和质量。这项研究为渲染领域提供了有价值的技术支持和应用潜力。

关键词：光照模型；计算机图形学；基于物理；视觉真实感

中图分类号：TP311 文献标识码：A

文章编号：1009-3044（2024）17-0123-04 开放科学（资源服务）标识码（OSID） ：

随着计算机图形学的发展，光照模型在三维场景渲染中的作用愈发重要，直接影响图像的逼真度和视觉效果。自1981年提出以来，Cook-Torrance光照模型[1]因其物理基础和逼真效果，广泛应用于工业和学术界。该模型通过模拟光与粗糙表面的交互，为金属和非金属材料提供了准确的光照计算方法。

尽管Cook-Torrance 模型在多个方面表现出色，但随着渲染技术的进步和应用场景的复杂化，原始模型在处理某些特定材质或光照条件时仍存在局限性，如极端条件下的反射率计算、高动态范围光照的适应性及能量守恒的严格性等方面，未能完全满足现代高质量渲染的需求。

本研究旨在改进Cook-Torrance 光照模型，引入新的物理参数和计算方法，提高其在复杂光照和材质条件下的适应性和准确性，特别关注模型在处理高光反射、折射、散射及不同材质表面特性时的表现，使渲染结果更符合真实世界的物理特性。此外，研究还考虑了能量守恒原则和菲涅尔效应，构建了更精确的光照计算框架。

通过对比分析改进前后的模型渲染效果，验证了改进措施的有效性，为计算机图形学领域提供了新的研究方向和实践应用的可能性，期望能在追求极致逼真度和高度复杂场景渲染的应用中发挥作用。

1 Cook-Torrance 光照模型分析[2]

该光照模型基于物理材质，主要考虑了光线照射到物体表面后发生的漫反射和镜面反射现象。其中，Cook-Torrance模型主要用于模拟不同材质的镜面反射效果。

1.1 Cook-Torrance 局部光照模型

Ic - t = Id + Is = kd Ip Rd + ks Ip Rs （1）

式中：Ic - t是cook-torrance模型的反射光强；Ip是入射光强；Id是漫反射光强，其中Rd = max（N·L，0），N是表面的法向量，L是光向量，计算方法仍沿用Blinn-Phong 局部光照模型[2]；Is是镜面反射光强，Rs是镜面反射项。

1.2 计算镜面反射项（Rs）

F项为菲涅尔系数；D项为微平面分布函数；G为几何衰减因子；N为表面法向量，L为光向量，V为视向量。

1.2.1 F 项-Fresnel-菲涅尔系数

描述每个光滑微镜面的反射光与入射光之间的关系：

F = f0 + （1 - f0）（1 - cosθ）5= f0 + （1 - f0）（1 - V ⋅ H）5 （3）

H是中分矢量，其中中分向量和光向量以及视向量之间的夹角是θ，f0为表面基础反射率。

真实世界中，当视线和表面的夹角不同时，反射效果会有差别。例如，站在湖边上，反射不明显，可以看到水下的东西；但是向远处的水面看，反射则十分明显，湖面像镜子一样。根据Schlick模型[3]可以近似计算出F，其中f0 是入射角度接近0°时，也就是光线垂直反射时的 Fresnel 反射率。

1.2.2 D 项-微平面分布函数

模拟物体表面是由无数微小的像镜子一样的平面组成，每一个微平面对于光线会根据自身的方向反射光线。这里采用的是Backmann 分布函数[5]，用分布函数D 来描述微镜面分布的概率：

k 是用于度量表面的粗糙程度，也就是微镜面的斜率。当k 很小时，微镜面只是轻微偏离平面的法线，表面较光滑，反射光具有很高的方向性；当k 很大时，微镜面的倾斜度很大，表面较粗糙，反射光线发散。

1.2.3 G 项-几何衰减因子

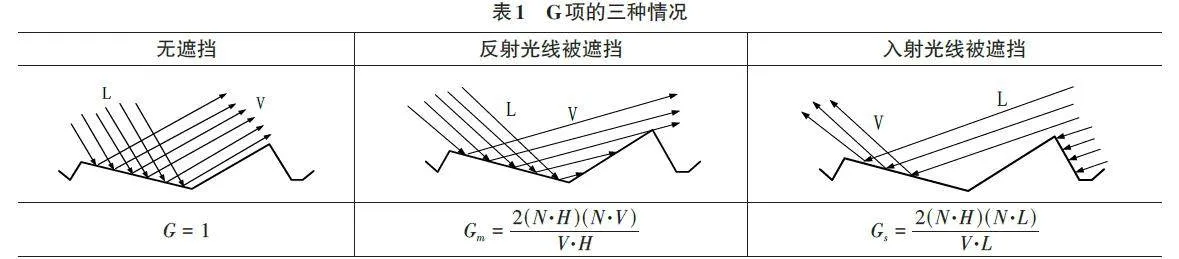
在微观表面层，入射光在抵达表面或反射之前，可能会受到邻近微镜面的遮挡，导致部分光线无法直接到达或反射。这些未被遮挡的光线会随机散射，最终形成漫反射光。几何衰减因子G 被用来量化这种遮挡效应，它描述了镜面反射的轻微变暗现象。

几何衰减因子项，代表微镜面之间的遮挡效果，实际应用中G 被定义为：到达观察者的光的最小强度，G取三种情况中的最小值 G 项的三种情况如表1所示。

2 对BRDF 的改进研究

2.1 微平面理论

微平面理论（Microfacets Theory） ，就是从微观角度去分析，其认为任何物体的表面在到达微观的尺度之后，都是由许许多多的更小的镜面所组成的，如图1和图2表示粗糙和光滑表面。

当这些微小的镜面的法线方向较为集中一致的时候如图3，从宏观角度去看，物体的镜面反射会比较明显，反之，当这些微小镜面的法线方向比较杂乱如图4，分布均匀的时候，表面则会相对粗糙。将表面粗糙度引入到光照模型中，表明镜面反射光颜色和物体的材质属性有关。

除了微观角度的镜面反射，漫反射也是同样重要的现象。在微观尺度上，光线照射到物体表面时，一部分会发生镜面反射，另一部分则折射进入物体内部。这符合能量守恒定律，出射光的能量不会超过入射光，因为部分入射光会被反射或折射，另一些则在物体内部转化为热量消散。镜面反射和漫反射的总和不超过1.0，确保能量守恒。根据这一原则，首先计算镜面反射部分，其值等于入射光被反射的能量百分比。

当光线折射进入物体内部时，会与微小粒子不断碰撞并散射到随机方向，同时部分光能会被吸收转化为热能，有些光线在多次碰撞后被完全吸收。还有一部分光线因散射方向随机性重新离开表面，形成漫反射。以上是从微观角度理解物体表面的镜面反射和漫反射现象，本研究中的BRDF考虑了这两种情况的BRDF。

fBRDF = kd flambert + ks fspecular （6）

2.2 镜面反射BRDF

2.2.1 菲涅尔（Fresnel） 方程（F 项）

在传统的Cook-Torrance局部光照模型中使用的是Fresnel-Schlick近似法求得菲涅尔系数，但是存在一些问题，Fresnel-Schlick 近似仅仅对电介质（非金属）表面有定义。对于导体（金属），使用它们的折射指数计算基础反射率不能得出正确的结果，这样就需要使用一种不同的菲涅尔方程来对导体表面进行计算。由于这样很不方便，所以预计算出表面对于法向入射的结果（f0，处于0度角，好像直接看向表面一样），然后基于相应观察角的Fresnel-Schlick近似对这个值进行插值，用这种方法来进行进一步的估算。这样就能对金属和非金属材质使用同一个菲涅尔方程来计算菲涅尔系数。

根据表2观察，电介质（绝缘体）表面的基础反射率通常小于0.17，而导体材质的基础反射率大多在0.5 至1.0之间。此外，金属表面的基础反射率具有颜色特性，因此需要用三原色来表示。为了模拟这种表面特性，实验中引入了金属度（Metalness） 参数。金属度用于描述表面是金属还是非金属。尽管理论上表面要么是金属要么是非金属，但为了实现更真实的视觉效果，大多数渲染管线允许在0.0至1.0之间调节金属度。这样做主要是因为材质纹理精度不足以精确描述如细沙或刮痕等细节的金属表面。对于电介质表面，一般使用近似的基础反射率，通常设定为0.04。而对于金属表面，则直接使用其颜色纹理作为基础反射率，因为金属表面吸收所有折射光线，没有漫反射。计算基础反射率的公式如下：

f0 = （1 - meltaless） × f0 + meltaless × suferColor.rgb （7）

F = f0 + （1 - f0）（1 - cosθ）5= f0 + （1 - f0）（1 - V ⋅ H）5 （8）

meltaless 金属度，f0 = 0.04为电介质基础反射率，suferColor.rgb 为材质纹理表面颜色。

在程序中实现如下：

double VdotH=max（DotProduct（V，H），0）;

CRGB F0=pMaterial->M_F0*（1.0-pMaterial->M_s）+pMaterial->Albedo*pMaterial->M_s;

CRGB F=F0+（1.0-F0）*pow（（1.0-VdotH），5.0）;

CRGB CLighting：：fresnelSchlickRoughness（float cosTheat，CRGB F0，float Roughness）

{

CRGB c=F0+（Max（（1.0-Roughness），F0）-F0）*pow（1.0-cosTheta，5.0）;;

return c;

}

2.2.2 法线分布函数（D 项）

在传统的Cook-Torrance 光照模型中，法线分布函数是核心组成部分之一，它负责模拟光和微观凹凸表面相互作用的效果。原模型通常采用Beckmann分布来近似这种交互，尽管这种方法效果显著，但是处理高粗糙表面时，Beckmann分布的准确性和现实感受限。本研究采用高斯微平面分布（DistributionGGX） [6]，这种分布在模拟高粗糙度表面时，相比Beckmann 分布，能提供更加真实和合理的结果。

H表示用来与平面上微平面作比较用的半程向量，而α 表示表面的粗糙度。

图6 中-20 到20 区间在上面的曲线代表Beck⁃mann分布，下面的曲线代表DistributionGGX分布，从图6中可以看出，DistributionGGX分布更加窄、拖尾更长，结合图7，说明高光衰减得更加慢、表示的范围更广泛，也更符合实际。

在程序中实现如下：

CVector3 H=（L+V）.Normalize（）;//H为中值矢量

double NdotH=max（DotProduct（N，H），0）;//N 与H 的点积

doubleNdotH2=pow（NdotH，2）;

double a=pow（pMaterial->M_a，2）;

double a2=pow（a，2）;

double d1=a2;

double d2=PI*pow（（NdotH2*（a2-1.0）+1.0），2）;

double NDF=d1/d2;

2.2.3 几何函数（G 项）

几何遮蔽用于计算微平面之间的相互遮挡比率，描述了微平面自身形成阴影的特性。当一个表面相对较粗糙时，表面上的微平面可能会相互遮挡，导致减少了表面反射的光线。几何函数以材质的粗糙度作为参数，对于粗糙度较高的表面，微平面相互遮挡的概率会增加。本研究采用的几何函数是GGX 与Beckmann近似的结合体，因此称之为SchlickGGX。

为了有效地估算几何部分，需要将几何遮蔽和几何阴影都考虑进去：

几何遮蔽在不同粗糙度下可以呈现如图8所示的视觉效果：

在程序中实现如下：

double NdotV = max（DotProduct（N， V）， 0）;//N 与V 的点积

doubleM_k=pow（（pMaterial->M_a+1.0），2）/8.0;

double g1=NdotV/（NdotV*（1.0-M.k）+M_k）;？/几何遮蔽

double g2 = NdotL / （NdotL * （1.0 - M_k） + M_k）;//几何阴影

double G = g1 * g2;

2.3 漫反射反射BRDF

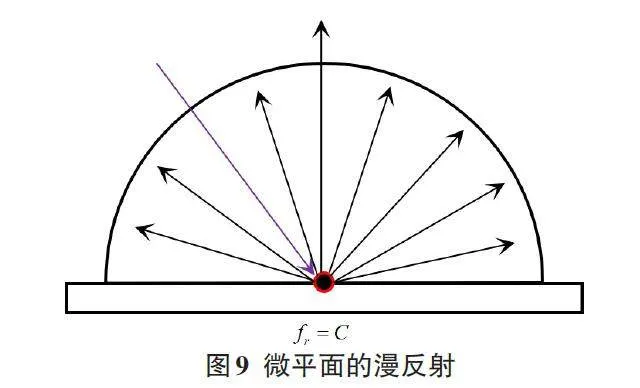
光线在场景各种的某一点入射后会朝四面八方均匀地散射出去。因此，漫反射的BRDF一定是一个常数。假设入射光线是均匀且遍布整个半球方向如图9，可以得到以下方程：

Lo（ωo ） = ∫H2 fr Li （ωo ）cos θi dωo = πfr Li （13）

由于假设入射光线是均匀遍布整个半球方向，所以Li与方向无关，且等于Lo，最终约去两边的L得到以下结果。

fr =1/π（14）

但是这里并没有考虑能量被吸收，将反射率考虑进来之后，得到最终的漫反射BRDF：

flambert = C/π（15）

C 可以类比为光栅化当中的漫反射系数去理解，本质上是一个三维向量，含有物体表面的颜色信息。除以π是为了对漫反射光进行标准化。

在程序中实现如下：

CRGB Ks=F;//反射部分等于Fresnel

CRGB Kd=1.0-Ks;//（漫反射部分）为了能量守恒Kd等于1-Ks

Kd*=（1.0-pMaterial->M_s）;

CRGB Lambert = Kd * pMaterial->Albedo / PI;

3 BRDF 的改变在MFC 下实现渲染效果及效果分析

MFC提供了一系列封装好的C++类，这些类封装了大量的Windows API调用，使得开发者可以使用更加面向对象的方式来创建GUI（图形用户界面）应用程序，利用MFC框架下创建GUI可以大大减少开发过程中的工作量。

在Win10系统环境下使用VisualStudio2017安装MFC，通过C++编程实现对渲染环境的搭建，实验分别使用不同材质对物体进行渲染得到以下渲染效果图：

通过表3的详细对比分析，我们观察到改进后的光照模型在模拟各种微表面结构，特别是金属表面方面展现出显著的优越性。在渲染高光效果时尤为出色，这一点可以通过图像直观地看出。这种改进不仅使得渲染出的图像视觉上更接近真实世界，而且显著增强了高光部分的光滑度和自然感，从而提升了图像的真实感和视觉质量。

改进后的光照模型通过精确模拟光线与复杂微表面的交互，捕捉到传统模型常忽略的细微光照变化。特别是在处理反射率高、光泽度强的材料如金属时，能够精确渲染出光与材料互动产生的细腻高光效果，充分展现材料的质感和光泽度。这不仅增强了图像的视觉效果，也提供了更丰富和深刻的视觉体验。这种光照模型的改进对于增强三维场景的真实感至关重要，其精度直接影响渲染图像的质量和真实性，能够更好地处理从光滑表面到粗糙表面的过渡，以及不同材质表面对光线的反射和吸收，从而在不同的光照条件和观察角度下，产生高度真实和细腻的渲染效果。综上所述，通过深入分析和实验验证，我们证明了改进后光照模型在模拟现实世界物体表面，特别是在高光渲染和材质真实感模拟方面的高效性和准确性。

4 结束语

在本研究中，改进了Cook-Torrance 光照模型的BRDF计算方式，通过引入新的微表面分布函数和优化的能量守恒考虑，提高了模型的真实性和效率。实验结果验证了改进方法在不同条件下的适用性，为物理基础渲染技术提供了新思路。尽管取得了一定成果，但仍需解决如何优化计算过程和处理非金属材质等问题。总之，本研究为渲染技术发展提供了基础，并期待未来进一步推动该领域的发展。

参考文献：

[1] COOK R L，TORRANCE K E. A reflectance model for com⁃puter graphics[J]. ACM Transactions on Graphics，1（1）：7-24.

[2] 孔令德，康凤娥. 三维计算机图形学[M]. 北京：高等教育出版社，2020.

[3] SCHLICK C. An inexpensive BRDF model for physically-basedrendering[J]. Computer Graphics Forum，1994，13（3）：233-246.

[4] Akenine-Möller T， Haines E， Hoffman N. Real-Time Render⁃ing （4th ed. ）[M]. Boca Raton， FL： CRC Press. （Published by Taylor & Francis Group， LLC），2018.

[5] BECKMANN P. Roughness-dependent Diffuse Reflection[J].Journal of the Optical Society of America，1963，53（10）：1394-1402.

[6] WALTER B，MARSCHNER S R，LI H S，et al. Microfacet mod⁃els for refraction through rough surfaces[C]//Proceedings of the18th Eurographics conference on Rendering Techniques. June25 - 27，2007，Grenoble，France. ACM，2007：195–206.

【通联编辑：李雅琪】