声学测温TOF 时延估计算法研究现状及前景

摘要：采空区等隐蔽区域煤自燃温度的精准判定一直未能更好地解决，难以对深部松散煤体真实温度进行实时、准确探测。声学测温是此类隐蔽火源探测的一种新方法，但声波飞渡时间（TOF） 的准确测量是松散煤体声学测温的前提及基础，而时延估计算法是精确获取TOF的关键。为此，文章从声波飞渡时间测量基本原理出发，综述各类互相关函数时延估计法，通过理论分析建立声波时延估计数学模型，探索合理的算法和技术对声源信号的相关参数进行设定和优化，将为声学法煤温探测基础研究和技术研发提供思路，为采空区等隐蔽区域火源精准探测提供新的方向。

关键词：声学测温；煤自燃；TOF；时延估计；隐蔽火源

中图分类号：TP3 文献标识码：A

文章编号：1009-3044（2024）17-0107-03 开放科学（资源服务）标识码（OSID） ：

0 引言

由于我国特殊的能源产业结构，在未来几十年内，煤炭仍是我国的主体能源。在我国25个主要产煤省和自治区中，大多数煤矿均存在煤自燃的潜在风险。煤自燃过程是一个具有非线性突变特性的自热加速反应过程，会导致温度逐渐升高，最终引发燃烧。煤矿井下采空区等隐蔽空间是煤自燃的重点防护区域，该区域存在漏风严重、煤体易碎和储热环境好等特点，极易引发煤自燃灾害。煤炭自燃的早期准确预警与防控是煤矿火灾防控的关键，但受限于矿山地质条件等因素，目前的测温技术难以实时、快速地实现隐蔽空间遗煤温度的精准检测，这对煤炭的绿色、安全和高效开采造成了极大影响。

声学测温法是一种基于声传播速率与介质温度的相关性来实现非接触式测温的技术，具有监测范围广、精度高、实时连续等特点。声学法测温最早用于海洋及大气温度的测量[1]，近年来已在工业高温炉及谷仓粮食的温度测量中取得良好效果[2-3]，鉴于松散煤体具有与仓储颗粒粮食相似的力学性质及多孔介质特征，声学测温法有望用于煤矿井下复杂环境松散煤体温度的实时监测[4-5]。而选择合适的声波时延估计算法是声波飞渡时间测量的关键要素，因此这是声学法探测煤温技术急需解决的技术难点。

本文根据文献资料，对声波飞渡时间的测量在消除背景噪声、声波衰减等方面的影响因素和研究进展进行了总结，综述了声波飞渡时间测量的相关函数算法，初步构建时延估计算法的相关特征参数及分析方法，分析探讨了声波飞渡时间在声波衰减和消除噪声等干扰方面的优越性，以解决声波飞渡时间准确性的现实难题。研究成果为声学法煤温探测基础研究和技术研发提供了思路，为采空区隐蔽火源精准探测提供了新的方向。

1 声波TOF 时延估计算法概述

声波飞渡时间作为声学测温的一个关键参量，其测量结果的准确性对声学测温十分重要。声波飞渡时间的测量误差主要来自声波传播过程中的多种因素，如声波传播速度的不确定性、声波传播路径的不确定性、声源和接收器的位置误差、环境噪声的干扰等。为了提高声学测温的精准度，需要对这些误差因素综合考虑和优化设计，并采用合适的算法和技术进行误差校正和数据处理。

目前，国内外学者主要利用互相关函数法来进行声波飞渡时间的测量，其原理是利用声波在各点之间传播的时间差，把参考信号对接收信号进行互相关计算，得出一个与声波传播时延相对应的峰值。在此基础上，对时间进行反演，得到了声波的传播速度和传播距离。但在实际应用中，由于环境噪声及声波衰减的影响，使得在测量声波飞渡时间时存在诸多问题。因此，研究适合的声波时延估计算法，能有效解决上述问题，确保声波飞渡时间的准确性。

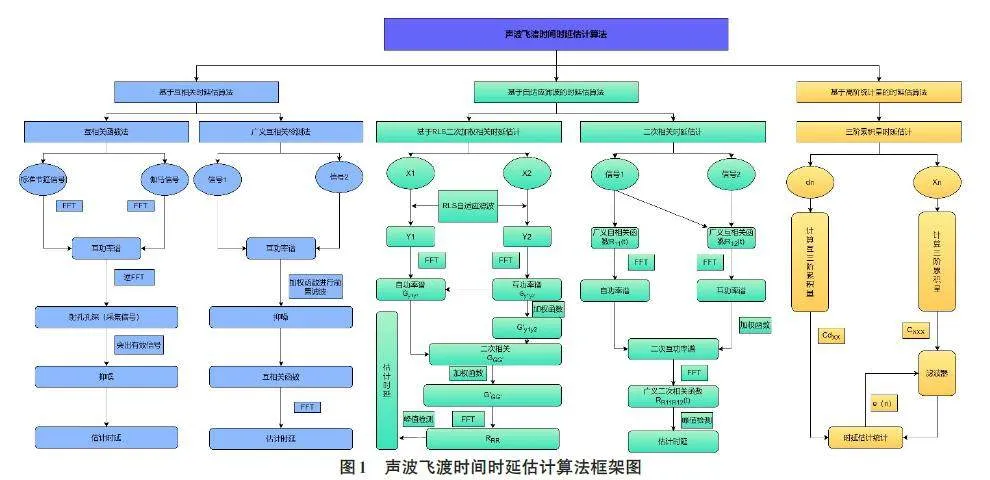
国内外有关学者围绕声波TOF的时延估计算法进行了大量研究，主要集中在基于互相关的时延估计法（广义互相关算法、互相关函数法）、基于高阶统计量的和自适应滤波的时延估计法等方面。因此，本文也主要从这几类算法方面开展调研和分析。

2 基于互相关的时延估计法

2.1 互相关函数法

互相关函数法作为最典型的时延估计方法，李缙等人[6]将测得的射孔深度信号进行互相关处理，可以有效地抑制背景噪声，且操作简便。马增强等人[7]提出一种利用互相关函数进行自适应共振解调的方法，经过精度测试和鲁棒性测试，证明了这种新方法不仅可以提高在噪声干扰条件下进行轴承故障诊断的精度，还可以应对带通滤波器失效和任意单一信号源自身突发性故障。Khosraviani等人[8]使用互相关损伤指数（CCDI） 来确定损伤位置，该方法可以在不同的损伤场景下以适当的精度确定损伤位置。

基于互相关函数的声波时延估计方法，具有易于理解、计算量小、易于实现等优点，但是也有以下不足：首先，其会因信号频率特征的变化或噪声的影响导致误差增大；其次，该方法需要保证信号在两个传声器上的采样时间间隔足够小，否则会导致时延估计的精度下降。因此，在实际应用中，需要综合考虑以上因素，并采用其他方法进行补充和优化，以提高时延估计的精度和可靠性。

2.2 广义互相关算法

Knapp等人[9]和Hero等人[10]等人在互相关时延估计算法上提出了广义互相关算法，以减弱或消除噪声对互相关时延估计造成的影响。该算法在对两不同位置的传声器接收的信号进行互相关分析前，采用加权函数对上述信号处理后，起到了对背景噪声滤除的作用，更有利于将声源信号与噪声信号分离开，相当于间接地提高了该信号的信噪比。在此基础上，广义互相关算法利用加权处理后信号的互相关曲线峰值对声波进行时延估计，从而提高声波飞渡时间测量精度。

Wiener-Khinchin理论证明，在时延估计过程中，其互相关函数和互功率谱函数都是由傅里叶变换（Fourier Transform） 获得的[11]。因此，首先对两不同传声器接收到的信号进行傅里叶变换以得到其功率密度函数，接着将功率密度函数通过傅里叶逆变换得到互相关函数，最后采用广义互相关法的不同加权函数对两接收信号的频谱进行滤波处理，降低噪声对时延估计结果的影响。通过这个流程，可以有效地处理信号，提高接收信号的质量，可以提高测量的精度和可靠性，从而更好地满足实际需求。

3 基于自适应滤波的时延估计法

对于声波飞渡时间测量环境来说，若声源信号的性质为随机的且整个过程平稳或已经明确了其统计特性，理论上可以通过选取合适的声波滤波器来减小噪声的影响，实现对声波飞行时间的精确测量。然而，在实际工程中，各个场景的强噪声的统计先验规律往往是不可知的，且声源信号和噪声的统计特性根据现场环境的变化而产生不同程度的畸变，所以对滤波器的研究很有必要。

李智超等人[12]提出了一种自适应滤波广义互相关的时延估计方法，解决了低信噪比情况下传统互相关时延难以估计的问题，在低信噪比情况下该方法对北斗导航弱干扰源定位具有优越性。罗乐等人[13]为解决在低信噪比条件下的时延估计精度差造成的难以对石油管道盗窃定位精准定位的难题，开展了基于PRLS的自适应滤波时延估计方法。通过进行仿真实验，结果表明在信噪比低于-10dB的情况下，该算法的误差不超过0.0995个采样点，并且定位误差不超过0.334千米，可以准确地确定石油管道盗取点的位置。徐菁等人[14]为解决测向定位中时延估计的问题，给出一种基于递推最小二乘算法的二次加权相关时延估计方法，在低信噪比环境下，基于RLS的二次加权相关时延估计法使谱峰更加尖锐，抑制了噪声的影响，提高了估计的准确度。

王宝仁等人[15]提出一种新的RLS-GCC算法，该算法在低信噪比条件下，与广义互相关算法和二次相关算法相比，能够获得较高的时延估计精度，且误差较小。魏文亮等人[16]基于希尔伯特差值与分段变步长LMS自适应滤波，提出了互相关时延估计优化算法，经在不同信噪比下进行测试后，该方法相较传统时延估计方法精度提高了2.2%以上，具有良好的抗噪声性能。

4 基于高阶统计量的时延估计法

前述时延估计算法的基础是使用二阶统计量进行计算，受加性噪声影响较大，需要在信号和噪声之间有明显的区别，才能准确地计算时延，故只能对加性白噪声的观测数据进行处理。但现实中二阶统计量的时延估计方法会受到数据长度受限、空间相关性有色噪声干扰等因素的影响，导致方法不能适用。这时就需要采用三阶及以上的高阶统计量，有效克服数据长度受限、背景噪声等因素对时延估计的影响，提升时延估计的准确性与可靠性。

Nikias等人[17-18]提出了一种利用三阶累积量进行时延估计的算法，其主要有频域法和时域法。频域法要求对两传声器间的接收信号进行双谱、互倒双谱等进行求解，前者用非参数化双谱方法来实现，后者可用来实现对信号时延参数的直接估计。时域方法是一种具有较低计算量的参数化估计方法[17]，但是，该方法需要求反矩阵，且当矩阵呈病态时，难以估计其时间延迟。并且所述的三阶统计量的时延估计方法，在某些分布呈对称分布的声源信号中因不能达到信号的均值为0和分布不均匀等要求导致时延估计算法难以达到预期的效果。

5 存在的不足及展望

围绕声波TOF的时延估计，国内外学者对该问题进行了广泛的研究，并提出多种估计算法，取得了巨大成果。然而现有的估计算法仅适用于某一特定场合，且具有局限性，对松散煤体的测温技术还处于理论研究阶段。

随着声波飞渡时间时延估计算法在各领域的广泛应用与不断发展，很多学者根据具体的应用场合和需要，提出了相应的方法。例如基于小波变换的广义相关、基于小波神经网络的时延估计法、基于遗传算法的自适应时延估计法、基于时频分析的结合相关处理思想的时延估计法等。然而，目前的研究还存在理论不够成熟、适用范围狭窄和计算量过大等不足。现有声波时延估算法暂无松散煤体煤温探测的应用成功案例，当将这些算法应用于松散煤体声波飞渡时间测量系统时，仍存在诸多不足。因此，需要对这些算法改进完善，以满足实际应用需求。

6 结束语

声波测温是一种新型的温度检测技术，在众多的温度检测领域中得到了广泛的应用，然而在煤自燃温度探测方面鲜见于文献，且煤自燃声波飞渡时间的特征参数和影响因素尚未明确，还须广大科研工作者继续发挥学科交叉融合作用，合理应用和优化时延估计算法，为声学法测温技术研究奠定基础，并为煤自燃精准预测提供新的思路和方向。

参考文献：

[1] CHEN C，YANG K D，DUAN R，et al.Acoustic propagation analy⁃sis with a sound speed feature model in the front area of Ku⁃roshio Extension[J].Applied Ocean Research，2017，68：1-10.

[2] YAN H，CHEN G N，ZHOU Y G，et al.Primary study of tempera⁃ture distribution measurement in stored grain based on acoustictomography[J].Experimental Thermal and Fluid Science，2012，42：55-63.

[3] 陈冠男.声学法仓储粮食温度检测关键技术的研究[D].沈阳：沈阳工业大学，2012.

[4] 郭军，昝若怡，文虎，等.基于双源复合声波的煤温感知技术展望[J].科技导报，2023，41（22）：83-90.

[5] 郭军，高文静，蔡国斌等.基于伪随机序列的松散煤体声学测温方法及应用研究[J/OL]. 煤炭科学技术，1-9.

[6] 李缙，刘玉海，张剑，等.互相关函数法在定位射孔深度上的应用[J].西南石油大学学报（自然科学版），2020，42（6）：42-48.

[7] 马增强，谷朝健，王建东.基于互相关函数的滚动轴承故障诊断方法研究[J].应用基础与工程科学学报，2017，25（3）：646-655.

[8] KHOSRAVIANI M J，BAHAR O，GHASEMI S H.Global and lo⁃cal damage detection in continuous bridge decks using instanta⁃neous amplitude energy and cross-correlation function methods[J].KSCE Journal of Civil Engineering，2021，25（2）：603-620.

[9] KNAPP C，CARTER G.The generalized correlation method forestimation of time delay[J]. IEEE Transactions on Acoustics，Speech，and Signal Processing，1976，24（4）：320-327.

[10] HERO A，SCHWARTZ S.A new generalized cross correlator[J].IEEE Transactions on Acoustics，Speech，and Signal Process⁃ing，1985，33（1）：38-45.

[11] ÁLVAREZ-MARCOS A， LUIS A. Phase-space quantumWiener-Khintchine theorem[J]. Optics Letters， 2022， 47（18）：4604-4607.

[12] 李智超，姚金杰，孙兴丽，等.基于自适应滤波的北斗弱干扰源定位方法[J].国外电子测量技术，2022，41（10）：33-38.

[13] 罗乐，于玲.石油管道盗取定位中的时延估计算法[J].电脑知识与技术，2022，18（13）：109-112.

[14] 徐菁，倪淑燕，廖育荣.基于RLS的二次加权相关时延估计算法[J].电讯技术，2022，62（12）：1835-1840.

[15] 王宝仁，曹明瑞.基于RLS自适应滤波算法的广义互相关时延估计方法研究[J].组合机床与自动化加工技术，2020（6）：27-31，36.

[16] 魏文亮，茅玉龙.一种基于LMS自适应滤波的互相关时延估计优化算法[J].电子科技，2020，33（6）：29-34.

[17] NIKIAS C L，PAN R.Time delay estimation in unknown Gauss⁃ian spatially correlated noise[J].IEEE Transactions on Acous⁃tics，Speech，and Signal Processing，1988，36（11）：1706-1714.

[18] NIKIAS C L，LIU F.Bicepstrum computation based on secondandthird-order statistics with applications[C]//InternationalConference on Acoustics，Speech，and Signal Processing.Albu⁃querque，NM，USA.IEEE，1990：2381-2385.

【通联编辑：代影】