基于贝叶斯优化XGBoost 算法的电影评分预测研究

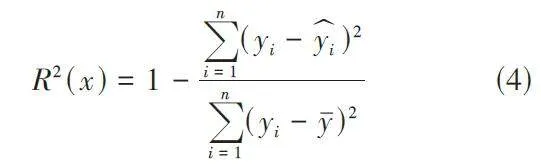
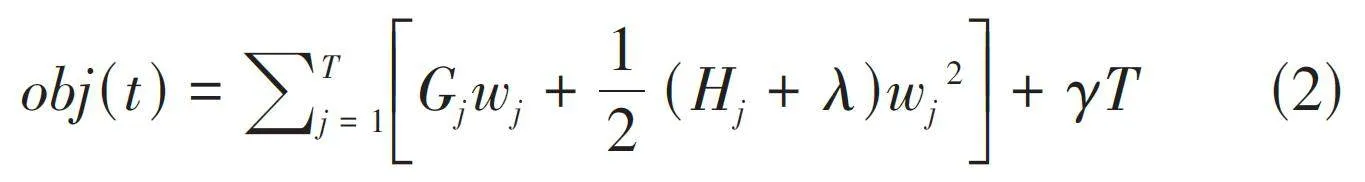
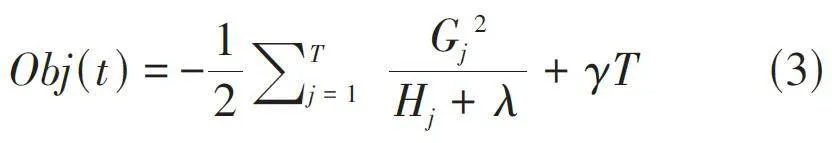
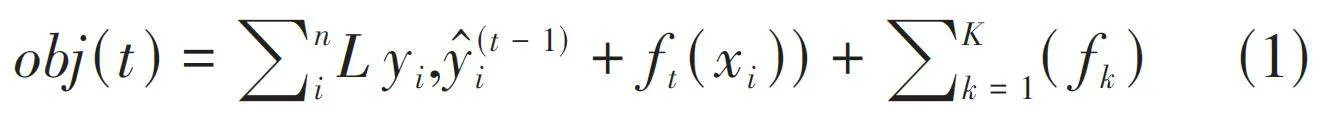
摘要：电影评分是反映观众对电影喜爱程度的重要依据。针对当前电影评分预测模型涵盖影响电影评分特征因素不足、预测准确率不高、模型过于简化等问题。为解决这些问题提出了一种基于贝叶斯优化XGBoost算法预测模型。该模型整合了影响电影评分的13个关键因素。首先收集电影网站数据，并进行数据预处理和文本向量化等操作，然后结合优化的贝叶斯算法筛选出与电影评分高度相关的特征，并进行最佳参数确定，最后根据最佳参数评估模型。实验表明，评价指标中的决定系数由优化前的0.577提升到0.763，增加了32.2%，均方误差和平均绝对误差分别降低了44.1%和29.7%。因此该模型具有较高的预测准确性，有望在实际应用中取得良好效果。

关键词：电影评分；机器学习；贝叶斯优化；XGBoost算法

中图分类号：TP391.1 文献标识码：A

文章编号：1009-3044（2024）17-0015-04 开放科学（资源服务）标识码（OSID） ：

0 引言

在数字化时代，中国电影产业展示出更加繁荣的景象，逐渐崭露头角成为全球电影市场的焦点。随着互联网技术的深度普及，观众可以通过各种平台观看和评价电影，而电影评分是观众对电影的综合评价，也是对电影效果最直观的反映。因此电影评分预测的重要性日益凸显，这不仅对电影的制作和市场策略产生影响，同时也直接关系到观众的观影体验。

目前，电影评分预测模型还存在以下问题：如模型使用的数据特征不足，且对观众评价数据的利用不足，同时使用的算法适应性较低，导致预测精度有待提高。针对以上问题，本研究旨在采用一种优化XG⁃Boost算法来预测电影评分。在特征选择方面，通过设计一种创新性的贝叶斯优化算法，用于计算特征的后验概率分布，可以更精确地筛选出与电影评分高度相关的特征，从而增强模型的预测性能[1]。在模型训练时，选择大量的观众评价作为数据集。此外还采用了贝叶斯方法进行超参数的优化，提高了参数选择的速度和准确性。

1 评分预测模型框架

本研究提出的基于贝叶斯优化XGBoost电影评分预测模型主要由数据处理、算法应用和结果分析这三部分组成。具体流程如图1所示。

2 算法优化原理

2.1 XGBoost 算法原理

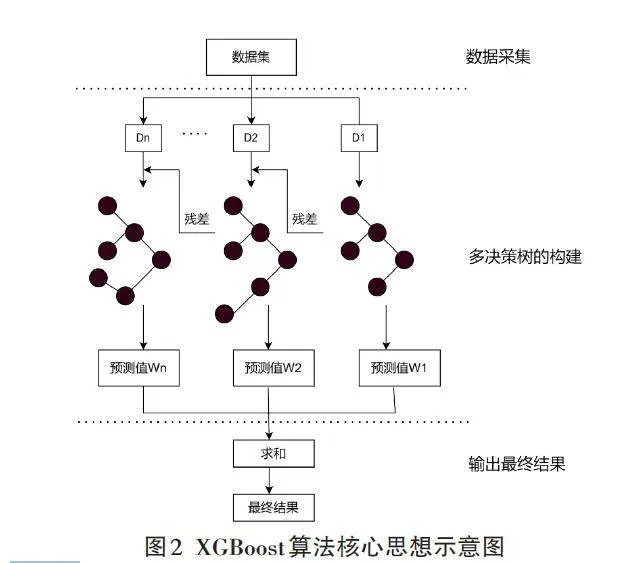
XGBoost算法是一种强大的机器学习算法，其核心思想是通过不断地添加树来进行特征分裂，每次添加一棵树，相当于学习一个新函数f（x），去拟合上次预测的残差[2]。XG⁃Boost 算法还通过正则化、并行计算等技术，大大提高了训练速度，并且减小了过拟合的风险。下面是核心思想执行示意图，如图2所示。

结合算法的基本步骤，对XGBoost算法进行简单推导[3]。

已知训练数据集T ={（x1，y1 ），（x2，y2 ），… ，（xn，yn ） }，损失函数为L （yi，ŷi ），正则化项为Ω（ fk ）。因此其目标函数可以表达为：

由式（1） 所示，其中obj （t） 是目标函数。yi 表示实际值，ŷ（t - 1） i 表示前t-1 棵决策树对样本i 的预测值。Ω（ fk ）表示模型的复杂项。ft （xi ）表示第t 棵决策树对样本i 的预测值。

上面公式需要进行二阶泰勒展开，正则化项展开，合并一次项系数、二次项系数，得到最终目标函数。

由式（2） 所示，Gj：叶子结点j 所包含样本的一阶偏导数累加之和，是一个常数。Hj ：叶子结点j 所包含样本的二阶偏导数累加之和，是一个常数。wj 表示叶子结点的权重向量。T：表示这棵树有T 个叶子结点。

其中一个wj 的一元二次函数（其中（Hj + λ） > 0） 。则f （wj ）取得最小值时，由式（3） 所示。

XGBoost目标函数的各个叶子结点的目标式子是相互独立的。即每个叶子结点的式子都达到最值点，整个目标函数也达到最值点。则每个叶子结点的权重w，即此时达到最优的Obj（t）目标值。

2.2 贝叶斯优化原理

本优化算法是实验核心。这是一种基于贝叶斯推理的全局优化方法。其基本思想是选择XGBoost 超参数样本，拟合高斯过程回归模型，得到R2的均值和方差。根据高斯分布特性，选择条件概率P （R2|x） 最大的值，即μ 最大σ2 最小的x。增加新的样本，重复上述过程，迭代接近模型的全局最优超参数。

通过这种方式，本研究引入了概率模型，基于统计规律进行全局搜索，以当前参数空间最优解为中心进行局部搜索避免陷入局部最优解。相比确定性算法，更具全局视角，能够更好地解决复杂的黑盒优化问题。

在代码中使用XGBoost 算法进行电影评分预测，其中模型的超参数需要调优。因此使用贝叶斯优化进行超参数调参。具体来说，目标函数是XGBoost 在测试集上的R2 ，表示方差得分：

由式（4） 所示。其中yi 是真实目标值，yi 是预测目标值，yˉ是目标值的均值。

设目标函数R2（x）服从高斯分布：

p（R2|x） = N （ μ （x），σ2 （x）） （5）

由式（5） 所示。其中μ （x）和σ2 （x）分别是目标函数在参数x处的均值和方差。均值μ （x）反映目标函数的全局特性，方差σ2 （x）反映目标函数的局部特性。然后可以从参数空间中随机选择一组样本参数X = x1，x2，...，xn，计算目标函数在这些参数下的函数值y = y1，y2，...，yn，并用这些数据估计高斯过程，由式（6） （7） 所示：

μ̂（x） = k（x）T K-1y （6）

σ̂2 （x） = k（x，x） - k（x）T K-1k（x） （7）

其中k（x） = [k（x，x1）， k（x，x2）， ... k（x，xn）]T，k 是样本点之间的核矩阵。μ̂（x）为x 与所有样本间的核函数向量。y 是目标函数在所有样本点上的观测值向量。利用x与所有样本点之间的相似度，结合样本点之间的相似度矩阵k 和目标函数值y，预测目标函数在x 点上的均值μ̂（x）。通过这个公式，建立起了x 和目标函数值之间的关系，从而可以进行概率推断。

k（x，x） 表示核函数k 在同一个样本x 上的计算，即样本点与自身的相似度。k（x）表示向量函数，表示样本x 与所有样本点（包括自身）之间的核函数值。

得到高斯过程估计后，可以采样新的候选参数，选择其预测效果的条件概率分布最大化的点，由式（8） 所示：

x* = argmaxx p（ŷ*|x）= argmaxx N （ μ̂（x），σ̂2 （x））σ̂2 （x） （8）

表示找到使后验分布p（ŷ*|x） 最大的x，也就是找到均值μ̂（x） 最大且方差σ̂2 （x） 最小的。argmax是数学符号，表示使函数取得最大值时对应的自变量的值。它常用于描述优化问题的最优解。

重复该过程，每次用新的样本更新高斯过程，逐步逼近全局最优解。在代码中选择了几个重要超参数作为优化变量，定义其范围，通过BayesianOptimiza⁃tion模块实现了贝叶斯优化，并得到了XGBoost的最优超参数组合。

3 实验

3.1 实验数据准备

1） 数据收集。本研究的数据源主要来自豆瓣电影网站[4]。涵盖了从2020至2022年间在中国公开上映的电影。在综合考虑以后，选取了电影名、导演、编剧、主演、语言、片长、类型、电影简介及观众评论等13个评分因素。本次数据集共采集了875部影视数据，每一部电影采集评论约252条，总评论数达22万条。

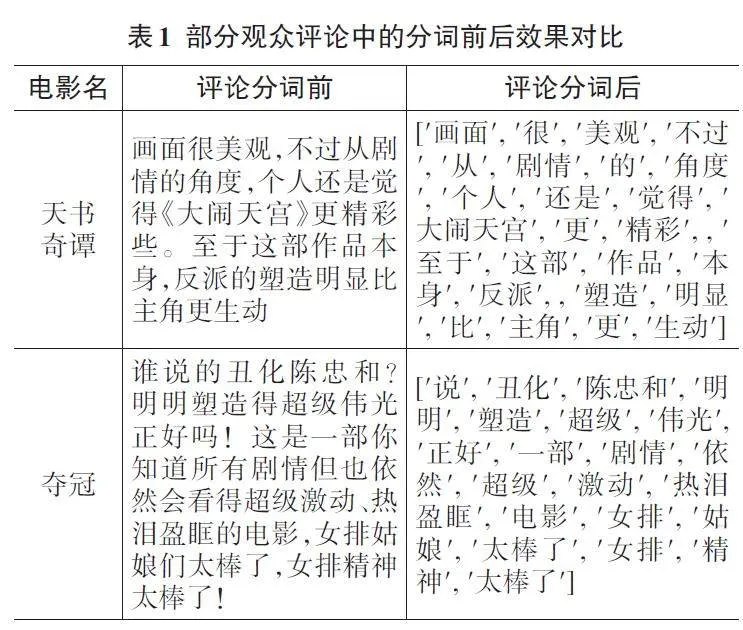
2） 数据分词。本研究采用了Jieba分词工具的精确模式作为数据分词的主要方法。为了提高分词效果，还引入了目前广泛应用的分词停用表，本研究整理了包括中文停用词库表、百度停用词表、哈尔滨工业大学停用词表在内的停用词表。如表1所示。

3） 数据集划分与数据向量化。实施监督学习任务时，通常会将数据集分为训练集和测试集。训练集主要用于模型的训练，而测试集则是评估模型对未知数据的预测能力。

在进行分词以及训练集与测试集划分后，需要对数据进行Term Frequency-Inverse Document Frequency（TF-IDF） 向量化处理。这是一种常用的统计方法，通过计算词语在文本中的词频（TF） 和该词语在语料库中的反向文档频率（IDF） ，来反映词语对文本主题的重要程度[5]。相比直接使用词频，TF-IDF向量化方法更能突出对文章主题分类有重大贡献的词语权重。

3.2 实验过程

经过对数据的采集以及预处理。现在关键的任务是使用XGBoost算法对数据进行处理，以便获得所需要的结果。其中超参数的设定尤为关键。

1） XGBoost模型超参数空间设定。在XGBoost模型训练之前，需要设定可能影响模型性能的关键超参数搜索空间。它直接影响到模型的性能。因此，对超参数进行适当的调整就显得尤为重要[6]。本研究选择调节的超参数包括：树的最大深度（max_depth） 、学习率（learning_rate） 、特征随机采样的比例（colsample_by⁃tree） 、树的数量（n_estimators） 以确定基学习器个数等共计10个超参数。

2） 贝叶斯超参数优化过程。在超参数空间确定后，将使用贝叶斯优化算法来寻找最优的参数配置。首先，定义目标函数xgb_eval，该函数以R2作为评价指标，接收不同的超参数组合来训练模型，并在测试集上进行预测，返回R2。接着构建贝叶斯优化器，将定义的超参数范围param_ranges 作为优化变量，以xgb_eval 为目标函数，并设定了随机种子ran⁃dom_state。

在贝叶斯优化的迭代过程中，优化器会根据目标函数的历史评估结果，利用高斯过程对未知目标函数的先验分布获取后验信息[7]。根据这个后验信息和获取新样本的成本，贝叶斯规则会输出下一个最可能产生最大收益的超参数组合。当获取新样本后，先验分布会使用贝叶斯定理进行更新。

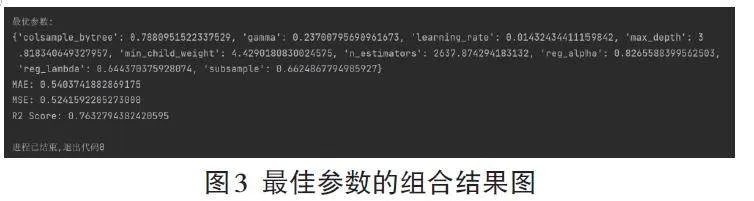
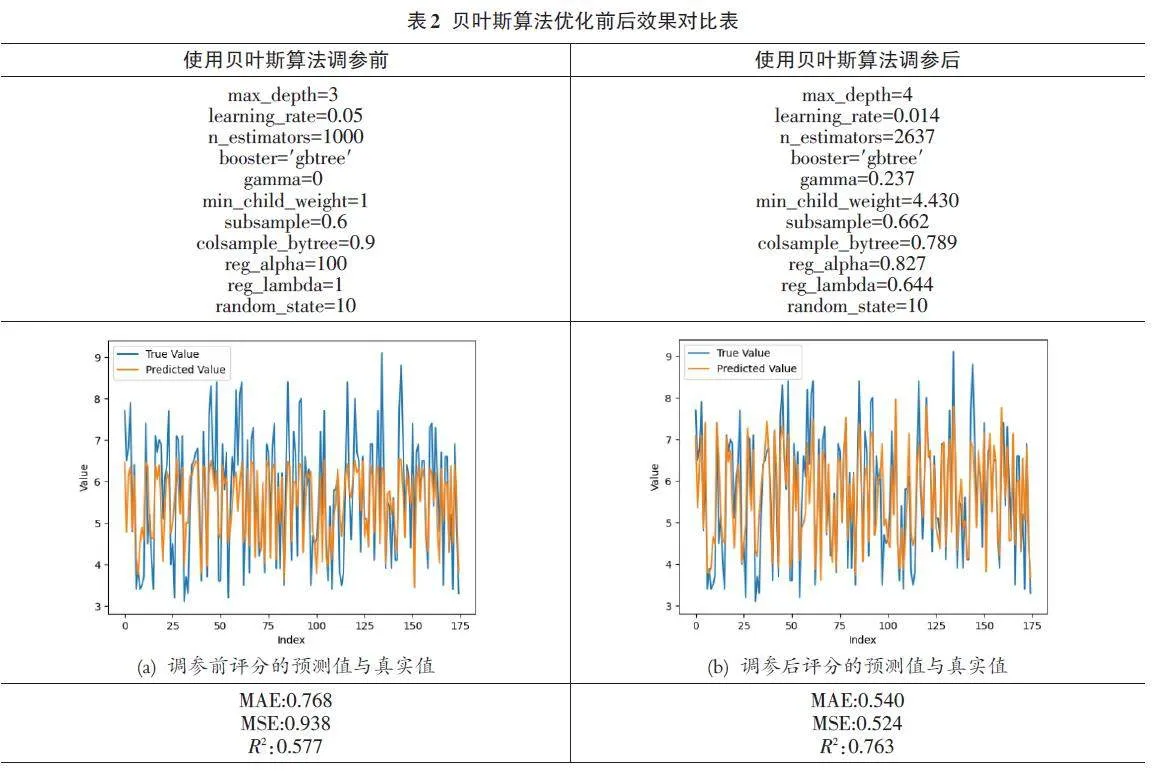
本研究设定了迭代次数为10次。每次迭代都会调用目标函数xgb_eval，输出一个R2，并更新超参数的先验分布。迭代结束后，可以得到一个最优的参数配置。最后使用这组参数重新训练模型，并在测试集上进行评估。表2展示了使用贝叶斯算法调参前后各参数的值、电影评分值的折线图以及算法评价指标值，而调参后的数值保留到小数点后三位。表2中图a和图b分别是在调参前后，电影的真实评分与预测评分的折线图。程序在PyCharm中寻找到的最佳参数的组合结果如图3所示。

3.3 实验结果对比分析

根据实验结果分析，该算法的MAE由调参前的0.768降低到0.540，减少了29.7%。MSE由调参前的0.938 降低到0.524，降低了44.1%。R2 由调参前的0.577提升到0.763，增加了32.2%。数据表明，经过贝叶斯优化后的模型在预测电影评分方面有了显著提升。MAE和MSE的显著降低表明模型的预测误差得到了有效减少，这意味着模型的预测结果更接近实际情况，具有更高的准确性。而R2的提升则意味着模型的拟合效果更好，更能解释目标变量的变异性。

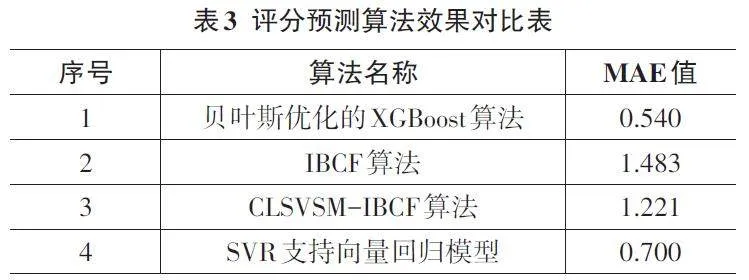
表3是本研究与目前其他研究者，利用不同算法来预测电影评分的对比。序号1是本研究算法，序号2是基于电影评分的推荐算法，序号3是在2的基础上提出的基于共现潜在语义向量空间模型，序号4为基于rbf（径向基函数）的SVR支持向量回归模型。评分预测算法采用的评价指标为MAE[8-9]。从表格可以看出，基于贝叶斯优化的XGBoost算法在预测电影评分中，评分的真实值与预测值之间的平均绝对误差更小，更有优势。

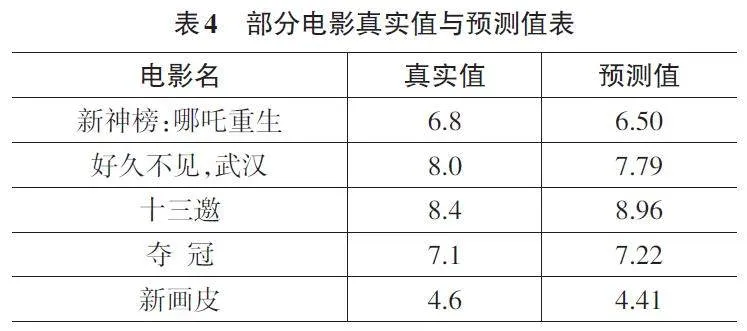
对比贝叶斯优化前后的实验结果，可以看出贝叶斯优化作为一种超参数调优方法是有效的，能够在有限的计算资源下搜索到更优的模型配置。结合贝叶斯优化，XGBoost算法在电影评分预测方面展现出了较高的精度和拟合能力[10]。这也表明此算法在处理类似的回归问题时具有广泛的应用潜力。下面是测试集中部分电影的预测结果，如表4所示。

4 结束语

本实验通过构建贝叶斯算法来优化XGBoost模型，将优化前后的实验结果对比，并与目前市面上其他电影评分预测模型对比，验证了基于贝叶斯优化的XGBoost算法在预测电影评分方面性能提升显著。本实验为超参数调优提供实证案例。同时实验结果突显机器学习算法在实际问题中的潜力，机器学习算法可广泛应用于各行各业，可以提高数据分析、预测和决策支持任务的效率和准确性。

参考文献：

[1] 方茜.基于XGBoost的网络舆情文章预警模型建立[J].智能计算机与应用，2023，13（6）：72-77.

[2] GUPTA A，RAJPUT I S，GUNJAN，et al.NSGA-II-XGB：Metaheuristic feature selection with XGBoost framework for diabe⁃tes prediction[J]. Concurrency and Computation： Practice andExperience，2022，34（21）.

[3] 崔逊龙.基于数据挖掘算法的个体出行行为预测[D].合肥： 安徽大学，2021.

[4] 豆瓣电影网.[EBOL].[2023-12-10].https：//movie.douban.com/explore.

[5] 陈平平，耿笑冉，邹敏，等.基于机器学习的文本情感倾向性分析[J].计算机与现代化，2020（3）：77-81，92.

[6] NI J J，CAI Y，TANG G Y，et al.Collaborative filtering recommen⁃dation algorithm based on TF-IDF and user characteristics[J].Applied Sciences，2021，11（20）：9554.

[7] 贾颖，赵峰，李博，等.贝叶斯优化的XGBoost信用风险评估模型[J/OL].计算机工程与应用，2023：1-15.（2023-06-27）.https：//kns.cnki.net/kcms/detail/11.2127.TP.20230626.1704.002.html.

[8] 崔榕峰，马海，郭承鹏，等.基于贝叶斯超参数优化的Gradient Boosting方法的导弹气动特性预测[J].航空科学技术，2023，34（7）：22-28.

[9] 李香君，肖小玲.基于机器学习的电影评分预测研究[J].电脑知识与技术，2021，17（27）：109-111.

[10] JANIZADEH S，VAFAKHAH M，KAPELAN Z，et al.Hybrid XGboost model with various Bayesian hyperparameter optimi⁃zation algorithms for flood hazard susceptibility modeling[J].Geocarto International，2022，37（25）：8273-8292.

【通联编辑：王力】