充分条件与必要条件:揭示逻辑推理的思维密码

数学是讲逻辑、重推理的学科，每一个结论都需要充分的推导．本文寻找充分、必要条件的知识源头并叙述新中国成立以来的教学要求，从高中数学的教学内容出发，对概念进行多视角阐释，以期促进学生对概念的理解;从教育功能出发，培养学生的逻辑推理能力和构建知识体系的能力，提升课堂教学效率．

１ 研究缘起

在教研活动中，经常有教师问：“为什么高中数学中要学习充分、必要条件？”在与数学教师的交流中，部分教师也表示“这部分知识是学生学习的一个难点”“学生不理解，做题错误率较高”“学不学该部分知识对其他数学知识的学习没有影响”等，导致教学的现状是部分教师让学生死记硬背，学生“知其然，而不知其所以然”，学生做题的错误率较高．那么，为什么无论是新教材还是老教材，都没有删去这部分内容？ 为什么从原来的数学教学大纲到数学课程标准都保留这部分内容？ 笔者从“充分、必要条件”的知识源头入手，重点阐释这一概念的教学思路与功能，以利于教师课堂教学的顺利开展，提升课堂教学的效率.

２ 概念的渊源、发展与教学要求

亚里士多德是古希腊三贤之一，在数学、物理、文学、逻辑学等诸多领域都有巨大的成就，其中“三段论”一直被现代数学所沿用，充分、必要条件的概念便源于他所创造的逻辑学理论，他指出充分、必要条件是描述一定语言符号所指概念范畴所必需的集合特征，这些集合特征是对客观世界中某一类实体的抽象概括，后来充分、必要条件在数理逻辑领域逐渐发展并广泛应用，直到今天．

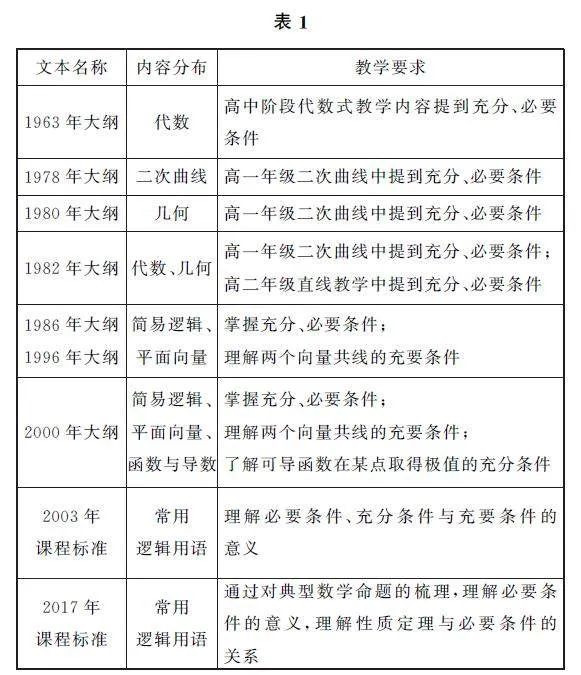
“有之则必然，无之则未必不然，是为大故，无之则必不然，有之则未必然，是为小故”出自战国时期思想家墨子的著作«墨经»，这也是我国关于充分、必要条件概念最早的描述，形象地解释了充分、必要条件的含义．新中国成立以来，教材版本不断发生变化，但这一概念一直存在于数学教材之中．表１罗列了新中国成立以来高中数学教学大纲（以下简称大纲）、普通高中数学课程标准（以下简称课程标准）中关于充分条件与必要条件的表述．

从表１可以看出，充分、必要条件一直存在于高中数学知识体系之中，起初这些概念分散于不同的章节之中，如解析几何、立体几何、向量等，后来从培养学生逻辑思维能力的视角出发，这部分内容逐渐被整合到一个系统的章节中，使得学生可以更好地理解和应用这些概念，显然，对于充分、必要条件知识的重要性的认识也是一个逐渐完善和加强的过程．

３ 充分、必要条件的概念阐释

３.１ 依据教材，理解概念

北师大版教材给出的定义如下：一般地，当命题“若p，则q”是真命题时，称q 是p 的必要条件，同时称p 是q 的充分条件;如果p⇒q，且q⇒p，那么称p是q 的充分且必要条件，简称p 是q 的充要条件，记作p⇔q．

在教学中，学生对充分条件易于理解，但对必要条件的理解较为困难，教材为了让学生突破这一难点，先通过实例分析数学中的性质和定理，再给出定义，让学生对必要条件语言有一个认识、归纳、理解的过程．在实际的教学中，效果依然不够理想，需要从多个维度加以分析，引导学生抓住概念的本质．

３.２ 基于学情，深化概念

１）利用“逆否命题”的知识

在“几何与图形”课程内容中有“定义、命题、定理”一节，该节的教学要求：能结合具体实例，会区分命题的条件与结论，了解原命题及其逆命题的概念．会识别两个互逆命题，知道原命题成立其逆命题不一定成立．为了增强学生的理解力，我们可以补充原命题的逆否命题的概念，利用逆否命题和原命题的等价性，充分、必要条件的定义如下．

“若p，则q”是真命题，则称p 是q 的充分条件;即如果条件A 成立，则结论B 也成立，我们就称条件A 是结论B 的充分条件．

“若￢q，则￢p”是真命题，则称q 是p 的必要条件，即如果条件A 不成立，则结论B 也不成立，我们就称条件A 是结论B 的必要条件．

这样就进一步诠释了必要条件的定义．例如，若两个三角形全等，则两个三角形的面积相等，称两个三角形全等是这两个三角形的面积相等的充分条件．显然，若两个三角形的面积不相等，则这两个三角形不全等，我们就称两个三角形的面积相等是这两个三角形全等的必要条件．这也是对古籍«墨经»中的“无之则必不然”的具体解释．

２）利用“集合”的知识

数学语言包括自然语言、符号语言、图形语言，我们可以认为p⇒q 为符号语言，p 是q 的充分条件，q是p 的必要条件为自然语言，借用集合知识A ⊆B 可以表示为如图１所示的图形语言，如果x∈A ，那么x∈B，我们就说x∈A 是x∈B 的充分条件，由于x∉B 时，x∉A 成立，我们也称x∈B 是x∈A 的必要条件．

我们知道，同一个研究对象，可以有不同的文字语言表征．同样，阐释同一件事物属性的表达也可以有不同的方法，如“若p，则q”是真命题、p⇒q、p 是q的充分条件、q 是p 的必要条件这四种说法，表达的意思本质上是等价的，都在描述特定的一个逻辑关系．

４ 紧扣数学本质，发挥知识功能

４.１ 为知识梳理提供方法，建构学生知识体系

充分、必要条件知识贯穿整个高中乃至以后的数学学习，对建构学生的知识体系有重大意义．德国数学家开普勒说过，数学就是研究千变万化中不变的规律．课程标准已经把“常用逻辑用语”等单独列为一个主题，作为高中数学的预备知识，这有利于初中、高中的平稳过渡，知道数学中的每一条性质定理都给出了相应数学结论成立的一个必要条件;每一条判定定理都给出了相应数学结论成立的一个充分条件;每一个定义都给出了结论成立的充要条件．让学生深度理解充分条件、必要条件、充要条件、判定定理、性质定理、定义之间的关系．利用充分、必要条件知识对所学知识进行总结，有利于学生站在更高的视角理解数学，学习数学．

４.２ 为解题提供思路，提升学生思维逻辑

１）分析法与充分条件

分析法是数学证明中常用的方法，其特点是执果索因．从充分、必要条件知识来看，这种方法的本质是从结论出发，然后一步步得到前一个结论成立所具备的充分条件或充要条件，直到归结为命题的已知条件，或者归结为定义、定理、公理等．

例１ 设a≥３，求证：

２）参数范围问题与充要条件

我们在一些导数的综合问题（如求参数的取值范围）中，经常采取迂回的策略———必要性探路的方法，得到参数的范围，然后再证明充分性成立．

例２ （２０２３年全国甲卷理２３）已知函数

至此，我们通过三角恒等变形以及不等式放缩，采用必要性探路的方法找到a 所满足的必要条件a≤３，完成了必要性探路，下面再去证明充分性成立，即当a≤３时，f（x）＜sin２x 成立．

当a≤３时，有

综上，a 的取值范围是（－∞，３]．

必要性探路策略能明晰解题路径，使问题化繁为简，是对充分、必要条件知识的灵活运用，可以培养学生的转化与化归思想，提升学生的逻辑推理、数据分析等数学核心素养．在许多数学问题中，确定一个条件是否充分或必要是解决问题的关键，学习充分、必要条件知识可以帮助学生更好地理解问题，从而提高问题解决的能力．

４.３ 为大概念获取提供路径，促进学生深度学习

北京师范大学的郭华教授说过：“所谓深度学习，就是指在教师引领下，学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程．”因此，利用充分、必要条件的功能可为大概念教学提供支撑．如“垂直”是中学数学中的一个核心概念，小学阶段学生已经有了两直线垂直的意识，初中的平面几何已给出判定两直线垂直的方法，高中数学也有相关内容，因此教师可以布置任务：如何利用充分、必要条件再次审视“垂直”这一概念呢？学生可以多角度深入思考高中数学中出现的关于“垂直”的相关知识．

若从向量的角度，当a，b 分别是直线a，b 的方向向量时，直线a⊥b 的充要条件是ab＝０;若从斜率的角度，当直线a，b 的斜率分别为k１，k２ 时，k１k２＝－１是直线a⊥b 的充分条件;在立体几何中，学生可以归纳出更多的内容，如直线b⊂α，a⊥b 是a⊥α 的必要条件、{b⊥α，a∥b 是a⊥α 的充分条件等．综上所述，关于“垂直”可以从向量的角度、斜率的角度和空间的角度来描述，这些方法不仅可以判断两条直线是否垂直，也可以为我们更好地提取大概念“垂直”创造条件，从而促进学生深度学习数学知识．

４.４ 为新命题的发现提供视角，促进知识自然生长

瑞士心理学家皮亚杰是建构主义理论的代表人物之一，他认为学生通过对概念的理解、应用，可以探索出新的知识，即知识是可以主动构建的．当我们尝试寻找新的数学命题或结论时，可以运用充分、必要条件的思维方法，假设我们尝试发现三角函数的某个性质，可以找到充分条件来表达该性质，也可以用必要条件来阐明在什么情况下不满足该性质．例如，函数y＝Asin（ωx＋θ）（A ＞０）取得最大值时x 的范围的充分条件既可以表述为{x|ωx＋θ＝２kπ＋π／２，k∈Z}，也可以是过图像最高点时x 的取值集合，即从数与形两个方面阐述．再如，已知△ABC 的三边分别是a，b，c，则△ABC 是等边三角形的充要条件是a２ ＋b２＋c２＝ab＋ac＋bc．这类问题可以为新命题的发现提供广阔的视角，帮助学生深入理解数学概念促进知识的生长，养成从不同的视角探索数学奥秘的习惯．

«普通高中数学课程标准（２０１７年版２０２０年修订）»在实施建议中指出：“树立以发展学生数学学科核心素养为导向的教学意识，将数学学科核心素养的培养贯穿于教学活动的全过程．”数学教学的核心就是培养学生的逻辑思维能力，充分、必要条件是推理过程中的常用概念之一，它对培养学生的逻辑思维能力，提高他们的分析和解决问题的能力有着重要意义．因此，从某种程度上可以说，充分、必要条件是揭示逻辑推理的一个思维密码．

本文系安徽省教育科学研究项目２０２３年度课题“‘教—学—评’一致性下的高中数学大单元教学的应用研究（课题编号：JK２３１５０）”的阶段性成果．

（完）