基于模糊聚类的遍历基线干涉仪测向算法

时瑞 罗元政 李志鹏 张一帆

摘要： 文章针对基于均匀圆阵的干涉仪测向技术由于测角模糊无法实现准确测向的问题，提出了基于模糊聚类的遍历基线干涉仪测向算法。该算法基于均匀圆阵分析了干涉仪测向技术的解模糊原理和流程，利用遍历方法求解每个相位差下可能存在的模糊数并解出对应的角度，最后采用模糊聚类方法确定正确的角度。仿真结果表明，文章所提算法能够实现基于均匀圆阵的干涉仪测向解模糊，有效提高了测向精度，拓宽了探测范围。

关键词：干涉仪测向；解模糊；遍历基线；模糊聚类

中图分类号：TN 971  文献标志码：A

0 引言

模糊聚类［2］是一种基于模糊集理论的聚类方法，将数据点根据它们之间的相似度或距离分配到不同的类别中，且每个数据点被分配到每个类别的隶属度都是一个介于0和1之间的数值，表示这个数据点属于每个类别的程度。与传统聚类方法不同，模糊聚类在某些情况下允许一个数据点同时属于多个类别，这使得它适用于一些复杂的分类问题［3］。

目前，虽然相位干涉仪测向算法已经在实际系统中广泛应用，但是如何解决测向精度与测向模糊之间的关系，一直是相位干涉仪需要解决的核心问题之一。针对这一问题，本文研究了一种基于模糊聚类的遍历基线干涉仪测向算法。首先对均匀圆阵的阵元间相位差进行分析［4］，从理论上给出均匀圆阵布阵方式下，干涉仪测向模糊数产生的原因，并进一步提出相应的解模糊算法，实现基于均匀圆阵的干涉仪测向解模糊，有效提高了相位干涉仪的测向精度，拓宽了探测范围。

1 阵列接收信号模型

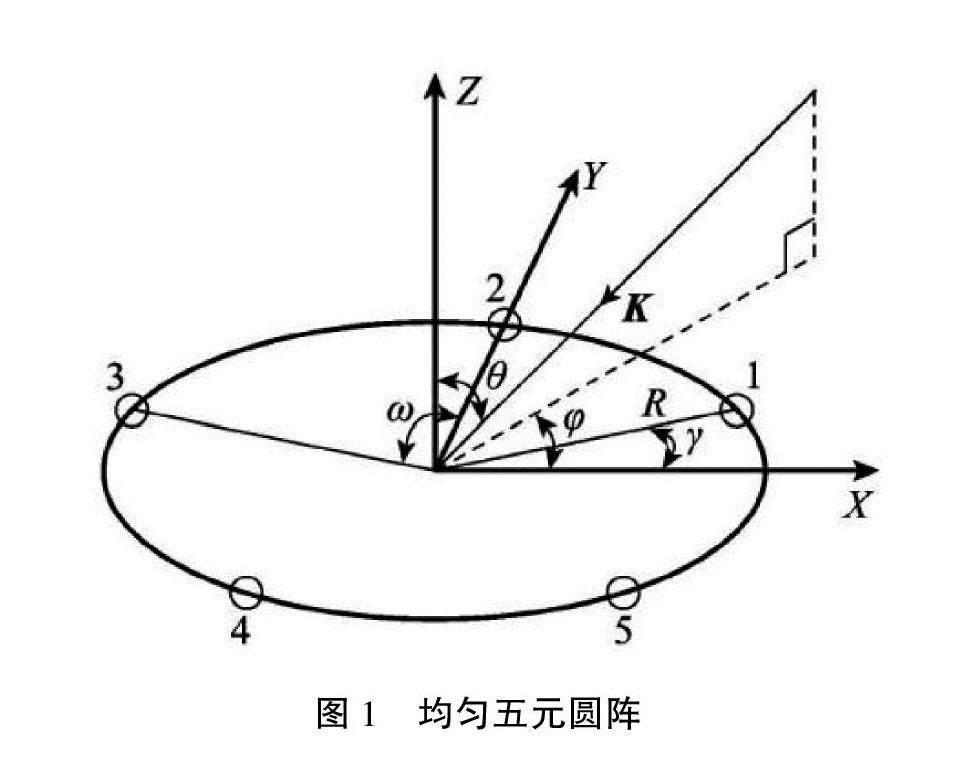
为了便于理解，本文以均匀五元圆阵为例进行分析，所提算法适用于阵元数任意的均匀圆阵。均匀五元圆阵如图1所示。阵列接收信号数学表达式为：

X（t）=AS（t）+N（t）（1）

其中，X（t）为阵列接收矢量，S（t）为空间信号源矢量，N（t）为噪声矢量。假设噪声为高斯白噪声［5］，A为入射信号源的阵列流型。

以五元均匀圆阵中的天线2为Y轴的正方向，建立空间直角坐标系。其中，γ为阵元的角度位置，方位角∈（0，2π）为入射信号在XOY平面的投影与X轴逆时针反方向的夹角，俯仰角θ∈（0，π/2）为入射信号与Z轴的夹角。

2 模糊数的产生

本文利用阵列接收信号求解所有基线间的相位差，模糊数的产生原理如下。

阵列使用的鉴相器所得到的相位差的取值范围为［-π，π］，如果实际得到的相位差在这个范围以外，那么鉴相器求得的相位差与实际两天线之间的相位差会相差2nπ。此处，n为整数，即模糊数［6］。

相位差与基线长度D有关系。当D的长度很大时，相位差的真实值φ就会超出［-π，π］的范围，这时根据鉴相器得到的相位差与真实值相差2nπ，可以得到如下公式：

φ=2nπ+=2πDλsinθ（2）

通过变换可得：

sinθ=λφ2πD=λ（2nπ+）2πD（3）

从以上式子可以看出，如果想提高干涉仪测向算法的准确度，在一般的情况下，除了需要知道天线间的相位差φ、信号波长λ和基线长度D以外，模糊值n也是必须知道的。

从上面可以清楚地知道，当相位差不在［-π，π］这一范围内时，就会产生模糊数n，这时如果不解决模糊数n的问题，那么求得的角度将会与实际值产生很大的偏差。因此，笔者引入模糊聚类算法来解决这一问题。

3 模糊聚类算法

K均值聚类算法具有算法简单、易于实现以及能够快速处理大规模数据等优点。

以误差平方和准则函数作为聚类的结果函数，定义为：

jk=∑kj=1∑nji=1‖x（j）i-mj‖2（4）

其中，

mj=1n∑nji=1xj（j）（5）

式（4）中，jk是误差平方和，式（5）中mj （j=1，2，…，k）是聚类类型x（j）所含样本的平均值，即聚类中心。样本集X给定的时候，jk的值取决于k个聚类中心的值，jk值的大小表现了误差的大小，误差越小说明聚类的结果越好。

Means算法属于动态聚类算法，每次迭代的过程中都要考虑所有样本的正确性。每一次迭代过程完毕后都要更新所有的聚类中心［7］。如果有一次迭代后所有的样本点都可以正确分类，就不需要再对样本进行调整，聚类中心也将不会再发生变化，这个时候的jk收敛，聚类分析结束。

利用均匀圆阵中的每组基线求得的所有模糊值都由一个真实值和多个模糊值组成，而每组基线对应的模糊值不同，因此，可以利用k均值聚类算法对遍历基线求得的所有可能模糊值进行聚类，从而求得真实模糊值。

4 基于模糊聚类的遍历基线法

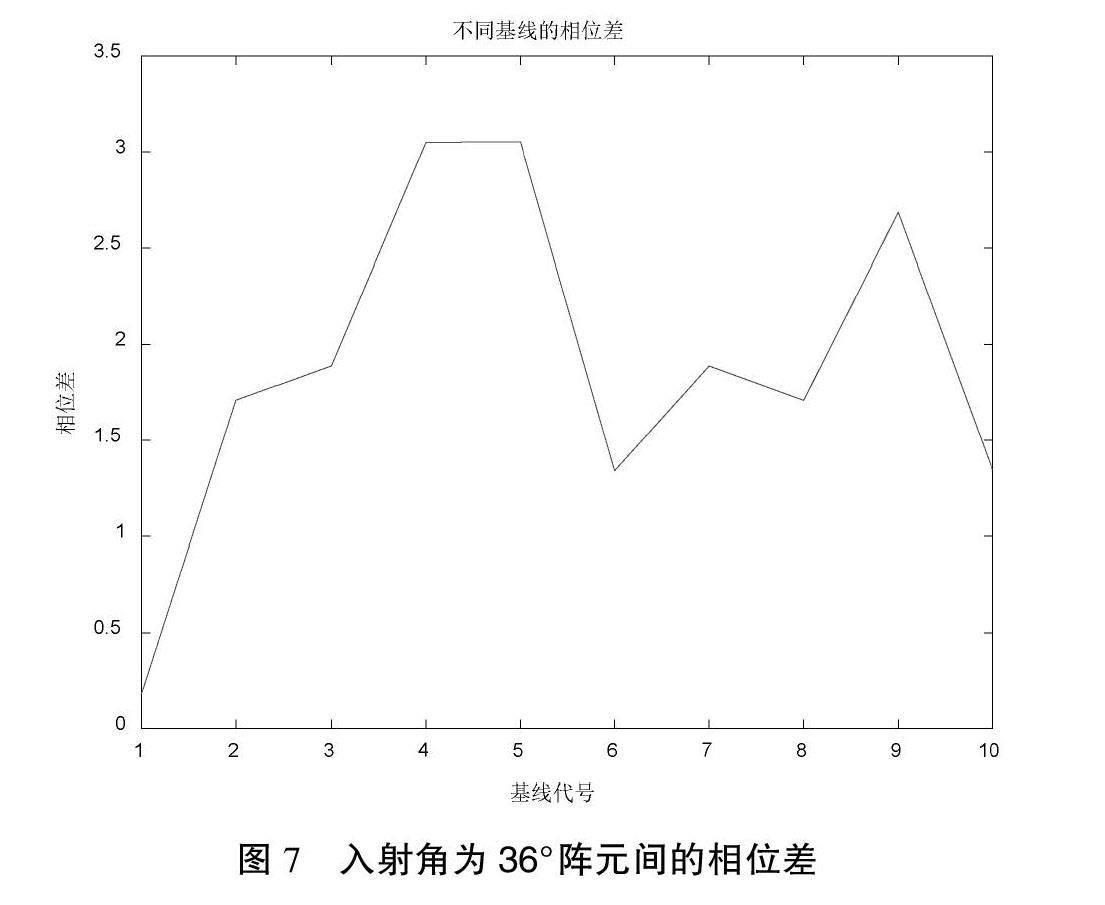
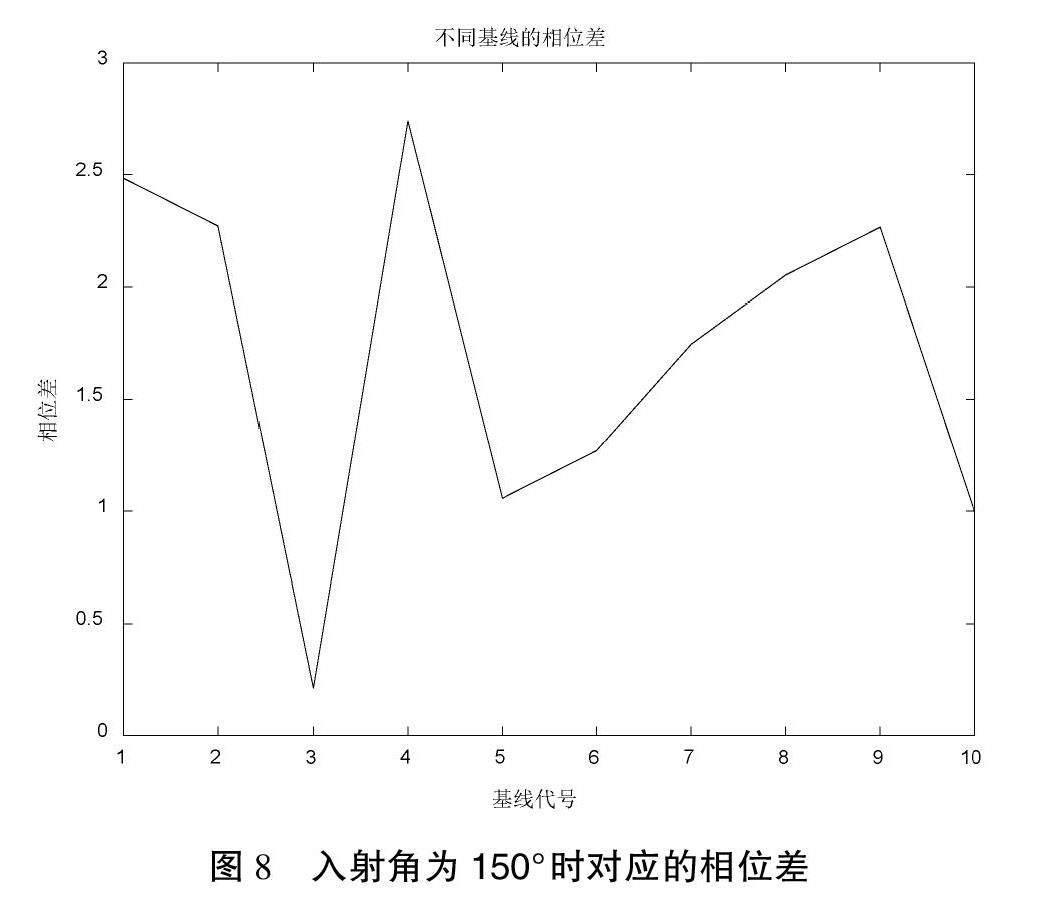
遍历基线法的核心是求出天线阵中所有可以求得的基线的相位差i （i=1，2，…，N），由于式中波长λ、圆周率π、基线长度D均为已知值，再根据-1

θ=arcsinλ（2nπ+）2πD（6）

由于不同基线对应的模糊值不同，求解得到的所有模糊值［8］的θ也不尽相同，但是都会求出同一个正确的θ值。因此，利用模糊聚类的方法，把得到的θ角度进行聚类，就能得到正确的角度值。

而要对模糊值n进行估计并反解出对应的方向角，还存在一个问题，即求得的方向角是在以该条基线为X轴，但是在设置五元阵［9］的时候是以圆心到天线2为Y轴方向，因此，有些基线通过式（6）计算出来的θ角并不是实际的θ角。

为了解决这个问题，需要对计算得到的方向角进行校正。一种常用的方法是通过标定基线来确定偏差角度，并将其纳入方向角的计算，即选取一个已知角度的基线，以其为基准，通过实际测量的角度与计算出的角度之差［10］，确定所有基线的偏差角度，并进行相应的修正。通过这样的校正和修正，可以得到更加准确、可靠的方向角度。

在采用以圆心到天线2为Y轴的方向，比如在确定由天线2和3组成的基线的θ角时，可以分为以下几种情况：

当入射角小于36°时，如图2所示，其中m角为天线2和3组成的基线与标定坐标轴的夹角，可以很清楚地知道该角度为36°，其中使用式（6）计算出来的角度θ2为角θ1的余角，因此，实际的入射角度θ测得角度θ1的关系为：

θ-θ2-（90-m）=θ2-54°（7）

当入射角大于36°小于126°时，如图3所示，其中m角为天线2和3组成的基线与标定坐标轴的夹角，可以很清楚地知道该角度为36°，使用式（6）计算出来的角度θ2为角θ1的余角，因此，实际的入射角度θ测得角度θ1的关系为：

θ=θ1+36°=126°-θ2（8）

最后一种情况就是如图4所示，当入射角大于126°小于180°时的情况，跟前2种情况分析的步骤一样，此时的入射角θ与反解求得的角θ1的关系为：

θ=126°+θ1（9）

综上所述可知，当算法到达计算反解入射角这一步时，需要先进行判断，根据角度的大小选择合适的公式才可以得出正确的结果。整体的计算流程如图5所示。

以上工作全部完毕以后即可进行模糊聚类的工作，就是要把得到的所有数据存入一个矩阵，然后利用K均值算法寻找最合适的点来作为最终所确定的角度。

5 仿真实验及结果分析

下面通过计算机仿真软件证明本文研究的实验具有可行性。使用计算机仿真软件，可以模拟实验中的各个步骤和变量，并得出与实际实验相似的结果。

5.1 实验过程

实验条件：假设有个频率为2 GHz的远场相干信号入射到均匀线阵中，信号的相位为随机产生；采用的天线阵为均匀五元圆阵，λ为信号波长，接收数据快拍数为50。根据来波方向与均匀阵线法线的夹角不同，设计了3组实验。

首先要得到的数据为求出天线阵中所有可以求得到的基线的相位差。因为是五元阵，所以可能出现的相位差个数为C25=10个。3组实验分别如图6—8所示。

由上图可知可以成功得到每组基线的相位差，接下来就要根据这些相位差利用式（10）求出可能的n值，如表1所示。

sinθ=λφ2πD=λ（2nπ+）2πD（10）

求出模糊值后就要对所有的n值进行处理，带入式（11）并反解出全部可能对应的θ角。

θ=arcsinλ（2nπ+）2πD（11）

最后对这些数据进行模糊聚类分析，得到正确的θ角，如表2所示。

由表2可知，所得到的θ角与预设的角基本一致，基本可以确定该算法能够很好地实现所预期的目标。从中可以看出，即使在36°这样特殊的角度，同样可以正确地解模糊从而得到准确的方向角，在大于126°的角度也是一样，这更加印证了文章所使用方法的可行性以及准确性。

5.2 数据分析

上述3个实验结果表明：本文研究的基于模糊聚类的遍历基线干涉仪测向算法非常可靠和精确。该算法能有效测量任意方向的入射信号角度，所得数据与输入角度之间的误差极小，小于0.1°。

6 结语

文章提出的研究方法旨在解决基于均匀圆阵的干涉仪测向解模糊问题。为了验证方法的准确度，本文采用了均匀五元圆阵的布局进行实验。遍历基线法的核心在于求出所有可测量的基线的相位差，并利用这些相位差进行后续计算。

文章仿真实验表明，基于模糊聚类的遍历基线干涉仪测向算法具有较高精度，这种精度足以证明该算法在解决干涉仪测向问题中能够实现非常高的正确率，从而提高了干涉仪测向的准确度和可靠性，为干涉仪测向技术的发展和应用提供了强有力的支持和保障。该算法在增强干涉仪测向算法的稳定性、准确性以及综合利用率方面具有重要的价值和应用前景。

参考文献

［1］张子鑫，胡国平，周豪，等.基于互协方差稀疏重构的MIMO雷达低仰角估计算法［J］.系统工程与电子技术，2021（5）：1218-1223.

［2］牛琨.聚类分析中若干关键技术及其在电信领域的应用研究［D］.北京：北京邮电大学，2007.

［3］BERSENEV I S，STAROSTIN A N.Analysis of pellets mineral composition using the solutions trees and k-means methods［J］.Ferrous Metallurgy Bulletin of Scientific，Technical and Economic Information，2019（7）：796-802.

［4］徐文君，赵荣琦，刘志永.基于基线比值法的多基线相位干涉仪解模糊算法研究［J］.舰船电子对抗，2023（5）：80-84.

［5］虞贵财，邵玉斌，肖笛.产生高斯白噪声的研究与实现［J］.电子科技，2006（11）：16-18.

［6］LIU L T，YU T.An analysis method for solving ambiguity in direction finding with phase interferometers［J］.Circuits，Systems，and Signal Processing：CSSP，2020（3）：1-18.

［7］胡赢双，陆亿红.基于MapReduce的强连通网格聚类算法［J］.计算机科学，2019（增刊2）：204-207，215.

［8］杨晶，罗冰，夏韶俊.相位干涉仪参差基线解模糊算法研究［J］.航天电子对抗，2012（3）：31-34.

［9］PAN Y J，ZHANG X F，XIE S Y.An ultra-fast DOA estimator with circular array interferometer using lookup table method［J］.Radio Eengineering，2015（3）：850-856.

［10］魏子翔，胡永芳，崔嵬，等.基于对称天线相位干涉仪的入射角估计及跟踪［J］.电子与信息学报，2015（10）：2369-2376.

（编辑 王雪芬）

Direction finding algorithm for traversing baseline interferometers based on fuzzy clustering

SHI  Rui1， LUO  Yuanzheng1， LI  Zhipeng1， ZHANG  Yifan2

（1.Tongda College， Nanjing University of Posts and Telecommunications， Yangzhou 225000， China;

2.Nanjing University of Posts and Telecommunications， Nanjing 210023， China）

Abstract：  The article proposes a traversal baseline interferometer direction finding algorithm based on fuzzy clustering to address the issue of inaccurate direction finding due to angle ambiguity in interferometer direction finding technology based on uniform circular arrays. This algorithm is based on the analysis of the principle and process of resolving ambiguity in interferometer direction finding technology using a uniform circular array. The traversal method is used to solve for the possible number of ambiguities under each phase difference and determine the corresponding angle. Finally， the fuzzy clustering method is used to determine the correct angle. The simulation results show that the proposed algorithm can achieve direction finding deblurring based on a uniform circular array interferometer， effectively improving direction finding accuracy and detection range.

Key words： interferometer direction finding; resolve ambiguity; traverse the baseline; fuzzy clustering