基于模糊聚类的宁波大红鹰学院教学质量评价研究

寇小鸿

摘要：结合实际工作将模糊聚类的理论应用于教师评价中，对数据进行了预处理，将清洗后的数据经过多次迭加，得到科学的分类。聚类结果为三类，其中第三类的教师教学水平最高，对课程投入较好；第二类的教师的教学水平较好，教师的教学风格比较受学生们喜爱；第一类教师的水平一般，课程难度却相对简单。运用逐步聚类方法分析教师教学质量，从而为具有不同教学特征的教学质量评价提供一定的参考。

关键词：模糊聚类；教学质量；数据挖掘

中图分类号：TP18 文献标识码：A 文章编号：1009-3044（2015）36-0092-03

高校是教学科研和培养人才的重要场所，教师资源作为高校中最重要的资源，对高校的生存和发展具有决定性影响。近年来，社会对教师的工作质量和效率提出了更高要求。学生对教师的评价在从中扮演着一个极为重要的角色，它把学生对教师在教学过程中遇到的问题反馈给教师，教师对一些在教学过程中出现的问题进行调整，从而达到最理想的教学模式。高校教师评价研究是高校师资队伍建设的重要环节，也是高等教育改革与发展的最为重要的基石。教师评价不仅仅是一种客观性评价，而且是用于诊断教学中存在的问题，以利于进一步改进教师的工作，为他们提供培训和自我发展的机会[1]。

本文以宁波大红鹰学院机电学院师生评教作为研究对象，运用数据挖局中模糊聚类的方法处理这些数据。从这些数据中挖掘出有价值的信息，进行不断的归纳总结，分析出教师在教学任务中存在利与弊。从而达到更深层次的教学质量，全面提高教师的教学素质。

1 研究方法

Zadeh提出的模糊集理论为软划分提供了充分有力的分析工具， 人们开始用模糊的方法来处理一些聚类问题，并称之为模糊聚类分析，由于模糊聚类得到的样本类别程度的不确定，体现了样本类属的中介性，即建立起了样本对于类别的不确定性的描述，又能客观地反映现实，从而成为现代聚类分析研究的主流。模糊聚类能够有效对类与类之间有联系的数据集进行分类，能够提高算法的寻优的概率[2]。

1.1 研究的数据

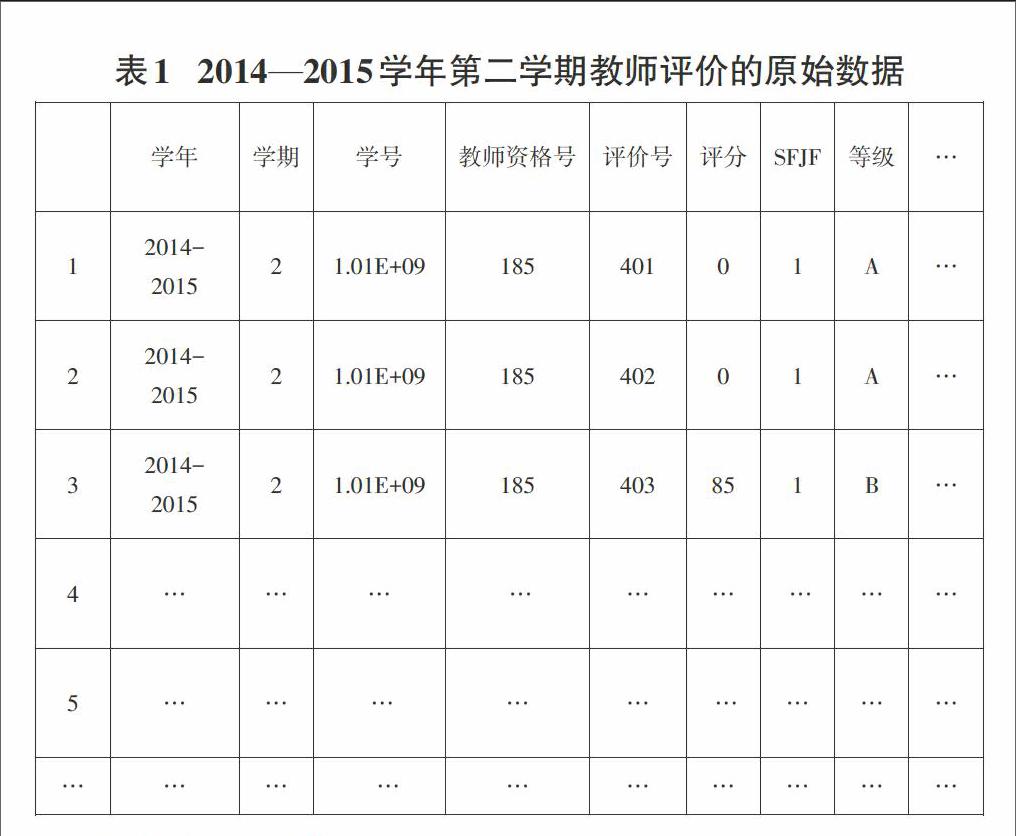
本课题的原始数据资料来源于宁波大红鹰学院某学院的数据，收集了2014—2015学年第二学期教师评价的数据6000个。通过计算机将服务器ACCESS数据库中的数据，提取到EXCEL文件中，录入到EXCEL中，如表1。

1.2 数据的清洗和简化

数据清洗的目的不只是要消除错误、冗余和数据噪声，还要将按不同的、不兼容的规则所得的各种数据集一致起来[3]。

数据简化是在对发现任务和数据本身内容理解的基础上，寻找依赖于发现目标的表达数据的有用特征，以缩减数据模型，从而在尽可能保持数据原貌的前提下最大限度的精简数据量。由于教师和学生数量过多，本文随即抽取了100个教师和教师所对应的100个学生。并且以9个指标来评价老师X1，X2…，X9。每个指标分为四个等级，A B C D，其中A最高4分，B其次3分，C为2分，D为1分。

1.3数据的变换

数据变换是找到数据的特征表示，用维变换或转换来减少有效变量的数目或找到数据的不变式，包括规格化、归约、切换和投影等操作。

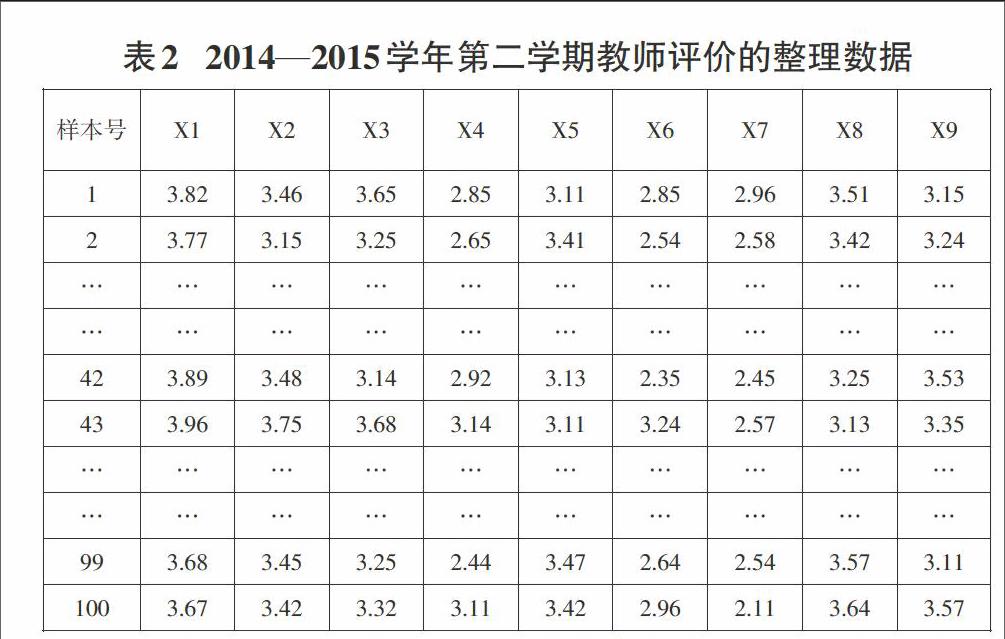
根据简化后的数据，计算每一个老师的每一个指标的平均数，表2为最终整理得到的最终数据。

（X1表示为该任课老师对教学非常投入；X2表示为该老师的教学能力和水平很高；X3表示为任课老师的总体满意程度高；X4表示为该课程较难掌握；X5表示非常投入的学习该门课程；X6表示为通过课程学习，我收获很大；X7表示为学习完该门课程后，我的收获很大；X8表示为该课程的设置价值较高；X9表示为对课程的总体满意程度高。）

1.4根据所选的凝聚点，每个样品按最近凝聚点分成几类

若与该数接近的整数为[k]，则将样本[xi]归入[k]类（[1≤k≤K]）。其中由表2中可得，

[MI=min1≤i≤nSUMi]=1.11319，[MA=max1≤i≤nSUMi]= 6.0087，[.]表示取整运算。对于[k]值的选取，根据医学知识的经验以及反复上机调试实验，将100个样本初始分为3类较为合适，根据公式（1）、（2），在DPS软件系统中进行初始分类。

1.5根据分类结果，再找出新的凝聚点

计算与上一组的凝聚点差异，若差异小于摸个设定值，则认为分类合理，过程结束。若差异大于设定值则分类不合理，继续按照前面方法进行分类。

因为选取的样品数量比较多，所以本文采用的是重心法[5]，初始凝聚点采用该样品的均值，计算公式为：

其中[gj]（[j=1，2，...m]）为第k类（[1≤k≤K]）类的重心坐标，[nk]为第k类的样本数。那么，根据（3）式计算初始分类的重心，得到凝聚点，由重心计算公式得到初始分类重心坐标如表3。

1.6 将所有的样本按最近凝聚点归类

这里，[ni]为第[i]个样本组的样本数，[xi]为其均值，[x]为N个样本的总均值，m为N个样本所分类的组数，[N=i=1mni]，S为样本[xi]与类凝聚点的距离。

从计算公式上可以看出，当[ni=1]时，[S]为[N]个样本分[N]组的总离差平方和；当[ni≥2]时，此时[S]则为[N]个样本被分为[m]组的组间平方和。根据方差分析的思想。如果分类正确，那么同类样品的离差平方和应当较小，即组内的同质性就越大，异质性就越小，类间离差平方和应当较大，即组内的同质性就越小，异质性就越大。计算所有样本到每一个类凝聚点的距离，并将样本归入到最近凝聚点所在的类[6]。

1.7修改分类，使分类趋于合理

本文将采用成批修改法，其步骤如下：在样品初始分类后，计算每一类的重心，并将重心作为新的凝聚点，重新将样品按最近的新凝聚点聚类。如果新的分类结果和原始分类有差异，再计算新的凝聚点，并重新进行分类，如无差异则分类终止。这样一直重新分类直到所有样品不再变动类别为止[7]。经过七次迭代得到的结果，如表4。

2 逐步聚类结果及结果分析

在DPS软件中完成上述逐步聚类算法的整个过程，包括初始分类、每次迭代后各个样本的类别，与距凝聚点的距离、最终分类结果见表5。聚类结果是，其中第一类样本12个，第二类样本66个，第三类样本22个。

（X1表示为该任课老师对教学非常投入；X2表示为该老师的教学能力和水平很高；X3表示为对任课老师的总体满意程度高；X4表示为该课程较难掌握；X5表示非常投入的学习该门课程；X6表示为通过课程学习，我收获很大；X7表示为学习完该门课程后，我的收获很大；X8表示为该课程的设置价值较高；X9表示为对课程的总体满意程度高。）

由表5可以得出：

1、第三类的教师水平最好，尤其是对教学非常投入，教学水平和能力很高，很受学生欢迎，但所教课程也有一定的难度，教师的教学经验丰富，由于课程难度较大导致学生对于知识的理解和吸收相对较低，所以本文觉得这类课程通常为专业必修课，课程时间安排比较紧凑，同学消化课程内容又相对较慢，另外由于学生的一些个人因素，使得同学对这类课程失去学习的兴趣，老师在上课的时候虽然把各类知识重点都讲到了，但是巨大的内容还是让学生感觉到学习压力。所以这类教师应该更加注重创新化教育，从学校培养人才计划的方向，从学生的角度出发，根据学生的自身能力安排课程。否则再好的师资力量，再好的课本，也无法教出优质的学生。

2、第二类教师的水平较高。课程难度却相对简单，学生相对来说也比较容易接受这类课程，并且收获也不小。教师的教学风格比较受学生们喜爱，学生接受知识的速度也较快，使得教师和同学之间的关系比较融洽，这类教师可能是一些年轻教师。学生和教师之间的沟通很重要，而这类教师又善于改变课堂教学模式，从学生角度出发，使得枯燥的课堂环境变成一个理想的吸收知识的海洋。

3、第一类的教师水平一般，并且而师资力量相对来说比较薄弱，学生的学习热情更不够高，无法激起对这门课程的兴趣。本文认为这类课程通常为选修课，由于这类课程性质的特殊性，使得很多学生觉得这类课程可学可不学，通常是为修满学分而学，因此这类教师应该忽略课程特殊性问题，所开课程应该转移课堂外为主，而不是传统的课堂PPT模式，多增加学生团队合作，动手能力，使乏味的课堂增加一些年轻人的活力。比如电影赏析这类课程，不是一味地在课堂上放电影，然后写观后感，在欣赏完好看的 电影后，而是让学生自己拿起工具去拍一部微电影，哪怕是一段小视频，同时在某一节课堂上与同学们分享他们的劳动成果。

3逐步聚类方法的讨论

本文采用的模糊聚类中逐步聚类法优缺点。

逐步聚类法是在一个平面层次上对所有的样本先做出某一种较为粗略的分类，然后按照最小距离值进行修正，通过算法的迭代执行，得到一个较为合理的聚类分类。其运算量小，能用于处理庞大的样本数据，也为实时处理提供了一定可能性。

缺点是它倾向于识别密度相近的，距离和大小相近的聚类，不能识别分布形状比较错综复杂的聚类，它要求类别数目K可以合理地估计，且初始聚类中心的选择和噪声会对聚类结果产生很大影响，一旦初始值选择的不好，可能无法得到有效的聚类结果。还需要用户预先指定聚类个数。

由于实际问题的复杂性和数据的多样性，使得无论采用哪一种算法都只能解决某一方面的问题。因此，我们应该根据具体问题具体分析的原则，选择适合自己的聚类算法。

参考文献：

[1] 石娟.高校教育质量发展性评价的研究与实践[J].现代教育管理，2009（1）：65-67

[2] 张维朋.基于模糊聚类的数据挖掘在临床检验信息系统中的应用研究[J]. 电脑知识与技术，2009，5（23）.

[3] 陈明浩.模糊分析学新论[M].北京：科学出版社，2009

[4] 唐启义，冯明光.实用统计分析及其DPS数据处理系统[M].北京：科学出版社，2013

[5] 朱星宇，陈勇强. SPSS多元统计分析方法及应用[M]. 北京：清华大学出版社，2011

[6] 张旭鹏，孙莉，于佳涵，等. 基于聚类分析和神经网络的风电场日前功率预测研究[J].黑龙江科技信息，2015（29）：29-29

[7] 李远成 阴培培 赵银. 基于模糊聚类的推测多线程划分算法[J].计算机学报，37（3）：580-592