借助GeoGebra软件探究水中物体折射成像位置问题
2024-07-08王韵涵侯汶君冯洁李红梅
王韵涵 侯汶君 冯洁 李红梅


[摘 要]对于水中物体的折射成像,教师常结合小孩叉鱼、池底变浅等例子进行讲解,但对于水中物体折射成像的位置描述却不够科学准确。文章借助GeoGebra软件对水中物体折射形成的虚像位置及其随视角变化的情况进行模拟演示,通过虚拟仿真手段直观、完整地展示水中物体折射成像问题的实质,并在教学中呈现更严谨的图示,帮助师生深度理解水中物体折射成像的原理。
[关键词]水中物体;折射成像;GeoGebra软件
[中图分类号] G633.7 [文献标识码] A [文章编号] 1674-6058(2024)14-0040-04
一、 问题的由来
[题目](2022年云南省初中学业水平考试物理第24题)小华偶然间竖直向下看到放在玻璃砖下面的字发生了错位。
(1)他想光斜射时才发生偏折,才会出现“池底变浅”的现象。那么,光在垂直入射时,光线不再偏折,还会有“池底变浅”的现象吗?上述过程,在科学探究中叫作 (选填“设计实验”“提出问题”或“分析论证”)。
(2)①联想到“平面镜成像”找像位置的方法,于是他按如图1甲所示将玻璃砖紧贴物体摆放在水平桌面上的一张白纸上,标记出物体的位置。按照图1乙的方式沿水平方向观察物体(观察盒上的条形码)。当看到物体经玻璃砖成的像时,前后移动小卡片,使小卡片与像在同一个平面上,将小卡片此时的位置标记在白纸上,这样就找到了放置一块玻璃砖时 的位置。
②随后,他将玻璃砖离开物体向观察者移动一小段距离后进行观察,发现像的位置不变,说明玻璃砖与物体的距离 影响成像位置(选填“会”或“不会”)。
[俯视图 一块玻璃砖 两块玻璃砖 三块玻璃砖][甲 乙 丙 丁][厚度][小卡片][小卡片][小卡片]
图1
(3)为了观察不同厚度玻璃的成像情况,他将第二块相同玻璃砖紧贴在第一块后面,如图1丙所示,观察并记录像的位置;他再将第三块相同玻璃砖紧贴在前两块后面,如图1丁所示,观察并记录像的位置。记录数据如图2所示。
[物体的位置][一块玻璃砖时像的位置][两块玻璃砖时像的位置][三块玻璃砖时像的位置][2.13 cm][2.15 cm][2.35 cm]
图2
①分析图2的数据可知,用一块玻璃砖观察时,像与物体的距离是 cm;
②三次实验都说明了光在垂直入射时,像的位置会 观察者(选填“靠近”或“远离”)。
(4)从图2的实验数据还可以得出:玻璃的厚度越厚,像与物的距离越 。
(5)从以上探究可知,从竖直方向看到的池底比它的实际位置 (选填“浅”或“深”)。
分析:这一道探究题,基于真实情境设置问题,从设计实验、进行实验、收集证据、分析论证等方面对学生的科学探究能力进行考查。光的折射是生活中常见的现象,教师常结合小孩叉鱼、池底变浅等例子来进行解释,但在解释这些现象背后的原理时往往只提到当光线斜射入其他介质时折射角小于入射角,当光垂直入射时光线的传播方向不变。在讲解时也只是进行了“虚像在鱼上方”“水看起来变浅”等的描述,而对于当视角变化时折射成像位置发生变化的情况以及光线垂直入射时折射成像的位置并不提及。
本题对于光线垂直水面入射时的成像位置提出疑问,而后用玻璃砖与小卡片进行定性探究,最后得出结论。按照题中的实验设计进行探究,发现虽然能够根据现象得出结论,但仍然无法清晰地体现变化规律以及成像特点。借助GeoGebra软件强大的数据运算以及动态模拟功能,建立物理模型,通过动态、立体图示,可以准确直观地表征和解释水中物体折射成像的位置问题,清晰体现其变化规律以及成像特点。
二、凭借主观经验绘图存在的缺陷
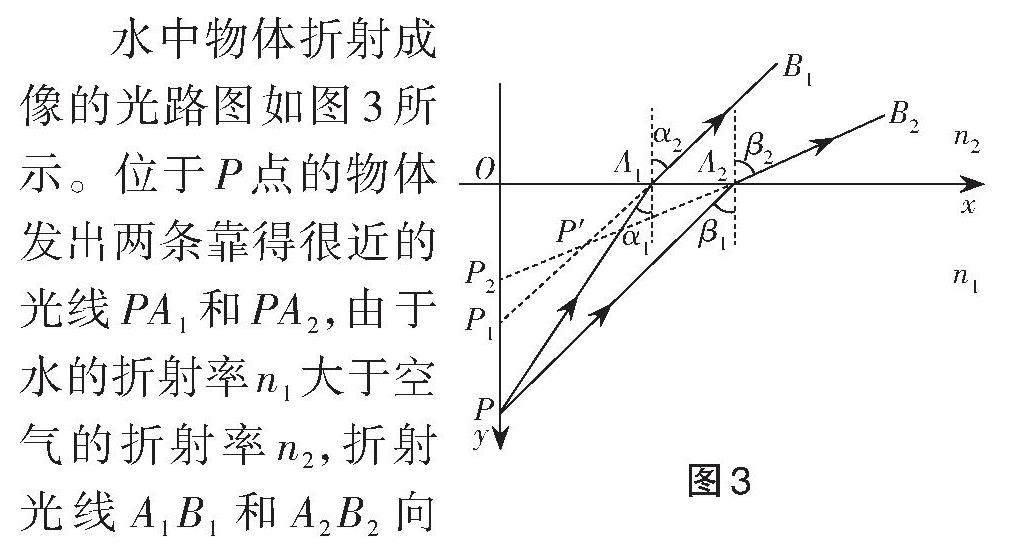
水中物体折射成像的光路图如图3所示。位于[P]点的物体发出两条靠得很近的光线[PA1]和[PA2],由于水的折射率[n1]大于空气的折射率[n2],折射光线[A1B1]和[A2B2]向远离法线的一侧偏折。精确的折射角度依据光的折射定律[n1sinθ1=n2sinθ2]来确定。此时,观察者逆着折射光线看向水中,看到的物体位置应位于两条折射光线[A1B1]和[A2B2]的反向延长线的交点[P′]处。
如图3所示,当水中的物体发出的光斜射入人眼时,物体的真实位置在竖直方向上且在观察者看到的像的位置下方,在水平方向上会比虚像更远离观察者[1]。但在实际作图时,由于折射角的计算涉及反三角函数,往往不能即时得出精确的角度,于是教师在讲解时常常通过估测,先画出两条折射光线,再标注折射角,最后反向延长使之相交,得出虚像的位置。教师由于没有利用光的折射定律进行计算,直接凭借主观经验画出折射光线,因此常会出现光线偏折程度不当,甚至出现入射角大于临界角的情况,与全反射规律相违背。这样的作图方式缺乏科学性与严谨性,于教师专业发展不利,同时也会影响学生实事求是、严谨认真的科学态度的培养。
另外,教师在黑板上即时绘图并不能连贯地向学生演示随着观察者视角的变化虚像位置的变化情况。即使严格按照光的折射定律进行计算,其过程也较为烦琐,耗费时间长且不够直观,学生难以发现其中的变化规律以及一些特殊情况下(如光线垂直入射时)的折射成像特点。
三、借助GeoGebra软件直观演示水中物体折射成像的位置变化
基于上述分析,借助GeoGebra软件来准确直观地演示水中物体折射成像的位置变化。
(一)基于单心光束的水中物体折射成像的位置演示
从水中物体发出的光束如果在水与空气的分界面发生折射后仍是单心光束,就说明光线的方向虽然改变,但折射光束中的所有光线的反向延长线仍能汇聚于同一个点,这个点就是像点。因此,只需要考虑任意两条折射光线,作出其反向延长线的交点,就能找到水中物体折射所成的虚像的位置。
如图4所示建立[xOy]平面,光源[P]在[y]轴上,考虑从[P]发出的两条光线[PA1]和[PA2],利用GeoGebra软件的“角度”工具直接测出入射角[α1]和[β1],输入光的折射定律公式,利用GeoGebra软件的运算功能即可直接得出折射角[α2]和[β2]的大小,再根据折射角绘制折射光线。将两条折射光线[A1B1]和[A2B2]反向延长分别交[y]轴于[P1]、[P2]点,并且它们在[xOy]平面上相交于[P′]点,这个点就是此时虚像的位置。
随着观察者在岸上走动,虚像的位置也会随之变化,因此设置[P′]的属性为显示踪迹,启动[A1]、[A2]动画,这两点将向右移动,表示观察者的视角发生变化,逐渐远离水中的物体[P],而虚像[P′]的位置将随观察者视角的改变而改变,并显示出其轨迹(如图5)。
[O][P2][P1][P][y][n2][n1][x][B2][B1][A1][A2][P′][β2=89.11°][β1=48.75°][α2=65.2°][α1=13.04°]
图5
根据光学原理,设[P]点的坐标为(0,y),则[P′]点的横坐标与纵坐标[2]分别为
[x'=yn21n22-1tanα31] (1)
[y'=yn2n11-n21n22-1tanα2132] (2)
(二)基于较大范围内光束的水中物体折射成像的位置演示
水中物体发出的光束如果所占范围较大,从[P]点发出时是一束单心空间光束,但经过折射后可能不再保持其单心性,那么就需要考虑折射光束的空间分布。由于平时在黑板或纸面上作图,受限于二维平面,因此难以描述三维空间中光的折射情况,而利用GeoGebra软件的3D绘图功能可以直观演示三维空间中光的折射成像情况。
建立三维坐标系,选[x]轴上的任意两点[A1]、[A2]为入射点,此时光源[P]在[A1A2]范围内发出的单心光束如图6所示。
输入光的折射定律公式后得到折射光线,并将其反向延长,可以看出折射光束中所有光线的延长线并不交于同一个点,而是交[y]轴于线段[P1P2]的范围内。同时,[P′]点描出一段很短的弧,可近似看作垂直于[xOy]平面的一小段直线,折射光束中所有光线的延长线也分别交于这一小段直线上的各个点[3],如图7所示。
[B1][B2][n2=1][n1=1.33][x][A2][β1=40.679°][β2=60.104°][A1][α2=28.593°][α1=21.09°][O][y][P2][P1][P′] [z]
(a)从z轴正向往z轴负向看
[y][z][n2=1][n1=1.33][B1][O][P2][P′][α2=28.593°][α1=21.09°]
(b)从x轴负向往x轴正向看
图7
由此可见,当水中物体发出的光束所占范围较大时,折射光束不再保持单心性,而成为像散光束,折射光线的反向延长线不再交于一点,整个区域有很多可能的交点[4]。因此,当观察者处于光束[PA1A2]范围内的不同空间位置处时,交点[P′]的位置也会有所不同,虚像的位置也会不同[5]。
当观察者在水中物体的正上方竖直向下看时,[P]点所发出的光线几乎垂直于分界面,即入射角[α1=0]时,由式(1)和式(2)得像点[P′]的坐标[6]为:
[x'=0],[y'=y1=y2=n2n1y] (3)
此时[P1]、[P2]、[P′]三点几乎重合在一起,折射光束仍保持单心性,由于[n1>n2],则[y′>y],虚像的位置位于真实物体的上方,如图8所示。
现在再来回顾2022年云南省初中学业水平考试物理试题第24题,这道实验探究题中物体的位置代表池底的位置,玻璃砖的厚度代表池子的深度,小卡片的位置代表光在垂直入射时池底折射成像的位置。题目的第(3)(4)问提出的问题是当玻璃砖的厚度不同时,求像与观察者的距离关系以及像与物的距离关系。利用GeoGebra软件建立的模型来模拟实验情境,[xOz]平面代表池子水面,池底[P]在[y]轴上,观察者位于[O]点处,改变入射角使光线垂直水面入射,题目中依次增加玻璃砖的数量意味着池底到观察者的距离越来越远,于是向[y]轴正方向拖动[P]点,表示逐渐增加池子的深度,如图9所示。
[O][A1][A2][P′][y][z][x][n2][n1][B1][B2][像的深度y′= 3.559][物体的深度y=4.734][像与物体的距离d=y-y'=1.175][(a)当池子深度为4.734时的折射成像情况] [O][A1][A2][P′][y][z][x][n2][n1][B1][B2][像的深度y′= 6.22][物体的深度y=8.272][像与物体的距离d=y-y'=2.052][(b)当池子深度为8.272时的折射成像情况][P][P]
[O][A1][A2][P′][y][z][x][n2][n1][B1][B2][像的深度y′=10.764][物体的深度y=14.316][像与物体的距离d=y-y'=3.552][P][(d)当池子深度为14.316时的折射成像情况][O][A1][A2][P′][y][z][x][n2][n1][B1][B2][像的深度y′= 8.326][物体的深度y=11.073][像与物体的距离d=y-y'=2.747][(c)当池子深度为11.073时的折射成像情况][P]
图9
用[y]来表示物体与观察者的距离,即物体的深度,用[y′]来表示像与观察者的距离,即像的深度,设置公式计算并显示出[y]与[y′]之差以及[y′]与[y]之比,精确度为保留3位小数。仔细观察[P]点折射所成像的位置[P′]点,分析[P]与[P′]点的坐标,得出以下结论:①光在垂直入射时,像的位置会比物体的实际位置更靠近观察者,也就是我们看到的“池底变浅”的现象;②物体与观察者的距离越大,折射所成的像与观察者的距离越大,像与物的距离也越大;③在光线垂直入射时,无论物体与观察者的距离是多少,像的深度与物体的深度之比始终不变,其值的大小为两种介质的折射率[n2]与[n1]之比,与式(3)相符合。
四、总结
受限于复杂的计算以及烦琐的绘图步骤,教师在讲解水中物体折射成像时往往根据主观经验,大概地画出光线的偏折程度以及所成虚像的位置。这样的绘画方式不够规范,甚至有可能产生科学性错误,影响学生形成科学严谨的学习态度。借助GeoGebra软件强大的数据运算以及动态模拟功能,可以准确地解释水中物体折射成像的规律,帮助学生加深对光的折射知识的理解。希望本文有关GeoGebra软件的应用能够对中学教师有所启发,促使中学教师应用GeoGebro软件辅助教学,从而取得更好的教学效果。
[ 参 考 文 献 ]
[1] 董霞,张雄,徐晓梅,等.“鱼在哪里”:中学物理教学中的折射解析[J].物理教师,2013(11):59-60,62.
[2][3][6] 姚启钧.光学教程[M].5版.北京:高等教育出版社,2014.
[4][5] 汪志荣,苏银凤.物理教科书光学插图设计问题与对策:基于8种版本初中物理教科书折射成像插图分析[J].物理教师,2019(2):27-32,36.
(责任编辑 黄春香)
[基金项目]2022年度教育部高等学校大学物理课程教学指导委员会大中物理教育衔接工作委员会教学研究课题(项目编号:WX202214)。
[通信作者]李红梅(1972— ),女,云南人,硕士研究生导师,研究方向为中学物理教学研究、实验创新研究。
