基于超材料的太赫兹波辐射特性与增强研究
2024-07-08徐新龙史明坚黄媛媛刘慧彪熊永臻
徐新龙 史明坚 黄媛媛 刘慧彪 熊永臻

摘要:太赫兹波的产生与调控对太赫兹技术发展至关重要。超材料的可设计几何结构与特异共振响应为产生与调控太赫兹波提供了新的途径。但超材料产生太赫兹波辐射的转换效率较低仍然是一个亟待解决的问题。设计了一种由金属谐振环阵列和全介质硅开口谐振器组成的超材料。利用麦克斯韦方程联合表述电子运动的流体动力模型的自洽方程组,研究了该超材料的太赫兹波辐射与调控过程。研究发现,通过优化分裂谐振环的开口方向,超材料产生的太赫兹波振幅提高了1倍。此外,通过改变入射光偏振角及超材料的几何尺寸实现了太赫兹波振幅调控。这为基于超材料的,紧凑型和可调谐的太赫兹源提供了新途径。
关键词:超材料;太赫兹辐射;分裂谐振环;共振耦合效应
中图分类号:O 437 文献标志码:A
Terahertz wave radiation characteristics and enhancementbased on metamaterials
XU Xinlong,SHI Mingjian,HUANG Yuanyuan,LIU Huibiao,XIONG Yongzhen
(School of Physics, Northwest University, Xi'an 710127, China)
Abstract: The generationand manipulation of terahertz wave is crucialfor the advancement of terahertz technology. The designable geometry and specific resonance response of metamaterials offeranovelapproachforgeneratingandmanipulatingterahertzwaves. However,thelow conversionefficiencyof terahertzwavefrommetamaterialsremainsachallengingissuetobe addressed. In this paper, a metamaterial was designed which consisted of metal resonator ring array and all-dielectric silicon split ring resonators. The terahertz wave radiation and manipulation of the metamaterial were studied by using self-consistent equations consisting of Maxwell's equation and the hydrodynamic model of the electron motion. It was discovered that by optimizing the opening directionofthesplitringresonators,theamplitudeofterahertzwavesgeneratedbythe metamaterial was doubled. Furthermore, control over the amplitude of terahertz wave was achieved by altering both the polarization angle of incident light and the geometry of the metamaterial. This work opens up new possibilities for compact and tunable terahertz sources based on metamaterials.
Keywords: metamaterial; terahertz radiation; split ring resonators; resonance coupling effect
引言
超材料是一种单元结构在亚波长尺度的人工结构,经过特定的结构设计,其可产生独特的共振模式,如法诺(Fano)共振、米氏(Mie)共振、明暗模式耦合等,从而实现对电磁场的有效调控。基于优异的线性光学响应,超材料被广泛应用于电磁波的振幅、相位、偏振和传播特性的调控。特别是在太赫兹(terahertz ,THz)波段,超材料展现了在圆偏振转换[1]、电磁诱导透明[2-3]、手性传感[4]等应用中的巨大潜力。有关超材料的非线性光学响应研究,虽然在二次谐波产生[5]、三次谐波产生[6]及谐波圆二向色性[5]方面已有部分研究进展,但在基于超材料的 THz波产生研究领域仍然处于起步阶段,且关于超材料产生 THz 波的物理机理仍存在一定争议。目前,电磁共振驱动的非线性光电流是 THz 波产生的主要物理机理之一。多光子电离引起的有质动力势、不均匀热分布也可在超材料结构中引起有效的 THz 波辐射。在实验中,Luo 等[7]观察到,开口环谐振器(split ring resonators , SRRs)中的磁偶极共振在超材料中引起有效的单周期宽带 THz 波辐射。在理论计算方面, Fang 等[8]运用麦克斯韦方程和描述电子运动的流体动力模型来描述 SRRs 的非线性光电流和 THz 波的产生。
基于超材料非线性光学响应产生 THz 波的相关研究主要分为两个方面。一方面,研究人员通过超材料几何结构的设计与排布实现对 THz 波相位与偏振态的调控,如自旋超原子的设计[9]、多层结构间的相互作用[10]、超原子的相位梯度排布[11]等。这些方式可以实现圆偏振/椭圆偏振 THz 波的发射,并可以灵活地调控 THz 波的取向角、椭偏率等特性。另一方面,通过设计有效的局域场增强来提高超材料的 THz 波转换效率。各种提高超材料的 THz辐射效率的方法被提出来,如明暗模式耦合[12]、等离子体天线[13]等。然而,基于超材料的 THz波产生仍面临着物理机理复杂多样,THz 波转换效率较低,调控与增强方式单一等科学问题。
本研究构建了由金属 L 型谐振器和全介质硅 SRRs 阵列组成的超材料。该超材料在飞秒脉冲激发下可以产生 THz波。相较于单层 L 型超材料结构,杂化超材料通过优化 SRRs 开口方向实现磁共振耦合,可以有效地提高超材料的THz 波振幅。此外,通过改变 L 型结构的几何尺寸,揭示了超材料对称性对产生 THz 波的影响。这种利用磁共振耦合效应的方法为增强超材料的 THz 波辐射提供了新的途径。
1 理论模型及结构设计
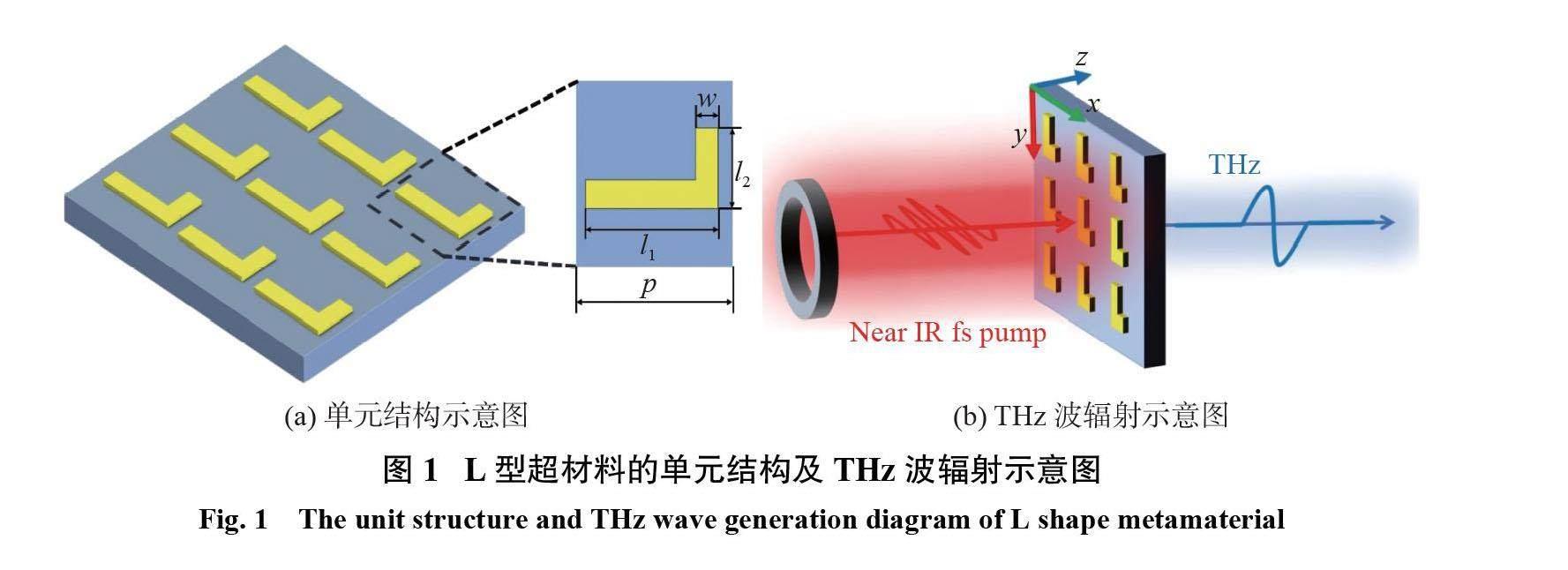
如图1(a)所示,本研究设计了一个 L 型金超材料, L 型结构周期地排列在介电常数ε=2.25的熔石英(fused silica)基底上。每个结构单元在 x ,y 方向的周期长度均为 P =480 nm。L 型结构的几何尺寸分别为 l1=350 nm , l2=170 nm ,w =50 nm。基底与金超材料的厚度分别为200 nm 和30 nm。
在线性光学响应中,金的振荡模式可以通过 Drude模型进行描述[2]
式中:参数 j 为表面电流;ω为峰值频率;高频相对介电常数ε凯=9;等离子振荡频率!p =√n0 e2/(ε0me )= 1.37×1016 rad/s,其中, me 为电子的质量, e 为电荷量,n0=5.92×1028 m?3为未被激发的本征电子密度;等离子体阻尼频率γ= 10.68×1013 rad/s[8]。
对于超材料的非线性光学响应与 THz波产生的研究是利用飞秒脉冲光激发超材料的样品面,在基底面探测 THz信号,如图1(b)所示。飞秒脉冲光的电场分布符合高斯函数 E = E0exp[一2ln2((t 一 t0)/τ)2]cos(!t),其中激发光的脉冲宽度τ=100 fs;入射光峰值时间 t0=300 fs;入射激光的峰值振幅为 E0=2×107 V/m。电场为 x 方向的泵浦光沿着 z 方向入射到 L 型超材料上,产生的 THz 波沿着 z 方向继续传播。
在理论模拟方面,采用麦克斯韦方程组?流体动力模型可以对金中的自由电子气进行非线性光学响应的描述
式中:H,E,P 分别为磁场强度、电场强度和电极化强度;和分别为真空磁导率和介电常数。
式中: me 和 e 是电子质量和电子电荷; v 项是极化电流速度;B 为磁感应强度;ev×B 为洛伦兹项;量子压力项p =(3π2)2/3·(h2/5me )· n5/3;(v ·Δ)v 是对流加速; n 为电子密度。
由金属的极化强度 P 的变化可以获得极化电流 J,可以表示为
脉冲光激发下的电子密度 = e(n 一 n0)。
利用有限元软件 COMSOL Multiphysics 对超材料的线性与非线性光学响应进行计算。通过飞秒脉冲光垂直激发超材料,并在远场设置面探针探测超材料产生的 THz波信号。在 z 方向采用散射边界条件与完美匹配层,防止入射波被边界反射影响计算结果,四周采用周期性边界条件模拟xy平面内无限大的周期性阵列。
2 结果与讨论
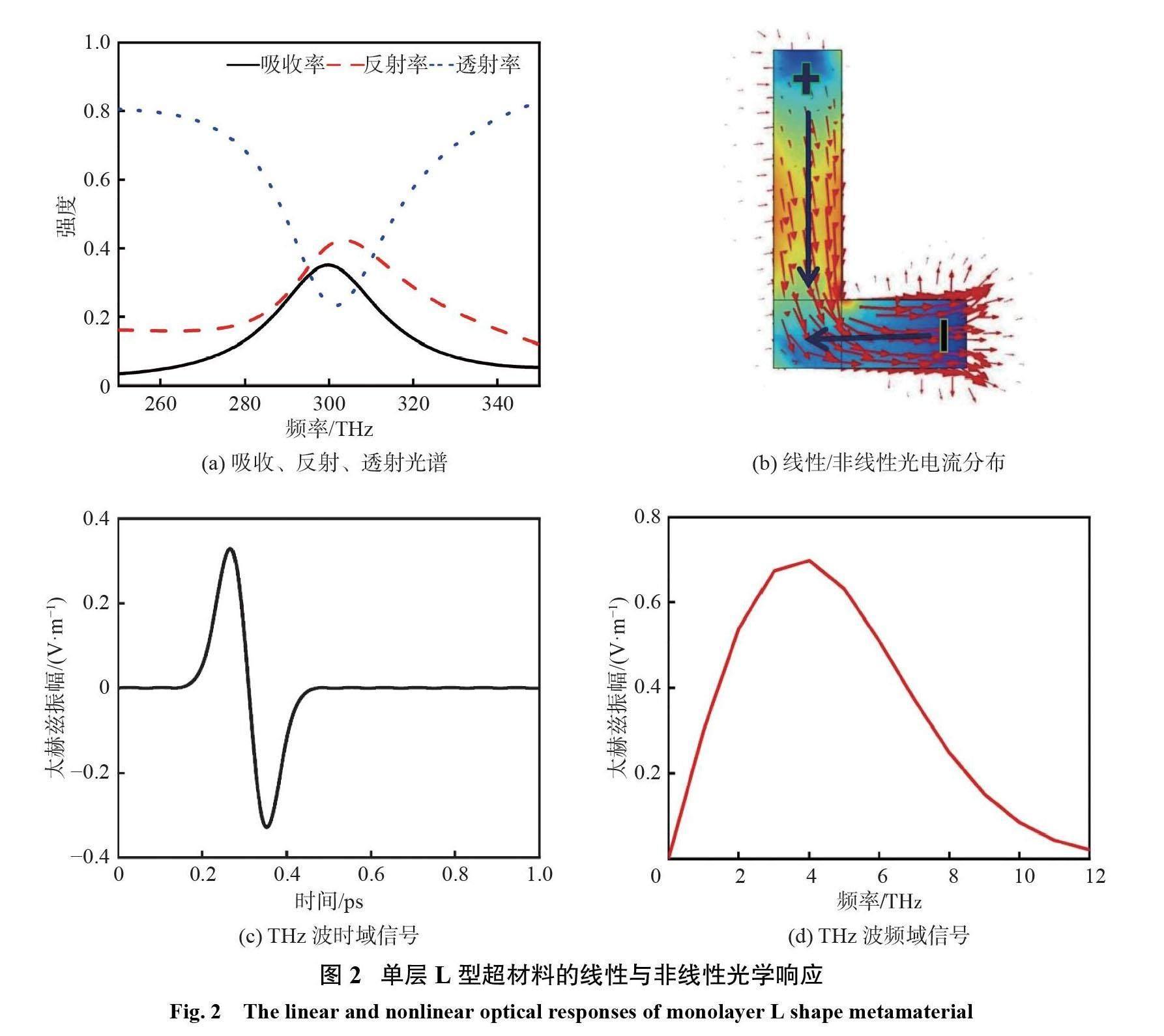
如图2(a)所示,计算了电场沿 x 方向的入射光垂直激发 L 型超材料产生的透射率、反射率、吸收率。其中,在频率为300 THz处存在一个强度为0.35的共振吸收峰。共振位置的脉冲光激发超材料可以得到最大的 THz信号[7],因此选用频率为300 THz 的光作为泵浦光。为了保证飞秒脉冲光不会损伤超材料,计算了该飞秒脉冲光的峰值功率 P = SE0(2)/ Z0 =0.06 W,其中 S 为单元结构的面积, E0是峰值电场, Z0为波阻抗。该峰值功率小于实验中的平均功率0.1 W,因此该强度的飞秒脉冲不会损伤超材料。为分析吸收峰处的共振模式,计算了 L 型超材料在共振位置的表面电流分布。如图2(b)所示,在激发光的激发下,L 型超材料在共振位置处产生了一个由 L 型结构长臂的顶部流向短臂的尾部的线性光电流。线性光电流的流动导致 L 型超材料长臂的顶部与短臂的尾部形成电荷积累区,在长臂与短臂交界处形成电荷耗尽区。这将导致L 型超材料沿长臂 y 方向产生由顶部指向尾部的非线性光电流,沿短臂 x 方向产生由尾部指向顶部的非线性光电流[14]。由于长臂方向的非线性光电流远大于短臂的非线性光电流,因此在远场探测了超材料产生的 Ey 分量的 THz信号。如图2(c)所示,计算得到 L 型超材料在 Ey 分量的 THz信号为0.65 V/m,高于之前研究的 SRRs产生的 THz振幅(0.5 V/m),表明 L 型超材料具有很好的 THz信号辐射响应[8]。通过傅里叶变换得到 THz频域信号,其频谱宽度达到12 THz,远大于传统非线性晶体产生的 THz频谱宽度(如图2(d))[15],同时避免了传统非线性晶体对THz 波的强吸收导致的 THz频谱不连续。
THz 波振幅作为 THz 波的主要特性之一,是衡量 THz 波强度的重要标准。为了进一步提高 L 型超材料产生的 THz信号,设计了厚度为100 nm 的全介质硅 SRRs覆盖在 L 型金属超材料上,两者之间熔石英层的厚度为100 nm,相邻开口环之间的距离为145 nm。通过改变硅 SRRs 的开口方向,优化硅 SRRs在泵浦光激发下产生的共振模式,从而增强 L 型超材料产生的 THz 波信号。其中硅也可以产生较弱的 THz 波,但需要打破结构对称性,而硅 SRRs 作为对称结构很难产生较大的 THz信号,因此在模拟中忽略了硅 SRRs产生的 THz信号。如图3(a)和(b)所示,设计了覆盖同向与反向开口的硅 SRRs超材料。相较于单层 L 型超材料,两种覆盖硅 SRRs超材料的共振吸收峰出现红移,共振峰的位置位于265 THz 附近(如图3(c)和(d))。通过模拟计算两种不同开口方向的硅SRRs 表面电流可知,当全介质硅 SRRs 的开口方向相同时,在泵浦光激发下,表面产生环形光电流(红色箭头),并形成相同方向的磁偶极矩(图3(e));当相邻硅 SRRs 的开口方向为反向时,泵浦光激发下两者都产生磁共振响应,并反向振荡,相邻 SRRs形成相反方向的磁偶极矩(图3(f))。为验证两种模式对 L 型超材料非线性响应的影响,分别计算了覆盖同向硅 SRRs 与反向硅 SRRs超材料产生的 THz信号。
如图4(a)所示,对比了单层 L 型超材料、覆盖开口方向同向的硅 SRRs 以及反向的硅SRRs 超材料产生的 THz信号。可以发现,覆盖同向硅 SRRs超材料产生的 THz 波振幅为0.78 V/m,相较于单层 L 型超材料产生的 THz 波仅提高0.13 V/m。然而,将硅 SRRs 的开口方向反转(反向硅开口谐振器),L 型超材料产生的 THz 波振幅提高至1.3 V/m,相较于单层 L 型超材料产生的 THz波提高了一倍。超材料的有效二阶非线性极化率χ(2)可以通过公式χ(2)= c √η/!dE0给出,其中 c 为光速, d 为超材料厚度,ω为泵浦光频率, E0为泵浦光电场,η= ITHz/I!为 THz 波的转换率。计算得到,同向硅 SRRs 与反向硅 SRRs覆盖的 L 型超材料的二阶极化率分别为1.09 V/m 和1.8 V/m,而单层 L 型超材料的二阶极化率为0.9 V/m 。3种超材料的二阶极化率都高于之前研究的 SRRs超材料(0.7 V/m)[8]。通过对比可知,硅 SRRs 的开口方向影响了超材料产生的 THz波的强度,这与全介质硅 SRRs之间的磁共振耦合有关。当同向硅SRRs 超材料被飞秒光照射时,每个 SRRs都产生相同方向的磁偶极矩,导致局域场增强。与单层 L 型超材料相比,这在一定程度上增强了THz 波的转换效率。而对于飞秒脉冲激发下的反向硅 SRRs超材料,在一对谐振环中产生了相反方向的磁偶极矩[16],从而通过首尾相连形成环偶极子共振[17-20]。这种谐振模式可以减少超材料的辐射损失,并产生高于前者的强局域场。超材料中二阶非线性光学过程可以表示为[21-22]
式中, E!和ε0分别表示泵浦光电场和真空介电常数。通过式(7)可知,环偶极子产生的强局域场可以更好地提高二阶非线性极化强度,从而增强 L 型超材料产生的 THz波信号。
L 型结构具有明显的几何不对称性,因此其对入射光偏振响应具有一定的敏感性。计算了单层 L 型超材料与覆盖反向硅 SRRs超材料在不同偏振角下产生的 THz 波。如图4(b)所示,两种超材料在不同偏振角下产生的 THz 波表现为2φ依赖关系。两种超材料都在偏振角为30°时, THz 波振幅达到最大值。其中,单层 L 型超材料产生的 THz波最大振幅为0.8 V/m,反向硅 SRRs 超材料产生的 THz 波最大振幅为1.8 V/m。在偏振角为120°时,两种超材料产生的 THz 波振幅都为最小值。其中,单层 L 型超材料产生的 THz 波振幅为0.05 V/m,反向硅 SRRs超材料产生的 THz波振幅为0.15 V/m。通过计算可知,单层 L 型超材料与覆盖反向硅 SRRs超材料在偏振角为30°时的 THz二阶非线性极率分别为1×10?2 pm/V 和2.4×10?2 pm/V。此外,通过公式(Emax ? Emin)/(Emax + Emin)计算可知,单层 L 型超材料的偏振角调制深度为88.2%,覆盖反向硅 SRRs 超材料的偏振角调制深度为84.6%。为评估超材料的调制能力,将覆盖反向硅 SRRs 超材料与其他 THz发射器进行比较。如表1所示,反向硅 SRRs超材料的 THz 波偏振调制深度几乎是二硒化钯与硫化铋材料的两倍[23-24],且远优于大部分实验中所取得的基于二维材料 THz 波偏振调制深度的数据[25]。这进一步展示了超材料在 THz 波产生与调制方面的应用潜力。
对于传统二阶非线性光学材料,需要具有对称性破缺,即材料的晶体结构中不存在反演对称,从而可以产生二阶非线性光学响应。类似地,超材料作为人工设计的结构,其二阶非线性过程也需要满足几何结构的不对称性[28]。L 型超材料在几何结构上不具备中心反演对称性,因此可以产生二阶非线性过程。为了确认 L 型超材料产生的 THz波可以进行人工调控,通过改变L 型超材料的几何结构,研究超材料产生THz 波与结构几何尺寸的关系。的长臂 l1固定,改变短臂 l2时,生的 THz 波振幅如图5(a)所示。当 L 型超材料两种超材料产当 l2从170 nm逐渐增加至350 nm,两种超材料产生的 THz波振幅都表现出逐渐递减的趋势。单层 L 型超材料产生的 THz 波振幅由0.65 V/m减小至0.13 V/m,覆盖反向硅 SRRs超材料产生的 THz 波振幅由1.3 V/m减小至0.26 V/m。这是因为随着 l2的不断增加,L 型超材料逐渐接近于中心对称结构。由于存在一定的几何对称性,难以满足超材料结构产生二阶非线性过程的基本要求[29]。因此, L 型超材料随着 l2的不断增加产生的THz 波振幅逐渐降低。上述结果表明,超材料的非线性响应和超材料结构的几何参数(包括臂宽、周期、角度等)以及几何对称性密切相关[30],与传统材料相比,超材料的优势是具有非线性光学性质的可设计性。
由于超材料产生的 THz波振幅与入射光的脉冲宽度密切相关,为进一步研究其中的变化规律,模拟了 THz波振幅随入射光脉冲宽度的变化趋势。如图5(b)所示,入射光的脉冲宽度由80 fs 逐渐增加至150 fs,超材料产生的 THz 波振幅随之减小。通过式(7)可知,超材料的二阶非线性极化强度与入射光电场的平方成正比,将入射光对应的高斯脉冲函数与式(7)结合,可以得到超材料产生的 THz波振幅ETHz与入射光脉宽τ的关系为
ETHz∝ P ∝ e?2A/τ2
利用式(8)对相关结果进行拟合,其中 A 为常数。可以发现,两种超材料产生的 THz 波振幅随脉冲宽度变化趋势可以被很好地拟合。通过时域模型计算的结果与使用频域模型得到的结果完全一致[31]。
3 结论
本文提出了一种由磁共振耦合效应提高超材料 THz 波辐射效率的新方法。通过优化全介质硅 SRRs 的开口方向,利用其磁共振耦合效应增强局域场,使得单层 L 型超材料产生的 THz 波振幅提高了一倍。此外,研究发现 L 型超材料和复合了介质硅 SRRs 的超材料产生的 THz 波随入射光偏振角呈现2φ依赖关系,且其调制深度优于目前大部分二维材料。通过计算得到,超材料产生的 THz波振幅与入射光的脉冲宽度呈指数关系,其 THz波振幅随着脉冲宽度的增加而减小。最后,该超材料的 L 型结构的几何尺寸对 THz 波振幅的影响表明,超材料的非线性光学响应具有较好的设计自由度。该研究结果为基于超材料的非线性光学研究奠定了理论基础,为提高基于超材料的集成化 THz 源的转换效率提供了理论指导。
参考文献:
[1] HUANGYY,YAOZH,HUFR,etal. Tunablecircularpolarizationconversionandasymmetrictransmission of planar chiral graphene-metamaterial interahertz region[J]. Carbon, 2017, 119:305–313.
[2] LIU C J, HUANG Y Y, YAO Z H, et al. Giant angulardependence of electromagnetic induced transparency in THzmetamaterials[J].EurophysicsLetters,2018, 121(4):44004.
[3] BOROVIKSS,KISELEVA,ACHOURIK,etal. Demonstrationofaplasmonicnonlinear pseudodiode[J]. NanoLetters, 2023, 23(8): 3362–3368.
[4] YU L L, HUANG Y Y, LIU C J, et al. Giant plasmonic modesplittinginTHzmetamaterialsmediatedby couplingwithLorentzphononmode[J]. Applied Physics Letters, 2018, 112(15):151101.
[5] YANG Y, LIU C J, HUANG Y Y, et al. Elliptically polarizedsecond-harmonicgenerationbylocal magneticfieldinterahertzchiralmetamaterials[J]. Optics Communications, 2022, 508:127668.
[6] KLEINMW,WEGENERM,FETHN,etal. Experiments on second- and third-harmonic generation from magnetic metamaterials[J]. Optics Express, 2007, 15(8):5238–5247.
[7] LUO L, CHATZAKIS I, WANG J G, et al. Broadband terahertzgenerationfrommetamaterials[J]. Nature Communications, 2014, 5(1):3055.
[8] FANG M, NIU K K, HUANG Z X, et al. Investigation of broadband terahertz generation from metasurface[J]. Optics Express, 2018, 26(11):14241–14250.
[9] MCDONNELLC,DENGJH,SIDERISS,etal. Terahertz metagrating emitters with beam steering and full linear polarization control[J]. Nano Letters, 2022, 22(7):2603–2610.
[10] SHI M J, LEI Z, XI Y Y, et al. Manipulating nonlinear photocurrentfrominterlayercouplinginbilayer metamaterialsforpolarizedterahertzgeneration[J]. Annalen der Physik, 2023, 535(12):2300314.
[11] LUYC,FENGX,WANGQW,etal. Integrated terahertzgenerator-manipulatorsusingepsilon-near- zero-hybridnonlinearmetasurfaces[J]. NanoLetters, 2021, 21(18):7699–7707.
[12] FANG M, SHEN N H, SHA W E I, et al. Nonlinearity inthedark: broadbandterahertzgenerationwith extremely high efficiency[J]. Physical Review Letters, 2019, 122(2):027401.
[13]靳延平, 杨勇, 徐新龙.基于纳米天线阵列非线性光学效应的太赫兹辐射特性研究[J].光学学报, 2022, 42(15):1506001.
[14] CIRAC? C, POUTRINA E, SCALORA M, et al. Origin of second-harmonic generation enhancement in opticalsplit-ringresonators[J]. PhysicalReviewB, 2012,85(20):201403.
[15] YAO Z H, HUANG Y Y, DU W Y, et al. Interface-inducedenhancementofTHzgenerationandmodulationinhexagonalboronnitride/Simixed-dimensionalvanderWaalsheterostructure[J]. IEEETransactionsonTerahertzScienceandTechnology,2020, 10(2):101–106.
[16] KAELBERER T, FEDOTOV V A, PAPASIMAKIS N,et al.Toroidal dipolar response ina metamaterial[J].Science, 2010, 330(6010):1510–1512.
[17] HAN S, GUPTA M, CONG L Q, et al. Toroidal andmagnetic Fano resonances in planarTHzmetamaterials[J]. JournalofAppliedPhysics, 2017,122(11):113105.
[18] BASHARIN A A, CHUGUEVSKY V, VOLSKY N, etal. ExtremelyhighQ-factormetamaterialsduetoanapole excitation[J]. Physical Review B, 2017, 95(3):035104.
[19] AHMADIVAND A, GERISLIOGLU B, TOMITAKAA,etal. Extremesensitivemetasensorfortargetedbiomarkers identification using colloidal nanoparticles-integrated plasmonic unitcells[J]. BiomedicalOpticsExpress, 2018, 9(2):373–386.
[20] CHEN X, FAN W H. Toroidal metasurfacesintegratedwithmicrofluidicforterahertzrefractiveindexsensing[J]. JournalofPhysicsD: AppliedPhysics,2019, 52(48):485104.
[21] HOOPER D C, KUPPE C, WANG D Q, et al. Secondharmonic spectroscopy of surface lattice resonances[J].Nano Letters, 2019, 19(1):165–172.
[22] LI G X, CHEN S M, PHOLCHAI N, et al. Continuouscontrolofthenonlinearityphaseforharmonicgenerations[J]. NatureMaterials, 2015, 14(6):607–612.
[23] XI Y Y, ZHOU Y X, LEI Z, et al. Thickness-dependentterahertzemissionfromBi2S3 filmsunderexcitationbelow and above the band gap[J]. Physical Review B,2023, 107(3):035307.
[24] WANG H, CHANG J W, HUANG Y Y, et al. Large in-planeanisotropicterahertzemissioninducedbyasymmetricpolarizationinlow-symmetricPdSe2[J].ACSAppliedMaterials & Interfaces, 2021, 13(45):54543–54550.
[25] XI F G, YANG H, KHAYRUDINOV V, et al. Enhanced terahertz emission from mushroom-shaped InAs nanowire network induced by linear and nonlinear optical effects[J]. Nanotechnology, 2022, 33(8):085207.
[26] ZHU L P, HUANG Y Y, HE C, et al. Transient anisotropic photocurrent induced terahertz emission from the surface of black phosphorus[J]. Physica Status Solidi (RRL)-Rapid Research Letters, 2021, 15(11):2100413.
[27] CHANG J W, WANG H, LEI Z, et al. Coherent elliptically polarized terahertz wave generation in WSe2 by linearly polarized femtosecond laser excitation[J]. The Journal of Physical Chemistry Letters, 2021, 12(41):10068–10078.
[28] FANG C Z, YANG Q Y, YUAN Q C, et al. Efficientsecond - harmonic generation from silicon slottednanocubes with bound states in the continuum[J]. Laser &Photonics Reviews, 2022, 16(5):2100498.
[29] LIU J J, BRIO M, ZENG Y, et al. Generalization of theFDTD algorithm for simulations of hydrodynamicnonlinear Drude model[J]. Journal of ComputationalPhysics, 2010, 229(17):5921–5932.
[30] LIU Y M, ZHANG X. Metamaterials: a new frontier ofscience and technology[J]. Chemical Society Reviews,2011, 40(5):2494–2507.
[31] SIDERIS S, ELLENBOGEN T. Terahertz generation inparallel plate waveguides activated by nonlinearmetasurfaces[J]. Optics Letters, 2019, 44(14):3590–3593.
(编辑:李晓莉)
