光电编码器检测装置的安装偏角对检测精度的影响

唐宁宁 李志斌 李映铮

摘要：针对编码器在检测过程中因安装误差产生安装偏角的情况，分析了安装偏角、旋转角度和测量误差之间的关系。建立由安装偏差引起的非同心检测系统安装偏角的模型，通过实验分析3种不同程度的安装偏角0。～0.002。、0.1。～0.102。、0.2。～0.202。对被检编码器检测静态精度、动态精度的影响，得出了3种不同实验结果。实验结果表明，在检测编码器时，初次安装可控的安装误差在0。～0.102。范围内可以满足编码器检测技术指标，超过此安装误差的安全范围会导致编码器检测技术指标偏离检测标准。实验结论对提高编码器的检测精度与可靠性有参考价值。

关键词：光电编码器；安装偏角；测量误差；检测精度

中图分类号： TN 253 文献标志码： A

Effect of installation angular deviation on accuracy for photoelectric encoder detection device

TANG Ningning，LI Zhibin，LI Yingzheng

（School of Automation Engineering， Shanghai University of Electric Power， Shanghai 200090， China）

Abstract： This article addresses the problem that installation errors in the encoder during the detection process result in the generation of installation angular errors. It analyzes the relationship of installation angular errors， rotation angles， and measurement errors. It establishes a model for determining the installation angular errors caused by misalignment in the non-concentric detection system. Through experiments， the impact of three different levels of installation angular errors， namely 0。to 0.002。， 0.1。to 0.102。， and 0.2。to 0.202。， on the static and dynamic accuracy of the detected encoder was analyzed. Three distinct experimental results were obtained. The experimental findings indicate that during encoder detection， initial controllable installation errors within the specified range meet the technical specifications. However， exceeding this safe range of installation errors would cause the deviation of the encoder's detection performance from the standard. Theconclusions drawn from the experiments hold importance in enhancing the accuracy and reliability of encoder detection technology. They also provide valuable reference points for future research aimed at improving encoder detection accuracy.

Keywords： photoelectricencoder; installationdeflectionangle; measurementerror; detection accuracy

引言

光电编码器具有高精度、高分辨力、低能耗、输出稳定等优点，在军事、航天、机器人、生物工程等领域的精密测量与控制设备中得到广泛应用[1]。在工业编码器精度检测领域中，小型编码器动态检测过程中的误差主要来源于被测编码器与基准编码器轴系中心线结构错位，这导致同轴转动产生偏角，并引入测量误差。由于目前没有相关参考数据对被测编码器检测指标的影响进行量化分析，文献[2]中提到基准编码器与被测编码器安装误差即同轴度误差是影响编码器测试准确度的主要因素之一；文献[3]中提到电编码器光栅码盘粘接的偏心量及旋转轴受力产生的偏心量会导致较大的系统测量误差；文献[4]中提到旋转机械的角度不对中是在旋转机械中引发故障的最常见原因；文献[5]的实验装置中存在的错位引起的串扰误差被认为是最大的误差源；文献[6]检测方法提出两个编码器之间任何结构错位都会产生不对称脉冲，降低角速度估计的精度。

通过对国内外学者关于光电编码器的研究进行总结，为了有效解决检测装置在安装过程中由于操作不当使被测编码器安装偏离水平的问题，结合现有的实验条件研究编码器轴线与棱体轴线不平行产生的安装偏角及其与测量误差之间的关系，通过建立数学模型计算出最大测量误差与安装偏角。本文在实验中考量3种不同程度的安装偏角，对每一种程度的安装偏角对检测精度的影响进行实验测量。安装偏角程度的选择按最大安装偏角的1/3～1/5[7]，预留安装偏角阈量为1/5。通过实验定量分析了步进电机在最高转速的5%～15%的情况下，不同安装偏角对检测精度的影响。

1 安装偏角建模分析

1.1 安装偏角来源

检测系统原理是基准编码器与被测编码器同轴转动，通过数据采集卡采集基准信号和被检信号送入上位机，由上位机进行计算[8]并输出检测结果。采集数据并比较基准编码器与被测编码器输出的角度信息。检测装置的设计图如图1所示。

由图1可以看出步进电机、基准编码器、被测编码器可以实现同轴转动，但被测编码器在初次安装过程中无专业仪器指导的情况下安装不当导致检测对象一侧会存在一定倾斜角度[9]，进而在被测编码器一侧产生安装偏角，造成检测精度不高。

1.2 安装偏角建模分析

在初次安装检测装置时，基准编码器与被检测编码器之间任何结构错位都会产生不对称脉冲，被测编码器的码盘与水平面存在角度不对中[10]，即为安装偏角。图2所示为存在安装偏角情况下，角度不对中模型示意图。

由角度不对中理论分析可以建立角度不对中模型，如图3所示。

图3中在安装不水平的情况下建立 x-y-z 空间直角坐标系，z 轴与从动轴重合，主动轴转过的转矩Te经过联轴器传到从动轴，可以沿着从动轴分解为Tz和 Ty ，其中实际码盘与理想码盘存在平行距离 d ，实际码盘圆心与理想码盘圆心距为δ ， 即存在一定的偏心距，为θ、、= arctan 。两种安装误差引起的测角误差均呈正弦函数分布规律[10]，叠加进行分析，则安装偏角θ=θ、+θ、、。

根据角度不对中模型示意图，分析主动轴的转矩与从动轴转矩之间的关系，得到

Tz = Tecos θ= Jrφr （1）

式中： Jr是从动轴的转动惯量；φr是从动轴转过的角度；θ为初次安装检测装置时码盘倾斜角度，即安装偏角。

对于存在安装偏角的检测装置系统来说，其主动轴与从动轴角速度满足以下关系

wr 4cos θ/（3+ cos 2θ）

wm =1+3（1） cos 2（cos 2）θ（θ）cos 2φ2

式中：wr是从动轴角速度；wm是主动轴角速度。

对于初次安装时存在安转偏角θ的检测系统来说，主动轴转过的角度为φ2，从动轴转过的角度为φr ，Δ是任意时刻引入的测量误差，由码盘偏心误差导致的测量误差计算原理可知

Δ=φ2?φr（3）

又因为任意时刻，主动轴瞬间转角与从动轴瞬间转角关系为

tanφr = tanφ2/ cos θ （4）

联立式（1）～（4）可得测量误差与安装偏角以及主动轴旋转角度之间的关系为

?= arctan （ t1（a） t（φ） cos（cos））（5）

式（5）为编码器安装不当产生角不对中时的测量误差表达式。由测量误差表达式可以看出，编码器安装倾斜产生的测量误差主要与主动轴旋转角度、码盘倾斜角、偏心角度有关。

2 安装偏角对被测编码器测量误差总体影响

2.1 安装偏角与测量误差的关系

安装偏角为θ ， 被测编码器分辨率为ε ， 基准编码器的输出信号为 A， 被测编码器输出信号为 B，测量误差 E 与安装偏角之间的关系为

E =（A? B） （6）

已知被测编码器刻度线为360°， 在θ分别为0?～0.002?、0.1?～0.102?、0.2?～0.202?3种不同的场景下被测编码器码盘安装倾斜角与测量误差关系如图4所示。

由图4可以看出，安装偏角越大，对编码器测量误差影响越大；在θ一定的情况下，在φ2=时，?最大；在φ2=时，?最小，此刻检测编码器精度结果最好。

2.2 被测编码器的最大测量误差值计算

由图4测量误差曲线图可以看出由于基准编码器与被测编码器存在安装偏角θ ， 基准编码器的输出是已知的、确定的，因此测量误差主要是由被测编码器的测量精度和安装偏角造成的。在安装偏角值固定不变时，测量误差?与主动轴旋转角φ2之间符合正弦关系，周期为π ， 在φ2=时，测量误差最小；在φ2= 时，?最大（ n =1， 2， 3···）。且测量误差?最大值可以计算得到

?max = arctan （1（1） cos（cos）θ（θ）） （7）

式（7）就是存在一定安装偏角的情况下，可以得到的测量误差最大值。

2.3 安装偏角控制范围

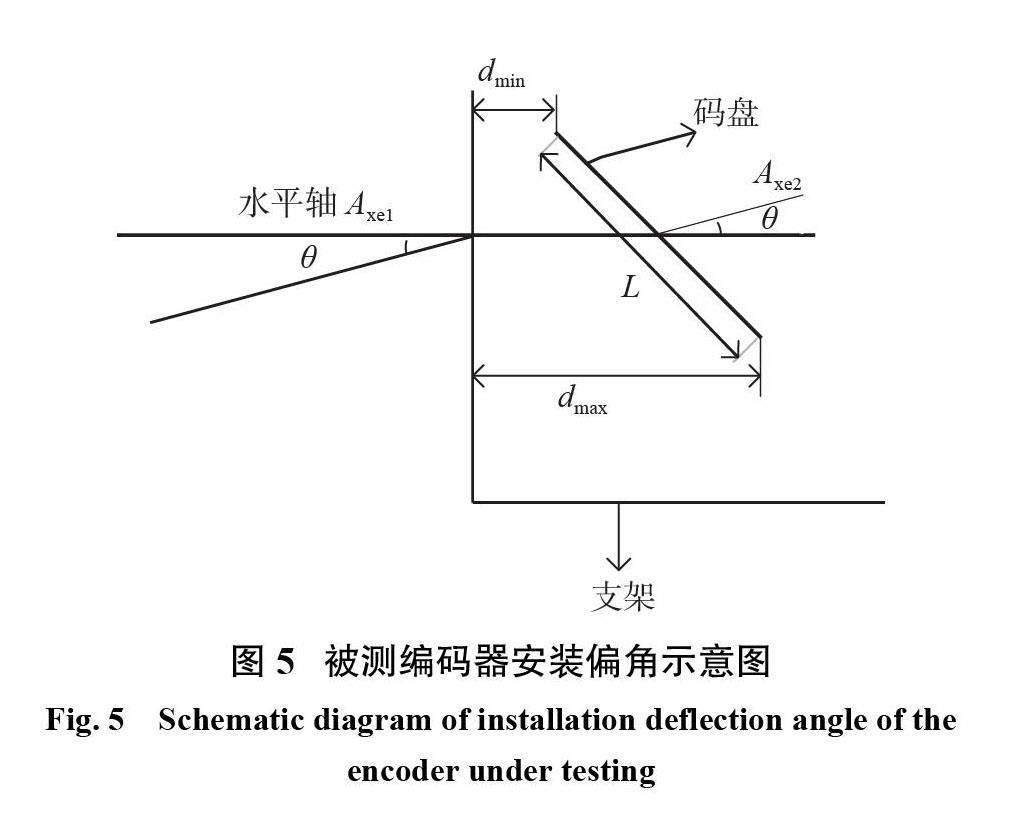
在编码器检测过程中，需要将被测编码器安装在支架上，如图5所示。

主动轴水平方向为 Axe1，从动轴的方向为Axe2，偏角值为θ。被测编码器码盘直径为 L ，法兰盘边缘到支架的最大距离和最小距离分别是dmin和dmax，安装偏角计算式为

θ′= arcsin（8）

基于全面检测法理论，被测编码器测量误差为|?|，被测编码器分辨率为ε ， 在保证检测平台的有效性的前提下，需要满足

将式（9）代入式（5），可得安装偏角与基准编码器旋转角之间的关系式为

tan φ2? tan

θ= arccos 'ε '

由2.2节可知，当φ2= 时，安装偏角最大，即

θmax = arccos （11）

将最大安装偏角代入式（7）中，可以得到被测编码器码盘距离支架允许的最大高度差为

1? tan

Dmax = Lsinarccostan +1（12）

根据式（10）、（11）可以计算出不同分辨率编码检测时的最大偏角及安装高度差。

3 安装偏角对检测精度的影响

3.1 安装偏角对检测编码器静态精度的影响

存在安装偏角时，检测编码器的静态精度理论计算式为

σ=|θi?θtrue |（13）

式中： N 表示测量次数；θi表示第i次测量编码器输出的角度值；θtrue 对应真实的角度值；σ表示静态精度。

编码器输出角度与安装偏角之间的关系为

θ=（C ? Stan α） （14）

式中： C 是输出周期的计数值； S 是标尺的等分距离。

3.2 安装偏角对检测编码器动态精度的影响

基准编码器与被测编码器之间存在安装偏角的情况下，对莫尔条纹信号的影响为

Δ?= × × sin θ （15）

式中： P 是光栅周期； d 是光栅条纹宽度； R 是基准编码器和被测编码器之间的距离；θ是安装偏角的大小。

修正系数为

存在安装偏角的情况下动态检测精度理论计算式为

δθ=Δθ? ccos （1?（17）

式中：δθ是动态检测精度；Δθ是基准编码器与被测编码器输出角度平均值； r 是基准编码器半径； N1是基准编码器刻度线； N2是被测编码器刻度线；α是安装偏角； K 是修正系数。

4 实验分析

图6是检测装置的实物图。实验中使用的基准编码器规格如下：基准编码器型号为GKT5815-001G，刻度线为8192，分辨率6′′，最大转速6000 r/min。在转过相同的角度时其输出的脉冲数远多于被检编码器时可以实现数据输出。被测编码器规格型号如下：刻度线为360，分辨率σ=50′′；步进电机调速范围为0～2000 r/min；被测编码器码盘直径为50 mm。实验装置要求基准编码器精度需远高于被测编码器，满足检测系统实验要求。

根据被测编码器的测量误差要小于被测编码器分辨率的1/2的原则，测量误差最大应该控制在25′′以内，即被测编码器静态精度标准控制在25′′以内，动态精度检测标准控制在35′′以内，此编码器为合格。

将标准测量误差代入式（7），根据此最大测量误差可以计算出最大安装偏角θmax =0.38? ， 最大高度差Dmax =0.36 mm 。

检测编码器精度实验步骤为：电机以不同的转速带动基准编码器与被测编码器同轴转动， 使用千分游标卡尺测量dmax，dmin的值，调节被测编码器与支架的距离来进行高度差 D = dmax ? dmin的计算，以获取不同的安装偏角进行实验。对比不同的安装偏角对编码器检测精度的影响。

本次实验所选的安装偏角以0.1?为步长区分安装偏角程度。选择0?～0.002?、0.1?～0.102?、0.2?～0.202?3种不同安装偏角范围来进行实验（表1）。

4.1 不同安装偏角对静态精度的影响

利用安装偏角与静态检测精度误差之间的关系式，可以得到不同安装偏角与静态检测精度误差之间的关系，如图7所示。

由此看出安装偏角与静态检测精度之间的关系：安装偏角越大，精度误差越大。

图7是利用数据采集系统在电机转速为100 r/ min ，安装偏角为0?～0.002?条件下采集到的被测编码器的静态检测精度误差。详细数据列于表2中。

表3是根据图7输出的18组静态精度误差数据。

由上述实验可以看出安装偏角在0?～0.002?范围内，安装良好的情况下，被测编码器精度误差在18.3676′′。

安装偏角为0.1?～0.102?时，根据上述检测理论，被测编码器检测精度误差已经达到了24.0203′′。随着安装偏角的增大，被测编码器检测精度下降。

安装偏角为0.2?～0.202?时，利用同样的检测方法，被测编码器检测精度已经达到了36.4339、、。安装偏角增大导致被测编码器检测精度大幅度下降，已超出编码器检测精度标准。

综上所述，在编码器进行静态精度检测时，安装偏角范围在0?～0.102?之间，被测编码器静态精度在检测标准范围内。

4.2 不同安装偏角对动态检测精度的影响

利用安装偏角与动态检测精度误差之间的关系式，当安装偏角在0?～0.002?范围内，步进电机不同转速下可以得到18组按离散时间采样的被测编码器动态精度误差数据，如表4所示。

当采样周期时间内连续采样时，利用式（12）可以计算出动态精度误差在不同转速下的变化趋势，转速为100 r/min 和300 r/min 时，动态检测精度随时间变化的趋势如图8所示。

由图8可以看出，随着转速的提升，编码器动态检测精度降低，检测精度最大相差20.5822、、。

根据动态精度与转速之间的关系，分析不同安装偏角条件下，安装偏角与动态检测精度之间的关系。电机转速为100 r/min 时，安装偏角与动态精度详细数据如表5所示。

电机转速为300r/ min 时，安装偏角与动态精度数据如表6所示。

根据上述各安装偏角的动态精度检测数据，转速100r/ min 逐渐加速至300r/ min ，安装偏角范围在0?～0.102?时，检测编码器动态精度结果符合动态检测精度标准。在安装偏角大于0.102?时，检测编码器动态精度大于40、、，无法满足检测标准。

5 结果

本文通过理论与实验对小型编码器在安装过程中被测编码器与基准编码器之间存在不对中的情况进行分析，推导出安装偏角与被测编码器测量误差之间的计算公式以及安装偏角的控制范围。为了使得编码器的检测能够准确反映检测精度与安装偏角之间的关系，继而进一步在安装偏角控制范围内，将安装偏角分为无安装偏角、安装偏角较小、安装偏角较大3种不同情况，对被测编码器检测的静态精度和动态精度进行实验测量与分析。综合实验数据可以得出以下实验结论：在安装偏角为0。～0.102。时，编码器的静态检测精度及动态检测精度误差结果较好，在安装偏角大于0.102。之后编码器检测精度结果无参考价值，偏离实际检测误差过多。

本文所推导出的精度检测公式以及安装偏角误差公式对于实际工业生产制造有很高的借鉴价值，对普通编码器检测精度的准确性与可靠性研究也有一定的参考价值。同时验证了基于超静定结构的检测系统可以运用在编码器的精度检测中，进一步证实了该检测系统的可靠性。

参考文献：

[1]邓方， 陈杰， 陈文颉， 等.一种高精度的光电编码器检测方法及其装置[J].北京理工大学学报 ， 2007， 27（11）：977–980，1008.

[2]赵建科， 张周峰.轴角编码器测量中偏心带来的误差分析[J].光子学报， 2007， 36（S1）：249–252.

[3]穆如传， 石洪， 周柏， 等.双读数系统编码器设计[J].电子质量， 2022（10）：63–66.

[4] YAO Y， LI Y S， YIN Q. A novel method based on self-sensingmotor drivesystemformisalignmentdetection[J].Mechanical Systems andSignalProcessing， 2019， 116：217–229.

[5] HAN Y D， NI K， LI X H， et al. An FPGA platform fornext-generationgratingencoders[J]. Sensors， 2020，20（8）：2266.

[6] PALACINJ，MARTINEZD. Improvingtheangularvelocitymeasuredwithalow-costmagneticrotaryencoderattachedtoabrushedDCmotorbycompensating magnet and Hall-effectsensormisalignments[J]. Sensors， 2021， 21（14）：4763.

[7]张怡芯， 李志斌， 李肇婷， 等. MBGD-RBF 自适应滤波器在光电编码器检测系统中的应用[J].电工电气，2020（11）：56–61.

[8]刘杨， 太兴宇， 姚红良， 等.双盘转子轴承系统不对中-碰摩耦合故障分析[J].振动、测试与诊断 ， 2013，33（5）：819–823，913，

[9]许自镍.圆光栅角度编码器测角误差补偿及新型结构研究[D].杭州：杭州电子科技大学， 2020.

[10]张洪波， 万秋华， 王树洁， 等.小型编码器动态精度检测的安装误差控制[J].光学精密工程 ， 2016， 24（7）：1655?1660.

（编辑：张磊）