基于虚拟质心的GSLQR最优控制和力前馈解耦控制算法
2024-06-30谢翰君王钦若
谢翰君 王钦若

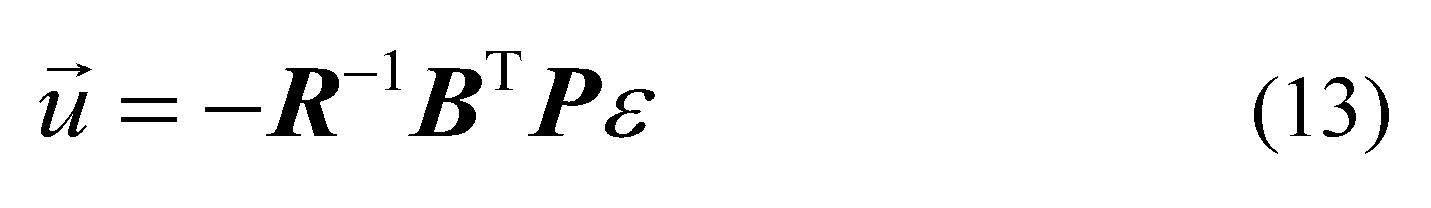

摘要:针对龙门同步双驱(GSD)平台因负载不均导致的同步误差影响加工精度的问题,目前的研究大多忽略了双驱轴之间的交叉耦合效应,或者重负载在龙门架横梁上的位置变化对同步误差的影响。为解决这一问题,首先,通过定义龙门架横梁的虚拟质心,量化双驱电机之间的交叉耦合力;然后,设计一种基于虚拟质心的GSLQR最优控制和力前馈解耦控制算法;最后,进行仿真实验。仿真实验结果表明,该算法的同步误差最大值比GSLQR最优控制算法和推力分配算法分别降低了约70%和60%,提高了GSD平台的同步性能和运动性能。
关键词:龙门同步双驱平台;龙门同步线性二次调节器;最优控制;力前馈解耦控制;虚拟质心;重负载
中图分类号:TP13 文献标志码:A 文章编号:1674-2605(2024)03-0003-07
DOI:10.3969/j.issn.1674-2605.2024.03.003
GSLQR Optimal Control and Force Feedforward Decoupling Control Algorithm Based on Virtual Centroid
Abstract: In response to the problem of synchronization errors affecting machining accuracy caused by uneven load on the gantry synchronous dual drive (GSD) platform, current research has mostly ignored the cross-coupling effect between the dual drive shafts, or the impact of changes in the position of heavy loads on the gantry crossbeam on synchronization errors. To solve this problem, first, quantify the cross-coupling force between the dual drive motors by defining the virtual center of mass of the gantry crossbeam; Then, design a GSLQR optimal control and force feedforward decoupling control algorithm based on virtual centroid; Finally, conduct simulation experiments. The simulation experiment results show that the maximum synchronization error of the algorithm is reduced by about 70% and 60% compared to the GSLQR optimal control algorithm and thrust allocation algorithm, respectively, improving the synchronization and motion performance of the GSD platform.
Keywords: gantry synchronous dual drive platform; gantry synchronous linear quadratic regulator; optimal control; force feedforward decoupling control; virtual centroid; heavy load
0 引言
在大跨度、长行程笛卡尔机器人系统中,龙门同步双驱(gantry synchronous dual drive, GSD)平台因具有较高的刚性和加速性能而受到广泛关注[1]。在GSD平台实际运行中,龙门架横梁上的重负载移动时,致使双驱电机的负载不均衡、运动不同步,从而导致
GSD平台的加工精度下降,甚至龙门架变形损坏。
目前,许多专家学者提出了多种解耦控制策略,以提高龙门双驱电机的同步性能和运动性能。MENG等[2]提出一种模型预测控制策略,基于面向线性时不变(linear time invariant, LTI)系统控制的切换模型,在双驱电机同步性能不佳的情况下,可保证轮廓公差,
但该模型忽略了激光切割工作头(负载)的转动惯量。HE等[3]引入一种商用控制器实现GSD平台的同步控制,但欠缺相关的理论分析。ISHIZAKI等[4]提出交叉耦合比例微分控制器,通过修改参考位置和速度命令来补偿龙门轴线性驱动之间的差分定位误差,但该控制器仅基于反馈控制,没有考虑因负载位置变化而导致的双驱同步误差。WANG等[5]提出一种模型参考自适应控制与变结构控制相结合的方法,可以在线确定并补偿双驱电机之间的同步运动误差,但该方法没有考虑横梁刚性结构对双驱电机产生的交叉耦合效应。YU等[6]提出一种改进型变结构控制的位置控制器解耦控制算法,不仅可以补偿因龙门结构而导致的耦合力,还能增强系统的鲁棒性,但该算法没有考虑负载位置变化而导致的双驱同步误差。KIM等[7]针对GSD平台提出线性二次调节器(linear quadratic regulator, LQR)最优控制方法,可提高双驱电机的同步精度,但该方法仅对单轴模型进行优化控制。QUAN[8]将GSD耦合系统的同步控制问题转化为线性二次最优控制问题,但计算过程复杂。GOMAND等[9]基于GSD物理模型推导出一种解耦控制算法,但没有考虑重负载在龙门架横梁上的位置变化对同步误差的影响。LI等[10]提出一种带推力分配的自适应鲁棒控制(adaptive robust control, ARC)算法,实现了双驱电机的运动同步及内力同步调节,但在前馈补偿策略方面,该算法较为简单。
本文提出基于虚拟质心的GSLQR最优控制和力前馈解耦控制算法。首先,针对GSD平台的重负载位置变化,采用全局的GSLQR优化方法对龙门双驱轴的交叉耦合力进行初步补偿;然后,在此基础上深化力前馈解耦算法的研究,有效处理因负载位置变化而导致的双驱同步误差。
1 GSD平台模型
双边直线电机驱动的GSD平台的双驱轴( 轴)由永磁直线电机(permanent magnet linear motor, PMLM)驱动,2条磁轨(PMLM定子)平行固定在大理石底座上;精密滚珠直线导轨平行于2条磁轨安装;2个PMLM动子(位于横梁两端的下方)与精密滚珠直线导轨滑块刚性连接;正交于精密滚珠直线导轨的龙门架横梁通过滑块与精密滚珠直线导轨刚性连接;龙门架横梁上的激光切割工作头(负载)由PMLM( 轴)驱动。GSD平台结构如图1所示。
GSD平台的等效集参数模型如图2所示[1]。当龙门架横梁转角 为0时,双驱PMLM的 电机同步运动;当 不为0时,双驱PMLM的 电机异步运动(为简便起见,图2中没有画出 电机,其位置分别与图2中的2个滑块位置重合)。精密滚珠直线导轨滑块的滚珠相对于结合部位的刚度较低,可看作是弹性元件[10]。
图2中, 为固定的惯性坐标系,原点 位于两条精密滚珠直线导轨中间, 轴与导轨平行; 为龙门架横梁的等效质心; 为龙门架横梁上的移动惯性坐标系, 轴平行于龙门架横梁的轴向; 为龙门架横梁上重负载的质量; 为龙门架横梁的质量; 分别为 电机的位置值(由线性光栅编码器获得); 分别为精密滚珠直线导轨的阻尼系数; 为龙门架横梁的长度; 、 分别为C到 电机之间的距离。上述变量的参数值详见文献[1]。
XIE等[1]给出了图2 GSD平台的准确数学模型,并通过实际系统的频率响应辨识实验证实了其有效性。该数学模型表明,双驱 电机耦合效应主要由龙门架横梁上重负载 的位置变化引起的。
2 GSLQR最优控制及力前馈解耦控制算法
GSD平台等效集参数模型的耦合状态方程为[1]
为减少GSD平台的双驱电机在动态重负载下的同步误差,首先,利用GSLQR最优控制算法对系统的交叉耦合力进行初步补偿;然后,提出基于虚拟质心的GSLQR最优控制和力前馈解耦控制算法,进一步提高 电机的同步精度。
2.1 GSLQR最优控制算法
一般情况下,设定系统的状态权值矩阵 和输入权值R后,最优反馈增益 可由Riccati方程计算[11]。
将公式(5)的最后一项用分部积分法展开,可得
为获得 的极小值,令公式(7)~(9)都等于零。
对公式(10)进行转置并整理,有
(12)
矩阵的数值解可由后向逼近动态规划(back-ward approximate dynamic programm, BADP)算法求解。将解出的 代入公式(8),可得到最优反馈增益 ,则控制律为
由公式(12)可知,GSLQR与LQR都具有无限增益裕度 ,保证相位裕度 。该结论可由李亚普诺夫第二方法证明[11]。
2.2 算法设计
由于GSLQR最优控制算法具有鲁棒性,在GSLQR中加入力前馈解耦可进一步提高系统的同步精度[12]。受B?AR?E等[13]提出的因果序图逆模型概念的启发,本文提出基于虚拟质心的GSLQR最优控制和力前馈解耦控制算法。
式中: 分别为龙门架横梁运动时不平衡负载对 电机的耦合力。注意,重负载 移动,导致质心C在龙门架横梁纵向上发生变化。
由此,基于虚拟质心的GSLQR最优控制和力前馈解耦控制算法的框图如图3所示。
至此,基于虚拟质心的GSLQR最优控制和力前馈解耦控制算法设计完成。
3 实验与分析
本文实验在MATLAB/Simulink环境下进行,采用的计算机配置为Intel(R) Core(TM) I7-7500U CPU,8 GB 内存,GSD平台模型参数详见文献[1]。仿真实验对比GSLQR最优控制算法(算法1)、文献[10]的推力分配算法 (算法2)和本文算法(算法3)。
3.1 GSLQR最优控制算法的仿真实验
图4仿真结果表明:当重负载 位于龙门架横梁的不同位置时,GSLQR最优控制算法可以保证 电机的响应速度基本相同;然而,由图4(a)、(c)可以看出,当双驱电机的重负载越来越不平衡时, 电机的同步误差趋于恶化。
需要指出的是,GSLQR最优控制算法的有效性主要取决于图2中 是否近似为零(此时 )。 得益于龙门架横梁与精密滚珠直线导轨的刚性连接,始终保证平台运动时 ,即平台的运动始终由线性方程组控制[1]。实际操作中, 的范围还与精密滚珠直线导轨的间隙有关:间隙越大, 越大。如果不满足 ,则需要非线性解决方案,这将在下一步的研究中讨论。
3.2 对比试验
设置 ,将重负载 的位置调整到 电机侧。权重设置为 , ,可得最优反馈增益为
设置 ,将重负载 的位置调整到 电机侧。权重设置为 , ,可得最优反馈增益为
从以上仿真结果可知,当重负载 位于龙门架横梁的不同位置时,本文算法比算法1和算法2的同步误差最大值分别降低了约70%和60%。
4 结论
针对重负载位置变化影响双驱电机耦合效应的问题,提出基于虚拟质心的GSLQR最优控制和力前馈解耦控制算法。GSLQR最优控制算法将系统的交叉耦合力初步解耦;为了进一步提高 电机的同步精度,提出基于虚拟质心的GSLQR最优控制和力前馈解耦控制算法,通过定义虚拟质心量化双驱电机之间的交叉耦合力,加入力前馈解耦控制进一步补偿系统的交叉耦合力。仿真实验结果显示,本文算法比GSLQR最优控制算法、推力分配算法的同步误差最大值分别降低了约70%和60%。
参考文献
[1] XIE H, WANG Q. Coupling modeling analysis of synchronous direct-drive gantry laser cutting stage with heavy-load[C]. 2022 4th International Conference on Control and Robotics (ICCR). IEEE, 2022:99-105.
[2] MENG Y, MANZIE C, LU G, et al. Modelling and contouring error bounded control of a biaxial industrial gantry machine[C]. The 3rd Conference on Control Technology and Applications (CCTA 2019), 2019: 388-393.
[3] HE YUNBO, YE WENTAO, GAO JIAN, et al. Research on dual-linear motor synchronous control in the high-precision gantry motion platform[C]. 2017 IEEE 19th Electronics Packa-ging Technology Conference (EPTC), 2017:1-5.
[4] ISHIZAKI KOSUKE, SENCER BURAK, SHAMOTO EIJI. Cross coupling controller for accurate motion synchronization of dual servo systems[J]. International Journal of Automation Technology, 2013,7(5):514-522.
